
Fraktalny Rendering
Krzywych i Powierzchni

2
Plan
1. Fraktal jako atraktor
2. Krzywe drugiego stopnia i inne jako fraktale
3. Odcinek fraktalnie
4. Trójkąt fraktalnie
5. Modelowanie konturu – przykłady
6. Triangulacja i modelowanie konturu z wypełnieniem
– przykłady
7. Kształty 3D fraktalnie – przykłady
8. Modyfikacja kształtu fraktala
9. Wnioski

3
1. Fraktal jako atraktor
1
2
{ ,
,...,
}
l
IFS
w w
w
1
2
( ) :
( )
( )
...
( )
l
W S
w S
w S
w S
1
(
),
0,1,...
k
k
S
W S
k
S
0
–
dowolny obraz początkowy
ˆ
ˆ
( )
,
W S
S
–
punkt stały, atraktor
ˆ
S

4
Analogie matematyczne
Przestrz. Euklidesa
• punkty
• odległość Euklidesa
• zbiory punktów
• odwzorowanie zwężające
• tw. Banacha o pkt. stałym
• alg. iteracje z dowolnego
pkt. startowego.
Przestrz. Fraktali
• zbiory zwarte
• metryka Hausdorffa
• atraktory
• IFS
• tw. Banacha o pkt. stałym
• alg. iteracje z dowolnego
zbioru startowego.

5
[ ', '] [ , ]
[ , ]
a
c
x y
x y
e f
b
d
0
[ ', ',1] [ , ,1]
0
1
a
c
x y
x y
b
d
e
f
Przekształcenie afiniczne
lub we współrzędnych jednorodnych

6
2. Krzywe drugiego stopnia jako
fraktale
1
1
,
,
P
L P P
M P
1
0
0
1 2 1 2
0
,
1 4 1 2 1 4
L
1 4 1 2 1 4
0
1 2 1 2 ,
0
0
1
M
0
0
1
1
2
2
1
1
1
x
y
P
x
y
x
y
IFS ma postać:
gdzie
7
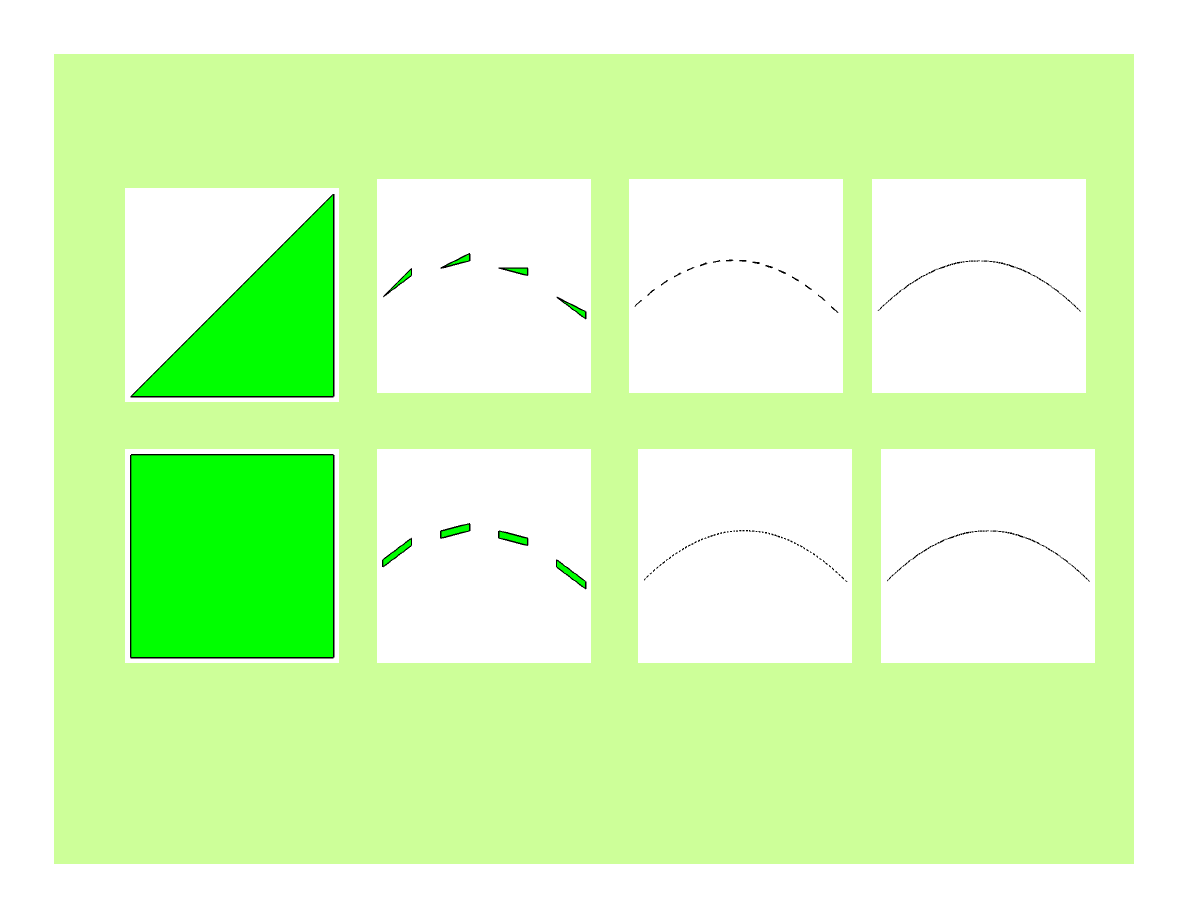
Przykład – iteracje: 0,2,4,8

8
UWAGA. Krzywe drugiego stopnia
są samopodobne! Powstają ze złożenia
przekształceń:
0
0
1
0
0
0
1
0
0
0
1
0
0
1
1
0
0
1
0
1
0
0
1
0
0
1
0
0
1
0
0
1
0
0
0
0
0
1
0
0
1
0
0
1
1
x
a
c
a
c
da bc
b
d
b a
a
e
f
fa
ec
e a
da bc
ac
a
da bc
da bc
b a
a
fa
ec
e a
da bc
Sh b
,
,
y
e
fa
ec
ac
da bc
a T
Sh
S a
a
da bc
da bc
a
ścinanie - translacja - ścinanie - skalowanie
9
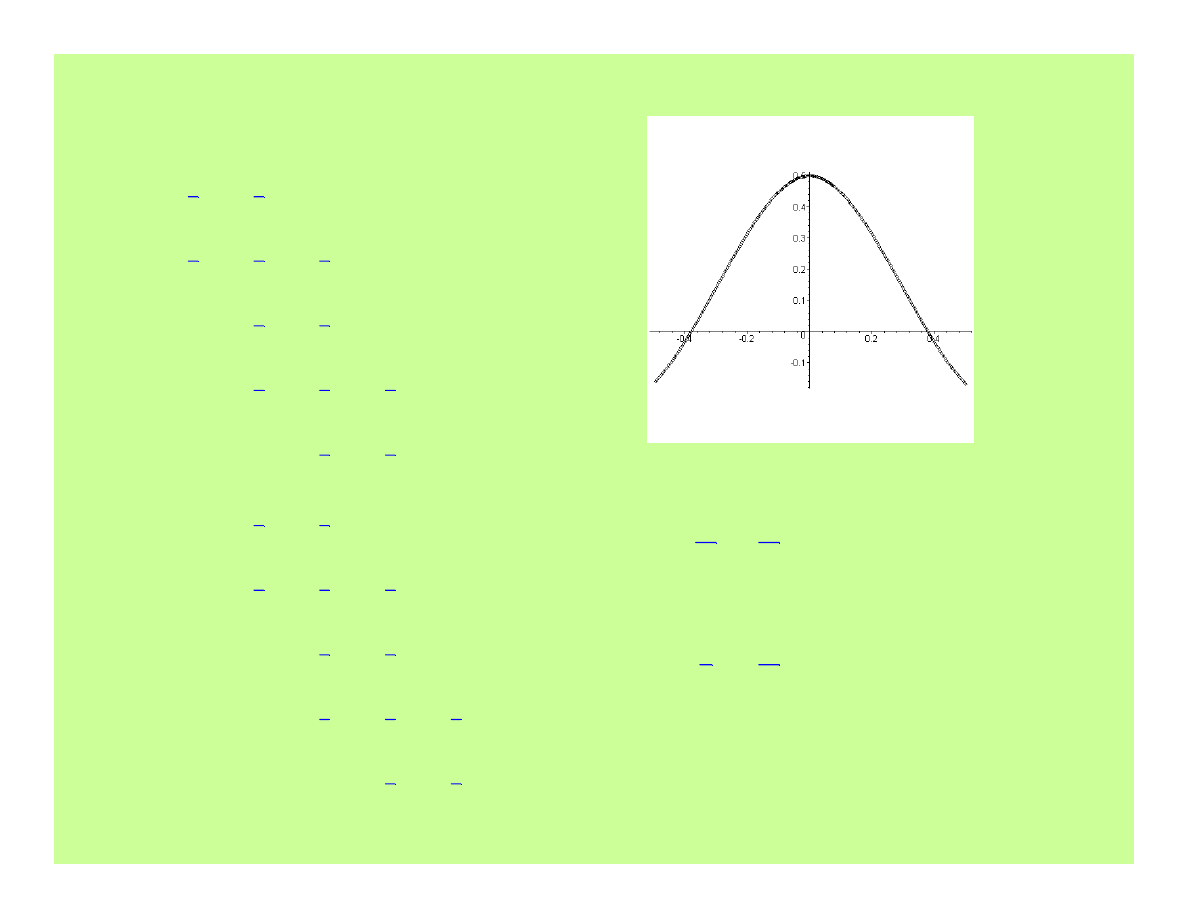
Inne krzywe – B-splajny
:=
S1
1
2
1
2
0
0
0
1
8
3
4
1
8
0
0
0
1
2
1
2
0
0
0
1
8
3
4
1
8
0
0
0
1
2
1
2
0
:=
S2
0
1
2
1
2
0
0
0
1
8
3
4
1
8
0
0
0
1
2
1
2
0
0
0
1
8
3
4
1
8
0
0
0
1
2
1
2
:=
P
-1
0
1
0
1
-1
2
-1
2
0
1
1
0
1
0
0
1
1
2
-1
2
0
0
1
1
0
0
0
1
1
1
1
2
{
,
}
IFS
P
S P P
S
P

10
1
0
0
1 2
0
0
0
1/ 2
0 ,
2
2
1
F
x
y
2
1
1
1 2
0
0
0
1 2
0
2
2
1
F
x
y
1
2
,
IFS
F F
IFS dla odcinka o wierzchołkach [x
0
,y
0
],[x
1
,y
1
]:
3. Odcinek 2D fraktalnie

11
4. Trójkąt fraktalnie
1
2
3
0
0
1
1
2
2
1/2
0
0
1/2
0
0
1/2
0
0
0
1/2 0 ,
0
1/2 0 ,
0
1/2 0 ,
2
/2 1
/2
/2 1
/2
/2 1
F
F
F
x
y
x
y
x
y
IFS dla trójkąta o wierzchołkach: [x
0
,y
0
], [x
1
,y
1
], [x
2
,y
2
].
1
2
3
4
,
,
,
IFS
F F F F
4
0
1
2
0
1
2
1/ 2
0
0
0
1/ 2
0
(
) 2
(
) / 2
1
F
x
x
x
y
y
y

12
Przykład: iteracje: 0,1,3,6
13
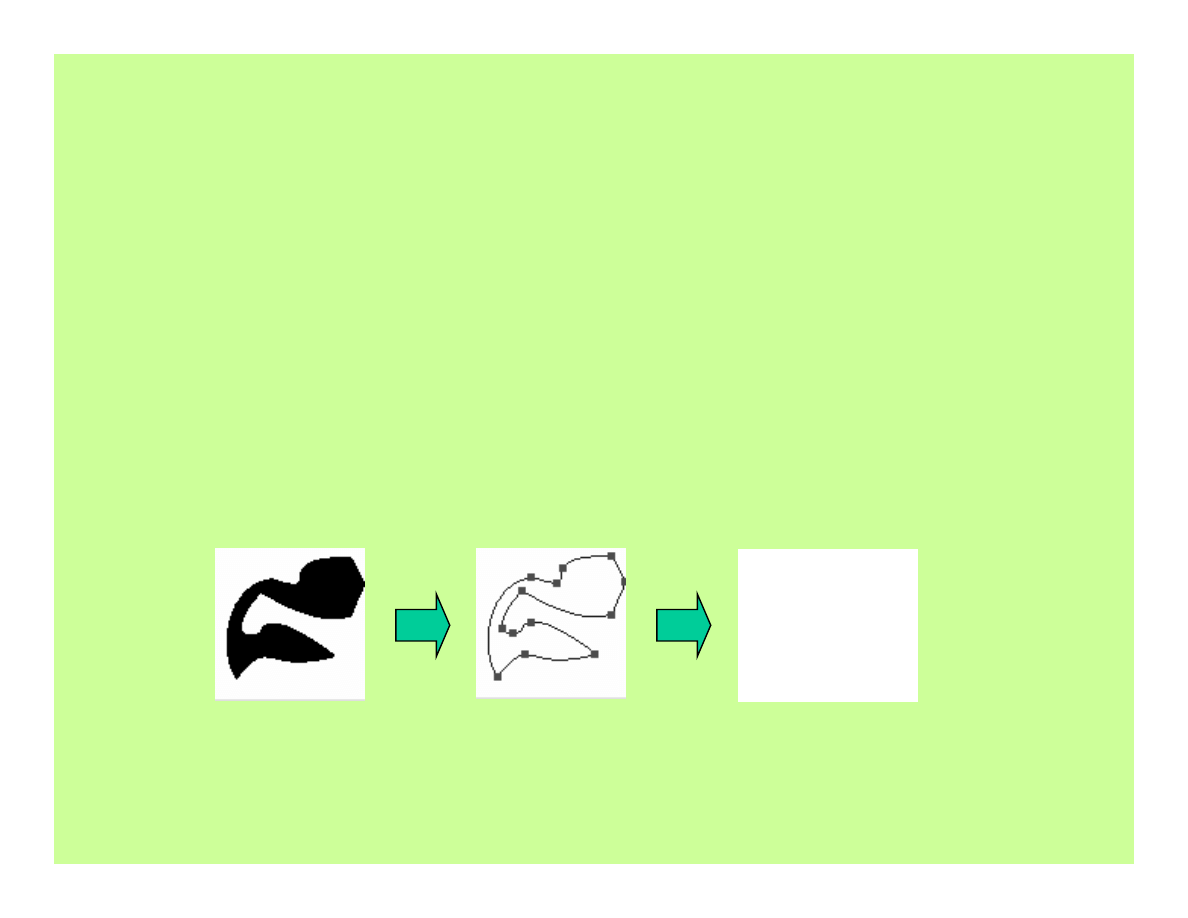
Etapy modelowania konturu 2D:
• wyodrębnienie konturu z obrazu,
• aproksymacja konturu łukami krzywych
i odcinkami prostych,
• wyznaczenie zbioru IFS-ów.
26 macierzy
składających
się na IFS
5. Modelowanie konturu

14
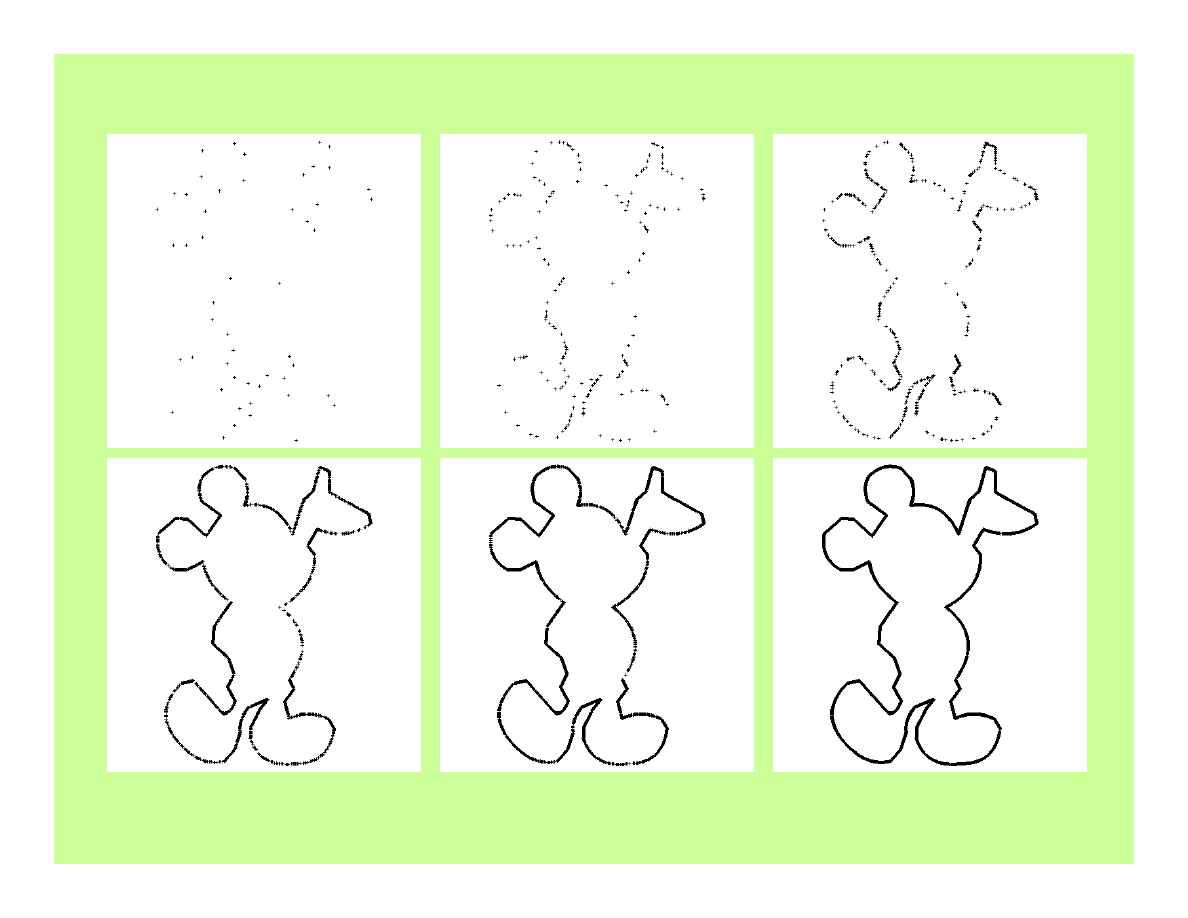
16 łuków + 35 odc.
Rendering deterministyczny: iteracje- 0,1,2,3,5,8
15
Rendering losowy: iteracje 1,3,5,20,50,200

16
6. Triangulacja i modelowanie
konturu z wypełnieniem
4 trójkąty
Rendering deterministyczny
17
7. Kształty 3D fraktalnie
Iteracje: 0,2,4,8

18
Odcinek 3D łączący punkty [x
0
,y
0
,z
0
],[x
1
,y
1
z
1
]
renderowany fraktalnie
1
2
,
,
IFS
FM FM
1
0
0
0
1 2
0
0
0
0
1 2
0
0
0
0
1 2
0
2
2
2
1
FM
x
y
z
2
1
1
1
1 2
0
0
0
0
1 2
0
0
0
0
1 2
0
2
2
2
1
FM
x
y
z

19
Krzywa 3D trzeciego stopnia fraktalnie
1
0
0
0
1 2 1 2
0
0
,
1 4 1 2 1 4
0
1 8
3 8 3 8 1 8
L
1 8 3 8 3 8 1 8
0
1 4 1 2 1 4
,
0
0
1 2 1 2
0
0
0
1
M
0
0
0
1
1
1
2
2
2
3
3
3
1
1
1
1
x
y
z
x
y
z
P
x
y
z
x
y
z
1
1
,
IFS
P
L P P
M P

20
Trójkąt 3D o wierzchołkach [x
0
,y
0
,z
0
], [x
1
,y
1
,z
1
],
[x
2
,y
2
,z
2
] fraktalnie
1
2
3
0
0
0
1
1
1
2
2
2
4
0
1
2
0
1
2
0
1
2
1 2
0
0
0
1 2
0
0
0
1 2
0
0
0
0
1 2
0
0
0
1 2
0
0
0
1 2
0
0
,
,
,
0
0
1 2
0
0
0
1 2
0
0
0
1 2
0
2
2
2
1
2
2
2
1
2
2
2
1
1 2
0
0
0
0
1 2
0
0
,
0
0
1 2
0
(
) 2
(
) 2
(
) 2
1
F
F
F
x
y
z
x
y
z
x
y
z
F
x
x
x
y
y
y
z
z
z
1
2
3
4
{ ,
,
,
}
IFS
F F F F
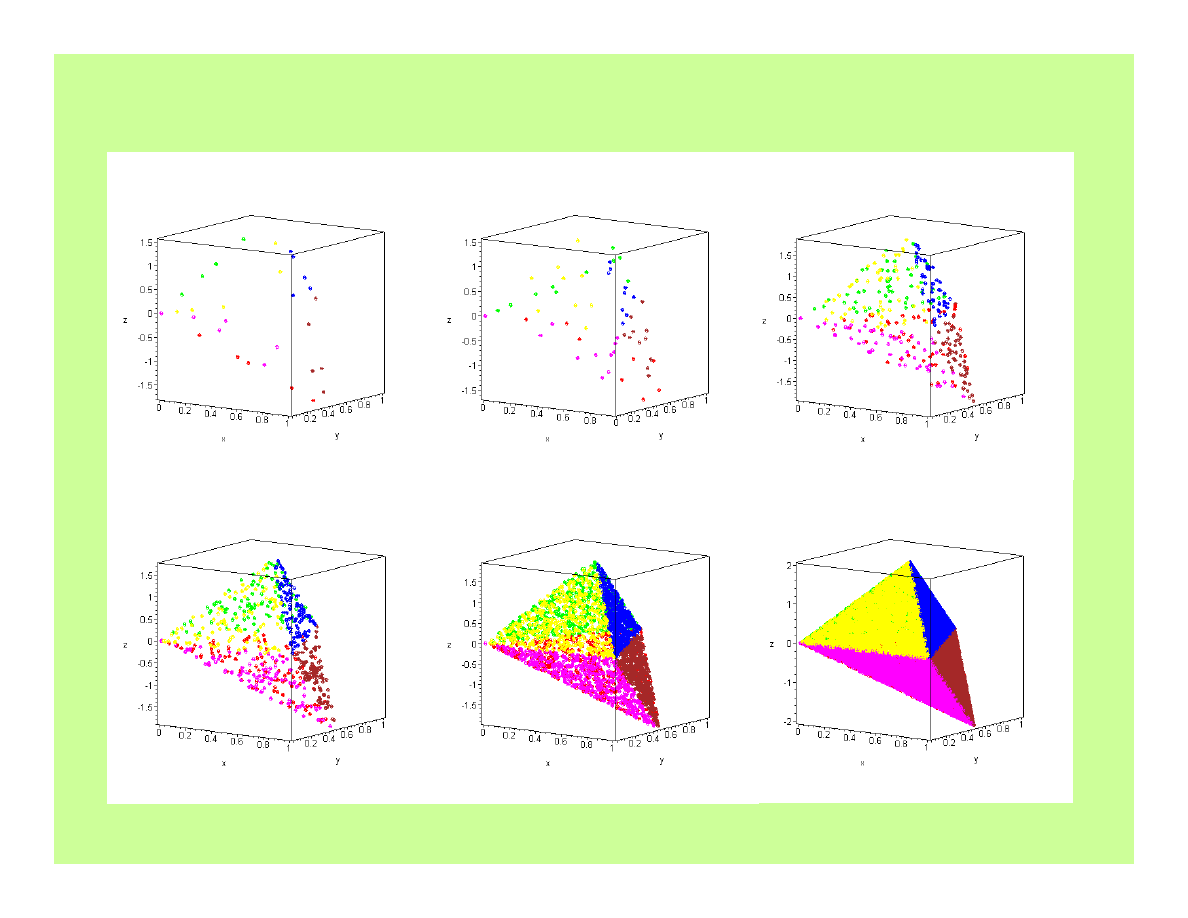
21
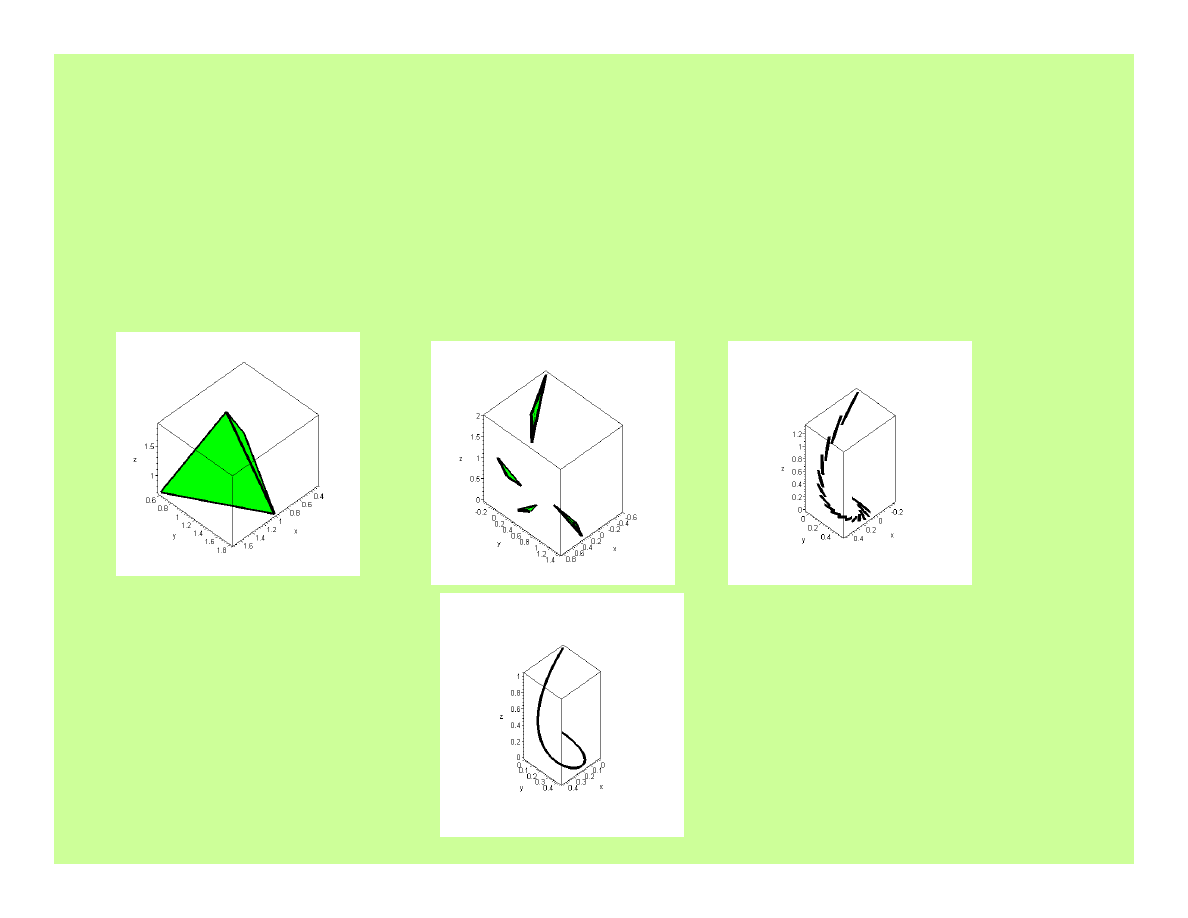
Bryła wielościenna fraktalnie
22
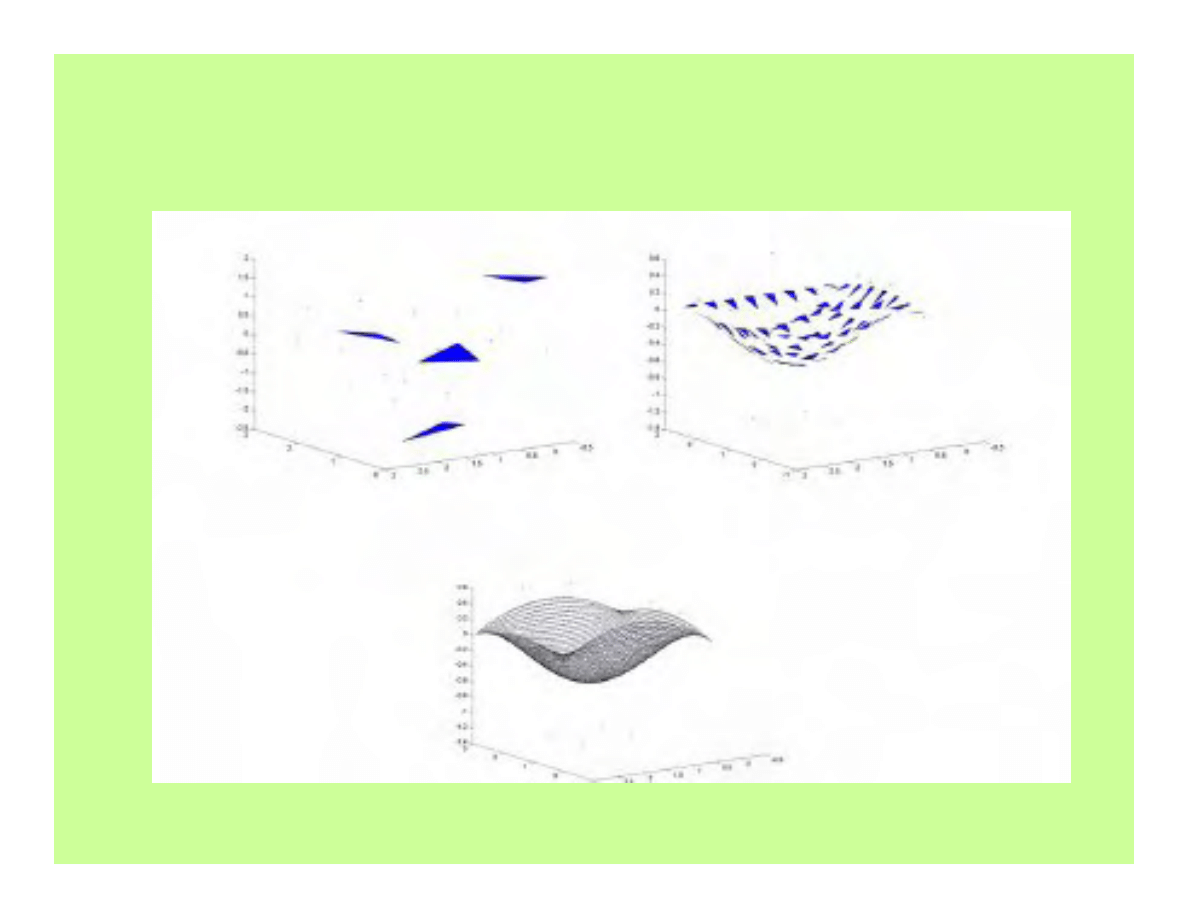
Płat powierzchni
23
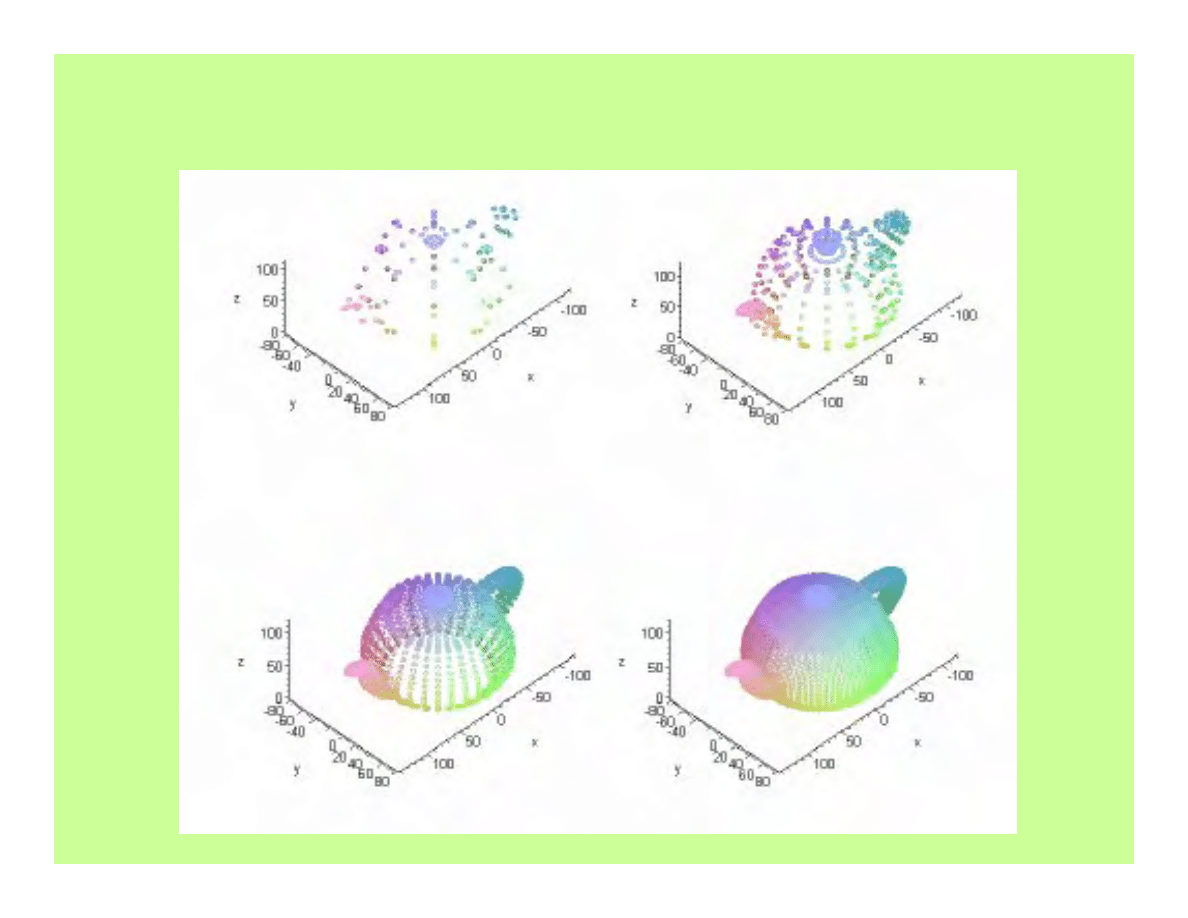
Fraktalny czajniczek z Utah

24
Modelowanie karoserii samochodu - można fraktalnie
25
:=
S1
1
0
0
0
0
0
3
8
3
4
-1
8
0
0
0
0
1
0
0
0
0
0
1
2
0
0
0
1
2
0
0
0
0
0
1
3
8
0
0
0
-1
8
3
4
:=
P
-1
0
1
0
0
1
-1
2
1
0
1
0
1
0
2
0
0
1
1
1
2
1
0
0
0
1
1
0
0
0
0
1
0
-1
0
0
0
1
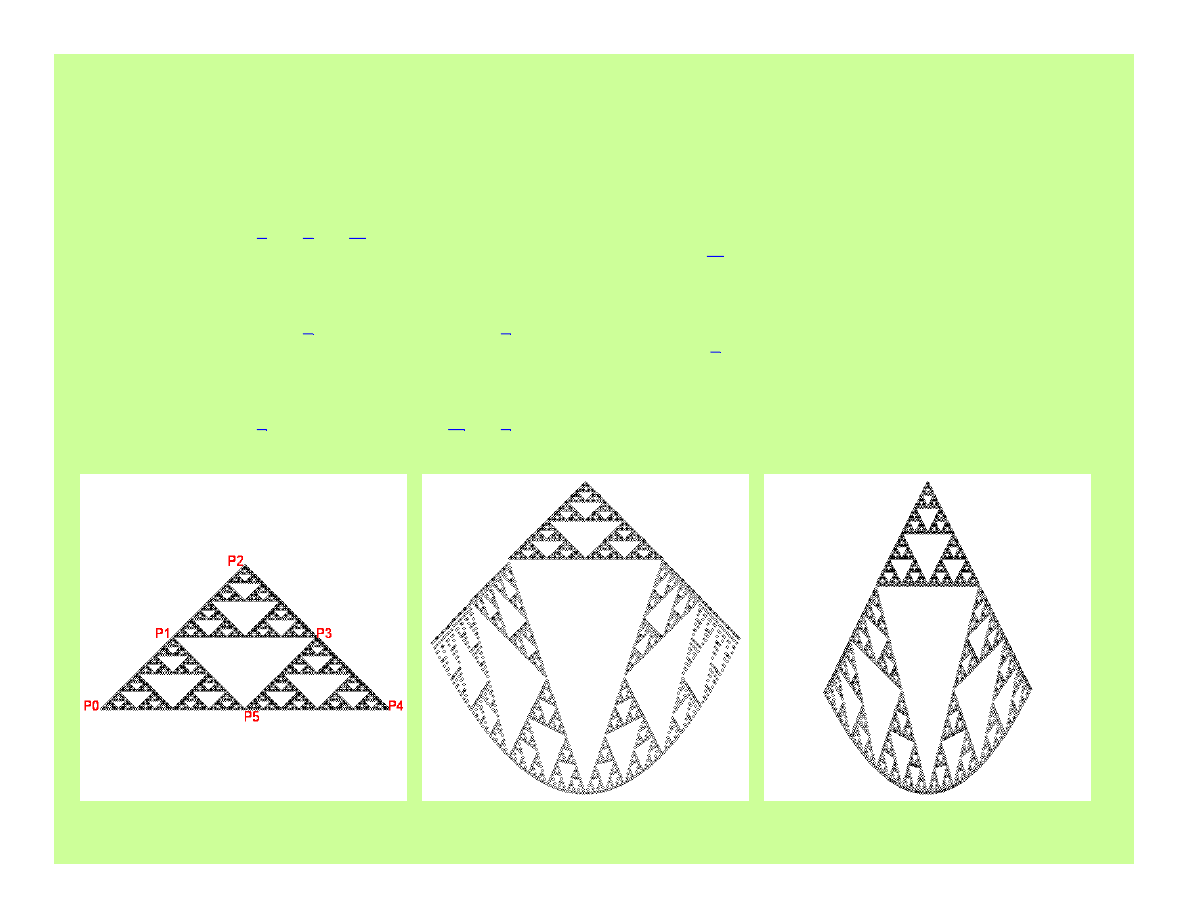
8. Modyfikacja kształtu fraktala

26
9. Wnioski
Modelowanie fraktalne ma charakter
progresywny w przeciwieństwie do
geometrycznego i jest niezależne
od rozdzielczości.
istnieje możliwość budowy progresywnego
kompresora fraktalnego kształtów 2D i 3D,
możliwe jest modelowanie fraktalne objętości.
Uwaga.
Prezentacja oparta jest na referacie przedstawionym na konferencji „Systemy Wspomagania
Decyzji”, Zakopane 2005, który powstał przy współpracy z dr Agnieszką Lisowską.
Wyszukiwarka
Podobne podstrony:
Geometria krzywych i powierzchn Nieznany
Geometria krzywych i powierzchni, zestaw 9
Geometria krzywych i powierzchni, zestaw 11
Geometria krzywych i powierzchni zestaw 9
Geometria krzywych i powierzchni, zestaw 8
GK 8 Modelowanie krzywych i powierzchni(1)
Geometria krzywych i powierzchni zestaw 11
Geometria krzywych i powierzchni zestaw 7
Geometria krzywych i powierzchni zestaw 14
Geometria krzywych i powierzchni zestaw 8
Geometria krzywych i powierzchni, zestaw 7
Geometria krzywych i powierzchni, zestaw 13
Geometria krzywych i powierzchni, zestaw 10
Geometria krzywych i powierzchni, zestaw 12
Geometria krzywych i powierzchn Nieznany
Geometria krzywych i powierzchni, zestaw 9
Geometria krzywych i powierzchni, zestaw 11
więcej podobnych podstron