Zagadnienie transportowe

Wykład 7

1

Zagadnienie transportowe

Zagadnienie transportowe jest specyficznym

problemem z zakresu programowania

liniowego.

2

ZT stosuje się najczęściej do:

• optymalnego planowania transportu towarów,

przy minimalizacji kosztów, lub czasu
wykonania zadania

• optymalnego rozdziału czynników produkcji,

celu maksymalizacji wartości produkcji, zysku
lub dochodu np. rolniczego

3



n – liczba dostawców (np., magazyny)



k – liczba odbiorców (np., sklepy)



a

i

– oferta i-tego dostawcy (podaż)



b

j

– zamówienie j-tego odbiorcy (popyt)



c

ij

– jednostkowy koszt transportu od i-tego

dostawcy do j-tego odbiorcy

Zagadnienie transportowe

4

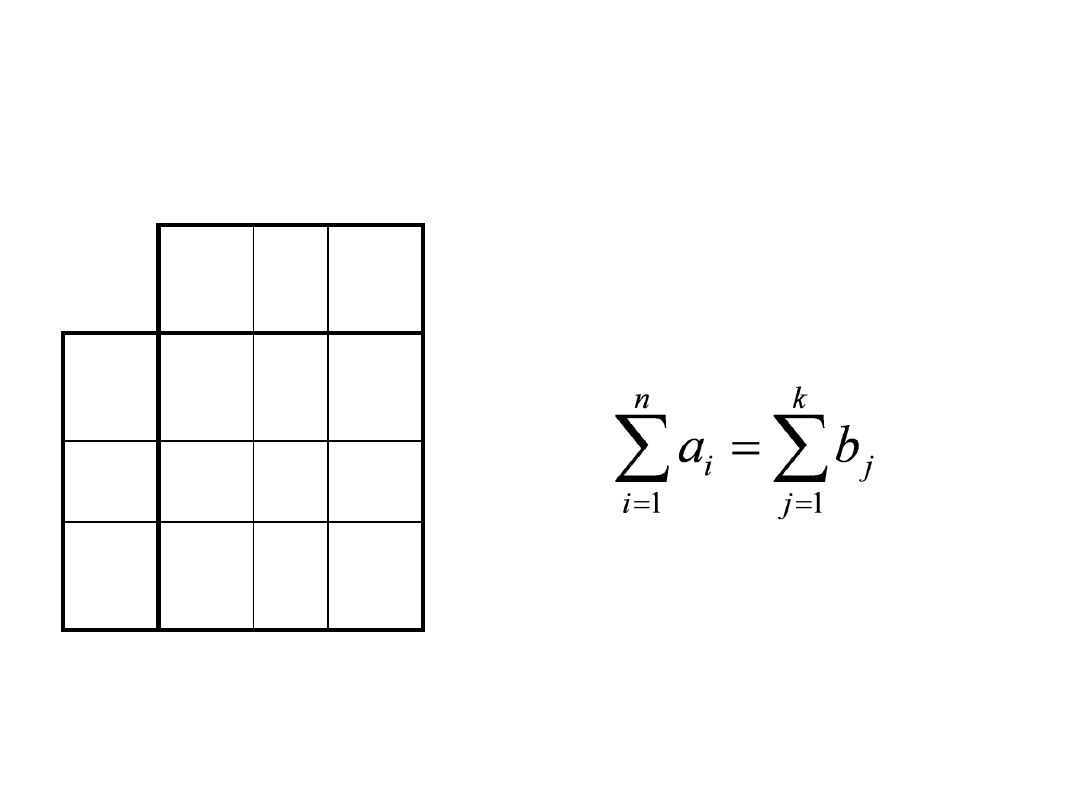
Zagadnienie transportowe

5

b

1

...

b

k

a

1

c

11

...

c

1k

...

a

n

c

n1

...

c

nk

ZT nazywamy

zbilansowanym

, jeżeli:

czyli ogólna podaż jest
równa całkowitemu
popytowi

(równowaga)

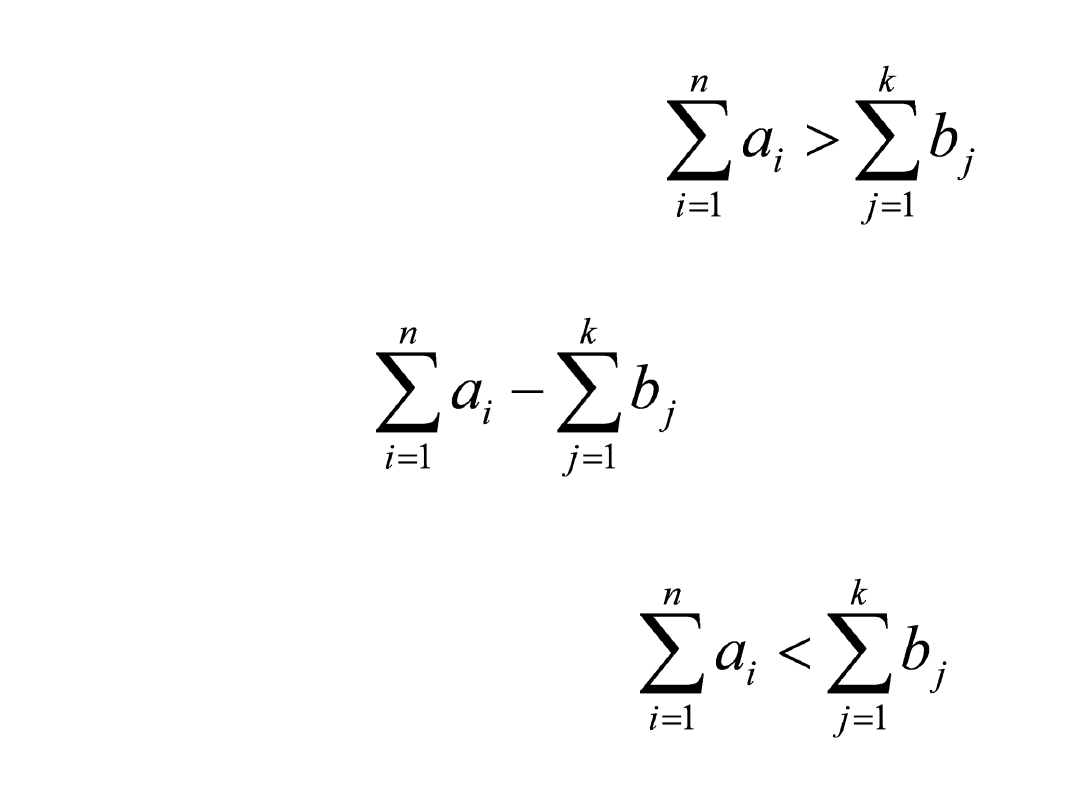
Zagadnienie transportowe niezbilansowane

Jeżeli w ZT podaż > popyt

zadanie bilansuje się wprowadzając fikcyjnego odbiorcę
(magazyn) z zapotrzebowaniem

Koszty jednostkowe transportu od dostawców do tego
odbiorcy = 0 lub jednostkowe koszty magazynowania.

Jeżeli w ZT podaż < popyt

zadania nie bilansujemy.

6

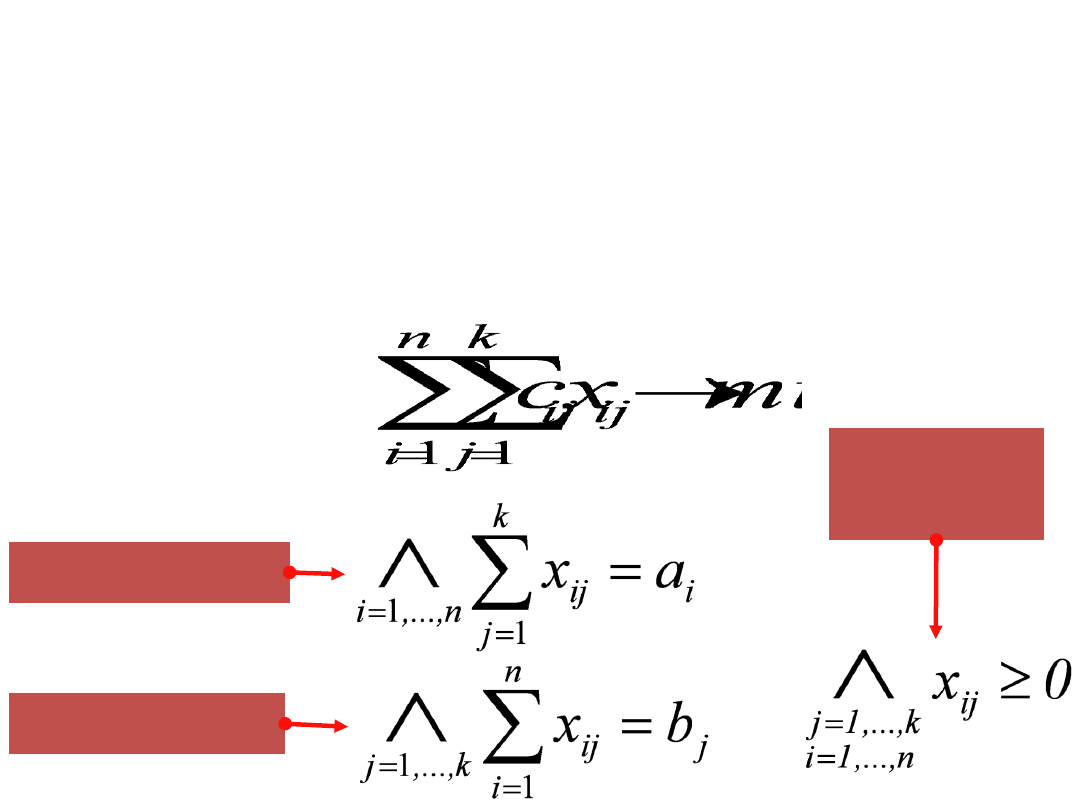
Problemem jest

zminimalizowanie kosztu całkowitego

transportu od dostawców do odbiorców, tak by popyt
odbiorców został całkowicie zaspokojony, a dostawcy
wysłali cały swój zapas

(zrealizowane są podaż i popyt).

Niech x

ij

oznacza wielkość transportu od i-tego dostawcy

do j-tego odbiorcy. Wówczas:

przy ogr.

ogr. podażowe

ogr. popytowe

nieujemne

przewozy

7

Przykład

Pewna firma za zakłady wytwórcze w

miejscowościach A, B, C oraz centra dystrybucyjne

miejscowościach D, E, F. Możliwości produkcyjne

zakładów wynoszą odpowiednio 50, 70 i 30 jednostek,

natomiast prognozy popytu w centrach – odpowiednio

20, 40 i 90 jednostek. Należy określić taki plan

przewozów, by przy uwzględnieniu możliwości

produkcyjnych zakładów oraz przewidywanego popytu w

centrach dystrybucyjnych zminimalizować łączne koszty

transportu.

8

Jednostkowe koszty transportu przedstawione są w
tablicy:

Miejscowość

D

E

F

A

3

5

7

B

12

10

9

C

13

3

9

9

Opis oznaczeń:

dostawcy

: D

1

, D

2

, D

3

– zakłady

produkcyjne w miejscowościach A, B, C

odbiorcy:

O

1

, O

2

, O

3

– centra dystrybucyjne

w miejscowościach D, E, F

10

Określenie popytu i podaży

Podaż:

50+30+70=150

Popyt:

20+40+90=150

Zadanie jest zbilansowane, ponieważ POPYT =

PODAŻ

11

x

ij

– wielkość przewozu od i-tego dostawcy do

j-tego odbiorcy

Funkcja celu:

12

Ograniczenia podażowe

:

1. Ilość towaru wysyłanego przez dostawcę D

1

odbiorcom O

1

, O

2

, O

3

jest równa podaży dla tego dostawcy i wynosi 50.

2. Ilość towaru wysyłanego przez dostawcę D

2

odbiorcom O

1

, O

2

, O

3

jest równa podaży dla tego dostawcy i wynosi 70.

3. Ilość towaru wysyłanego przez dostawcę D

3

odbiorcom O

1

, O

2

, O

3

jest równa podaży dla tego dostawcy i wynosi 30.

oraz

13

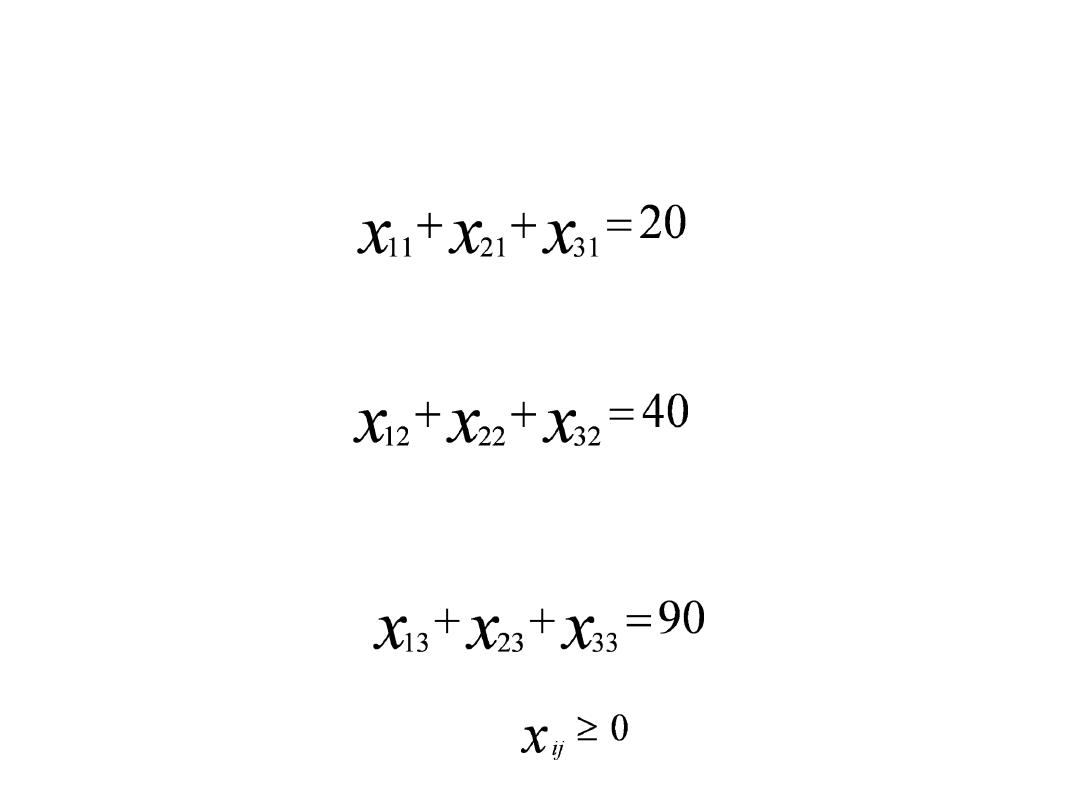
Ograniczenia popytowe

:

1. Ilość towaru otrzymana przez odbiorcę O

1

od dostawców D

1

, D

2

, D

3

jest równa popytowi dla tego odbiorcy i wynosi 20.

2. Ilość towaru otrzymana przez odbiorcę O

2

od dostawców D

1

, D

2

, D

3

jest równa popytowi dla tego odbiorcy i wynosi 40.

3. Ilość towaru otrzymana przez odbiorcę O

3

od dostawców D

1

, D

2

, D

3

jest równa popytowi dla tego odbiorcy i wynosi 40.

oraz

14

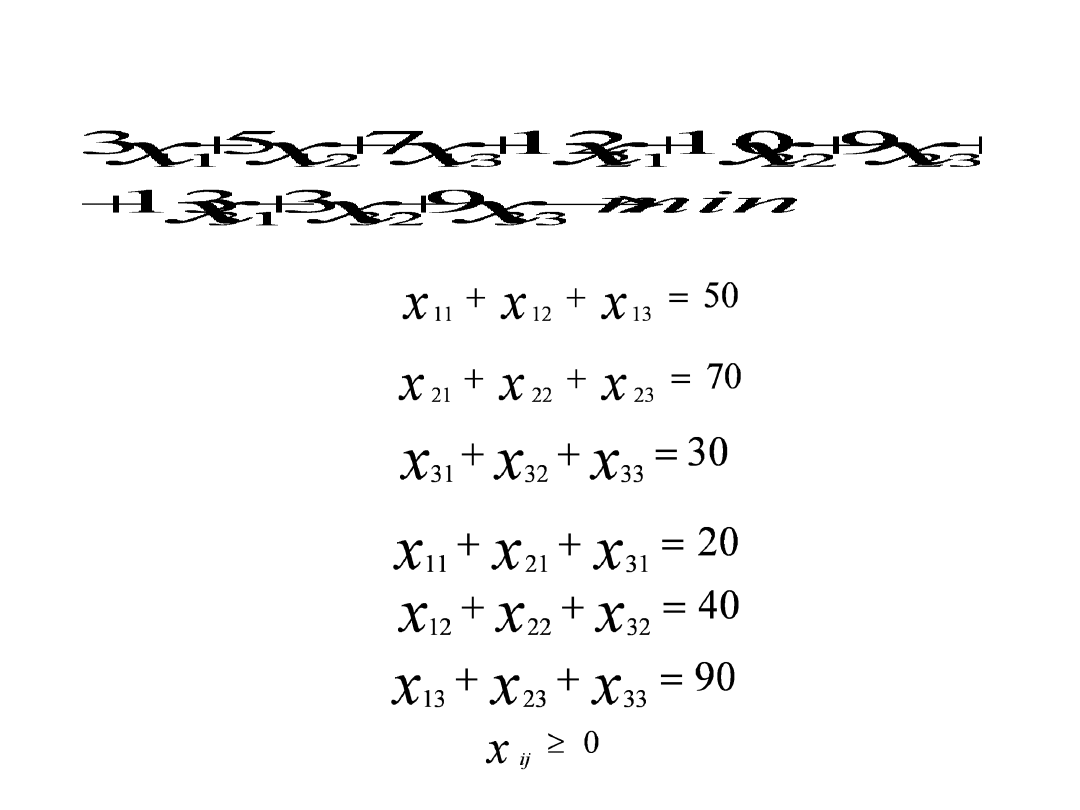
Model PL przyjmuje postać:

15

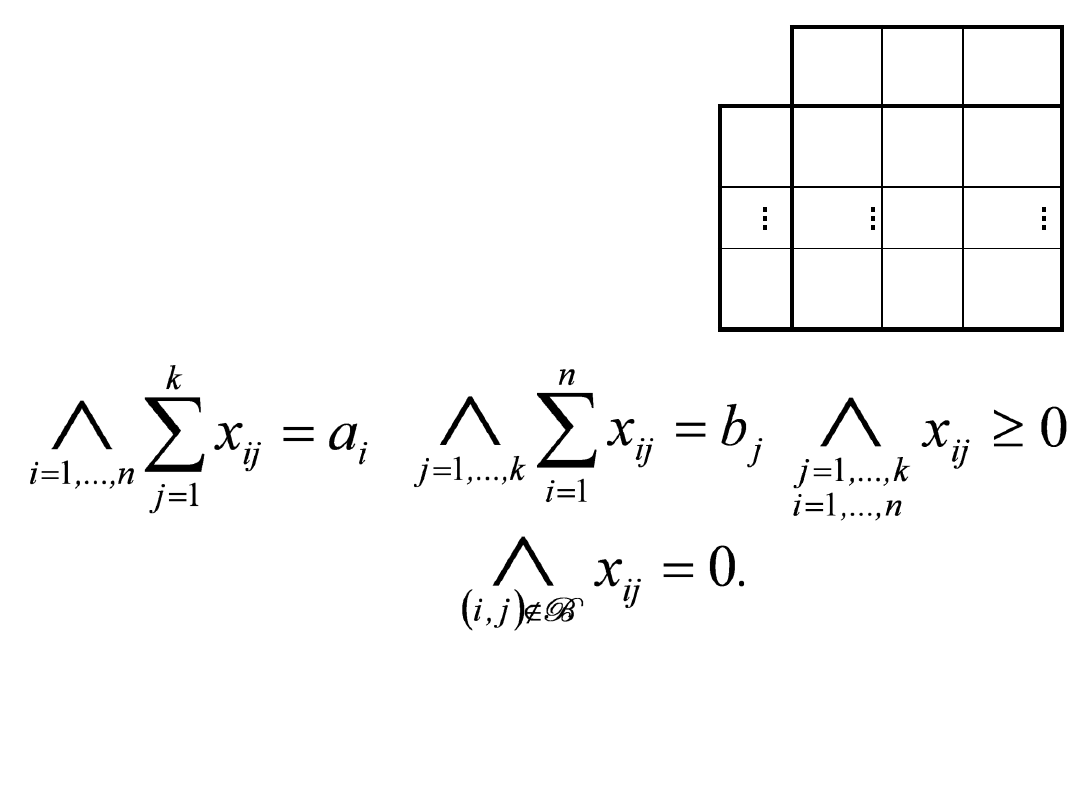
b

1

...

b

k

a

1

c

11

...

c

1k

...

a

n

c

n1

...

c

nk

Dopuszczalne rozwiązanie bazowe ZT

jest macierzą X n



k-wymiarową

spełniającą następujące warunki:

istnieje baza B t.że

16

Liczba węzłów bazowych w dopuszczalnym

rozwiązaniu bazowym ZT wynosi:

n+k-1

gdzie:

n – liczba dostawców

k – liczba odbiorców

17

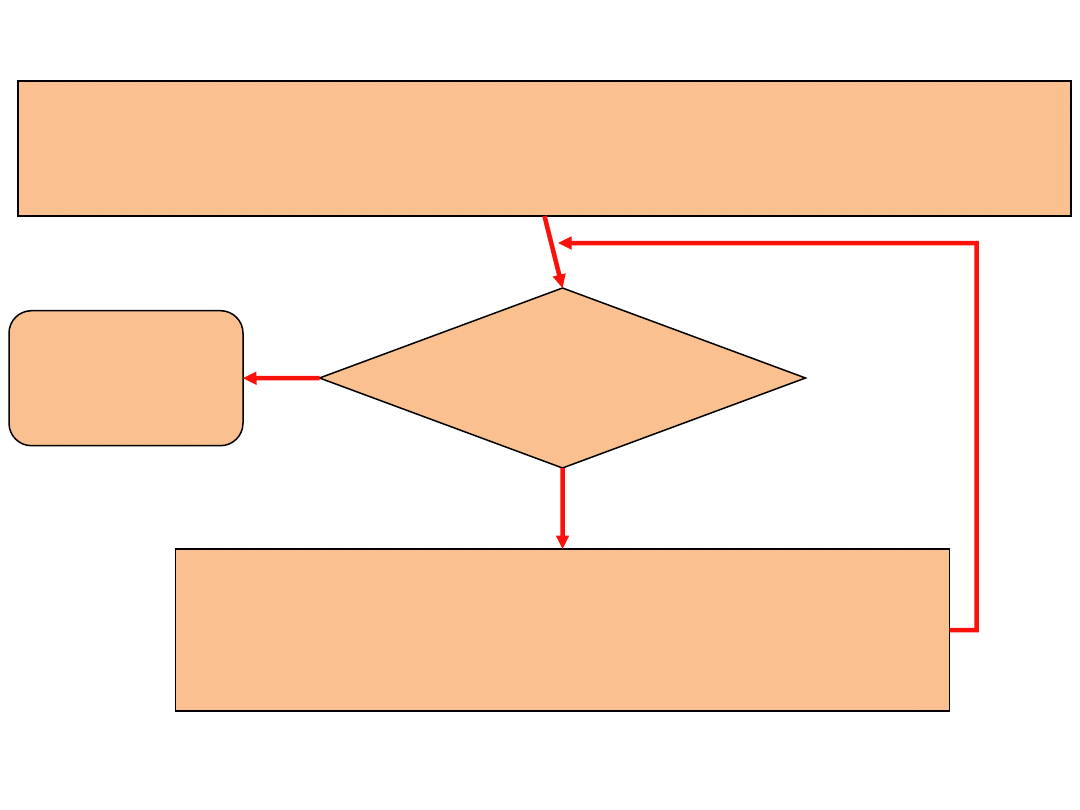
Znajdujemy pierwsze dopuszczalne rozwiązanie bazowe

Czy jest optymalne?

STOP

Tak

Wybieramy następne rozwiązanie bazowe

Nie

18

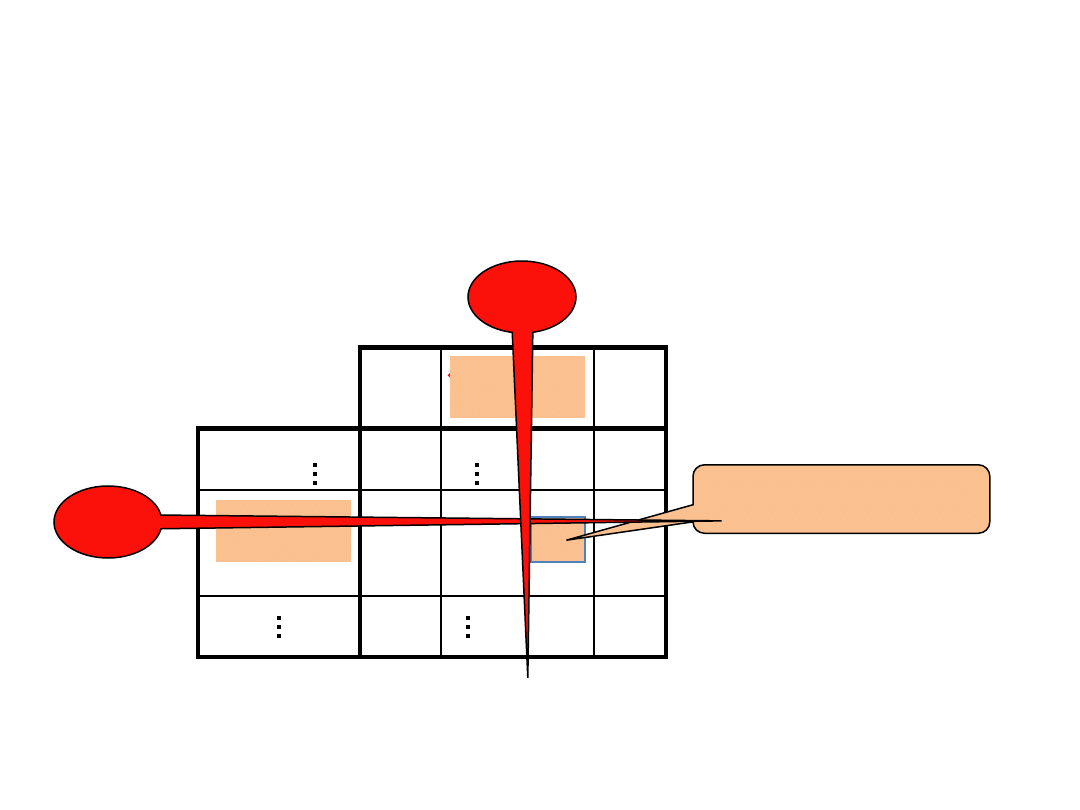
Metody otrzymywania pierwszego

dopuszczalnego rozwiązania bazowego

Metody

różnią

się

tylko

wyborem

węzłów

bazowych, w których przewozy mogą być dodatnie.

... b

j

...

...

...

a

i

... c

ij

...

...

...

x

ij

= min(a

i

,b

j

)

b

j

- x

ij

a

i

- x

ij

0=

0=

Jeżeli w obu przypadkach otrzymujemy 0, to wykreślamy
albo wiersz albo kolumnę (

nigdy jedno i drugie

).

19



M

etoda

K

ąta

P

ółnocno-

Z

achodniego

wybierany jest węzeł leżący na północnym-zachodzie,
czyli w górnym, lewym rogu



M

etoda

M

inimalnego

E

lementu

M

acierzy

wybierany jest węzeł z najmniejszym jednostkowym
kosztem przewozu, a jeżeli jest ich więcej, to ten z
nich, który leży na północnym-zachodzie.



V

ogel’s

A

pproximation

M

ethod

Najprostsza – MKPZ, ale dająca rozwiązanie dalekie od

optymalnego

Najlepsza – VAM, ale najbardziej skomplikowana.

20

Postępowanie w metodzie MEM:

•

wybieramy

węzły,

którym

odpowiada

najmniejszy element macierzy kosztów;

•

spośród

węzłów

wybranych

w

punkcie

pierwszym wybieramy węzły leżące w wierszu o
najmniejszym numerze;

•

spośród węzłów wybranych w punkcie drugim
wybieramy

węzeł leżący w

kolumnie

o

najmniejszym numerze

21

Postępowanie w metodzie VAM:

•

dla każdej linii (wiersza lub kolumny) wyznaczamy

wartość

bezwzględną

różnicy

między

dwoma

najmniejszymi

elementami

macierzy

kosztów

jednostkowych znajdujących się w tej linii;

•

wybieramy linię, której odpowiada największa różnica;

•

w wybranej linii wybieramy węzeł, któremu odpowiada
najmniejszy element macierzy kosztów jednostkowych.

•

może się zdarzyć przy wykonywaniu czynności z punktu
drugiego, że co najmniej dwie linie mają tę samą

największą różnicę. Dla jednoznaczności umówimy się,

że w takim wypadku spośród linii o największej różnicy

będziemy wybierać wiersz o najmniejszym numerze, zaś
w przypadku, gdy ta największa różnica odpowiada
tylko kolumnom – kolumnę o najmniejszym numerze.

22