Ekonometria

Wykład 1

mgr Marzanna Gawryluk

Literatura

• Buga J., Nykowski I. Zagadnienie transportowe w

programowaniu liniowym, PWN, Warszawa 1974

• Busłowski A. Stabilność rozwiązania optymalnego zadania

programowania liniowego, UwB, Białystok 2000

• Doroszkiewicz S., Koładkowski D., i in: Ekonometria, SGH,

Warszawa 1996 i następne wydania

• Gajda J. Ekonometria praktyczna, Absolwent, Łódź 1998
• Kukuła K. [red.] Badania operacyjne w przykładach i

zadaniach, PWN, Warszawa 1993

• Kukuła K. [red.] Wprowadzenie do ekonometrii w

przykładach i zadaniach, PWN, Warszawa 1996 i następne
wydania

• Nowak E. Zarys metod ekonometrii, PWN,

Warszawa 1997

• Maddala G. S. Ekonometria, WN PWN,

Warszawa 2006

• Sadowski W. [red.] Elementy ekonometrii i

programowania matematycznego, PWN,
Warszawa 1985

• Welfe A. Ekonometria, PWE, Warszawa 1995 i

następne wydania

• Welfe A. Ekonometria. Zbiór zadań, PWE,

Warszawa 1997

Co to jest ekonometria?

Ekonometria to dziedzina nauk społecznych,

zajmująca

się

zastosowaniem

metod

statystycznych

i

matematycznych

do

mierzenia, analizy i prognozowania zjawisk i
relacji gospodarczych.

Wśród uprawiających ekonometrię nie ma

zgodności w sprawie pełnej definicji tej
dziedziny, a także w kwestii jej faktycznych
możliwości aplikacyjnych.

Większość ekonometryków przychyla się do
poglądu, że zadania ekonometrii to:
• opis rzeczywistości gospodarczej,
• weryfikacja hipotez ekonomicznych,
• prognozowanie wyników działalności

gospodarczej.

Jednak realizacja tych zadań zależy od

wielu okoliczności i nie zawsze jest

możliwa.

Ekonometria a inne dziedziny

Z określenia ekonometrii wynika, że stanowi

ona połączenie teorii ekonomii, ekonomii

matematycznej, statystyki ekonomicznej i

statystyki matematycznej. Jest to jednak

dziedzina odrębna. Mimo znacznego związku

z teorią i metodami wypracowanymi w innych

dyscyplinach, ekonometria posiada własną

teorię i metodologię. Podstawy klasycznej

ekonometrii powstały w latach 40 i 50-tych

minionego wieku. Współczesna ekonometria

rozwija się nadal, starając się odpowiadać na

najpilniejsze pytania nauki ekonomii i praktyki

gospodarczej

Model ekonometryczny

Podstawowym narzędziem ekonometrii jest

model ekonometryczny. Jest to równanie lub
zestaw równań opisujących relacje między
wybranymi

zmiennymi

ekonomicznymi

(kategoriami

ekonomicznymi). Co najmniej

jedno z równań modelu ekonometrycznego
jest

równaniem

stochastycznym,

czyli

zawierającym tzw. składnik losowy.

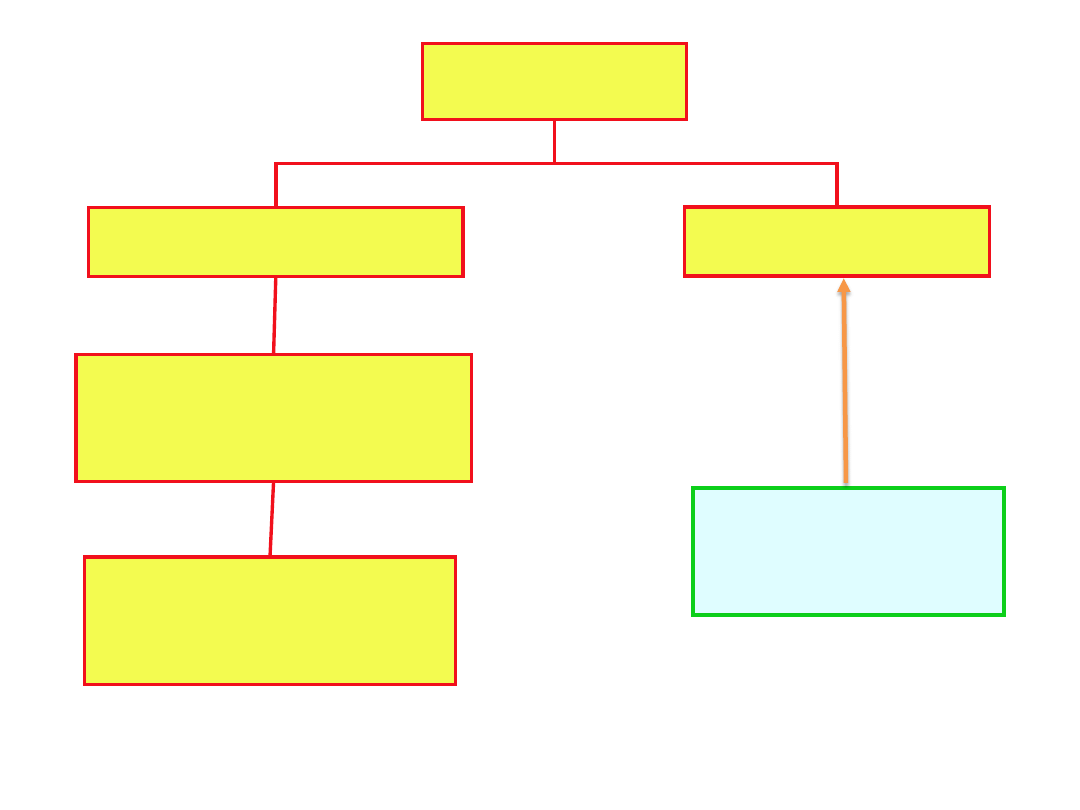
MODELE

deterministyczne

stochastyczne

programowanie

matematyczne

programowanie

liniowe

wnioskowanie

statystyczne

Formułowanie problemów

decyzyjnych

W zależności od rodzaju działalności jednostka podejmująca decyzje

może się znaleźć w różnych sytuacjach, w których może chodzić o
ustalenie np.:

• takiego planu produkcji uzyskanej z wykorzystaniem dostępnych

środków, przy którym przychód uzyskany ze sprzedaży wyrobów

będzie jak największy;

• takiego planu rozwozu produktów, aby przy możliwie niskim

koszcie

wykorzystać podaż dostawców i zaspokoić popyt

odbiorców;

• takiego harmonogramu prac, aby – przy zachowaniu pewnej

kolejności wykonywania czynności – całe przedsięwzięcie

zakończyć w możliwie krótkim czasie.

Nie dysponując dowolną, lecz ograniczoną

ilością środków, powinniśmy tak nimi
dysponować, aby cel, na którym nam
zależy, zrealizować w jak najwyższym
stopniu. Podjęcie decyzji sprowadza się
więc do ustalenia, które środki i w jakich
ilościach należy zaangażować. Gdy istnieje
więcej niż jeden wariant decyzji, mamy do
czynienia z problemem decyzyjnym.

Decyzję najlepszą do podjęcia w danej

sytuacji, to znaczy najlepszą z punktu
widzenia

przyjętego

celu

i

przy

uwzględnieniu

istniejących

ograniczeń,

nazywamy decyzją optymalną.

W

każdej sytuacji decyzyjnej pewne

decyzje są możliwe do realizacji, takie
decyzje będą nazywane dopuszczalnymi.
Pewne inne decyzje zaś są niemożliwe do
realizacji, takie decyzje będą nazywane
niedopuszczalnymi. Decyzje dopuszczalne

tworzą

zbiór

rozwiązań

(decyzji)

dopuszczalnych

(ZRD).

To

czy

dana

decyzja

jest

dopuszczalna

czy

jest

niedopuszczalna

zależy

od

warunków ograniczających narzuconych
przez sytuację decyzyjną.

Po

odpowiednim

„przetłumaczeniu”

problemu

decyzyjnego

na

język

matematyczny otrzymujemy model tego
problemu i na jego podstawie wyznaczamy
decyzję optymalną. Taki model nazywa się
modelem

decyzyjnym

(modelem

optymalizacyjnym).

Kryterium

według

którego ocenia się decyzje nosi nazwę
kryterium wyboru.

Metody wyznaczania optymalnych decyzji

należą do dziedziny, która nosi nazwę
badań operacyjnych. W ramach naszego
przedmiotu rozpatrywać będziemy modele
programowania

matematycznego

(PM),

a szczególnie ich podklasę, mianowicie
zadania programowania liniowego (PL).

Modelowanie decyzji

Warunki, w jakich podejmowane są decyzje,

nie pozwalają na wybór dowolnej decyzji,
ponieważ musi być ona zgodna z warunkami
ograniczającymi. W świetle celów, jakie sobie
stawia decydent, jedne decyzje mogą być
lepsze,

a

inne

gorsze.

Wybór decyzji

optymalnej wymaga przyjęcia określonego
kryterium, według którego oceniamy decyzje
jako lepsze lub gorsze.

Przykład

Możemy podjąć jedną z trzech decyzji

inwestycyjnych. Nakłady inwestycyjne oraz
oczekiwany roczny zysk osiągnięty z tych
inwestycji przedstawiono poniżej.

Która z trzech decyzji jest optymalna?

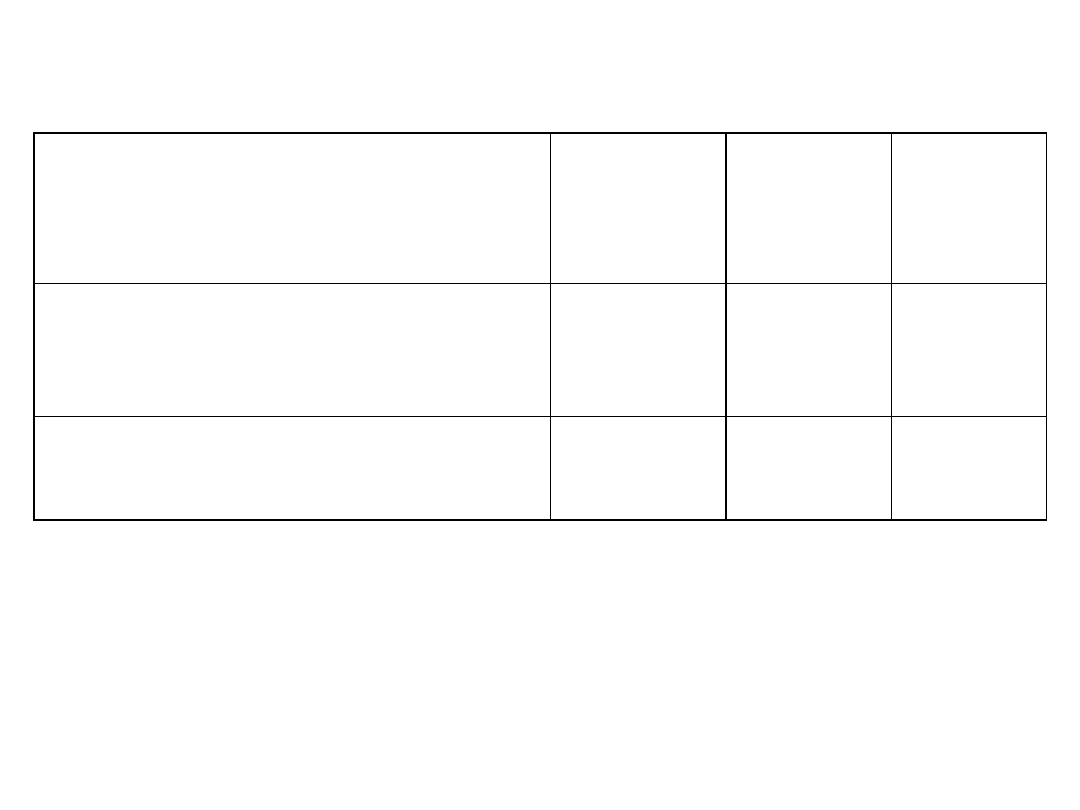
Decyzje

A

B

C

Nakłady inwestycyjne
(w mln zł)

40

50

30

Zyski (w mln zł)

8

4

6

Na pytanie to nie możemy odpowiedzieć, gdyż

nie zostało określone żadne kryterium wyboru.

a) Gdy kryterium oceny będzie minimalizacja

nakładów,

to

najlepszą

decyzją

jest

decyzja C.

b) Gdy jako kryterium wyboru przyjmiemy

maksymalizację zysku, to najlepszą decyzją
jest decyzja A.

c) W przypadku maksymalizacji stopy zysku

najlepsze są decyzje A i C.

Budowanie zadania PL

Proces budowy modelu służącego do wyznaczania

decyzji optymalnej przy ograniczonej swobodzie
wyboru można ująć w następujące etapy:

• zdefiniowanie pojęcia decyzji (c);
• zdefiniowanie zbioru D decyzji możliwych do

podjęcia – decyzje dopuszczalne;

• określenie sposobu oceny poziomu realizacji celu

przez każdą decyzję, jakiemu mają służyć te decyzje;

• określenie pojęcia decyzji optymalnej ze względu na

zadany cel i ustalony sposób oceny poziomu jego
realizacji;

• wybór decyzji optymalnej.

Przykład

Przedsiębiorstwo może wytwarzad dwa

wyroby, używając w tym celu dwóch
surowców. Normy zużycia, limity surowca,
ceny produktów podaje tabela.

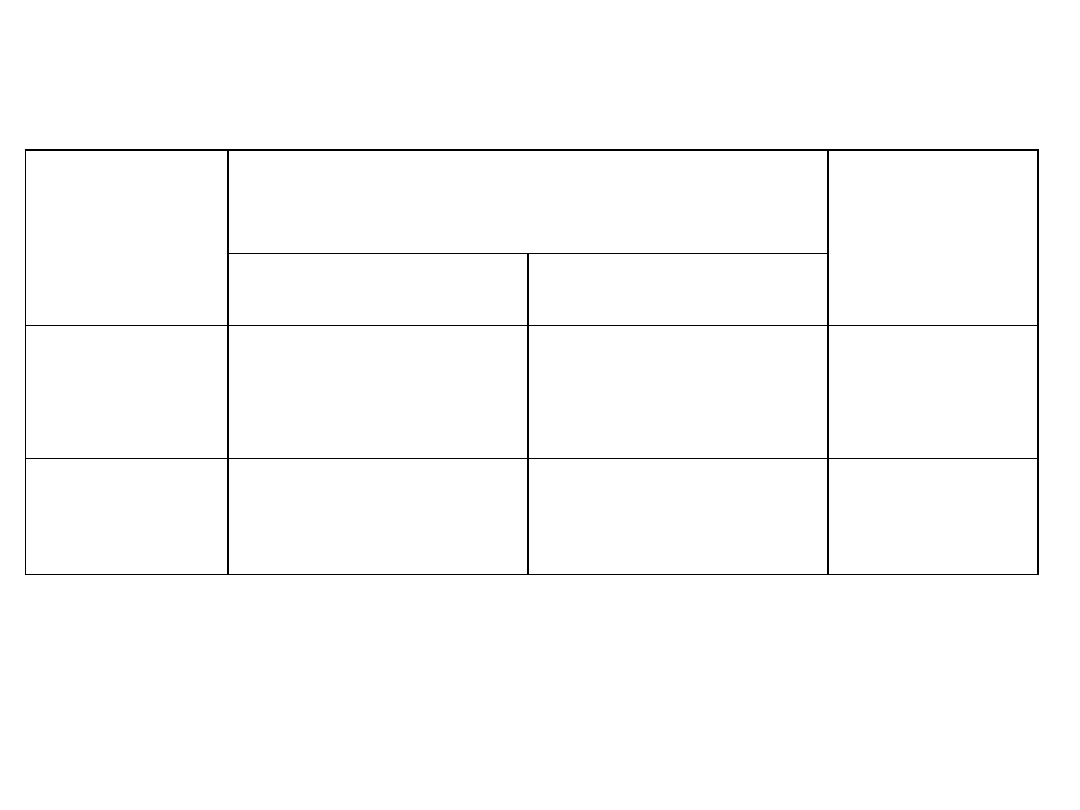
Wyroby

Surowiec

Ceny

I

II

1
2

8
4

6
9

18
15

Limit

52

69

Decydent ma określić, produkcję których

wyrobów i w jakiej wysokości podjąć, aby
przychód uzyskany ze sprzedaży był
możliwie

wysoki.

Sformułować

odpowiednie zadanie decyzyjne.

Zmienne decyzyjne:

• x

1

– ilość wyrobu 1

• x

2

– ilość wyrobu 2

Parametry:

Wszystkie parametry zadania podane są w

tabeli.

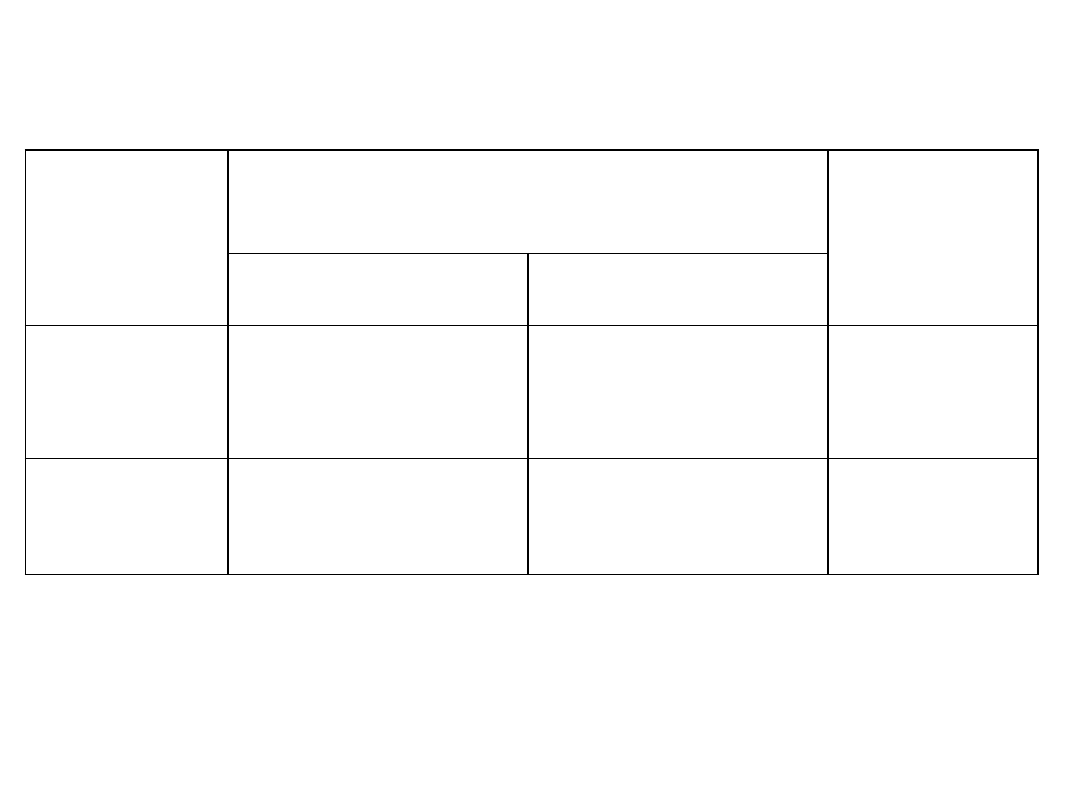
Wyroby

Surowiec

Ceny

I

II

1
2

8
4

6
9

18
15

Limit

52

69

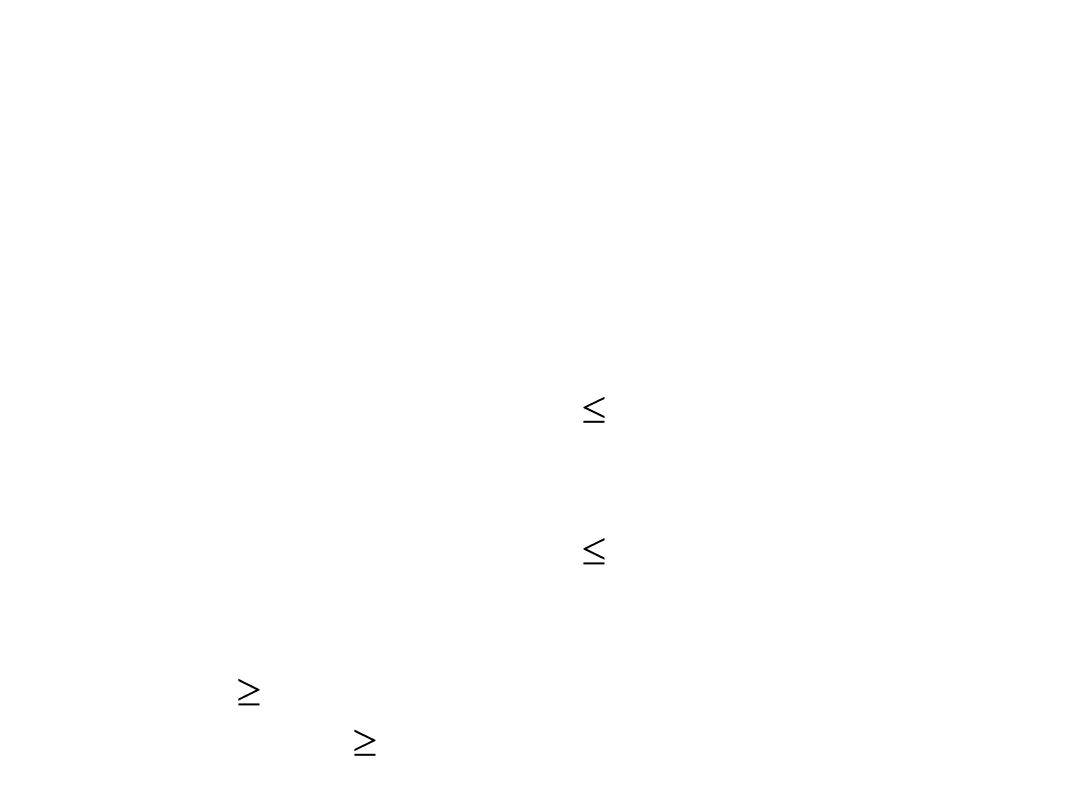
Warunki ograniczające:

• Dwa czynniki (surowce) ograniczają rozmiary produkcji.

Weźmy surowiec I. Jeżeli przedsiębiorstwo wytworzy x

1

jednostek wyrobu I oraz x

2

jednostek wyrobu 2, to łączne

zużycie surowca I wyniesie: 8x

1

+ 4x

2

jednostek. Z uwagi

na to, że limit surowca I wynosi 52 jednostki, odpowiedni
warunek ograniczający ma postać nierówności:

8x

1

+ 4x

2

52.

• Podobne rozważania w odniesieniu do surowca II

prowadzą do nierówności:

6x

1

+ 9x

2

69.

• Oczywiście, przedsiębiorstwo albo będzie wytwarzać

wyrób 1, albo nie będzie go wytwarzać wcale.

• Zatem x

1

0.

• Analogicznie x

2

0.

Funkcja kryterium:

Przy założeniu, że cała produkcja jest

sprzedawana, przychód ze sprzedaży x

1

jednostek wyrobu I oraz x

2

jednostek

wyrobu 2 wynosi 18x

1

+15x

2

złotych.

Celem

decydenta

jest

maksymalizacja

przychodu.

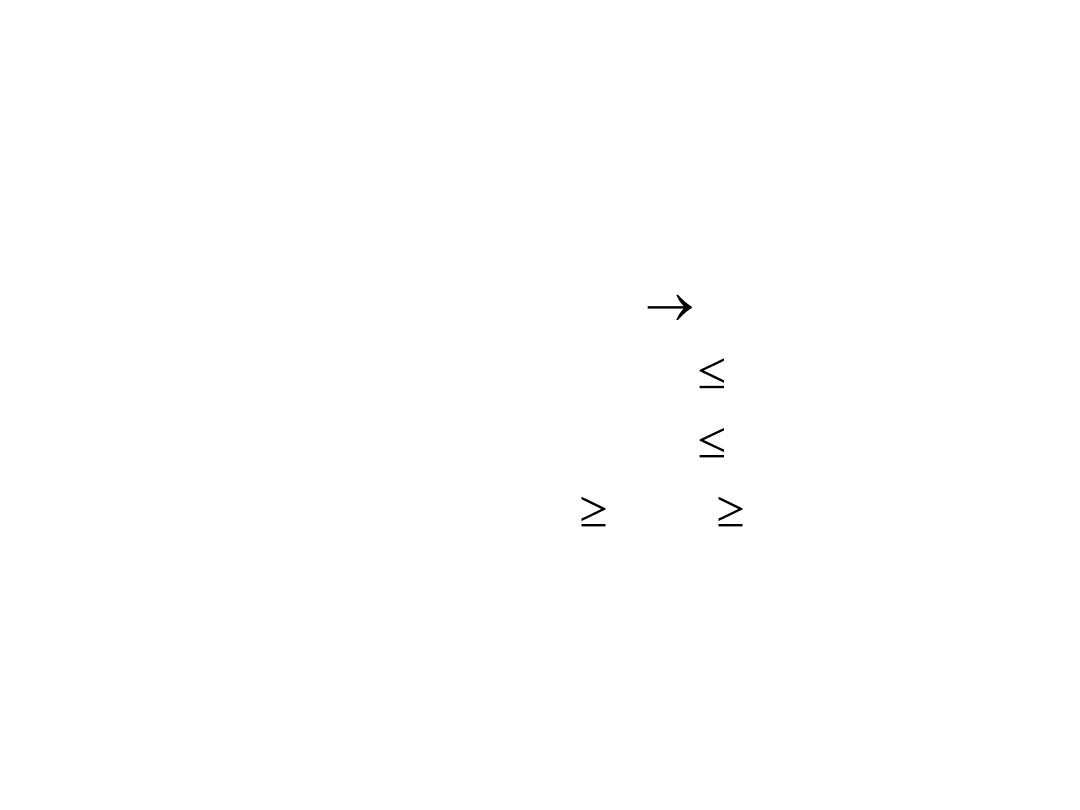
Zadanie decyzyjne:

Zadanie ma następującą postać:

f

c

: 18x

1

+ 15x

2

max

w.o.:

8x

1

+ 4x

2

52

6x

1

+ 9x

2

69

x

1

0; x

2

0

W sformułowanym zadaniu zarówno warunki

ograniczające jak i funkcja celu są liniowe.
Jest to więc liniowe zadanie decyzyjne

Matematyczny

model

problemu

optymalnego

wyboru jest zadaniem programowania liniowego,

jeśli spełnia następujące warunki:

• dowolną decyzję można wyrazić za pomocą

wektora „c” o „k” składowych:

c=[x

1

x

2

... x

k

]

T

R

k

i k

2.

x

1

, ... , x

k

– składowe decyzji

c – zmienne decyzyjne;

• zmienne decyzyjne muszą być liczbami

nieujemnymi (spełniać warunki nieujemności):

x

1

0, ... , x

k

0

• każdy z warunków ograniczający swobodę

wyboru (definiujący zbiór D) różny od
warunku nieujemności jest nierównością
lub równaniem liniowym nałożonym na
zmienne decyzyjne:

a

i1

x

1

+ a

i2

x

2

+ ... + a

ik

x

k

( =) b

i

dla i=1, ... ,m;

gdzie „m” oznacza liczbę tych warunków.

• ocena jakości decyzji dokonuje się za

pomocą tzw. funkcji celu, która jest funkcją
liniową

zmiennych

decyzyjnych

(składowych decyzji c):

f

c

: c

1

x

1

+ c

2

x

2

+ ... + c

k

x

k

.

• w zbiorze D szukamy decyzji co

wyznaczającej największą (maksymalną)
albo najmniejszą (minimalną) wartość
funkcji celu f w zależności od
sformułowanego problemu. Taką decyzję, o
ile istnieje, nazywamy decyzją optymalną i
stanowi ona rozwiązanie sformułowanego
problemu wyboru.

Zadania programowania liniowego

dotyczą najczęściej następujących
przejawów

działalności

ekonomicznej:

• ustalenia wielkości i struktury produkcji
• problemu diety
• zagadnienia transportowego
• problemu rozkroju itp.