Ekonometria 

Wykład 2

mgr Marzanna Gawryluk

1

Ważną rolę przy formułowaniu zadań

programowania

liniowego

i

ich

rozwiązywaniu

odgrywają

dwie

postacie szczegółowe:

• klasyczna

• standardowa

2

Zadaniem

postaci

klasycznej

nazywamy

zadanie,

w

którym

wszystkie warunki ograniczające są
nierównościami typu ≤ dla zadań na
maksimum, bądź nierówności typu ≥
dla zadań na minimum

3

Postać kanoniczna i standardowa PL



Postać kanoniczna (klasyczna)

przy ogr.

przy ogr.

przy ogr.

przy ogr.

4

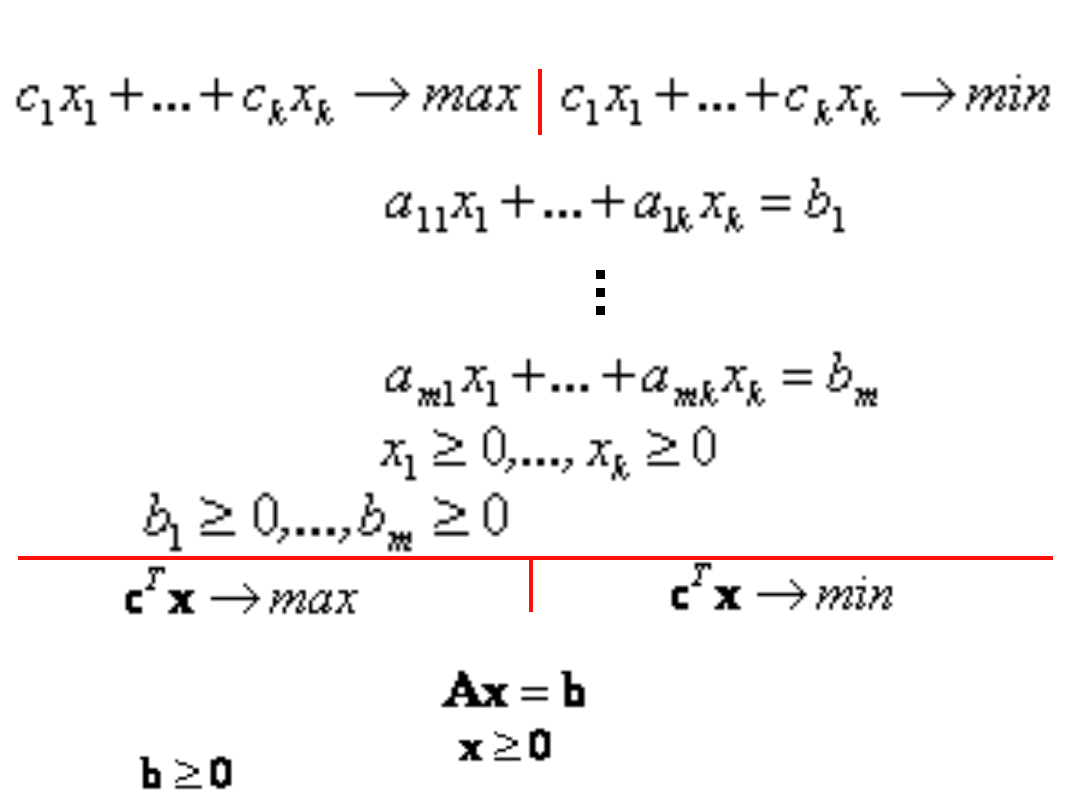
przy ogr.



Postać standardowa

oraz

przy ogr.

oraz

5

Zad. Sprowadź do postaci klasycznej i standardowej
zagadnienie PL:

– 4x

1

+ 6x

2

+ x

3

+ x

4

max

3x

1

– 5x

2

+ 2x

3

+ x

4

≥ 6

warunki ograniczające:

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0, x

4

R

x

1

+ x

2

– x

3

– 2x

4

≥ 14

6

3x

1

– 5x

2

+ 2x

3

+ x’

4

– x’’

4

≥ 6

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0, x’

4

≥ 0, x’’

4

≥ 0

x

1

+ x

2

– x

3

– 2 x’

4

+ 2x’’

4

≥ 14

x

4

= x’

4

– x’’

4

– 4x

1

+ 6x

2

+ x

3

+ x’

4

– x’’

4 

max

7

postać klasyczna:

–3x

1

+ 5x

2

– 2x

3

– x’

4

+ x’’

4

≤ –6

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0, x’

4

≥ 0, x’’

4

≥ 0

–x

1

– x

2

+ x

3

+ 2 x’

4

– 2x’’

4

≤ –14

– 4x

1

+ 6x

2

+ x

3

+ x’

4

– x’’

4 

max

8

postać standardowa:

3x

1

– 5x

2

+ 2x

3

+ x’

4

– x’’

4

– x

d

5

= 6

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0, x’

4

≥ 0, x’’

4

≥ 0, x

d

5

≥ 0, x

d

6

≥ 0

x

1

+ x

2

– x

3

– 2 x’

4

+ 2x’’

4

– x

d

6

= 14

– 4x

1

+ 6x

2

+ x

3

+ x’

4

– x’’

4 

max

9

Metoda geometryczna 

rozwiązywania zadań PL

10

Metodą

geometryczną

można

rozwiązywać liniowe zadania decyzyjne
o

dwóch

i

wyjątkowo

o

trzech

zmiennych.

Liczba zmiennych (k) wyznacza wymiar
przestrzeni, w której znajduje się zbiór
rozwiązań

dopuszczalnych

(ZRD)

i

rozwiązań optymalnych (RO).

11

Graficznie ZRD jest częścią wspólną
półpłaszczyzn (które są wyznaczane przez
nierówność) i/lub prostych (które są
wyznaczane

przez

równanie) oraz I

ćwiartki układu współrzędnych (wynika to
z

warunku

nieujemności

zmiennych

decyzyjnych),

czyli

jest

wypukłym

wielokątem (może nim być prosta, punkt,
wielobok).

12

Rozwiązywanie metodą geometryczną

polega

na

wyszukaniu

w

zbiorze

rozwiązań dopuszczalnych punktu, dla
którego funkcja celu przyjmuje wartości
najkorzystniejsze.

Taki

punkt

nosi

nazwę

punktu

optymalnego

,

a

jego

współrzędne

stanowią rozwiązanie optymalne zadania.

13

Przy

wyznaczaniu

punktu

optymalnego

pomocna

jest

izokwanta funkcji

celu tzw. prosta

odpowiadająca

pewnej

zadanej

wartości funkcji celu.

14

Gradientem

funkcji (f) w punkcie x

0

nazywamy (o ile istnieje) wektor,
który

wskazuje

kierunek

najszybszego, przy max. wzrostu
(przy min. spadku) wartości funkcji

15

Izokwanta 

jest prostą  prostopadłą do 

gradientu funkcji.

16

x

1

x

2

x

1

x

2

D

D

x

1

x

2

D

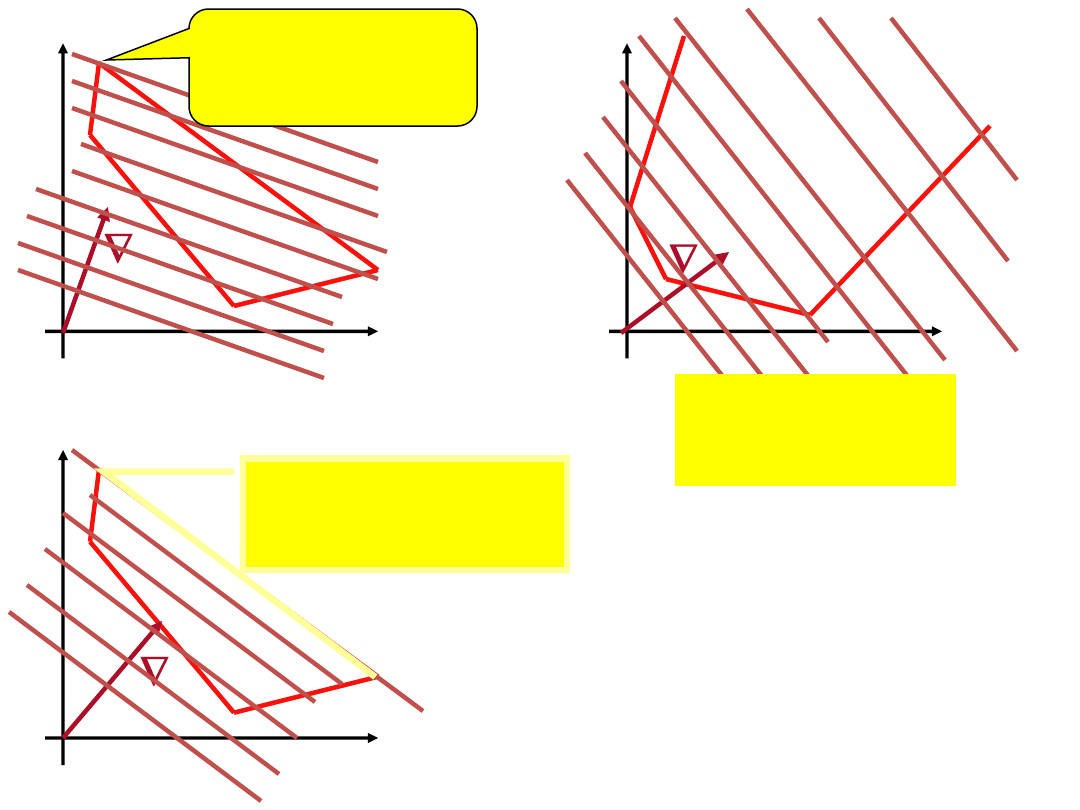
Rozwiązanie 

optymalne

Rozwiązania 

optymalne

Rozwiązanie 

nieskończone

17

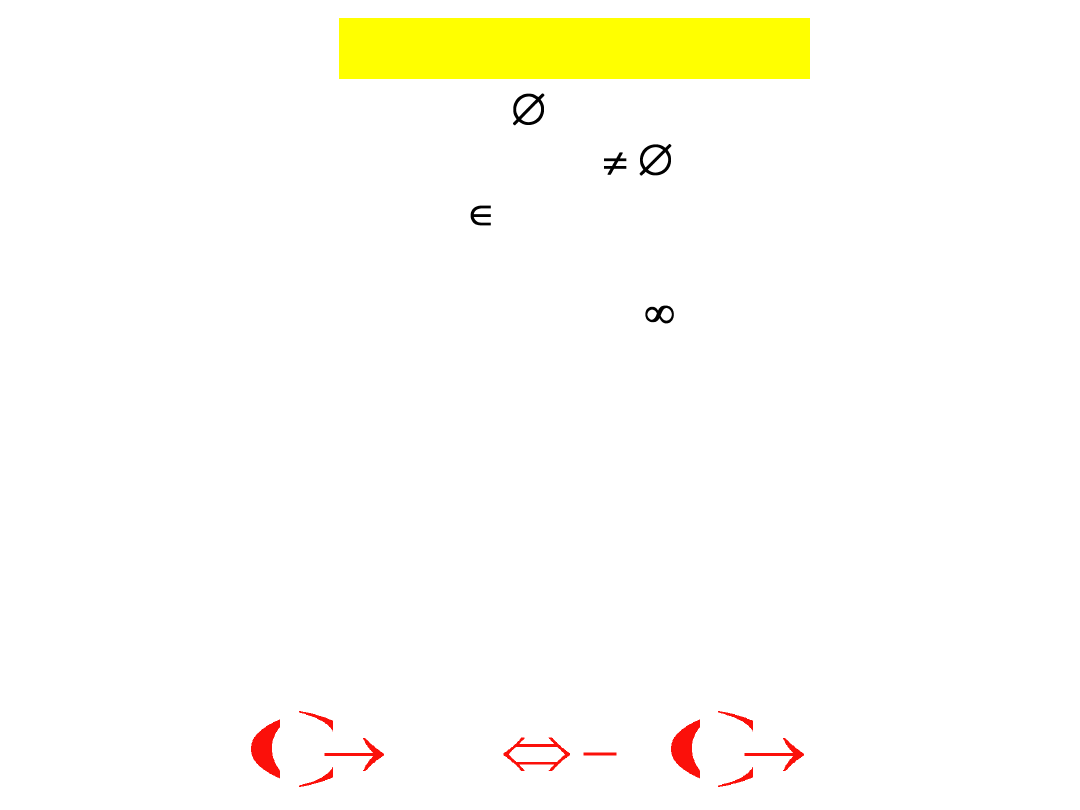
Rodzaje rozwiązań



program sprzeczny

: 

D=

(nie ma z czego wybierać)



rozwiązanie nieskończone 

(

D

oraz dla każdej 

liczby r istnieje x

D t.że f(x)>r, czyli funkcja 

celu nie posiada maksimum na zbiorze rozwiązań 
dopuszczalnych (dąży do + ) – D jest za mało 
ograniczony)



rozwiązanie jednoznaczne 

(jedyne)



rozwiązanie niejednoznaczne 

(istnieje więcej niż jedno 

rozwiązanie optymalne – dla nich wszystkich 
wartość funkcji celu jest taka sama).

Uwaga:

Szukanie najmniejszej wartości funkcji celu f jest 

równoważne szukaniu największej wartości funkcji –f:

max

f

min

f

x

x

18