
Temat:
Metoda rzutów Monge’a
Obrót

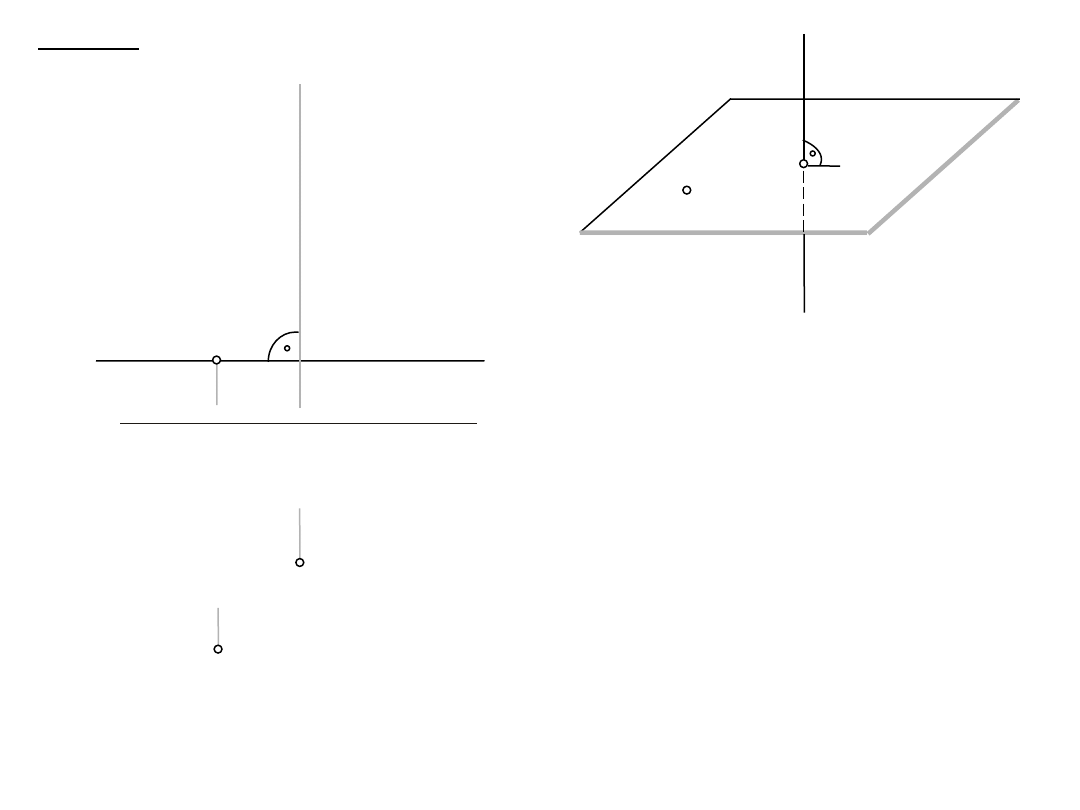
1. obrót
1.1. l
p
1
l
A'
A"
l'
l"
A
D: A, l
p
1
,
j
1
, j
2
=
p
2
'
X
12
=
p
1
"
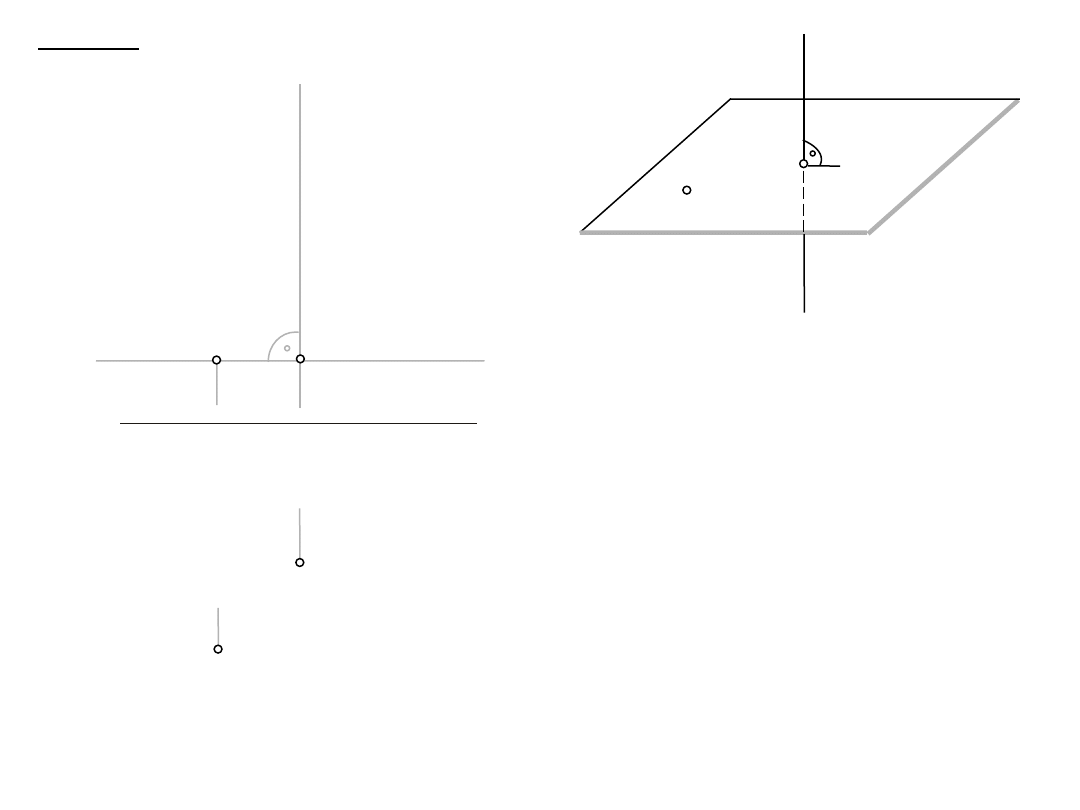
1. obrót
1.1. l
p
1
l
e
A
e
"
A
A'
A"
l'
l"
A
D: A, l
p
1
,
j
1
, j
2
e
A
l
e
A
A
=
p
2
'
X
12
=
p
1
"
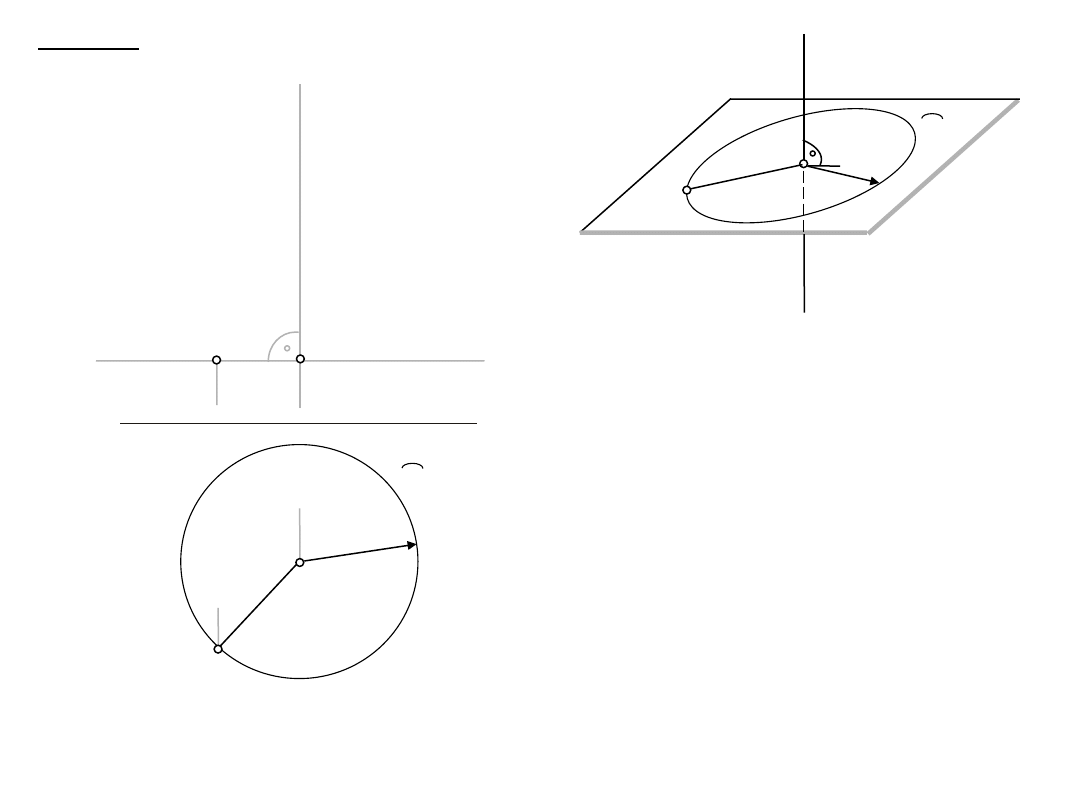
1. obrót
1.1. l
p
1
l
e
A
e
"
A
A'
A"
S"
A
l'
=S'
A
l"
S
A
A
D: A, l
p
1
,
j
1
, j
2
e
A
l
e
A
A
S
A
=l
e
A
=
p
2
'
X
12
=
p
1
"
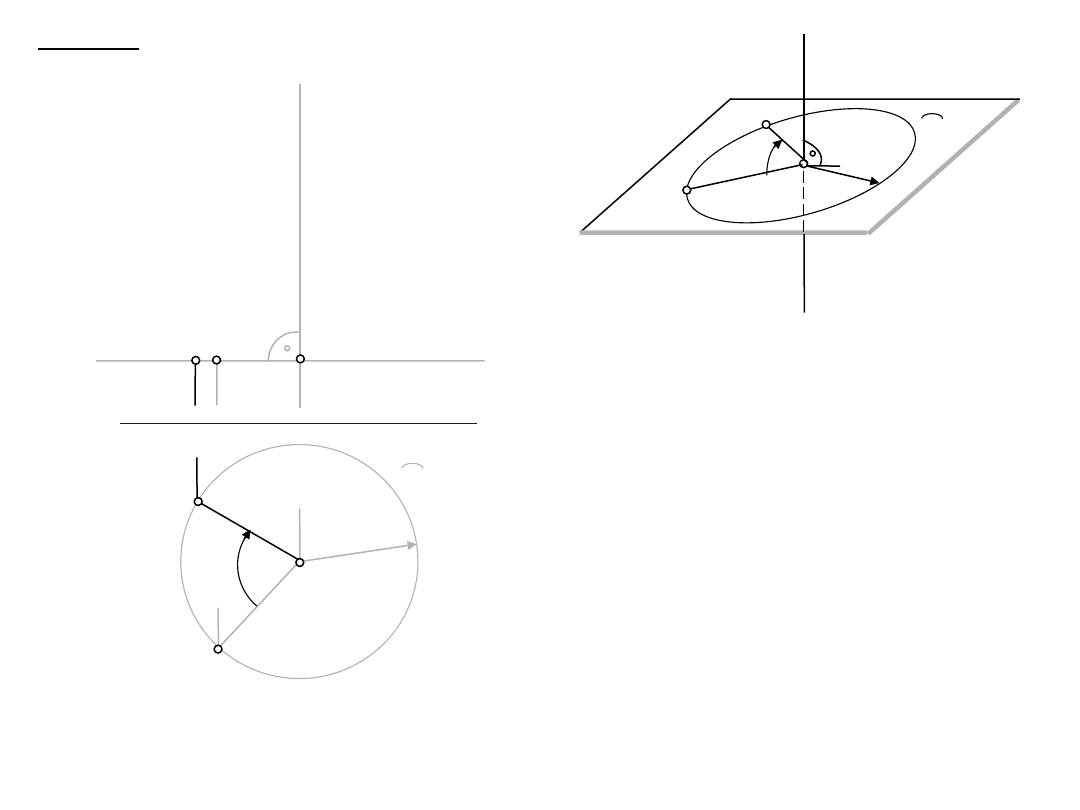
1. obrót
1.1. l
p
1
l
e
A
e
"
A
r
A
o'
A
r
A
A'
A"
S"
A
l'=S'
A
l"
S
A
A
o
A
D: A, l
p
1
,
j
1
, j
2
e
A
l
e
A
A
S
A
=l
e
A
r
A
=
AS
A
=
p
2
'
X
12
=
p
1
"
1. obrót
1.1. l
p
1
l
e
A
e
"
A
j
1
r
A
o'
A
r
A
A'
1
A'
A"
1
A"
S"
A
l'=S'
A
j
1
l"
S
A
A
A
1
o
A
D: A, l
p
1
,
j
1
, j
2
e
A
l
e
A
A
S
A
=l
e
A
r
A
=
AS
A
A
1
– punkt po obrocie o
j
1
=
p
2
'
X
12
=
p
1
"
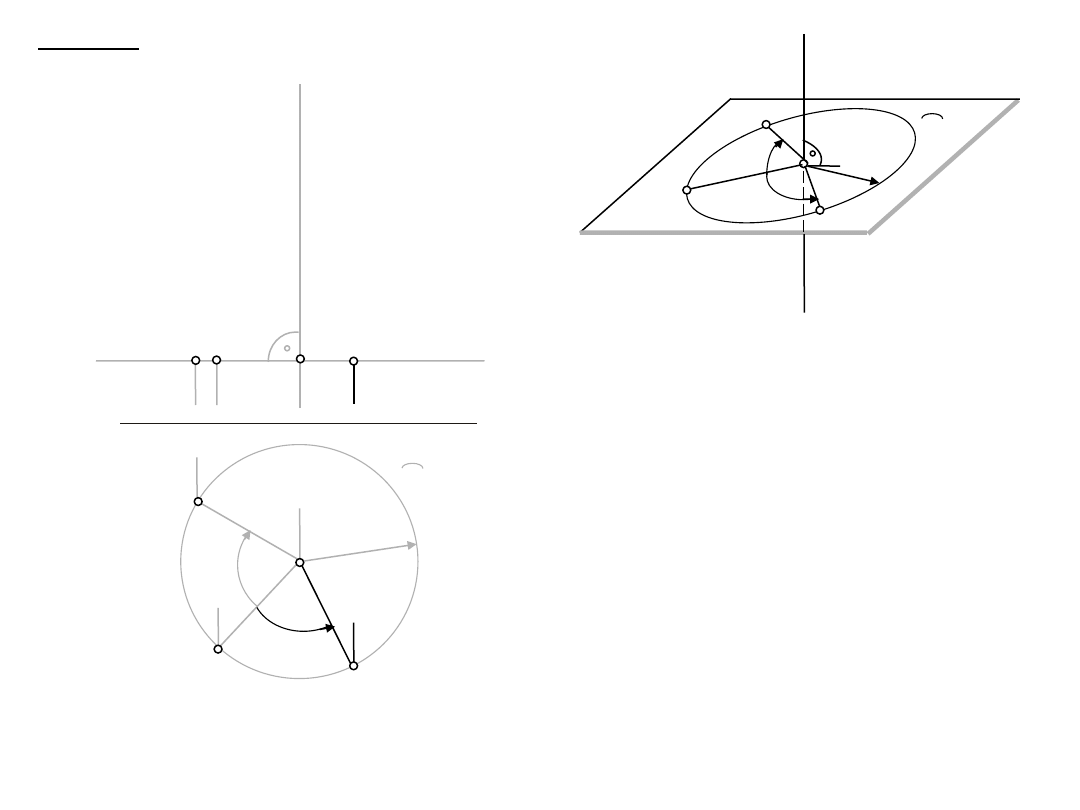
1. obrót
1.1. l
p
1
l
e
A
e
"
A
j
1
j
2
r
A
o'
A
r
A
A'
1
A'
A'
2
A"
1
A"
A"
2
S"
A
l'=S'
A
j
1
j
2
l"
S
A
A
A
1
A
2
o
A
D: A, l
p
1
,
j
1
, j
2
e
A
l
e
A
A
S
A
=l
e
A
r
A
=
AS
A
A
1
– punkt po obrocie o
j
1
A
2
– punkt po obrocie o
j
2
=
p
2
'
X
12
=
p
1
"
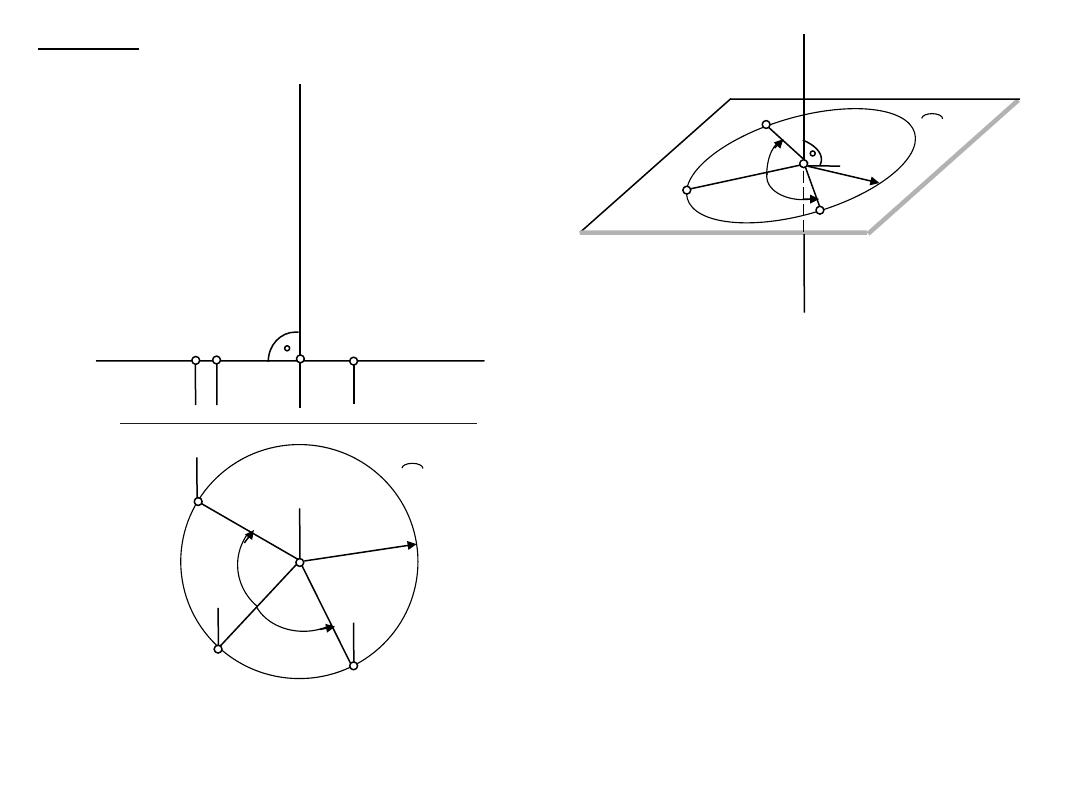
1. obrót
1.1. l
p
1
l
A
e
A
e
"
A
D: A, l
p
1
,
j
1
, j
2
e
A
l
e
A
A
S
A
=l
e
A
r
A
=
AS
A
A
1
– punkt po obrocie o
j
1
A
2
– punkt po obrocie o
j
2
A
1
A
2
j
1
j
2
r
A
o
A
o'
A
r
A
A'
1
A'
A'
2
A"
1
A"
A"
2
S"
A
l'=S'
A
j
1
j
2
l"
S
A
=
p
2
'
X
12
=
p
1
"

Temat:
Metoda rzutów Monge’a
wyznaczenie długości odcinka za
pomocą obrotu

1.2.
Wyznaczyć długość odcinka AB
D: A,B
A'
B"
A"
B'
=
p
2
'
X
12
=
p
1
"
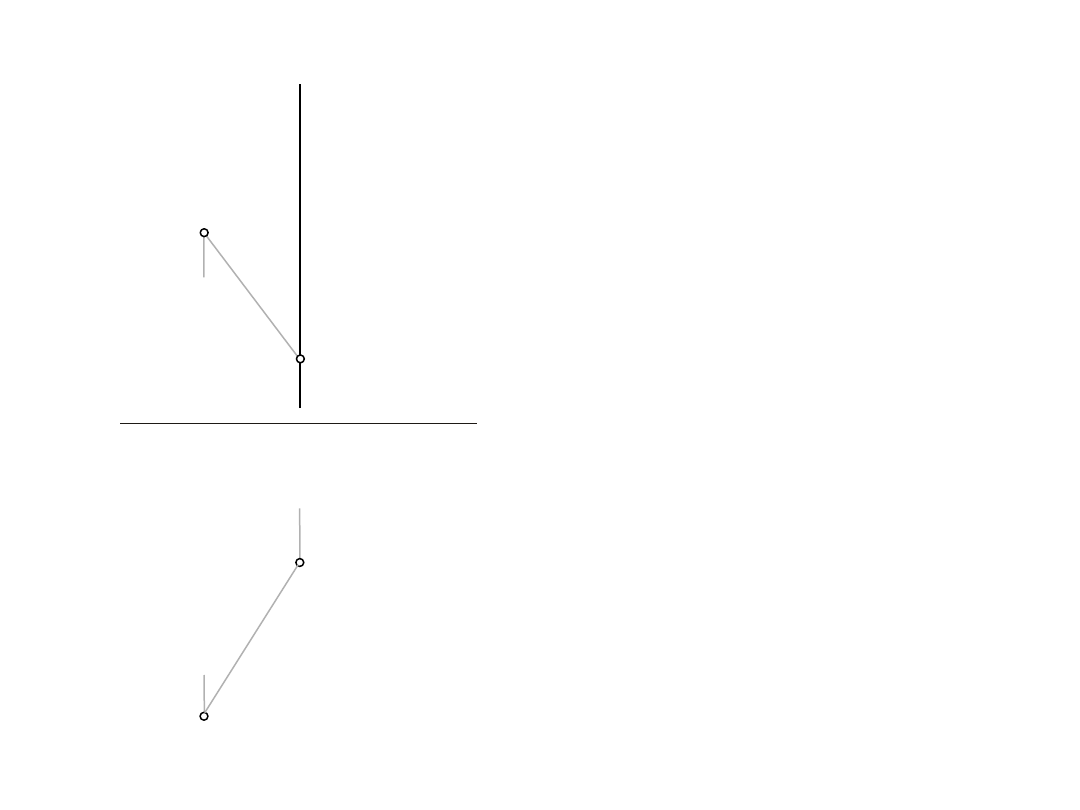
1.2.
Wyznaczyć długość odcinka AB
D: A,B
l
p
1
B
l
A'
B"
A"
B'
=l'
l"
=
p
2
'
X
12
=
p
1
"
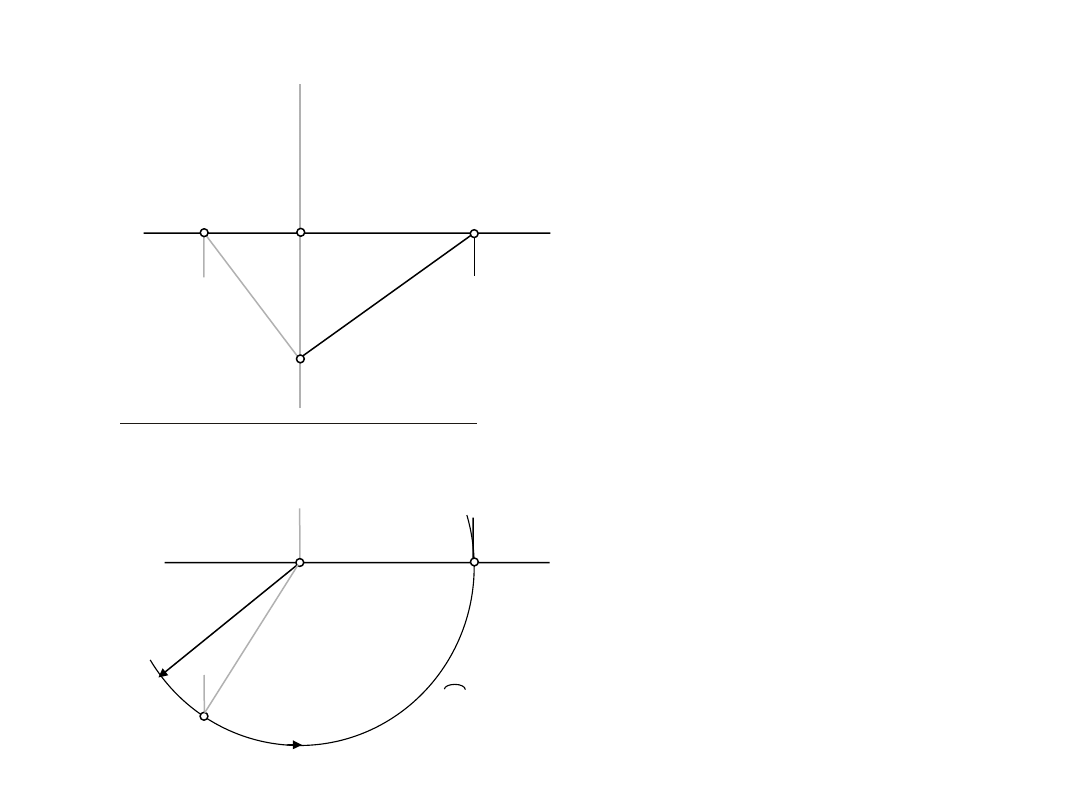
1.2.
Wyznaczyć długość odcinka AB
e
"
A
D: A,B
l
p
1
B
l
o'
A
r
A
A'
1
A'
B"
A"
A"
1
B'=l'
l"
=B"
1
=B'
1
S"
A
=S'
A
B
1
=B
e
A
l
e
A
A
r
A
=
AS
A
A
1
– punkt po obrocie
do momentu,
kiedy A
1
B
1
będzie
prostą czołową
~
~
=
p
2
'
X
12
=
p
1
"
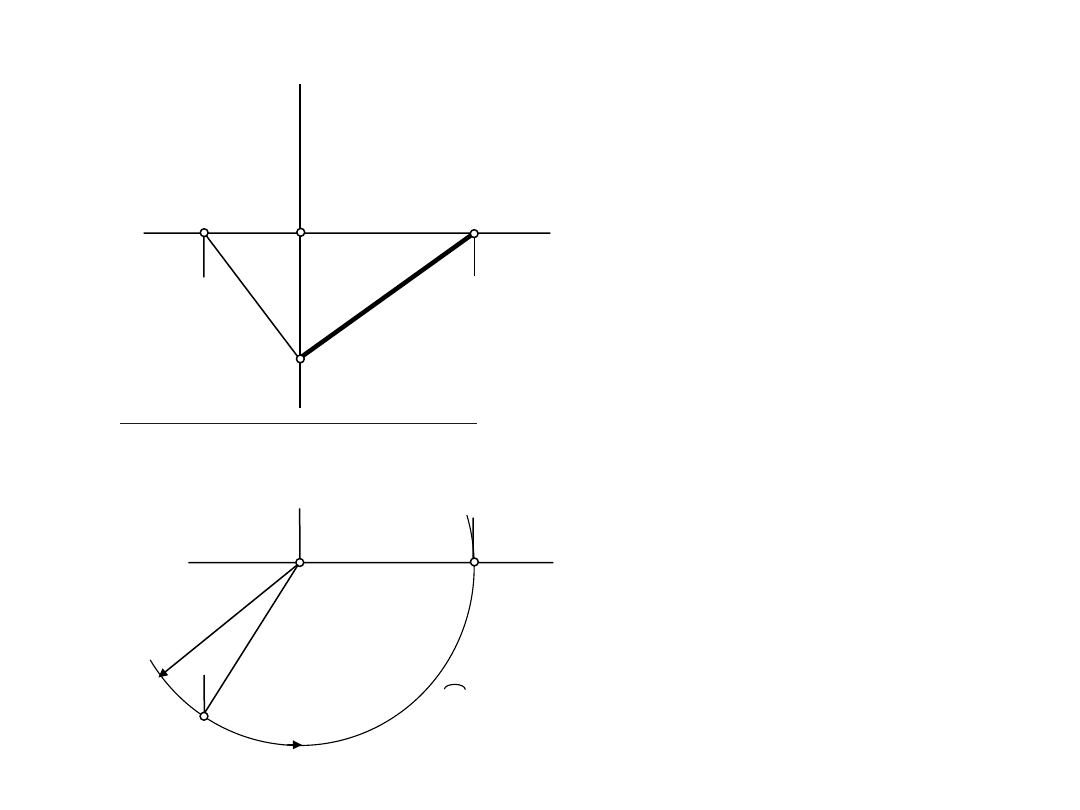
A"
1
1.2.
Wyznaczyć długość odcinka AB
e
"
A
D: A,B
l
p
1
B
l
B
1
=B
e
A
l
e
A
A
r
A
=
AS
A
A
1
– punkt po obrocie
do momentu,
kiedy A
1
B
1
będzie
prostą czołową
o'
A
r
A
A'
1
A'
B"
A"
B'=l'
l"
=B"
1
=B'
1
S"
A
=S'
A
~
~
=
p
2
'
X
12
=
p
1
"
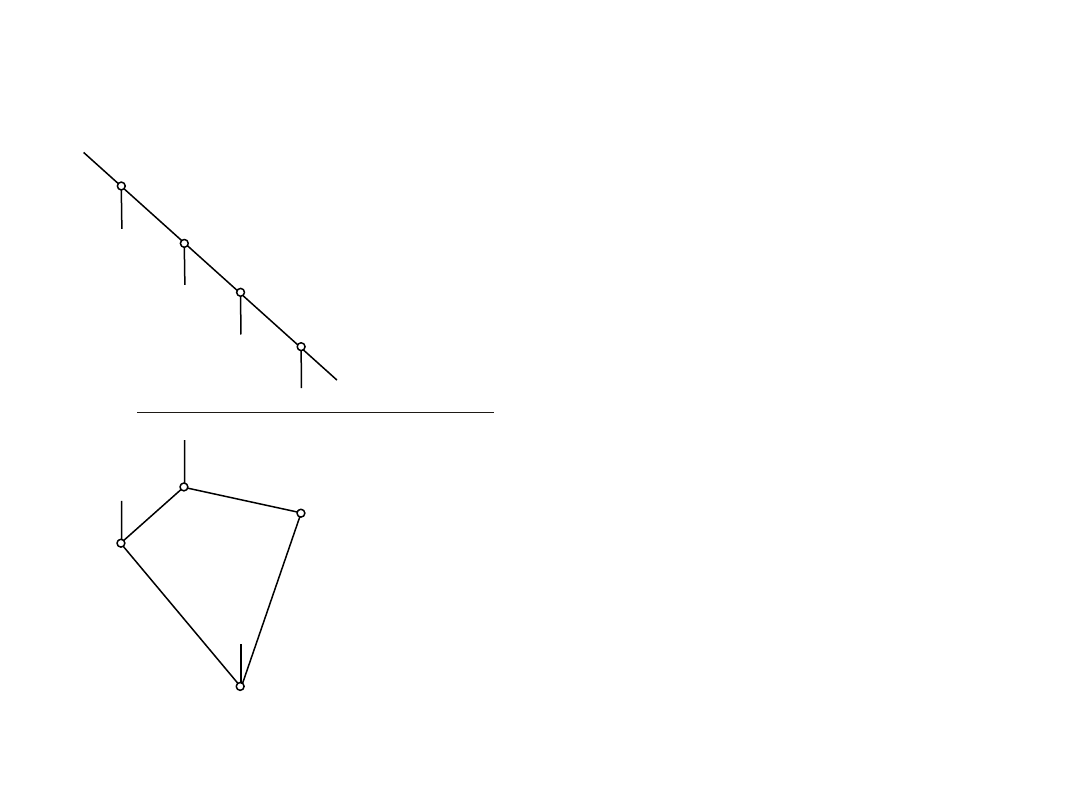
1.3.
Wyznaczyć rzeczywistą wielkość czworokąta ABCD
D:
a
=ABCD,
ap
2
B'
A'
B"
A"
C"
D"
a
"
D'
C'
=
p
2
'
X
12
=
p
1
"
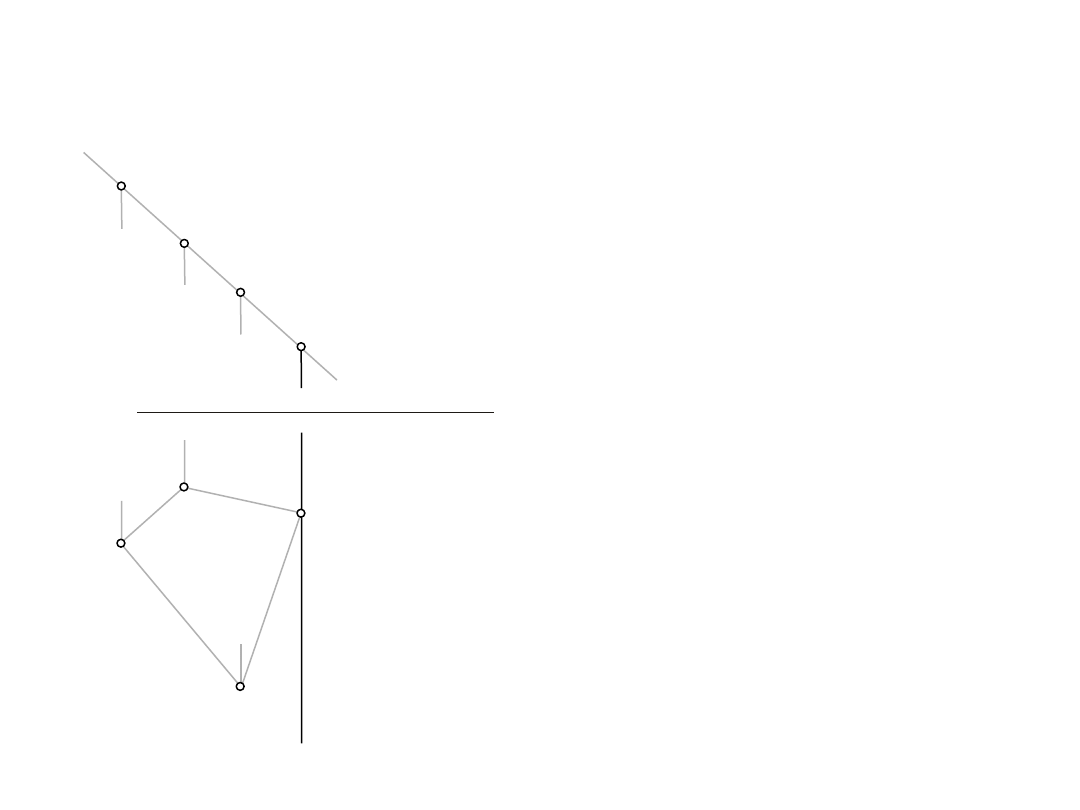
1.3.
Wyznaczyć rzeczywistą wielkość czworokąta ABCD
D:
a
=ABCD,
ap
2
l
p
2
A
l
B'
A'
B"
l'
A"
=l"
C"
D"
a
"
D'
C'
=
p
2
'
X
12
=
p
1
"
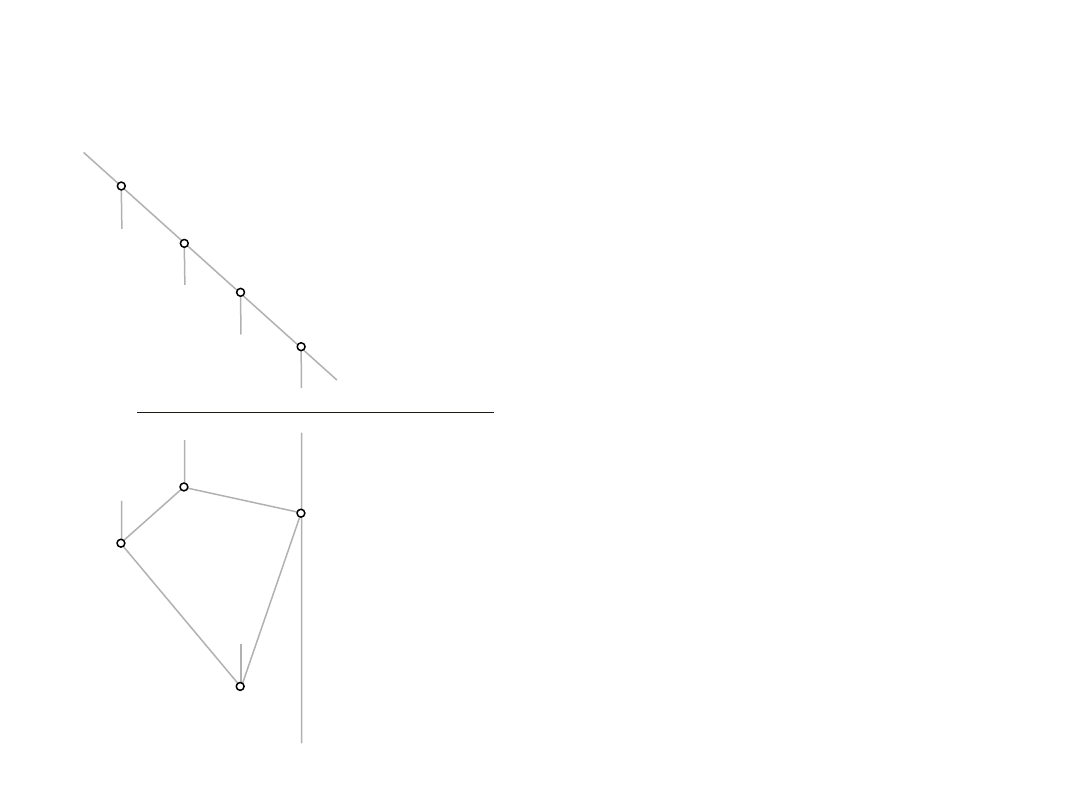
1.3.
Wyznaczyć rzeczywistą wielkość czworokąta ABCD
D:
a
=ABCD,
ap
2
l
p
2
A
l
A
1
=A
B'
A'
=A'
1
B"
l'
A"=l"
=A"
1
C"
D"
a
"
D'
C'
=
p
2
'
X
12
=
p
1
"
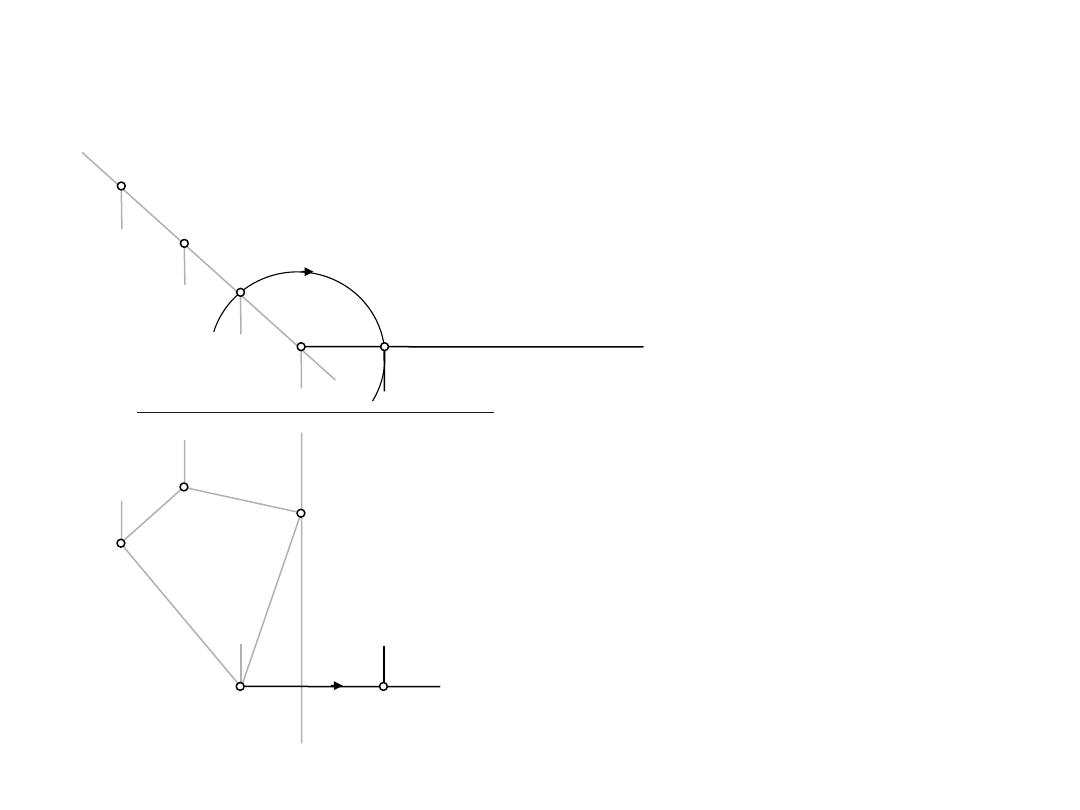
1.3.
Wyznaczyć rzeczywistą wielkość czworokąta ABCD
D:
a
=ABCD,
ap
2
l
p
2
A
l
A
1
=A
B'
1
B'
A'=A'
1
B"
l'
A"=l"=A"
1
C"
D"
a
"
D'
C'
B"
1
e
'
B
a
"
1
B
e
B
e
B
l
a
1
ll
p
1
B
1
e
B
~
~
=
p
2
'
X
12
=
p
1
"
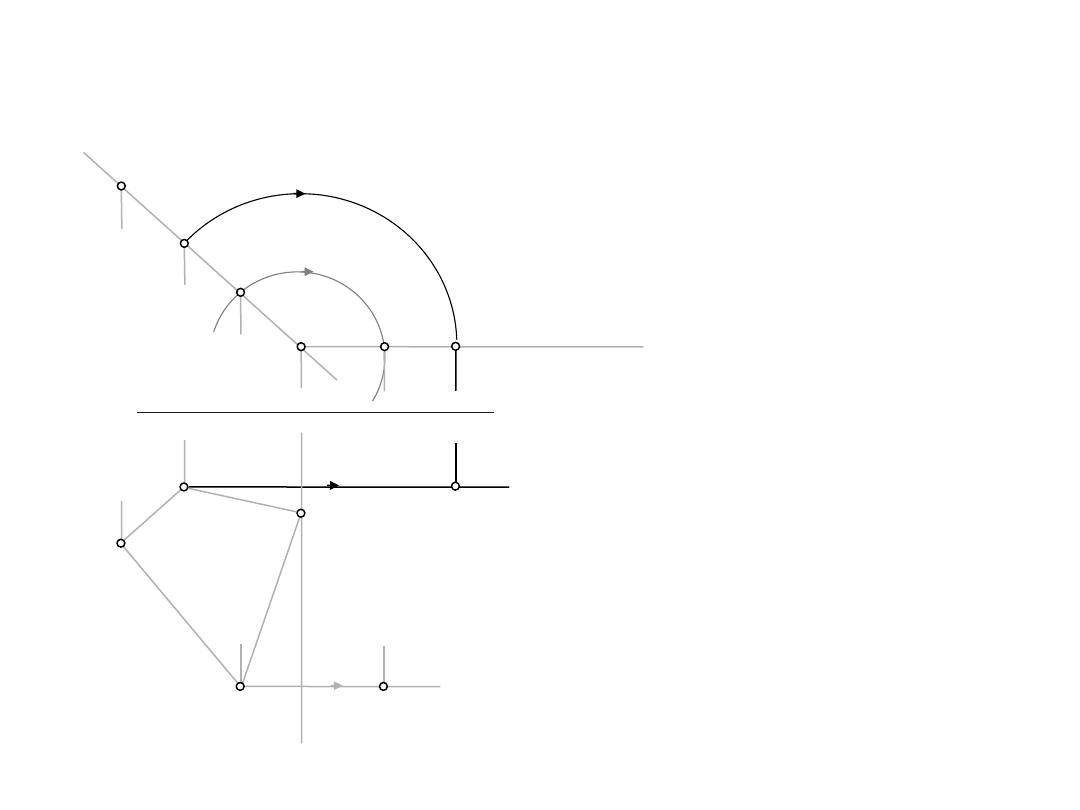
1.3.
Wyznaczyć rzeczywistą wielkość czworokąta ABCD
D:
a
=ABCD,
ap
2
l
p
2
A
l
A
1
=A
a
1
ll
p
1
B
e
B
e
B
l
B
1
e
B
B'
1
B'
A'=A'
1
B"
l'
A"=l"=A"
1
C"
D"
a
"
C'
1
D'
C'
B"
1
C"
1
e
'
C
e
'
B
a
"
1
~
~
~
=
p
2
'
X
12
=
p
1
"
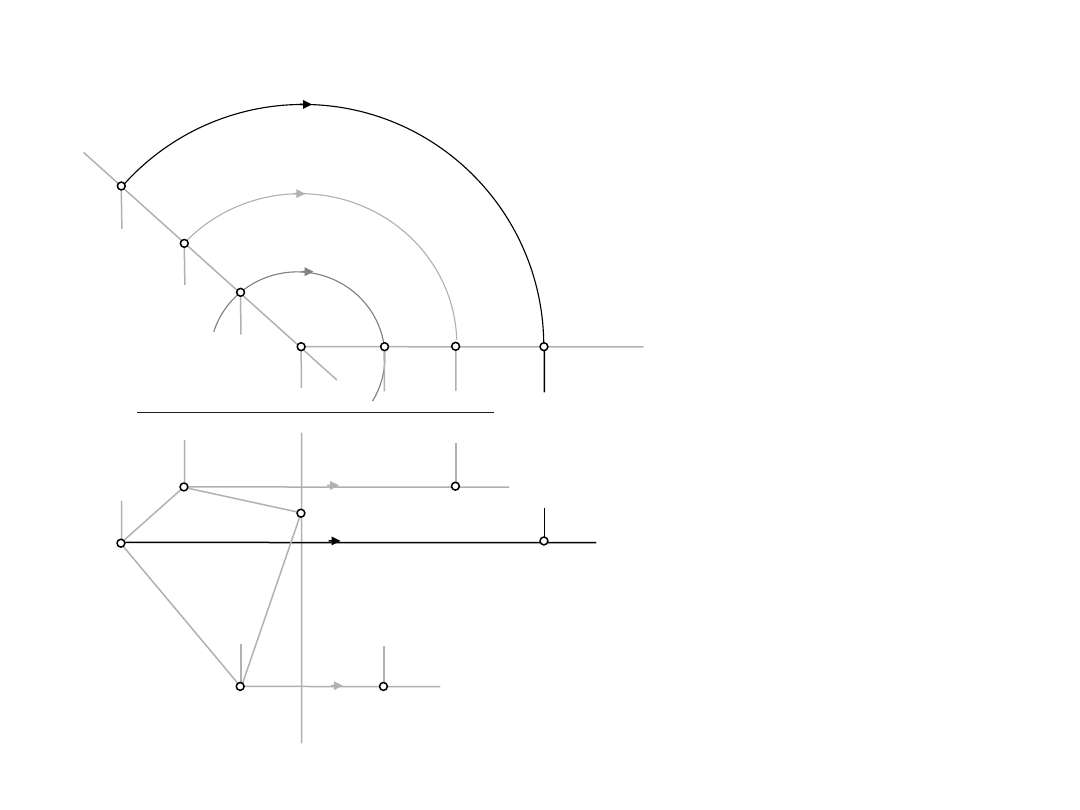
1.3.
Wyznaczyć rzeczywistą wielkość czworokąta ABCD
D:
a
=ABCD,
ap
2
l
p
2
A
l
A
1
=A
a
1
ll
p
1
B
e
B
e
B
l
B
1
e
B
B'
1
B'
A'=A'
1
B"
l'
A"=l"=A"
1
C"
D"
a
"
C'
1
D'
1
D'
C'
B"
1
C"
1
D"
1
e
'
C
e
'
D
e
'
B
a
"
1
~
~
~
~
=
p
2
'
X
12
=
p
1
"
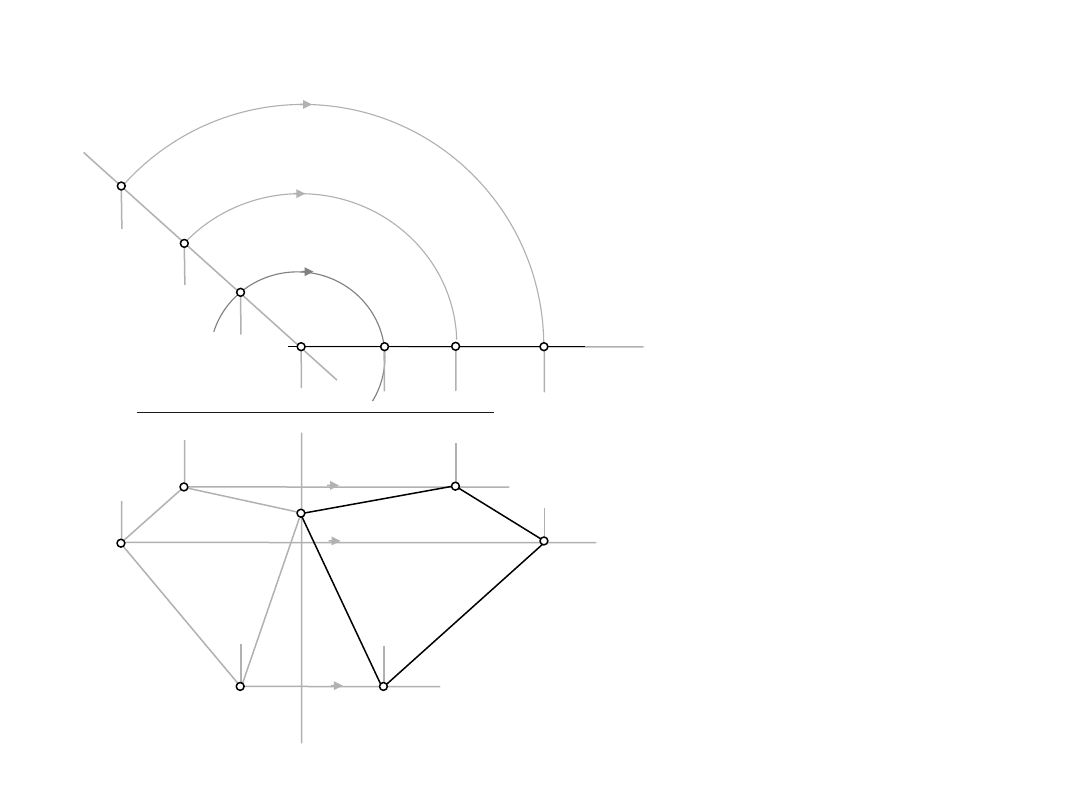
1.3.
Wyznaczyć rzeczywistą wielkość czworokąta ABCD
D:
a
=ABCD,
ap
2
l
p
2
A
l
A
1
=A
a
1
ll
p
1
B
e
B
e
B
l
B
1
e
B
B'
1
B'
A'=A'
1
B"
l'
A"=l"=A"
1
C"
D"
a
"
C'
1
D'
1
D'
C'
B"
1
C"
1
D"
1
a
"
1
e
'
C
e
'
D
e
'
B
a
1
=A
1
B
1
C
1
D
1
ABCD
~
~
~
~
=
p
2
'
X
12
=
p
1
"
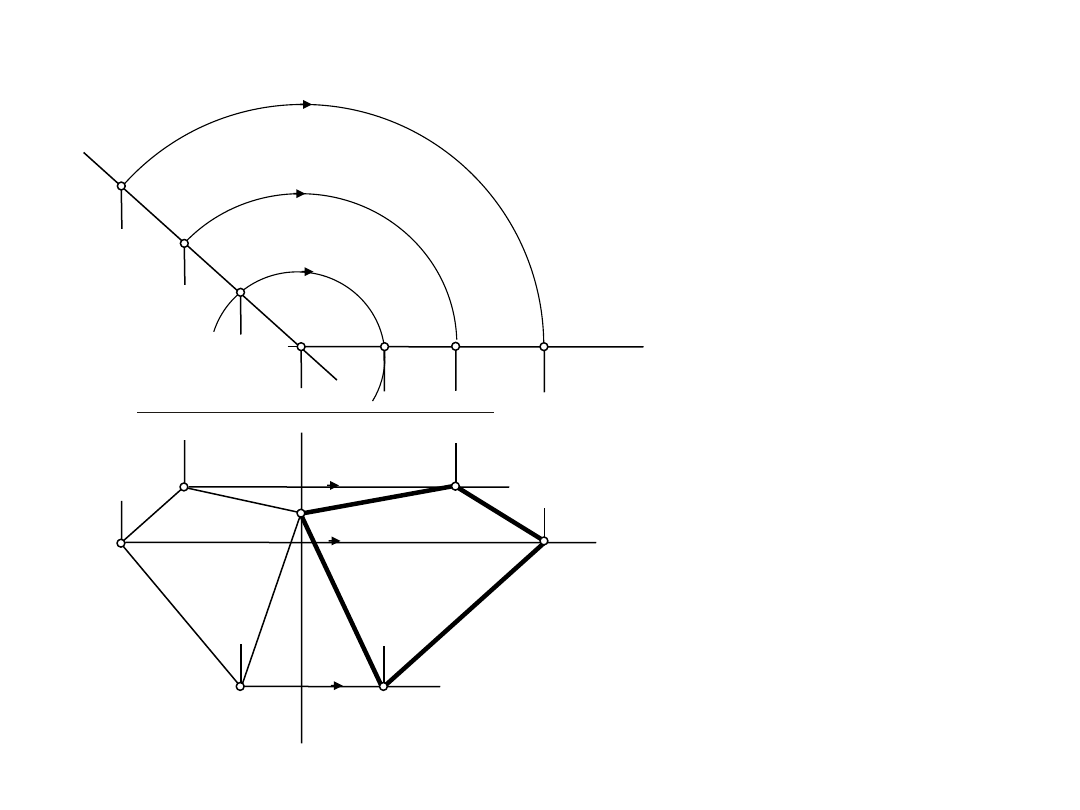
1.3.
Wyznaczyć rzeczywistą wielkość czworokąta ABCD
D:
a
=ABCD,
ap
2
l
p
2
A
l
A
1
=A
a
1
ll
p
1
B
e
B
e
B
l
B
1
e
B
a
1
=A
1
B
1
C
1
D
1
ABCD
B'
1
B'
A'=A'
1
B"
l'
A"=l"=A"
1
C"
D"
a
"
C'
1
D'
1
D'
C'
B"
1
C"
1
D"
1
a
"
1
e
'
C
e
'
D
e
'
B
a
1
ll
p
1
~
~
~
~
=
p
2
'
X
12
=
p
1
"

Temat:
Metoda rzutów Monge’a
Wielościany – ostrosłup
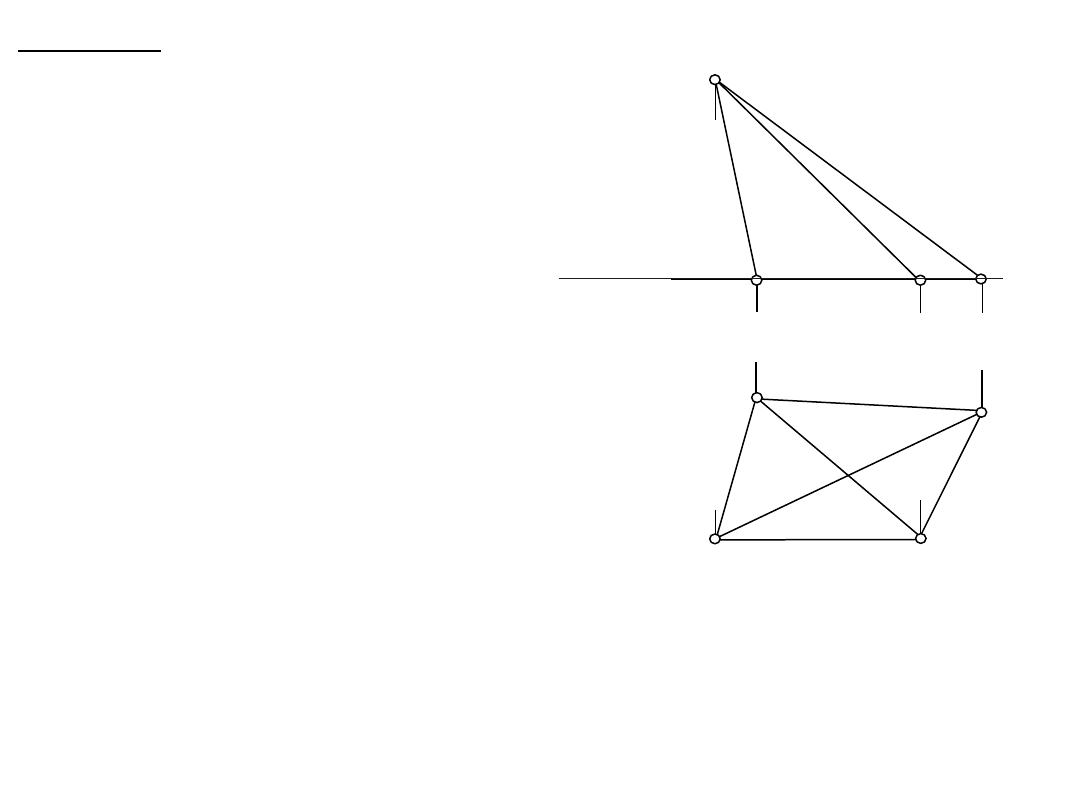
Wielościany
Ostrosłup
C"
B"
A"
W"
C'
A'
W'
B'
=
p
2
'
X
12
=
p
1
"
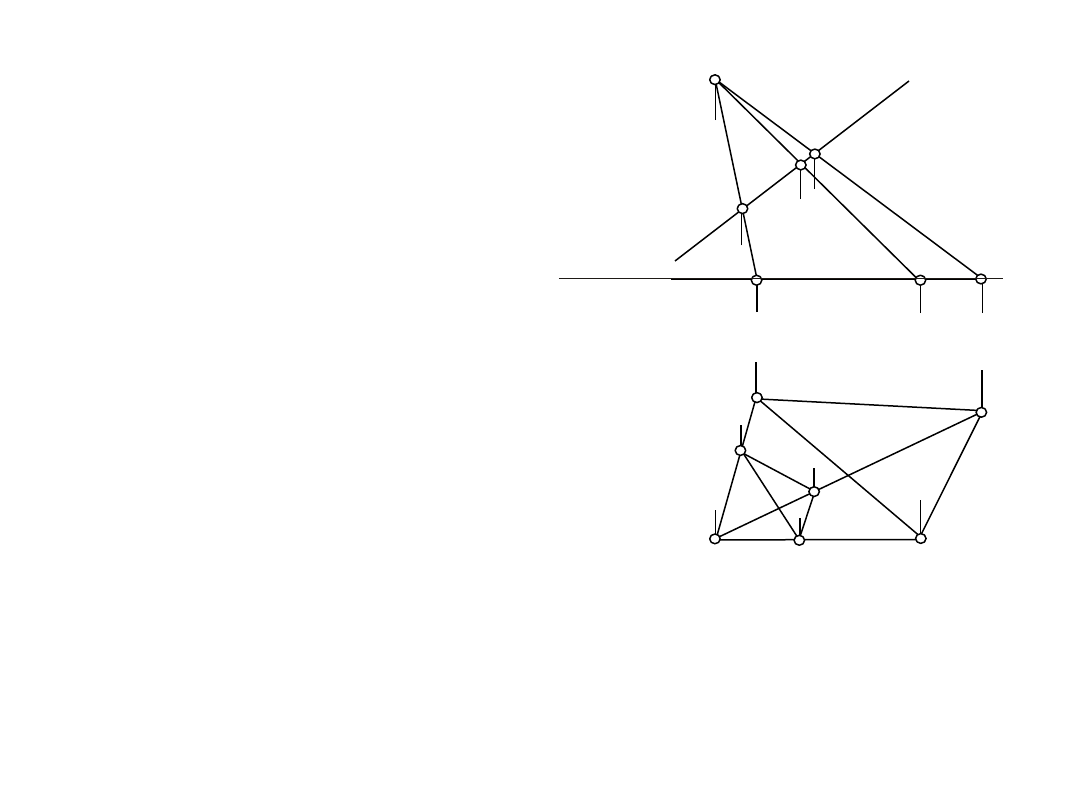
C"
a
"
B"
A"
W"
C'
A'
W'
1'
2'
3'
1"
2"
3"
B'
=
p
2
'
X
12
=
p
1
"
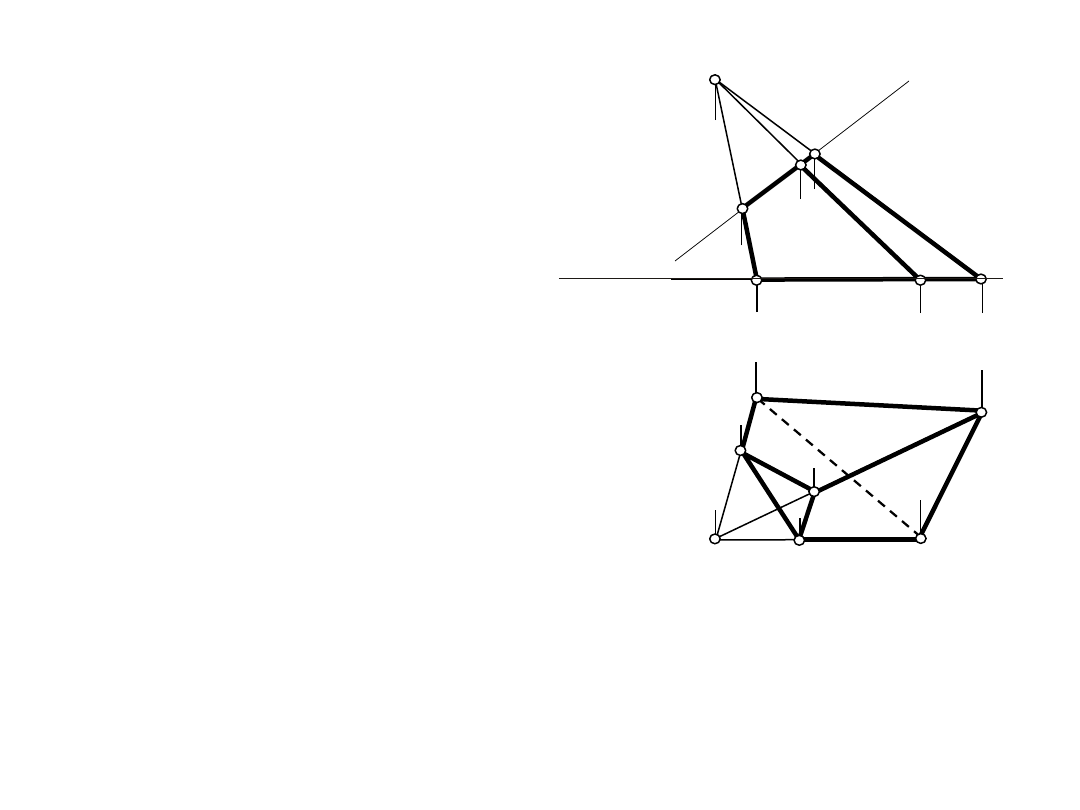
C"
a
"
B"
A"
W"
C'
A'
W'
1'
2'
3'
1"
2"
3"
B'
=
p
2
'
X
12
=
p
1
"
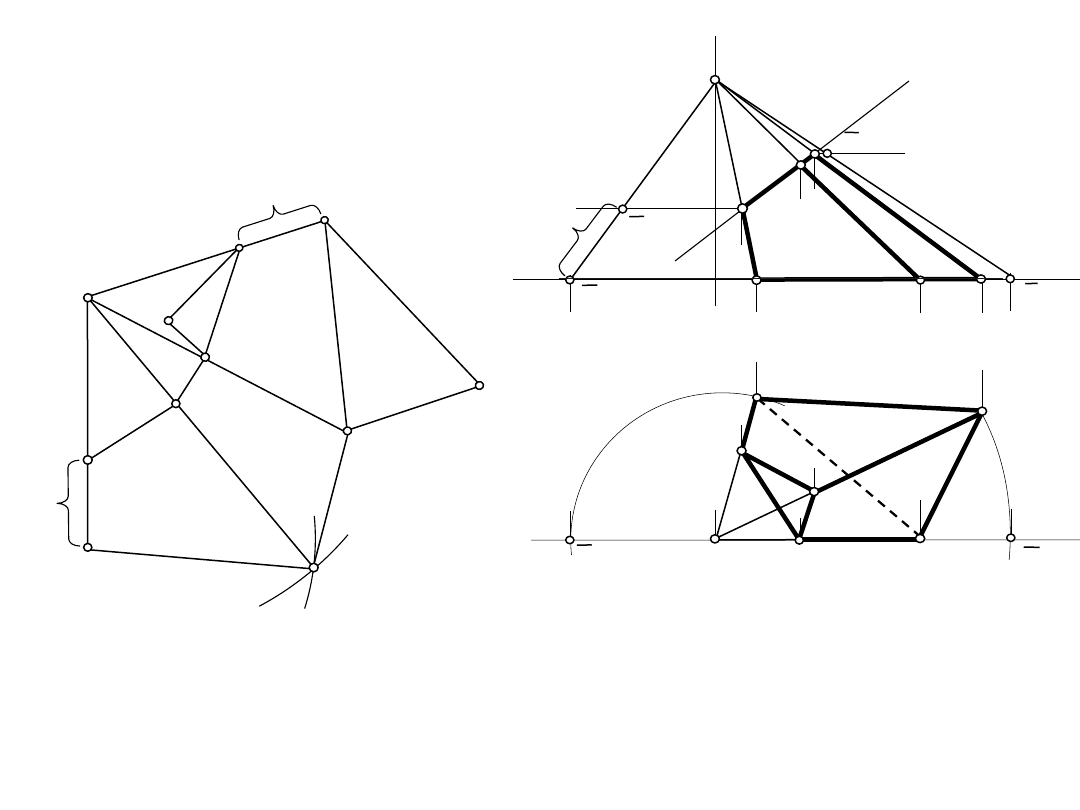
C"
a
"
B"
A"
W"
C'
B'
A'
W'
1'
2'
3'
1"
2"
3"
l"
t
'
A'
C'
e
A
"
A"
C"
e
1
"
1"
3"
e
3
"
A
A
B
C
W
1
1
3
2
3
=l'
C
=
p
2
'
X
12
=
p
1
"
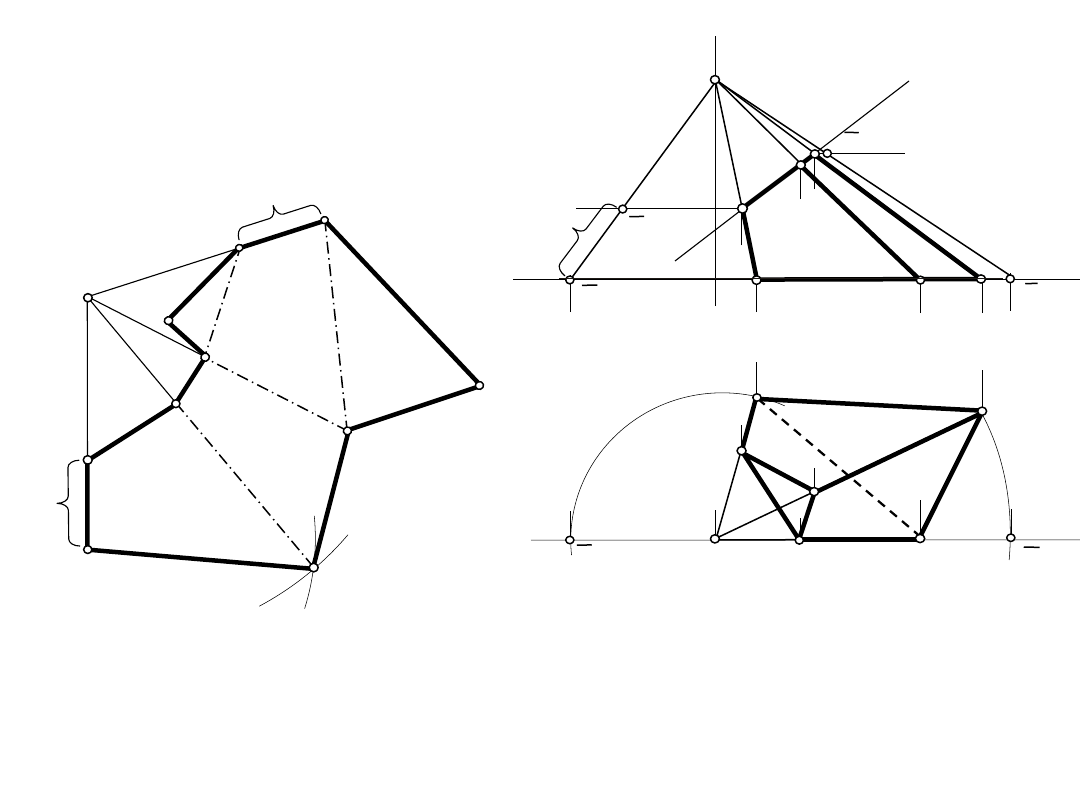
C"
a
"
B"
A"
W"
C'
B'
A'
W'
1'
2'
3'
1"
2"
3"
l"
t
'
A'
C'
e
A
"
A"
C"
e
1
"
1"
3"
e
3
"
A
A
B
C
W
1
1
3
2
3
=l'
C
=
p
2
'
X
12
=
p
1
"

Temat:
Metoda rzutów Monge’a
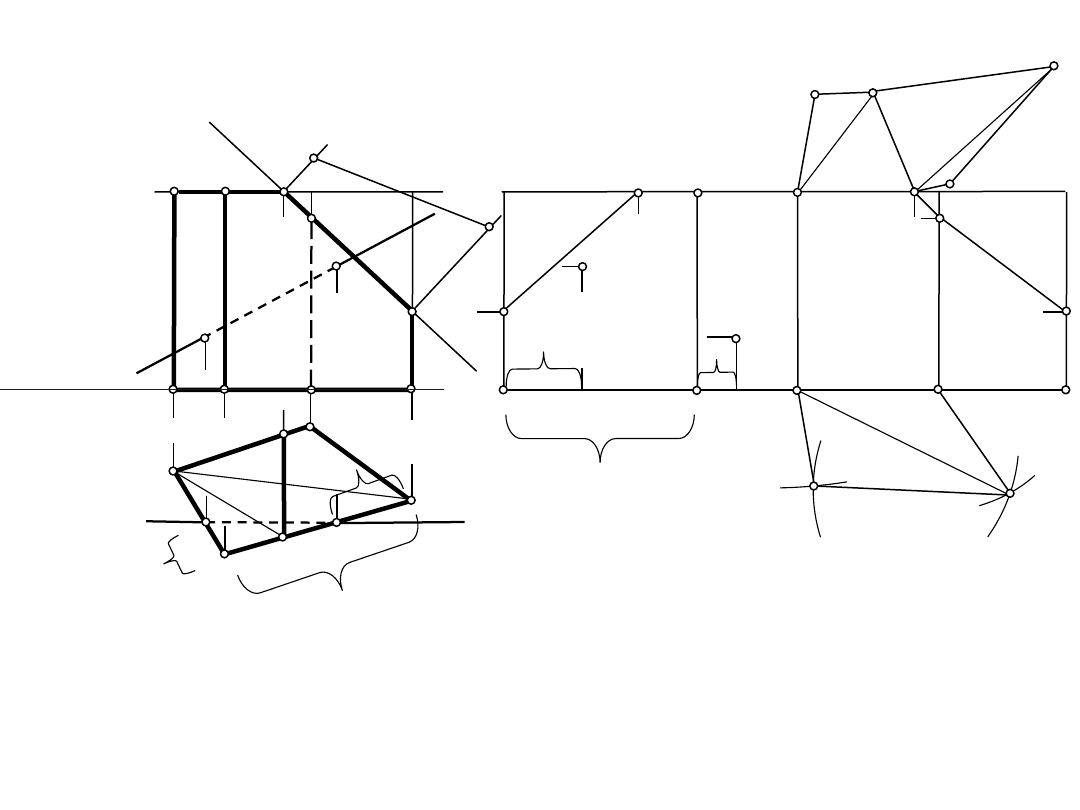
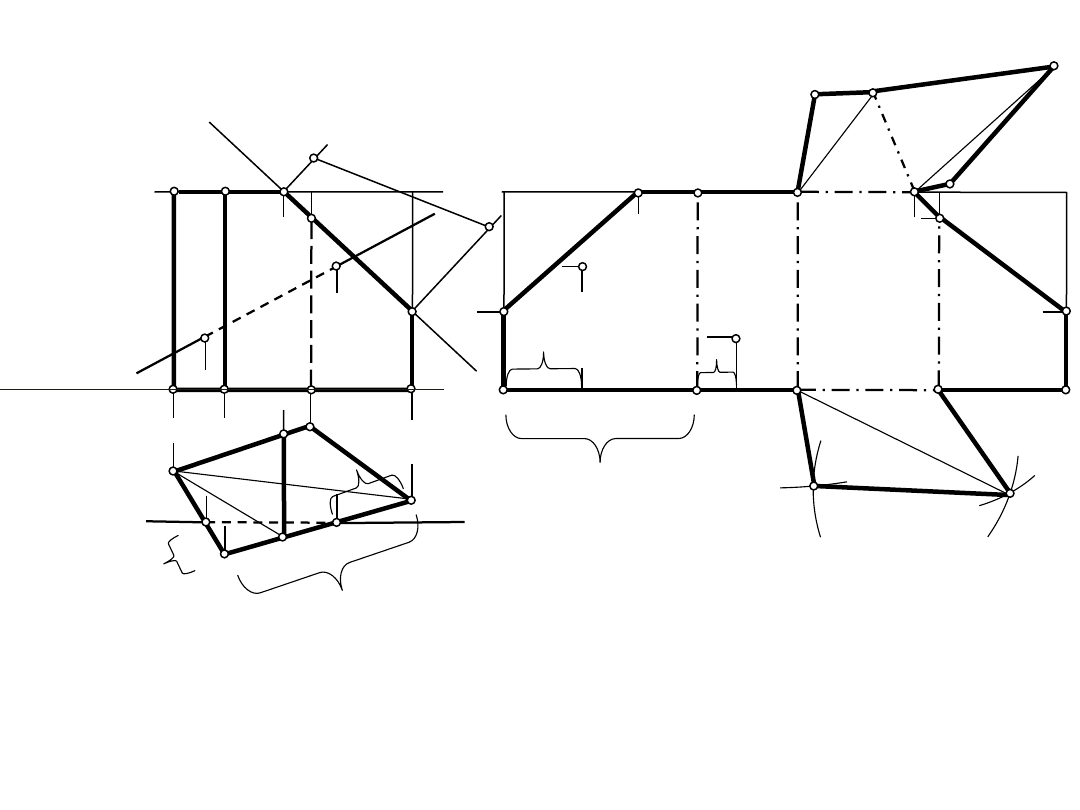
Wielościany – graniastosłup prosty
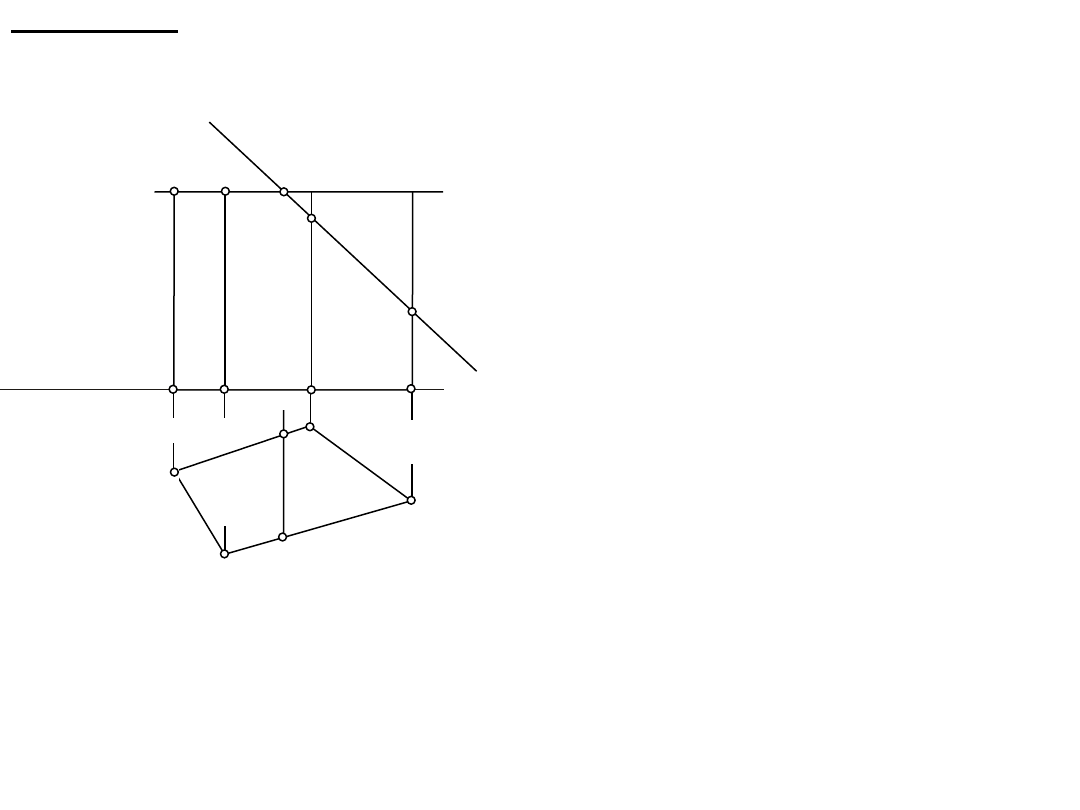
A'
Wielościany
Graniastosłup prosty
A"
C'
B'
D"
B"
C"
A
1
"
D
1
"
1"
2"
3"
a
"
4'
1'
b
"
=2'
=3'
A'=A
1
'
D'=D
1
'
1"=4"
=
p
2
'
X
12
=
p
1
"
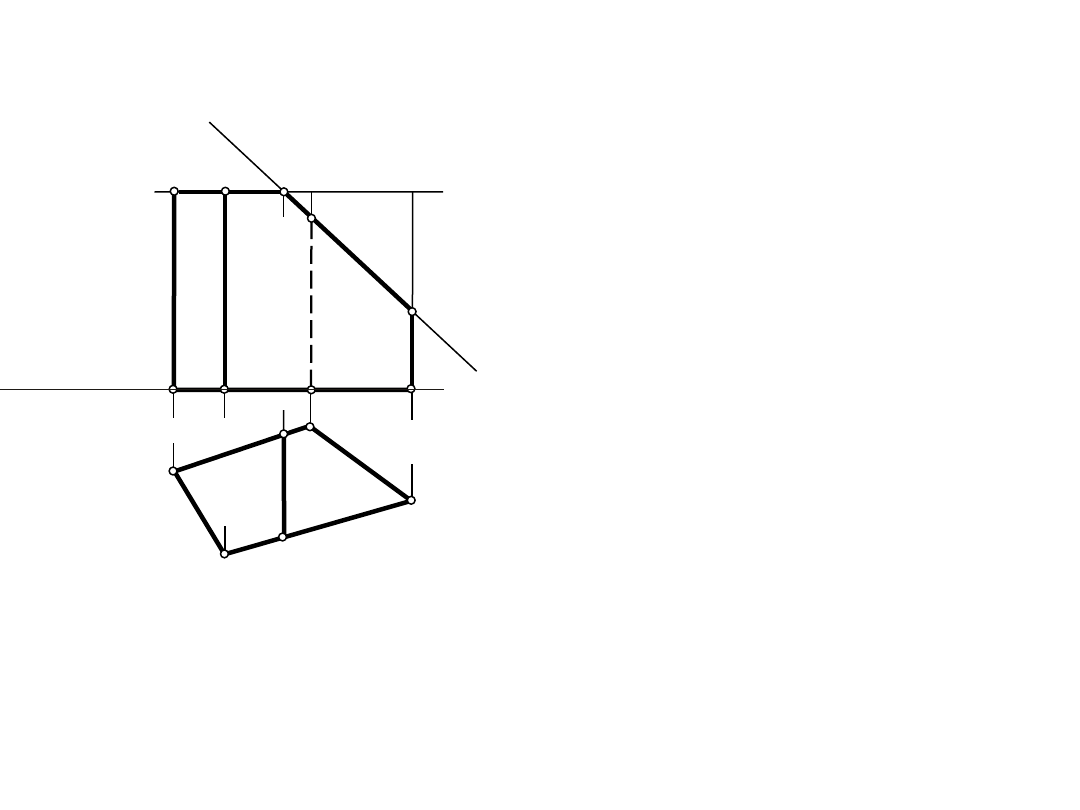
A"
D'=D
1
'
C'=3'
B'=2'
D"
B"
C"
A
1
"
D
1
"
1"=4"
2"
3"
a
"
4'
1'
b
"
A'=A
1
'
=
p
2
'
X
12
=
p
1
"
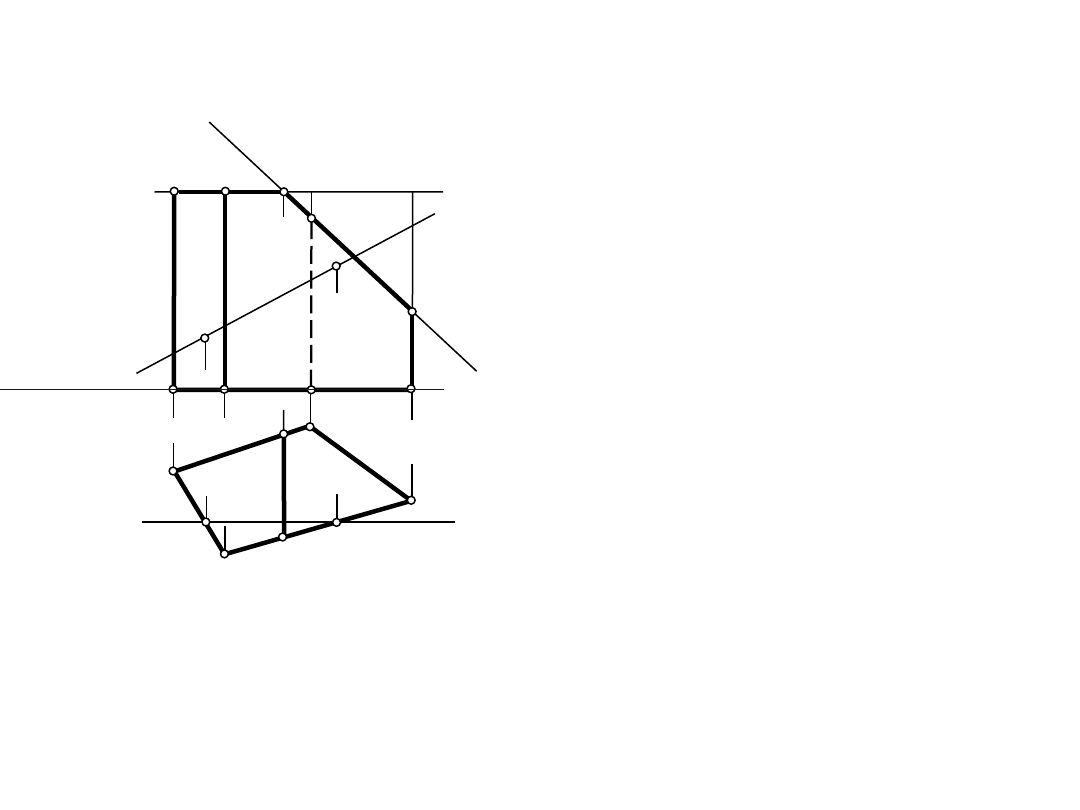
A"
C'=3'
B'=2'
D"
B"
C"
A
1
"
D
1
"
1"=4"
2"
3"
P
1
"
P
2
"
a
"
p"
p'
P
1
'
P
2
'
4'
1'
b
"
D'=D
1
'
A'=A
1
'
=
p
2
'
X
12
=
p
1
"
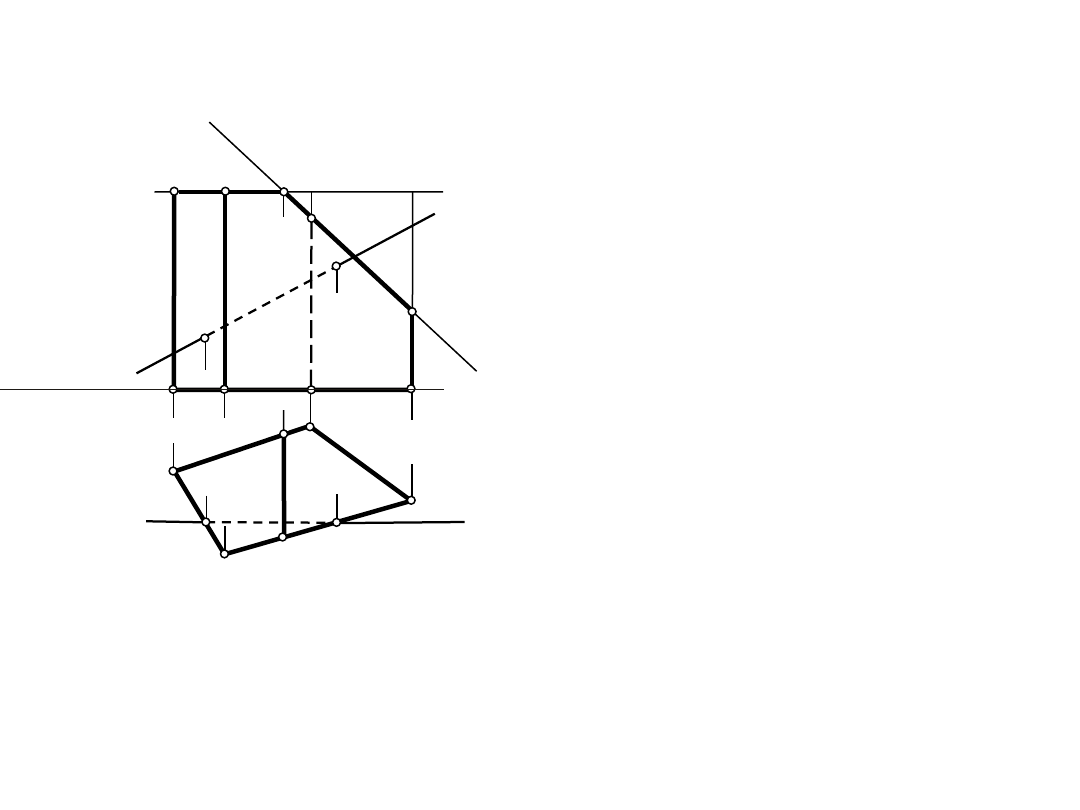
A"
C'=3'
B'=2'
D"
B"
C"
A
1
"
D
1
"
1"=4"
2"
3"
P
2
"
a
"
p"
p'
P
2
'
4'
1'
b
"
D'=D
1
'
A'=A
1
'
P
1
"
P
1
'
=
p
2
'
X
12
=
p
1
"
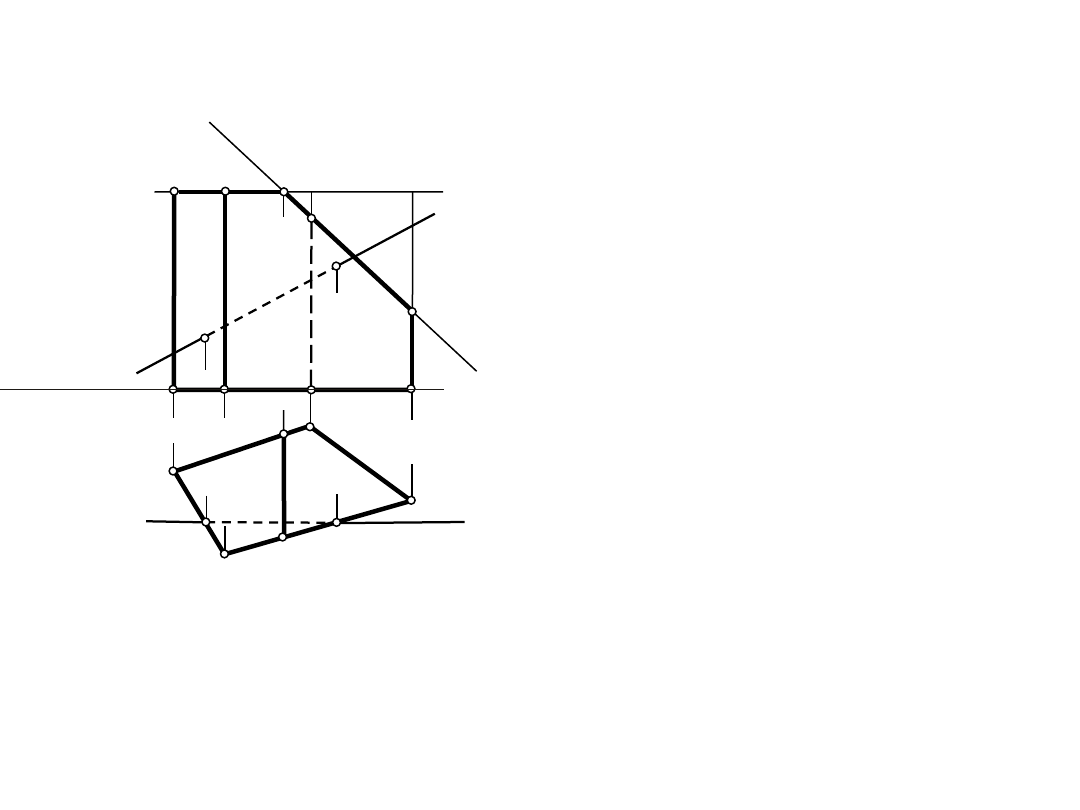
A"
C'=3'
B'=2'
D"
B"
C"
A
1
"
D
1
"
1"=4"
2"
3"
P
2
"
a
"
p"
p'
P
2
'
4'
1'
b
"
D'=D
1
'
A'=A
1
'
P
1
"
P
1
'
=
p
2
'
X
12
=
p
1
"
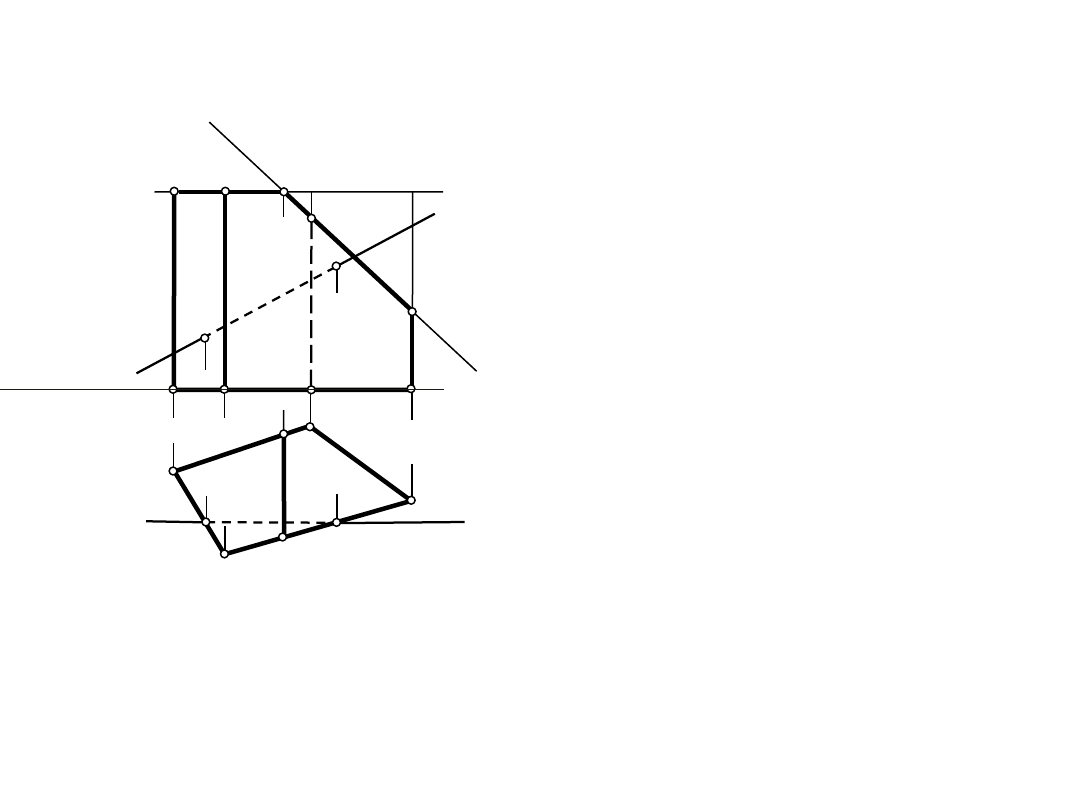
A"
C'=3'
B'=2'
D"
B"
C"
A
1
"
D
1
"
1"=4"
2"
3"
P
2
"
a
"
p"
p'
P
2
'
4'
1'
b
"
D'=D
1
'
A'=A
1
'
P
1
"
P
1
'
=
p
2
'
X
12
=
p
1
"
D'=D
1
'
A"
C'=3'
B'=2'
D"
B"
C"
A
1
"
D
1
"
1"=4"
1
x
2"
3"
3
x
P
2
"
a
"
p"
p'
P
2
'
4'
1'
C
B
A
D
C
C
D
3
4
D
1
A
1
P
2
P
1
1
4
D
1
2
3
b
"
A'=A
1
'
P
1
"
P
1
'
2
3
=
p
2
'
X
12
=
p
1
"
D'=D
1
'
A"
C'=3'
B'=2'
D"
B"
C"
A
1
"
D
1
"
1"=4"
1
x
2"
3"
3
x
P
2
"
a
"
p"
p'
P
2
'
4'
1'
C
B
A
D
C
C
D
3
4
D
1
A
1
P
2
3
1
4
D
1
2
b
"
A'=A
1
'
P
1
"
P
1
'
P
1
2
3
=
p
2
'
X
12
=
p
1
"

Temat:
Metoda rzutów Monge’a
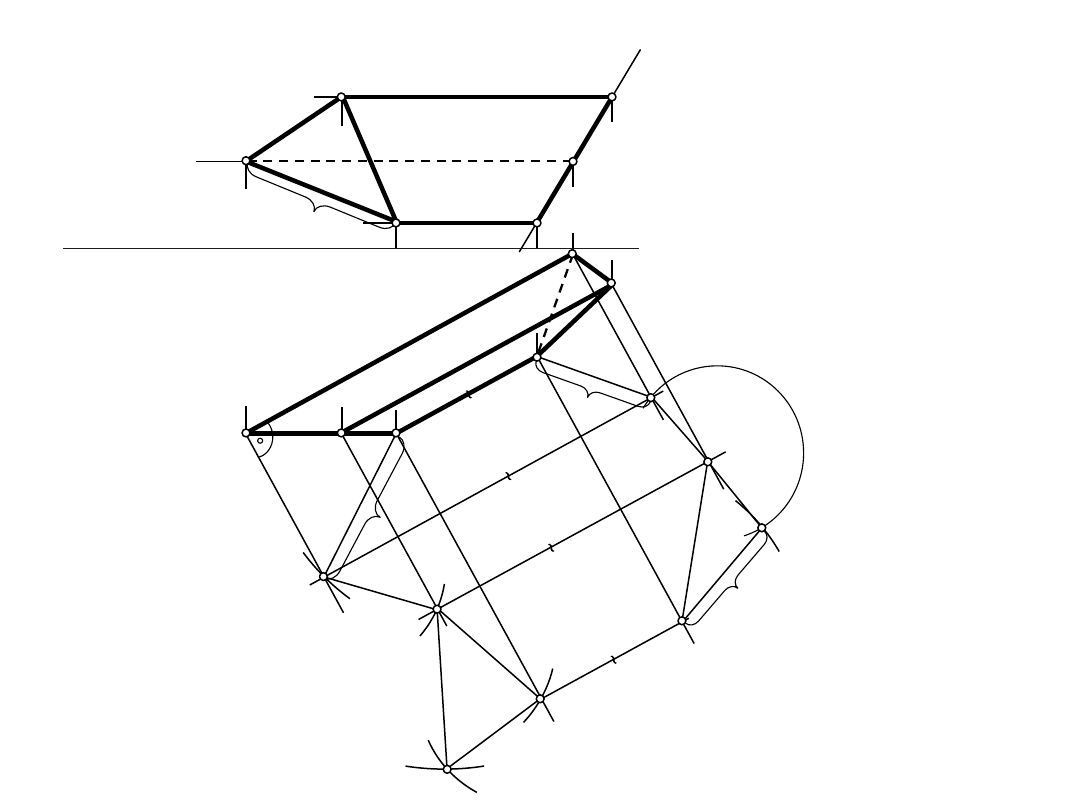
Wielościany – graniastosłup pochyły
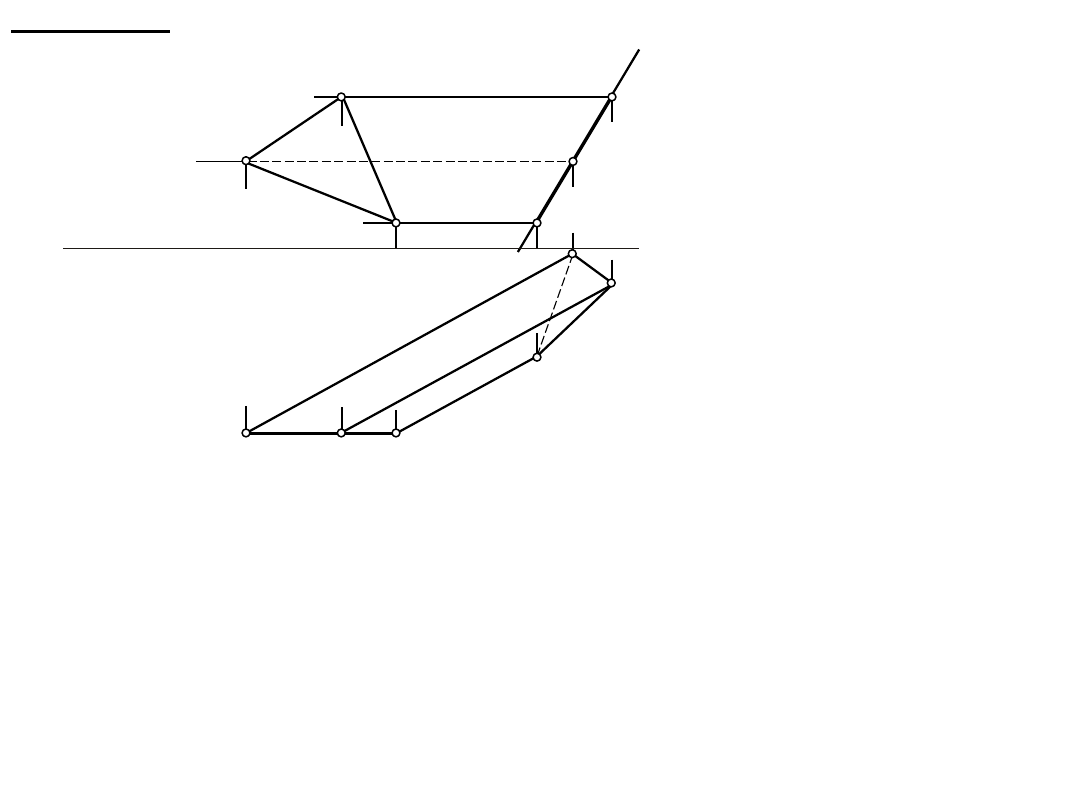
Wielościany
Graniastosłup pochyły
a
"
A'
C'
B'
A"
B"
C"
K"
L"
M"
M'
K'
L'
=
p
2
'
X
12
=
p
1
"
a
"
A'
C'
B'
A"
B"
C"
K"
L"
M"
M'
K'
L'
B
=C
=M
A
K
L
M
K
C
A
e
A
=
p
2
'
X
12
=
p
1
"
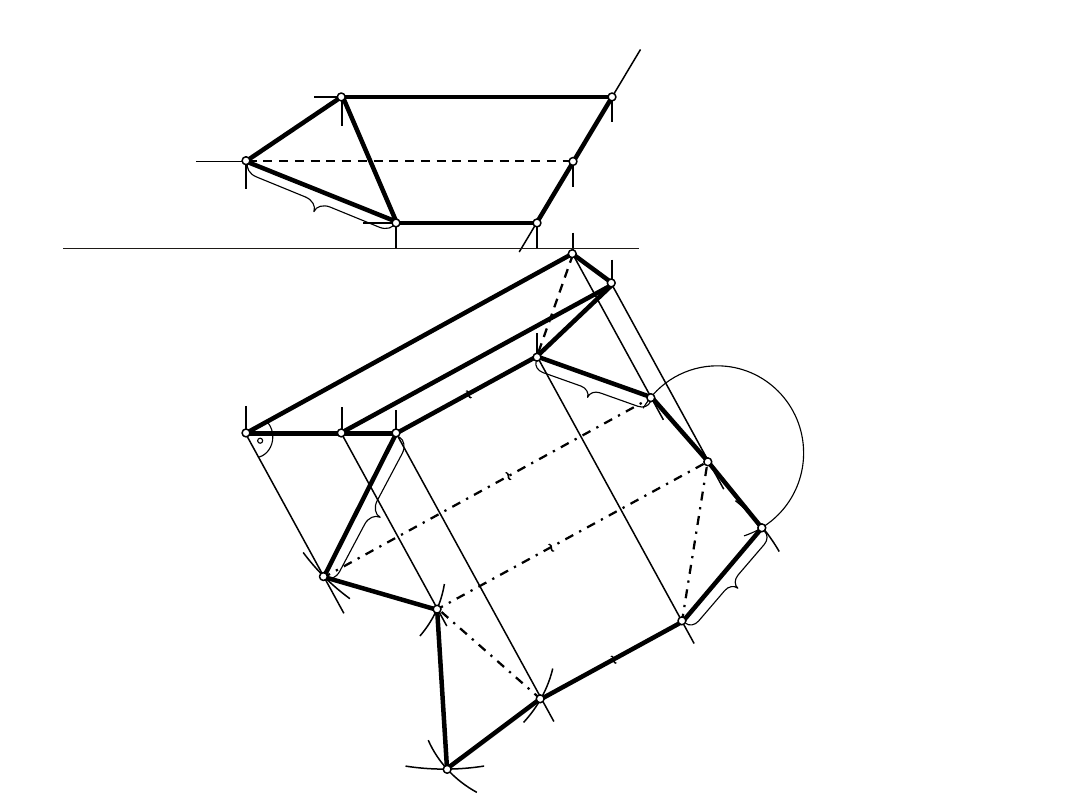
a
"
A'
C'
B'
A"
B"
C"
K"
L"
M"
M'
K'
L'
B
=C
=M
A
K
L
K
C
A
M
=
p
2
'
X
12
=
p
1
"
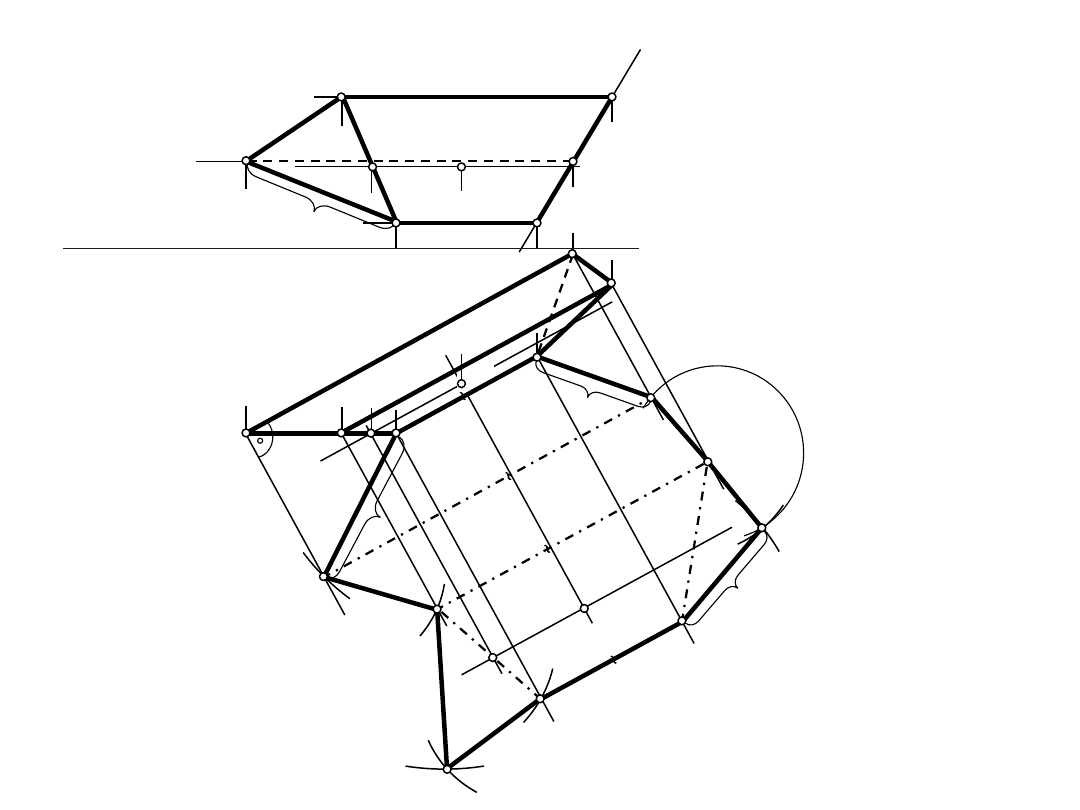
a
"
A'
C'
B'
A"
B"
C"
K"
L"
M"
M'
K'
L'
B
=C
=M
A
K
L
K
C
A
P
1
a
1"
a"
P"
1'
a'
P'
M
=
p
2
'
X
12
=
p
1
"
Wyszukiwarka
Podobne podstrony:
AiSD Wyklad4 dzienne id 53497 Nieznany (2)
3 Wyklad OiSE id 33284 Nieznany
or wyklad 4b id 339029 Nieznany
Materialy do wykladu nr 5 id 28 Nieznany
Finanse Wyklady FiR id 172193 Nieznany
AiSD Wyklad9 dzienne id 53501 Nieznany
Folie wyklad2 Krakow id 286699 Nieznany
OP wyklad nr 3 id 335762 Nieznany
prc wyklad zagad 5 id 388963 Nieznany
hydrologia wyklad 06 id 207845 Nieznany
hydrologia wyklad 05 id 207839 Nieznany
F II wyklad 11 id 167234 Nieznany
BHP Wyklad 10 id 84576 Nieznany (2)
AiSD Wyklad11 dzienne id 53494 Nieznany
elektro wyklad 03b id 157928 Nieznany
fcs wyklad comment 2 2 id 16907 Nieznany
5 wyklad ciagi id 40772 Nieznany (2)
więcej podobnych podstron