Zestaw 1.

1. rednia pr dko poci gu osobowego v = 54 km/h. Wyrazi t pr dko w cm/s.

2. Mi dzy dwoma punktami na rzece oddalonymi od siebie o L = 100 km kursuje kuter.
Drog t przebywa on z pr dem w ci gu czasu t

1

= 4 h, a w kierunku przeciwnym w czasie t

2

=

10 h. Znale pr dko pr du w rzece

υ

1

i pr dko kutra wzgl dem wody

υ

2

.

3. Na szynach porusza si pusty wóz kolejowy ruchem jednostajnym z pr dko ci v = 10 m/s.
Nagle pad strza rewolwerowy w kierunku prostopad ym do toru i w p aszczy nie poziomej.
Kula przebi a obie ciany wozu. Stwierdzono, e otwór wylotowy by przesuni ty wstecz w
stosunku do otworu wlotowego o a = 12.5 cm. Szeroko wozu d = 2 m. Obliczy pr dko
kuli.

4. Szos biegn

równolegle do toru kolejowego jedzie cyklista na rowerze ze redni

pr dko ci 12 km/h. W pewnej chwili dogania go poci g po pieszny d ugo ci 70 m i mija po
up ywie 4 s. Obliczy pr dko tego poci gu.

5. Znale czas, po up ywie którego poci g o d ugo ci L = 300 m poruszaj cy si z
pr dko ci

υ

1

= 75 km/h minie pasa era znajduj cego si w poci gu jad cym w przeciwnym

kierunku z pr dko ci

υ

2

= 54 km/h.

6. Wio larz mo e nada

ódce pr dko 2.5 m/s. Pr dko pr du jest 7.2 km/h. W jakim

kierunku powinien wio larz odbi od brzegu, aby przejecha rzek w poprzek w kierunku
prostopad ym do jej biegu.

7. Równanie ruchu s = 15 t + 0.4 t

2

, gdzie t w sekundach, a s w metrach. Znale pr dko

pocz tkow

υ

0

, przyspieszenie ruchu a, pr dko

υ

2

po up ywie 15 s oraz sporz dzi wykres

zale no ci pr dko ci od czasu.

8. Podczas pierwszych 4 sekund trwania ruchu samochód przejecha drog 10 m. Jak drog
przejedzie podczas 8 sekund? Jak drog przejedzie w ci gu 8-smej sekundy?
-----------------------------------------------------------------------------------------------------------------

9. Sporz dzi wykres przebytej drogi i przyspieszenia pewnego cia a w zale no ci od czasu,
je li jego pr dko

υ

[m/s] jest przedstawiona na rysunku jako funkcja czasu t [s].

v

t

1

1

10. Z balonu znajduj cego si na wysoko ci h = 300 m spad kamie . W ci gu, jakiego czasu
kamie b dzie spada na ziemi , je li:

a.) balon jest nieruchomy,
b.) balon podnosi si z pr dko ci

υ

0

= 5 m/s,

c.) balon opada z pr dko ci

υ

0

= 5 m/s ?

Opór powietrza zaniedba .

(1500cm/s)

(7,5 17,5)

(160)

20 5/6

8,37

(9,37 40)

(7,7
8,72
7,3)

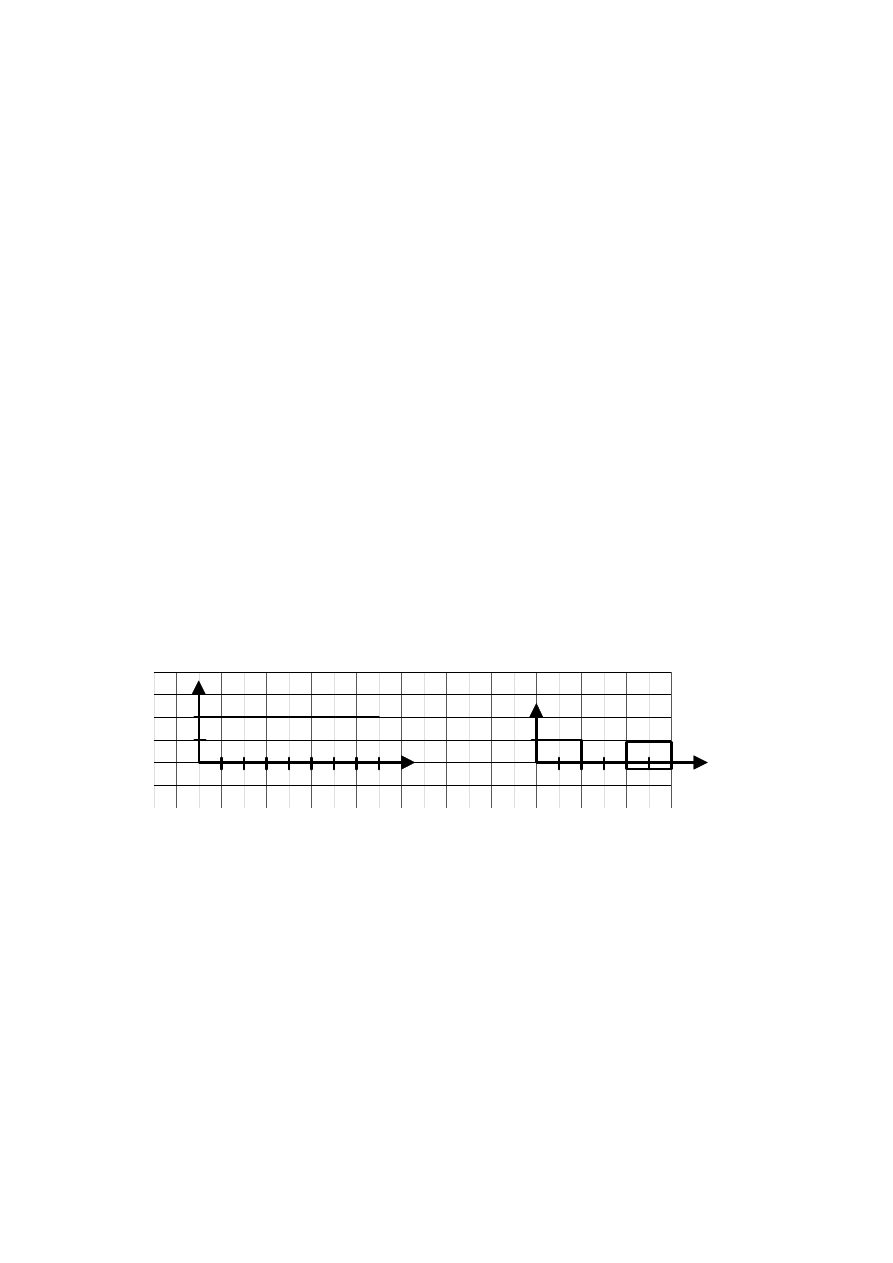
11 Cia o swobodnie spadaj ce przeby o w ostatniej sekundzie drog s = 23.1 m. Z jakiej
wysoko ci spad o cia o?

12. Z wysoko ci h

1

= 40 m spada cia o A. Po up ywie czasu t = 2 s zacz o spada z tej samej

wysoko ci h

1

cia o B. Na jakiej wysoko ci znajdowa si b dzie cia o B w chwili upadku

cia a A na ziemi .

13. Strza a wypuszczona pionowo do góry z pr dko ci

υ

0

= 30 m/s trafia w cel po up ywie

czasu, t = 2 s. Na jakiej wysoko ci znajduje si cel i z jak pr dko ci strza a go osi gn a?

14. Samolot startuj c przebiega po betonowej nawierzchni drog s = 790 m i w chwili
oderwania si od ziemi posiada pr dko

υ

= 240 km/h. Ile czasu trwa przebieg i jakie jest

przyspieszenie samolotu podczas rozbiegu? Zak adamy ruch prostoliniowy jednostajnie
zmienny.

15. Samochód osobowy przebywa tras z odzi do Warszawy z pr dko ci

υ

1

= 80 km/h, a z

Warszawy do odzi z pr dko ci

υ

2

= 100 km/h. Obliczy

redni pr dko samochodu na

ca ej trasie z odzi do Warszawy i z powrotem.

16. Cia o spadaj ce swobodnie ma w punkcie A pr dko

υ

1

= 34.43 m/s, a w punkcie B

υ

2

=

49.05 m/s. Jaka jest d ugo odcinka AB i w jakim czasie cia o przeby o ten odcinek?

17. Znale pr dko ko cow i redni cia a spadaj cego swobodnie z wysoko ci h = 200 m.

18. Poda wykres drogi i pr dko ci w zale no ci od czasu t [s], je li wykresy przyspieszenia
cia a [m/s

2

] maj posta przedstawion na rysunku. Pr dko pocz tkowa we wszystkich

przypadkach jest równa zeru.

a

t

1

1

a

t

1

1

19. Rozg

nia w Krakowie nadaje koncert z Wawelu. Koncertu s uchaj bezpo rednio na

Wawelu z odleg

ci 25 m oraz przez radio w Pary u. Gdzie s ysz muzyk wcze niej?

Odleg

z Krakowa do Pary a wynosi oko o 1300 km, pr dko g osu w powietrzu jest 340

m/s, a pr dko fal radiowych wynosi 300000 km/s.

20. Jak wysoko wzniesie si cia o rzucone pionowo do góry z pr dko ci pocz tkow v =
42 m/s? Po ilu sekundach spadnie na ziemi cia o rzucone pionowo do góry z pr dko ci
pocz tkow v = 24.5 m/s?

(2,81)

(36,6)

(40
10)

(24 2,8)

(89)

(1,5)

(63 31,75)

(88,2 4,9)

m

0

0

m

1

m

2

H

R

m

Zestaw 2.

1. Kula o ci arze P = 50 kG wisi na lince. Za pomoc drugiej poziomej linki odchylono t
kul tak, e pierwsza linka utworzy a z pionem k t

α

= 30

°

. Obliczy napi cie obu linek.

2. Prostopad

cian o podstawie kwadratowej i wysoko ci n = 4 razy wi kszej od kraw dzi

podstawy stoi na poziomej desce. Desk unosimy jednym ko cem zwolna do góry. Przy
jakim wspó czynniku tarcia zacznie si ten prostopad

cian zsuwa , jednocze nie nie

wywracaj c?

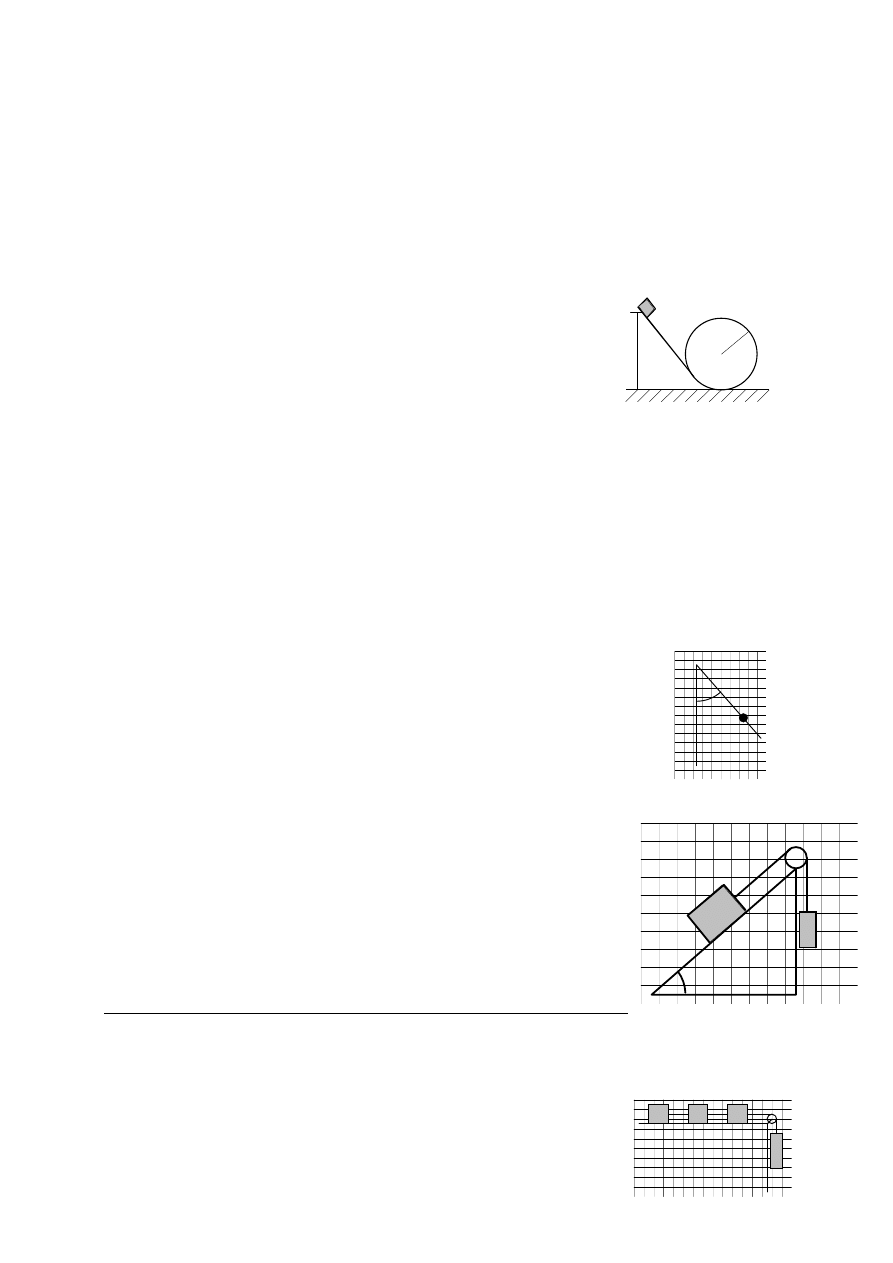
3. Z jakiej wysoko ci H musi by puszczone cia o o masie m, aby
nie spad o pod dzia aniem si y ci ko ci (patrz rysunek). Promie

tli wynosi R.

4. Na równi pochy ej nachylonej do poziomu pod k tem

α

= 30

°

znajduje si g adkie cia o o ci arze P = 50 kG, utrzymywane w równowadze przez si
równoleg do d ugo ci równi. Obliczy wielko ci tej si y oraz nacisk, jaki wywiera cia o na
równi .

5. Ma e cia o stacza si po powierzchni kuli o promieniu R. Na jakiej wysoko ci od
wierzcho ka kuli cia o oderwie si od jej powierzchni? Tarcie zaniedba .

6. Na nici o wytrzyma

ci F = 40 N ch opiec obraca w p aszczy nie pionowej mas m =

1 kg. O obrotu znajduje si w odleg

ci h = 4 m od ziemi, promie okr gu, jaki opisuje

kamie R = 1 m. Z jak pr dko ci k tow musi ch opiec obraca kamie , aby ni si
zerwa a? W jakiej odleg

ci s od ch opca, licz c w p aszczy nie poziomej, upadnie kamie ?

7*. Niewa ki pr t 00 zgi ty jak na rysunku obraca si z pr dko ci k tow

ω

wokó osi 00. Na pr t nasuni to wydr on kulk o masie m. Znale , w
jakiej odleg

ci l od punktu 0 znajduje si po

enie równowagi kulki, je li

wspó czynnik tarcia mi dzy kulk a pr tem wynosi f.

8. Na poziomej tarczy zamocowano na statywie ni o d ugo ci l z kulk o
masie m na ko cu. Z jak pr dko ci k tow

ω

obraca si tarcza, je eli ni tworzy z pionem

t

α

= 45

°

, l = 6 cm, odleg

statywu od rodka osi obrotu x = 10

cm.

9. Na górnym brzegu równi pochy ej przymocowany jest nieruchomy
blok, przez który przerzucono ni . Na jednym jej ko cu przywi zane
jest cia o o masie m

1

, le ce na równi a na drugim ko cu nici wisi

ci ar o masie m

2

. Z jakim przyspieszeniem a poruszaj si ci arki i

jakie jest napr enie nici N? Równia pochy a tworzy z pionem k t

α

.

Wspó czynnik tarcia mi dzy cia em a równi wynosi f.

10. Trzy odzie o jednakowym ci arze P p yn jedna za drug z jednakow pr dko ci

υ

. Ze

rodkowej odzi przerzucono jednocze nie do przedniej i tylnej odzi ci ary P

1

z pr dko ci

u wzgl dem odzi rodkowej. Jakie b

pr dko ci odzi po przerzuceniu ci arów?

11. Do masy m

1

le cej na stole przymocowano ni mi jedna za drug

masy m

2

i m

3

. Masa klocka zwisaj cego swobodnie wynosi M (patrz

m

3

m

2

m

1

M

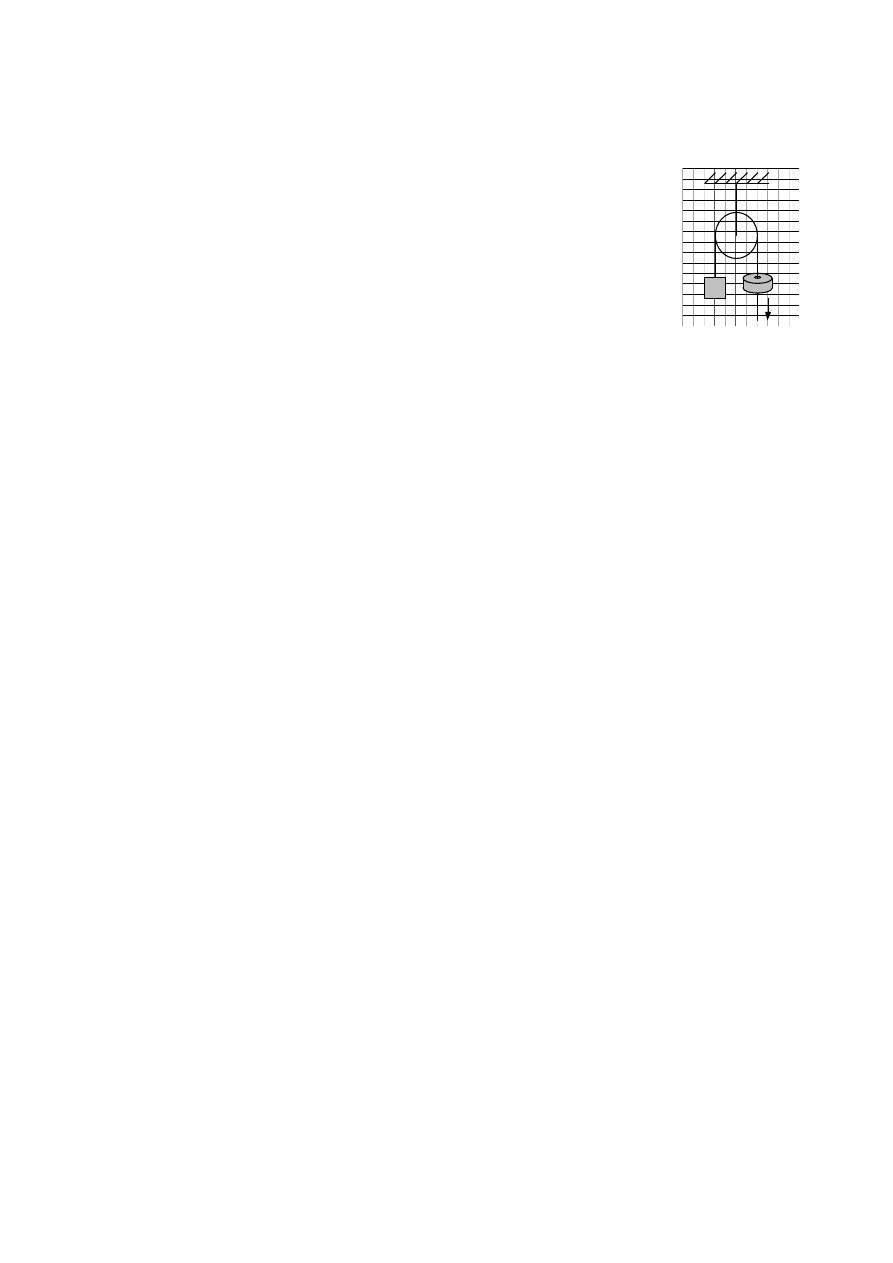
rysunek). Znale przyspieszenie a uk adu. Znale napr enia wszystkich nici. Tarcie
zaniedba .

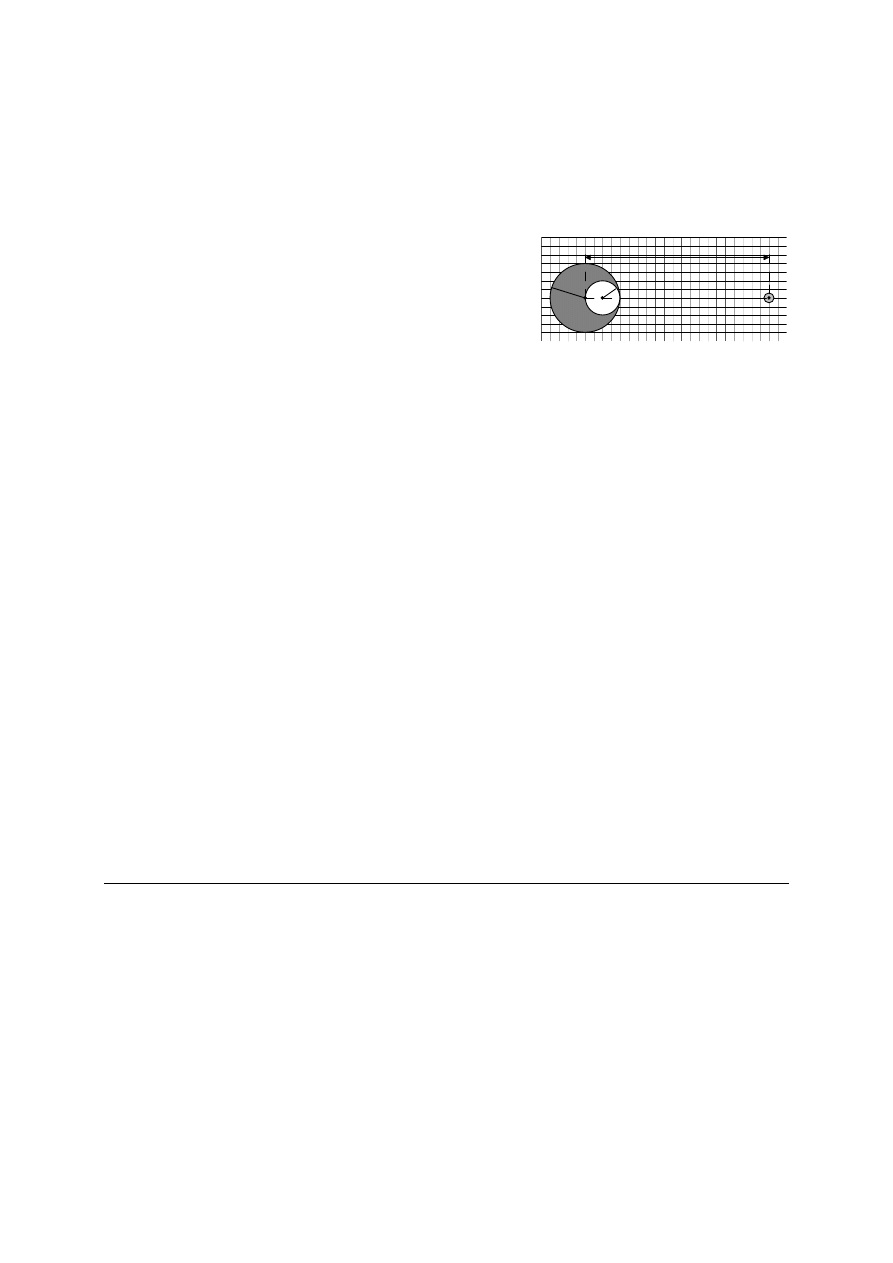
12*. Przez lekki blok przerzucony jest sznurek. Na jednym jego ko cu wisi
ci ar o masie m

1

. Wzd

drugiej po owy sznurka zsuwa si pier cie o

masie m

2

ze sta ym wzgl dem sznurka przyspieszeniem a

2

. Znale

przyspieszenie a

1

masy m

1

i si tarcia R pier cienia o sznurek. Mas sznurka

mo na zaniedba .

13. Ze swobodnie ze lizguj cego si po równi pochy ej dzia a, które przeby o
ju drog l oddano wystrza w kierunku poziomym. Jaka powinna by
pr dko

υ

pocisku, aby dzia o po wystrzale zatrzyma o si ? Wyrazi szukan pr dko

υ

pocisku za po rednictwem jego masy m, masy dzia a M i k ta nachylenia

α

równi wzgl dem

poziomu. Zak adamy, e m jest mniejsze od M.

14. Na klin o masie M stoj cy nieruchomo pada poziomo lec ca kula o masie m i po
zderzeniu spr

ystym z powierzchni klina odskakuje pionowo do góry. Na jak wysoko

podniesie si kula, je li pr dko klina po zderzeniu wynosi V? Tarcie zaniedba .

15. Dwie deski nachylone jedna do drugiej pod k tem

α

= 60

°

tworz korytko, przy czym

ka da cianka korytka nachylona jest do poziomu równie pod k tem

α

= 60

°

. W korytku

le y kula o ci arze P =10 k G. Jaki nacisk wywiera ta kula na ciany korytka?

16. Przy jakim k cie nachylenia równi zsuwaj ce si po niej cia a zu ywaj n = 2 razy wi cej
czasu ni przy swobodnym spadku z tej samej wysoko ci?

17. W ci gu czasu t = 1 s cia o zsuwaj ce si wzd

równi pochy ej przeby o drog s =

200 cm.. Obliczy k t nachylenia tej równi pochy ej do poziomu.

18. Z jakim opó nieniem posuwa si cia o po równi pochy ej ku górze, je eli wspó czynnik
tarcia f = 0,2, a k t nachylenia równi do poziomu

α

= 30

°

?

m

1

m

2

a

2

Zestaw 3.

1. Promie Ziemi R = 6370 km. Jak zmieni si przyspieszenie si y ci ko ci: a.) przy
zanurzeniu a do rodka kuli ziemskiej, b.) przy oddalaniu si od powierzchni Ziemi a do
odleg

ci równej 5-ciu promieniom Ziemi.

2. W metalowej kuli o promieniu R i masie M wydr ono
mniejsz kul o promieniu r = R/2, w sposób
uwidoczniony na rysunku. Obliczy si , z jak b dzie
dzia

pozosta a cz

du ej kuli na ma kuleczk o

masie m, znajduj

si w odleg

ci d od rodka du ej

kuli.

3. Sztuczny satelita Ziemi porusza si na wysoko ci h = 670 km. Znale pr dko oraz czas
obiegu sputnika wokó Ziemi. Promie Ziemi R = 6370 km.

4. Cia o o g sto ci

ξ

1

= 0.8 g/cm

3

zsuwa si bez tarcia z równi pochy ej o wysoko ci h = 3 m i

wpada u jej podstawy do wody o g sto ci

ξ

2

= 1 g/cm

3

. Jak daleko wyp ynie to cia o z wody ?

Równia tworzy z poziomem k t

α

= 30

°

.

5. Cel po

ony na wzgórzu wida z miejsca gdzie stoi dzia o pod k tem

α

wzgl dem

poziomu. Odleg

liczona w kierunku poziomym od dzia a do celu wynosi L. Cel jest

ostrzeliwany przy k cie

β

dzia a wzgl dem poziomu. Wyznaczy pr dko

υ

0

pocisku, który

trafi w cel.

6. Sanki ze lizguj si z pagórka, którego zbocze ma d ugo l = 10 m i nachylone jest pod

tem

α

= 30

°

do poziomu. Jak drog przeb

sanki na odcinku poziomym po zjechaniu z

górki, je eli na ca ej drodze wspó czynnik tarcia wynosi k = 0.02?

7. Pi eczk pingpongow o promieniu r = 15 mm i masie m = 5 g zanurzono w wodzie do

boko ci h = 30 cm. Po puszczeniu pi eczka wyskoczy a na wysoko H = 10 cm nad

powierzchni wody. Jaka ilo energii zamieni a si na ciep o na skutek tarcia powierzchni o
wod ?

8. Jak prac nale y wykona , aby przewróci prostopad

cian o wymiarach 1l, 2l, 4l z boku

1l

×

2l na bok 2l

×

4l? W którym z po

równowaga jest najbardziej pewna?

9. Na biegunie pewnej kulistej planety cia o wa y n razy wi cej ni na równiku. Pr dko

towa ruchu planety wynosi

ω

, a sta a grawitacji G. Oblicz g sto tej planety.

10. Ksi

yc obiega doko a Ziemi w okresie T = 27.3 dni. redni promie orbity Ksi yca R =

380 000 km. Znale pr dko liniow

υ

ruchu Ksi yca doko a Ziemi i jego przyspieszenie

do rodkowe.

11. Masa Ksi yca jest 81 razy mniejsza od masy Ziemi. Stosunek za promieni Ksi yca i
Ziemi wynosi 3/11 a odleg

pomi dzy nimi wynosi d = 380 000 km. a.) Obliczy

przyspieszenie si y ci ko ci g

K

na powierzchni Ksi yca. b.) Znale punkt niewa ko ci

pomi dzy Ziemi a Ksi ycem.

d

r

R

M

m

12. Z jak pr dko ci pocz tkow

υ

0

trzeba wyrzuci rakiet pod k tem

α

= 45

°

wzgl dem

poziomu, aby rozb ys a ona w najwy szym punkcie swego toru, je eli czas palenia si
zapalnika rakiety wynosi 6 sekund?

13. Samolot leci poziomo po torze prostoliniowym z pr dko ci

υ

na wysoko ci h. Lotnik ma

zrzuci bomb na cel le cy przed samolotem. Pod jakim k tem wzgl dem pionu powinien on
widzie cel w chwili zrzutu bomby? Jaka jest w tej chwili odleg

od celu do punktu, nad

którym znajduje si samolot?

14. Ch opiec opieraj c si o barierk rzuci kamie o masie m = 1 kg w kierunku poziomym z
pr dko ci

υ

1

= 5 m/s. Masa ch opca M = 49 kg. Jak pr dko mo e on nada kamieniowi,

je eli b dzie go wyrzuca z tak sam si jak poprzednio stoj c na

wach na g adkim

lodzie? Jaka b dzie pr dko kamienia wzgl dem ch opca w drugim przypadku?

15. Samolot, aby wznie si do góry powinien mie pr dko

υ

= 80 km/h. D ugo rozbiegu

s = 100 m. Masa samolotu M = 1000 kg. Wspó czynnik tarcia k = 0.2. Jaka powinna by
minimalna moc silników aby samolot móg wznie si do góry? Ruch samolotu podczas
rozbiegu przyj za jednostajnie zmienny.

16. Poci g o masie m = 150 ton ma osi gn na poziomym torze pr dko

υ

= 10 m/s po

up ywie czasu t = 40 s od wyruszenia ze stacji. Oblicz moc parowozu, je eli wspó czynnik
tarcia f = 0.004.

17. Spr

yna o wspó czynniku spr ysto ci k = 2 N/m, której mas zaniedbujemy

umocowano poziomo. Ze spr

yn t zderza si cia o o masie m = 1 kg, powoduj c jej

ci ni cie o 0.4 m licz c od po

enia równowagi. Obliczy pr dko , jak mia o cia o w

chwili zderzenia si , je eli jego kinetyczny wspó czynnik tarcia o powierzchni poziom , po
której porusza o si f = 0.25

18. Dwa wagoniki rozje

aj si w przeciwnych kierunkach na skutek wybuchu mi dzy nimi

adunku prochowego. Wagonik o masie m

1

= 100 g przeby do chwili zatrzymania si drog

s

1

= 18 m. Jak drog s

2

przejedzie drugi wagonik o masie m

2

= 300 g? Wspó czynnik tarcia

jest sta y dla obu wagoników.

19. W kierunku poziomym oddano dwa strza y do ciany znajduj cej si w odleg

ci s = 50

m. Po pierwszym wystrzale przed luf karabinu ustawiono desk . Druga kula po przebiciu
deski uderzy a w cian w odleg

ci 0.5 m poni ej pierwszej. Jak prac wykona a kula w

czasie przebijania deski, je li pr dko pocz tkowa kuli wynosi

υ

0

= 300 m/s a ci ar kuli m

=5 g?

20. Po pomiaru pr dko ci kuli stosuje si wahad o balistyczne. Jest to skrzynka z piaskiem
zawieszona na linie. Kula wpadaj c do skrzynki utkwi w niej, ale przy tym skrzynka zostanie
odepchni ta na pewn wysoko . Oblicz pr dko kulki na podstawie nast puj cych danych:
masa kulki m, masa skrzynki M, wysoko wyniesienia skrzynki h.

21. Poci g elektryczny o masie 500 ton przebywa ruchem jednostajnym drog 3 km pod gór
o wzniesieniu 4m na 1 km drogi. Wspó czynnik tarcia f = 0.02.
a.) Wyznaczy prac wykonan przez poci g.
b.) Wyznaczy moc poci gu wiedz c, e drog 3 km przeby on w ci gu 5 min

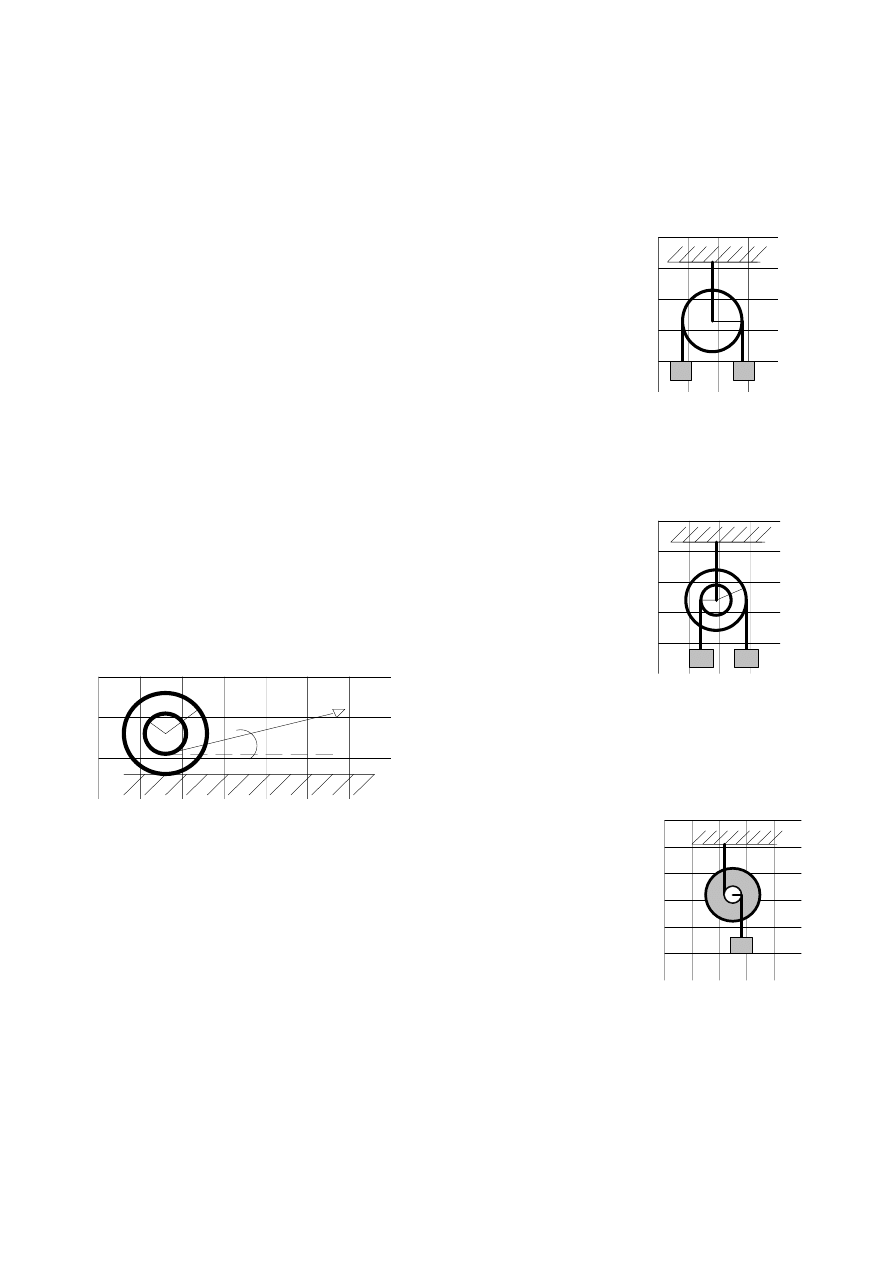
Zestaw 4.

1. Dr ek o d ugo ci d = 100 cm ma ci ar P = 160 G i jest wsz dzie jednakowej grubo ci.
Na ko cach tego dr ka zawieszono ci arki P = 100 G i Q = 240 G. W którym punkcie
nale y go podeprze , aby osi gn równowag ?

2. Znale przyspieszenie ci arków oraz napr enie nici w urz dzeniu
przedstawionym na rysunku uwzgl dniaj c moment bezw adno ci
obracaj cego si bloku pod warunkiem, e ni nie lizga si po bloku.
Wyznaczy napi cia nici oraz napr enie w punkcie zawieszenia A, je eli
masa bloku wynosi M. a promie r.

3. Drut ABC zgi to w punkcie B pod k tem prostym, przy czym AB = a =
20 cm i BC = b = 30 cm. Jaki k t utworzy z pionem rami AB, je eli drut
zawiesi w punkcie B na nitce?

4. Jednorodny walec ko owy o masie m i promieniu r stacza si bez po lizgu po p aszczy nie
pochylonej do poziomu pod k tem

β

wzd

drogi s. Obliczy pr dko ko cow osi walca i

czas staczania si .

5. Na ko owrót o promieniach r i R nawini te s w kierunkach
przeciwnych dwie lekkie nici obci one masami m

1

i m

2

. Znale

przyspieszenie k towe ko owrotu i napi cie nici T

1

i T

2

bior c pod uwag

dany moment bezw adno ci ko owrotu I.

6. Na poziomym stole le y szpulka nici (patrz rysunek). Z jakim
przyspieszeniem liniowym a b dzie porusza si o szpulki, je eli

dziemy ci gn za nitk si F ?

a)

W jaki sposób nale y ci gn za nitk , aby
szpulka porusza a si w stron , w któr
ci gniemy nitk ?

b)

Znale warto si y tarcia szpulki o stó .

Szpulka toczy si po stole bez po lizgu.

7*. Z jakim przyspieszeniem a b dzie obni

si du y kr ek o masie M w

uk adzie przedstawionym na rysunku, je eli na innych dwóch niciach
nawini tych na ma y kr ek o promieniu r zawieszono ci arek o masie
m? Wyznaczy napr

enie nici.

8. Na stoliku obrotowym stoi cz owiek obracaj c si z cz sto ci f

1

= 0,5

obr./min. Moment bezw adno ci cia a cz owieka wzgl dem osi obrotu
wynosi I

0

= 1,6 kg

⋅

m

2

. W wyci gni tych poziomo r kach trzyma dwa

ci arki o masie m = 1 kg ka dy, odleg

mi dzy którymi wynosi l

1

= 1,6 m. Ile obrotów

dzie wykonywa cz owiek, je eli opu ci on r ce i odleg

mi dzy ci arkami wyniesie l

2

= 0,4 m ? Moment bezw adno ci stolika zaniedba .

9*. Kula o promieniu r i masie m stacza si (bez po lizgu) z wysoko ci h po równi pochy ej
nachylonej do poziomu pod k tem

α

. Znale drog , któr przeb dzie kula na p aszczy nie

poziomej po stoczeniu si z równi, je eli wspó czynnik tarcia jest sta y i wynosi k.

m

m

1

2

r

A

M

m

m

1

2

2

T

T

1

r

R

I

F

α

r

R

I

m

M

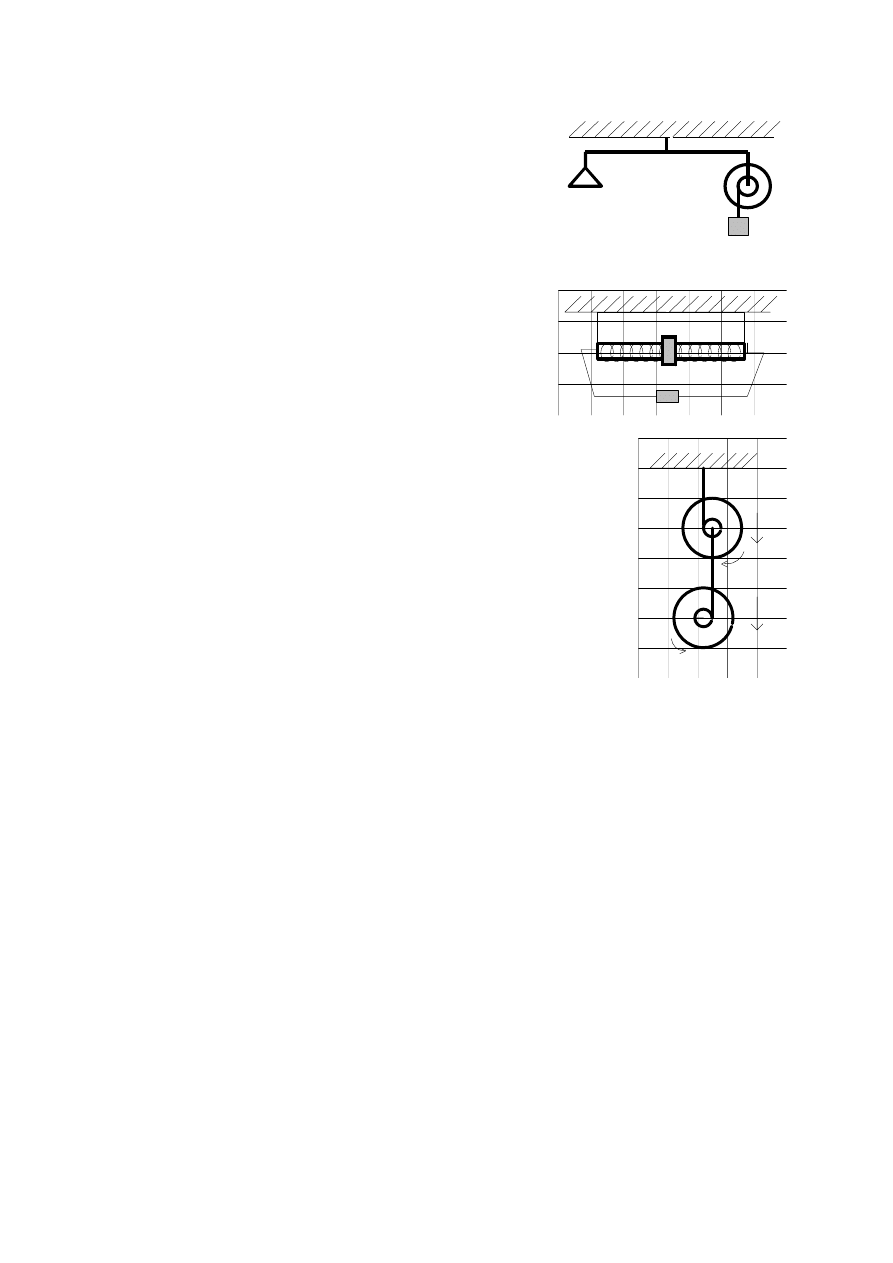
10. Model ko owrotu przymocowany jest do jednej z szalek
wagi. Na ko owrót o momencie bezw adno ci I i promieniu
r nawini to ni z ci arkiem o masie m. Waga jest w
równowadze, gdy ko owrót jest zahamowany. O ile trzeba
zmieni obci enie drugiej szalki, aby zosta a przywrócona
równowaga, gdy ko owrót zacznie obraca si pod
wp ywem opadaj cego ci arka? Znale napr enie nici w
obu przypadkach.

11*. Obliczy przyspieszenie a, z którym b dzie opada
kr ek o masie M przedstawiony na rysunku, je eli na
pr ciku swobodnie przesuni tym przez otwór w walcu
zawieszono na niciach mas m. Moment bezw adno ci
kr ka I, promie wa ka kr ka r. Ci ar nici i pr cika
zaniedba .

12*. Znale przyspieszenia a

1

i a

2

, z którym b

si obni

y rodki

dwóch jednakowych kr ków oraz si y napr

enia nici przyrz du

przedstawionego na rysunku. Moment bezw adno ci kr ka jest I, masa
m, promie , na którym nawini ta jest ni r.

13. Do cia a o masie m

1

= 3 kg umieszczonego na równi pochy ej (

α

=

30

°

) przyczepiono ni przerzucon przez ko owrotek o masie M = 0.1

kg przytwierdzony do szczytu równi. Na drugim ko cu nici
zawieszono ci ar o masie m

2

= 2 kg. Znale napi cia nici oraz

przyspieszenie liniowe ruchu uk adu. Za

, e nie ma po lizgu a

wspó czynnik tarcia wynosi f = 0.02.

14. Obliczy moment bezw adno ci dr ka o d ugo ci 1= 60 cm i o masie ml = 75 g, na
ko cach, którego umocowano kulki o masie m2 = 100 g ka da, je eli o przechodzi przez

rodek pr ta i jest do niego prostopad a.

15. Obliczy moment bezw adno ci dwóch jednakowych cienkich pr tów skrzy owanych w

rodku pod k tem prostym i osadzonych na osi przechodz cej przez punkt skrzy owania.

ugo ka dego pr ta l = 60 cm, masa m = 120 g.

16. Obliczy moment bezw adno ci ramki kwadratowej o kraw dzi a = 40 cm, je eli o
przechodzi przez rodki przeciwleg ych boków. Ramk zrobiono z pr ta, którego metr
bie cy wa y P = 120 G.

17. Zadanie jak wy ej, ale o pokrywa si z jednym z boków ramki.

18. Obliczy energi kinetyczn kuli o promieniu r = 6cm i o masie m = 6 kg mkn cej z
szybko ci v = 4 m/s i wykonuj

n = 10 obr./s. (I = 0.4 m r

2

)

19. Obliczy energi kinetyczn kuli o masie m = 500 g tocz cej si z pr dko ci v = 2 m/s.

20. Jak prac nale y wykona aby zatrzyma ko o zamachowe o masie m = 2000 kg i o
promieniu r = 1 m wykonuj ce n = 50 obr./min. (I = 0.5 m r

2

)

m

I

M

I

r

m

a

a

r

1

2

Zestaw 1.

pr dko

dt

dx

v

=

przyspieszenie

2

2

dt

x

d

dt

dv

a

=

=

ruch jednostajny

t

v

s

⋅

=

ruch

jednostajnie

przyspieszony

t

v

t

a

s

0

2

2

1

+

⋅

=

transformacja Galileusza

t

t

t

v

x

x

=

⋅

−

=

'

'

czas spadku swobodnego

g

h

t

2

=

pr dko

ko cowa

hg

v

2

=

zasi g rzutu uko nego

( )

α

2

sin

2

0

g

v

z

=

Zestaw 2.

zasady dynamiki Newtona

a

m

F

⋅

=

BA

AB

F

F

−

=

p d

cia a

v

m

p

⋅

=

ci ar cia a

mg

P

=

, energia

potencjalna

mgh

E

pot

=

, energia kinetyczna

2

2

mv

E

kin

=

si a od rodkowa

r

m

F

r

⋅

=

2

ω

równia:

si

ci gaj ca

( )

α

sin

P

S

=

, si a

nacisku

( )

α

cos

P

N

=

, tarcie

N

f

T

⋅

=

Zestaw 3.

si a grawitacji Newtona

2

R

Mm

G

F

=

, G=6.67 10

-11

Nm

2

kg

-2

, przyspieszenie ziemskie

2

Z

Z

R

GM

g

=

energia potencjalna pola grawitacyjnego

R

GMm

E

pot

−

=

i jego potencja

R

GM

V

−

=

si a wyporu Archimedesa

g

V

F

cieczy

w

⋅

= ρ

praca

s

F

W

r

r

⋅

=

moc

dt

dW

P

=

Zestaw 4.

pr dko k towa

dt

d

ϕ

ω =

przyspieszenie

k towe

2

2

dt

d

dt

d

ϕ

ω

ε

=

=

moment si y

F

r

M

r

r

r

×

=

moment

p du

p

r

L

r

r

r

×

=

moment bezw adno ci walca

2

2

r

m

I

⋅

=

i kuli

5

2

2

r

m

I

⋅

=

dynamika bry y sztywnej

ε

⋅

=

I

M