2009-10-19

1

Geodezja i astronomia geodezyjna

Ćwiczenie 1

Trójkąty sferyczne

Podstawy trygonometrii sferycznej

LITERATURA

•

Janusz Śledziński: „Geodezja satelitarna”. PPWK, Warszawa, 1978.

•

Rocznik Astronomiczny na rok 2008 (

www.igik.edu.pl

).

•

Jan Kryński, Jerzy Rogowski: „Systemy i układy współrzędnych w

y

,

y

g

„ y

y

y

p

ę

y

geodezji, geodynamice i astronomii”

•

Eugeniusz Rybka: „Astronomia ogólna”

•

Wiesław Opalski, Ludosław Cichowicz: „Astronomia Geodezyjna”

•

Barbara Kołaczek: „Astronomia sferyczna z ćwiczeniami”

•

Ludosław Cichowicz: „Astronomia sferyczna”

„

y

•

Tadeusz Jarzębowski: „Elementy astronomii”

•

Internet (n.p. www.geoforum.pl,

www.nauticalissues.com/astronomy.html)...

2009-10-19

2

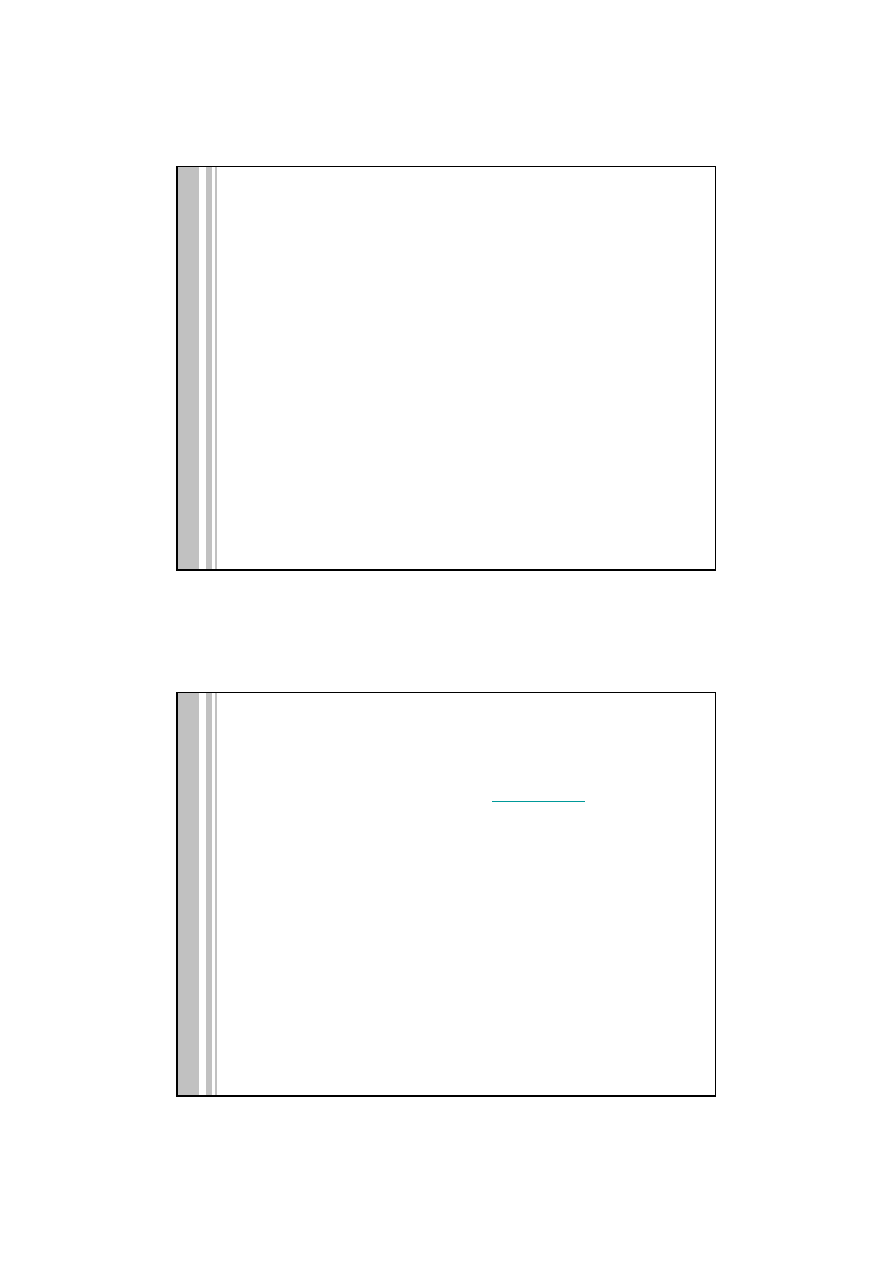
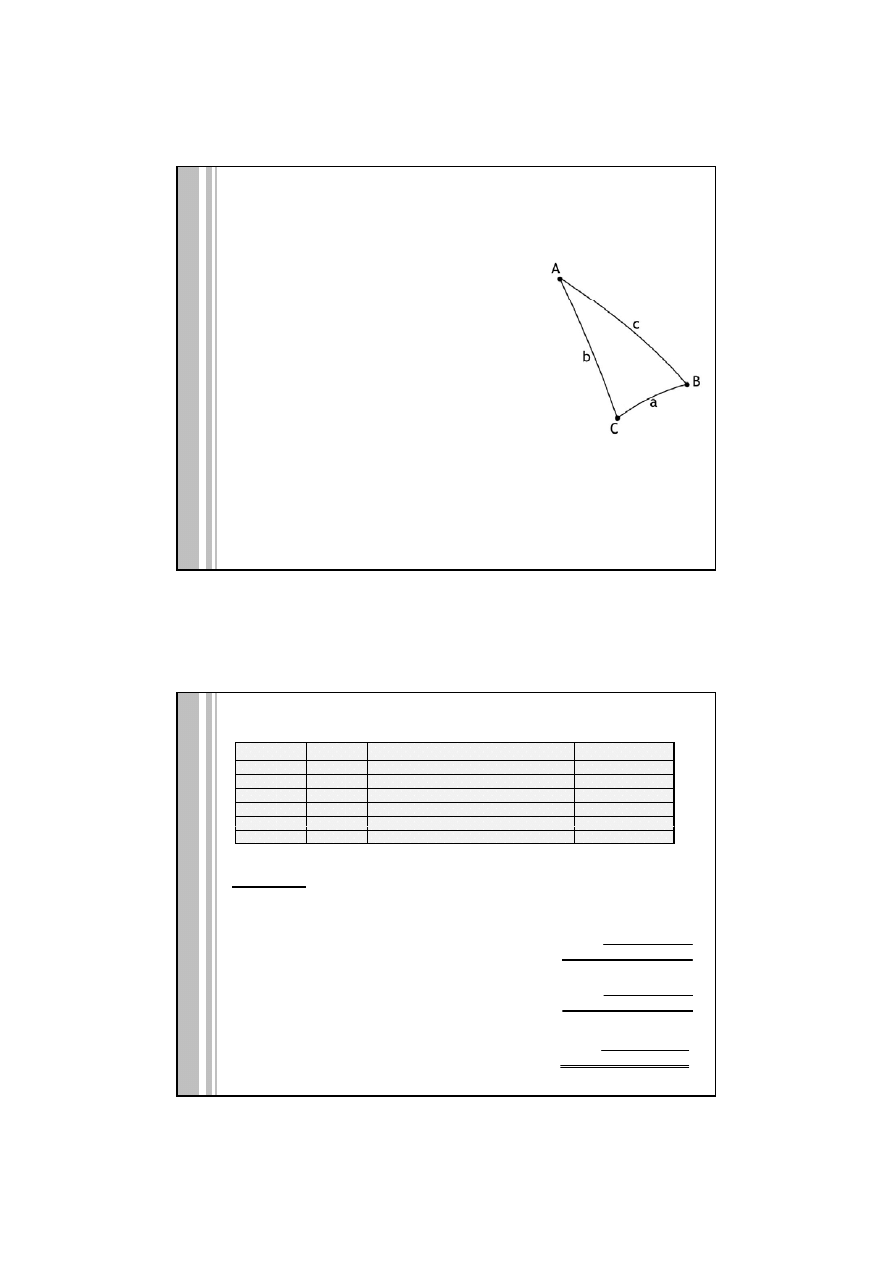
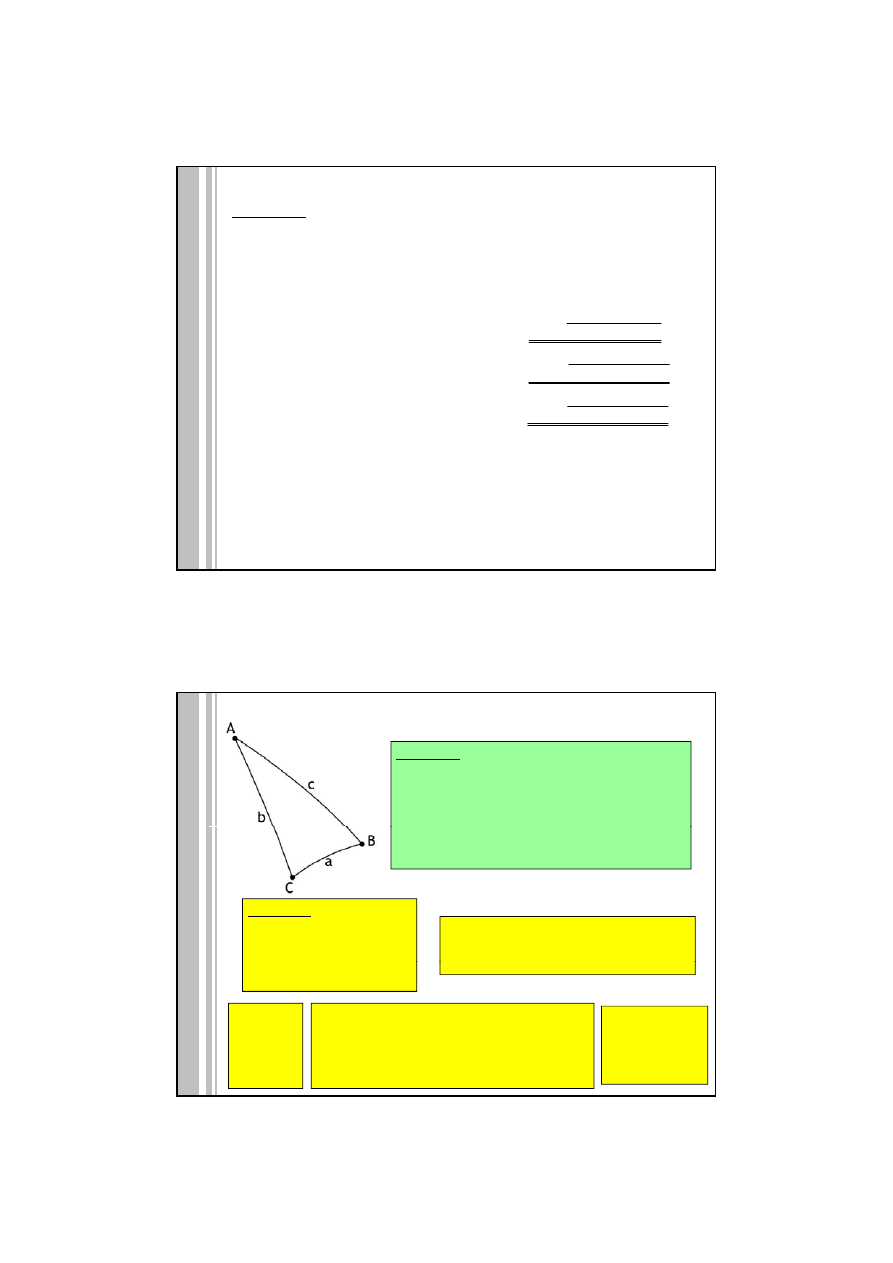
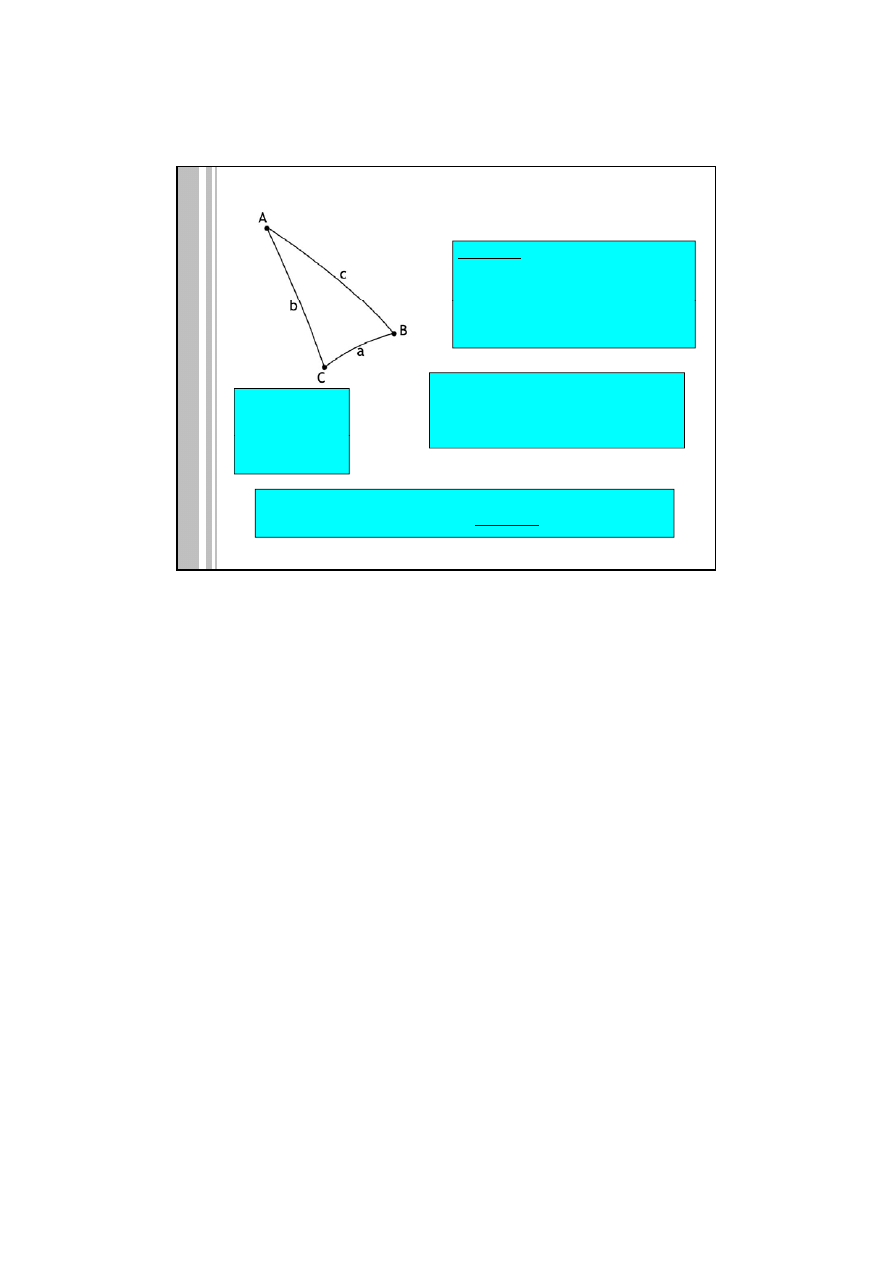
Trójkąt sferyczny – figura powstała z trzech łuków kół wielkich (kąty i boki

mierzone w mierze kątowej)

W każdym z trójkątów rozważa się sześć elementów:

3 kąty A, B, C i 3 boki (kąty środkowe oparte na łukach kół wielkich) a, b, c.

2009-10-19

3

GEOMETRIA SFERY

GEOMETRIA SFERY

2009-10-19

4

GEOMETRIA SFERY

GEOMETRIA SFERY

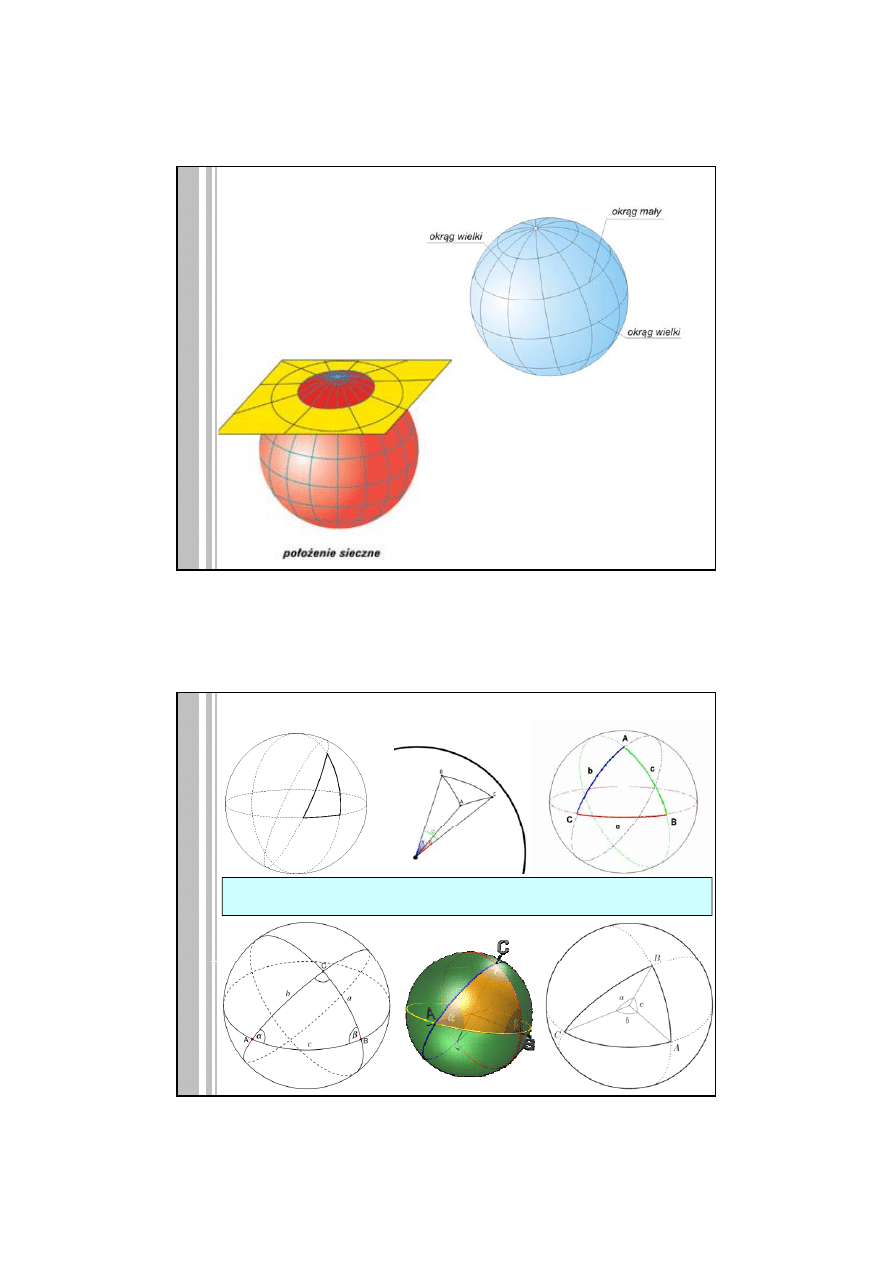
Pomiędzy elementami trójkąta danego
(bokami a, b, c i kątami A, B, C),
a elementami trójkąta biegunowego
(bokami a’, b’, c’ i kątami A’, B’, C’)
zachodzą zależności:

a + A’ = 180°;

A + a’ = 180°

b + B’ = 180°; B + b’ = 180°

c + C’ = 180°;

C + c’ = 180°

2009-10-19

5

Wzory sinusowe:
sin b · sin A = sin a · sin B

(1a)

sin c · sin B = sin b · sin C

(1b)

sin a · sin C = sin c · sin A

(1c)

Wzory cosinusowe:
cos a = cos b · cos c + sin b · sin c · cos A

(2a)

TRYGONOMETRIA SFERYCZNA

( )

cos b = cos c · cos a + sin c · sin a · cos B

(2b)

cos c = cos a · cos b + sin a · sin b · cos C

(2c)

Wzory mieszane:
sin a · cos B = cos b · sin c – sin b · cos c · cos A (3a)
sin b · cos C = cos c · sin a – sin c · cos a · cos B (3b)
sin c · cos A = cos a · sin b – sin a · cos b · cos C (3c)
sin a · cos C = cos c · sin b – sin c · cos b · cos A (3d)
sin b · cos A = cos a · sin c – sin a · cos c · cos B (3e)
sin c · cos B = cos b · sin a – sin b · cos a · cos C (3f)
Wzory na podstawie zależności trójkąta biegunowego (przykłady):
sin A · sin b = sin a · sin B (4a)
cos A = - cos B · cos C + sin B · sin C · cos a (4b)
sin A · cos b = cos B · sin C + sin B · cos C · cos a (4c)
sin A · cos c = cos C · sin B + sin C · cos B · cos a (4d) …….

ROZWIĄZYWANIE TRÓJKĄTÓW SFERYCZNYCH

DANE

OPIS DANYCH

WYZNACZANE

Wariant 1

a, b, c

3 boki

A, B, C

Wariant 2

a, b, C

2 boki i kąt między nimi

A, B, c

Wariant 3

a, b, A

2 boki i kąt przyległy do jednego z nich

B, C, c

Wariant 4

B, C, c

2 kąty i bok przyległy do jednego z nich

A, a, b

Wariant 5

A, B, c

2 kąty i bok pomiędzy nimi

C, a, b

, ,

ą y

p

ę y

, ,

Wariant 6

A, B, C

3 kąty

a, b, c

WARIANT 1

DANE: a, b, c

WYZNACZANE: A, B, C

Wzór cosinusowy:

c

b

c

b

a

A

A

c

b

c

b

a

sin

sin

cos

cos

cos

cos

cos

sin

sin

cos

cos

cos











Wzór cosinusowy:

Wzór cosinusowy:

a

c

a

c

b

B

B

a

c

a

c

b

sin

sin

cos

cos

cos

cos

cos

sin

sin

cos

cos

cos











b

a

b

a

c

C

C

b

a

b

a

c

sin

sin

cos

cos

cos

cos

cos

sin

sin

cos

cos

cos











2009-10-19

6

WARIANT 2

DANE: a, b, C

WYZNACZANE: a, b, C

Wzór cosinusowy:

cos

cos cos

sin sin cos

c

a

b

a

b

C





Wzory sinusowo-cosinusowe

sin cos

cos sin

sin cos cos

cos

cos sin

sin cos cos

sin

sin cos

cos sin

sin cos cos

cos

cos sin

sin cos cos

sin

c

B

b

a

b

a

C

B

b

a

b

a

C

c

c

A

a

b

a

b

C

A

a

b

a

b

C

c

















=

-

WARIANT 3

DANE: a, b, A

WYZNACZANE: B, C, c

Wzór sinusowy:

a

A

b

B

a

A

b

B

sin

sin

sin

sin

sin

sin

sin

sin







Wzory sinusowo-cosinusowe

sin cos

cos sin

sin cos cos

sin cos

cos sin

sin cos cos

cos

cos sin cos

cos sin cos

sin cos cos

sin cos cos

c

A

a

b

a

b

C

c

B

b

a

b

a

C

C

a

b

B

b

a

A

b

B

b

A



















Warunek:

b > a



B > A

lub

b < a



B < A

sin cos cos

sin cos cos

sin

sin

cos

cos

sin

sin cos cos

cos sin cos

a

b

B

b

a

A

c

a

b

a

b

a

b

B

a

b

A








2

2

2

2

Warunek:

C > B



c > b

lub

C < B



c < b

2009-10-19

7

WARIANT 4

DANE: B, C, c

WYZNACZANE: a, b, A

Wzór sinusowy:

sin

sin

sin

sin

sin

sin sin

sin

B

b

C

c

b

B

C

c







Wzory sinusowo-cosinusowe

Warunek:

B > C



b > c

lub

B < C



b < c

sin cos

cos sin

sin cos cos

sin cos

cos sin

sin cos cos

cos

cos sin cos

cos sin cos

i

i

a

B

b

c

b

c

A

a

C

c

b

c

b

A

A

c

b

B

b

c

C

b

B

b

C



















sin cos cos

sin cos cos

sin

sin

cos

cos

sin

sin cos cos

cos sin cos

c

b

B

b

c

C

a

b

c

b

c

b

c

C

b

c

B








2

2

2

2

Warunek:

A > C



a > c

lub

A < C



a < c

WARIANT 5

DANE: A, B, c

WYZNACZANE: C, a, b

Wzór na ‘trójkąt biegunowy’:

cos

cos sin sin

cos cos

C

c

A

B

A

B





Wzory sinusowe:

C

c

A

a

c

C

a

A

sin

sin

sin

sin

sin

sin

sin

sin







C

c

B

b

c

C

b

B

sin

sin

sin

sin

sin

sin

sin

sin







Warunek:

A > C



a > c

lub

A < C



a < c

Warunek:

B > C



b > c

lub

B < C



b < c

2009-10-19

8

WARIANT 6

DANE: A, B, C

WYZNACZANE: a, b, c

Wzory na ‘trójkąt biegunowy’:

cos

cos sin sin

cos cos

sin sin

cos

cos sin sin

cos cos

cos

cos

cos cos

sin sin

cos

cos sin sin

cos cos

cos

cos

cos cos

sin sin

A

a

B

C

B

C

B

C

B

b

C

A

C

A

b

B

C

A

C

A

C

c

A

B

A

B

c

C

A

B

A

B



























cosa =

cosA + cosBcosC

TRYGONOMETRIA SFERYCZNA - PRZYKŁADY

Przykład 1:
Dane: b, c, A
Szukane: a, B
Korzystamy ze wzorów:
sin b · sin A = sin a · sin B (1a)

s b s

s a s

( a)

sin a · cos B = cos b · sin c – sin b · cos c · cos A (3a)
cos a = cos b · cos c + sin b · sin c · cos A

(2a)

Przykład 2:
Wzory sinusowe:
sin b · sin A = sin a · sin B
sin c · sin B = sin b · sin C

Ze wzorów sinusowych korzystamy, gdy
znamy trzy elementy trójkąta, z których dwa
są do siebie przeciwległe

sin c · sin B = sin b · sin C
sin a · sin C = sin c · sin A

są do siebie przeciwległe.

Dane:

a = 61º 42’

b = 81º 33’

A = 39º 10’

sin B = sin b * sin A / sin a

sin B = 0,989144*0,631578/0,880477 = 0,709527

B = arcsin (0,709527)

B = 45º 12’ lub B = 134º 48’

Z analizy
wielkości trójkąta
wynika, że obie
wartości są
poprawne

2009-10-19

9

Przykład 3:

Wzory cosinusowe:

cos a = cos b · cos c + sin b · sin c · cos A

TRYGONOMETRIA SFERYCZNA - PRZYKŁADY

cos a = cos b · cos c + sin b · sin c · cos A
cos b = cos c · cos a + sin c · sin a · cos B
cos c = cos a · cos b + sin a · sin b · cos C

Ze wzorów cosinusowych korzystamy, gdy
mamy trzy boki trójkąta lub gdy znamy dwa
boki i kąt między nimi zawarty (wtedy
znajdujemy trzeci bok)

Dane:

a = 59º 13’

znajdujemy trzeci bok).

b = 117º 45’

C = 76º 23’

cos c = 0,511793*(-0,465615)+0,859109*0,884988*0,235425 = -0,059305

c =93º24’ (c2 = 266º36’)