2013-12-01

Podstawy automatyki -

ćwiczenia

1

Charakterystyki

czestotliwościowe

Podstawy automatyki

2013-12-01

Podstawy automatyki -

ćwiczenia

2

Charakterystyka częstotliwościowa:

x(t)=A

1

sin

ωt

y(t)=A

2

sin (

ωt + φ)

Jest to przebieg odpowiedzi

y(t)=A2sin (

ωt + φ)

układu dynamicznego

na podane na jego wejście wymuszenie

x(t)=A1sin

ωt

.

Zmienną niezależną jest pulsacja –

ω

Charakterystyki częstotliwościowe określają zachowanie się obiektu

dynamicznego w stanach ustalonych przy wymuszeniach harmonicznych

(sinusoidalnych).

2013-12-01

Podstawy automatyki -

ćwiczenia

3

Charakterystyki częstotliwościowe:

Transmitancja widmowa





)

(

)

(

j

s

s

G

j

G





G(j



)

x(

t

)=A

1

sin



t

y(

t

)=A

2

sin(



t+

j

)

]

[sin

)]

[sin(

t

L

e

t

L

s



j





j







Zgodnie z tw. o przesunięciu w dziedzinie zmiennej rzeczywistej:

2013-12-01

Podstawy automatyki -

ćwiczenia

4

Charakterystyki częstotliwościowe:

Transmitancję operatorową układu automatyki można zapisać:

 















sin

)

sin(

1

2

t

A

L

t

A

L

s

G



j

















sin

)

sin(

1

2

t

L

t

L

A

A



j



s

e

A

A



j

1

2



















t

L

t

L

e

A

A

s

sin

sin

1

2







j

2013-12-01

Podstawy automatyki -

ćwiczenia

5

Charakterystyki częstotliwościowe:





























j



j

s

s

e

A

A

j

G

1

2

)

(

Zgodnie z def. tr. widmowej:







j

j

e

A

A

1

2

j

j

e

A



gdzie:

A

– moduł transmitancji

φ

– przesunięcie fazowe

(argument)

są funkcjami częstotliwości

2013-12-01

Podstawy automatyki -

ćwiczenia

6

Charakterystyki częstotliwościowe:

Transmitancja widmowa

jest więc

liczbą zespoloną

,

której moduł

A(

ω

)

jest równy stosunkowi amplitud

sinusoidalnego sygnału wyjściowego i wejściowego:





)

(



j

G



)

(



A

1

2

A

A







j

j

e

A

A

1

2

a argumentem

φ

(

j

ω

)

jest przesunięcie fazowe sygnału

wyjściowego względem wejściowego:



)

(



j





)

(

arg



j

G

















j

j

e

A

A

1

2

arg

2013-12-01

Podstawy automatyki -

ćwiczenia

7

Charakterystyki częstotliwościowe:

2013-12-01

Podstawy automatyki -

ćwiczenia

8

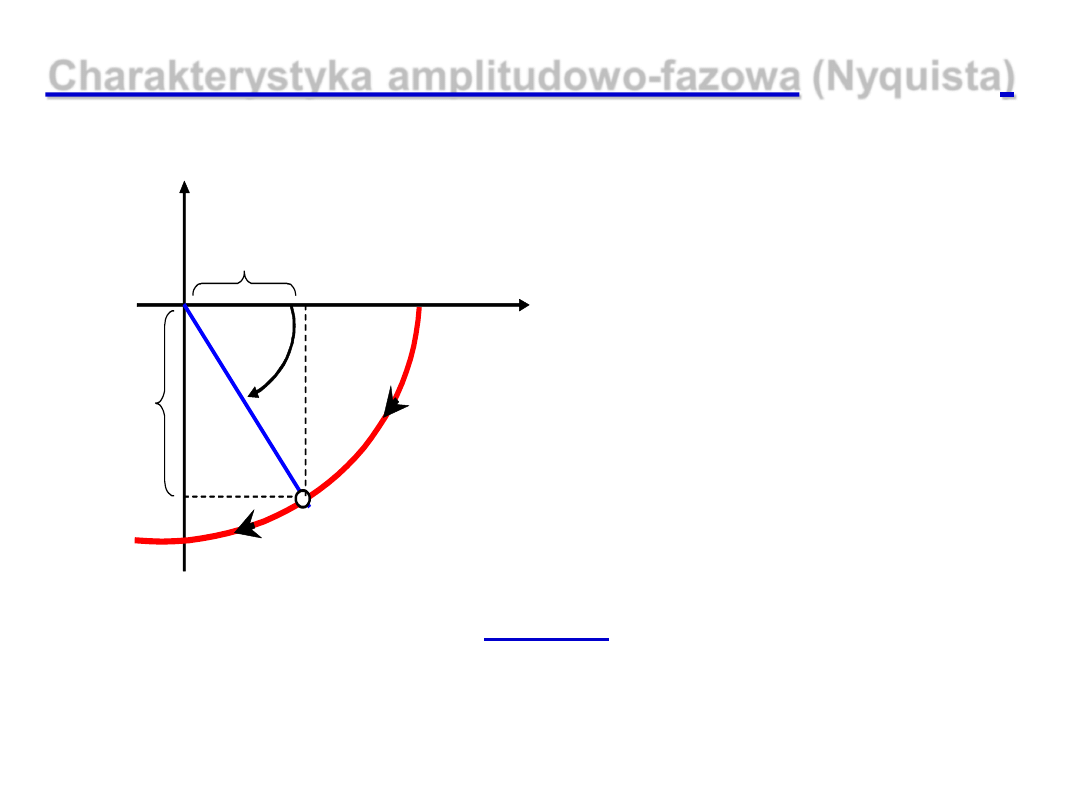
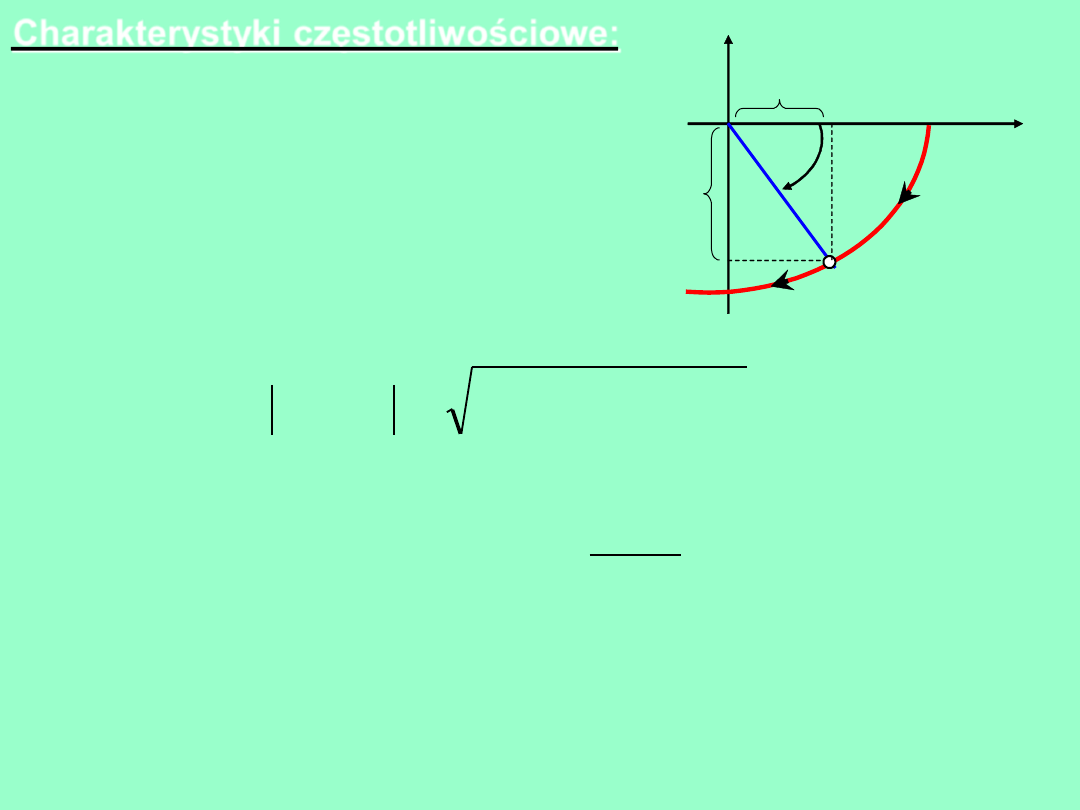
Charakterystyka amplitudowo-fazowa (Nyquista)

Im G (j



)

R e G (j



)



0



i

j

(



i

)

A (



i

)

0

P (



)

Q (



)

Ch-ka A-F

– miejsce

geometryczne punktów, jakie

zakreśla wektor G(

j

ω)

, na

płaszczyźnie zespolonej przy
zmianie częstotliwości
(pulsacji) sygnału wejściowego

od

0

do



UWAGA:

Ch-ka A-F

określa zachowanie się elementu lub układu przy

wszystkich

częstotliwościach sygnału wejściowego.

2013-12-01

Podstawy automatyki -

ćwiczenia

9

Charakterystyki częstotliwościowe:

Korzystając z tw. Eulera dla liczb zespolonych:

j

j

j

sin

cos

j

e

j





transmitancję widmową można zapisać jako:



)

(



j

G





j

j

Ae

)

sin

(cos

j

j

j

A





co daje:

)

(

)

(

)

(







Q

j

P

j

G





gdzie:



)

(



P





)}

(

Re{



j

G

)]

(

cos[

)

(



j







A



)

(



Q





)}

(

Im{



j

G

)]

(

sin[

)

(



j







A

2013-12-01

Podstawy automatyki -

ćwiczenia

10

Charakterystyki częstotliwościowe:

- na podstawie rysunku (ch-ka A-F) mamy:

Im G (j



)

R e G (j



)



0



i

j

(



i

)

A (



i

)

0

P (



)

Q (



)





)

(



j

G



)

(



A

)

(

)

(

2

2





Q

P







)

(



j





)

(

arg



j

G

)

(

)

(





P

Q

tg

arc



2013-12-01

Podstawy automatyki -

ćwiczenia

11

Inne charakterystyki częstotliwościowe

2.

A(

ω)

– charakterystyka amplitudowa

3.

φ(ω)

– charakterystyka fazowa

oraz

charakterystyki logarytmiczne

(oś odciętych ma podziałkę

logarytmiczną – log

ω )

:

4.

L(

ω)

– logarytmiczna charakterystyka amplitudowa

5.

φ(ω)

– charakterystyka fazowa

[dB]

)

(

log

20

)

(





A

L



2013-12-01

Podstawy automatyki -

ćwiczenia

12

Jak wyznaczać ch-ki częstotliwościowe ?

• kreślimy odpowiednie ch- ki

1)

Układ opisany równaniem różniczkowym:

• dokonujemy przekształcenia Laplace’a r. różniczkowego;
• i wyznaczamy –

G(s)

• korzystając z def. transmitancji widmowej wyznaczamy:





j

s

s

G

j

G





)

(

)

(

• mnożymy i dzielimy G(j

ω

) przez liczb

ę sprzężoną

2)

Układ opisany transmitancją operatorową

G(s)

• doprowadzamy do wyznaczenia części Re{G(jω)} i Im{G(jω)}

jb

a

z

jb

a

z











2013-12-01

Podstawy automatyki -

ćwiczenia

13

Przykład (1/3):

Wyznaczyć ch-kę A-F układu o transmitancji operatorowej:

 





1





Ts

s

k

s

G

gdzie: k=20 T=0,1 s











1





Tj

j

k

Rozwiązanie:





j

T

k







2

 





j

G









j

s

s

G

)

(

 

































j

T

j

T

j

T

k

j

G

2

2

2













2

2

4

2

2

4

2













T

k

j

T

T

k

2013-12-01

Podstawy automatyki -

ćwiczenia

14

Przykład (2/3):

Wyznaczyć ch-kę A-F układu o transmitancji operatorowej:

 





1





Ts

s

k

s

G

gdzie: k=20 T=0,1 s

Rozwiązanie c.d.:

















2

3

2

2

1

T

k

j

T

kT

stąd

 

1

2

2







T

kT

P





 













2

3

T

k

Q

po podstawieniu danych liczbowych:

 

1

01

,

0

2

2











P

 













3

01

,

0

20

Q

2013-12-01

Podstawy automatyki -

ćwiczenia

15

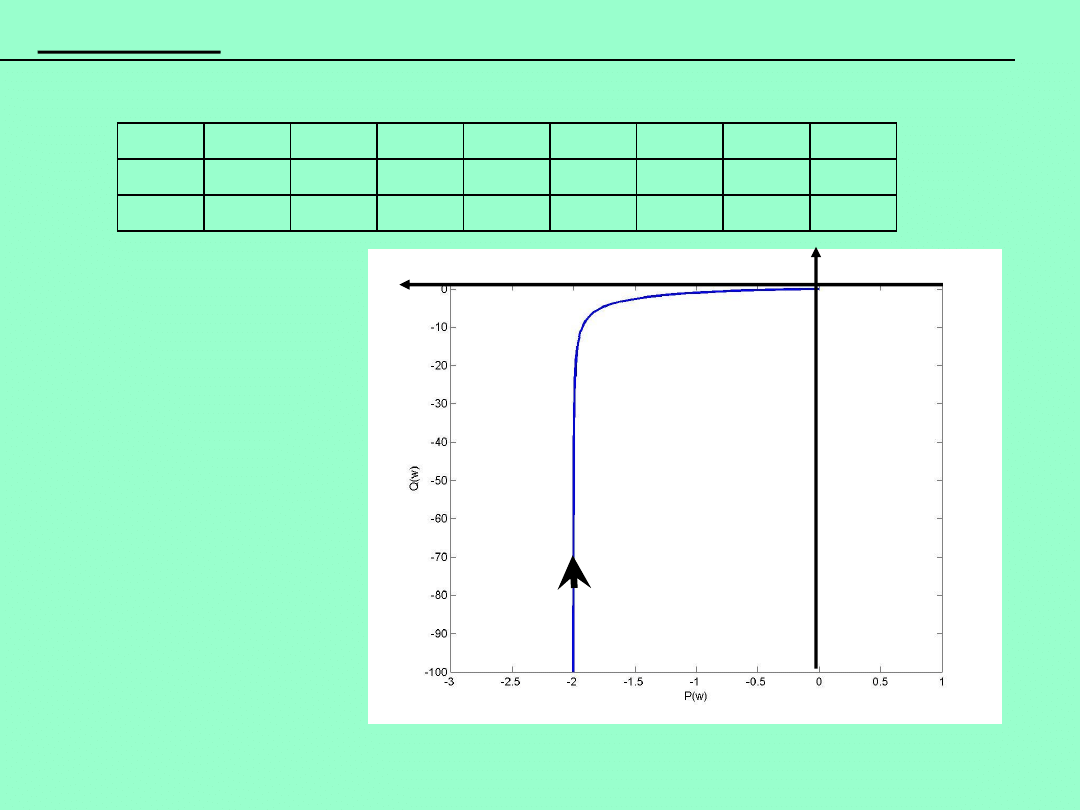
Przykład (3/3):

Rozwiązanie c.d.:

otrzymujemy wykres:



0

0,5

1

5

10

20

50

∞

P(



)

-2

-1,995

-1,98

-1,6

-1

-0,4

-0,077

0

Q(



)

-∞

-39,9

-19,8

-3,2

-1

-0,2

-0,015

0

Wyliczając wartości w tabeli: