Metoda Eulera

Weźmy równanie różniczkowe w postaci:
y’(x)=f(x,y) dla a<=x<=b
y(a)=y

a

Takie równanie wraz z podanym warunkiem początkowym nazywamy zagadnieniem
początkowym Cauchy’ego.
Niech x

i

=a+ih, i=0,1,…,N, gdzie h=(b-a)/N. Pochodną y’(x) przybliżamy ilorazem

różnicowym pierwszego rzędu opartym na węzłach x i x+h. Jeżeli funkcja f jest ciągła na
przedziale [a,b] i posiada pochodną, to ze wzoru Taylora otrzymamy:

)

(

"

2

)

(

)

(

)

(

'



y

h

h

x

y

h

x

y

x

y









, gdzie

]

,

[

h

x

x







.

Wykorzystując warunek początkowy dla x=x

i

i odrzucając resztę we wzorze Taylora

dostajemy:















a

i

i

i

i

y

a

y

x

y

x

hf

x

y

x

y

)

(

))

(

,

(

)

(

)

(

1

Schemat metody Eulera:















a

i

i

i

i

y

y

y

x

hf

y

y

0

1

)

,

(

Przykład:
Oblicz y(0,3) dla y spełniającego równanie:
y’(x)=x

2

+y

y(0)=0,1
Rozwiązanie:
Przyjmujemy h=0,1
x

0

=0

y

0

=0,1

x

1

=x

0

+h=0,1

y

1

=y(0,1)=y

0

+h(x

0

2

+y

0

)=0,1+0,1(0

2

+0,1)=0,11

x

2

=x

1

+h=0,2

y

2

=y(0,2)= y

1

+h(x

1

2

+y

1

)=0,11+0,1(0,01+0,11)=0,122

x

3

=0,3

y

3

=0,122+0,1(0,04+0,122)=0,1382.

Odpowiedź: y(0,3)=0,1382.

Metoda Rungego-Kutty

Metody Rungego-Kutty to metody numerycznego rozwiązywania równania różniczkowego

pierwszego rzędu w postaci:

y’=f(x,y).

Rozwiązaniem takiego zagadnienia jest funkcja f(x,y(x))=y’(x) dla

]

,

[ b

a

x



. Rozwiązanie to

nie jest jednoznczne, dlatego by uzyskać jednoznaczne rozwiązanie konieczne jest zadanie na

przykład warunku początkowego:

y(a)=y

a

.

Takie zagadnienie nosi nazwę zagadnienia Cauchy’ego [1].

Metoda Rungego-Kutty jest zdefiniowana wzorem:

)

,

,

(

1

h

y

x

h

y

y

i

i

i

i









, i=0,1,…,N-1

y

0

=y

a

gdzie:














































r

j

r

j

j

ij

ij

i

i

r

i

i

i

k

b

h

y

b

h

x

f

h

y

x

k

k

k

c

h

y

x

1

1

1

,

)

,

,

(

)

,

,

(



dla i=1,2,…,r.

Rząd metody Rungego-Kutty jest równy r. Najczęściej stosuje się metodę Rungego-Kutty

czwartego rzędu (RK4), dla której powyższe wzory przyjmują postać:

)

2

2

(

6

1

)

,

,

(

4

3

2

1

k

k

k

k

h

y

x











,

)

,

(

1

y

x

f

k



,

)

2

1

,

2

1

(

1

2

hk

y

h

x

f

k







,

)

2

1

,

2

1

(

2

3

hk

y

h

x

f

k







,

)

,

(

3

4

hk

y

h

x

f

k







.

Metoda

Rungego-Kutty

drugiego

rzędu

(zmodyfikowana

metoda

Eulera):

)

(

2

1

)

,

,

(

2

1

k

k

h

y

x







,

)

,

(

1

y

x

f

k



,

)

,

(

1

2

hk

y

h

x

f

k







.

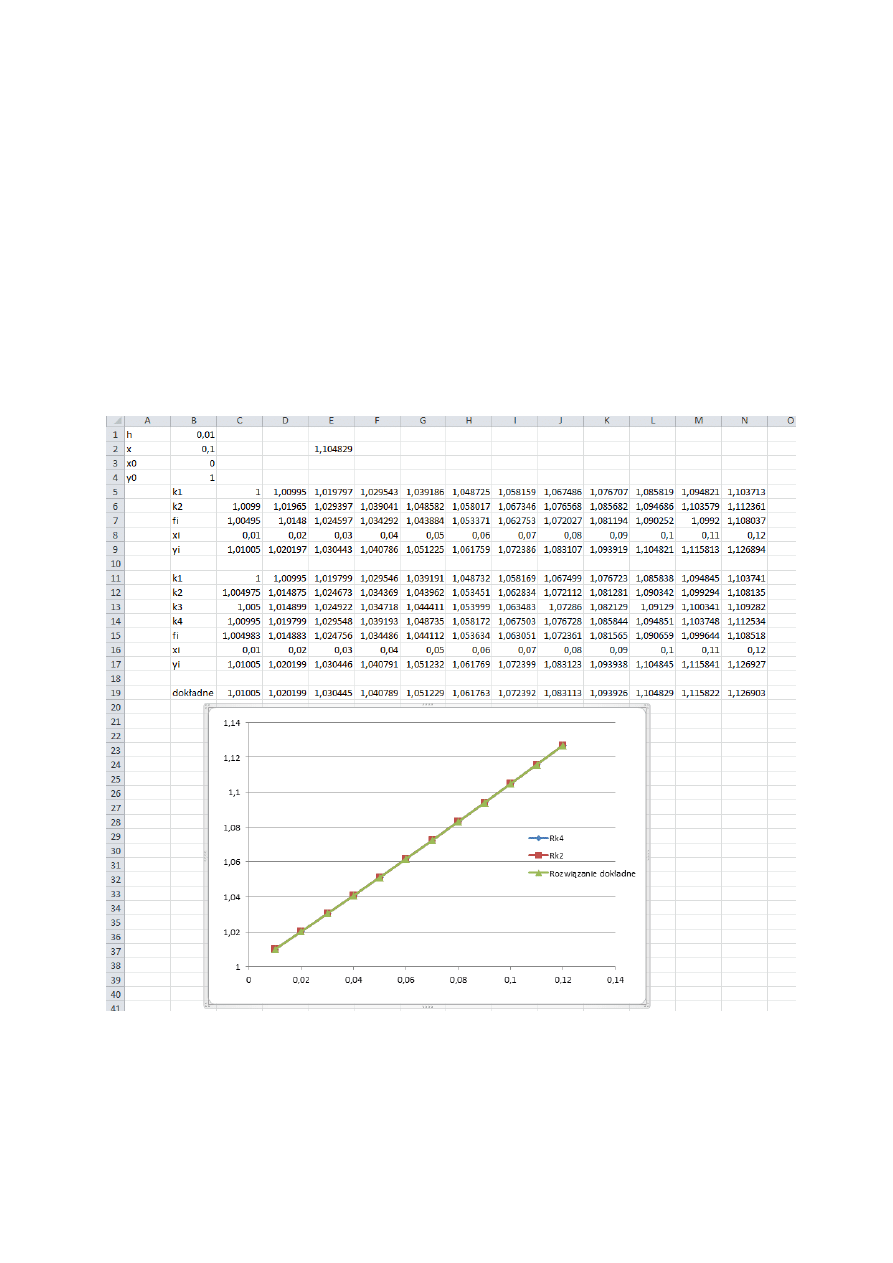
Przykład:

y'=y-x

2

, y

0

=1, h=0,01.

Obliczymy wartość rozwiązania y w punkcie x=0,1.

Dla metody RK4:

y(0,1)= 1,104845

Dla metody RK2:

k

1

=1, k

2

=1,09, φ=1,045, y

i

=1,1045

y(0,1)=1,104821

Rozwiązanie dokładne to funkcja y=2+2x+x

2

-e

x

, która w punkcie x=0,1 przyjmuje wartość

1,104829.

1. Jankowscy, Janina i Michał. Przegląd Metod i Algorytmów Numerycznych, cz.1.
Warszawa : Wydawnictwa Naukowo-Techniczne, 1981. ISBN 83-204-0226-3.