Numeryczne całkowanie

układów dynamicznych

metodą Rungego-Kutty

dr Joanna Napiórkowska

Instytut Matematyki i

Informatyki Uniwersytet

Opolski

W wielu dziedzinach nauki pojawiają się
problemy natury dynamicznej, zmienne w

czasie:

- w naukach społecznych, np. problemy

dotyczące zbiorowisk ludzkich,

- w naukach ekonomicznych np. mechanizmy

cyklu ekonomicznego,

- w naukach przyrodniczych, np. podukłady

takie jak serce i jego neurologiczny system
sterowania,

- w naukach fizycznych, np. zagadnienie trzech

ciał.

W modelowaniu takich układów

dynamicznych

często stosuje się numeryczne całkowanie
równań różniczkowych zwyczajnych.

Rozwój metod numerycznych:
I.

praca Adamsa i Bashfortha (1883 r.)
praca

C.Rungego (1895 r.)

praca

M.W.Kutty (1901 r.)

II. zastosowanie elektronicznych maszyn

cyfrowych (od początku lat 60-tych XX w.)

Martin Wilhelm Kutta

(1867-1944)

Carl Runge
(1856-1927)

Rozważmy zagadnienie początkowe

Niech

będą punktami przedziału

oraz

i . Niech każdemu punktowi

odpowiada liczba będąca przybliżeniem
wartości rozwiązania dokładnego . Obliczenia
mogą być wykonywane ze stałą lub ze zmienną
długością kroku całkowania

.

 















0

)

(

,

)),

(

,

(

)

(

'

y

a

y

b

a

t

t

y

t

f

t

y

)

,

2

,

1

,

0

(





i

t

n

 

b

a,

1





n

n

t

t

a

t 

0

n

t

n

y

)

(

n

t

y

1







n

n

n

t

t

h

Metody Rungego-Kutty określamy ogólnie

wzorem

(1)

gdzie

(2)

przy czym

(3)

Liczba m określa ilość etapów metody.

.

,

,

2

,

1

,

0

,

1

1

const

h

n

k

w

h

y

y

m

i

i

i

n

n

















,

,

,

1

),

,

(

1

m

i

k

a

h

y

h

c

t

f

k

m

j

j

ij

n

i

n

i















.

,

,

1

,

1

m

i

a

c

m

j

ij

i











Współczynniki

wygodnie jest

przedstawić w postaci tablicy

ij

i

i

a

c

w

,

,

1

c

2

c

m

c



1

w

2

w



1



m

w

m

w

21

a

31

a

32

a

1

m

a

2

m

a



1

, 

m

m

a

 

11

a

3

c

m

a

1

mm

a



22

a



Jeżeli macierz kwadratowa

ma

zerowe

elementy na głównej przekątnej oraz

nad nią,

to metoda Rungego-Kutty jest jawna.
Wtedy współczynniki redukują się do

postaci

]

[

ij

a

),

,

(

1

n

n

y

t

f

k 

,

1

),

,

(

1

1















i

k

a

h

y

h

c

t

f

k

i

j

j

ij

n

i

n

i

.

1

,

1

1











i

a

c

i

j

ij

i

i

k

Załóżmy, że zamiast wstawiamy do wzoru (1)
wartość dokładną

. Wówczas dla wartości

dokładnej

, dla

prawdziwa jest

następująca zależność

gdzie

jest błędem spełnienia wzoru (1)

przez

wartości rozwiązania dokładnego oraz.

Wielkość błędu aproksymacji określa dokładność
metody.

)

(

1



n

t

y

),

(

)

(

)

(

)

(

1

1

h

r

h

k

w

h

t

y

h

t

y

n

m

i

i

i

n

n















h

t

t

n

n





1

)

(

1

h

r

n

)

(

n

t

y

)

(

1



n

t

y

n

y

)

(

n

t

y

Metoda Rungego-Kutty jest rzędu , jeżeli dla
każdego zagadnienia początkowego

oraz

Metoda Rungego-Kutty rzędu wymaga
ustanowienia warunków wiążących

współczynniki
.

p

0

)

0

(

,

,

0

)

0

(

,

0

)

0

(

)

(

1

'

1

1













p

n

n

n

r

r

r



.

0

)

0

(

)

1

(

1







p

n

r

p

ij

i

i

a

c

w

,

,

Dla metody rzędu pierwszego mamy

warunek

Dla metody rzędu drugiego, oprócz warunku

poprzedniego, mamy .

Dla metody rzędu trzeciego dodajemy

warunki

.

1

1







m

i

i

w







m

i

i

i

c

w

1

2

1

.

6

1

,

3

1

1

1

1

1

2



















i

j

j

ij

m

i

i

m

i

i

i

c

a

w

c

w

Dla metody rzędu czwartego dodatkowo

mamy

Liczba warunków rośnie wraz ze

wzrostem

rzędu aproksymacji

,

8

1

,

4

1

1

1

1

1

3



















m

i

i

j

j

ij

i

i

m

i

i

i

c

a

c

w

c

w

.

24

1

,

12

1

1

1

1

1

1

1

1

1

2

  

 





















m

i

i

j

j

k

k

jk

ij

i

m

i

i

j

j

ij

i

c

a

a

w

c

a

w

p

200

85

37

17

8

4

2

1

8

7

6

5

4

3

2

1

p

l

l

Zależność między ilością etapów m a

rzędem

aproksymacji p:

dla

dla

dla

7

,

6

,

5



m

1



m

p

2



m

p

8



m

4

,

3

,

2

,

1



m

m

p 

Dla (metoda jednoetapowa):

, gdzie

.

W tym przypadku jedyną możliwością jest rząd
aproksymacji

. Z warunku

gwarantującego, że

metoda jest rzędu pierwszego wynika, że

.

Wówczas dostajemy

metoda Eulera

Postać tabelaryczna: 0 0

1

1

1

1

k

hw

y

y

n

n







)

,

(

1

n

n

y

t

f

k 

1



p

)

,

(

1

n

n

n

n

y

t

hf

y

y







1



m

1

1



w

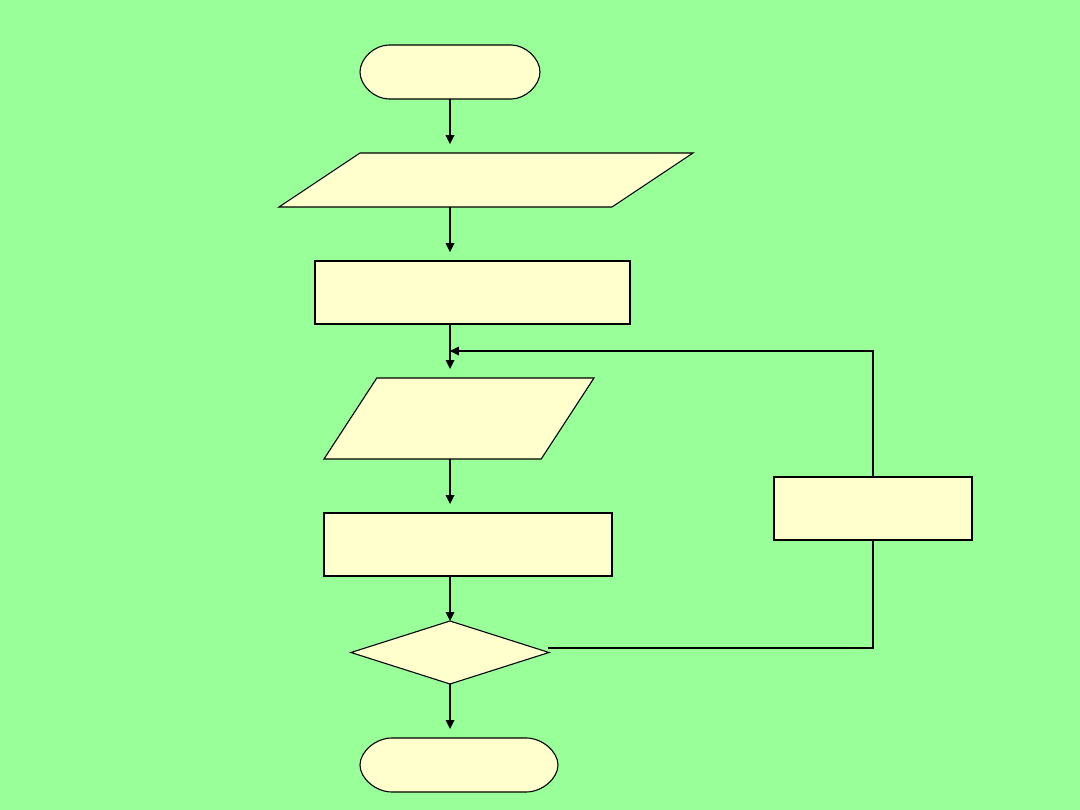
Algorytm
metody
Eulera

n

t

t 

N

0

:

,

:

y

y

a

t





Podaj

h

y

b

a

,

,

,

0

Koniec

Początek

b

t 

)

,

(

:

y

t

hf

y

y





Drukuj y

t,

h

t

t





:

T

Istnieje nieskończenie wiele dwuetapowych
metod Rungego-Kutty rzędu drugiego
(dowód: A. Krupowicz, Metody numeryczne...)

Przykład 1: ulepszona metoda Eulera

gdzie

0 0 0

½ ½ 0

0 1

,

2

1

hk

y

y

n

n







),

,

(

1

n

n

y

t

f

k 

).

2

1

,

2

1

(

1

2

hk

y

h

t

f

k

n

n







Przykład 2: metoda Eulera-Cauchy’ego

gdzie

0 0 0

1 1 0
½ ½

Podobnie istnieje nieskończenie wiele

metod

trójetapowych rzędu trzeciego oraz metod
czteroetapowych rzędu czwartego.

,

2

1

2

1

2

1

1





















k

k

h

y

y

n

n

),

,

(

1

n

n

y

t

f

k 

).

,

(

1

2

hk

y

h

t

f

k

n

n







Popularna metoda czteroetapowa rzędu

czwartego

najczęściej kojarzona z nazwiskami Rungego i

Kutty

gdzie

0 0 0 0 0
½ ½ 0 0 0
½ 0 ½ 0 0
1 0 0 1 0

),

2

2

(

6

1

4

3

2

1

1

k

k

k

k

h

y

y

n

n













),

,

(

1

n

n

y

t

f

k 

),

2

1

,

2

1

(

2

3

hk

y

h

t

f

k

n

n







),

2

1

,

2

1

(

1

2

hk

y

h

t

f

k

n

n







).

,

(

3

4

hk

y

h

t

f

k

n

n







6

1

6

1

3

1

3

1

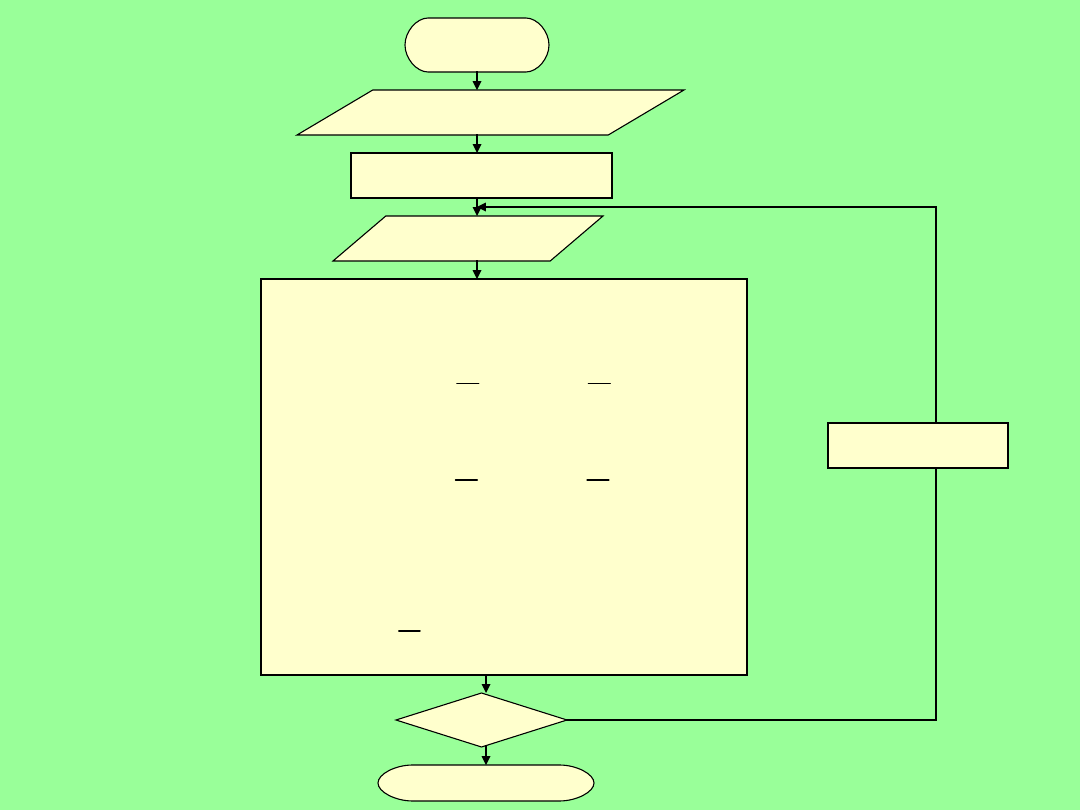
Algorytm

Początek

Podaj

h

y

b

a

,

,

,

0

0

:

,

:

y

y

a

t





Drukuj

y

t,

)

2

2

(

6

1

:

)

,

(

:

)

2

1

,

2

1

(

:

)

2

1

,

2

1

(

:

)

,

(

:

4

3

2

1

3

4

2

3

1

2

1

k

k

k

k

h

y

y

hk

y

h

t

f

k

hk

y

h

t

f

k

hk

y

h

t

f

k

y

t

f

k

n

n

n

n

n

n

n

n































b

t 

Koniec

N

h

t

t





:

T

Zastosowanie metody Rungego-Kutty:

Rozwiązanie równania różniczkowego

z warunkiem początkowym

1. Metoda Rungego-Kutty
Obliczamy kolejno dla kroku

y

t

y





'

1

)

0

( 

y

2

,

0



h

8

,

0

))

1

(

2

,

0

2

1

1

(

2

,

0

2

1

)

2

1

1

,

2

1

(

1

)

1

,

0

(

1

2

1





























hk

h

f

k

f

k

...
Następne przybliżenia obliczamy

analogicznie.

636

,

0

))

82

,

0

(

2

,

0

1

(

2

,

0

)

1

,

(

82

,

0

))

8

,

0

(

2

,

0

2

1

1

(

2

,

0

2

1

)

2

1

1

,

2

1

(

3

4

2

3









































hk

h

f

k

hk

h

f

k

8708

,

0

))

636

,

0

(

)

82

,

0

(

2

)

8

,

0

(

2

)

1

((

2

,

0

6

1

1

)

2

2

(

6

1

)

(

)

2

,

0

(

4

3

2

1

0

1

1















































k

k

k

k

h

y

y

t

y

y

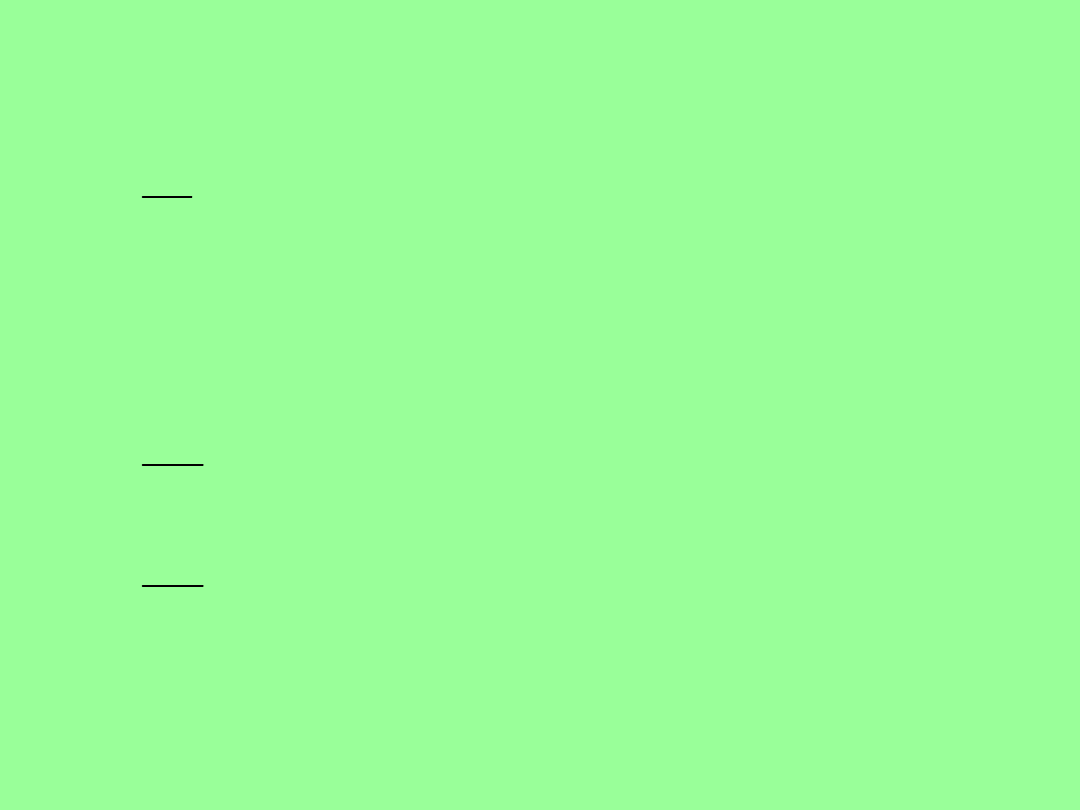
2. Metoda analityczna

R

C

e

C

t

t

y

C

e

te

t

C

te

dt

dC

Ce

t

e

C

e

dt

dC

e

t

C

t

y

R

C

Ce

t

y

y

t

dt

dy

t

t

t

t

t

t

t

t

t

















































~

,

~

1

)

(

~

)

(

)

(

)

(

)

(

,

)

(

Po uwzględnieniu warunku początkowego

Stąd

...

Dla uzyskania większej dokładności wyników
można zastosować mniejszy krok

całkowania.

t

e

t

t

y









2

1

)

(

84

,

0

82

,

0

2

1

2

,

0

2

1

2

,

0

)

2

,

0

(

2

,

0





















e

y

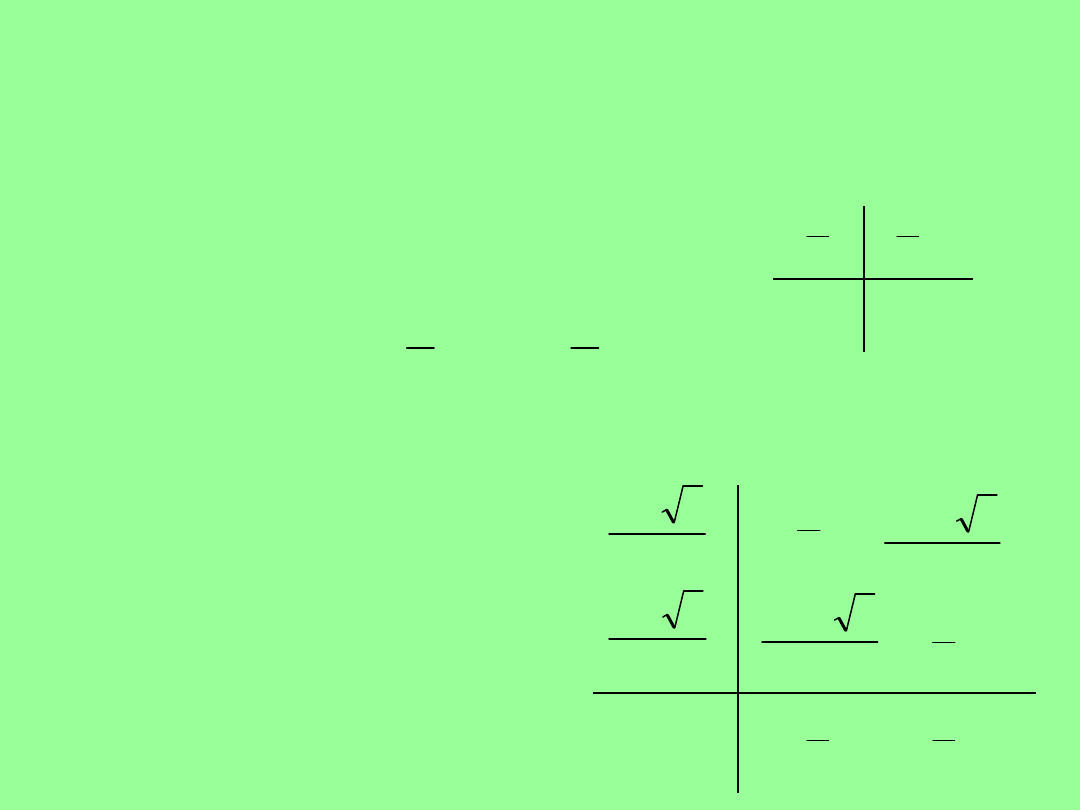
Przykład jednoetapowej metody niejawnej

rzędu

drugiego (

)

Przykład dwuetapowej metody niejawnej

rzędu

czwartego ( )

2

,

1 

 p

m

)

2

1

,

2

1

(

,

1

1

1

1

hk

y

h

t

f

k

hk

y

y

n

n

n

n













4

,

2 

 p

m

6

3

3

6

3

3

4

1

4

1

12

3

2

3

12

3

2

3

2

1

2

1

2

1

2

1

1

W przypadku układów równań

różniczkowych

wzory określające metodę Rungego-

Kutty mają tę

samą postać, ale odpowiednie wielkości

skalarne

zastępuje się wielkościami

wektorowymi

.

,

,

2

,

1

,

0

,

1

1

const

h

n

k

w

h

y

y

m

i

i

i

n

n























.

,

,

1

),

,

(

1

m

i

k

a

h

y

h

c

t

f

k

m

j

j

ij

n

i

n

i























Do rozwiązania układu równań

stosujemy zasadę jednej trzeciej Kutty-Simpsona

gdzie współczynniki są
określone analogicznie jak w metodzie Rungego-
Kutty czwartego rzędu dla pojedynczego

równania.











)

,

,

(

'

)

,

,

(

'

z

y

t

g

z

z

y

t

f

y

),

2

2

(

6

1

),

2

2

(

6

1

4

3

2

1

1

4

3

2

1

1

l

l

l

l

h

z

z

k

k

k

k

h

y

y

n

n

n

n

























4

3

2

1

4

3

2

1

,

,

,

,

,

,

,

l

l

l

l

k

k

k

k

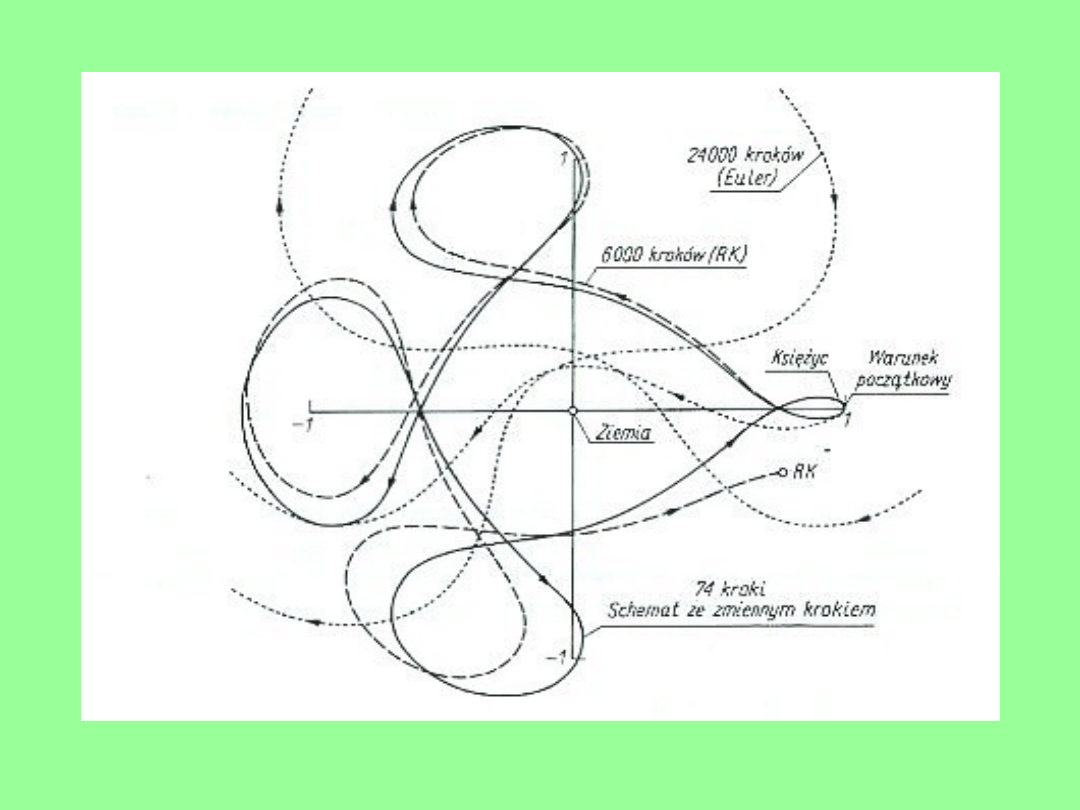
Zastosowanie metody Rungego-Kutty:
Zagadnienie trzech ciał w mechanice

nieba

Rozważmy układ równań opisujących ruch
satelity między Ziemią a Księżycem

gdzie






































2

1

2

1

)

1

(

2

1

)

1

(

2

D

z

D

z

y

z

z

D

y

D

y

z

y

y



















.

01228

,

0

,

)

)

1

((

,

)

)

((

2

/

3

2

2

2

2

/

3

2

2

1























z

y

D

z

y

D

Współrzędne opisują położenie satelity
względem środka masy układu Księżyc-Ziemia.
Ziemia znajduje się w punkcie , a Księżyc
w punkcie

. Dla dostatecznie małych

i warunków początkowych

zagadnienia tego typu mają rozwiązania

okresowe

z okresem

.



)

,

( z

y

)

0

,

(





)

0

,

1

(





,

0

)

0

(

,

0

)

0

(





y

y



06522

,

17



T

00159

,

2

)

0

(

,

0

)

0

(







z

z



Obliczenia numeryczne wykonano
- metodą Eulera (24000 kroków, ),
- metodą Rungego-Kutty rzędu czwartego (6000

kroków,

),

- metodą rzędu czwartego ze zmiennym krokiem

z dokładnością 10

-3

.

Wynik obliczeń metodą Rungego-Kutty był
dokładniejszy niż metodą Eulera.

Najdokładniejszy

wynik uzyskano w trzecim przypadku. Ta metoda
była też najszybsza (74 kroki obliczeń) (rys.).

24000

/

T

h 

6000

/

T

h 

Podsumowanie:

Metody Rungego-Kutty

- mają prostą formułę je określającą,

- są metodami jednokrokowymi,
- są metodami samostartującymi,
- dla dużej aproksymacji mają duży koszt

obliczeń,

- są pracochłonne, zakres ich

stosowalności jest ograniczony.

Literatura:
K.E. Atkinson, An Introduction to Numerical

Analysis, John Wiley & Sons.

J.C. Butcher, Numerical methods for ordinary

differential equations (wersja elektroniczna).

E. Hairer, S.P. Nørsett, G. Wanner, Solving

Ordinary Differential Equations, Springer.

A. Krupowicz, Metody numeryczne zagadnień

początkowych równań różniczkowych, PWN.

A. Ralston, Wstęp do analizy numerycznej, PWN.