G. Wieczorkowska & J. Wierzbiński (2005)
1
2.6. Testowanie hipotez
Wiemy już, że informacja o tym, że liczba pochodzi z rozkładu normalnego o znanej
średniej i o odchyleniu standardowym, pozwala nam na określanie prawdopodobieństw. Znając
średnią oraz odchylenie standardowe tego rozkładu i korzystając z tablic, możemy określić, jaki
procent populacji będzie miał wynik w danym przedziale. Ten procent populacji przekłada się na
odpowiedź na pytanie o prawdopodobieństwo, że wylosowana osoba otrzyma wynik z danego
przedziału.
Odpowiadanie na pytanie, jakie jest prawdopodobieństwo otrzymania danego wyniku,
jest jedną z najczęstszych aktywności osób zajmujących się statystyką. Statystyka niczego nie
wyklucza, ale wylicza prawdopodobieństwa otrzymania określonego wyniku. Przeanalizujmy sposób
wnioskowania zastosowany przez Krystynę.
Gdy wypełniłam test mierzący szybkość czytania, okazało się, że mój wynik to 140 słów na
minutę. Otrzymałam informację, że wyniki w tym teście mają rozkład normalny o średniej 200 słów na
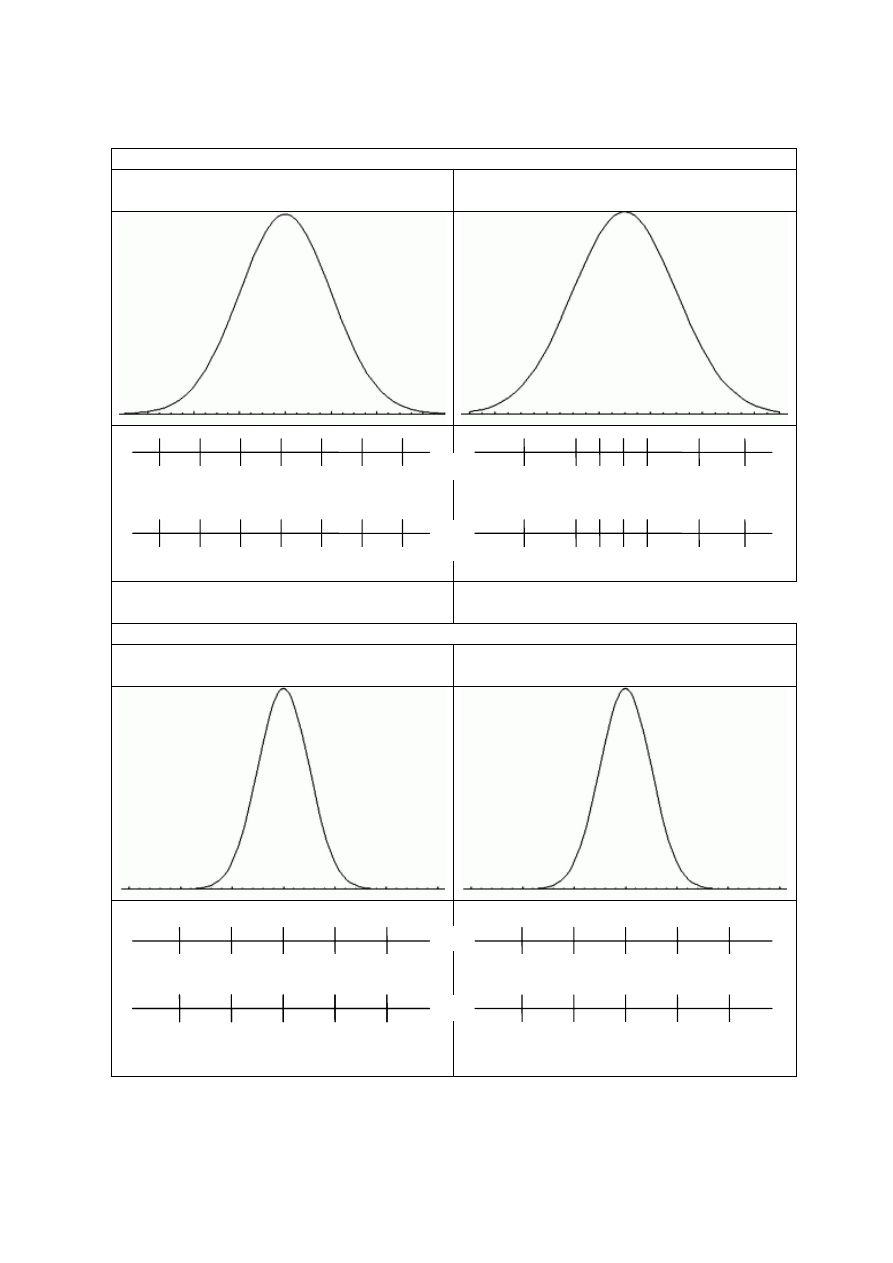
minutę i odchyleniu standardowym 20 [N(200, 20), rys. 2.6 - diagram A1]. Oznacza to, że mój wynik
plasuje mnie na bardzo skrajnej pozycji, ponieważ jeśli wystandaryzuję ten wynik, czyli od 140 odejmę
200, a następnie podzielę przez 20, okaże się, że mój wynik odpowiada z = - 3. W rozkładzie
normalnym 95% przypadków mieści się w granicach dwóch odchyleń standardowych – poniżej i
powyżej średniej. Jeżeli otrzymałam wynik z = - 3, oznacza to, że jestem niesłychanie unikalną osobą,
należę do bardzo małej frakcji osób w populacji. Jak to możliwe? Może tekst był napisany w obcym
języku? Jeżeli jednak był napisany w języku dobrze mi znanym, może wypełniałam go z przerwami –
robiłam w między czasie makijaż albo poszłam się czegoś napić? Jeżeli jednak jestem pewna, że nic
takiego nie miało miejsca, mogę podejrzewać, że informacja mówiąca, że wyniki tego testu pochodzą
z rozkładu normalnego o średniej 200 i odchyleniu standardowym 20, jest nieprawdziwa. Biorąc pod
uwagę liczbę lat, jaką spędziłam w ławach szkolnych, stwierdzenie, że należę do tak „elitarnej” grupy
(tak wolno czytającej w porównaniu z resztą populacji), wydaje się być mało prawdopodobnym. Mam
więc silne podstawy do kwestionowania informacji, że średnia w populacji wynosi 200. Jeżeli
dowiem się, że średnia w populacji wynosi 150 [N(150, 20), rys. 2.6 - diagram A2], uzyskany przeze
mnie wynik (140) oznaczać będzie1/2 odchylenia standardowego poniżej średniej. Nadal nie jest
to wynik, który by mnie satysfakcjonował, ale należę już do dość licznej grupy osób. Tym samym
prawdopodobieństwo otrzymania takiego wyniku wcale nie jest niskie, a co za tym idzie - nie mam
podstaw do kwestionowania założenia, że średnia w populacji to 150.
G. Wieczorkowska & J. Wierzbiński (2005)
2
Rozkład zmiennej SZYBKOŚĆ CZYTANIA w populacji
N(200, 20)
Diagram A1
N(150, 20)
Diagram A2
200
180
220
150
140
160
180
200
130
110
-1 -0.5 0
0.5
1.5
2.5
-2
x
Rozkład średnich z prób 16-osobowych
N(200, 5)
Diagram B1
N(150, 5)
Diagram B2
Rys. 2.6. Rozkład zmiennej SZYBKOŚĆ CZYTANIA w populacji (diagramy A1 i A2) i rozkład średnich
z prób 16-osobowych (diagramy B1 i B2)
150
140
160
170
120
0
-2
-4
2
4
200
190
210
220
180
0
-2
-4
2
4
240
260
160
140
240
z
-3
0
3
2
-1
-2
1
M
z
M
G. Wieczorkowska & J. Wierzbiński (2005)
3
Należy zwrócić uwagę na sposób wnioskowania. Krystyna założyła, że otrzymana informacja
o parametrach rozkładu (rozkład normalny o znanej średniej i odchyleniu standardowym) jest
prawdziwa – i, wykorzystując tablice rozkładu normalnego, określiła, jak bardzo prawdopodobne jest
otrzymanie jej wyniku. Dla rozkładu normalnego wyniki, dla których z>1,96 lub z<-1,96 można określić
jako mało prawdopodobne, ponieważ prawdopodobieństwo ich otrzymania jest mniejsze niż 0,05.
Wartość progowa p=0,05, która służy oddzielaniu wyników prawdopodobnych od mało
prawdopodobnych, jest wynikiem umowy społecznej. W niektórych przypadkach próg ten jest
ustalony wyżej, na p=0,01 lub p=0,001. Wynik empiryczny jest rzeczą stałą, czyli nie można go
zmienić bez powtarzania badań, natomiast można zmieniać hipotezy (założenia, dla których
wyliczamy rozkład). W przytoczonym przykładzie Krystyna zmieniła założenia (hipotezy) – pierwsza
hipoteza mówiła, że średnia w populacji wynosi 200 słów na minutę, druga – że 150. Biorąc pod
uwagę swój wynik, uznała, że pierwsza hipoteza jest fałszywa. Nie miała jednak podstaw, aby
odrzucić drugą hipotezę - mówiącą, że średnia w populacji wynosi 150 słów na minutę, ponieważ jej
wynik należał do grupy wyników typowych (-1<z<1). Aby odrzucić założenie, że µ=200, jej wynik
w teście powinien być większy niż 239 lub mniejszy niż 189. Aby odrzucić założenie, że µ=150, jej
wynik w teście powinien być większy niż 160 lub mniejszy niż 110.
N(200, 20)
N(150, 20)
z>1,96
X >239,2
X >189,2
z<-1,96
X <160,8
X <110,8
Powtórzmy: hipotezę odrzucamy, gdy otrzymany przez nas wynik należy do zbioru wyników
mało prawdopodobnych. Należy pamiętać, że to, otrzymanie jakich wyników uznamy jako mało
prawdopodobne, zależy nie tylko od ustalonego progu prawdopodobieństwa (0,05 czy też np. 0,001),
ale także od hipotezy (założenia, na podstawie którego wyliczamy prawdopodobieństwa).
Hipotezy zerowe, które poddajemy testowi, muszą być precyzyjnie sformułowane. Gdyby
hipoteza była sformułowana nieprecyzyjnie, np.: „Średnia w populacji jest większa od 160”, nie
moglibyśmy wyliczyć prawdopodobieństw. W tabeli poniżej mamy kilka przykładów par precyzyjnie
sformułowanych hipotez zerowych i hipotez badawczych, które badacz chciałby potwierdzić.
Hipoteza badawcza (to, czego chcielibyśmy
dowieść)
Hipoteza zerowa, wykorzystywana do
wyliczania prawdopodobieństw
Uczeni przez nas studenci nie pochodzą z populacji o
średniej równej 200.
[μ ≠ 200]
Uczeni przez nas studenci pochodzą
z populacji o średniej równej 200.
[μ = 200]
Kwiatki w jednej doniczce są wyższe od kwiatków w
doniczce drugiej.
Kwiatki w obu doniczkach pochodzą z tej
samej populacji (różnica w wysokości między
kwiatkami jest nieistotna statystycznie).
Kobiety mają wyższy poziom empatii niż mężczyźni.
Kobiety i mężczyźni nie różnią się w poziomie
empatii (pochodzą z populacji o tej samej
średniej).
Naświetlanie kwiatków promieniami A powoduje ich
wzrost.
Średni przyrost wysokości naświetlanych
kwiatków wynosi w określonej populacji zero.
Istnieje dodatnia korelacja między ilością wypijanej
zielonej herbaty a poziomem energii.
Korelacja między ilością wypijanej zielonej
herbaty a poziomem energii wynosi w
populacji zero.
2.7. Testowanie hipotezy dotyczącej średniej w grupie
G. Wieczorkowska & J. Wierzbiński (2005)
4
Jak pisaliśmy w pierwszym rozdziale, nie mając klonów do badań, w naukach społecznych
posługujemy się zbiorowymi klonami, czyli badamy różnice między grupami. Testowane hipotezy
dotyczą populacji, z których pochodzą te grupy, a nie samych grup.
Jeżeli chcemy sprawdzić szybkość czytania grupy naszych studentów, musimy poprosić ich o
przeprowadzenie testu, któremu poddała się Krystyna, a następnie policzyć średnią w badanej grupie.
Podstawowe pytanie - z czym możemy porównać taką średnią? Liczba 150 może być wynikiem
pojedynczej osoby lub średnim wynikiem 20-osobowej grupy osób. Choć pozornie liczba wygląda tak
samo, to nie można porównywać średnich z grupy wyników z wynikiem pojedynczych osób. Te liczby
pochodzą z różnych rozkładów. Dzięki pracy matematyków wiemy, z jakiego rozkładu pochodzi
średnia arytmetyczna.
Średnią z grupy wyników porównujemy
z rozkładem średnich
ze wszystkich możliwych prób o danej liczebności.
1
Szczęśliwie dla nas matematycy udowodnili bardzo ważne twierdzenie, które mówi, że
rozkład średnich z dużych prób jest rozkładem normalnym. Ma on średnią równą średniej
w populacji, a jego odchylenie standardowe zależy od odchylenia standardowego zmiennej
i wielkości badanej próby.
Odchylenie standardowe rozkładu średnich jest dla nas bardzo ważną informacją, więc
otrzymało specjalną nazwę - nazywa się je błędem standardowym średniej. Aby go obliczyć,
wystarczy podzielić odchylenie standardowe zmiennej przez pierwiastek kwadratowy z liczebności
próby. W naszym przykładzie odchylenie standardowe zmiennej wynosiło 20, a więc błąd
standardowy średniej dla próby 16-osobowej wyniesie: 20/√16=5 (porównaj diagram A1 i B1 oraz A2
i B2 – rys. 2.6). Gdyby próba była 100-elementowa, błąd standardowy średniej wyniósłby: 20/√100=2.
Jest to zgodne z tym, co podpowiada intuicja - nie można porównywać średniej z próby 100-
elementowej ze średnią z próby 10-elementowej.
Zauważmy, że średnie są skupione wokół średniej swojego rozkładu dużo bardziej niż wyniki
pojedynczych osób. Wynik 140, uzyskany w teście czytania przez pojedynczą osobę [N(150,20)],
oznacza z=-1/2 (rys. 2.6. - diagram A2). Średnia dla 16-osobowej grupy, wynosząca w tym samym
teście M=140 [N(150,5)], oznacza z
M
=-2 (rys. 2.6. - diagram B2).
Powtórzmy: Rozkład średnich ma tę samą średnią, co rozkład zmiennej w populacji, ale
mniejsze odchylenie standardowe. Znając rozkład średnich, możemy określić, jakie wyniki
musielibyśmy otrzymać w badaniu, aby były mało prawdopodobne - przy założeniu o prawdziwości
hipotezy zerowej. Sposób wnioskowania jest analogiczny jak poprzednio. Zakładamy, że wylosowana
próba pochodzi z populacji o znanej średniej, a następnie patrzymy, czy wynik grupy (średnia) należy
do zbioru wyników mało prawdopodobnych - przy założeniu, że hipoteza zerowa jest prawdziwa, czy
też należy do wyników prawdopodobnych. Jeżeli otrzymujemy wynik, który należy do zbioru wyników
mało prawdopodobnych, mamy podstawy do odrzucenia naszego założenia (hipotezy zerowej).
Postępujemy analogicznie, czyli jak wtedy, gdy uznaliśmy, że wynik w teście czytania Krystyny (równy
trzem odchyleniom standardowym poniżej średniej) podważa założenie, które przyjęliśmy jako
prawdziwe, obliczając jej wynik standaryzowany. Gdy oceniamy średnią grupy, postępujemy tak
samo. Jeżeli otrzymujemy wynik należący do klasy wyników mało prawdopodobnych - przy założeniu
prawdziwości hipotezy zerowej, odrzucamy hipotezę zerową (uznajemy ją za fałszywą).
Warto zauważyć, że hipoteza zerowa (założenie używane do wyliczania prawdopodobieństw)
jest przeciwstawna do hipotezy, którą chcemy potwierdzić. Jeżeli chcemy stwierdzić, że nasi studenci
czytają szybciej niż populacja, zakładamy, że pochodzą z populacji o średniej równej 200 (μ = 200),
1
Aby zapoznać się ze sposobem wyliczania rozkładu średnich dla małej populacji, należy sięgnąć do literatury
[20].
G. Wieczorkowska & J. Wierzbiński (2005)
5
przy tym założeniu przeliczamy średnią w grupie studentów na z-ty - i sprawdzamy, czy otrzymana
wartość z
M
należy do wyników mało prawdopodobnych, czy też nie.
Struktura dowodzenia statystycznego jest podobna do „dowodzenia nie wprost”. Chcemy
wykazać, że studenci pochodzą z populacji μ ≠ 200, więc zakładamy, że prawdziwe jest
przeciwieństwo tego, co chcemy pokazać, czyli μ = 200. Stosując klasyczne wnioskowanie „nie
wprost”, powinniśmy doprowadzić do sprzeczności. W przypadku wnioskowania statystycznego nie
doprowadzamy do sprzeczności, ale wykazujemy, że otrzymany wynik jest mało prawdopodobny, co
pozwala na odrzucenie hipotezy zerowej i staje się „dowodem” – nie wprost – prawdziwości zdania
zapisanego w hipotezie badawczej, które chcieliśmy potwierdzić.
Jeżeli wyliczone prawdopodobieństwa pozwalają na odrzucenie hipotezy zerowej (są
mniejsze od 0,05), mówimy, że otrzymaliśmy wyniki istotne statystycznie. Jeżeli nie mamy podstaw
do odrzucenia hipotezy zerowej, mówimy, że wyniki tego badania są nieistotne statystycznie.
2.8. Testowanie istotności różnicy między dwiema niezależnymi grupami
wyników
Aby porównywać średnie pochodzące z dwóch małych grup, wyliczamy według podanego
wzoru wartość t. Wzór na t wymaga wprowadzenia informacji o charakterystykach dwóch zbadanych
prób (średnich: M
1
, M
2
i odchyleniach standardowych: s
1
, s
2
).
2
Nie wchodząc w szczegóły - ważne dla
nas jest to, że statystyka t ma znany rozkład, dzięki któremu możemy określić prawdopodobieństwo
otrzymywania różnych średnich w badaniach, tak jak robiliśmy to poprzednio. Pokażemy to na
przykładzie porównywania wysokości kwiatków w dwóch doniczkach (rysunki 2.7
i 2.8).
Zauważyliśmy, że kwiatki posadzone w doniczce lewej są niższe (M
1
=200) niż kwiatki
w doniczce prawej (M
2
=330). Testowana hipoteza zerowa mówi, że kwiatki w obu doniczkach
pochodzą z populacji o tej samej średniej wysokości. Mierząc wysokości kwiatków w obu doniczkach,
możemy wyliczyć statystykę t. Aby otrzymany wynik, wyliczony na podstawie różnicy średnich
kwiatków
z doniczki lewej i prawej, można było uznać jako nieprawdopodobny (p<0,05), wartość bezwzględna
t musi być większa niż 2,179 (tę wartość odczytujemy z tablic rozkładu statystyki t, analogicznie jak to
robiliśmy w przypadku rozkładu normalnego). Wynik nieprawdopodobny pozwala nam na odrzucenie
hipotezy zerowej mówiącej o braku różnic w wysokości kwiatków w populacji - i nazywany jest
wynikiem istotnym statystycznie. Wyniki, które nie pozwalają na odrzucenie hipotezy zerowej,
określane są jako nieistotne statystycznie.
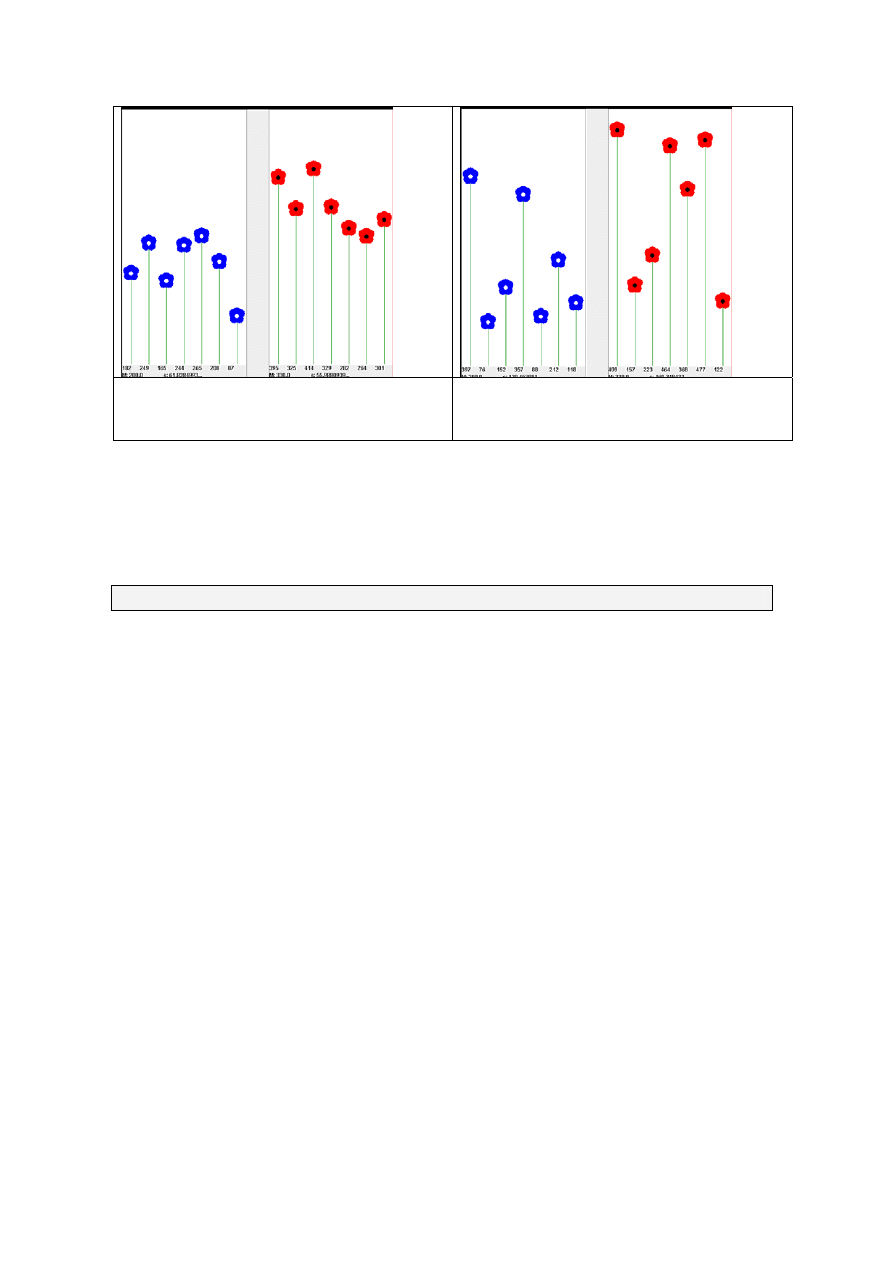
Na rysunkach poniżej możemy zobaczyć, że wartość t zależy nie tylko od różnicy średnich,
ale i od różnicy wariancji w doniczkach.
2
Wzór na t różni się w zależności od tego, czy odchylenia standardowe w badanych próbach są równe czy nie, ale różnice
w wielkości t są nieznaczne, dlatego pominiemy je tutaj.
G. Wieczorkowska & J. Wierzbiński (2005)
6
Rys. 2.7. Porównanie wysokości kwiatków w obu
doniczkach. Wartości statystyk wynoszą:
t
n
=4,12 t
z
=3,72 r=-0,22
Rys. 2.8. Porównanie wysokości kwiatków w obu
doniczkach. Wartości statystyk wynoszą:
t
n
=1,76 t
z
=3,33 r=0,76
Różnicę średnich (wynoszącą 130) między kwiatkami przedstawionymi na rysunku 2.7
uznamy za istotną statystycznie, bo t
n
=4,12 >2,179.
Różnicę średnich (wynoszącą 130) między kwiatkami przedstawionymi na rysunku 2.8
uznamy za nieistotną statystycznie, bo t
n
=1,76 <2,179.
2.9. Testowanie istotności różnicy między dwiema zależnymi grupami wyników
Różnicę między średnimi będziemy liczyć inaczej, jeżeli wyniki w obu grupach pochodzą od
tych samych osób - w takiej sytuacji naprawdę mamy do czynienia z parami wyników. To, że średnia
zamożność społeczeństwa po zmianie systemowej wzrosła, może być wynikiem tego, że prawie
wszyscy wzbogacili się - ale może też być konsekwencją tego, że tylko niektórzy bardzo się
wzbogacili, a reszta zubożała. Jeżeli kwiatki z prawej doniczki przedstawiają te same kwiatki, co
w doniczce lewej - po np. naświetlaniu, to dla każdego kwiatka możemy policzyć jego zmianę
wysokości i zastosować wzór na t dla prób zależnych (t
z).
Abyśmy mogli uznać różnicę między
wysokością kwiatków przed i po naświetlaniu za mało prawdopodobną (gdy hipoteza zerowa zakłada
brak różnic), wartość bezwzględna wyliczonego t
z
musi być większa niż 2,447.
Na rysunku 2.8 różnica między kwiatkami jest nieistotna statystycznie - jeżeli wiemy, że
kwiatki pochodzą z dwóch niezależnych prób, ale byłaby istotna, gdyby doniczka z prawej
przedstawiała kwiatki z lewej doniczki, np. po intensywnym naświetlaniu. W takim wypadku
moglibyśmy policzyć współczynnik korelacji miedzy wysokością kwiatków przed i po naświetlaniu. Dla
kwiatków na rysunku 2.8 współczynnik korelacji jest dodatni i wynosi 0,76.
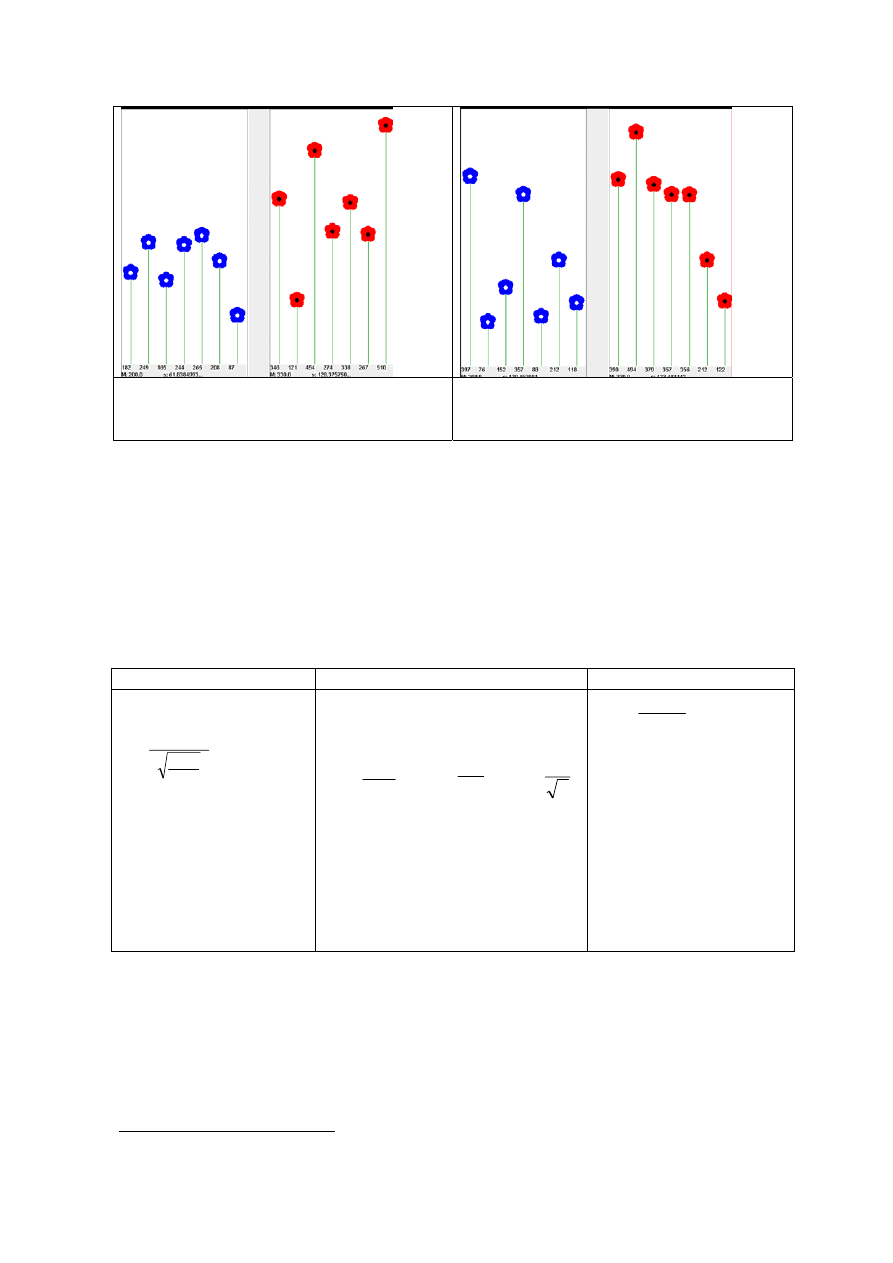
Może się jednak okazać, że współczynnik korelacji jest ujemny - jak na rysunku 2.9, gdzie r=-
0,79. Oznacza to, że mimo tego, że po naświetlaniu średnia wzrosła z 200 do 330, to jednak kwiatki
duże przed naświetlaniem teraz zmarniały, gdy tymczasem małe urosły. Na rysunku 2.10 korelacja
między wysokością kwiatków przed i po naświetlaniem jest „zerowa” (r=0,06).
G. Wieczorkowska & J. Wierzbiński (2005)
7
Rysunek 2.9. Porównanie wysokości kwiatków w
obu doniczkach. Wartości statystyk wynoszą:
t
n
=-2,41 t
z
=-1,9 r=-0,79
Rysunek 2.10. Porównanie wysokości kwiatków
w obu doniczkach. Wartości statystyk wynoszą:
t
n
=1,92 t
z
=-1,98 r=0,06
Podsumowując - ta sama różnica średnich może okazać się istotna lub nieistotna
statystycznie. Zależy to od zróżnicowania w grupach oraz tego, czy porównywane średnie dotyczą
tych samych (dane zależne/ pary wyników) czy różnych (dane niezależne) obiektów. Choć analizy
danych wykonywane są przy użyciu pakietów statystycznych, dla tych Czytelników, którzy lubią
oglądać wzory, zestawiliśmy je dla wykorzystywanych w tym rozdziale statystyk (tabela 2.8). Rozkład
statystyki t Studenta (nazwanej od pseudonimu matematyka, który go opisał) zależy od liczebności
próby, co jest podawane w postaci wartości df
3
.
Tab. 2.8. Wzory na obliczanie statystyk wykorzystywanych w tym rozdziale
t
n
dla prób niezależnych
t
z
dla prób zależnych
r-współczynnik korelacji
dla prób o równych
liczebnościach
:
n
s
s
M
M
2
2
2
1
2
1
n
t
+
−
=
df = 2(n – 1),
gdzie:
n – liczebność każdej z prób
M
1
, M
2
-
średnie w
poszczególnych grupach
s
1
, s
2
- odchylenia
standardowe w
poszczególnych grupach
dla każdej osoby tworzymy zmienną
D=│X 1-X 2│, następnie liczymy średnią
i jej odchylenie standardowe
:
D
M
D
s
D
M
D
z
s
M
t
=
N
D
M
D
Σ
=
n
s
s
D
M
D
=
df = n-1
n- liczba par wyników
gdzie:
- średnia różnica
D
M
D
s
– odchylenie standardowe różnic
D
M
s
– błąd standardowy różnicy
1
−
Σ
=
n
z
z
r
Y
X
XY
gdzie:
n- liczba par wyników
Y
X
z
z
Σ
oznacza sumę
iloczynów wyników
standaryzowanych
Te proste przykłady miały unaocznić, że wnioskowanie statystyczne opiera się zawsze na
tych samych zasadach. Na podstawie wyników empirycznych wyliczamy - według podanego wzoru -
jakąś wartość (statystykę), która dzięki pracy matematyków ma znany rozkład. Na podstawie
znajomości rozkładu, zakładając prawdziwość sformułowanej przez badacza hipotezy zerowej,
wyliczamy prawdopodobieństwo otrzymania naszych wyników. Jeżeli to prawdopodobieństwo jest
3
O interpretacji stopni swobody (df) można przeczytać w literaturze
[20].
G. Wieczorkowska & J. Wierzbiński (2005)
8
mniejsze niż 0,05, uznajemy hipotezę zerową za fałszywą i ogłaszamy światu ☺, że otrzymaliśmy
wyniki istotne statystycznie.