SYSTEMY INFORMACJI PRZESTRZENNEJ – OPRACOWANIE:

Piksel - najmniejszy, jednolity element obrazu. Obraz składa się z bardzo dużej liczby pikseli, których kolory mogą byd zmieniane. Każdy piksel składa się
z 3 subpikseli, świecących w kolorach: czerwonym, zielonym i niebieskim. Sterowanie intensywnościami świecenia subpikseli powoduje powstanie
wypadkowego koloru całego piksela. Rozdzielczośd to liczba pikseli, jakie obraz zawiera w pionie i poziomie.

GIS = SIP (Geographical information System) - zintegrowany zestaw komputerowy z oprogramowaniem, danymi przestrzennymi („geograficznymi”)
i personelem, wykorzystywany w celu pozyskiwania, przechowywania, unowocześniania, operowania, analizowania i prezentowania wszelkich postaci
danych lokalizowanych na powierzchni Ziemi. Prościej to komputerowo wspomagany system do przechowywania i obróbki danych odnoszących się do
powierzchni Ziemi, czyli po prostu cyfrowa mapa i baza danych w komputerze. Narodził się w Ameryce ok. 45 lat temu.

Dane mogą byd przestrzenne i nieprzestrzenne:



Nieprzestrzenne = atrybutowe - linijka pozioma w bazie danych to rekord (nieograniczona liczba), odnoszący się do 1 obiektu na mapie, ma
charakter klucza głównego, składający się z pewnej liczby atrybutów (pxi), które najczęściej są liczbami (chod mogą byd tekstowe), każdy piksel
jest opisany atrybutem. Atrybuty możemy sobie nadad, np. przypisując 15 dla piaskowców. Atrybut – informacja liczbowa lub tekstowa dołączona
do każdego obiektu.



Przestrzenne = mapy:
a.

wektorowa:
Zalety:
1.

wysoka jakośd grafiki wektorowej

2.

bardzo wysoka precyzja i rozdzielczośd, skalowalnośd

3.

mała objętośd danych

4.

bardzo wysoka pojemnośd - możemy wprowadzid nieskooczenie wiele punktów, bo tu podstawą nie jest px, ale właśnie punkt.

Wady:

1.

bardzo złożona i skomplikowana struktura danych

2.

skomplikowane edytowanie i przetwarzanie danych

3.

skomplikowane operacje analityczne

4.

drogie oprogramowanie

Mamy tu 3 elementy, do każdego przypisany jest atrybut:

- punkt – podstawowy (na jego atrybut liczbowy składają się: dane współrzędne oraz nr Id)

- linia łamana, czyli łuk - z połączenia punktów, co najmniej dwóch

- poligon - linia łamana zamknięta, gdzie wstawiamy centroid (w środku ciężkości)

Zastosowanie:

* inwentaryzacja,

* zbieranie i przechowywanie danych,

Inwentaryzacja, zbieranie i przechowywanie danych: Aby wprowadzid dane do komputera, należy przeprowadzid digitalizację. Zawsze jej
efektem jest mapa wektorowa, potem zamieniana na rastrową.

Schemat:

dane wejściowe (mapy papierowe, dane tabelaryczne)  digitalizacja  dane wyjściowe (przestrzenne = mapy, które trzeba skonwertowad
do mapy rastrowej i dane atrybutowe = tabele baz danych)  dystrybucja (mapy, płyty CD)

* przeglądanie i kompilacja zasobów WMS (Web Map Service- międzynarodowy standard udostępniania map w Internecie - map
użytkowania terenu, katastralnych, geologicznych, infrastruktury technicznej i in.),

* „produkcja” kartograficzna (druk, plotowanie),

* zastosowanie we wspomaganiu decyzyjnym i zarządzaniu

b.

rastrowa:
- siatka punktów (pxi o określonym atrybucie) zorganizowanych w wiersze i kolumny
Zalety:
1.

bardzo prosta struktura danych

2.

prosta edycja i przetwarzanie danych

3.

proste, liczne i efemtywne narzędzia analityczne

4.

tanie oprogramowanie

Wady:

1.

„zgrzebna” grafika rastrowa

2.

ograniczona precyzja i rozdzielczośd, brak skalowalności bez zmiany rozdzielczości – rozdzielczośd mierzymy wielkością pxi, a nie ich
ilością. Chcąc zwiększyd rozdzielczośd 2x, wielkośd pliku musimy zwiększyd 4x.

3.

„pamięciożernośd” – im wyższa rozdzielczośd, tym większa wielkośd plików

4.

niska pojemnośd

Zastosowanie:

* analiza
* zastosowanie we wspomaganiu decyzyjnym i zarządzaniu
* nauczanie GIS

Zastosowanie GIS rozwijało się wraz z upływem lat. Wyróżniamy 3 stadia rozwoju:

1.

Zbieractwa = zastosowanie inwentaryzacyjne, czyli budowa baz danych. W Polsce takie zastosowanie wykorzystują głównie agendy rządowe i
samorządowe

2.

Zastosowania analityczne - uniwersytety i instytucje badawcze

3.

Wspomaganie decyzyjne - firmy inżynierskie

Oprogramowanie:



Arc GIS (ESRI - firma produkująca)- najlepszy program, adresowany głównie dla analizy map wektorowych, chod nie tylko, darmowy, ale dośd
skomplikowany



Idrisi (Clarck Labs) - do interpretacji danych dyskretnych (skokowe - mogą przyjmowad ograniczoną liczbę wartości)



Surfer (Golden Software) - do interpretacji danych ciągłych (mogą przyjmowad nieskooczoną liczbę wartości, np. dane wysokościowe)



Access (Microsoft)



ER Mapper (ERM)

WMS = Web Mapping Service - międzynarodowy standard udostępniania map w Internecie, czyli dane GIS dostępne są w sieci, to zasób sieciowy. Źródłem
danych geodezyjnych jest GUGiK = Główny Urząd Geodezji i Kartografii, Główny Geodeta Kraju. Dysponuje on zasobami BDO = Baza Danych
Ogólnogeograficznych, obejmujących prawie cały obszar Polski. Są tu dostępne za darmo dane: skany map topograficznych, mapy hydrologiczne,
sozologiczne, ortofotomapy, kataster, oficjalny rejestr nazw geograficznych i granic. W celu wyświetlenia mapy, należy połączyd się z tym serwerem WMP,
pobrad z serwera meta dane, wybrad z nich interesujące nas warstwy (rzeki, linie kolejowe, podział administracyjny itp.), do serwera zostaje wysłane
zapytanie o wycinek mapy.

Jeśli chodzi o dane GIS za opłatą, dostarczane one są na zamówienie, na płytach CD/ DVD w kilku formatach GIS i układach współrzędnych (krajowych
i uniwersalnych UTM) i są to: mapy wektorowe i baza danych, skany map topograficznych, hydrologicznych i sozologicznych, kataster, oficjalny rejestr nazw
geograficznych i granic, ortofotomapa (jej treśd przedstawiona jest obrazem aerofoto graficznym, zwykle zdjęcie lotnicze lub satelitarne), zdjęcia lotnicze,
CMT (model „drutowy”= wireframe, model cieniowany) w siatce 5-20m, TIN lub ASCII text)

Za opłata dostarczane są też dane tematyczne, np. geologiczne - z PIG, zasoby CBDG= Centralnej bazy danych geologicznych, na płytach CD/DVD, prawie cały
obszar Polskie, to dane wektorowe z bazą , SMGP, MGGP, MHP i In., też w kilku formatach GIS i układach współrzędnych (krajowych lub uniwersalnych
(UTM)).

Do przeglądania danych nie potrzeba programu, wystarczy przeglądarka sieciowa, są tam dane z:



BDO (Baza danych Ogólnogeograficznych) www.geoportal.gov.pl Możemy tu znaleźd mapę sozologiczną, hydrograficzną, topograficzną, granice
administracyjne i paostwowe, oficjalne nazwy geograficzne, ortofotomapy i CMT w siatce 50m



CBDG www.pig.gov.pl – mapy wektorowe i bazy danych oraz rastrowe mapy tematyczne

Najbardziej zaawansowanym wykorzystaniem GIS jest analiza przestrzenna - procedura wykonywana na danych geograficznych z użyciem technik i metod
dostępnych oprogramowaniu do Systemów Informacji Przestrzennej w celu pozyskania nowej informacji geograficznej, często w celu odpowiedzi na
konkretne pytanie przy pewnych założeniach.

Idea analizy przestrzennej:



WEJŚCIE: dane przestrzenne (mapy), dane nieprzestrzenne (atrybuty, bazy danych), obrazy teledetekcyjne (satelitarne i lotnicze)



 ANALIZA (narzędzia i procedury analityczne)



 WYJŚCIE: nowe mapy, nowe atrybuty (nowa bazy danych), wykresy, dane statystyczne

Narzędzia i procedury analityczne:

1.

Kwerenda danych (DB Querry) - zapytanie do bazy danych, umożliwiające znalezienie i wyświetlenie informacji żądanych, odpowiada na proste
pytania, np. co znajduje się w tym miejscu?, gdzie znajduje się taki obiekt?, a także na pytania złożone, np. gdzie znajduje się obiekt o określonych
cechach?, jakie cechy ma obiekt znajdujący się w danym miejscu?; specyficznym rodzajem kwerendy jest ekstrakcja danych. Z jednej mapy dane
są ekstrahowane, np. z mapy CMT ekstrahujemy, czyli wyodrębniamy dane wysokościowe dla innej mapy - tzw. filtru. W tym przypadku filtrem
może byd mapa zagospodarowania terenu. Wynikiem jest statystyka wysokości dla każdej kategorii użytkowania powierzchni.

2.

Reklasyfikacja - służy zmianie wartości atrybutów liczbowych, np. jeśli na mapie geologicznej opisane jest każde wydzielenie (np. 1- piaski i żwiry
Qh, 2- mułki i gliny Qh, 3- piaski eoliczne Qh itd.), aby utworzyd mapę, na której widoczna będzie tylko stratygrafia (poszczególne systemy),
wszystkim osadom Qh nadajemy jedną wartośd, wszystkim osadom Qp inną wartośd itd.; specyficznym rodzajem reklasyfikacji jest binaryzacja,
gdzie obiekt może przyjmowad tylko wartośd 0 lub 1 - otrzymujemy mapę binarną = „zero-jedynkowa”). Najczęściej mapa binarna jest
„półproduktem” do wykonania innych procedur, takich jak: buforowanie, obliczanie odległości, analiza dyskryminacyjna, wieloczynnikowa (jako
kryterium dyskryminacyjne). Jako mapa wynikowa ukazuje elementy wyekstrahowane spośród większego zbioru. Reklasyfikację stosujemy dla
map dyskretnych (np. mapa geologiczna zakryta) i map ciągłych (np. mapa wysokościowa).

3.

Operatory odległości:



Euklidesowe (w ośrodkach izotropowych) = odległośd z pkt A do B = odległośd z pkt B do A,
np. mapa odległości euklidesowej od huty, którą można przeliczyd na stężenie fluoru w glebie:

Im dalej od huty we wszystkich kierunkach, tym mniejsze jej oddziaływanie na środowisko. Jeśli przyjąd, że stężenie będzie malało
z kwadratem odległości, oddziaływanie będzie bardzo mocne w obszarach nieodległych, a malało drastycznie dla obszarów położonych
dalej (zgodnie z funkcją), aż do momentu, kiedy wpływ będzie znikomy. Nie uwzględniamy tu innych czynników, jedynie odległośd od
huty oraz formułę przeliczeniową.

- buforowanie - to szczególny przypadek operatora odległości, przedstawiony w postaci rastrowej lub wektorowej



Nie-euklidesowe (w ośrodkach anizotropowych) = odległośd z pkt A do B nie musi byd równa odległości z pkt B do A:
a) nieukierunkowane - nie ma zależności od kierunku, np. powyższy przypadek należy rozważyd pod względem czynnika
anizotropozującego, niekierunkowy, którym jest różna własnośd sorpcyjna poszczególnych typów gleb (a te rozmieszczone w sposób
nieregularny, niekierunkowy od huty). W związku z tym, rozmieszczenie stężenia fluoru nie będzie sferyczne, ukierunkowane,
a nieukierunkowane. Konieczne jest tutaj założenie o braku wpływu czynnika anizotropozującego, kierunkowego.

b) ukierunkowane - zależnośd od kierunku, np. przypadek euklidesowej analizy skażenia fluorem przez hutę można rozpatrzyd
w następujący sposób: czynnikiem anizotropozującym, niekierunkowym może byd wiatr (jego kierunek i siła) oraz stoki (kierunki ich
nachylenia oraz stopnie). Jeśli wiatr będzie wiał z W na E, to rozprzestrzenianie stężenia fluoru będzie wyglądało jak na rysunku
(sferyczne rozprzestrzenianie). Z reguły wiatr wieje z różnych kierunków i o różnej sile, dlatego sfery te byłyby mniej lub bardziej
zniekształcone. Do tego można dołączyd stoki – im większe nachylenie, tym mniejszy opór spływu zanieczyszczeo.

4.

Algebra map - to operacje algebraiczne (matematyczne), statystyczne (min., max., średnia itp.) i logiczne (z użyciem operatorów Boole’a),
najczęściej na mapach rastrowych, wykonywane na liczbach będących atrybutami odpowiadających sobie pxi wszystkich map, czyli pxi z tego
samego rzędu i kolumny (o identycznych współrzędnych), np. dodawanie 2 map polega na dodawaniu atrybutów odpowiadających sobie px.
Przykład: mnożenie CMT przez mapę binarną, gdzie 1 to tereny zabudowane, 0 to inne tereny. Mapa binarna to tzw. maska. Gdy mnożymy przez
1, otrzymujemy wartośd z mapy CMT, gdy przez 0, otrzymujemy 0, czyli wynik jest maskowany. W efekcie dostajemy CMT na terenach
zabudowanych.
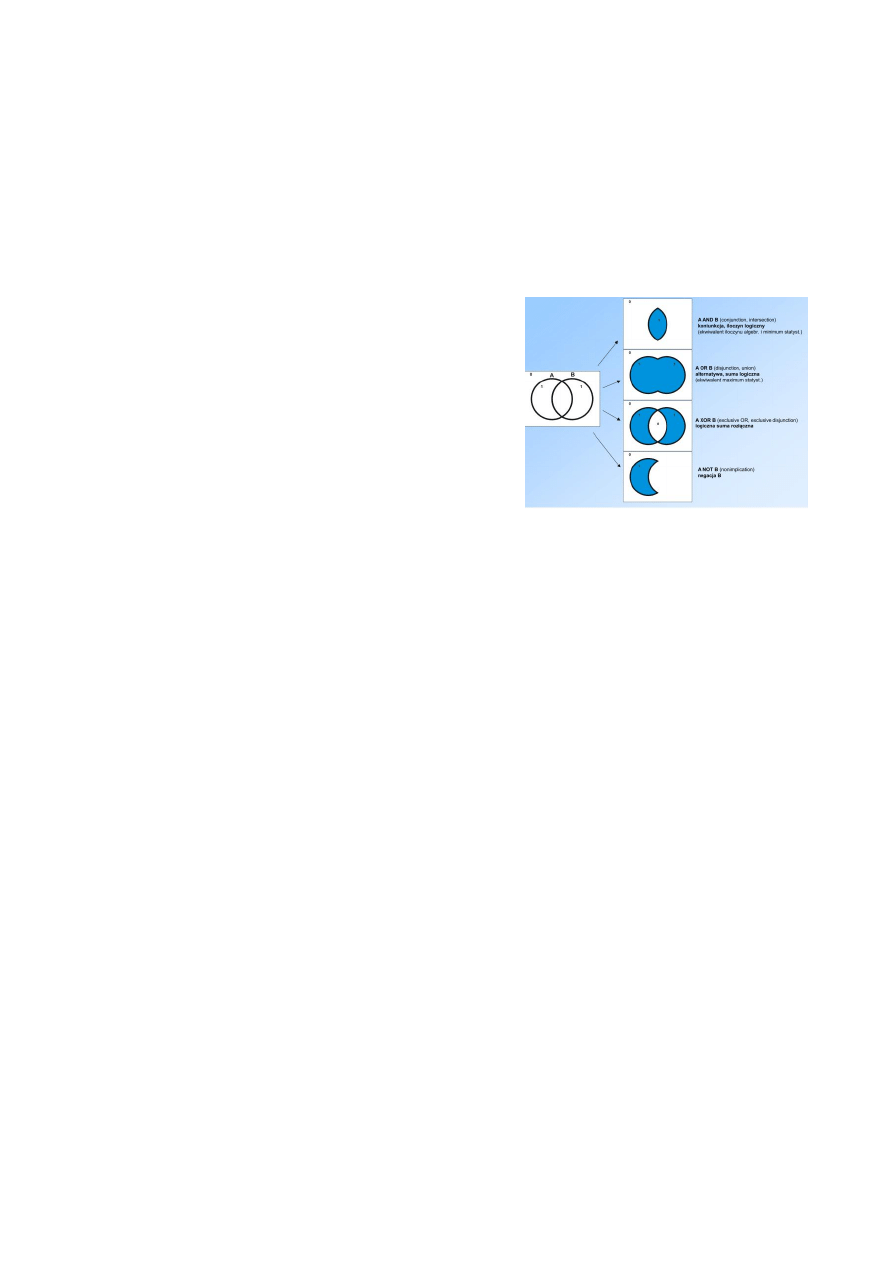
Szczególnym przypadkiem algebry map są operacje logiczne na mapach binarnych, do których używa się operatorów Boole’a. Istnieje 16
możliwych kombinacji elementów 0 i 1 dwóch map binarnych, ale tylko kilka jest praktycznie stosowanych w analizie przestrzennej. Są to:
koniunkcja, czyli iloczyn logiczny A and B, alternatywa, czyli suma logiczna A or B, logiczna suma rozłączna A xor B oraz negacja B A not B (rysunki)




Przykład: strefa zalewów powodziowych A i zabudowa zwarta B
A AND B= zabudowa zagrożona powodzią
A OR B = zabudowa i tereny powodziowe
A XOR B = zabudowa niezagrożona powodzią i niezabudowane tereny powodziowe
B NOT A = zabudowa niezagrożona powodzią

5.

Operacje skalarne – wykonywanie operacji algebraicznych na mapach rastrowych i liczbach lub funkcjach. Mapę rastrową (dokładniej liczbową
wartośd atrybutu każdego px) traktuje się jako zmienną niezależną funkcji. Wynikiem jest również mapa rastrowa (dokładniej liczbowa wartośd
atrybutu odpowiedniego px) jako zmienna zależna funkcji.
Przykład: tworzenie mapy czasów podejścia w górach. Zmienną niezależną jest mapa nachylenia stoków (X), Po utworzeniu funkcji f(X).
otrzymujemy mapę wynikową, w której wyższa wartośd atrybutu odpowiada dłuższemu czasowi podejścia.

6.

Analiza dyskryminacyjna:
- ma na celu wyznaczenie obszarów spełniających wszystkie kryteria
- każde z kryteriów należy przedstawid na mapie binarnej, gdzie 1 - obszary spełniające kryterium, 0 – niespełniające
- następnie mapy wszystkich kryteriów poddaje się procedurze algebry map (stosując operatory mnożenia, ekstrakcji min lub logiczne OR)
- wynikiem jest mapa binarna, gdzie 1 – obszary spełniające wszystkie kryteria, 0 – obszary nie spełniające chod jednego z kryteriów

7.

Analiza = selekcja wieloczynnikowa (MCE= Multi-Criteria Evaluation, LWC= Linear Weighted Combination- średnia ważona liniowo):
- ma na celu wyznaczenie obszarów spełniający mniej lub bardziej poszczególne kryteria

- zamiast selekcji typu „nadaje się” czy „nie nadaje się”, stosuje się selekcję typu „nadaj się bardzo”, „…średnio” itp. – czynniki niedyskryminujące

- te kryteria zaś, które ostro określają przydatnośd bądź nieprzydatnośd jakiegoś terenu dalej traktuje się jako czynniki dyskryminujące

- na mapach czynników przestrzennych niedyskryminujących, może występowad różna ilośd klas przydatności, dlatego najpierw mapy należy
znormalizowad do wspólnego zakresu; następnie każdemu kryterium, możemy nadad wagę w zależności od jego znaczenia tak, by suma wag=1
(atrybuty każdego px mnożymy przez tę wagę); dodajemy czynniki niedyskryminujące (powstaje średnia ważona) i mnożymy przez mapy
czynników dyskryminujących (w ten sposób usuwamy tereny całkowicie nieprzydatne); z pomocą histogramu (rozkład wielkości obszarów
względem kategorii), przeprowadzamy reklasyfikację w celu zredukowania zakresu atrybutów (do 3 lub 4 max); granice klas umieszcza się
w przerwach lub minimach histogramu.

8.

Modelowanie:
Przykład: Modelowanie zanieczyszczenia gleb metalami ciężkimi w Nowej Hucie w celu stworzenia i przetestowania modelu z uwzględnieniem
czynników przestrzennych, takich jak: odległośd od emiterów, typy genetyczne gleb, zabudowa, obszary zielone, kąty nachylenia stoków itp.
Metoda opiera się na badaniu korelacji wielorakiej. Czynniki przedstawiamy w postaci zreklasyfikowanych map - im wyższa wartośd atrybutu, tym
gorzej - większa podatnośd terenu na kumulację metali. Sporządzone mapy są weryfikowane przez badanie ich skorelowania z danymi
terenowymi. Czynniki słabo - lub nieskorelowane są reklasyfikowane ponownie, gdy to nie polepszy ich korelacji - odrzucane. Na podstawie
skorelowanych czynników, tworzy się modele rozmieszczenia metali ciężkich, uwzględniając tylko 1 czynnik przestrzenny, za pomocą operacji
skalarnych, gdzie mapa czynnika jest zmienną niezależną w równaniu regresji. Powstałe modele podstawowe są kompilowane metodą MCE -
przypisuje im się wagi proporcjonalnie do współczynników korelacji. Powstały model koocowy jest znów weryfikowany przez badanie
skorelowania z danymi laboratoryjnymi. Gdy współczynnik korelacji >0,7  model poprawny.
- 3 próby na /km

2

- czynniki wpływające na zanieczyszczenia gleb metalami ciężkimi:

- wysokośd – im niżej, tym zanieczyszczenie jest większe

- kąty nachylenia stoków – im b. strome, tym mniejsze zanieczyszczenie

- kierunki nachylenia stoków – na stokach zawietrznych sedymentacja jest lepsza

- zabudowa

- zieleo

- typ gleby
- odległośd od emiterów

- korelacja do próbek

DIGITALIZACJA (cyfrowanie) - sposób pozyskiwania danych do analiz. To najdroższy etap analizy przestrzennej (>75% wszystkich kosztów), czasochłonny,
polegający na zamianie mapy w postaci analogowej (papierowej) na cyfrową. Produktem digitalizacji jest mapa wektorowa, którą można zamienid na
rastrową w procesie konwersji. Digitalizację można przeprowadzid na różne sposoby:

a)

przy użyciu digitalizatora (urządzenie służące do tworzenia obrazu cyfrowego na specjalnej tablicy elektronicznej, tzw. tablecie, funkcjonalnie
odpowiadające myszy komputerowej, charakteryzuje się jednak znacznie wyższą dokładnością)

b)

digitalizacja ekranowa - w tym celu używamy skanera (skan mapy o wysokiej rozdzielczości (ok. 2000dpi lub więcej)) i uzyskujemy obraz mapy,
który może byd wykorzystany jako „półprodukt” do dalszej obróbki. Mapa przed skanowaniem nie powinna byd ponaginana ani poplamiona.
Dalej, dokonujemy procesu wektoryzacji – obrysowujemy (wodzimy) obiekty, zaznaczamy co określoną odległośd punkty, linie łamane (łuki),
zaczynające i kooczące się w punktach węzłowych oraz linie zamknięte, czyli poligony, wewnątrz których umieszczamy centroidy = lokatory
o określonym atrybucie, do którego przypisana jest cała niezbędna informacje o danym poligonie, zamieszczonym w bazie danych.

c)

przez wyciąg graficzny - na kalce dobrej jakości obrysowujemy b. cienkimi i dobrymi pisakami te elementy, które potrzebujemy, zaznaczamy węzły
siatki, skanujemy w b. wysokiej rozdzielczości i otrzymujemy mapę binarną. Na skanie trzeba zretyfikowad błędy, uzupełnid braki oraz nadad
odpowiednie współrzędne (kalibracja) i w konsekwencji wymazad węzły. Następnie przy pomocy oprogramowania dokonujemy automatycznej
wektoryzacji wyciągu graficznego, czego efektem jest tzw. mapa spaghetti – mapa bez danych. Automatycznie odbywa się też topologizacja - czyli
uzyskujemy informacje topologiczną o wszystkich elementach oraz o wzajemnych stosunkach między różnymi elementami, np. linia oddzielająca
2 poligony. Mapa spaghetti + baza danych = mapa wektorowa topologiczna z bazą danych. Ostatecznie uzyskujemy mapę wektorową obiektową
z bazą danych, w której każdy z obiektów nie ma części wspólnej ze swoim sąsiadem, jak w przypadku mapy wektorowej topologicznej.

SYSTEMY POZYCJONOWANIA SATELITARNEGO - są 3 globalne:

1.

GPS (Global Positioning System) – USA

2.

GloNaSS - Rosja

3.

Galileo - UE

+ lokalne, np. Indie i inne

GPS składa się z 3 powiązanych ze sobą zespołów:

a)

segmentu kosmicznego - satelitów okrążających Ziemię
Segment ten składa się z 24 satelitów. Na każdej z 6 orbit konstelacji znajdują się 4 satelity na wysokości 20 200 km (ok. 11 tys. mil), okrążające
Ziemię w ciągu 12h. Nie są to satelity geostacjonarne (na wys. 36km), tak jak satelity telekomunikacyjne czy meteorologiczne. Orbity te są
rozmieszczone wokół całej Ziemi i nachylone do powierzchni równika pod kątem 55°, co gwarantuje dobrą ich widocznośd nawet z niskich
i średnich szerokości geograficznych. Navstar posiada 4-8 satelitów zapasowych.

b)

segmentu kontroli - stacji kontrolujących i monitorujących prowadzonych przez Departament Obrony USA (U. S. Department of Defense - DOD),

c)

segmentu użytkownika - odbiorników GPS, będących w posiadaniu osób prywatnych, instytucji, firm i wojska.

Zasada działania:

GPS to systemy bierne, tzn. wykorzystują tylko sygnał wysyłane przez satelitę do odbiornika, bez sygnału zwrotnego. Każdy satelita wysyła sygnał swoisty dla
siebie, tj. sygnał binarny - o mniejszej mocy niż modulowany, ale odporny na zakłócenia i szumy, dzięki czemu dociera do odbiornika. W sekwencji „pisków
i cisz” zapisany jest kod każdego satelity, a w nim informacja efemeryczna (pozycja na orbicie), czyli łatwo można zidentyfikowad satelitę. Odbiornik oblicza
czas dojścia sygnału (ze względu na koniecznośd dużej precyzji, czas musi byd zmierzony bardzo dokładnie, do ns, dlatego musimy wiedzied dokładnie, kiedy
sygnał opuszcza satelitę), mnoży prędkośd światła (ok. 300 000 km/s) przez ten czas i w efekcie otrzymujemy odległośd między satelita i odbiornikiem. Znana
odległośd od satelity lokuje odbiornik na sferze o promieniu równym zmierzonej odległości (ok. 11tys. mil). Znana odległośd od dwóch satelitów lokuje
odbiornik na okręgu będącym przecięciem dwóch sfer. Kiedy odbiornik zmierzy odległośd od trzech satelitów, istnieją tylko dwa punkty, w których może się
on znajdowad. Jeden z tych punktów można wykluczyd jako znajdujący się zbyt wysoko lub poruszający się zbyt szybko, drugi zaś jest nieruchomy i to właśnie
ten drugi to przybliżona tymczasowa pozycja odbiornika. Aby sprawdzid dokładnośd pozycji, wykorzystuje się sygnał od 4 satelity i 4 sfera przechodzi tylko
przez 1 z 2 punktów. Błąd między rzeczywistą a prowizoryczną odległością wynika ze stosowania różnych zegarów - na powierzchni satelitów występują po 2
zegary atomowe, natomiast w odbiornikach zegary kwarcowe  różnicę czasu wylicza się jako poprawkę, do czego potrzebny jest właśnie sygnał od 4
satelity. Jeśli dokładnośd przekracza wartośd graniczną, sygnał nie wyświetli się na odbiorniku. Bardzo ważna więc jest synchronizacja zegarów na drodze
iteracji wielokrotnej. Odczytanie pozycji następuje co 1 sek. Biorąc pod uwagę pozycje satelitów, można przeliczyd to na współrzędne punktu, w którym
znajduje się odbiornik. Opisana wyżej zasada wyznaczania pozycji odbiornika nosi nazwę przestrzennej triangulacji „wcięcia wstecz”.

Zimny start odbiornika - gdy urządzenie musi zlokalizowad położenie satelitów i policzyd czas podróży sygnału z satelity do odbiornika, po zsynchronizowaniu
zegara w odbiorniku

Gorący start odbiornika - gdy położenie nie zmieniło się od ostatniego wyłączenia odbiornika.

Od czego zależy dokładnośd odczytanej pozycji?:

1.

Klasa odbiornika:



Nawigacyjne (turystyczne) - kilka-kilkanaście m



Kartograficzne (kodowo-fazowe) - <1m



Geodezyjne (fazowe) - rzędu cm i mm, ale pomiar trwa bardzo długo (godzinę lub więcej godzin)

2.

Czas spędzony na pomiarze

3.

Odchyłka konstelacyjna satelitów (GDOP) - parametr, który opisuje dokładnośd położenia punktu w 4 wymiarach (3 wymiary przestrzenne i czas)
- pozycja wyznaczona przez odbiornik rzeczywistości nie jest punktem, ale rombem (im większe jego pole powierzchni, tym mniejsza dokładnośd);
dokładnośd maleje, gdy satelity zbliżają się do siebie (zwiększa się pole rombu). Miarą odchyłki jest przedział od 1 do nieskooczoności, a wartości
te są wynikiem stosunku maksymalnej objętości ostrosłupa utworzonego przez 4 satelity na nieboskłonie do chwilowej objętości ostrosłupa.
Przedziały:
*<1;4) – akceptowalne *<4;6) – może byd w ostateczności *>= 6 – odbiornik nie podaje pozycji lub wyświetla informację na czerwono

4.

Czynniki topograficzne – zasłonięcie nieboskłonu przez lasy (lasy liściaste odbijają sygnał, a iglaste tłumią go), góry, zabudowę; ponadto jednolite
gładkie powierzchnie (tafle wody, budynki, lasy liściaste) powodują wielodrożnośd sygnału – droga się zwiększa (nie wykrywa tego odbiornik),
a czas pozostaje ten sam

5.

Opóźnienia atmosferyczne i jonosferyczne - ewentualne burze magnetyczne w jonosferze, pyły, wilgod zniekształcają i opóźniają sygnał w drodze
na Ziemię

6.

S/A (Selective Availability) – ograniczenie dostępności (celowe obniżanie dokładności GPS, możliwośd jego wyłączenia) przez twórców - głównie
Departament Obrony Stanów Zjednoczonych, błąd to ok. 100 stóp od jednego satelity, likwidacja przed DGPS (ale w czasie – brak znaczenia dla
społeczeostwa, duże znaczenie w wojsku)

GPS różnicowy (DGPS):

- służy do usunięcia zakłóceo S/A (w czasie 1-3s) oraz do zmniejszenie pozostałych zakłóceo o kilka-kilkanaście %

Aby wyeliminowad większośd błędów, stosuje się wyznaczanie współrzędnych punktów metodą względną, nie bezwzględną (absolutną). Do metody
bezwzględnej wykorzystuje się jeden odbiornik i otrzymujemy współrzędne odniesione do początku układu, czyli środa ciężkości Ziemi (elipsoidy WGS84).
To najmniej dokładny sposób pomiaru.

Częściej stosuje się metodę względną - wykorzystuje się min. 2 odbiorniki GPS, nie otrzymujemy współrzędnych x, y, z stanowisk , ale różnice współrzędnych
Δx, Δy i Δz pomiędzy wszystkimi punktami satelitarnymi uczestniczącymi w pomiarze. Polega to na tym, że jeden odbiornik jest nieruchomy (stacjonarny),
drugi się porusza. Jeżeli ustawi się odbiornik GPS w ustalonym punkcie (stacja bazowa), to na skutek zakłócenia sygnału pozycja przez niego wyznaczona
będzie się ciągle zmieniad. Jeżeli obliczymy różnicę pomiędzy zmierzoną przez odbiornik pozycją, a pozycją rzeczywistą odbiornika to otrzymamy tzw. wektor
błędu (na zasadzie poprawki różnicowej). Drugi odbiornik (zbieracz) musi mied możliwośd odbioru tych poprawek. Otrzymane w ten sposób informacje,
tzw. dane korekcyjne, odejmuje się od danych odbieranych przez GPS-y dokonujące pomiarów w terenie (korekta pomiarów). Uzyskana w ten sposób
pozycja jest tym dokładniejsza, im bliżej znajduje się zbieracz od bazy stacjonarnej. Korektę pomiarów można stosowad w czasie rzeczywistym wtedy, kiedy
baza wysyła poprawkę drogą radiową do odbiornika, który przed podaniem wyniku uwzględnia ją, albo jako późniejsze przetworzenie danych w tzw.
postprocessingu. Ewentualnie można uzyskad wartośd poprawek dzięki istniejącym bazom - ściągnąd z Internetu.

Innym sposobem minimalizacji zakłóceo jest nawigacja SBAS. System występuje w trzech kompatybilnych ze sobą wersjach regionalnych:

WAAS w Ameryce + EGNOS w Europie + MSAS w Azji. System z założenia nie działa samodzielnie, lecz jest uzupełnieniem systemu GPS. Pozwala na
zmniejszenie błędu pomiaru do poniżej 3 metrów w odbiornikach przystosowanych do odbioru sygnału WAAS.

Inne systemy pozycjonowania satelitarnego:

- GloNaSS - rosyjski, bez S/A, ogólnie dokładniejszy, ale bardzo awaryjny, ze względu na brak satelitów zapasowych

- GALILEO - UE, w trakcie rozruchu, jeszcze niedostępny

Wykorzystanie GPS-u w GIS-ie:

- dostarcza danych wektorowych

- lokalizacja punktów (wierceo, miejsc opróbowania, odsłonięd) i marszrut (np. zarysów odsłonięd, kamieniołomów, wychodni, krawędzi teras itp.)

- przez specjalistyczne oprogramowanie (dostarczane z odbiornikiem) możliwe jest „zrzucenie” i obróbka danych w PC

UKŁADY ODWZOROWAO KARTOGRAFICZNYCH:

Geoida – powierzchnia prostopadła do lokalnego pionu wyznaczonego przez siłę ciężkości i przebiegająca na średnim poziomie oceanów, przedłużonych pod
powierzchnią lądów; ze względu na nierównomierne rozmieszczenie mas w skorupie ziemskiej, piony odchylają się od normalnej do elipsoidy obrotowej
o 50-100m; na obszarach lądowych geoida wznosi się ponad elipsoidę obrotową (przy rzutowaniu powierzchni lądów na elipsoidę odcinki ulegają skróceniu),
a na oceanicznych jest obniżona względem niej (odcinki ulegają wydłużaniu); geoidę nie da się opisad matematycznie.

Elipsoida obrotowa – powierzchnia powstała z obrócenia elipsy wokół jednej z jej osi, której kształt w wystarczająco dużym stopniu przybliża kształt Ziemi;
elipsoidę obrotową można opisad i opisuje się matematycznie.

Dziś na świecie używane jest ok. 30 elipsoid. Oś x jest zawsze równoległa do orbity Ziemi, a elipsoida jest rotowana względem osi y (y w kierunku południka
zerowego) i z. Elipsoidę opisuje 5 parametrów - 2 półosie oraz współrzędne środka x, y, z (w tym przesunięcie środka ciężkości względem środka ciężkości
Ziemi, wielkośd elipsoidy i rotacje). Elipsoida może byd lokalna lub geocentryczna.

Obecnie powszechnie stosowaną elipsoidą obrotową jest międzynarodowa elipsoida WGS84 (geocentryczna), stanowiąca podstawę wszystkich systemów
satelitarnych. WGS84 podobna jest do jej poprzedniczki GRS80, lecz różnica między nimi ma znaczenie jedynie dla pomiarów bardzo dokładnych.

Układy współrzędnych:

a)

geograficznych (globalny):
- odniesione do geoidy
- układ ten określa położenie punktu P na powierzchni Ziemi za pomocą dwóch współrzędnych kątowych:

- długośd geograficzna – (λ) kąt dwuścienny pomiędzy płaszczyzną południka początkowego (Greenwich), a płaszczyzną południka
miejscowego (W lub E, 0-180

o

)

- szerokośd geograficzna - (φ) kąt, jaki tworzy kierunek pionu (R geoidy) w danym punkcie z płaszczyzną równika (N lub S, 0-90

o

)

- południki – połowy kół wielkich, tzw. wertykałów, czyli obwodowych kół Ziemi zbiegających się na biegunach
- równoleżniki – płaszczyzny wzajemnie równoległe i prostopadłe do osi Ziemi, mające kształt kół małych, tzw. almukantaratów
- układ południków i równoleżników tworzy układ współrzędnych geograficznych

b)

geodezyjnych (geograficznych elipsoidalnych – globalny):
- odniesione do elipsoidy geocentrycznej

- długośd L i szerokośd B danego punktu jest definiowana podobnie jak na geoidzie z tym, że zamiast kierunku pionu używamy pojęcia normalnej
do elipsoidy; dodatkowo dochodzi wysokośd H nad elipsoidą, mierzona od powierzchni elipsoidy do fizycznego punktu na powierzchni Ziemi po
normalnej do elipsoidy
- położenie punktu może byd również ustalone za pomocą współrzędnych kartezjaoskich: x, y, z w prostokątnym układzie geocentrycznym, gdzie
oś x leży na przecięciu płaszczyzn: równika i południka zerowego, oś y na przecięciu: równika i południka 90

o

, zaś oś z pokrywa się z osią obrotu

elipsoidy

c)

prostokątnych na płaszczyźnie (lokalny)
- do wiarygodnego przedstawienia położenia danego punktu na powierzchni Ziemi stosuje się siatki płaszczyznowe (geodezyjne), które obejmują
taki obszar, dla którego linie siatki będą się pokrywały (w granicach pewnego błędu) z liniami siatki geograficznej elipsoidalnej; jest to inaczej
siatka kilometrowa, w której wzdłuż południka centralnego nie ma zniekształceo. Osie x i y są zamienione miejscami. Ze względu na duże
zniekształcenia siatki te nie są stosowane w dużych i rozciągniętych krajach (tam najlepsze odwzorowanie walcowe). Obszar, który nie wymaga
uwzględniania krzywizny Ziemi to obszar o powierzchni 750km

2

i średnicy max 31,2km.

Metody odwzorowywania powierzchni elipsoidy na płaszczyznę:

a)

ze względu na rodzaj powierzchni rzutowania:



płaszczyznowe (=azymutalne) – rzutowanie na płaszczyznę styczną do elipsoidy lub przecinającą ją:
- centralne (=gnomiczne) – środek rzutu znajduje się w środku elipsoidy
- stereograficzne (=wiernokątne) – środkiem rzutu jest punkt elipsoidy
- ortograficzne – rzutowanie na płaszczyznę realizowane jest wzdłuż prostych stycznych do elipsoidy oraz prostopadłych do tej płaszczyzny



stożkowe – rzutowanie na pobocznicę stożka stycznego do elipsoidy lub tnącego ją (siecznego) – najlepsze dla krajów wydłużonych



walcowe – rzutowanie na pobocznicę walca stycznego do elipsoidy lub tnącego ją (siecznego) – najbardziej uniwersalne; najlepsze do
przedstawienia rozległych obszarów (ukośne); nie da się przedstawid okolic biegunowych (normalne)
Ponadto, wśród każdego z powyższych odwzorowao można wyróżnid:
* odwzorowania normalne (płaszczyzna, oś obrotu stożka i walca jest prostopadła do osi obrotu elipsoidy)
* odwzorowanie poprzeczne (płaszczyzna, oś obrotu stożka i walca jest równoległa do osi obrotu elipsoidy).
* odwzorowanie ukośne (płaszczyzna, oś obrotu stożka i walca przecina oś obrotu elipsoidy pod pewnym kątem 0-90

o

)

Podczas odwzorowao zniekształceniu ulegają:



Kąty - zachowujące stałe kąty to odwzorowanie wiernokątne



Kształt - zachowujące bez zniekształceo długośd w jednym z kierunków głównych to odwzorowanie wiernokształtne



Wielkośd – zachowujące bez zniekształceo wielkośd to odwzorowanie wiernopowierzchniowe

Na półkuli północnej oś wartości układu współrzędnych maleją na zachód i na południe. Na półkuli południowej - na odwrót.

Rodzaje odwzorowao:

a)

odwzorowanie Gaussa-Krugera (=Mercatora):
- wiernokątne, walcowe poprzeczne odwzorowanie elipsoidy obrotowej na płaszczyznę, realizowane w wąskich pasach południkowych
- spełnia następujące warunki:

- południk środkowy odwzorowuje się wiernie jako odcinek prostej (gdyż tutaj przyłożono walec), a pozostałe południki są liniami
krzywymi zbiegającymi się ku biegunom, symetrycznymi i wypukłymi względem południka środkowego
- równik odwzorowuje się wiernie jako odcinek prostej, a pozostałe równoleżniki są liniami krzywymi symetrycznymi i wypukłymi
względem obrazu równika

- aby nie dopuścid do powstania nadmiernych zniekształceo, obszar dzieli się ekwideformatami na południkowe strefy o szerokości 3 lub 6

o

,

symetrycznie względem południka środkowego; każdy pas odwzorowuje się oddzielnie
- układy w tym odwzorowaniu:



„1942”:
- obszar Polski podzielony na 2 strefy odwzorowawcze (3 i 4) 6-stopniowe, z południkami środkowymi 15 i 21

o

E (linie zniekształcenia

zerowego, m=1)
- obszar Polski podzielony na 4 strefy odwzorowawcze (5, 6, 7 i 8) 3-stopniowe, z południkami środkowymi 15, 18, 21 i 24

o

E

- oparte na elipsoidzie Krassowskiego

- odwzorowanie styczne



„1992”:
- obszar Polski przedstawiony jako jedna strefa odwzorowawcza o południku środkowym 19

o

E (współczynnik skali m = 0,9993)

- zniekształcenia na południku środkowym wynoszą -70, na skrajnym zachodnim obszarze +60, a na skrajnym wschodnim +90cm/km
- oparte na elipsoidzie WGS84
- odwzorowanie sieczne

b)

Odwzorowanie UTM:
- wersja odwzorowania walcowego, poprzecznego, siecznego
- oparte na elipsoidzie WGS84
- cała Ziemia jest podzielona na 60 stref północnych i południowych (jedne na N, a inne na S od równika), każda o szerokości 6 stopni długości
geograficznej oraz posiadająca swój południk środkowy
- numeracja stref zaczyna się od południka 183

o

na E, gdzie spotykają się strefy 0 i 60

- Polska leży w strefach 33, 34 i mała częśd w strefie 35, południki środkowe 15E, 21E i 27

o

E

c)

Odwzorowanie stereograficzne (=quasi-stereograficzne):
- odwzorowanie stożkowe sieczne
- stosunkowo małe zniekształcenia
- układy w tym odwzorowaniu:



„1965”:
- Polska podzielona na 5 stref odwzorowawczych ( strefy 1-4 na bazie odwzorowania quasi-stereograficznego, a strefa 5 została
zobrazowana dzięki odwzorowaniu Gaussa-Krugera siecznym
- oparte na elipsoidzie Krassowskiego

GIS: to system, w którego skład wchodzą ludzie, sprzęt komputerowy, oprogramowanie oraz procedury, mający na celu pozyskanie, zarządzanie,
przetwarzanie, analiza, modelowanie i prezentowanie danych przestrzennych

DANE PRZESTRZENNE:

a)

dane dyskretne – dane reprezentowane przez tzw. obiekty proste: punkty, linie i poligony, pomiędzy którymi nie ma przejścia, są oddzielne,
tj. posiadające inne atrybuty, np. dom, drzewa, rzeka, województwo

b)

dane ciągłe – dane zmieniające się w sposób ciągły na powierzchni Ziemi, dające się interpolowad, np. temperatura, stężenie metalami,
wysokośd n.p.m., ciśnienie:
- potrzebne są specjalne procedury, by je przedstawid
- procedura zapisu i przedstawienia danych ciągłych:

- próbkowanie: nieregularne i regularne (punktowe (współrzędne x, y i h) lub tekstowe)  reprezentacja tych danych, to chmura pktw

- w dalszej kolejności dane interpolujemy poprzez utworzenie modeli (izolinii, TINu lub GRIDu):

* TIN – tzw. nieregularna siatka trójkątów:

- sąsiadujące punkty łączy się liniami w ten sposób, by powstające trójkąty miały najmniejszą powierzchnię

- maksymalna liczba trójkątów równa jest liczbie wszystkich punktów pomiarowych -2

- liczbę trójkątów oraz ich średnią wielkośd można sobie założyd

- każdy trójkąt opisany jest 3 parametrami (wierzchołkami), a każdy parametr 3 wartościami

- metoda często stosowana do tworzenia CMT

*GRID – tzw. regularna siatka kwadratów:
- każdy z kwadratów jest identyczny oraz reprezentowany 2 parametrami (2 bokami) – jest to wielka zaleta nad TINem, gdyż obliczenia
matematyczne są bardzo uproszczone
- jednak żeby uzyskad ową sied należy wyliczyd wartości, które przypadają na węzły sieci kwadratów (punkty pomiarowe znajdują się
wewnątrz kwadratów, a nie jak w przypadku TINu, w wierzchołkach trójkątów)
- punkty węzłowe posiadają określone wysokości
- im gęstsza zastosowana siatka, tym model dokładniejszy (jednak do pewnego stopnia, gdyż zwiększanie ilości kwadratów może
wiązad się ze wzrostem w miejscach o małym urozmaiceniu terenu, co jest zupełnie niepotrzebne); rozwiązaniem jest uzupełnienie
struktury o punkty charakterystyczne i linie szkieletowe lub zastosowanie siatki o strukturze hierarchicznej dostosowującej gęstośd do
stopnia skomplikowania rzeźby

- na czym tak naprawdę polega interpolacja?:

- w naukach o Ziemi istotne są 3 interpolatory; niektóre z nich:



triangulacja + interpolacja liniowa (rys)



IDW (średnia ważona odwrotności potęgi odległości) (rys)

- utworzone modele stosujemy m.in. do:

- wizualizacji danych 3D

- do tworzenia modeli cieniowanych