1

G – całkowita konsumpcja benzyny w USA (w mld galonów)
Pop – populacja (w mln), Y – dochód per capita (w 100 $), Pg – cena benzyny (w $),
Pnc – średnia cena nowych samochodów (w 1000$), Puc – średnia cena używanych samochodów (w 1000$),
Ppt – ceny transportu publicznego (w 10$)

G

i

=

β

0

+

β

1

Pop

i

+

β

2

Y

i

+

β

3

Pg

i

+

β

4

Pnc

i

+

β

5

Puc

i

+

β

6

Ppt

i

+ ε

i

p-value jest to prawdopodobieństwo popełnienia błędu przy odrzuceniu prawdziwej hipotezy zerowej.
Porównujemy je z poziomem istotności, na którym pracujemy (np.

0, 05

α

=

). Poziom istotności rozumiemy jako

nasze maksymalne przyzwolenie na prawdopodobieństwo popełnienia błędu przy odrzuceniu prawdziwej
hipotezy zerowej. Jęśli więc p value

α

−

<

, to odrzucamy prawdziwą

0

H

z mniejszym prawdopodobieństwem

niż maksymalne przez nas dopuszczane, więc

0

H

można odrzucić. Jeśli natomiast p value

α

−

>

, to szansa, że

popełnimy błąd przy odrzuceniu

0

H

jest większa niż dopuszczana, więc nie ma podstaw do odrzucenia

0

H

.

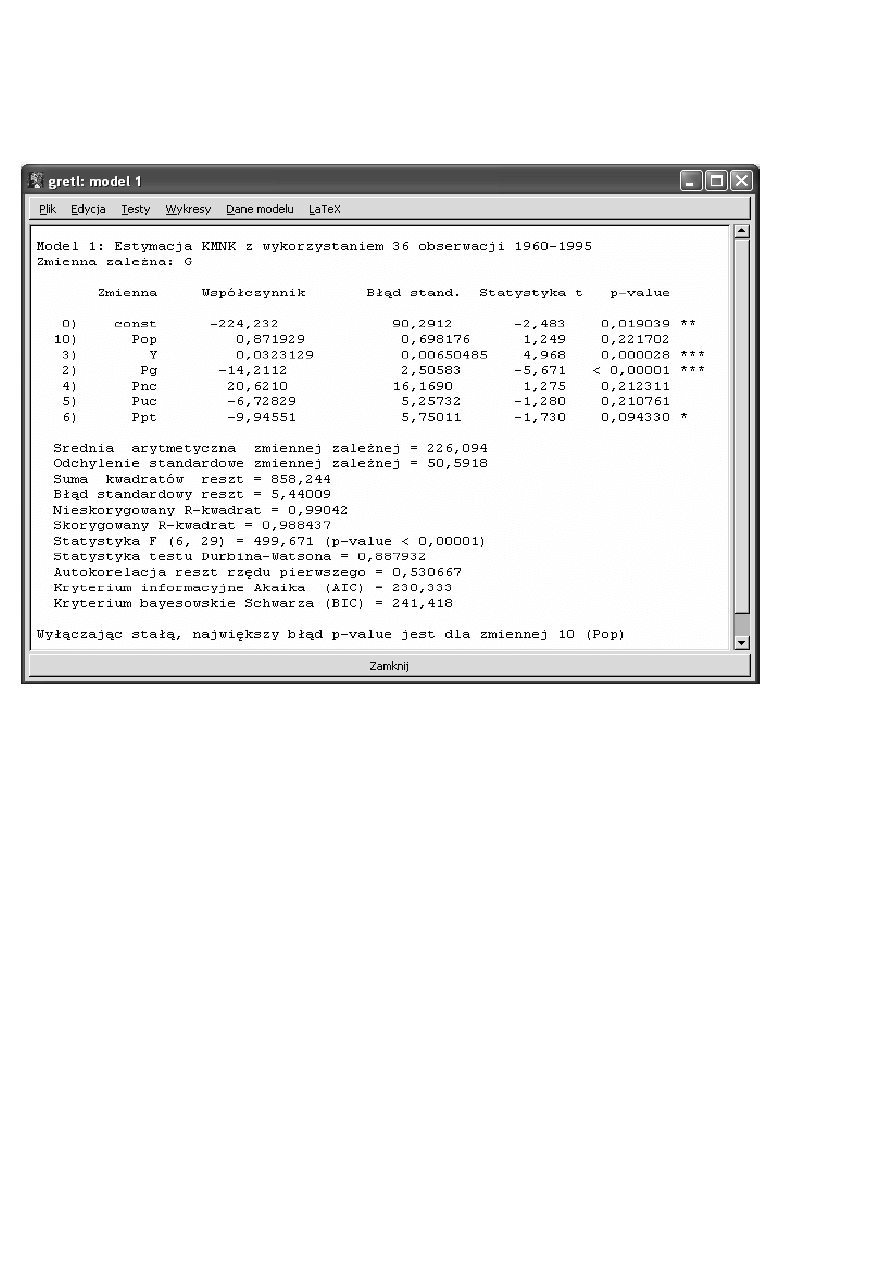
Np. p-value podane w ostatniej kolumnie powyższego wydruku z pakietu ekonometrycznego Gretl dotyczy
testów istotności poszczególnych zmiennych w modelu. Dla zmiennej Ppt p-value wynosi 0,094, zaś hipotezy
testu istotności dla tej zmiennej to (patrz równanie modelu nad wydrukiem):

0

6

:

0

H

β

= i

1

6

:

0

H

β

≠ .

Przyjmując

0, 05

α

=

, mamy

0, 094

0, 05

p value

α

−

=

>

=

, a więc prawdopodobieństwo, że popełnimy błąd przy

odrzuceniu hipotezy zerowej jest większe niż maksymalne przez nas dopuszczane. Nie odrzucamy więc

0

H

,

czego wynikiem jest uznanie zmiennej Ppt za nieistotną (na poziomie istotności

0, 05

α

=

, czyli na poziomie

istotności 5%-wym). Łatwo zauważyć, że wybierając inny poziom istotności (np.

0,1

α

=

), może się zdarzyć, że

wynik analizy będzie inny. Teraz zachodzi

0, 094

0,1

p value

α

−

=

<

=

, a więc szansa na popełnienie błędu przy

odrzuceniu

0

H

jest mniejsza niż maksymalnie dopuszczalna, odrzucamy ją więc i przyjmujemy hipotezę

alternatywną, co oznacza, że zmienna jest w modelu istotna (na poziomie istotności 10%-wym).

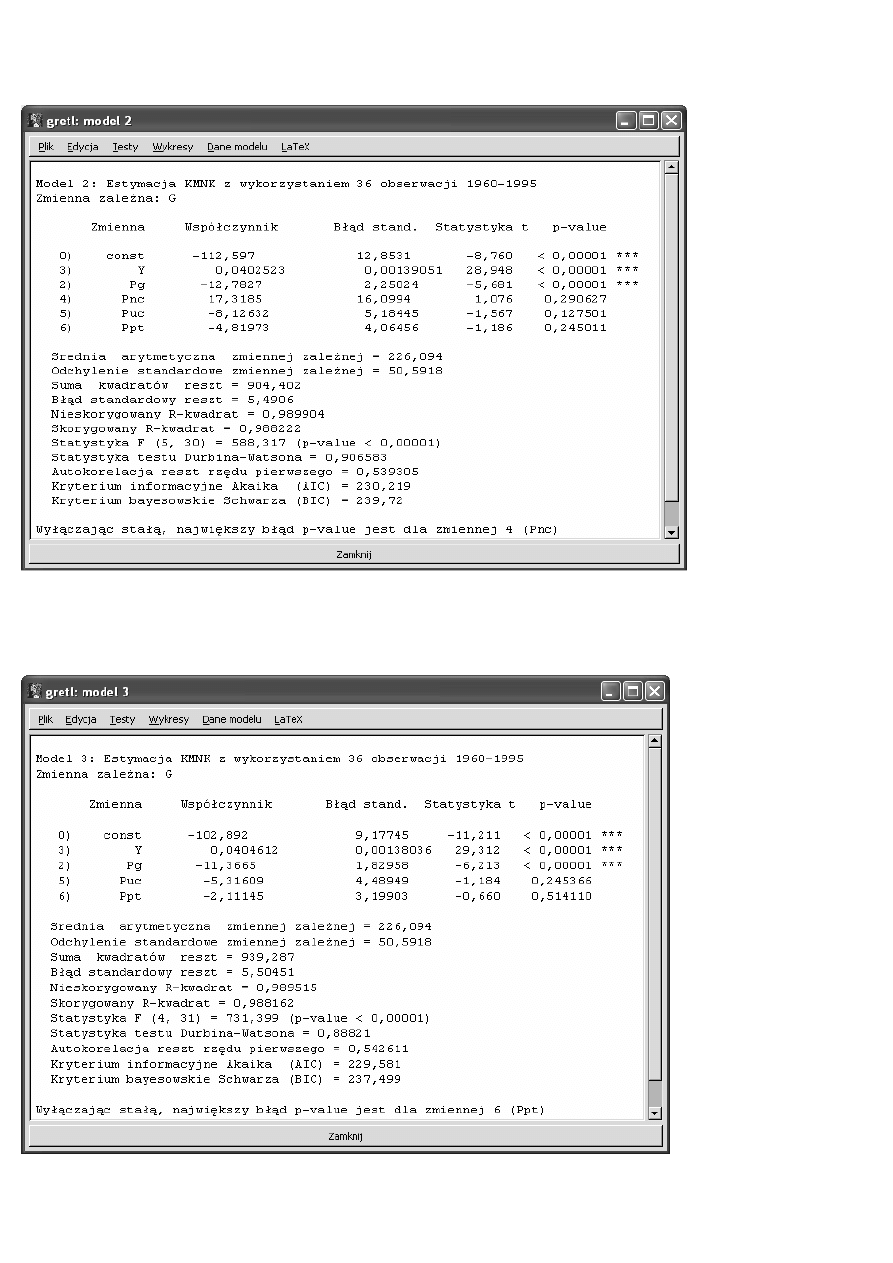
2

G

i

=

β

0

+

β

1

Y

i

+

β

2

Pg

i

+

β

3

Pnc

i

+

β

4

Puc

i

+

β

5

Ppt

i

+ ε

i

G

i

=

β

0

+

β

1

Y

i

+

β

2

Pg

i

+

β

3

Puc

i

+

β

4

Ppt

i

+ ε

i

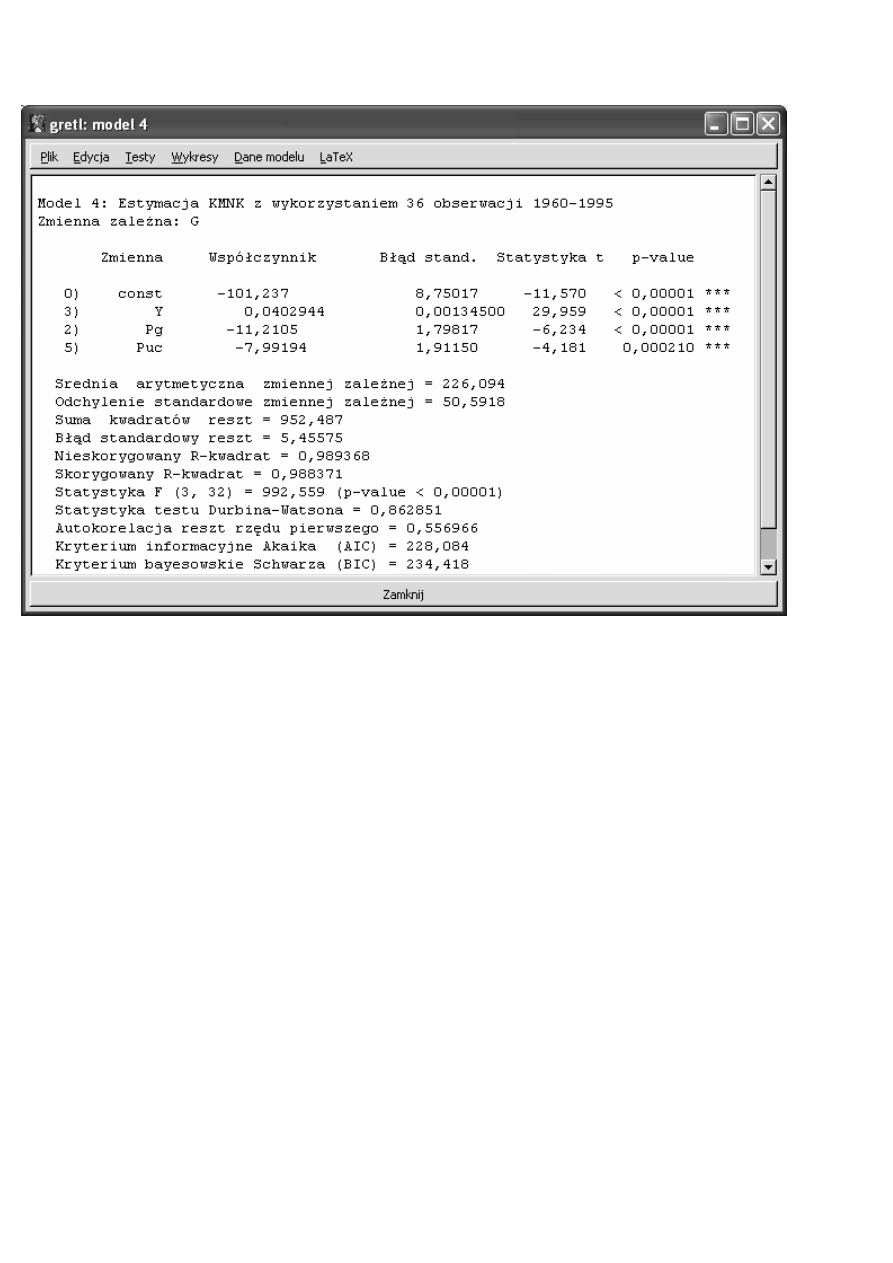
3

G

i

=

β

0

+

β

1

Y

i

+

β

2

Pg

i

+

β

3

Puc

i

+ ε

i

Teraz wszystkie zmienne objaśniające w analizowanym przez nas modelu są statystycznie istotne (i poszczególne
z nich są istotne i łącznie są one istotne). Jednak w procesie dochodzenia do tej postaci modelu, pominęliśmy z
modelu trzy zmiennej objaśniające. Czy mogliśmy to zrobić? Czy łącznie nie były one w stanie wyjaśnić choć
części zmienności zmiennej objaśnianej (konsumpcji benzyny)?

Aby odpowiedzieć sobie na to pytanie, przeanalizujmy przypadek teoretyczny:

Test na łączną istotność podzbioru regresorów / Test pominiętych zmiennych

Załóżmy, że mamy dwa konkurencyjne modele:

1

2 2

3 3

...

i

i

i

k

ki

i

i

i

y

x

x

x

X

β

β

β

β

ε

β ε

=

+

+

+

+

+

=

+

(1)

1

2 2

3 3

1 1

2 2

...

...

i

i

i

k

ki

i

i

m mi

i

i

i

i

y

x

x

x

z

z

z

X

Z

β

β

β

β

α

α

α

ε

β

α ε

=

+

+

+

+

+

+

+

+

+

=

+

+

(2)

Modele te są bardzo do siebie podobne, z tymże w modelu (1) na

i

y

wpływa (k-1) zmiennych objaśniających

zawartych w macierzy X, zaś w modelu (2), na tę samą zmienną wpływają znowu zmienne z macierzy X, ale
również wpływa na nią m zmiennych z macierzy Z. Model (2) nazwiemy modelem bez ograniczeń/bez restrykcji
(modelem ogólnym), zaś model (1) – modelem z ograniczeniami/restrykcjami (modelem szczególnym), jako, że
na parametry zmiennych z macierzy Z nałożyliśmy ograniczenia, że są one równe zero, więc zmiennych tych w
tym modelu nie ma, bo są nieistotne.
Jeśli chcielibyśmy szacować model (1), musimy przeprowadzić test na łączną istotność zmiennych zawartych w
macierzy Z (które są podzbiorem regresorów modelu (2)). Jeśli test nie pozwoli odrzucić hipotezy zerowej, którą
jest

0

:

0

H

α

= , to regresory z macierzy Z można pominąć, czyli poprawny jest model (1). Przyjęcie hipotezy

alternatywnej (

1

:

0

H

α

≠ ) wskazuje na poprawność modelu (2).

Rozróżnienie, który z modeli jest poprawny jest o tyle ważne, że gdy szacujemy model (1), a poprawny jest
model (2) (problem zmiennych pominiętych), to estymatory są obciążone. Gdy sytuacja jest odwrotna i

4

szacujemy model (2) gdy poprawny jest model (1) (problem zmiennych nieistotnych), to estymatory są
nieefektywne, ale pozostają nieobciążone. Oczywiście problem zmiennych pominiętych (obciążoność
estymatorów) niesie ze sobą dużo bardziej negatywne konsekwencje dla oszacowań parametrów modelu niż
problem zmiennych nieistotnych (estymatory mniej efektywne), jednakże obydwa przypadki są niepożądane w
czasie estymacji i powinniśmy się ich wystrzegać.
Test przeprowadzamy w następujący sposób:
- szacujemy model bez ograniczeń (2) i obliczamy jego współczynnik determinacji, nazywając go

2

R

.

- szacujemy model z ograniczeniami (1) i obliczamy jego współczynnik determinacji, nazywając go

2

R

R

.

- wyznaczamy statystykę testową:

2

2

2

(

) /

~

( ,

(

))

(1

) /(

(

))

R

R

R

J

F

F J n

k

m

R

n

k

m

−

=

−

+

−

−

+

, gdzie J oznacza ilo

ść

restrykcji nało

ż

onych na model (1) (a wi

ę

c ilo

ść

zmiennych z macierzy Z – ilo

ść

zmiennych, które

chcemy pomin

ąć

), n jest ilo

ś

ci

ą

obserwacji, a (k+m) ilo

ś

ci

ą

zmiennych obja

ś

niaj

ą

cych modelu bez

ogranicze

ń

(2). Znaj

ą

c rozkład statystyki testowej, mo

ż

emy odczyta

ć

z tablic warto

ść

krytyczn

ą

i je

ś

li

kr

F

F

>

, to przyjmujemy hipotez

ę

alternatywn

ą

o prawdziwo

ś

ci modelu (2), za

ś

gdy

kr

F

F

<

, to nie ma

podstaw do odrzucenia hipotezy zerowej, a wi

ę

c przyjmujemy poprawno

ść

modelu (1). Wynik testu

cz

ę

sto wygodniej jest odczyta

ć

z p-Value (cz

ę

sto podawanego przez pakiety ekonometryczne), które

mówi nam o prawdopodobie

ń

stwie popełnienia bł

ę

du przy odrzuceniu prawdziwej hipotezy zerowej.

W naszym przypadku, test na mo

ż

liwo

ść

pomini

ę

cia zmiennych Pop, Pnc i Ppt wygl

ą

dałby nast

ę

puj

ą

co:

2

0,99042

R

=

,

2

0,989368

R

R

=

,

3

J

=

,

36

n

=

,

7

k

m

+

=

. Obliczamy

F

:

(0,99042 0,989368) / 3

1, 0615

(1 0,99042) /(36 7)

F

−

=

=

−

−

. Odczytujemy z tablic F-Snedecora (o J=3 i (n-k-m)=29 stopniach

swobody) warto

ść

krytyczn

ą

. Wynosi ona:

2,93

kr

F

=

. Poniewa

ż

zachodzi

kr

F

F

<

, to ma podstaw do odrzucenia

hipotezy zerowej, parametry przy zmiennych Pop, Pnc i Ppt s

ą

równe zero, czyli zmienne te s

ą

ł

ą

cznie nieistotne

i mogli

ś

my je z modelu pomin

ąć

.

Te sam test, przeprowadzony przez pakiet ekonometryczny Gretl, wygl

ą

da nast

ę

puj

ą

co:

Interpretuj

ą

c p-value, dochodzimy do tych samych wniosków.