Instytut Sterowania i Systemów Informatycznych

Uniwersytet Zielonogórski

Sieci Neuronowe

Laboratorium

Dyskretne sieci Hopfielda

Wiadomości wstępne

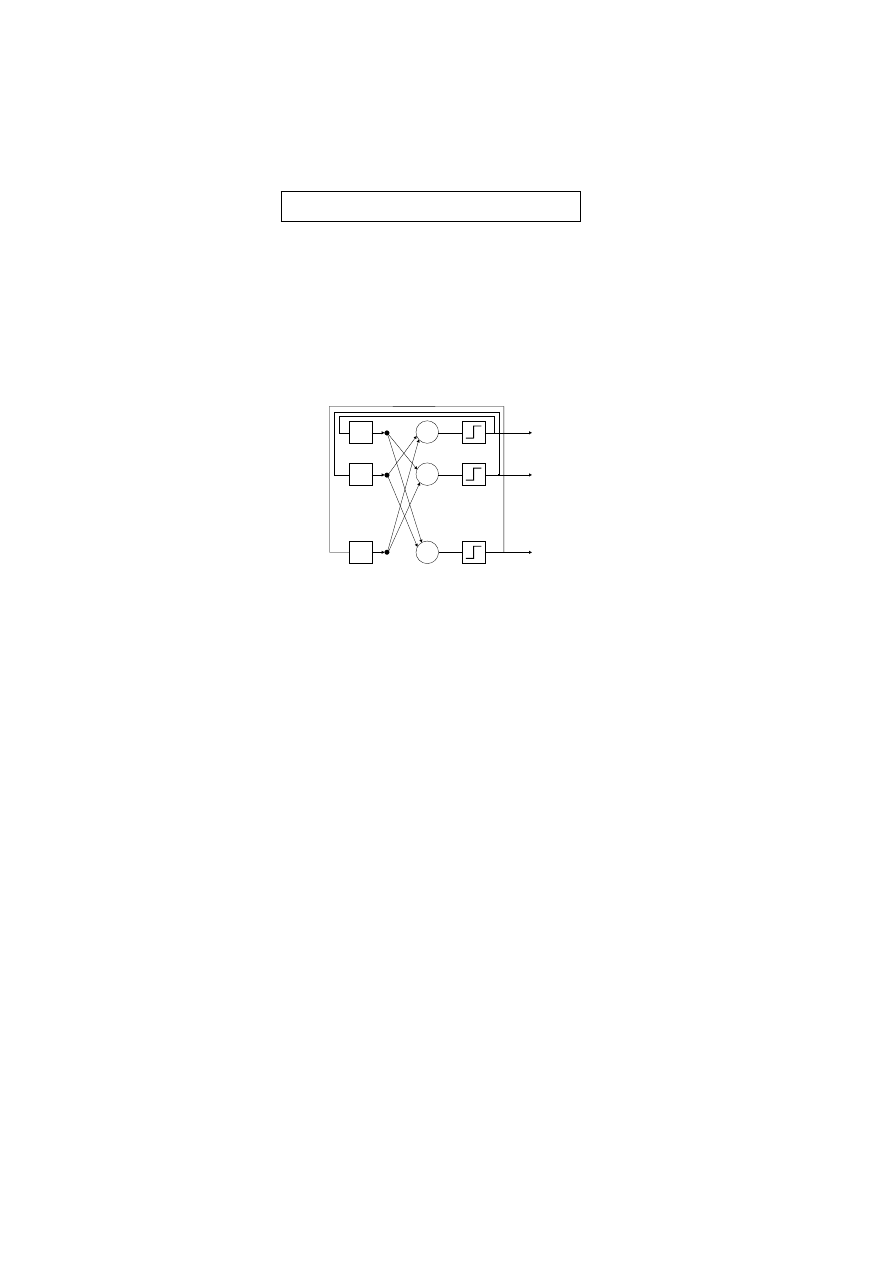
• Architektura sieci

..

.

..

.

..

.

S

S

S

y

N

z

-1

z

-1

z

-1

w

ij

i

j

y

2

y

1

• Algorytm uczenia

1 dla zbioru uczącego o rozmiarze M i elementach {x

(1)

, x

(2)

, . . . , x

(M )

} ∈ R

N

, ko-

rektę parametrów sieci przeprowadza się wg wzoru:

w

ij

=

(

P

M
m=1

(2x

(m)
i

− 1)(2x

(m)
j

− 1)

dla

i 6= i

0

dla

i = j

• Stabilność

sieci Hopfielda zawsze osiągają stan stabilny po pewnej określonej liczbie iteracji
(proces odtwarzania wzorca), w którym:

x

i

(k + 1) = x

i

(k), ∀i

Stany stabilne, odpowiadające minimum funkcji energii nazywa się atraktorami.
Każdemu z nich można przyporządkować zbiór warunków początkowych x(0), które
inicjują ewolucję sieci kończącą się w tym atraktorze. Zbiór ten nazywamy niecką
przyciągania danego atraktora.

• Pojemność pamięci asocjacyjnej

Istotnym parametrem pamięci asocjacyjnej jest jej pojemność. Przez pojemność
rozumie się maksymalną liczbę wzorców zapamiętanych i odtwarzanych z akcepto-
walnym błędem ε

max

. Maksymalna pojemność pamięci asocjacyjnej dla dużej liczby

elementów przetwarzających N i błędzie ε

max

= 1% wynosi:

p

max

= 0.138N

• Pamięć autoasocjacyjna

Sieć Hopfielda często stosowana jest jako pamięć autoskojarzeniowa inaczej nazy-
wana pamięcią autoasocjacyjną. Załóżmy, że dany jest zbiór M różnych wzorców
{x

(1)

, x

(2)

, . . . , x

(M )

} ∈ R

N

. Pamięcią autoskojarzeniową związaną z tym zbiorem

nazywamy układ realizujący odwzorowanie F : R

N

→ R

N

takie, że F (x

(m)

) =

x

(m)

,

m = 1, . . . , M oraz F (x) = x

(l)

, jeżeli x

(l)

jest najbardziej podobny do x

spośród wszystkich wzorców. Stopień podobieństwa dwóch wektorów a i b można
wyznaczyć stosując odległość Hamminga.

Zadania

1. Jak definiuje się odległość Hamminga? Wyznaczyć odległości pomiędzy wektorami

a i b zdefiniowanymi poniżej:

• a = [0 1 1 1 0 0 1 0], b = [1 0 0 0 1 1 0 1]

• a = [0 1 1 1 0 0 1 0], b = [0 1 1 1 0 0 1 0]

• a = [0 1 1 1 0 0 1 0], b = [1 0 1 0 0 1 1 0]

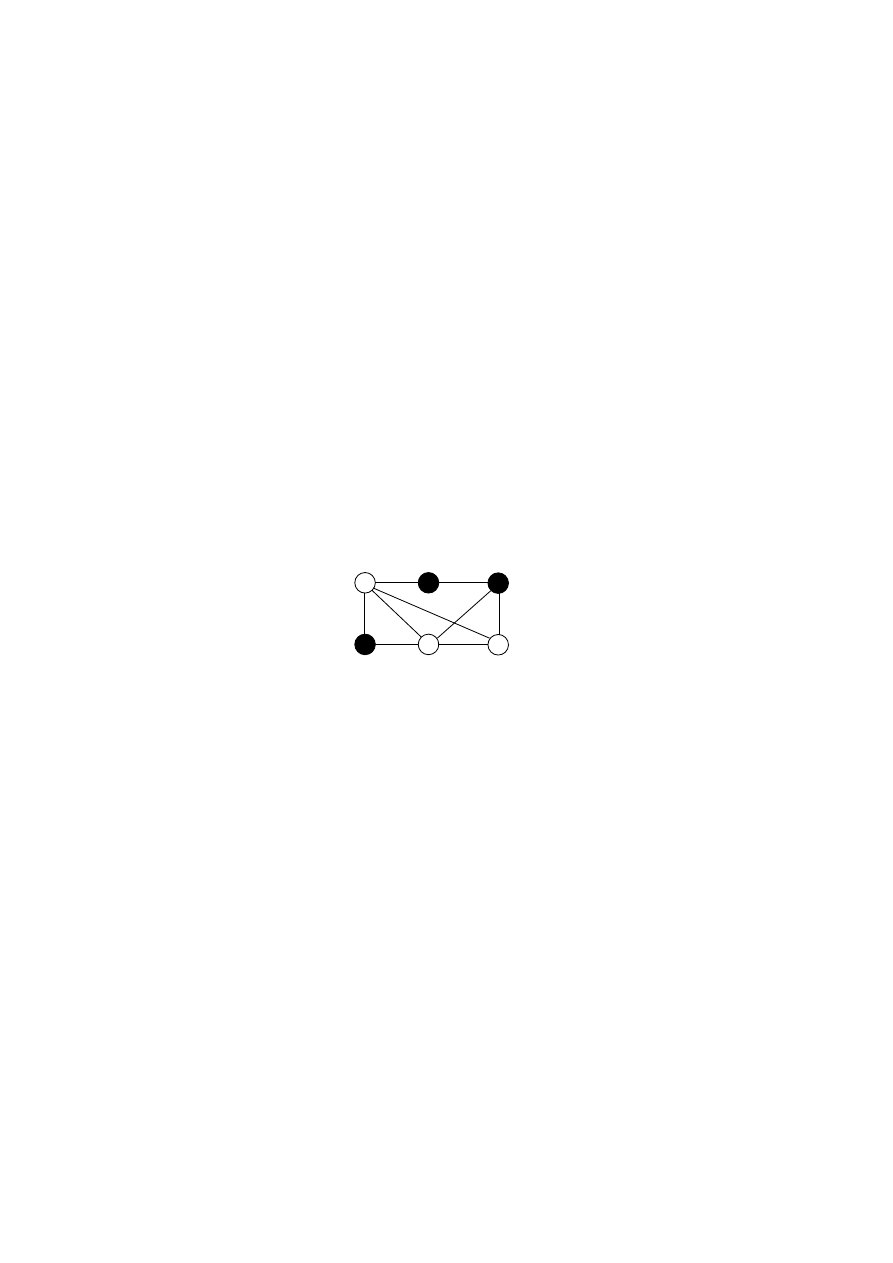
2. Wyznaczyć stan stabilny następującej sieci Hopfielda. Czy dla danego stanu począt-

kowego mogą istnieć dwa różne stany stabilne?

1

1

-1

-2

-2

2

2

3

-1

3. Zapoznać się z następującymi funkcjami przybornika NNET dotyczącymi dyskretnej

sieci Hopfielda:

• simuhop - symulacja sieci Hopfielda

• solvehop - projektowanie sieci Hopfielda

4. Zastosować sieć Hopfielda złożoną z pięciu neuronów do zapamiętania trzech wzor-

ców: Ψ

1

= [+1, +1, +1, +1, +1]

T

, Ψ

2

= [+1, −1, −1, +1, −1]

T

, Ψ

3

= [−1, +1, −1, +1, +1]

T

.

(a) Wyznaczyć macierz połączeń synaptycznych.

(b) Za pomocą asynchronicznego odtwarzania stanu sieci pokazać, że wszystkie

trzy wzorce zostały poprawnie zapamiętane.

(c) Przebadać jak zostaną odtworzone zapamiętane wzorce przy pomocy synchro-

nicznego odtwarzania stanu sieci.

(d) Przebadać zachowanie się sieci w przypadku prezentacji wzorca Ψ

1

w którym

wartość drugiego elementu został zmieniona na −1.

(e) Pokazać, że wzorce Ψ

0
1

= [−1, −1, −1, −1, −1]

T

, Ψ

0
2

= [−1, +1, +1, −1, +1]

T

,

Ψ

0
3

= [+1, −1, +1, −1, −1]

T

są także zapamiętane przez sieć neuronową.

2

(f) Przypuśćmy, że pierwszy element wzorca Ψ

3

jest brakujący (równy 0). Określić

odpowiedź sieci na taki wzorzec. Porównać odpowiedź sieci z wzorcem orygi-
nalnym.

5. W oparciu o dyskretną sieć Hopfielda zaprojektować system rozpoznawania znaków

alfanumerycznych. Przetestować nauczoną sieć, wykorzystując wzorce oryginalne i
zaszumione.

3