S

TEROWANIE

R

OBOTAMI

C

WICZENIA

L

ABORATORYJNE NR

5

M

IEJSCA GEOMETRYCZNE PIERWIASTKÓW

Akademia Górniczo – Hutnicza w Krakowie

Laboratorium nr 5 – miejsca geometryczne pierwiastków

Cwiczenia – czesc pierwsza

Cwiczenie 1

a.

Wykresl MGP dla ukladu G(s) = (3s - 4) / (s

2

- 2s + 2).

b. Wykresl MGP dla ukladu G(s) = -(3s - 4) / (s

2

- 2s + 2).

c.

Czy istnieje taka wartosc k , dla której jeden z powyzszych ukladów bedzie stabilny?

Cwiczenie 2

a.

Wykresl MGP dla ukladu G(s) = 1 /s(s + 1) (s

2

+ as + 4), gdzie a zmienia sie od 0,01 do 4,0

b. Sprawdz czy mozna znalezc dokladna wartosc a, dla której dwa niestabilne bieguny ustabilizuja sie.

Cwiczenie 3

a.

Wykresl MGP dla ukladu G(s) = (s

2

+ s + a) / s (s + 1) (s

2

+ s + 1.25) (s

2

+ s + 4.25), gdzie a zmienia sie

od 1,25 do 4,25 z przyrostem 1.

b. Wykresl MGP dla ukladu :

G(s) = (s

2

+ s + 9.25) (s

2

+ 2s + 10) (s

2

+ 3s + 11.25) / s (s + 2) (s

2

+ 2s + 5) (s

2

+ 2s + 17).

Cwiczenia – czesc druga

Cwiczenie 4

Dany jest skrypt ssrloc.m

ssrloc.m
% ssrloc
% This illustrate s the use of rlocus with a system
% in state space form.
clf
a = [ -1.5 -13.5 -13.0 0
1 0 0 0
0 1 0 0
0 0 1 0];
b = [ 1; 0; 0; 0 ];
c = [ 0 0 0 1 ];
d = 0;
rlocus (a, b, c, d);

Projektanci ukladów automatyki zawsze daza do skasowania wplywu sprzezonych biegunów (rezonansowych)
umieszczajac w ich poblizu sprzezone zera. Poniewaz liczba zer nie moze byc wieksza niz liczba biegunów,
musza równiez dodac nowe bieguny o zblizonej czestosci wlasnej, ale wiekszym tlumieniu. Operacje taka
nazywa sie notch filter.
a.

Dodaj notch filter do ssrloc.m – umiesc zera dokladnie na biegunach rezonansowych, bieguny filtru niech
maja te sama czestotliwosc, ale pieciokrotnie wieksze tlumienie.

b. Powtóz czesc a ale umiesc zera nieco powyzej i na lewo od biegunów rezonansowych.
c.

Powtóz czesc a ale umiesc zera nieco ponizej i na lewo od biegunów rezonansowych.

d. Poniewaz w warunkach rzeczywistych znamy tylko przyblizone polozenie biegunów, podaj które polozenie

zer jest lepsze: z podpunktu b czy c?
Podpowiedz: odpowiedz zalezy od zapasu stabilnosci. Jaka zmiana spowoduje utrate stabilnosci przez twój
uklad

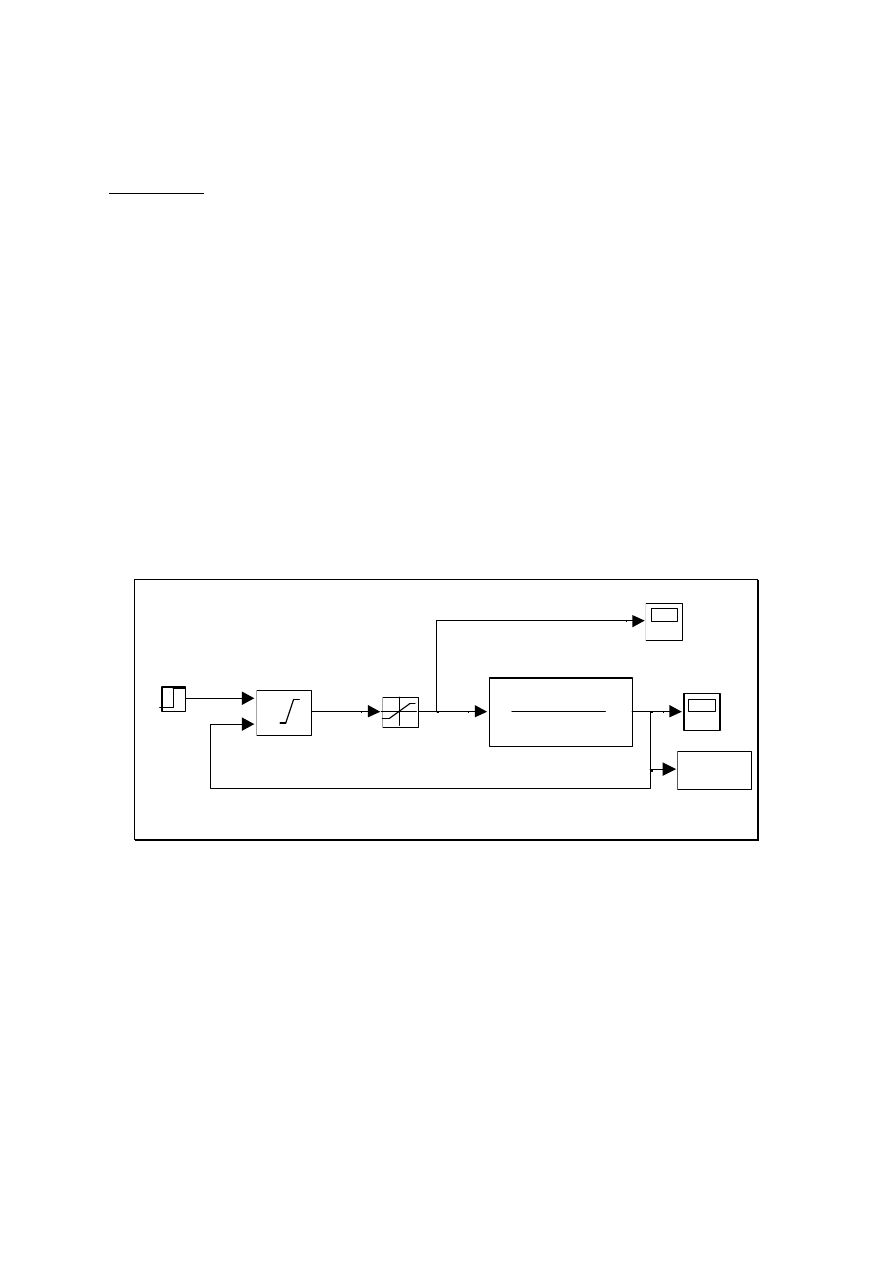
Cwiczenie 5

Dany jest skrypt ukazujacy przyklad projektowania ukladów sterowania w oparciu o MGP

.rlocdesignex.m
% rlocdesignex
% An example of design by means of the root locus
clf
num = 1;
den = conv ( conv ( [ 1 0], [1 1] ), [ 0.2 1] );
rlocus (num, den);
v1 = 0.1; v2 = 2.5; h1 = 4; h2 = 0.1;
axis ( [-h1 h2 -v1 v2] ); damping=0.707;
wn = 1:1:4;
sgrid (damping, wn)

a.

Wykresl MGP ukladu danego w skrypcie z kompensatorem wyprzedzajacym z kompensujacym zerem w
punkcie –0,9. Pamietaj aby bieguny kompensatora znalazly sie 10 razy dalej na lewo niz zero.

b. Powtórz czesc a. ale umiesc zero kompensatora w punkcie –1.1. Który z kompensatorów jest lepszy.
c.

Wykresl MGP ukladu danego w skrypcie z kompensatorem opózniajacym. Jak polozenie biegunów
kompensatora wplywa na wyglad MGP.

d. Wykresl MGP dla ukladu plus wszystkie trzy kompensatory.

Cwiczenie 6

Zbuduj nastepujacy uklad w SIMULINKU

20

(s+.1)(s+2)(s+10)

Zero-Pole

y

To Workspace

Step Input

PID

Set point PID

with Anti-Windup

Scope

Scope

Saturation

Znajdz niezerowa wartosc Td, która poprawi odpowiedz powyzszego ukladu. Niewykluczone, ze konieczna
bedzie równiez korekta wartosci N.