S

TEROWANIE

R

OBOTAMI

C

WICZENIA

L

ABORATORYJNE NR

3

D

EFINICJA UKLADÓW STEROWANIA W

M

ATLABIE

Akademia Górniczo – Hutnicza w Krakowie

Cwiczenia laboratoryjne nr 3. Definiowanie ukladów sterowania w Matlabie

1

Definicja ukladów sterowania w Matlabie

Dobre zrozumienie zwiazku pomiedzy róznymi opisami liniowych ukladów o parametrach nie zmieniajacych sie w czasie
jest niezbedne aby projektowac uklady sterowania typu SISO (single input, single output). Inzynierowie automatycy, jak
i teoretycy sterowania operuja na funkcjach przejscia, zmiennych stanu, biegunach i zerach oraz odpowiedzi impulsowej
ukladu w swych próbach zaprojektowania ukladów sterowania. Kazda z powyzszych metod opisu ukladu ma swoje wady
i zalety, ale kazda jest potrzebna poniewaz ukazuje inne cechy jego zachowania.
Matlab dostarcza narzedzia do definiowania ukladów w kazdy z powyzszych sposobów oraz do przelaczania sie miedzy
nimi. Umozliwia równiez graficzna reprezentacje róznych rodzajów opisów. Poprzednie cwiczenia dotyczyly podstaw
poslugiwania sie Matlabem jako oprogramowaniem inzynierskim. Nastepne cwiczenia dotycza zastosowania Matlaba
jako przykladowego narzedzia wirtualnego prototypowania do analizy i projektowania liniowych ukladów sterowania
typu SISO. To cwiczenie pokazuje jak w Matlabie zdefiniowac funkcje przejscia lub zmienne stanu jakiegokolwiek
rozwazanego ukladu.

Tworzenie funkcji przejscia

Rozwaz uklad opisany przez:

)

4

.

0

)(

25

)(

15

(

)

20

(

18

)

(

)

(

)

(

+

+

+

+

=

=

s

s

s

s

s

G

s

U

s

Y

gdzie transmitancja G(s) jest stosunkiem wyjscia Y(s) do wejscia U(s). Powyzszy przyklad funkcji przejscia wiaze
predkosc obrotowa walu Y(s) z zasilaniem w paliwo U(s) turbiny gazowej napedzajacej okret wojenny. Skrypt marinep.m
tworzy funkcje przejscia powyzszego ukladu w Matlabie.

marinep.m
% marinep
% This creates1 multiplies out, and prints
% the transfer function.
% G (s) = 18 (S+20) / (S+15) (S+25) (S+0.4)
num = 18*[1 20];
den = conv ( conv( [1 15], [1 25] ), [1 0.4] );
printsys (num, den, 's')

Zmienna num reprezentuje wielomian licznika funkcji przejscia G(s). Wielomiany sa zdefiniowane jako wektory
wierszowe, których elementy równe sa wspólczynnikom przy kolejnych potegach zmiennej. Podobnie den to wielomian
mianownika funkcji przejscia. Komenda printsys uzyta w marinep.m wypisuje funkcje przejscia ukladu w formie zgodnej
z zapisem matematycznym. Parametr ‘s’ okresla, ze transmitancje jest w dziedzinie s. Wykonanie marinep.m zwróci:

18 s + 360

----------------------------------------

s

3

+ 40.4 s

2

+ 391 s + 150

Uklad masa, sprezyna tlumik ma funkcje przejscia drugiego rzedu w formie:

K

s

Ms

s

G

s

F

s

X

m

+

+

=

=

µ

2

1

)

(

)

(

)

(

gdzie X(s) jest pozycja masy, a F(s) sila przylozona do niej,

µ

to wspólczynnik tlumienia i K sztywnosc sprezyny.

Uklady bardziej zlozone moga byc niekiedy aproksymowane dynamikami drugiego rzedu. Uklady drugie rzedu sa
zapisywane w standardowej formie:

2

2

2

2

)

(

)

(

)

(

n

n

s

s

k

s

G

s

U

s

Y

ω

ζω

+

+

=

=

gdzie

ϖ

n

to czestotliwosc drgan wlasnych, a

ζ znormalizowany wspólczynnik tlumienia ukladu. Gdy przekonwertujemy

uklad masa, sprezyna, tlumik do powyzszego formatu otrzymamy

M

k

/

1

=

,

M

K

n

/

=

ω

, i

M

K /

2

/

µ

ζ

=

.

Cwiczenia laboratoryjne nr 3. Definiowanie ukladów sterowania w Matlabie

2

Poniewaz powszechnym jest opisywanie ukladów takiej formie Matlab posiada polecenie ord2 , do generowania opisu
ukladu przy parametrach wejsciowych

ζ

i

ϖ

n

. Na przyklad plik massprdm.m zawiera polecenia definiujace uklad drugiego

rzedu dla k=1,

ϖ

n

=2 i

ζ=0.707 (tzn. M=1, K=4, µ=2,828 ).

massprdm.m
% masspringdamp
% Illustration of the use of ord2.
wn = 2;
damping = 0.707;
[num2, den2] = ord2 ( wn, damping );
printsys (num2, den2, ‘s’)

Polecenie ord2 wykorzystuje dwa parametry wejsciowe: czestotliwosc drgan wlasnych i znormalizowany wspólczynnik
tlumienia. Zwraca równiez dwie wielkosci, odpowiednio licznik i mianownik funkcji przejscia zadanego ukladu.
Wykonanie pliku massprdm.m spowoduje wypisanie w przestrzeni roboczej Matlaba:

num/den =

1

------------------------------

s

2

+ 2.828 s + 4

Matlab zapewnia równiez srodki do generowania losowych funkcji przejscia. Komenda [numr,denr] = rmodel(n) tworzy
licznik numr i mianownik denr stabilnej funkcji przejscia n-tego rzedu o losowo wybranych parametrach.
W Matlabie istnieje mnóstwo narzedzi do analizowania ukladów sterowania opisanych przez transmitancje. Na przyklad
mozesz obejrzec odpowiedz ukladu na skok jednostkowy wykorzystujac step, wygenerowac miejsca geometryczne
pierwiastków przy pomocy rlocus, lub charakterystyki Bodego uzywajac bode.

Tworzenie opisów modeli równaniami stanu

Generowanie opisu modelu przy pomocy zmiennych stanu jest analogiczne do opisywania go funkcja przejscia. Rozwaz
równania stanu standardowego liniowego ukladu SISO:

x’(t) = ax(t) + bu(t)
y(t) = cx(t) + du(t)

gdzie wektor x(t) reprezentuje zmienne stanu, skalar u(t) wejscie, a skalar y(t) wyjscie z ukladu. Stala a to macierz, b
wektor kolumnowy, c wektor wierszowy, a d to skalar. Poniewaz tworzenie i manipulacja na macierzach i wektorach jest w
Matlabie bardzo prosta, definiowanie ukladów przy pomocy równan stanu jest równiez wygodne i szybkie. Plik
ssmarine.m tworzy równania stanu dla napedu okretu opisanego uprzednio.

ssmarine.m
% ssmarine
% State space version of the marine propulsion plant.
a = [ -40.4 –391 -150; 1 0 0; 0 1 0 ];
b = [ 1 0 0 ]';
c = [ 0 18 360 ];
d = 0;
printsys(a, b, c, d)

Stale a, b, c i d zostaly wygenerowane przy uzyciu standardowej notacji Matlaba dla macierzy i wektorów. Jak mozna
przewidywac polecenie printsys uzyte w powyzszy sposób wypisze równania stanu w przestrzeni roboczej Matlaba.
Wykonanie ssmarine.m spowoduje:

a =

x1

x2

x3

x1

-40.40000

-391.00000

-150.00000

x2

1.00000

0

0

x3

0

1.00000

0

Cwiczenia laboratoryjne nr 3. Definiowanie ukladów sterowania w Matlabie

3

b =

u1

x1

1.00000

x2

0

x3

0

c =

x1

x2

x3

y1

0

18.00000

360.00000

d =

u1

y1

0

Podobnie polecenie ord2 moze zostac wykorzystane do wygenerowania równan stanu dla ukladów drugiego rzedu, przy
tych samych argumentach wejsciowych jak w przypadku transmitancji. Wystarczy zdefiniowac jako parametry
wyjsciowe stale z równan stanu w miejsce licznika i mianownika funkcji przejscia. Skrypt ssmasspd.m zwraca równania
stanu dla przykladu wspomnianego wczesniej gdzie

ζ=0,707

a

ϖ

n

=2.

ssmasspd.m
% ssmasspd
% Illustration of the state space version of ord2.
wn = 2;
damping = 0.707;
[a2, b2, c2, d2] = ord2(wn,

damping);

printsys (a2, b2, c2, d2)

Komenda rmodel równiez ma zastosowanie do tworzenia równan stanu stabilnego ukladu losowego o zadanym rzedzie
n. Polecenie minreal tworzy nowe równania stanu z juz istniejacych, eliminujac zmienne stanu, które sa niepotrzebne.
Polecenie to moze byc równiez uzuwane do modyfikacji funkcji przejscia. Redukcja rzedu równan stanu moze byc
równiez wykonana poleceniami modred i balreal.

Przejscie z równan stanu do funkcji przejscia

Jak wspomniano na poczatku tego cwiczenia, inzynierowie automatycy musza byc biegli w przechodzeniu miedzy
róznymi typami opisów modeli. Matlab bardzo ulatwia to zadanie. Na przyklad polecenie ss2tf powoduje przejscie z
opisu zmiennymi stanu (ss) do (2) opisu funkcja przejscia (tf). Zauwaz, ze jesli nauczysz sie tych mnemoników to latwo
bedzie ci wymyslic nazwy innych komend o podobnym dzialaniu. Na przyklad, tf2ss, która przelacza opis modelu z
funkcji przejscia do równan stanu.
Po wykonaniu skryptu ssmasspd.m, który tworzy równania stanu o parametrach a2, b2 , c2, d2 spróbuj uruchomic
converts.m, który konwertuje model uprzednio powstaly na funkcje przejscia.

converts.m
% converts
% This converts the second-order state space system
% created earlier into transfer function form
% (a2, b2, c2, d2 must already be present in workspace)
[numcss, dencss] = ss2tf ( a2, b2, c2, d2, 1);
printsys (numcss, dencss, 's')

Matlab wyswietli

num/den =

1

---------------------
s

2

+ 2.828 s + 4

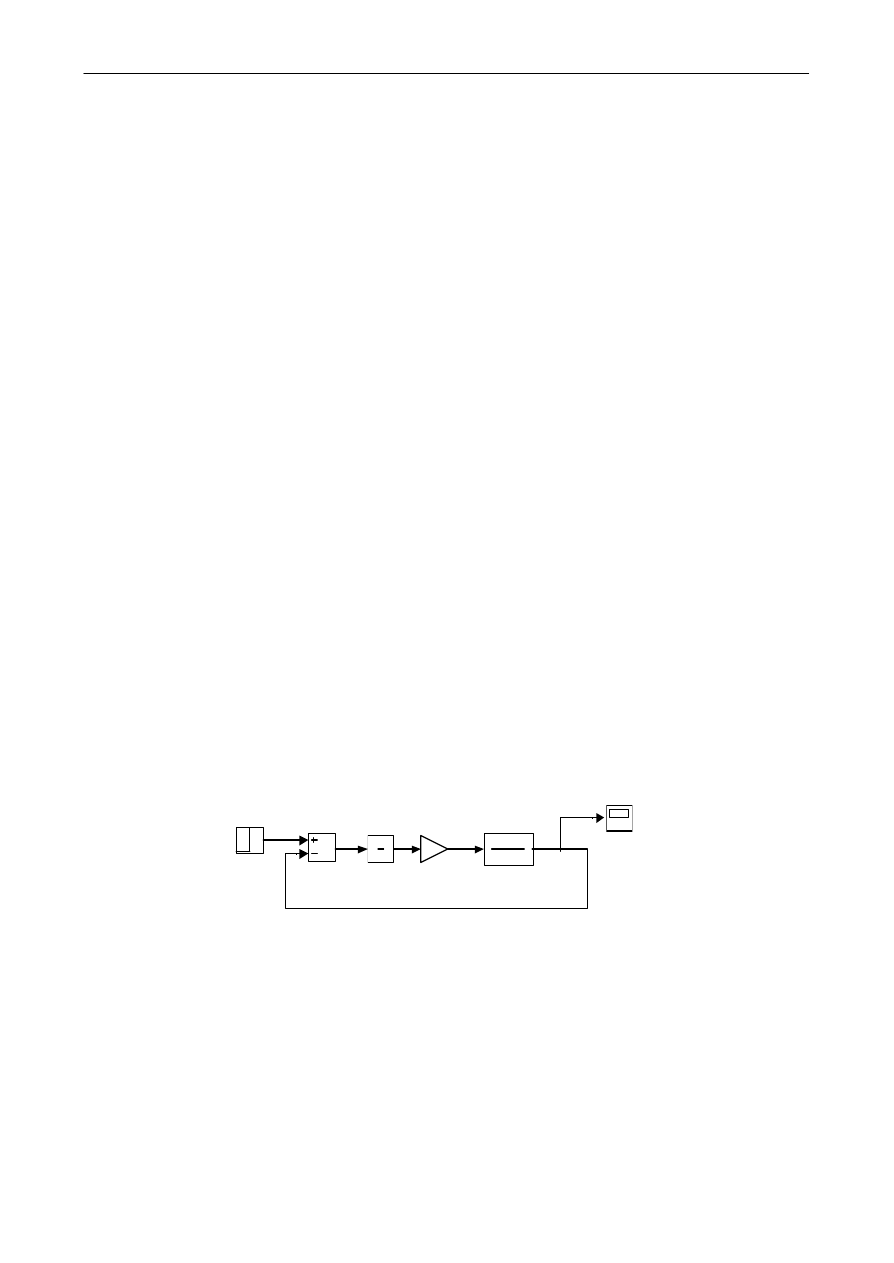
Cwiczenia laboratoryjne nr 3. Definiowanie ukladów sterowania w Matlabie

4

co jest funkcja przejscia identyczna do oryginalnej, wyliczonej dla masy, tlumienia i sprezystosci z pliku massprdm.m.
Ostatni argument wejsciowy polecenia ss2tf okresla, które wejscie modelu opisanego równaniami stanu mamy na mysli.
Dla ukladów typu SISO parametr ten zawsze powinien miec wartosc 1 lub moze zostac pominiety. Jednakze dla ukladów
wielowejsciowych parametr moze przyjmowac inne wartosci.
Polecenie ss2tf dziala poprawnie dla ukladów niskiego rzedu, jednak uzywa ono numerycznie niestabilnego algorytmu,
zachowaj wiec ostroznosc uzywajac go dla ukladów wyzszego rzedu.

Budowanie modeli z wykorzystaniem SIMULNIKA

Simulink jest narzedziem Matlaba, które udostepnia proste i intuicyjne srodki do budowania modeli z bloczków.
Umozliwia wymuszanie ich róznymi wejsciami i obserwacje wyjsc. Jak wskazuje nazwa Simulink jest przede wszystkim
narzedziem do symulowania ukladów. Szczególnie przydatny jest przy obserwowaniu nieliniowosci w ukladach.
Interfejs uzytkownika w Simulinku odpowiada standardom Macintosha, PC lub Unixa i jest oparty na systemie
okienkowym z rozwijanymi menu. Wiele ukladów, które chcemy modelowac moze zostac zbudowanych z prostszych
systemów juz zamodelowanych i dostepnych w Simulinku w postaci bloczków. Sa one reprezentowane przez ikony.
Ikony te moga byc otwierane przez podwójne klikniecie myszy i przeciagane mysza po nacisnieciu i przytrzymaniu
klawisza.

Cwiczenia

Cwiczenie 1

Dany jest uklad masa, sprezyna, tlumik o parametrach: m=2, k=3 i

µ=0.8. Znajdz funkcje przejscia G(s) = X(s)/F(s),

gdzie X(s) to pozycja masy, a F(s) to sila przylozona do masy. Jakie sa czestosci wlasne ukladu i znormalizowany
wspólczynnik tlumienia. Wygeneruj takze równania stanu tego ukladu. (wykorzystaj polecenie ord2 ).

Cwiczenie 2

Zalóz, ze system opisany funkcja przejscia H(s) jest polaczony równolegle do ukladu z cwiczenia 1 opisanego przez G(s).
Napisz skrypt, który wygeneruje funkcje przejscia takiego ukladu zakladajac, ze H(s) to stabilny uklad trzeciego rzedu o
losowych parametrach. (wykorzystaj polecenie rmodel).

Cwiczenie 3

a). Uzyj SIMULINKA do stworzenia ukladu jak na rysunku

s+1

s +5s+6

2

Transfer Fcn

Sum

Step

Scope

s

1

Integrator

80

Gain

b). W miejsce czlonu calkujacego wstaw blok saturation nonlinearity.
c). Zasymuluj system przed i po zmianie,
d). Dodaj kolejny scope po bloku nieliniowym, jaki ma on wplyw na sygnal?

Literatura

[1] Brzózka J.: Cwiczenia z automatyki w Matlabie i Simulinku. MIKOM, Warszawa 1997

[2] Matlab User’s Guide

[3] Simulink User’s Guide

[4] Leonard N., Levine W.: Using Matlab to Analyze and Design Control System. The Benjamin/Cummings Publishing

Company, 1995

Cwiczenia laboratoryjne nr 3. Definiowanie ukladów sterowania w Matlabie

5

[5] Zalewski A., Cegiela R.: Matlab – obliczenia numeryczne i ich zastosowania. NAKOM, Poznan 1996