Aula 06 Parte 01

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

Aula 6 – Parte 1

Problemas do 1º grau ........................................................................................................................................ 2

Relação das questões comentadas.................................................................................................................. 22

Gabarito ........................................................................................................................................................... 27

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

Olá, pessoal!

Aprenderemos a resolver os chamados “problemas do 1º grau”. São problemas contextualizados
cuja solução decai em uma equação ou um sistema de equações do 1º grau.

O maior problema encontrado pelos alunos não é o ato de resolver a equação propriamente dita.
O maior problema é interpretar o problema e escrevê-lo na linguagem matemática. Assim, durante
a resolução dos problemas, darei algumas dicas para que você tenha um pouco mais de facilidade
neste processo de transformar um texto em uma equação.

Algumas questões englobarão também assuntos gerais de matemática como proporcionalidade,
porcentagens, regra de três, MMC, MDC e conjuntos numéricos.

Problemas do 1º grau

01.

(RIOPREVIDÊNCIA 2010/CEPERJ) Considere um número real e faça com ele as

seguintes operações sucessivas: multiplique por 2, em seguida some 1, multiplique por 3 e
subtraia 5. Se o resultado foi 220, o valor de está entre:

a) 30 e 35
b) 35 e 40
c) 40 e 45
d) 45 e 50
e) 50 e 55

Resolução

Considere um número real .

Multiplicando-o por 2, obtemos

2 ∙ .

Somando 1 ao resultado, obtemos

2 ∙ + 1.

Em seguida, multiplicamos o resultado por 3. Assim, tem-se

3 ∙ 2 ∙ + 1 .

Finalmente subtrai-se 5 e obtemos:

3 ∙ 2 ∙ + 1 − 5.

Este resultado é igual a 220.

3 ∙ 2 ∙ + 1 − 5 = 220

Vamos aplicar a propriedade distributiva.

6 ∙ + 3 − 5 = 220

6 − 2 = 220

6 = 220 + 2

6 = 222 ⇔ =

222

6 = 37

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

Letra B

02.

(Pref. de São Gonçalo 2007/CEPERJ) Considere um número real e faça com ele as

seguintes operações sucessivas: multiplique por 4, depois some 31, em seguida divida por 3,
multiplique por 5 e subtraia 23. Se o resultado foi 222, o valor de é:

a) um número múltiplo de 7.
b) um número entre 30 e 40.
c) um número par.
d) um número cuja soma dos dígitos é 10.
e) um número primo.

Resolução

Multiplicando o número obtemos

4 ∙ .

Em seguida some 31

→ 4 ∙ + 31.

Depois divida por 3

→

Multiplique por 5

→ 5 ∙

Subtraia 23

→ 5 ∙

− 23

O resultado é igual a 222.

5 ∙

4 + 31

− 23 = 222 ⇔ 5 ∙

4 + 31

= 222 + 23

5 ∙

4 + 31

= 245 ⇔

4 + 31

245

4 + 31

= 49 ⇔ 4 + 31 = 3 ∙ 49

4 + 31 = 147 ⇔ 4 = 147 − 31

4 = 116 ⇔ =

116

4 = 29

Como o número 29 é primo (número primo é aquele que possui apenas dois divisores naturais).

Letra E

03. (SEE/RJ 2010/CEPERJ) No sistema

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

0,3 + 1,2 = 2,4

0,5 − 0,8 = −0,9

O valor de é:

a) 1
b) -1
c) 0
d) 2
e) 2/3

Resolução

Para deixar o sistema um pouco mais “limpo”, podemos multiplicar as duas equações por
10 com o intuito de eliminar as casas decimais.

0,3 + 1,2 = 2,4 ∙ 10

0,5 − 0,8 = −0,9 ∙ 10

3 + 12 = 24

5 − 8 = −9

Olhemos para a primeira equação:

3 + 12 = 24

Podemos, para simplificar, dividir ambos os membros da equação por 3.

+ 4 = 8

= 8 − 4

Vamos substituir esta expressão na segunda equação. Ou seja, trocaremos por

8 − 4 .

5 − 8 = −9

5 ∙ 8 − 4 − 8 = −9

40 − 20 − 8 = −9

−28 = −9 − 40

−28 = −49

Multiplicando os dois membros da equação por

−1 :

28 = 49 ⇔ =

Vamos simplificar esta fração por 7. Para simplificar, devemos dividir o numerador e o
denominador por 7.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

49/7

28/7 =

Como

= 8 − 4 :

= 8 − 4 ∙

4 = 8 − 7 = 1

Letra A

04. (TCE-RN 2000/ESAF) Um homem caridoso observou alguns mendigos em uma praça e

pensou: “Se eu der R$ 5,00 a cada mendigo, sobrar-me-ão R$ 3,00. Ah, mas se eu
tivesse apenas mais R$ 5,00, eu teria a quantia exata para poder dar a cada um deles R$
6,00”. O número de mendigos era, portanto:

a) 5
b) 6
c) 7
d) 8
e) 9

Resolução

Digamos que o homem caridoso possua reais e que existam

$ mendigos.

Vejamos a primeira situação. “Se eu der R$ 5,00 a cada mendigo, sobrar-me-ão R$ 3,00.”

O homem entrega 5 reais para cada um dos

$ mendigos. Portanto, ele gastou 5$ reais. Ele ainda

ficou com 3 reais. Desta forma, a quantia que o homem possui é igual a

5$ + 3 %&'().

= 5$ + 3

“Se eu tivesse apenas mais R$ 5,00, eu teria a quantia exata para poder dar a cada um deles R$
6,00.”

O homem possui reais. Se ele tivesse mais R$ 5,00, então ele teria

+ 5 reais. Esta quantia

daria para entregar exatamente 6 reais para cada um dos

$ mendigos.

+ 5 = 6$

= 6$ − 5

Ora, se

= 5$ + 3 e = 6$ − 5, então 5$ + 3 = 6$ − 5

5$ + 3 = 6$ − 5

5$ − 6$ = −5 − 3

−$ = −8

∴ $ = 8

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

São 8 mendigos.

Letra D

05. (Prefeitura Municipal de Pinheiral 2006/CETRO) Hoje a idade de João é a metade da idade

de sua mãe. Há quatro anos, a idade de João era a terça parte da idade de seu pai. Se a
soma das idades dos três é 100 anos hoje, calcule quantos anos o pai de João é mais
velho que sua mãe.

a) 8
b) 10
c) 12
d) 13
e) 15

Resolução

Uma dica: procure sempre utilizar letras que façam referência ao nome das pessoas
envolvidas. Esqueça essa “mania” de sempre usar x,y,z... Pois ao terminar a questão você
terá que procurar quem é x,y,z...

Por exemplo: a idade de João é J, a idade da mãe é M e a idade do pai é P.

Hoje a idade de João é a metade da idade de sua mãe. Assim,

+ =

. Assim,

. = 2 ∙ +.

Há quatro anos, a idade de João era a terça parte da idade de seu pai.

Ora, há quatros anos, João tinha (J – 4) anos e o seu pai tinha (P – 4) anos. A idade João era a
terça parte da idade de seu pai.

/0102 02 34ã4 =

/0102 04 516

3 − 8 =

9 − 8

9 − 8 = 7 ∙ 3 − 8

9 − 8 = 7 ∙ 3 − :;

9 = 7 ∙ 3 − :; + 8

9 = 7 ∙ 3 − <

A soma das idades dos três é 100 anos hoje.

3 + = + 9 = :>>

3 + ; ∙ 3 + 7 ∙ 3 − < = :>>

? ∙ 3 = :><

3 = :<

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

Assim, a mãe de João tem

= = ; ∙ 3 = 7?.

O pai de João tem

9 = 7 ∙ 3 − < = 7 ∙ :< − < = 8?.

O pai de João é 10 anos mais velho do que a sua mãe.

Letra B

06. (AFC/SEPLAG-GDF 2009/FUNIVERSA) A diferença entre as idades de dois irmãos é de

três anos. Após três anos do nascimento do segundo, nasceu o terceiro e assim foi
acontecendo até se formar uma família com cinco irmãos. Sabendo-se que, hoje, a idade
do último irmão que nasceu é a metade da idade do primeiro irmão nascido, é correto
afirmar que, hoje, o irmão mais velho está com idade igual a

a) 18 anos.
b) 20 anos.
c) 22 anos.
d) 24 anos.
e) 26 anos.

Resolução

Considere que o irmão mais novo tem anos. Portanto, as idades dos outros irmãos são iguais a

+ 3, + 6, + 9 & + 12.

A idade do irmão mais novo é a metade da idade do irmão mais velho.

@A'A& AB (%$ãB $'() DBEB =

@A'A& AB (%$ãB $'() E&FℎB

+ 12

2 = + 12

= 12

Assim, as idades dos irmãos são 12, 15, 18, 21, 24.

O irmão mais velho está com 24 anos.

Letra D

07. (EPPGG – SEPLAG/RJ 2009 – CEPERJ) Uma pessoa terá no ano de 2012 o triplo da

idade que tinha em 1994. Essa pessoa tem hoje:

a) 22 anos.
b) 23 anos.
c) 24 anos.
d) 25 anos.
e) 26 anos.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

Resolução

Prestemos atenção ao fato de que a prova foi realizada no ano de 2009. Digamos que a pessoa
tenha anos em 2009. Dessa maneira, terá

+ 3 anos em 2012 e − 15 anos em 1994. Isso

porque 2012 – 2009 = 3 e 2009 – 1994 = 15.

Ano

1994

2009

2012

Idade

− 15

+ 3

A idade da pessoa em 2012 é o triplo da idade da mesma pessoa em 1994.

@A'A& A' H&))B' &$ 2012 = 3 ∙ @A'A& A' H&))B' &$ 1994

+ 3 = 3 ∙ − 15

+ 3 = 3 − 45

− 3 = −45 − 3

−2 = −48

= 24 'DB)

Letra C

08. (TRF 1ªR 2001/FCC) No almoxarifado de certa empresa há 68 pacotes de papel sulfite,

dispostos em 4 prateleiras. Se as quantidades de pacotes em cada prateleira
correspondem a 4 números pares sucessivos, então, dos números seguintes, o que
representa uma dessas quantidades é o:

Resolução

Se o primeiro número par for ,então os próximos números pares sucessivos serão

+ 2, +

4 & + 6. A soma destes 4 números deve ser igual a 68.

+ + 2 + + 4 + + 6 = 68

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

4 + 12 = 68

4 = 56 ⇔ = 14

Desta maneira, se na primeira prateleira há 14 pacotes, nas outras prateleiras haverá 16,

e 20

pacotes.

Letra C

09. (Prefeitura Municipal de Arujá 2006/CETRO) Três números pares e consecutivos têm por

soma 90. A divisão do menor deles por 7 nos dá um quociente igual a:

a) 2
b) 3
c) 4
d) 5
e) 6

Resolução

Seja x o primeiro número par. Os próximos números pares serão x+2 e x+4. A soma dos
três é igual a 90. Assim,

I + I + ; + I + 8 = J>

7 ∙ I + ? = J>

7 ∙ I = <8

I = ;<

O quociente da divisão de 28 por 7 é igual a 4.

Letra C

010.

(MF 2009/ESAF) Existem duas torneiras para encher um tanque vazio. Se

apenas a primeira torneira for aberta, ao máximo, o tanque encherá em 24 horas.
Se apenas a segunda torneira for aberta, ao máximo, o tanque encherá em 48
horas. Se as duas torneiras forem abertas ao mesmo tempo, ao máximo, em
quanto tempo o tanque encherá?

a) 12 horas
b) 30 horas
c) 20 horas
d) 24 horas
e) 16 horas

Resolução

Existe uma tática muito boa para resolver problemas envolvendo produção e tempo. A
tática é a seguinte: perguntar o que cada objeto produz na unidade de tempo.

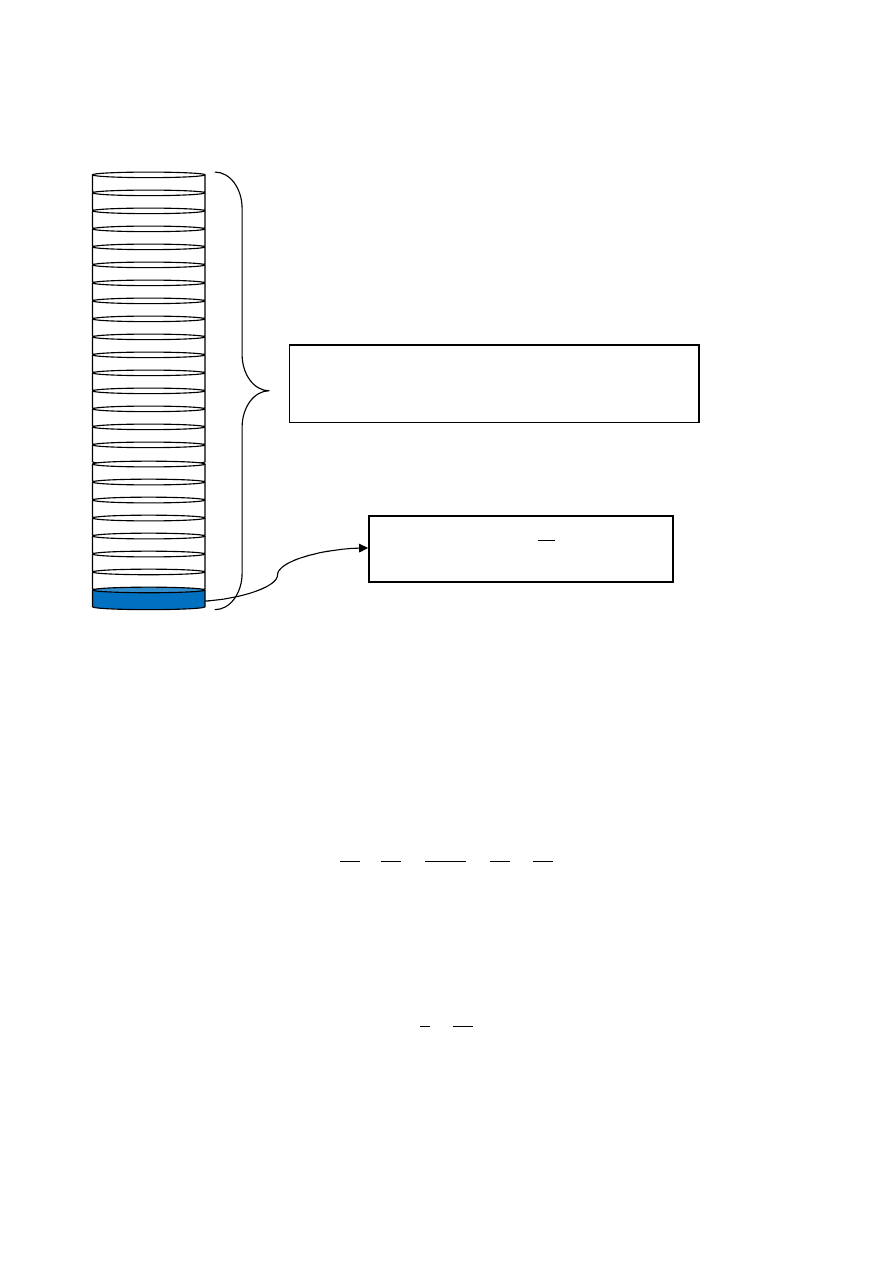
A primeira torneira enche o tanque em 24 horas. Isto significa que eu posso dividir o
tanque em 24 partes iguais e a torneira enche cada parte em 1 hora.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

Desta maneira, a primeira torneira enche 1/24 do tanque em 1 hora.

A segunda torneira enche o tanque em 48 horas. Isto significa que eu posso dividir o
tanque em 48 partes iguais e a torneira enche cada parte em 1 hora. Como o tanque foi
dividido em 48 partes, cada parte representa 1/48 do tanque. Ou seja, a segunda torneira
enche 1/48 do tanque em 1 hora.

Ora, se a primeira torneira em 1 hora enche 1/24 do tanque e a segunda torneira em 1
hora enche 1/48 do tanque, então juntas em 1 hora encherão:

24 +

48 =

2 + 1

48 =

Analogamente, se juntas as torneiras enchem o tanque completamente em horas, em 1
hora encherão 1/x.

Assim:

= 16 ℎB%').

Letra E

Vamos agora criar uma resolução geral para problemas de produção e tempo?

O tanque foi dividido em 24 partes iguais. A torneira

enche cada parte em 1 hora, totalizando 24 horas.

Cada parte representa

do tanque.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

Considere que um objeto execute um serviço em

' horas, outro objeto execute um serviço

o mesmo serviço em

K horas, outro objeto execute o mesmo serviço em L horas e assim

por diante. Considere ainda que juntos, os objetos executem o serviço em horas. Temos
a seguinte relação:

' +

K + ⋯ =

No nosso caso, a primeira torneira enche o tanque em 24 horas e a segunda torneira
enche o tanque em 48 horas. Elas enchem o tanque em

ℎB%').

24 +

48 =

2 + 1

48 =

⇔

48 =

Como o produto dos meios é igual ao produto dos extremos:

3 ∙ = 1 ∙ 48

3 = 16 ℎB%').

011.

(Oficial de Chancelaria – MRE 2009/FCC) Certo dia, Alfeu e Gema foram

incumbidos de, no dia seguinte, trabalharem juntos a fim de cumprir uma certa
tarefa; entretanto, como Alfeu faltou ao serviço no dia marcado para a execução de
tal tarefa, Gema cumpriu-a sozinha. Considerando que, juntos, eles executariam a
tarefa em 3 horas e que, sozinho, Alfeu seria capaz de executá-la em 5 horas, o
esperado é que, sozinha, Gema a tenha cumprido em

a) 6 horas e 30 minutos.
b) 7 horas e 30 minutos.
c) 6 horas.
d) 7 horas.
e) 8 horas.

Resolução

Alfeu executa o serviço sozinho em 5 horas. Gema executa o serviço sozinha em

N horas.

Juntos, executariam o serviço em 3 horas.

5 +

N =

3 −

5 ⇔

N =

5 − 3

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

N =

Como o produto dos meios é igual ao produto dos extremos:

2 ∙ N = 1 ∙ 15

2 = 7,5 ℎB%') = 7 ℎB%') & 30 $(DOPB)

Letra B

012.

(ANEEL 2004/ESAF) Para

≠ 5, a simplificação da expressão

10 − 50

25 − 5

é dada por:

−2

−5

d) 5
e)

Resolução

Vejamos o numerador:

10 − 50 = 10 ∙ − 5

Vejamos o denominador:

25 − 5 = 5 ∙ 5 −

= −5 ∙ − 5

Desta forma:

10 − 50

25 − 5 =

10 ∙ − 5

−5 ∙ − 5

Como

≠ 5, podemos cortar os fatores − 5 .

10 − 50

25 − 5 =

10 ∙ − 5

−5 ∙ − 5 =

−5 = −2

Dê uma olhada nas alternativas. A resposta não depende do valor de x. Portanto,
podemos escolher um valor arbitrário para x. Vamos, por exemplo, substituir x por 1.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

10 − 50

25 − 5 =

10 ∙ 1 − 50

25 − 5 ∙ 1 =

10 − 50

25 − 5 =

−40

20 = −2

Bem melhor, não?

Letra A

013.

(SEE/RJ 2010/CEPERJ) Carlos e Márcio são irmãos. Carlos dá a Márcio tantos

reais quantos Márcio possui e, em seguida, Márcio dá a Carlos tantos reais quantos Carlos
possui. Se terminaram com 16 reais cada um, a quantia que Carlos tinha inicialmente era
de:

12 reais

15 reais

18 reais

20 reais

24 reais

Resolução

Uma dica: procure sempre utilizar letras que façam referência ao nome das pessoas
envolvidas. Esqueça essa “mania” de sempre usar x,y,z...

No nosso caso, Carlos tem

R reais e Márcio tem S reais.

1ª informação: Carlos dá a Márcio tantos reais quantos Márcio possui.

Já que Márcio possui

$ reais, Carlos dará $ reais para Márcio. Vejamos o que acontece com as

quantias de cada um:

Carlos

Márcio

Início

Carlos dá

S reais para

Márcio

R − S

S + S = ;S

É óbvio notar que se Carlos dá

$ reais para Márcio, então Carlos perde $ reais e Márcio ganha

$ %&'().

1ª informação: Márcio dá a Carlos tantos reais quantos Carlos possui.

Atualmente, Carlos possui

L − $ %&'(). Portanto, Márcio dará a Carlos L − $ %&'().

Carlos

Márcio

Início

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

Carlos dá

reais para

Márcio

R − S

S + S = ;S

Márcio dá

(

R − S reais a

Carlos

R − S + R − S = ;R − ;S

;S − R − S = 7S − R

As duas quantias são iguais a 16 reais.

T2L − 2$ = 16

3$ − L = 16

Olhemos para a primeira equação:

2L − 2$ = 16

Podemos dividir os dois membros da equação por 2.

L − $ = 8

L = $ + 8

Vamos substituir esta expressão na segunda equação.

3$ − L = 16

3$ − $ + 8 = 16

3$ − $ − 8 = 16

2$ = 16 + 8 ⇔ 2$ = 24 ⇔ $ = 12

Como

L = $ + 8:

L = 12 + 8 = 20 %&'().

Letra D

014.

(SERPRO 2001/ESAF) Três meninas, cada uma delas com algum dinheiro,

redistribuem o que possuem da seguinte maneira: Alice dá a Bela e a Cátia dinheiro
suficiente para duplicar a quantia que cada uma possui. A seguir, Bela dá a Alice e a Cátia
o suficiente para que cada uma duplique a quantia que possui. Finalmente, Cátia faz o
mesmo, isto é, dá a Alice e a Bela o suficiente para que cada uma duplique a quantia que
possui. Se Cátia possuía R$ 36,00 tanto no início quanto no final da distribuição, a quantia
total que as três meninas possuem juntas é igual a:

a) R$ 214,00
b) R$ 252,00
c) R$ 278,00
d) R$ 282,00
e) R$ 296,00

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

Resolução

Vamos montar uma tabela com a evolução da quantia que cada pessoa possui.

Alice

Bela

Cátia

Início

Alice dá a Bela e a Cátia dinheiro suficiente para duplicar a quantia que cada uma possui.

Para que Bela duplique sua quantia, ela deve receber

K reais. Para que Cátia duplique sua

quantia, ela deve receber 36 reais.

Alice

Bela

Cátia

' − K − 36

K + K = 2K

36 + 36 = 72

Bela dá a Alice e a Cátia o suficiente para que cada uma duplique a quantia que possui.

Para que Alice duplique sua quantia, ela deve receber

' − K − 36. Para que Cátia duplique a sua

quantia, ela deve receber 72 reais.

Alice

Bela

Cátia

2 ∙ ' − K − 36

2K − ' − K − 36 − 72

2 ∙ 72 = 144

Manipulando a expressão da quantia de Bela:

Alice

Bela

Cátia

2 ∙ ' − K − 36

3K − ' − 36

2 ∙ 72 = 144

Cátia faz o mesmo, isto é, dá a Alice e a Bela o suficiente para que cada uma duplique a quantia
que possui.

Para que Alice duplique a sua quantia, ela deve receber

2 ∙ ' − K − 36 . Para que Bela duplique a

sua quantia, ela deve receber

3K − ' − 36.

Cátia possuía 144 reais. Como deu

2 ∙ ' − K − 36 para Alice e 3K − ' − 36 para Bela, então ficou

com:

144 − 2 ∙ ' − K − 36 – 3K − ' − 36

No final, Cátia ficou com 36 reais. Portanto,

144 − 2 ∙ ' − K − 36 – 3K − ' − 36 = 36

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

144 − 2' + 2K + 72 − 3K + ' + 36 = 36

−' − K = −216

Multiplicando os dois membros por

−1 :

' + K = 216

A quantia total que as três meninas possuem juntas é igual a:

' + K + L = 216 + 36 = 252

Letra B

015.

(CEAGESP 2006/CONSULPLAN) Rui diz a Pedro: Se você me der 1/5 do dinheiro

que possui, eu ficarei com uma quantia igual ao dobro do que lhe restará. Por outro lado,
se eu lhe der R$ 6,00 do meu dinheiro, nós ficaremos com quantias iguais. Quanto de
dinheiro possui Rui?

a) R$ 42,00
b) R$ 31,00
c) R$ 25,00
d) R$ 28,00
e) R$ 47,00

Resolução

Vamos assumir que Rui possui

% reais e que Pedro possui H reais.

“Rui diz a Pedro: Se você me der 1/5 do dinheiro que possui, eu ficarei com uma quantia igual ao
dobro do que lhe restará.”

Se Pedro der 1/5 do seu dinheiro, ficará com 4/5 da sua quantia.

Ou seja, se Pedro possuía

H %&'(), ficará com

∙ H.

Rui receberá 1/5 da quantia de Pedro. Como Rui possuía

% %&'(), ficará com % +

∙ H.

Sabemos que a quantia que Rui fica é o dobro da quantia de Pedro.

% +

5 ∙ H = 2 ∙

5 ∙ H

% +

5 ∙ H =

5 ∙ H

% =

5 ∙ H −

5 ∙ H

% =

5 ∙ H

5% = 7H

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

Rui diz a Pedro:

“Por outro lado, se eu lhe der R$ 6,00 do meu dinheiro, nós ficaremos com quantias iguais.”

Pedro ficará com

H + 6 reais e Rui ficará com % − 6 reais. Estas duas quantias devem ser iguais.

H + 6 = % − 6

H = % − 12

Substituindo esta expressão na equação obtida acima:

5% = 7H

5% = 7 ∙ % − 12

5% = 7% − 84

−2% = −84 ⇔ 2% = 84 ⇔ % = 42 %&'().

Letra A

016.

(Pref. de São Gonçalo 2007/CEPERJ) Antônio, Bruno e Carlos compraram um

barco por R$ 600,00. Antônio pagou a metade do que os outros dois juntos pagaram.
Bruno pagou a terça parte do que os outros dois juntos pagaram. Então Carlos pagou:

a) R$150,00
b) R$200,00
c) R$250,00
d) R$300,00
e) R$350,00

Resolução

Vamos utilizar as letras

', K, L para indicar as quantias pagas por Antônio, Bruno e Carlos,

respectivamente.

1ª informação

→ Antônio, Bruno e Carlos compraram um barco por R$ 600,00.

' + K + L = 600

2ª informação

→ Antônio pagou a metade do que os outros dois juntos pagaram.

' =

K + L

2 ⇔

W + R = ;1

3ª informação

→ Bruno pagou a terça parte do que os outros dois juntos pagaram.

K =

' + L

3 ⇔ ' + L = 3K

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

Voltemos à primeira equação:

' +

W + R

= 600

Sabemos que

W + R = ;1.

Portanto,

' +

= 600

3' = 600

' = 200

Vamos utilizar o mesmo artifício com a terceira informação.

Sabemos que

1 + R = 7W

e que

+ K

+ R

= 600.

K +

= 600

4K = 600

K = 150

' + K + L = 600

200 + 150 + L = 600

350 + L = 600

L = 250

Letra C

017.

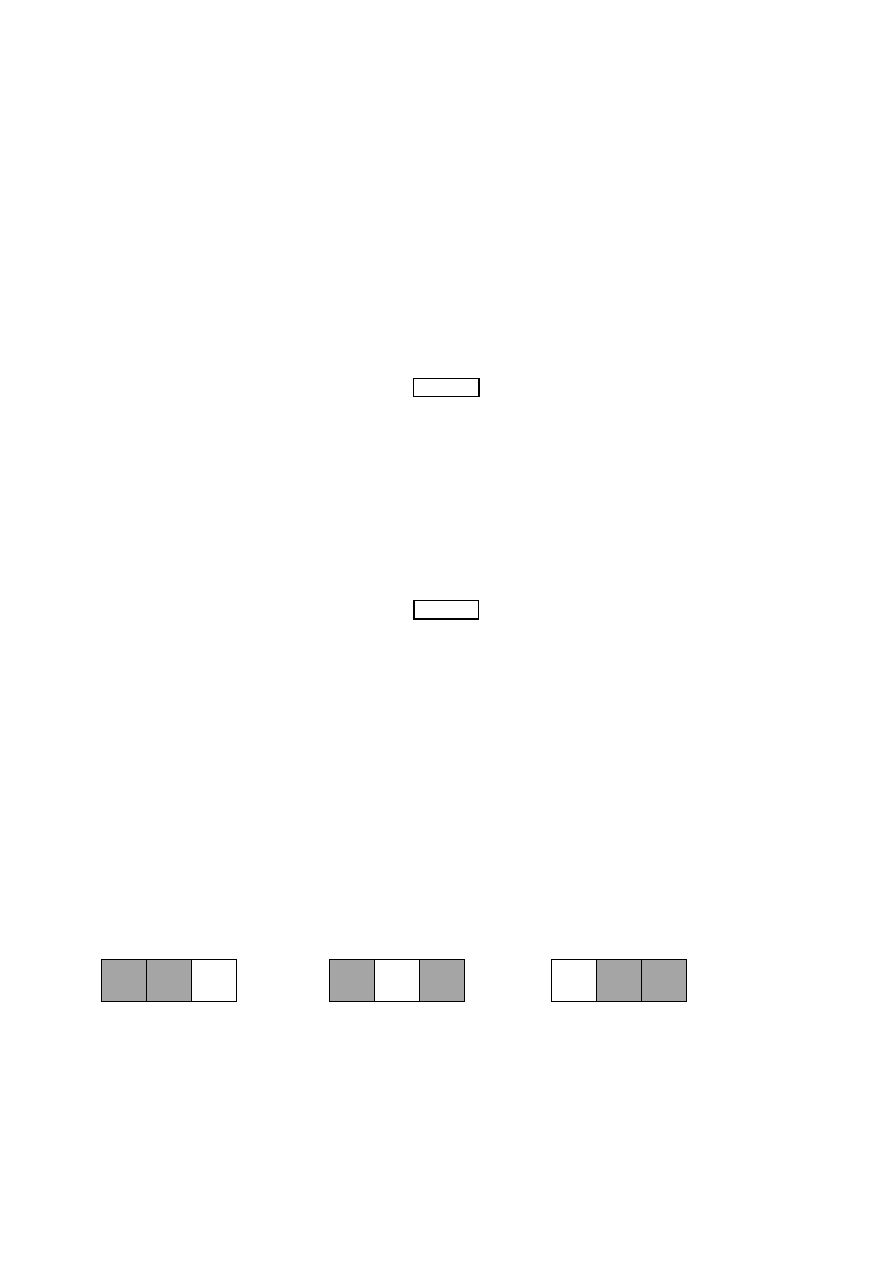
(EPPGG – SEPLAG/RJ 2009 – CEPERJ) Em cada quadradinho da figura abaixo há

um número escondido.

Nas figuras a seguir, está escrita, abaixo de cada uma, a soma dos números dos quadradinhos
sombreados.

16 21 11

O número que está no primeiro quadradinho é:

a) 3
b) 5
c) 8

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

d) 11
e) 13

Resolução

Chamemos o número escondido no primeiro quadrado de , o segundo número de e o terceiro
de

Concluímos que:

+ = 16

+ X = 21

+ X = 11

Este é um sistema linear muito famoso em questões de matemática. É um sistema com 3
incógnitas. Só que em cada equação aparece a soma de duas das três incógnitas. O processo
mais rápido para resolver esse tipo de sistema é o seguinte:

i) Escolha a incógnita que você quer calcular.
ii) Multiplique por (-1) os dois membros da equação que não tem a incógnita escolhida por você.
iii) Some as três equações.

Como queremos calcular o número do primeiro quadradinho, então a incógnita escolhida é .

A equação que não aparece o é a terceira. Portanto, vamos multiplicar os dois membros da
terceira equação por -1.

+ = 16

+ X = 21

− − X = −11

Ao somar as três equações,

& X serão cancelados.

Ficamos com:

+ = 16 + 21 − 11

2 = 26

= 13

Letra E

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

018.

(Assistente Administrativo – SERGIPE GAS 2010/FCC) Três equipes, X, Y e Z,

trabalham em obras de canalização e distribuição de gás natural. Considere que, em certo
período, a soma dos comprimentos dos dutos montados por X e Y foi 8,2 km, por Y e Z foi
8,9 km e por X e Z foi 9,7 km. O comprimento dos dutos montados pela equipe

(A) X foi 4 200 m.
(B) X foi 4 500 m.
(C) Y foi 3 500 m.
(D) Y foi 3 900 m.
(E) Z foi 5 000 m.

Resolução

De acordo com o enunciado temos:

+ = 8,2

+ X = 8,9

+ X = 9,7

O processo mais rápido para resolver esse tipo de sistema é o seguinte:

i) Escolha a incógnita que você quer calcular.
ii) Multiplique por (-1) os dois membros da equação que não tem a incógnita escolhida por você.
iii) Some as três equações.

Vamos multiplicar a última equação por

−1 .

+ = 8,2

+ X = 8,9

− − X = −9,7

o somar as três equações,

& X serão cancelados.

Ficamos com:

+ = 8,2 + 8,9 − 9,7

2 = 7,4

= 3,7

Substituindo este valor na primeira equação:

+ 3,7 = 8,2

= 4,5

Como

+ X = 8,9:

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

3,7 + X = 8,9

X = 5,2

Desta maneira,

comprimento dos dutos montados pela equipe:

Y foi = 4,5 Z$ = 4.500 $

[ foi = 3,7 Z$ = 3.700 $

\ foi X = 5,2 Z$ = 5.200 $

Letra B

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

Relação das questões comentadas

01. (RIOPREVIDÊNCIA 2010/CEPERJ) Considere um número real e faça com ele as

seguintes operações sucessivas: multiplique por 2, em seguida some 1, multiplique por 3 e
subtraia 5. Se o resultado foi 220, o valor de está entre:

a) 30 e 35
b) 35 e 40
c) 40 e 45
d) 45 e 50
e) 50 e 55

02.

(Pref. de São Gonçalo 2007/CEPERJ) Considere um número real e faça com ele as

seguintes operações sucessivas: multiplique por 4, depois some 31, em seguida divida por 3,
multiplique por 5 e subtraia 23. Se o resultado foi 222, o valor de é:

a) um número múltiplo de 7.
b) um número entre 30 e 40.
c) um número par.
d) um número cuja soma dos dígitos é 10.
e) um número primo.

03. (SEE/RJ 2010/CEPERJ) No sistema

0,3 + 1,2 = 2,4

0,5 − 0,8 = −0,9

O valor de é:

a) 1
b) -1
c) 0
d) 2
e) 2/3

04. (TCE-RN 2000/ESAF) Um homem caridoso observou alguns mendigos em uma praça e

a) 5
b) 6
c) 7
d) 8
e) 9

05. (Prefeitura Municipal de Pinheiral 2006/CETRO) Hoje a idade de João é a metade da idade

de sua mãe. Há quatro anos, a idade de João era a terça parte da idade de seu pai. Se a

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

soma das idades dos três é 100 anos hoje, calcule quantos anos o pai de João é mais
velho que sua mãe.

a) 8
b) 10
c) 12
d) 13
e) 15

06. (AFC/SEPLAG-GDF 2009/FUNIVERSA) A diferença entre as idades de dois irmãos é de

a) 18 anos.
b) 20 anos.
c) 22 anos.
d) 24 anos.
e) 26 anos.

07. (EPPGG – SEPLAG/RJ 2009 – CEPERJ) Uma pessoa terá no ano de 2012 o triplo da

idade que tinha em 1994. Essa pessoa tem hoje:

a) 22 anos.
b) 23 anos.
c) 24 anos.
d) 25 anos.
e) 26 anos.

08. (TRF 1ªR 2001/FCC) No almoxarifado de certa empresa há 68 pacotes de papel sulfite,

dispostos em 4 prateleiras. Se as quantidades de pacotes em cada prateleira
correspondem a 4 números pares sucessivos, então, dos números seguintes, o que
representa uma dessas quantidades é o:

09. (Prefeitura Municipal de Arujá 2006/CETRO) Três números pares e consecutivos têm por

soma 90. A divisão do menor deles por 7 nos dá um quociente igual a:

a) 2
b) 3
c) 4
d) 5
e) 6

010.

(MF 2009/ESAF) Existem duas torneiras para encher um tanque vazio. Se

apenas a primeira torneira for aberta, ao máximo, o tanque encherá em 24 horas.
Se apenas a segunda torneira for aberta, ao máximo, o tanque encherá em 48

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

horas. Se as duas torneiras forem abertas ao mesmo tempo, ao máximo, em
quanto tempo o tanque encherá?

f) 12 horas
g) 30 horas
h) 20 horas
i) 24 horas
j) 16 horas
011.

(Oficial de Chancelaria – MRE 2009/FCC) Certo dia, Alfeu e Gema foram

a) 6 horas e 30 minutos.
b) 7 horas e 30 minutos.
c) 6 horas.
d) 7 horas.
e) 8 horas.

012.

(ANEEL 2004/ESAF) Para

≠ 5, a simplificação da expressão

10 − 50

25 − 5

é dada por:

−2

−5

d) 5
e)

013.

(SEE/RJ 2010/CEPERJ) Carlos e Márcio são irmãos. Carlos dá a Márcio tantos

reais quantos Márcio possui e, em seguida, Márcio dá a Carlos tantos reais quantos Carlos
possui. Se terminaram com 16 reais cada um, a quantia que Carlos tinha inicialmente era
de:

12 reais

15 reais

18 reais

20 reais

24 reais

014.

(SERPRO 2001/ESAF) Três meninas, cada uma delas com algum dinheiro,

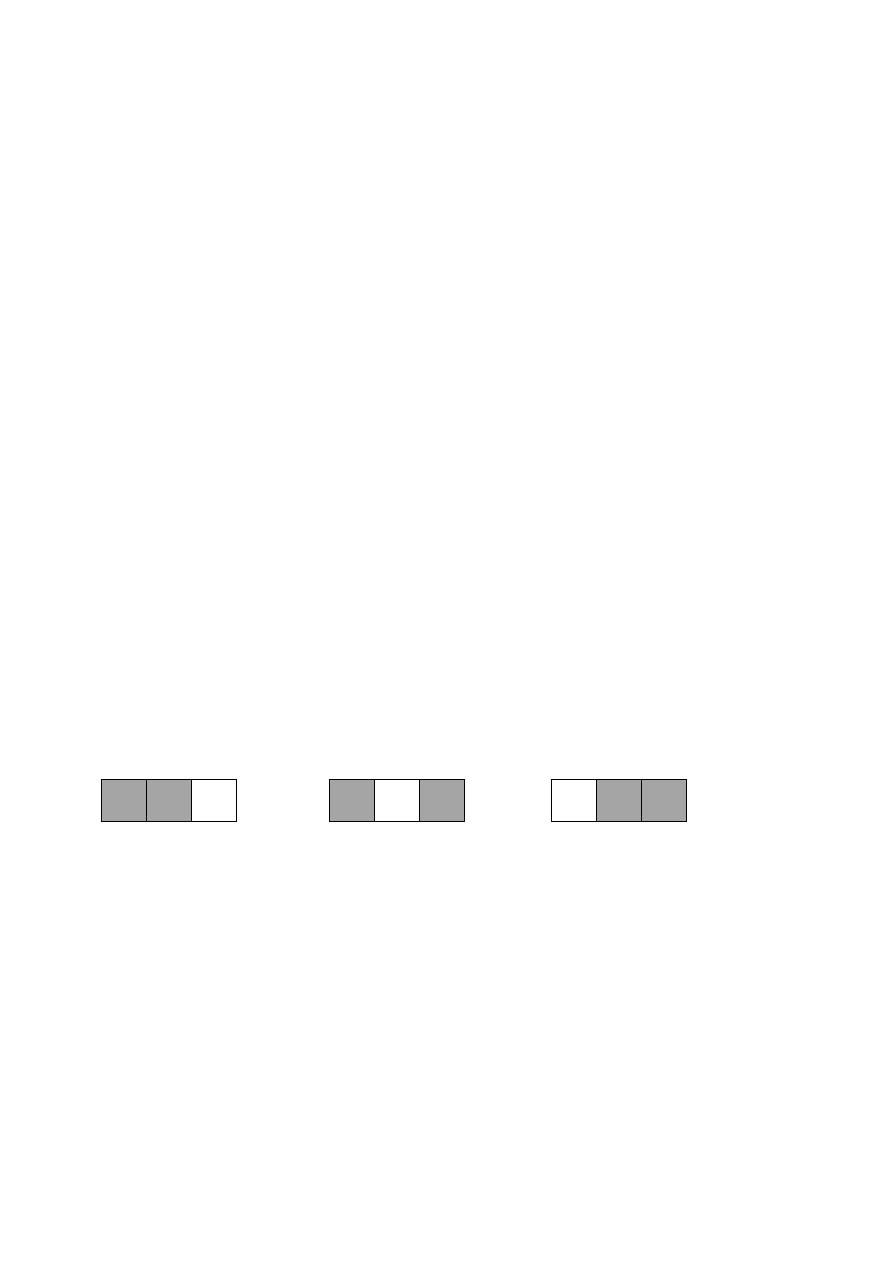
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

possui. Se Cátia possuía R$ 36,00 tanto no início quanto no final da distribuição, a quantia
total que as três meninas possuem juntas é igual a:

a) R$ 214,00
b) R$ 252,00
c) R$ 278,00
d) R$ 282,00
e) R$ 296,00

015.

(CEAGESP 2006/CONSULPLAN) Rui diz a Pedro: Se você me der 1/5 do dinheiro

que possui, eu ficarei com uma quantia igual ao dobro do que lhe restará. Por outro lado,
se eu lhe der R$ 6,00 do meu dinheiro, nós ficaremos com quantias iguais. Quanto de
dinheiro possui Rui?

a) R$ 42,00
b) R$ 31,00
c) R$ 25,00
d) R$ 28,00
e) R$ 47,00

016.

(Pref. de São Gonçalo 2007/CEPERJ) Antônio, Bruno e Carlos compraram um

barco por R$ 600,00. Antônio pagou a metade do que os outros dois juntos pagaram.
Bruno pagou a terça parte do que os outros dois juntos pagaram. Então Carlos pagou:

a) R$150,00
b) R$200,00
c) R$250,00
d) R$300,00
e) R$350,00

017.

(EPPGG – SEPLAG/RJ 2009 – CEPERJ) Em cada quadradinho da figura abaixo há

um número escondido.

Nas figuras a seguir, está escrita, abaixo de cada uma, a soma dos números dos quadradinhos
sombreados.

16 21 11

O número que está no primeiro quadradinho é:

a) 3
b) 5
c) 8
d) 11
e) 13

018.

(Assistente Administrativo – SERGIPE GAS 2010/FCC) Três equipes, X, Y e Z,

(A) X foi 4 200 m.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

(B) X foi 4 500 m.
(C) Y foi 3 500 m.
(D) Y foi 3 900 m.
(E) Z foi 5 000 m.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB

PROFESSOR: GUILHERME NEVES

Prof. Guilherme Neves

www.pontodosconcursos.com.br

Gabarito

01.

02.

03.

04.

05.

06.

07.

08.

09.

10.

11.

12.

13.

14.

15.

16.

17.

18.

Wyszukiwarka

Podobne podstrony:
Aula 06 Parte 01 B
Aula 06 Parte 01 A
Aula 06 Parte 01 B
Aula 06 Parte 01 A
Aula 06 Parte 03
Aula 07 Parte 01
Aula 12 Parte 01
Aula 05 Parte 01
Aula 07 Parte 01
Aula 10 Parte 01
Aula 14 Parte 01
Aula 09 Parte 01
Aula 08 Parte 01
Aula 06 Parte 02
Aula 15 Parte 01
Aula 14 Parte 01
Aula 10 Parte 01

więcej podobnych podstron