
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
1
PORCENTAGEM ................................................................................................................................................. 2
Razão e Proporção ........................................................................................................................................... 37
GRANDEZAS DIRETAMENTE/INVERSAMENTE PROPORCIONAIS ..................................................................... 57
Regra de Três ................................................................................................................................................... 62
Aula 5 - P a r t e 1

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
2
Olá, pessoal!
Tudo bem?
Faremos uma pequena mudança no cronograma das próximas aulas.
Aula 2
Razão e proporção, divisão proporcional, regra de três simples e composta. Porcentagem.
Matrizes, Determinantes e Sistemas Lineares
Aula 3
Equivalências lógicas, negação de proposições compostas e de proposições quantificadas.
Diagramas Lógicos.
Aula 4
Verdades e Mentiras. Problemas de Associação. Problemas gerais de Raciocínio Lógico
Aula 5
Introdução à Teoria dos Conjuntos. Operações e relações entre conjuntos. Conjuntos Numéricos
(Naturais, Inteiros, Racionais, Irracionais, Reais e Complexos). Operações: Adição, Subtração,
Multiplicação, Divisão, Potenciação e Radiciação. Mínimo Múltiplo Comum e Máximo Divisor
Comum. Sistemas de Medidas.
Da aula 6 em diante o cronograma seguirá o mesmo.
PORCENTAGEM
As razões de denominador 100 são chamadas taxas percentuais, razões centesimais,
percentagem ou porcentagem.
Em geral, podemos trocar o denominador 100 pelo símbolo % (por cento).
Ou seja,
100 = %
Podemos expressar as porcentagens sob a forma decimal (taxa unitária). Para obter a taxa
unitária, basta dividir o numerador por 100.
80% =
80
100 = 0,8
47% =
47
100 = 0,47
100% =
100
100 = 1
280% =
280
100 = 2,8
1
Percentual de um valor
Para calcular x% de um valor, basta multiplicar o valor pelo número x/100.
Exemplo: Calcular 30% de 500.
Resolução

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
3
30% 500 =
30
100 ∙ 500 = 150
Exemplo: Calcular 20% de 30% de 40% de 1.000.
Resolução
20
100 ∙
30
100 ∙
40
100 ∙ 1.000
Neste caso, podemos simplificar as frações. 20/100 pode ser simplificado por 20, tornando-se 1/5.
30/100 pode ser simplificado por 10, tornando-se 3/10. 40/100 pode ser simplificado por 20,
tornando-se 2/5.
1
5 ∙
3
10 ∙
2
5 ∙ 1.000 =
6.000
250 = 24
Portanto, 20% de 30% de 40% de 1.000 é igual a 24.
2
Transformação de uma fração ordinária em taxa percentual
Este tópico é importante, pois quando queremos expressar algum crescimento ou desconto,
sempre o fazemos em termos percentuais.
Para transformar uma fração ordinária qualquer em taxa percentual, basta multiplicá-la por 100%.
Exemplo: Transformar a fração 5/2 em taxa percentual.
Resolução
5
2 =
5
2 ∙ 100% =
500
2 % = 250%
Exemplo: Transformar a fração 3/8 em taxa percentual.
Resolução
= ∙
% =
% =
, %
Exemplo: Transformar o número 0,4 em forma de taxa percentual.
Resolução
, = , ∙
% =
%
Lembre-se que para multiplicar um número decimal por 100 basta deslocar a vírgula duas casas
decimais para a direita. Se não houver casas decimais, então deveremos adicionar zeros a direita.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
4
É comum querermos saber qual é a participação percentual de uma parte do todo. Por exemplo,
imagine que em um grupo de 300 pessoas, 120 são homens. Como calculamos a participação
percentual dos homens? Ora, basta dividir a “parte” pelo “todo”. E para transformar o resultado em
porcentagem, devemos multiplicar o resultado por 100%.
120
300 ∙ 100% = 40%
Isto significa que 40% das 300 pessoas são homens.
3
Variação Percentual
i) Imagine a seguinte situação. Você pretende comprar um computador que custa
R$ 1.500,00. Como bom “comprador”, pergunta ao vendedor se existe algum tipo de “ajudinha” se
você efetuar o pagamento em dinheiro vivo. O vendedor então informa que se o pagamento for
feito assim, haverá um desconto de R$ 300,00. Ou seja, você pagará apenas R$ 1.200,00. Ótimo
negócio...!!
ii) Imagine agora outra situação. Você pretende comprar um automóvel no valor de
R$ 80.000,00. Como bom “comprador”, pergunta ao vendedor se existe algum tipo de “ajudinha”
se você efetuar o pagamento em dinheiro vivo. O vendedor então informa que se o pagamento for
feito assim, haverá um desconto de R$ 300,00. Ou seja, você pagará apenas R$ 79.700,00. Ótimo
negócio!?
Em valores absolutos, o desconto do valor do computador foi igual ao desconto do valor do
automóvel. Qual dos dois descontos foi mais significativo em relação ao valor inicial do objeto?
Obviamente um desconto de R$ 300,00 em um produto que custa R$ 1.500,00 é bem mais
representativo do que um desconto de R$ 300,00 em um produto que custa R$ 80.000,00.
Pois bem, a maneira de comparar esses descontos é a chamada variação percentual.
Definição
A razão entre a diferença de valores (valor final menos o valor inicial) e o preço inicial, expressa
em forma de porcentagem, é chamada variação percentual.
Generalizemos: Considere um objeto com valor inicial
na data 0 e valor final
em uma
data futura
!. A variação percentual dessa grandeza entre as datas consideradas é o número "
(expresso em porcentagem) dado por:
" =
−
Voltemos aos nossos exemplos:
i)
= 1.500,00 e
= 1.200,00
Assim, a taxa percentual é:
" =
1.200 − 1.500
1.500
=
−300
1.500
Devemos escrever i em forma percentual. Vimos anteriormente que temos que multiplicar a fração
por 100%.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
5
" =
−300
1.500 =
−300
1.500 ∙ 100% = −20%
ii)
= 80.000,00 e
= 79.700,00
Assim, a taxa percentual é:
" =
79.700 − 80.000
80.000
=
−300
80.000
Devemos escrever i em forma percentual. Vimos anteriormente que temos que multiplicar a fração
por 100%.
" =
−300
80.000 =
−300
80.000 ∙ 100% = −0,375%
Observe que o desconto no pagamento do computador foi de 20% e o desconto no pagamento do
carro foi de apenas 0,375%. Apesar de os valores absolutos dos descontos terem sido iguais,
percentualmente a diferença foi gritante.
Exemplo: Guilherme decidiu comprar uma televisão no valor de R$ 1.200,00. Esperou o seu
salário entrar no início do mês, para que ficasse mais “folgado”. Quando então foi à loja efetuar o
pagamento, soube que o preço da televisão tinha subido para R$ 1.500,00. Qual foi o percentual
de aumento no preço da televisão?
" =
−
=
1.500 − 1.200
1.200
=
300
1.200 =
300
1.200 ∙ 100% = 25%
Portanto, o aumento foi de 25%.
Vamos comparar o que aconteceu no caso do computador e no caso da televisão.
i)
O computador custava
R$ 1.500,00
e sofreu um desconto de
20%
. Assim, o valor pago
foi de
R$ 1.200,00
.
ii)
A televisão custava
R$ 1.200,00
e sofreu um aumento de
25%
. Assim, o valor pago foi
de
R$ 1.500,00
.
4
Variações percentuais sucessivas
Suponha que uma mercadoria recebeu um desconto de 30%. Se você fosse pagar essa
mercadoria sem o desconto, você iria desembolsar 100%. Porém, com o desconto concedido,
Atenção!
Se
% > 0, a taxa percentual é de crescimento.
Se
% < 0, o módulo da taxa percentual é de decrescimento (desconto).

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
6
você irá pagar 100% - 30% = 70%. Assim, para calcular o valor após o desconto, devemos
multiplicar o valor original por 70%=70/100.
Em geral, ao diminuir p%, para calcular o valor final, devemos multiplicar por 100% - p%.
Da mesma forma, para aumentar p% de certo valor, devemos multiplicá-lo por
100% + p%. Por exemplo, se uma mercadoria aumenta 20%, você irá pagar
100% + 20% = 120%.
Exemplo: Uma mercadoria custa R$ 300,00. Em uma primeira ocasião, sofreu um aumento de
40%. Dois meses depois, a loja anunciou uma liquidação e a mercadoria sofreu um desconto de
25%. Qual o valor final da mercadoria? Qual a variação percentual acumulada?
Resolução
Quando a mercadoria sofre um aumento de 40%, o cliente além de ter que pagar os 100% (valor
da mercadoria) terá que pagar os 40% de aumento. Pagará, portanto, 140% do valor da
mercadoria. Dessa forma, a mercadoria, após o aumento, vale:
140% ($300,00 =
140
100 ∙ 300 = 420 * +",.
A mercadoria (que agora vale R$ 420,00) sofre um desconto de 25%. Você não pagará o valor
total da mercadoria (100%), já que foi concedido um desconto. O cliente pagará 100% - 25% =
75% do valor da mercadoria. Dessa forma, a mercadoria, após o desconto, vale:
75% ($ 420,00 =
75
100 ∙ 420 = ($ 315,00
Portanto, o valor final da mercadoria é igual a R$ 315,00.
Poderíamos ter efetuado este cálculo de uma maneira mais “objetiva”. Toma-se o valor da
mercadoria e multiplica-se pelas taxas de aumentos e de descontos.
Assim,
= 300 ∙
140
100 ∙
75
100 = 315 * +",.
Inicialmente a mercadoria valia R$ 300,00 e após as variações seu valor é de R$ 315,00. Ou seja:
= 300
= 315
A taxa de variação acumulada é de:
" =
−
=
315 − 300
300
" =
15
300 =
15
300 ∙ 100% = 5%
Assim, o aumento de 40% seguido do desconto de 25% equivale a um único aumento de 5%.
Vamos agora resolver algumas questões para sedimentar os conhecimentos.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
7
1.
(Agente Executivo – SUSEP 2006/ESAF) Um indivíduo tinha uma dívida de R$
1.200,00 três meses atrás. Considerando que o valor dessa dívida hoje é R$ 1.440,00,
calcule a porcentagem de aumento da dívida no período.
a) 12%
b) 15%
c) 20%
d) 25%
e) 30%
Resolução
Para qualquer questão em que precisemos calcular o aumento ou desconto percentual,
dados o valor inicial e o final, podemos utilizar a seguinte fórmula:
" =
−
Valor inicial: R$ 1200,00
Valor final: R$ 1440,00
Diferença entre os valores: R$ 1440,00 – R$ 1200,00 = R$ 240,00.
" =
240
1200 ∙ 100% =
240
12 % = 20%
Letra C
2.
(ESAF-AFC/CGU-2004) Durante uma viagem para visitar familiares com diferentes
hábitos alimentares, Alice apresentou sucessivas mudanças em seu peso. Primeiro, ao
visitar uma tia vegetariana, Alice perdeu 20% de seu peso. A seguir, passou alguns dias
na casa de um tio, dono de uma pizzaria, o que fez Alice ganhar 20% de peso. Após, ela
visitou uma sobrinha que estava fazendo um rígido regime de emagrecimento.
Acompanhando a sobrinha em seu regime, Alice também emagreceu, perdendo 25% de
peso. Finalmente, visitou um sobrinho, dono de uma renomada confeitaria, visita que
acarretou, para Alice, um ganho de peso de 25%. O peso final de Alice, após essas visitas
a esses quatro familiares, com relação ao peso imediatamente anterior ao início dessa
sequência de visitas, ficou:
a) exatamente igual
b) 5% maior
c) 5% menor
d) 10% menor
e) 10% maior
Resolução
Suponha que Alice tinha 100 kg antes das mudanças em seu peso.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
8
Primeiro, ao visitar uma tia vegetariana, Alice perdeu 20% de seu peso. Se ela perdeu
20% de peso, então para calcular o peso que ela ficou após essa mudança, devemos
multiplicar o valor original por 100% - 20% = 80% = 80/100.
A seguir, passou alguns dias na casa de um tio, dono de uma pizzaria, o que fez Alice
ganhar 20% de peso. Se ela ganhou 20% de peso, para calcular o seu peso final,
devemos multiplicar o valor por 100% + 20% = 120% = 120/100.
Após, ela visitou uma sobrinha que estava fazendo um rígido regime de emagrecimento.
Acompanhando a sobrinha em seu regime, Alice também emagreceu, perdendo 25% de
peso. Se ela perdeu 25% de peso, devemos multiplicar o valor do peso por 100% - 25% =
75% = 75/100.
Finalmente, visitou um sobrinho, dono de uma renomada confeitaria, visita que acarretou,
para Alice, um ganho de peso de 25%. Devemos multiplicar por 100% + 25% = 125% =
125/100.
Assim, o peso final de Alice será calculado da seguinte maneira:
Seu peso final será:
100 ∙
80
100 ∙
120
100 ∙
75
100 ∙
125
100 = 90 -.
Então, já que Alice possuía 100 kg, ficou com um peso 10% menor.
Letra D
3.
(Fiscal do trabalho 2003/ESAF) Uma estranha clínica veterinária atende apenas
cães e gatos. Dos cães hospedados, 90% agem como cães e 10% agem como gatos. Do
mesmo modo, dos gatos hospedados 90% agem como gatos e 10% agem como cães.
Observou-se que 20% de todos os animais hospedados nessa estranha clínica agem
como gatos e que os 80% restantes agem como cães. Sabendo-se que na clínica
veterinária estão hospedados 10 gatos, o número de cães hospedados nessa estranha
clínica é:
a) 50
b) 10
c) 20
d) 40
e) 70
Resolução:
Na clínica temos 10 gatos. 90% destes agem como gatos e 10% agem como cães. Logo:
Nove gatos agem como gatos e um gato age como cão.
Vamos considerar que há
/ cães na clínica. Destes, 90% agem como cães e 10% agem
como gatos. Logo:
0,9/ cães agem com cães e 0,1/ cães agem como gatos

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
9
Em resumo, temos:
Nove gatos e
, 0 cães agem como gatos.
Um gato e
0,9/ cães agem como cães.
Há 10 gatos e
/ cães. Desta forma, o total de animais é igual a 10 + /.
Sabemos pelo enunciado que 20% dos animais desta clínica agem como gatos. Assim:
20% 2, +3"4+", +. 4 5242 .+!2,
20% 610 + /7 = 9 + 0,1/
0,20 ∙ 610 + /7 = 9 + 0,1/
2 + 0,2/ = 9 + 0,1/
0,2/ − 0,1/ = 9 − 2
0,1/ = 7
/ =
7
0,1 = 70
Há 70 cães.
Letra E
4.
(AFT 2010/ESAF) Em uma universidade, 56% dos alunos estudam em cursos da
área de ciências humanas e os outros 44% estudam em cursos da área de ciências
exatas, que incluem matemática e física. Dado que 5% dos alunos da universidade
estudam matemática e 6% dos alunos da universidade estudam física e que não é
possível estudar em mais de um curso na universidade, qual a proporção dos alunos que
estudam matemática ou física entre os alunos que estudam em cursos de ciências
exatas?
a) 20,00%.
b) 21,67%.
c) 25,00%.
d) 11,00%.
e) 33,33%.
Resolução
Vamos imaginar, sem perda de generalidade, que a universidade possua 100 estudantes.
Pelo enunciado, sabemos que 56 alunos são da área de ciências humanas, 44 alunos
estudam em cursos da área de ciências exatas.
Sabemos ainda que 5 alunos estudam matemática e 6 alunos estudam física. Assim, a
quantidade de alunos que estuda matemática ou física é igual a 5+6=11.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
10
O problema pede a proporção dos alunos que estudam matemática ou física ENTRE OS
ALUNOS QUE ESTUDAM EM CURSOS DE CIÊNCIAS EXATAS.
Lembra que para calcular a participação percentual devemos dividir a “parte” pelo “todo”?
Pois bem, neste caso devemos dividir 11 (alunos que estudam matemática ou física) por
44 (alunos da área de ciências exatas).
Observe que ele não pede a participação percentual em relação a todos os estudantes da
universidade. É por isso que devemos dividir por 44 e não por 100.
11
44 ∙ 100% =
1
4 ∙ 100% = 25%
Letra C
5.
(SMF-RJ 2010/ESAF) Em uma determinada cidade, 25% dos automóveis são da
marca A e 50% dos automóveis são da marca B. Ademais, 30% dos automóveis da
marca A são pretos e 20% dos automóveis da marca B também são pretos. Dado que só
existem automóveis pretos da marca A e da marca B, qual a percentagem de carros
nesta cidade que são pretos?
a) 17,5%
b) 23,33%
c) 7,5%
d) 22,75%
e) 50%
Resolução
Vamos imaginar que existam 1.000 automóveis nesta cidade. Vinte e cinco por cento são
da marca A, ou seja, 250 são da marca A.
Trinta por cento dos carros da marca A são pretos.
30
100 ∙ 250 = 75 +8!24ó: ", * !2, + 4+*5+ ;
Cinquenta por cento são da marca B, ou seja, 500 automóveis são da marca B. Vinte por
cento dos automóveis da marca B são pretos.
20
100 ∙ 500 = 100 +8!24ó: ", * !2, + 4+*5+ <
O total de automóveis pretos é 175. Como o total de automóveis na cidade é 1.000, então
a porcentagem de carros pretos é

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
11
175
1.000 ∙ 100% = 17,5%
Letra A
6.
(Agente Executivo – SUSEP 2006/ESAF) Em um concurso, de cada 100
candidatos, 60 eram mulheres e 40 homens. Considerando que a porcentagem de
aprovação entre os candidatos mulheres foi de 20% e entre os homens foi de 15%,
calcule a porcentagem de aprovação em geral entre os candidatos, independentemente
do sexo.
a) 15%
b) 17%
c) 18%
d) 19%
e) 20%
Resolução
Supondo que são 100 pessoas, temos 60 mulheres e 40 homens.
Vinte por cento das mulheres foram aprovadas.
20
100 ∙ 60 = 12 48=ℎ * , + *2:+ +,
Quinze por cento dos homens foram aprovados.
15
100 ∙ 40 = 6 ℎ24 3, + *2:+ 2,.
O total de pessoas aprovadas é igual a 12+6=18. Como o total de pessoas é 100, então o
percentual de aprovados é igual a 18/100 (parte dividido pelo todo), ou seja, 18%.
Letra C
7.
(SMF-RJ 2010/ESAF) O PIB de um país que entrou em recessão no fim de 2008
tinha crescido 10% no primeiro trimestre de 2008, 5% no segundo trimestre, tinha ficado
estável no terceiro trimestre e tinha caído 10% no último trimestre daquele ano. Calcule a
taxa de crescimento do PIB desse País, em 2008.
a) 1,25%.
b) 5%.
c) 4,58%.
d) 3,95%.
e) -5%.
Resolução
Para calcularmos a taxa de crescimento, vamos atribuir um valor qualquer ao PIB no
início de 2008. Digamos que este valor inicial seja 100.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
12
Quando o PIB cresce 10% no primeiro trimestre, devemos multiplicar o seu valor por
100%+10% = 110% = 110/100.
Quando o PIB cresce 5% no segundo trimestre, devemos multiplicar o seu valor por 100%
+ 5% = 105%.
Se o PIB fica estável no terceiro trimestre, não precisamos multiplicar por número algum,
ou seja, devemos multiplicar por 100% + 0% = 100% = 100/100 = 1. Multiplicar por 1 não
altera o resultado, então não precisamos incluir este número na operação.
No último trimestre o PIB caiu 10%, ou seja, devemos multiplicá-lo por 100% - 10% = 90%
= 90/100.
Assim, o PIB no final de 2008 será igual a:
100 ∙
110
100 ∙
105
100 ∙
90
100 = 103,95
Se o PIB no início de 2008 era 100 e no final o PIB era de 103,95, então houve um
aumento de 3,95%.
Letra D
8.
(AFT 2010/ESAF) Em um grupo de pessoas, há 20 mulheres e 30 homens, sendo
que 20 pessoas estão usando óculos e 36 pessoas estão usando calça jeans. Sabe-se
que, nesse grupo, i) há 20% menos mulheres com calça jeans que homens com calça
jeans, ii) há três vezes mais homens com óculos que mulheres com óculos, e iii) metade
dos homens de calça jeans estão usando óculos. Qual a porcentagem de pessoas no
grupo que são homens que estão usando óculos mas não estão usando calça jeans?
a) 5%.
b) 10%.
c) 12%.
d) 20%.
e) 18%.
Resolução
Há muitas informações no enunciado. Vamos analisar cada uma delas separadamente e ir
montando as equações correspondentes.
i) há 20% menos mulheres com calça jeans que homens com calça jeans
Digamos que haja m
j
mulheres com calça jeans e h
j
homens com calça jeans. Sabemos
que existem 36 pessoas com calça jeans, ou seja,
ℎ
?
+ 4
?
= 36.
Como há 20% menos mulheres com calça jeans que homens com calça jeans, então
4
?
é
igual a
ℎ
?
multiplicado por 100% - 20% = 80% = 0,8.
4
?
= 0,8ℎ
?

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
13
Vamos substituir esta expressão na equação
ℎ
?
+ 4
?
= 36.
ℎ
?
+ 0,8ℎ
?
= 36
1,8ℎ
?
= 36
ℎ
?
= 20
Consequentemente,
4
?
= 16. Resumindo: há 20 homens com calça jeans e 16 mulheres
com calça jeans.
ii) há três vezes mais homens com óculos que mulheres com óculos.
O enunciado ainda afirma que há 20 pessoas com óculos.
Vamos considerar que a quantidade de mulheres com óculos é
4
@
e a quantidade de
homens com óculos é
ℎ
@
.
4
@
+ ℎ
@
= 20
A quantidade de homens com óculos é o triplo da quantidade de mulheres com óculos, ou
seja,
ℎ
@
= 34
@
. Substituindo na equação acima, temos:
4
@
+ 34
@
= 20
44
@
= 20
4
@
= 5
Consequentemente, a quantidadade de homens com óculos é igual a 15, ou seja,
ℎ
@
= 15.
iii) metade dos homens de calça jeans estão usando óculos.
E o problema pergunta: Qual a porcentagem de pessoas no grupo que
são homens que
estão usando óculos mas não estão usando calça jeans
?
Sabemos que há 20 homens de calça jeans. Metade deles usam óculos, ou seja, há 10
homens de calça jeans usando óculos. Como há 15 homens de óculos, 5 homens usam
óculos, mas não usam calça jeans.
Como o total de pessoas no grupo é 50, então a porcentagem pedida é 5/50 = 0,1 = 10%.
Letra B
9.
(ANA 2009/ESAF) Um rio principal tem, ao passar em determinado ponto, 20% de
águas turvas e 80% de águas claras, que não se misturam. Logo abaixo desse ponto
desemboca um afluente, que tem um volume d’água 30% menor que o rio principal e que,
por sua vez, tem 70% de águas turvas e 30% de águas claras, que não se misturam nem
entre si nem com as do rio principal. Obtenha o valor mais próximo da porcentagem de
águas turvas que os dois rios terão logo após se encontrarem.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
14
a) 41%
b) 35%
c) 45%
d) 49%
e) 55%
Resolução
Vamos supor que, para cada 1 litro de água do rio principal, temos 700 mL de água do
afluente (pois este tem volume 30% menor).
No rio principal, neste volume de 1 L, temos:
·
200 mL de águas turvas (20% de 1 L)
·
800 mL de águas claras (80% de 1 L)
No afluente, dos 700 mL de água, temos:
·
490 mL de águas turvas (70% de 700 mL)
·
210 mL de águas claras (30% de 700 mL)
Somando tudo, temos um volume de 1.700 mL (rio principal + rio afluente). Deste total,
são 690 mL de águas turvas (200+490).
Assim, o percentual de águas turvas fica:
690
1.700 ∙ 100% ≅ 40,58%
Letra A
10.
(TFC-CGU 2008/ESAF) Uma pequena cidade possui 10.000 habitantes, dos quais
40% são produtores rurais e 60% são do sexo masculino. Sabe-se que 40% das mulheres
são produtoras rurais. Desse modo, o número de habitantes do sexo masculino e que são
produtores rurais é igual a:
a) 1750
b) 2200
c) 3600
d) 6000
e) 4000
Resolução
40% dos 10.000 habitantes são produtores rurais.
40% 10.000 =
40
100 ∙ 10.000 = 4.000 *2 8!2* , *8*+",
60% dos 10.000 habitantes são do sexo masculino.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
15
60
100 ∙ 10.000 = 6.000 ℎ24 3,
Ora, como há 10.000 habitantes dos quais 6.000 são homens, então são 4.000 mulheres.
Sabe-se que 40% das mulheres são produtoras rurais.
40% +, 48=ℎ * , = 40% 4.000 =
40
100 ∙ 4.000 = 1.600
São 1.600 mulheres produtoras rurais.
Vamos montar uma tabela para detalhar bem a situação:
O total de produtores rurais é igual a 4.000. Como 1.600 são mulheres, então se tem um
total de
4.000 − 1.600 = 2.400 produtores rurais do sexo masculino.
Não há alternativa compatível e a questão foi anulada pela ESAF.
11.
(SEFAZ-SP 2009/ESAF) A e B são os lados de um retângulo I. Ao se aumentar o
lado A em 20% e reduzir-se o lado B em 20% obtem-se o retângulo II. Se, ao invés disso,
se aumentar o lado B em 20% e diminuir-se o lado A em 20%, tem-se o retângulo III.
Pode-se afirmar que:
a) os três retângulos têm a mesma área.
b) o retângulo III tem a maior área.
c) o retângulo II tem a maior área.
d) o retângulo I tem a maior área.
e) os retângulos II e III têm uma área igual, maior que a do retângulo I.
Resolução
Vamos considerar que o retângulo I tem lados A=10 e B=100. Assim, a sua área é igual a
10x100=1.000.
Ao se aumentar o lado A em 20% e reduzir-se o lado B em 20% obtem-se o retângulo II.
Assim, os lados do retângulo II são iguais a 12 e 80. Sua área é igual a 12x80=960.
Se, ao invés disso, se aumentar o lado B em 20% e diminuir-se o lado A em 20%, tem-se
o retângulo III. Assim, os lados do retângulo III são iguais a 120 e 8. Sua área é igual a
120x8 = 960.
Letra D
12.
(ATA-MF 2009/ESAF) Em um determinado curso de pós-graduação, 1/4 dos
participantes são graduados em matemática, 2/5 dos participantes são graduados em
geologia, 1/3 dos participantes são graduados em economia, 1/4 dos participantes são
graduados em biologia e 1/3 dos participantes são graduados em química. Sabe-se que
não há participantes do curso com outras graduações além dessas, e que não há
participantes com três ou mais graduações. Assim, qual é o número mais próximo da
porcentagem de participantes com duas graduações?

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
16
a) 40%
b) 33%
c) 57%
d) 50%
e) 25%
Resolução
Vamos ver um exemplo mais simples para você entender. Imagine que em um grupo de
pessoas, 40% são homens e 80% são mulheres. Isso é possível? Não! Por quê? Ora,
porque a soma total tem que ser 100%, e como não há elementos comuns entre os
homens e as mulheres, essa situação é impossível.
Agora imagine que em um grupo de pessoas, 40% gostam de Matemática e 80% gostam
de física. Essa situação é possível!!
Por que agora é possível? Porque deve existir um grupo de pessoas que gosta das duas
matérias. Quando somamos 40% com 80%, obtemos 120%. Essa porcentagem que
passou de 100% é justamente o grupo que gosta das duas matérias, no caso, 20%.
Voltemos ao enunciado.
1/4 dos participantes são graduados em matemática: 1/4 = 25% (Matemática)
2/5 dos participantes são graduados em geologia: 2/5 = 40% (Geologia)
1/3 dos participantes são graduados em economia: 1/3 = 33,33% (Economia). Esse valor
é aproximado. Não tem problema, o enunciado pediu um valor aproximado.
1/4 dos participantes são graduados em biologia: 1/4 = 25% (Biologia)
1/3 dos participantes são graduados em química: 1/3 = 33,33% (Química)
Somando as porcentagens, obtemos: 156,66%. Então a porcentagem de pessoas que
possuem duas graduações é igual a 56,66%.
Letra C
13.
(AFRFB 2009/ESAF) Em uma repartição, 3/5 do total dos funcionários são
concursados, 1/3 do total dos funcionários são mulheres e as mulheres concursadas
correspondem a 1/4 do total dos funcionários dessa repartição. Assim, qual entre as
opções abaixo, é o valor mais próximo da porcentagem do total dos funcionários dessa
repartição que são homens não concursados?
a) 21%
b) 19%
c) 42%
d) 56%
e) 32%
Resolução

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
17
Vamos atribuir valores. Para não trabalharmos com números decimais, vamos pegar um
número que seja múltiplo de 3, 4 e 5. Vamos supor que a repartição tem 60 pessoas.
3/5 dos funcionários são concursados.
3
5 × 60 = 36
São 36 concursados.
1/3 do total de funcionários são mulheres.
1
3 × 60 = 20
São 20 mulheres. Consequentemente, o número de homens é 40, de modo que o total de
pessoas seja 60.
1/4 dos funcionários são mulheres concursadas.
1
4 × 60 = 15
São 15 mulheres concursadas. Já sabemos que o total de concursados é 36. Assim, o
número de homens concursados é 36 – 15 = 21.
Como temos 40 homens e, destes, 21 são concursados, então 19 homens não são
concursados.
O percentual de homens não concursados, em relação ao total de funcionários, é:
19
60 × 100% ≅ 31,67%
Letra E
14.
(SMF-RJ 2010/ESAF) O álcool X
o
GL tem X% de fração em volume composto por
álcool etílico e o restante por água. Sendo assim, 750 ml de uma mistura em volumes
iguais de álcool 96
o
GL e álcool 70
o
GL são, por sua vez, misturados com 250 ml de álcool
com fração em volume desconhecida, resultando em um litro de álcool 76
o
GL. Calcule a
fração em volume desconhecida desses 250 ml de álcool.
a) 46%
b) 50%
c) 55%
d) 76%
e) 83%
Resolução

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
18
O que significa um álcool 96
o
GL? Significa que 96% do seu volume é composto por
álcool etílico e o restante de água.
Temos uma mistura de 750 ml em volumes iguais de álcool 96
o
GL e álcool 70
o
GL.
Ou seja, temos 375 ml de álcool 96
o
GL e 375 ml de álcool 70
o
GL.
A quantidade de álcool etílico é:
96% 375 + 70% 375
96
100 ∙ 375 +
70
100 ∙ 375 = 360 + 262,5 = 622,50
Concluímos que dos 750 ml da mistura, temos 622,50 ml de álcool etílico. O restante é
água.
Vamos misturar estes 750 ml com 250 ml de um outro álcool com fração em volume
desconhecida. Teremos como resultado uma mistura (750ml+250ml = 1.000 ml) de álcool
76
o
GL. Isto quer dizer que 76% da mistura de 1.000ml será de álcool etílico.
A quantidade de álcool etílico na mistura é igual a:
76% 1.0004= =
76
100 ∙ 1.000 = 760 4=
Como já tínhamos 622,50 ml de álcool etílico, então a quantidade de álcool etílico
correspondente ao terceiro álcool é igual a 750 – 622,50 = 137,50 ml.
Ora, o terceiro álcool tem um total de 250 ml, dos quais 137,50 ml são de álcool etílico. A
porcentagem de álcool puro é igual a:
137,50
250 ∙ 100% = 55%
Lembre-se que para calcular o percentual devemos dividir a “parte” pelo “todo”.
Letra C
15.
(ATRFB 2009/ESAF) Em um determinado período de tempo, o valor do dólar
americano passou de R$ 2,50 no início para R$ 2,00 no fim do período. Assim, com
relação a esse período, pode-se afirmar que:
a) O dolar se desvalorizou 25% em relação ao real.
b) O real se valorizou 20% em relação ao dólar.
c) O real se valorizou 25% em relação ao dólar.
d) O real se desvalorizou 20% em relação ao dólar.
e) O real se desvalorizou 25% em relação ao dólar.
Resolução

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
19
Inicialmente um dólar custava R$ 2,50 e no final custava R$ 2,00. A variação percentual
do dólar é igual a:
" =
−
" =
2,00 − 2,50
2,50
=
−0,50
2,50 ∙ 100% = −20%
Isto significa que o dólar desvalorizou 20%.
A questão deu o valor de 1 dólar. Disse que inicialmente,
CD$1,00 = ($ 2,50 e que no final
CD$1,00 = ($ 2,00. E qual é o valor de R$ 1,00?
Ora, se
CD$1,00 = ($ 2,50, então ($1,00 = CD$
E
F,GH
= CD$0,40.
Se você tiver dificuldade em fazer esta operação, faça uma regra de três:
Real Dólar
2,50
1
1
x
Multiplicando cruzado, temos:
2,50/ = 1
/ =
1
2,50 = 0,40
Ou seja, no início do período, 1 real correspondia a 40 centavos de dólar.
No final do período, temos que
CD$1,00 = ($ 2,00, ou seja, ($1,00 = CD$
E,HH
F,HH
= US$ 0,50.
Poderíamos novamente ter feito uma regra de três.
Real Dólar

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
20
2,00
1
1
x
2,00/ = 1
/ =
1
2,00 = 0,50
Isto significa que, no fim do período, 1 real correspondia a 50 centavos de dólar. Concluímos que
o real se valorizou. E valorizou quantos por cento?
" =
−
" =
0,50 − 0,40
0,40
=
0,10
0,40 ∙ 100% = +25%
O real se valorizou 25%.
Letra C
Observe que os percentuais não são iguais. Dizemos que uma desvalorização de 20% do
dólar equivale a uma valorização de 25% do real.
Isto ocorre porque, em cada caso, a base de cálculo para definição do percentual é
diferente.
No caso do dólar, a base de cálculo era o valor maior (2,50).
No caso do real, a base de cálculo era o valor menor (0,40).
16.
(BB 2010/FCC) As estatísticas da Campanha Nacional de Prevenção ao Câncer de Pele,
organizada há 11 anos pela Sociedade Brasileira de Dermatologia, revelam que o brasileiro não
se protege adequadamente do sol: 70% dos entrevistados afirmaram não usar qualquer tipo de
proteção solar, nem mesmo quando vão à praia (adaptado de www.sbd.org.br). Se foram
entrevistadas 34 430 pessoas, o número delas que usam protetor solar é
(A) 24 101
(B) 15 307
(C) 13 725
(D) 12 483
(E) 10 329
Resolução
O texto informou que 70% dos entrevistados afirmaram não usar qualquer tipo de proteção solar.
Como o total de pessoas corresponde a 100%, então 30% dos entrevistados usam protetor solar.
Devemos calcular 30% de 34.430 pessoas.
30% 34.430 =
30
100 ∙ 34.430

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
21
Observe que não precisamos efetuar este cálculo completamente. O número 100 que está no
denominador pode ser simplificado. Ficamos com:
3
10 ∙ 34.430 = 3 ∙ 3.443
Imagine que você estivesse efetuando esta multiplicação na hora da prova.
3.443
× 3
Começamos multiplicando o algarismo das unidades.
3.443
× 3
9
Neste momento, já podemos marcar a alternativa E, pois é a única que termina em 9.
Letra E.
De fato,
3 ∙ 3.443 = 10.329.
17.
(TRE – AC 2010/FCC) Relativamente ao total de registros de candidaturas protocolados
certo mês por três Técnicos Judiciários, sabe-se que: 8/15 foi protocolado por Alciléia, 5/12 por
Berenice e os demais por Otacílio. Assim sendo, a quantidade protocolada por Otacílio
corresponde a que parte do total de registros protocolados nesse mês?
a) 5%
b) 12,5%
c) 15%
d) 17,5%
e) 20%
Resolução
Alciléia protocolou 8/15 do total de registros e Berenice protocolou 5/12. Juntas, elas
protocolaram:
8
15 +
5
12 =
32 + 25
60 =
57
60
O que significa 57/60?
Significa que elas dividiram o trabalho total em 60 partes e protocolaram 57 destas 60 partes.
Portanto, ainda faltam ser protocoladas 3 das 60 partes. Esta parte será feita por Otacílio.
3
60 =
1
20
Para transformar esta fração ordinária em porcentagem, devemos multiplicá-la por 100%.
1
20 ∙ 100% = 5%
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
22
Letra A
18.
(MPE-RS 2010/FCC) Devido a uma promoção, um televisor está sendo vendido com 12%
de desconto sobre o preço normal. Cláudio, funcionário da loja, está interessado em comprar o
televisor. Sabendo que, como funcionário da loja, ele tem direito a 25% de desconto sobre o preço
promocional, o desconto que Cláudio terá sobre o preço normal do televisor, caso decida adquiri-
lo, será de
a) 37%
b) 36%
c) 35%
d) 34%
e) 33%
Resolução
Temos dois descontos sucessivos: 12% (devemos multiplicar por 100% - 12% = 88%) e
25% (devemos multiplicar por 100% - 25% = 75%).
Sempre que não for dada uma referência inicial, vale a pena utilizar o valor 100. Então,
vamos supor que o valor inicial do produto fosse igual a 100. O valor final após os
descontos será de:
100 ∙
88
100 ∙
75
100
A fração 75% pode ser simplificada por 25, obtendo, então, a fração 3/4.
O primeiro 100 pode cortar com o segundo 100 que está no denominador.
88 ∙
3
4 = 66
Ora, se o produto custava R$ 100,00 e agora custa R$ 66,00, é porque houve um
desconto de 34%.
Letra D
Esta é a vantagem de utilizar o valor inicial 100. A diferença entre os valores já é a taxa
percentual.
19.
(MPE-RS 2010/FCC) A empresa X possui 60 funcionários, dos quais 15% são
mulheres. De acordo com uma lei aprovada recentemente, toda empresa do ramo onde
atua a empresa X deverá ter, no mínimo, 40% de mulheres entre seus funcionários. Para
que a empresa X se adapte à nova lei sem demitir nenhum de seus atuais funcionários e
não contratando novos funcionários homens, ela deverá admitir um número de mulheres,
no mínimo, igual a
a) 25
b) 22
c) 20

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
23
d) 18
e) 15
Resolução
Sabemos que dos 60 funcionários, 15% são mulheres.
15% 60 =
15
100 ∙ 60 = 9 48=ℎ * ,
Assim, há um total de 51 homens (60 – 9 = 51).
Vamos considerar que serão admitidas
/ novas mulheres. Assim, o total de funcionários da
empresa será igual a
60 + / e o total de funcionárias será igual a 9 + /. Queremos que essas
9 + / mulheres representem 40% do total de funcionários.
9 + / 52** , 23 + 40% 2 !2!+= K835"23á*"2,
9 + / = 40% 660 + /7
9 + / =
40
100 ∙ 660 + /7
9 + / = 0,4 ∙ 660 + /7
9 + / = 24 + 0,4/
/ − 0,4/ = 24 − 9
0,6/ = 15
/ =
15
0,6 = 25
Portanto, deverão ser admitidas 25 mulheres.
Letra A
20.
(TRE-AC 2010/FCC) Na última eleição, ao elaborar o relatório sobre o
comparecimento dos eleitores inscritos numa Seção Eleitoral, o presidente da mesa de
trabalhos observou que 40% do total de inscritos haviam votado pela manhã e 75% do
número restante no período da tarde. Considerando que foi constatada a ausência de 27
eleitores, o total de inscritos nessa Seção era
a) 108
b) 125
c) 150
d) 172
e) 180
Resolução

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
24
Vamos considerar que há um total de
/ inscritos. Como 40% deste total votaram pela manhã,
então ainda faltam votar 60% dos inscritos (100% - 40% = 60%).
M+=!+4 :2!+*: 60% /
Destas pessoas que faltam votar, 75% votaram no período da tarde. Portanto, ainda faltam votar
25% das pessoas restantes.
M+=!+4 :2!+*: 25% 60% /
Foi constatada a ausência de 27 eleitores. Portanto:
25% 60% / = 27
25
100 ∙
60
100 ∙ / = 27
0,25 ∙ 0,6 ∙ / = 27
0,15/ = 27
/ =
27
0,15 = 180
O total de inscritos é igual a 180.
Letra E
21.
(PROMINP 2006/CESGRANRIO) Na Copa do Mundo de Futebol de 2002, havia, na
seleção brasileira, 10 jogadores que atuavam no exterior. Em 2006, esse número subiu para 21.
Qual o percentual de aumento do número de jogadores que atuam no exterior convocados para a
seleção brasileira, de 2002 para 2006?
(A) 210%
(B) 150%
(C) 110%
(D) 21%
(E) 11%
Resolução
Para calcular a taxa percentual de aumento, basta aplicar a fórmula que vimos anteriormente.
" =
−
Inicialmente (em 2002) eram 10 jogadores atuando no exterior. No final (em 2006) eram 21
jogadores atuando no exterior.
" =
−
=
21 − 10
10 =
11
10 ∙ 100% = 110%
Letra C

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
25
22.
(Agente Administrativo DNOCS 2010/FCC) Das 96 pessoas que participaram de
uma festa de confraternização dos funcionários do Departamento Nacional de Obras
Contra as Secas, sabe-se que 75% eram do sexo masculino. Se, num dado momento
antes do término da festa, foi constatado que a porcentagem dos homens havia se
reduzido a 60% do total das pessoas presentes, enquanto que o número de mulheres
permaneceu inalterado, até o final da festa, então a quantidade de homens que haviam se
retirado era
(A) 36.
(B) 38.
(C) 40.
(D) 42.
(E) 44.
Resolução
A quantidade de mulheres é constante. Se no início 75% das pessoas presentes na
confraternização eram homens, então 25% eram mulheres.
25% 96 =
25
100 ∙ 96 =
1
4 ∙ 96 = 24 48=ℎ * ,
Então, no início da festa havia
96 − 24 = 72 ℎ24 3,.
Antes do término da festa, o percentual de homens se reduziu a 60%. Então as mulheres
correspondem a 40% do total de pessoas na festa. Como o número de mulheres
permaneceu constante, então estes 40% correspondem a 24 pessoas.
Porcentagem
Pessoas
40%
24
60%
/
Vamos calcular quantos homens estavam presentes no final da festa.
Aumentando o percentual, aumenta-se o número de pessoas. As grandezas
(porcentagem e número de pessoas) são diretamente proporcionais (vamos estudar
detalhadamente as regras de três ainda nesta aula...).
40
60 =
24
/
2
3 =
24
/
2 ∙ / = 3 ∙ 24
2/ = 72
/ =
72
2 = 36 ℎ24 3,
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
26
Tínhamos inicialmente 72 homens. Como no final ficaram 36 homens, então o número de
homens que saiu é igual a:
72 − 36 = 36
Letra A
23.
(TRT 4ª Região 2006/FCC) Considere que em certo mês 76% das ações distribuídas em
uma vara trabalhista referiam-se ao reconhecimento de vínculo empregatício e que, destas, 20%
tinham origem na área de indústria, 25% na de comércio e as 209 ações restantes, na área de
serviços. Nessas condições, o número de ações distribuídas e NÃO referentes ao reconhecimento
de vínculo empregatício era
(A) 240
(B) 216
(C) 186
(D)
)
120
(E) 108
Resolução
Vamos considerar que o total de ações distribuídas na vara trabalhista seja igual a
/.
76% das ações distribuídas referiam-se ao reconhecimento de vínculo empregatício. Portanto,
100% − 76% = 24% NÃO são referentes ao reconhecimento de vínculo empregatício.
As ações distribuídas que se referem ao reconhecimento de vínculo empregatício são dividas em
três grupos:
Origem na área de indústria: 20%
Origem na área de comércio: 25%
Origem na área de serviços: 209 ações
Como as áreas de indústria e comércio totalizam 45%, então as ações que têm origem na área de
serviço totalizam 55% (100% - 45%).
Assim:
55% 76% / = 209 +çõ ,
x ações
76% são referentes ao
reconhecimento de vínculo
empregatício
Indútria: 20% de
76%
Comércio: 25% de 76%
Serviços: 55% de 76%
24% não são referentes ao
reconhecimento de vínculo
empregatício

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
27
55
100 ∙
76
100 ∙ / = 209
0,418/ = 209
/ =
209
0,418
Para efetuar tal divisão, devemos igualar a quantidade de casas decimais e depois apagar as
vírgulas.
/ =
209,000
0,418 =
209.000
418 = 500 +çõ ,
O problema pede o número de ações distribuídas e NÃO referentes ao reconhecimento de vínculo
empregatício.
24% / =
24
100 ∙ 500 = 120 +çõ ,
Letra D
24.
(METRO-SP 2007/FCC) Em um relatório sobre as atividades desenvolvidas em um
dado mês pelos funcionários lotados em certa estação do Metrô, foi registrado que:
− 25% do total de funcionários eram do sexo feminino e que, destes, 45% haviam
cumprido horas-extras;
− 60% do número de funcionários do sexo masculino cumpriram horas-extras;
− 70 funcionários não cumpriram horas-extras.
Com base nessas informações, nesse mês, o total de funcionários lotados em tal estação
era
(A) 120
(B) 150
(C) 160
(D) 180
(E) 190
Resolução
Vamos considerar que há
/ funcionários. Sabemos que 25% são mulheres e, portanto,
75% são homens. Podemos escrever:
4 = 0,25/
ℎ = 0,75/
O enunciado informou que 45% das mulheres cumpriram horas-extras. Desta forma,
concluímos que 55% (= 100% - 45%) não cumpriram horas-extras.
Não cumpriram horas extras: 55% das mulheres
= , Q.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
28
Sabemos também que 60% dos homens cumpriram horas-extras. Assim, 40% (=100% -
60%) não cumpriram horas-extras.
Não cumpriram horas extras: 40% dos homens
= , R.
Como 70 funcionários não cumpriram horas-extras, então:
, Q + , R =
Vamos substituir
4 2* 0,25/ ℎ 2* 0,75/.
,
∙ , S 0 + ,
∙ , 0 =
,
0 + , 0 =
,
0 =
0 = ,
= T UVWX%YWáZ%Y[
Letra C
25.
(METRO-SP 2007/FCC) Sabe-se que a área de uma superfície retangular é
calculada pelo produto
\ ∙ ], em que C e L são as respectivas medidas do comprimento e
da largura do retângulo, numa dada unidade. Suponha que a plataforma de embarque nos
trens que servem certa estação do Metrô tenha a forma de um retângulo e que, após uma
reforma, uma de suas dimensões foi diminuída em 20%, enquanto que a outra foi
acrescida de 20%. Nessas condições, é correto afirmar que, após a reforma, a área da
superfície original
(A) não foi alterada.
(B) foi aumentada em 2,4%.
(C) foi diminuída de 2,4%.
(D) foi aumentada de 4%.
(E) foi diminuída de 4%.
Resolução
Vamos considerar que o comprimento seja igual a 10 e a largura também seja igual a 10.
Assim, a área da superfície é igual a
10 × 10 = 100.
Diminuindo 20% do comprimento (o comprimento agora mede 8) e aumentando 20% da
largura (a largura agora mede 12), a área será igual a
8 × 12 = 96.
Resumindo: originalmente a área era de 100 e foi reduzida para 96, diminuindo, portanto,
4%.
Letra E
Vamos agora resolver algebricamente esta questão.
A área é o produto do comprimento pela largura.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
29
; = \ ∙ ]
Ao reduzir o comprimento em 20%, devemos multiplicá-lo por 100% - 20% = 80%. Ao
aumentar a largura em 20%, devemos multiplicá-la por 100% + 20% = 120%. Assim, a
nova área será igual a:
80
100 ∙ \ ∙
120
100 ∙ ] = 0,96 ∙ \ ∙ ] =
96
100 ∙ \ ∙ ]
Ou seja, área final é igual a área inicial multiplicada por 96%. Significando uma diminuição
de 4%.
26.
(METRO-SP 2010/FCC)
Especialistas dizem que, em um carro bicombustível
(álcool e gasolina), o uso de álcool só é vantajoso se o quociente do preço por litro de
álcool pelo do de gasolina for, no máximo, igual a 70%. Se o preço do litro da gasolina é
R$ 2,60, então NÃO é vantajoso usar álcool quando o preço por litro de álcool
(A) é no máximo de R$ 1,70.
(B) é superior a R$ 1,82.
(C) está compreendido entre R$ 1,79 e R$ 1,86.
(D) é igual a R$ 1,78.
(E) é menor que R$ 1,80.
Resolução
Os especialistas dizem que
o uso de álcool só é vantajoso se o quociente do preço por
litro de álcool pelo do de gasolina for, no máximo, igual a 70%. Podemos concluir que o
uso de álcool NÃO é vantajoso usar álcool se o referido quociente for maior que 70%.
Á=522=
_+,2="3+ > 70%
Á=522=
_+,2="3+ > 0,70
Á=522= > 0,70 ∙ 6_+,2="3+7
Á=522= > 0,70 ∙ 2,60
Á=522= > 1,82
Assim, não é vantajoso usar álcool se o preço do seu litro for maior que
R$ 1,82.
Letra B
27.
(METRO-SP 2010/FCC) A área de um círculo é igual ao produto do número π pelo
quadrado da medida do seu raio. Se a razão entre os raios de dois círculos concêntricos é
4, então a área do menor é quantos por cento da área do maior?
(A) 25%.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
30
(B) 12,5%.
(C) 6,25%.
(D) 4%.
(E) 3,25%.
Resolução
Vamos considerar que o raio do círculo menor é igual a
* e a raio do círculo maior é igual
a
(. A razão entre os raios é igual a 4, portanto:
(
* = 4 ⇔ ( = 4*
Para saber a porcentagem pedida, devemos dividir a área do menor pela área do maior
(posteriormente, estudaremos áreas de figuras planas detalhadamente).
a*²
a(²
Podemos cortar
a com a.
*²
(² = c
*
(d
F
= c
*
4*d
F
= e
1
4f
F
=
1
16 = 0,0625 = 6,25%
Letra C
28.
(Agente de Fiscalização Judiciária – TJSP 2010/VUNESP) Renato foi abastecer
seu carro. A bomba de combustível forneceu 25 litros em 2 minutos e 20 segundos, com
um fluxo de combustível constante. Então, houve um problema nessa bomba e o frentista
pediu para Renato continuar abastecendo em outra bomba, mais adiante. A 2.ª bomba
forneceu 26 litros em 2 minutos e 40 segundos, também com fluxo constante. O fluxo de
combustível dessa 2.ª bomba, em relação à 1.ª, foi
(A) 9% menor.
(B) 5% menor.
(C) 2% maior.
(D) 4% maior.
(E) 10% maior.
Resolução
Vamos transformar os tempos para segundos, lembrando que um minuto equivale a 60
segundos.
A primeira bomba forneceu 25 litros em 2 minutos e 20 segundos.
2 min 20 , = 2 ∙ 60 + 20 = 140 ,
Portanto, o fluxo da primeira bomba foi de
25 litros/140 s
.
A segunda bomba forneceu 26 litros em 2 minutos e 40 segundos.
2 min 40 , = 2 ∙ 60 + 40 = 160 ,

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
31
Portanto, o fluxo da primeira bomba foi de
26 litros/160 s
.
A variação percentual é dada por:
" =
−
" =
26
160 −
25
140
25
140
Para dividir duas frações, devemos repetir o numerador e multiplicar pelo inverso do
denominador. Assim,
" = e
26
160 −
25
140f ∙
140
25 =
26
160 ∙
140
25 −
25
140 ∙
140
25
" =
3.640
4.000 − 1 = 0,91 − 1 = −0,09 = −9%
Letra A
29.
(Casa da Moeda do Brasil 2009/CESGRANRIO) “Essa semana, o Banco Central
lançou campanha para que a população use mais moeda e aprenda a identificar notas
falsas. Este ano, até agosto, foram apreendidas 251 mil notas falsas, totalizando
R$12.386.000,00. Desse valor, cerca de 10% correspondiam a notas de 20 reais.”
O Globo, 24 out. 2009 (Adaptado).
De acordo com essas informações, quantas notas falsas de 20 reais foram apreendidas
até agosto desse ano?
(A) Menos de 20 mil
(B) Entre 20 mil e 40 mil
(C) Entre 40 mil e 60 mil
(D) Entre 60 mil e 80 mil
(E) Mais de 80 mil
Resolução
Vamos, inicialmente, calcular 10% do valor total apreendido.
10% ($ 12.386.000,00 =
10
100 ∙ 12.386.000,00 = ($ 1.238.600,00
Esse valor corresponde ao total apreendido com notas de R$ 20,00. Para saber a
quantidade de notas de R$ 20,00, basta dividir o valor total apreendido por 20.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
32
1.238.600
20
= 61.930 32!+, ($ 20,00
Letra D
30.
(Casa da Moeda do Brasil 2009/CESGRANRIO) Um comerciante aumentou em
20% o preço de suas mercadorias. Com isso, as vendas diminuíram, e ele resolveu
oferecer aos clientes um desconto de 30% sobre o preço com aumento. Desse modo,
qual é, em reais, o preço com desconto de uma mercadoria que inicialmente custava R$
200,00?
(A) 144,00
(B) 168,00
(C) 180,00
(D) 188,00
(E) 196,00
Resolução
Em geral, ao diminuir p%, para calcular o valor final, devemos multiplicar por 100% - p%.
Da mesma forma, para aumentar p% de certo valor, devemos multiplicá-lo por
100% + p%.
Assim, quando o comerciante aumenta o preço da mercadoria em 20%, devemos
multiplicar o seu valor por 100% + 20% = 120%.
Em seguida, quando o comerciante dá um desconto de 30% sobre o preço, devemos
multiplicar o valor por 100% - 30% = 70%.
O valor final será igual a:
200 ∙
120
100 ∙
70
100 = 168 * +",
Letra B
31.
(PROMINP 2009/CESGRANRIO) Paulo aproveitou uma promoção e comprou por
R$ 1.280,00 um computador novo, vendido com 20% de desconto. Qual era, em reais, o
preço desse computador sem o desconto?
(A) 1.420,00
(B) 1.488,00
(C) 1.536,00
(D) 1.580,00
(E) 1.600,00
Resolução
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
33
Vamos supor que o preço do computador, inicialmente, fosse de
/ reais. Quando ocorre a
promoção com 20% de desconto, devemos multiplicar o valor do computador por 100% -
20% = 80%.
/ ∙
80
100 = 1.280
O 100 que está dividindo passa para o segundo membro multiplicando. O 80 que está
multiplicando passa para o segundo membro dividindo.
/ = 1.280 ∙
100
80 = 1.600
Inicialmente, o computador valia R$ 1.600,00.
Letra E
32.
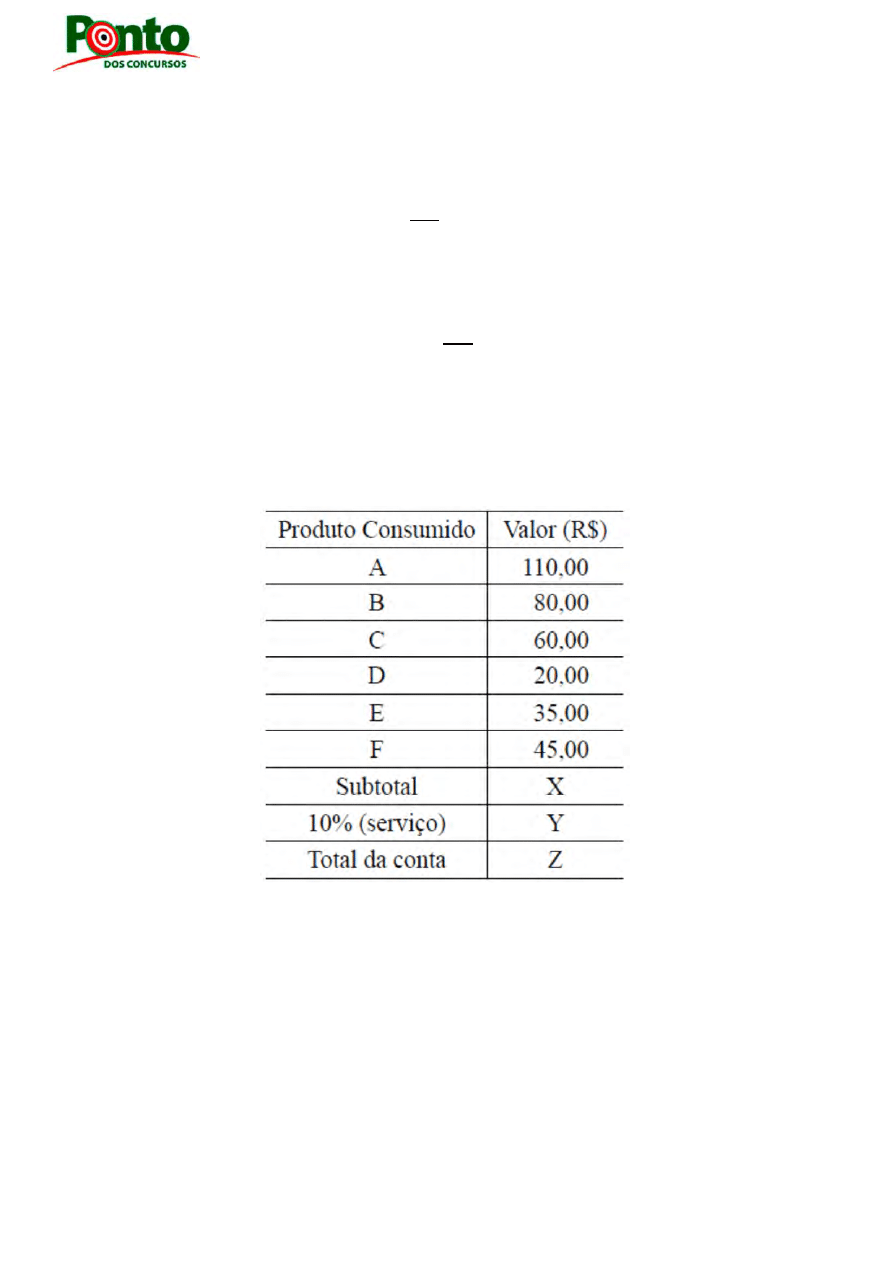
(Agente Administrativo CRF-SP 2009/VUNESP) Um grupo de amigos foi a um
restaurante, e a conta apresentada pelos serviços tinha a seguinte descrição:
Ao conferirem a conta, perceberam que os 3 últimos itens não haviam sido consumidos e
pediram para o garçom refazer a conta, calculando novamente o que havia sido
consumido e recalculando também o valor do serviço, que corresponde a 10% do valor do
que foi consumido. Desse modo, o valor total que seria cobrado a mais, incluindo o
serviço, representa, em relação ao valor total da conta correta,
(A) 28%.
(B) 36%.
(C) 38%.
(D) 40%.
(E) 42%.
Resolução

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
34
O
valor
que
seria
cobrado
a
mais
corresponde
a
j+k+M=20+35+45=100 reais. Devemos ainda acrescentar a taxa de 10% de serviço.
10% 100,00 =
10
100 ∙ 100 = 10 * +",
Desta forma, o valor total cobrado a mais é igual a 110 reais.
A conta correta é a seguinte:
Produto Consumido
Valor (R$)
A
110,00
B
80,00
C
60,00
Subtotal
110,00 + 80,00 + 60,00 = 250
10% (serviço)
10% de 250 = 25 reais
Total da conta
250 + 25 = 275 * +",
Desse modo, o valor total que seria cobrado a mais, incluindo o serviço, representa, em
relação ao valor total da conta correta,
110
275 = 0,4 = 40%
Letra D
33.
(PROMINP 2009/CESGRANRIO) (...) estamos nos tornando uma sociedade cada
vez mais em rede; atualmente 82 em cada 100 lares nos EUA têm acesso à Internet, um
aumento de 11% desde 2006.”
O Globo Digital, 03 nov. 2008. (Adaptado)
Considerando-se as informações apresentadas no texto acima, a quantidade de lares
norte americanos que tinham acesso à Internet em 2006 era de, aproximadamente,
(A) 67%
(B) 68%
(C) 71%
(D) 74%
(E) 77%
Resolução
Vamos considerar que, em cada 100 lares, x tinham acesso à Internet em 2006. Como
houve um aumento de 11%, então devemos multiplicar este valor por 100% + 11% =
111%.
111
100 ∙ / = 82

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
35
/ = 82 ∙
100
111 ≅ 73,87
Este valor indica que, em 2006, aproximadamente 74 em cada 100 lares nos EUA tinham
acesso à Internet.
Letra D
34.
(PROMINP 2010/CESGRANRIO) Um técnico em informática resolveu reajustar o
valor de seus serviços em 30%, mas, para os clientes antigos, manteve o preço sem
reajuste. Em relação ao novo preço, os clientes antigos terão, aproximadamente, um
desconto de
(A) 17%
(B) 23%
(C) 27%
(D) 30%
(E) 33%
Resolução
Vamos supor que o preço do serviço do técnico, inicialmente, fosse de R$ 100,00.
Quando ele resolve reajustar o valor dos seus serviços em 30%, ele passa a cobrar
R$ 130,00.
O preço agora é de R$ 130,00 e ele fará o serviço por R$ 100,00 para seus clientes
antigos. Para calcular a taxa de desconto, devemos utilizar a fórmula ensinada
anteriormente.
" =
−
=
100 − 130
130
= −
30
130 ∙ 100% ≅ −23%
Letra B
35.
(PROMINP 2010/CESGRANRIO) Da receita de certa editora, 20% correspondem
às vendas on-line e o restante, às vendas em livrarias. Essa editora tem como meta
dobrar o faturamento das vendas on-line e aumentar em 50% o faturamento das vendas
em livrarias. Se essa meta for cumprida, que parcela da receita total dessa editora as
vendas on-line passarão a representar?
(A) 25%
(B) 30%
(C) 35%
(D) 40%
(E) 45%
Resolução
Vamos considerar que a receita da editora seja de R$ 100,00. Desta forma, R$ 20,00
correspondem às vendas on-line e R$ 80,00 às vendas em livrarias.
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
36
Dobrando o faturamento das vendas on-line, temos um total de R$ 40,00 correspondentes
às esse tipo de venda.
Vamos aumentar em 50% o faturamento das vendas em livrarias. Como 50% de R$ 80,00
é igual a R$ 40,00, então o faturando deste tipo de venda será de R$ 120,00 (80 +40).
O faturamento total agora é de R$ 40,00 + R$ 120,00 = R$ 160,00.
Para saber a parcela representativa das vendas on-line, devemos dividir o faturamento
das vendas on-line pelo faturamento total.
40
160 = 0,25 = 25%
Letra A
36.
(PROMINP 2010/CESGRANRIO) Segundo o Código Florestal Brasileiro, o
percentual de mata nativa que o proprietário de um imóvel rural é obrigado a preservar
varia de acordo com a região. Na Amazônia, esse percentual é de 80%. Já, no Cerrado, é
de 35%. Duas propriedades, A e C, a primeira na Amazônia e a segunda, no Cerrado, têm
a mesma área de mata nativa preservada. Se a área total da propriedade A é 315 ha, qual
é, em ha, a área total da propriedade C?
(A) 505
(B) 630
(C) 720
(D) 904
(E) 1.102
Resolução
A área total da propriedade A é de 315 hectares. Segundo o Código Florestal Brasileiro, o
percentual de mata nativa que os proprietários de imóveis rurais devem preservar na
Amazônia é de 80%.
Portanto, a área preservada na propriedade A deve ser de:
80% 315 =
80
100 ∙ 315 = 0,8 ∙ 315 = 252 ℎ 5!+* ,
De acordo com o enunciado, esta área preservada na propriedade A é igual a área
preservada na propriedade C.
Á
* + * , *:+ + 3+ *2 *" + \ = 252 ℎ 5!+* ,
Vamos considerar que a área total da propriedade C seja de
/ hectares. De acordo com o
Código Florestal Brasileiro, o percentual de mata nativa que os proprietários de imóveis
rurais devem preservar no Cerrado é de 35%. Portanto:
35% / = 252

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
37
35
100 ∙ / = 252
O 100 que está dividindo “passa” multiplicando e o 35 que está multiplicando “passa”
dividindo.
/ = 252 ∙
100
35
/ = 720 ℎ 5!+* ,
Letra C
37.
(PROMINP 2010/CESGRANRIO) Durante o primeiro semestre de 2009, as
montadoras de veículos venderam, no Brasil, 1,45 milhão de automóveis. Nos primeiros
seis meses de 2010, as vendas foram ainda maiores, registrando um crescimento de 9%
em relação ao mesmo período do ano anterior. Quantos milhões de automóveis,
aproximadamente, foram vendidos no Brasil, no primeiro semestre de 2010?
(A) 1,64
(B) 1,58
(C) 1,52
(D) 1,48
(E) 1,30
Resolução
Para aumentar a quantidade de veículos vendidos em 9%, devemos multiplicar a
quantidade por 100% + 9% = 109%.
1,45 ∙
109
100 = 1,5805
Letra B
Razão e Proporção
Vamos começar com algumas definições formais que serão fundamentais para um bom
entendimento das resoluções das questões.
Razão de um número a para um número b, sendo b diferente de zero, é o quociente de a
por b.
Então quando aparecer a palavra razão, devemos sempre nos lembrar que haverá uma
divisão!!
Denotamos por a : b = a / b a razão entre os números a e b. O número a é chamado de
antecedente e o número b de consequente.
O conceito de razão nos permite fazer comparações de grandeza entre dois números.
Há, por exemplo, um tipo especial de razão: a escala.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
38
A escala é a relação entre as distâncias representadas num mapa e as correspondentes
distâncias reais. Escala é a razão entre a medida no desenho e o correspondente na
medida real.
real
desenho
do
Medida
Medida
Escala =
Desta forma, quando você lê em um mapa que a escala é de 1 : 100, isto significa que
para cada unidade de comprimento no desenho, teremos 100 unidades de comprimento
na realidade.
Escala = 1 :100
Isto significa que:
1 centímetro no desenho equivale a 100 centímetros na realidade.
1 decímetro no desenho equivale a 100 decímetros na realidade.
1 metro no desenho equivale a 100 metros na realidade.
E assim por diante...
Proporção é a igualdade entre duas razões. A proporção entre
d
c
e
b
a
é a igualdade:
d
c
b
a
=
. Podemos escrever
+
l =
5
⇔ +/l = 5/
Com a notação da esquerda, dizemos que a e c são os antecedentes; b e d são os
consequentes.
Com a notação da direita, dizemos que a e d são os extremos, e que b e c são os meios.
Em toda proporção, é válida a seguinte propriedade (chamada de Propriedade
Fundamental das Proporções): o produto dos meios é igual ao produto dos extremos.
+
l =
5
⇔ l ∙ 5 = + ∙
Por exemplo,
4
6 =
8
12 ⇔ 6 ∙ 8 = 4 ∙ 12 = 48
É importantíssima a seguinte propriedade: A soma dos antecedentes está para a soma
dos consequentes assim como qualquer antecedente está para o seu consequente.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
39
+
l =
5
=
+ + 5
l +
Por exemplo,
4
6 =
8
12 =
4 + 8
6 + 12 =
12
18
Ou seja, podemos “prolongar” toda proporção, somando os numeradores das frações e
somando os denominadores. Utilizaremos diversas vezes esta propriedade na resolução
de questões envolvendo divisão proporcional.
Isso é o básico que devemos saber para resolver questões sobre razões,
proporções e divisão proporcional. Ao longo da resolução das questões, colocarei
mais algumas propriedades e definições.
Vamos ver alguns exemplos para, em seguida, resolvermos questões de concursos
recentes.
Exemplo: A definição de densidade demográfica é dada pela
razão
entre o número de
habitantes de uma região e a área dessa região. Pedro fez uma pesquisa, em sua cidade,
para calcular qual seria a densidade demográfica da região onde mora. Ele conseguiu,
junto à prefeitura, as seguintes informações: a área da cidade era de 2.651 km
2
e a
quantidade de pessoas que residiam na localidade era de 151.107 habitantes. De posse
dessas informações, ele concluiu que a densidade demográfica de sua cidade é de:
Resolução
O enunciado informou que a definição de densidade demográfica é dada pela
razão
entre
o número de habitantes de uma região e a área dessa região.
Vimos anteriormente que a palavra RAZÃO tem o mesmo significado de quociente
(divisão)!!!
j 3," + 42.*áK"5+ =
3ú4 *2 ℎ+l"!+3! ,
á
* + + * ."ã2
=
151.107 ℎ+l"!+3! ,
2.651 -4
F
j 3," + 42.*áK"5+ = 57 ℎ+l"!+3! ,/-4
F
Exemplo: Em uma fábrica trabalham 216 funcionários, sendo que 135 são do sexo
masculino e 81 pertencem ao sexo feminino. Calcule a razão entre o número de
funcionários do sexo masculino e o número do sexo feminino.
Resolução
Para calcular a razão entre o número de funcionários do sexo masculino e o número do
sexo feminino basta dividir o número de homens pelo número de mulheres.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
40
n24 3,
o8=ℎ * , =
135
81 =
45
27 =
15
9 =
5
3
A fração 135/81 foi simplificada por 3, por 3, e por 3. Se você já tivesse percebido que 135
e 81 são divisíveis por 27, poderia ter simplificado direto.
Exemplo: Em uma proporção contínua, a terceira proporcional dos números 1 e 5 é igual
a:
Resolução
Uma proporção é contínua quando os meios são iguais. Ou seja, é uma proporção do tipo
+
l =
l
5
E o número c é chamado de terceira proporcional dos números a e b.
Assim,
1
5 =
5
5
1 ∙ 5 = 5 ∙ 5
5 = 25
Portanto, 25 é a terceira proporcional dos números 1 e 5.
O momento é oportuno para lembrar que na proporção
+
l =
5
O número d é a quarta proporcional dos números a, b, c.
Exemplo: A razão entre dois segmentos de reta x e y é 2/5, então a razão entre o
quíntuplo do segmento x e a metade do segmento y é igual a:
Resolução
Pelo enunciado, podemos escrever que
/
p =
2
5
Queremos calcular a seguinte razão:

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
41
5/
p
2
Lembre-se que para dividir frações, repetimos a fração do numerador, invertemos a fração
do denominador e multiplicamos. Dessa forma,
5/
p
2
= 5/ ∙
2
p = 10 ∙
/
p = 10 ∙
2
5 =
20
5 = 4
Exemplo: Na proporção x/y = 2/5. Sabendo-se que x+y=49, o valor de x e y será de:
Resolução
/
p =
2
5
Dica: É preferível que você coloque as incógnitas no numerador e os números no
denominador. Você poderá fazendo isso trocando os meios de lugar, ou trocando os
extremos. Por exemplo, podemos trocar o y com o 2. Essa troca é válida porque o produto
dos meios é igual ao produto dos extremos, e a ordem dos fatores não altera o produto.
Assim, a mesma proporção pode ser escrita como
/
2 =
p
5
Vamos agora utilizar uma propriedade que mencionei anteriormente.
Podemos “prolongar” toda proporção, somando os numeradores das frações e somando
os denominadores.
/
2 =
p
5 =
/ + p
2 + 5 =
49
7 = 7
Dessa forma,
/
2 = 7 ⇔ / = 14
p
5 = 7 ⇔ p = 35
Exemplo: Considere dois números x e y que sejam diretamente proporcionais a 8 e 3 e
cuja diferença entre eles seja 60.
Determine o valor de ( x + y ).
Resolução
Se os números x e y são diretamente proporcionais a 8 e 3, podemos escrever
/
8 =
p
3
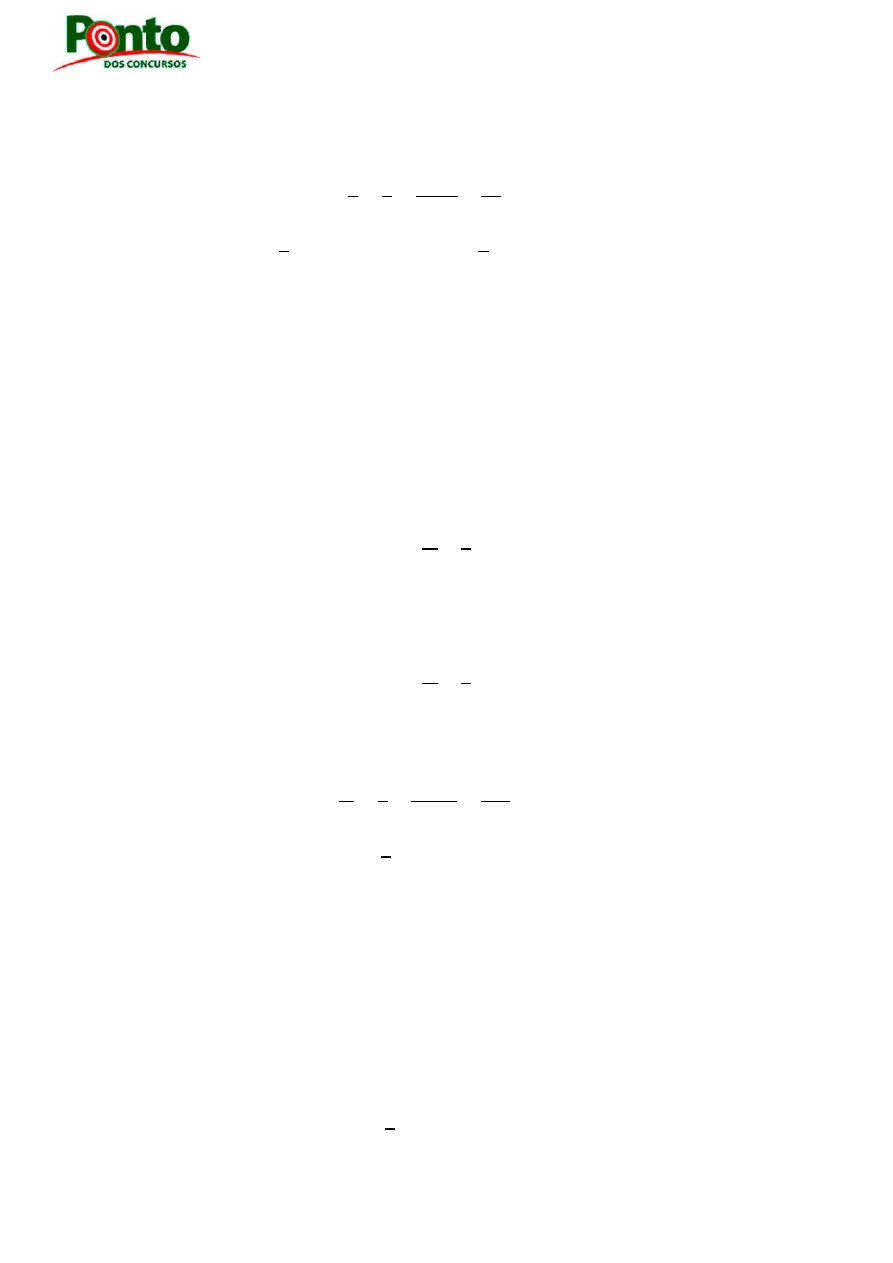
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
42
E da mesma forma que podemos “prolongar” a proporção somando os numeradores e os
denominadores, podemos também subtrair. Assim,
/
8 =
p
3 =
/ − p
8 − 3 =
60
5 = 12
/
8 = 12 ⇔ / = 96
p
3 = 12 ⇔ p = 36
Portanto,
/ + p = 96 + 36 = 132
Exemplo: Em uma festa, a razão entre o número de moças e o de rapazes, é de 3/2. A
porcentagem de rapazes na festa é:
Resolução
Se a razão entre o número de moças e o de rapazes é 3/2, então
4
* =
3
2
Falamos anteriormente que é preferível que você coloque as incógnitas no numerador e
os números no denominador. Você poderá fazendo isso trocando os meios de lugar, ou
trocando os extremos.
4
3 =
*
2
Queremos saber o percentual de rapazes. Podemos supor que o total de pessoas é igual
a 100. Se o total de pessoas (m+r) for igual a 100, então quantos serão rapazes?
4
3 =
*
2 =
4 + *
3 + 2 =
100
5 = 20
*
2 = 20 ⇒ * = 40
Ou seja, se fossem 100 pessoas no total, 40 seriam rapazes. Portanto, o percentual de
rapazes é 40%.
Exemplo: Se a razão entre dois números é 5 e a soma entre eles é 30, pode-se afirmar
que a diferença entre eles é:
Resolução
Sejam x e y os números.
/
p = 5 ⇒ / = 5p

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
43
Como a soma deles é 30,
/ + p = 30
Vamos substituir
/ por 5p.
5p + p = 30 ⇒ 6p = 30 ⇒ p = 5
Como
/ = 5p, 3!ã2 / = 5 ∙ 5 = 25
A diferença entre eles é 25 – 5 = 20.
Exemplo: Paulo tem três filhos, Rodrigo de 15 anos, Ricardo de 20 anos e Renato de 25
anos. Paulo pretende dividir R$ 3.000,00 para os três filhos em valores proporcionais as
suas idades. É correto afirmar que o valor que Rodrigo deve receber é:
Resolução
Queremos dividir R$ 3.000,00 em três partes diretamente proporcionais a 15, 20 e 25
anos, que são as idades de Rodrigo, Ricardo e Renato, respectivamente.
Assim,
(2
15 =
("
20 =
(
25
Obviamente
(2 + (" + ( = 3.000.
Assim, somando os numeradores e somando os denominadores, podemos prolongar a
proporção.
(2
15 =
("
20 =
(
25 =
(2 + (" + (
15 + 20 + 25 =
3.000
60 = 50
Temos então:
(2
15 = 50 ⇒ (2 = 15 ∙ 50 = 750
Exemplo: Três técnicos receberam, ao todo, por um serviço R$3.540,00. Um deles
trabalhou 2 dias, o outro 4 dias e o outro 6 dias. Sabendo-se que a divisão do valor é
proporcional ao tempo que cada um trabalhou, o técnico que trabalhou mais dias recebeu:
Resolução
Devemos dividir R$ 3.540,00 em partes diretamente proporcionais a 2,4 e 6 dias. Assim,
temos a seguinte proporção:

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
44
+
2 =
l
4 =
5
6
Obviamente, a soma das três partes (a+b+c) é igual a R$ 3.540,00. Dessa forma,
+
2 =
l
4 =
5
6 =
+ + l + 5
2 + 4 + 6 =
3.540
12 = 295
O técnico que mais trabalhou (6 dias) recebeu
5
6 = 295 ⇒ 5 = 6 ∙ 295 = 1.770 * +",
Exemplo: Uma gratificação de R$ 5.280,00 será dividida entre três funcionários de uma
empresa na razão direta do número de filhos e na razão inversa das idades de cada um.
André tem 30 anos e possui 2 filhos; Bruno com 36 anos tem 3 filhos e Carlos tem 48
anos e 6 filhos. É correto que o mais velho receberá:
Resolução
Temos agora uma divisão diretamente proporcional ao número de filhos e inversamente
proporcional às idades.
Em divisões desse tipo, a proporção tomará a seguinte forma:
+
"* !+
"3: *,+
=
l
"* !+
"3: *,+
=
5
"* !+
"3: *,+
No nosso exemplo, a divisão será diretamente proporcional a 2, 3 e 6 (ficam no
numerador) e será inversamente proporcional a 30, 36 e 48 (ficam no denominador).
+
2
30
=
l
3
36
=
5
6
48
Podemos simplificar as frações:
+
1
15
=
l
1
12
=
5
1
8
Podemos facilitar nossas vidas adotando o seguinte procedimento:
Sempre que numa proporção houver frações nos denominadores, devemos calcular o
m.m.c dos denominadores das frações.
No caso, o m.m.c. entre 8,12 e 15 é igual a 120. Devemos agora dividir 120 por 15 e
multiplicar por 1. Devemos dividir 120 por 12 e multiplicar por 1. Devemos dividir 120 por 8
e multiplicar por 1.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
45
+
8 =
l
10 =
5
15
Agora temos uma proporção muito parecida com às dos quesitos anteriores. Devemos
somar os numeradores e os denominadores.
+
8 =
l
10 =
5
15 =
+ + l + 5
8 + 10 + 15 =
5.280
33 = 160
O mais velho, Carlos, receberá:
5
15 = 160 ⇒ 5 = 15 ∙ 160 = 2.400 * +",
38.
(MPU 2004/ESAF) Se Y é diferente de zero, e se X/Y=4 , então a razão de 2X–Y
para X, em termos percentuais, é igual a
a) 75%.
b) 25%.
c) 57%.
d) 175%.
e) 200%.
Resolução
O problema informa que X/Y = 4, ou seja, X = 4Y.
Queremos calcular a razão de 2X – Y para X. Razão significa divisão. Devemos dividir 2X-
Y por X.
2r − s
r
Ora, X=4Y.
2 ∙ 4s − s
4s
=
8s − s
4s =
7s
4s =
7
4
Queremos este resultado em termos percentuais. Para tanto, devemos multiplicar este
resultado por 100%.
7
4 ∙ 100% = 175%
Letra D

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
46
39.
(PECFAZ 2013/ESAF) Em uma secretaria do Ministério da Fazenda, trabalham 63
pessoas. A razão entre o número de homens e o número de mulheres é igual 4/5. A diferença
entre o número de mulheres e o número de homens que trabalham nessa secretaria é igual a:
a) 8
b) 7
c) 6
d) 9
e) 5
Resolução
Vamos considerar que o número de homens é
ℎ e o número de mulheres é 4. Sabemos que há
63 pessoas, ou seja, a soma do número de homens com o número de mulheres é 63.
ℎ + 4 = 63
Sabemos ainda que a razão entre o
número de homens e o número de mulheres é igual 4/5.
ℎ
4 =
4
5
Temos, portanto, um sistema de equações para resolver.
Existem várias maneiras de resolver este sistema. Como não estudamos teoria alguma ainda, vou
resolver da maneira mais comum. Utilizaremos o método da
substituição
.
Na primeira equação, vamos isolar uma das incógnitas:
ℎ = 63 − 4
Vamos agora
substituir
esta expressão na segunda equação.
ℎ
4 =
4
5
63 − 4
4 =
4
5
Apliquemos a propriedade fundamental das proporções: “em toda proporção, o produto dos meios
é igual ao produto dos extremos”.
Muita gente gosta de falar de uma maneira mais simples: “multiplicando cruzadoc”.
4 ∙ 4 = 5 ∙ 663 − 47
44 = 315 − 54
44 + 54 = 315
94 = 315
4 =
315
9 = 35

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
47
Concluímos que o número de mulheres é 35. Como o total de pessoas é 63, então o número de
homens é
ℎ = 63 − 35 = 28.
A questão pede
a diferença entre o número de mulheres e o número de homens que trabalham
nessa secretaria.
4 − ℎ = 35 − 28 = 7
Poderíamos resolver esta questão um pouco mais rápido utilizando propriedades das proporções.
ℎ
4 =
4
5
Podemos trocar os lugares de “m” e 4.
ℎ
4 =
4
5
Vamos agora prolongar a proporção, somando os numeradores e os denominadores.
ℎ
4 =
4
5 =
63
9 = 7
Assim,
ℎ = 4 × 7 = 28
4 = 5 × 7 = 35
A diferença é 35-28 = 7.
Letra B
40.
(TFC-CGU 2008/ESAF) As idades de três irmãos encontram-se na razão 4:6:8.
Sabendo-se que a soma das idades é igual a 180 anos, então a idade do irmão mais
velho, em anos, é igual a:
a) 40
b) 45
c) 80
d) 70
e) 60
Resolução
Vamos considerar que as idades dos três irmão em ordem crescente são iguais a
/, p, t.
Como estas três idades encontram-se na razão 4:6:8, então:
/
4 =
p
6 =
t
8
Sabe-se que a soma das idades é igual a 180, logo:
/
4 =
p
6 =
t
8 =
/ + p + t
4 + 6 + 8 =
180
18 = 10
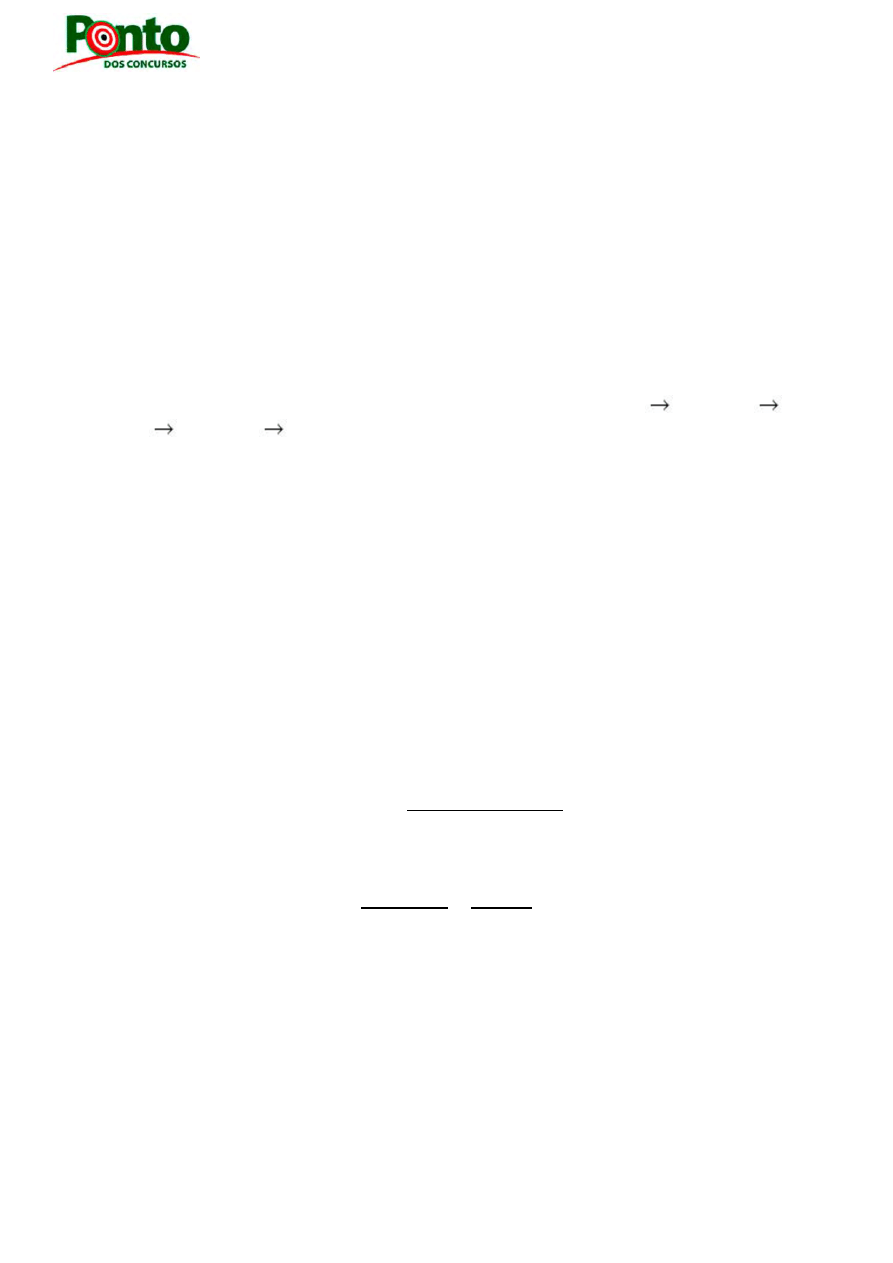
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
48
A constante de proporcionalidade é igual a 10. A idade do irmão mais velho é igual a
t = 8 × 10 = 80.
Letra C
41.
(TRE – AC 2010/FCC) Suponha que, para transportar as urnas eletrônicas usadas
em uma eleição foi utilizada uma viatura do TRE do Estado do Acre. Na ocasião, o
motorista responsável pela condução de tal viatura consultou um mapa feito na escala 1 :
20 000 000, ou seja, 1 unidade de medida no mapa correspondem a 20 000 000 unidades
de medida real. Se nesse mapa o município de Rio Branco distava 1,19 cm do de
Brasiléia e o município de Tarauacá distava 2,27 cm do de Rio Branco, quantos
quilômetros a viatura deve ter percorrido no trajeto: Rio Branco
Brasiléia
Rio
Branco
Tarauacá
Rio Branco?
a) 1.482
b) 1.384
c) 1.146
d) 930
e) 692
Resolução
No mapa, o trajeto indicado dá um total de:
1,19 + 1,19 + 2,27 + 2,27 = 6,92 54
Esta é a medida do desenho.
Sabemos que:
k,5+=+ =
4 " + 2 , 3ℎ2
4 " + * +=
1
20.000.000 =
6,92 54
/
Portanto:
/ = 6,92 ∙ 20.000.000 = 138.400.000 54
Pelo “tipo” de número, começando por 1384 só podemos marcar a alternativa B (pois ele
quer a resposta em quilômetros). Vamos à transformação.
Como 1 metro equivale a 100 cm, para transformar aquela medida para metros devemos
dividir por 100 (cortar dois zeros).

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
49
/ = 1.384.000 4 !*2,
Para transformar de metro para quilômetro, devemos dividir por 1000 (cortar três zeros),
já que 1 km = 1.000 m.
/ = 1.384 -4
Letra B
42.
(MPE-RS 2010/FCC) A tabela a seguir mostra as participações dos três sócios de
uma empresa na composição de suas ações.
Os lucros da empresa em determinado ano, que totalizaram R$ 560.000,00, foram
divididos entre os três sócios proporcionalmente à quantidade de ações que cada um
possui. Assim, a sócia Maria Oliveira recebeu nessa divisão
a) R$ 17.500,00
b) R$ 56.000,00
c) R$ 112.000,00
d) R$ 140.000,00
e) R$ 175.000,00
Resolução
As divisões foram feitas em partes diretamente proporcionais. Vamos denominar os lucros
de cada sócio com a letra inicial do nome de cada um.
15.000 =
4
10.000 =
5
7.000
Vamos simplificar os denominadores por 1.000.
15 =
4
10 =
5
7
Agora temos uma proporção muito parecida com às dos quesitos anteriores. Devemos
somar os numeradores e os denominadores.
15 =
4
10 =
5
7 =
+ 4 + 5
15 + 10 + 7 =
560.000
32
= 17.500
A parte de Maria Oliveira será igual a:

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
50
4 = 10 × 17.500 = 175.000
Letra E
43.
(TRF 5ª Região 2008/FCC) A razão entre as idades de dois técnicos é igual a 5/9.
Se a soma dessas idades é igual a 70 anos, quantos anos o mais jovem tem a menos que
o mais velho?
a) 15
b) 18
c) 20
d) 22
e) 25
Resolução
Vamos considerar que a idade do mais novo é igual a
3 e a idade do mais velho é igual a
:. A razão entre essas idades é igual a 5/9.
3
: =
5
9
Falamos anteriormente que é preferível que você coloque as incógnitas no numerador e
os números no denominador. Você poderá fazendo isso trocando os meios de lugar, ou
trocando os extremos.
3
5 =
:
9
A soma das idades é igual a 70 anos. Vamos então prolongar a proporção somando os
numeradores e somando os denominadores.
3
5 =
:
9 =
3 + :
5 + 9 =
70
14 = 5
Portanto:
3 = 5 × 5 = 25
: = 9 × 5 = 45
A idade do mais novo é 25 e a idade do mais velho é 45.
A diferença entre as idades é igual a 20 anos.
Letra C
44.
(SUSEP 2010/ESAF) Um pai deseja dividir uma fazenda de 500 alqueires entre
seus três filhos, na razão direta da quantidade de filhos que cada um tem e na razão
inversa de suas rendas. Sabendo-se que a
renda do filho mais velho é duas vezes a
renda do filho mais novo
e que
a renda do filho do meio é três vezes a renda do
mais novo
, e que, além disso,
o filho mais velho tem três filhos
,
o filho do meio tem

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
51
dois filhos
e o
filho mais novo tem dois filhos
, quantos alqueires receberá o filho do
meio?
a) 80
b) 100
c) 120
d) 160
e) 180
Resolução
Digamos que a renda do filho mais
n
ovo seja igual a 1. Portanto a renda do filho mais
v
elho será igual a 2 e a renda do filho do
m
eio será igual a 3.
Temos a seguinte proporção:
u
S
=
Q
S =
W
S
O mínimo múltiplo comum entre 2, 3 e 1 é igual a 6. Podemos desenvolver a proporção da
seguinte maneira: dividimos pelo denominador e multiplicamos pelo numerador (com as
frações que se encontram no denominador). Por exemplo, olhe para a primeira fração:
3/2. Dividimos 6 (m.m.c.) por 2 e multiplicamos por 3. Obtemos o número 9. A segunda
fração: 6 dividido por 3, vezes 2: obtemos o número 4. Finalmente a última fração: 6
dividido por 1, vezes 2: obtemos o número 12. A proporção ficará:
u
v =
Q
=
W
S
Temos uma divisão diretamente proporcional aos números 9, 4 e 12.
u
v =
Q
=
W
S =
u + Q + W
v + + S = S = S
Assim, o filho do meio receberá 4 x 20 = 80 alqueires.
Letra A
45.
(Pref. de São Paulo 2008/FCC) Lourival e Juvenal são funcionários da Prefeitura
Municipal de São Paulo há 8 e 12 anos, respectivamente. Eles foram incumbidos de
inspecionar as instalações de 75 estabelecimentos comerciais ao longo de certa semana
e decidiram dividir esse total entre si, em partes inversamente proporcionais aos seus
respectivos tempos de serviço na Prefeitura. Com base nessas informações, é correto
afirmar que coube a Lourival inspecionar
(A) 50 estabelecimentos.
(B) 15 estabelecimentos a menos do que Juvenal.
(C) 20 estabelecimentos a mais do que Juvenal.
(D) 40% do total de estabelecimentos.
(E) 60% do total de estabelecimentos.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
52
Resolução
Vamos considerar que Lourival inspecionará
= estabelecimentos e Juvenal inspecionará w
estabelecimentos.
Já que a divisão será em
partes inversamente proporcionais aos seus respectivos tempos
de serviço na Prefeitura, a proporção ficará assim:
=
1
8
=
w
1
12
Vamos adotar a mesma estratégia da questão anterior. O mínimo múltiplo comum entre 8
e 12 é igual a 24. Olhe para as frações dos denominadores. Devemos dividir 24 por 8 e 24
por 12. A proporção ficará assim:
=
3 =
w
2
Aplicando a propriedade das proporções. Devemos somar os numeradores e somar os
denominadores. Lembre-se que o total de estabelecimentos inspecionados é igual a 75.
=
3 =
w
2 =
= + w
3 + 2 =
75
5 = 15
= = 3 ∙ 15 = 45
w = 2 ∙ 15 = 30
Desta forma, Lourival inspecionou 45 estabelecimentos e Juvenal inspecionou 30
estabelecimentos.
Vamos agora analisar as alternativas:
É correto afirmar que coube a Lourival inspecionar:
(A) 50 estabelecimentos (FALSO)
(B) 15 estabelecimentos a menos do que Juvenal (FALSO, pois foram 15
estabelecimentos a mais do que Juvenal).
(C) 20 estabelecimentos a mais do que Juvenal (FALSO, pois foram 15 estabelecimentos
a mais do que Juvenal).
(D) 40% do total de estabelecimentos. (FALSO, pois 40% de 75 é igual a 30).
(E) 60% do total de estabelecimentos (VERDADEIRO, pois 60% de 75 é igual a 45).
Resposta: Letra E

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
53
46.
(Agente de Estação – METRO-SP 2007/FCC) Certo dia, três funcionários da
Companhia do Metropolitano de São Paulo foram incumbidos de distribuir folhetos
informativos contendo orientações aos usuários dos trens. Para executar tal tarefa, eles
dividiram o total de folhetos entre si, em partes inversamente proporcionais aos seus
respectivos tempos de serviço no Metrô: 2 anos, 9 anos e 12 anos. Se o que trabalha há 9
anos ficou com 288 folhetos, a soma das quantidades com que os outros dois ficaram foi
(A) 448
(B) 630
(C) 954
(D) 1 512
(E) 1 640
Resolução
Vamos considerar que as quantidades de folhetos de cada um dos funcionários são iguais
a
+, l, 5 (em ordem crescente do tempo de serviço).
Já que a divisão é inversamente proporcional ao tempo de serviço, então a proporção
ficará assim:
+
1
2
=
l
1
9
=
5
1
12
O mínimo múltiplo comum entre 2, 9 e 12 é igual a 36. Devemos dividir 36 por 2, por 9 e
por 12, obtendo 18, 4 e 3, respectivamente.
+
18 =
l
4 =
5
3
O funcionário que trabalha há 9 anos ficou com 288 folhetos, portanto
l = 288.
+
18 =
288
4 =
5
3
+
18 = 72 =
5
3
+ = 18 ∙ 72 = 1.296
l = 3 ∙ 72 = 216
Portanto,
+ + l = 1.512.
A soma das quantidades com que os outros dois ficaram foi 1.512.
Letra D
47.
(BAHIA GAS 2010/FCC) Para realizar a partilha de uma herança de R$ 28.500,00,
quatro irmãos, que nasceram em dias diferentes, marcaram encontro em um sábado. O
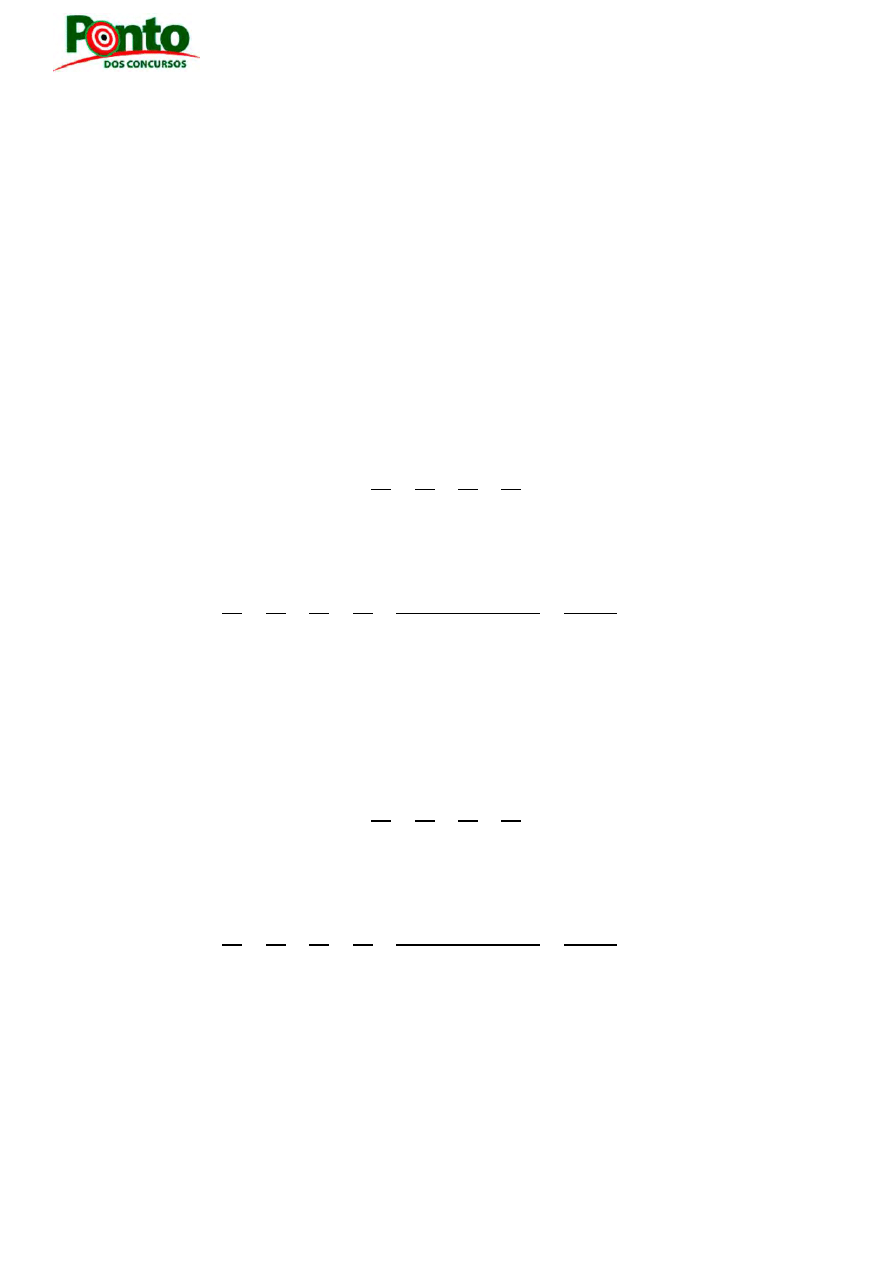
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
54
testamento determinava que eles receberiam partes diretamente proporcionais às
respectivas idades, em anos completos, que nesse sábado seriam: 15, 17, 21 e 22 anos.
O irmão mais novo só compareceu no domingo, um dia depois do combinado, e que era
exatamente o dia de seu aniversário. Supondo que a partilha tenha sido feita no domingo,
a quantia somada que os dois irmãos mais velhos deixaram de receber por conta do
adiamento de um dia é:
(A) R$ 50,00.
(B) R$ 155,00.
(C) R$ 180,00.
(D) R$ 205,00.
(E) R$ 215,00.
Resolução
As divisões foram feitas em partes diretamente proporcionais. Se a partilha fosse feita no
sábado, então a proporção ficaria assim:
+
15 =
l
17 =
5
21 = 22
Como a herança total é igual a R$ 28.500,00, então somando os numeradores e somando
os denominadores:
+
15 =
l
17 =
5
21 = 22 =
+ + l + 5 +
15 + 17 + 21 + 22 =
28.500
75 = 380
O irmão que tem 21 anos receberia
5 = 21 ∙ 380 = 7.980 * +",.
O irmão que tem 22 anos receberia
= 22 ∙ 380 = 8.360 * +",.
Mas a partilha foi feita no domingo, dia de aniversário do irmão mais novo. No domingo, o
irmão mais novo completou 16 anos e a partilha foi feita de acordo com a seguinte
proporção:
+
16 =
l
17 =
5
21 = 22
Como a herança total é igual a R$ 28.500,00, então somando os numeradores e somando
os denominadores:
+
16 =
l
17 =
5
21 = 22 =
+ + l + 5 +
16 + 17 + 21 + 22 =
28.500
76 = 375
O irmão que tem 21 anos recebeu
5 = 21 ∙ 375 = 7.875 * +",.
O irmão que tem 22 anos recebeu
= 22 ∙ 375 = 8.250 * +",.
O irmão de 21 anos deixou de receber
7.980 − 7.875 = 105 * +",.
O irmão de 22 anos deixou de receber
8.360 − 8.250 = 110 * +",.
A quantia somada que os dois irmãos mais velhos deixaram de receber por conta do
adiamento de um dia é
105 + 110 = 215 reais.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
55
Letra E
48.
(Pref. de Salvador 2008/FCC) Foi solicitada, à Guarda Municipal, a distribuição de
colaboradores que se responsabilizassem por ações que garantissem a preservação dos
parques públicos de três municípios da região metropolitana do Salvador. Fez-se a opção
de distribuir os 72 colaboradores, de forma diretamente proporcional à população de cada
um dos municípios.
Tabela de valores aproximados de população
Qual é o número de colaboradores destinados ao município Lauro de Freitas?
(A) 36
(B) 30
(C) 26
(D) 13
(E) 10
Resolução
Vamos considerar que os números de colaboradores aos municípios de Camaçari, Dias
D’Ávila e Lauro de Freitas são iguais a
5, =, respectivamente.
A divisão é feita de forma proporcional à população de cada cidade.
5
180.000 = 50.000 =
=
130.000
Podemos simplificar a proporção dividindo todos os termos dos denominadores por
10.000 (cortar 4 zeros).
5
18 = 5 =
=
13
Vamos agora somar os numeradores e somar os denominadores.
5
18 = 5 =
=
13 =
5 + + =
18 + 5 + 13 =
72
36 = 2
Desta forma,
= = 13 ∙ 2 = 26.
O município de Lauro de Freitas receberá 26 colaboradores.
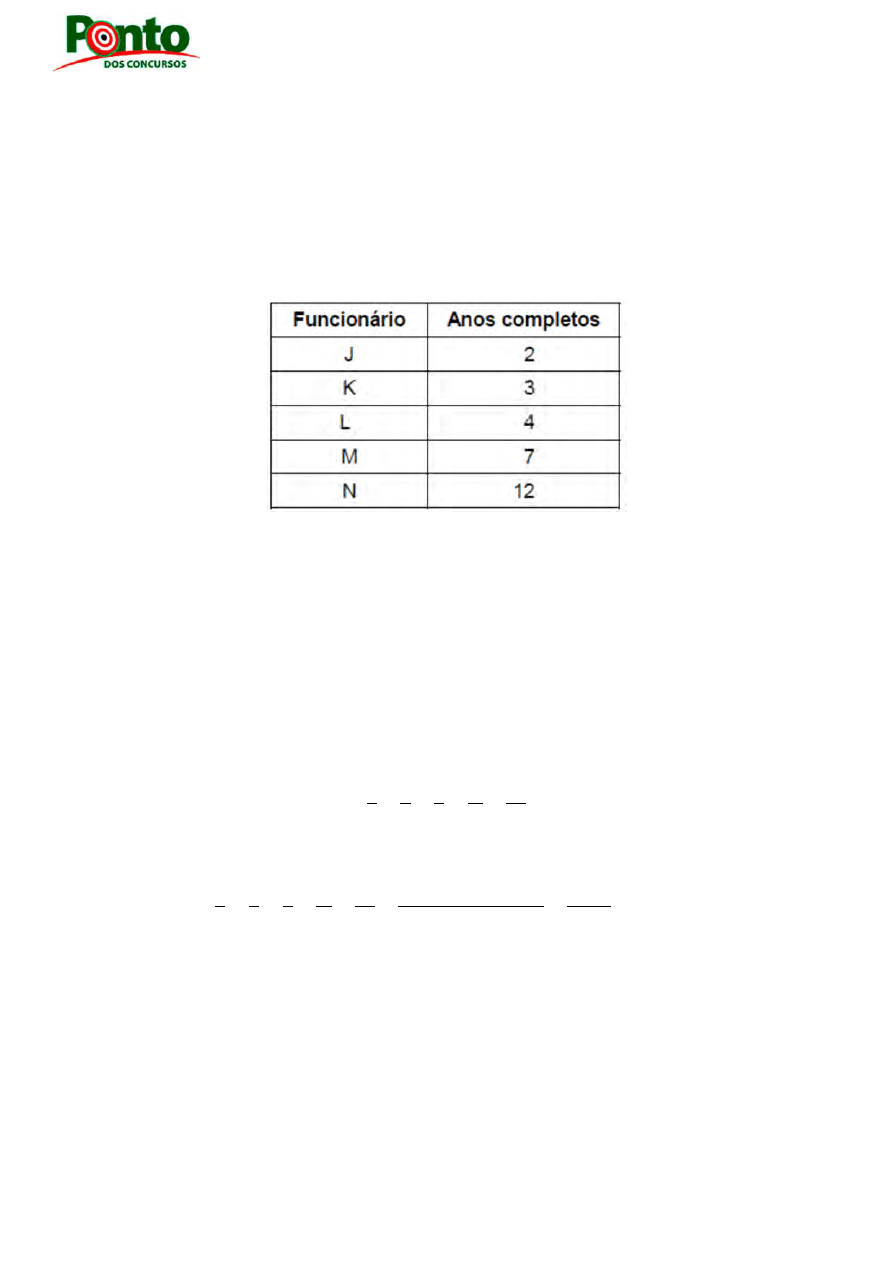
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
56
Letra C
49.
(MPE-AP 2009/FCC) O dono de uma loja resolveu distribuir a quantia de R$
3.570,00 entre seus funcionários, como premiação. Cada um dos cinco funcionários
receberá uma parte diretamente proporcional ao número de anos completos trabalhados
na loja. A tabela mostra o número de anos completos trabalhados na loja pelos cinco
funcionários.
A diferença entre o prêmio recebido pelo funcionário M e o prêmio recebido pelo
funcionário K, em reais, é
(A) 127,50
(B) 255,00
(C) 382,50
(D) 510,00
(E) 892,50
Resolução
A divisão será feita em partes diretamente proporcionais ao número de anos completos
trabalhados na loja. A proporção será a seguinte:
w
2 =
-
3 =
=
4 =
4
7 =
3
12
A soma das quantias recebidas pelos funcionários é igual a R$ 3.570,00.
w
2 =
-
3 =
=
4 =
4
7 =
3
12 =
x + - + = + 4 + 3
2 + 3 + 4 + 7 + 12 =
3.570
28 = 127,5
Desta forma:
4 = 7 ∙ 127,5 = 892,50
- = 3 ∙ 127,5 = 382,50
A diferença entre o prêmio recebido pelo funcionário M e o prêmio recebido pelo
funcionário K, em reais, é
892,50 − 382,50 = 510.
Letra D
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
57
50.
(DPE-SP 2010/FCC) O orçamento de um município para transporte público é de
R$ 770.000,00. Esse orçamento será repartido entre três regiões (A, B e C) do município
em proporção direta ao número de habitantes de cada uma. Sabe-se que o número de
habitantes da região A é o dobro da região B, que por sua vez é dobro da região C. Nas
condições dadas, as regiões B e C receberão, juntas,
(A) R$ 280.000,00.
(B) R$ 290.000,00.
(C) R$ 300.000,00.
(D) R$ 310.000,00.
(E) R$ 330.000,00.
Resolução
Não foi informada a população de cada uma das regiões. Apenas foi dito que o número de
habitantes da região A é o dobro da região B, que por sua vez é dobro da região C.
Vamos considerar que a população da região C seja igual a 1. Desta forma, a população
da região B será igual a 2 e a população da região A será igual a 4.
Desta maneira, devemos dividir R$ 770.000,00 em partes diretamente proporcionais a 4,2
e 1.
+
4 =
l
2 =
5
1 =
+ + l + 5
4 + 2 + 1 =
770.000
7
= 110.000
l = 2 ∙ 110.000 = 220.000
5 = 1 ∙ 110.000 = 110.000
As regiões B e C receberão juntas, 220.000+110.000 = 330.000 reais.
Letra E
GRANDEZAS DIRETAMENTE/INVERSAMENTE PROPORCIONAIS
Duas sequências de números são ditas
diretamente proporcionais
se o
quociente
entre
os elementos correspondentes for constante.
Ou seja, as sequências (
+
E
, +
F
, … , + 7 e (l
E
, l
F
, … , l 7 são diretamente proporcionais se
+
E
l
E
=
+
F
l
F
= ⋯ =
+
l = -
O número k é a chamada constante de proporcionalidade.
Duas sequências de números são ditas
inversamente proporcionais
se o
produto
entre
os elementos correspondentes for constante.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
58
Ou seja, as sequências (
+
E
, +
F
, … , + 7 e (l
E
, l
F
, … , l 7 são inversamente proporcionais se
+
E
∙ l
E
= +
F
∙ l
F
= ⋯ = + ∙ l = -
O número k é a chamada constante de proporcionalidade.
51.
(AFC-STN 2000/ESAF) Em um processo de fabricação, o custo total é
inversamente proporcional ao quadrado das quantidades produzidas. Quando são
produzidas 5 unidades, o custo total é igual a 225. Assim, quando forem produzidas 12
unidades, o custo total será igual a:
a) 625/25
b) 625/24
c) 625/16
d) 625/15
e) 625/12
Resolução
Chamemos a grandeza custo de C e a grandeza quantidade produzida de Q. Sabemos
que o custo total é inversamente proporcional ao quadrado das quantidades produzidas.
Quando duas grandezas são inversamente proporcionais, o produto entre os valores
correspondentes é constante. Assim,
\
E
∙ {
E
F
= \
F
∙ {
F
F
225 ∙ 5
F
= \
F
∙ 12
F
\
F
=
225 ∙ 25
144
Podemos simplificar 225 e 144 por 9.
\
F
=
25 ∙ 25
16 =
625
16
Letra C
52.
(Vestibular FGV 2002) Uma variável y é inversamente proporcional ao quadrado de
outra variável x. Para x = 3, y vale 15. Então, se x = 4, y deverá valer:
a) 1/16
b) 15/16
c) 45/16
d) 135/16
e) 625/16

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
59
Resolução
Grandezas inversamente proporcionais variam a produto constante.
p
E
∙ /
E
F
= p
F
∙ /
F
F
15 ∙ 3
F
= p
F
∙ 4
F
135 = 16 ∙ p
F
p
F
=
135
16
Letra D
53.
(FNDE 2007/FGV) A grandeza
/ é diretamente proporcional às grandezas + e l e
inversamente proporcional à grandeza
5. Quando + = 20, l = 12 e 5 = 30, o valor de / é
42. Então, quando os valores de
+, l e 5 forem respectivamente 25, 8 e 70, o valor de /
será:
a) 15
b) 21
c) 30
d) 56
e) 35
Resolução
Grandezas diretamente proporcionais variam a quociente constante e grandezas
inversamente proporcionais variam a produto constante. Portanto:
/
E
∙ 5
E
+
E
∙ l
E
=
/
F
∙ 5
F
+
F
∙ l
F
Vamos substituir os valores:
42 ∙ 30
20 ∙ 12 =
/
F
∙ 70
25 ∙ 8
1.260
240 =
/
F
∙ 70
200
O produto dos meios é igual ao produto dos extremos, portanto:
240 ∙ /
F
∙ 70 = 1.260 ∙ 200

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
60
Assim,
/
F
=
1.260 ∙ 200
240 ∙ 70 = 15
Letra A
54.
(AFRFB 2012/ESAF) A taxa cobrada por uma empresa de logística para entregar uma
encomenda até determinado lugar é proporcional à raiz quadrada do peso da encomenda. Ana,
que utiliza, em muito, os serviços dessa empresa, pagou para enviar uma encomenda de 25kg
uma taxa de R$ 54,00. Desse modo, se Ana enviar a mesma encomenda de 25kg dividida em
dois pacotes de 16kg e 9kg, ela pagará o valor total de
a) 54,32.
b) 54,86.
c) 76,40.
d) 54.
e) 75,60.
Resolução
A taxa cobrada é proporcional (diretamente) à raiz quadrada do peso. Quando as grandezas são
diretamente proporcionais, devemos dividir uma grandeza pela outra.
|
E
}~
E
=
|
F
}~
F
Na primeira situação, temos uma encomenda de 25kg com uma taxa de R$ 54,00.
54
√25
=
|
F
}~
F
Vamos calcular o valor do pacote de 16 kg e o valor do pacote de 9kg.
54
√25
=
|
F
√16
54
5 =
|
F
4
10,8 =
|
F
4
|
F
= 43,20
O pacote de 16kg custou R$ 43,20. Vamos agora calcular o preço do pacote de 9kg.
54
√25
=
|
€
√9

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
61
54
5 =
|
€
3
10,8 =
|
€
3
|
€
= 32,40
O pacote de 9kg custou R$ 32,40.
A soma dos dois pacotes é R$ 43,20 + R$ 32,40 = R$ 75,60.
Letra E
55.
(EPPGG – MPOG 2013/ESAF) Em um país distante, as tarifas ferroviárias são diretamente
proporcionais à raiz quadrada da distância percorrida. A distância da cidade Bengé até a cidade
Mengé, por trem, é de 1250 km e a tarifa é de R$ 182,00. Um turista que está em Bengé quer ir
até Mengé, viajando sempre de trem. No entanto, em vez de o turista ir diretamente de Bengé
para Mengé, ele vai de Bengé para Cengé, que fica distante 800 km de Bengé. No outro dia, ainda
de trem, o turista, sai de Cengé para Mengé, cuja distância é de 450 km. Desse modo, se o turista
tivesse ido diretamente de Bengé para Mengé, a redução percentual dos gastos com as tarifas de
trem, considerando duas casas após a vírgula, seria aproximadamente de:
a) 28,57%
b) 27,32%
c) 25,34%
d) 43,78%
e) 22,33 %
Resolução
A tarifa cobrada é diretamente proporcional à raiz quadrada da distância. Quando as grandezas
são diretamente proporcionais, devemos dividir uma grandeza pela outra.
|
E
}j
E
=
|
F
}j
F
Na primeira situação, temos que a distância de Bengé até Mengé é de 1.250 km e a tarifa é de
182 reais.
182
√1.250
=
|
F
}j
F
Entretanto, o sujeito irá de Bengé até Cengé e de Cengé para Mengé.
Vamos calcular o valor da tarifa de Bengé até Cengé (distância = 800 km).
182
√1.250
=
|
F
√800
|
F
∙ √1.250 = 182 ∙ √800

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
62
|
F
= 182 ∙ √
800
√1.250
= 182 ∙ •
800
1.250 = 182 ∙ }0,64 = 182 ∙ 0,8 = 145,60
A tarifa de Bengé até Cengé é R$ 145,60.
Vamos agora calcular a tarifa de Cengé até Mengé (distância = 450 km).
182
√1.250
=
|
€
√450
|
€
∙ √1.250 = 182 ∙ √450
|
€
= 182 ∙
√450
√1.250
= 182 ∙ •
450
1.250 = 182 ∙ }0,36 = 182 ∙ 0,6 = 109,20
A tarifa de Cengé até Mengé é de R$ 109,20.
A tarifa total do trajeto Bengé – Cengé – Mengé é R$ 145,60 + R$ 109,20 = R$ 254,80.
Indo de Bengé diretamente para Mengé a tarifa é de R$ 182,00.
Desse modo, se o turista tivesse ido diretamente de Bengé para Mengé, a redução percentual dos
gastos com as tarifas de trem, considerando duas casas após a vírgula, seria aproximadamente
de:
= 254,80 →
= 182
" =
−
=
182 − 254,80
254,80
=
−72,80
254,80 ∙ 100% = −28,57%
Letra A
Regra de Três
Vamos agora resolver questões sobre Regra de Três. Lembremos que para resolver
questões deste assunto, devemos construir uma tabela agrupando as grandezas da
mesma espécie em colunas e mantendo na mesma linha as grandezas de espécies
diferentes em correspondência. Em seguida devemos determinar se as grandezas são
direta ou inversamente proporcionais. O último passo é montar a proporção.
Quando as grandezas são diretamente proporcionais (ou seja, quando uma delas
aumenta
(
diminui
), a outra também
aumenta
(
diminui
) na mesma proporção), devemos
armar as frações no mesmo sentido das setas.
Quando as grandezas são inversamente proporcionais (ou seja, quando uma delas
aumenta
(
diminui
), a outra
diminui
(
aumenta
) na mesma proporção), devemos armar as
frações no sentido oposto aos das setas.
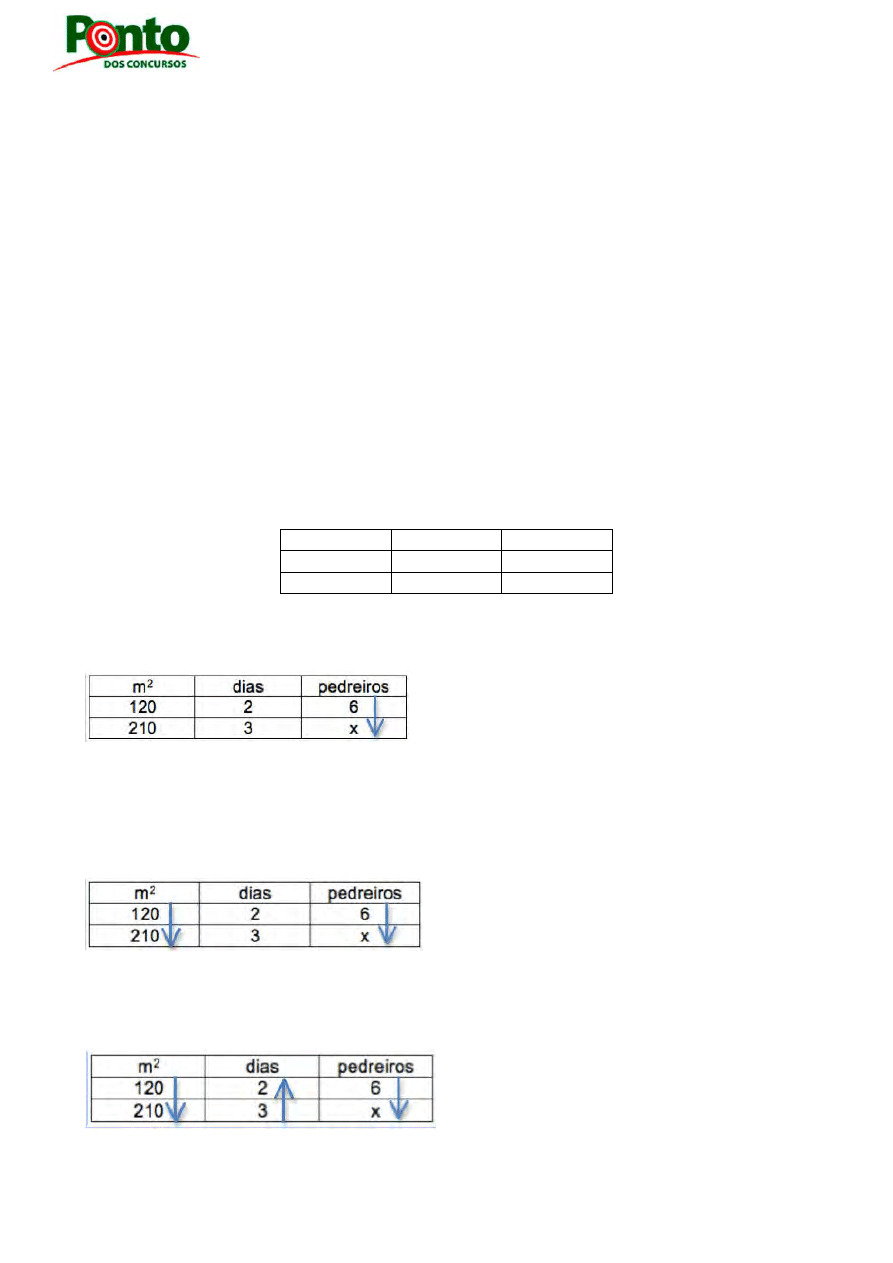
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
63
Por fim, a seta da coluna da grandeza desconhecida sempre fica para baixo!
56.
(ATRFB 2012/ESAF) Para construir 120 m
2
de um muro em 2 dias, são
necessários 6 pedreiros. Trabalhando no mesmo ritmo, o número de pedreiros
necessários para construir 210 m
2
desse mesmo muro em 3 dias é igual a
a) 2
b) 3
c) 4
d) 5
e) 7
Resolução
Vamos montar uma tabela para que possamos comparar as grandezas.
m
2
dias
pedreiros
120
2
6
210
3
x
A seta da coluna em que se encontra a incógnita fica sempre voltada para baixo.
Vamos comparar as grandezas com a coluna em que se encontra o “x”.
A área do muro aumentou de 120 para 210. Assim, a quantidade de pedreiros deverá aumentar.
Como as duas grandezas aumentam, elas são diretamente proporcionais. A seta ficará para
baixo.
A quantidade de dias aumentou, ou seja, o prazo para construir o muro aumentou. Se o prazo é
maior, a quantidade de pedreiros pode diminuir. Como uma grandeza aumenta enquanto a outra
diminui, as grandezas são inversamente proporcionais (seta para cima).

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
64
Agora é só armar a proporção.
6
/ =
120
210 ∙
3
2
6
/ =
360
420
6
/ =
36
42
6
/ =
6
7
/ = 7
Letra E
57.
(Agente Executivo – SUSEP 2006/ESAF) Um tratorista trabalhando 8 horas por dia
gradeia 100 hectares em 10 dias. Nas mesmas condições quantos hectares ele gradeará
em 6 dias trabalhando 10 horas por dia?
a) 60
b) 75
c) 80
d) 90
e) 100
Podemos juntar algumas grandezas. Temos um tratorista que trabalha 8 horas por dia
durante 10 dias. Isto quer dizer que ele trabalhou durante 80 horas.
Depois ele trabalhará 10 horas por dia durante 6 dias, ou seja, ele trabalhará durante 60
horas.
Vamos montar uma tabela para comparar as grandezas.
Horas
hectares
80
100
60
x
Diminuindo a quantidade de horas trabalhadas, diminuirá também a quantidade de
hectares. A seta ficará voltada para baixo, porque as grandezas são diretamente
proporcionais.
100
/ =
80
60
80/ = 6.000
/ = 75
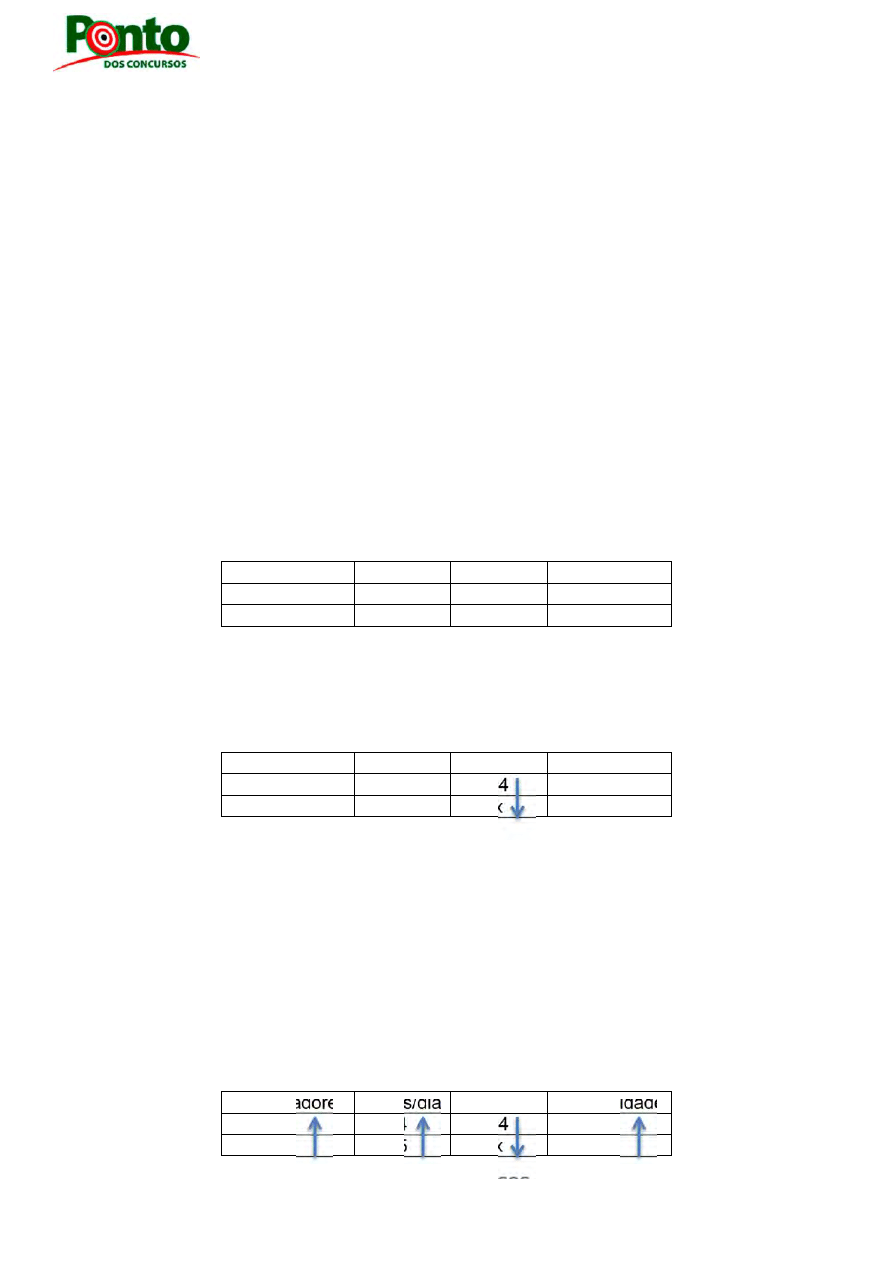
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
65
Letra B
58.
(ATA-MF 2009/ESAF) Com 50 trabalhadores, com a mesma produtividade,
trabalhando 8 horas por dia, uma obra ficaria pronta em 24 dias. Com 40 trabalhadores,
trabalhando 10 horas por dia, com uma produtividade 20% menor que os primeiros, em
quantos dias a mesma obra ficaria pronta?
a) 24
b) 16
c) 30
d) 15
e) 20
Resolução
Vamos atribuir um valor à produtividade do primeiro grupo. Suponhamos que a
produtividade do primeiro grupo seja igual a 100. Destarte, a produtividade do segundo
grupo será igual a 80 (20% menor).
Trabalhadores Horas/dia
dias
produtividade
50
8
24
100
40
10
x
80
Antes de verificarmos a situação das grandezas, vamos simplificar as colunas. A primeira
coluna pode ser simplificada por 10, a segunda coluna pode ser simplificada por 2 e a
última coluna pode ser simplificada por 20.
Trabalhadores Horas/dia
dias
produtividade
5
4
24
5
4
5
x
4
A coluna do x sempre fica com a seta voltada para baixo. Comparemos a grandeza
“trabalhadores” com a grandeza “dias”. A quantidade de trabalhadores diminuiu, então a
quantidade de dias deve aumentar. As grandezas são inversamente proporcionais. A seta
fica para cima.
A quantidade de horas trabalhadas por dia aumentou, então eles deverão trabalhar
durante menos dias. As grandezas são inversamente proporcionais. A seta fica para cima.
A produtividade diminuiu, assim, eles deverão aumentar a quantidade de dias. As
grandezas são inversamente proporcionais. A seta fica para cima.
Trabalhadores Horas/dia
dias
produtividade
5
4
24
5
4
5
x
4
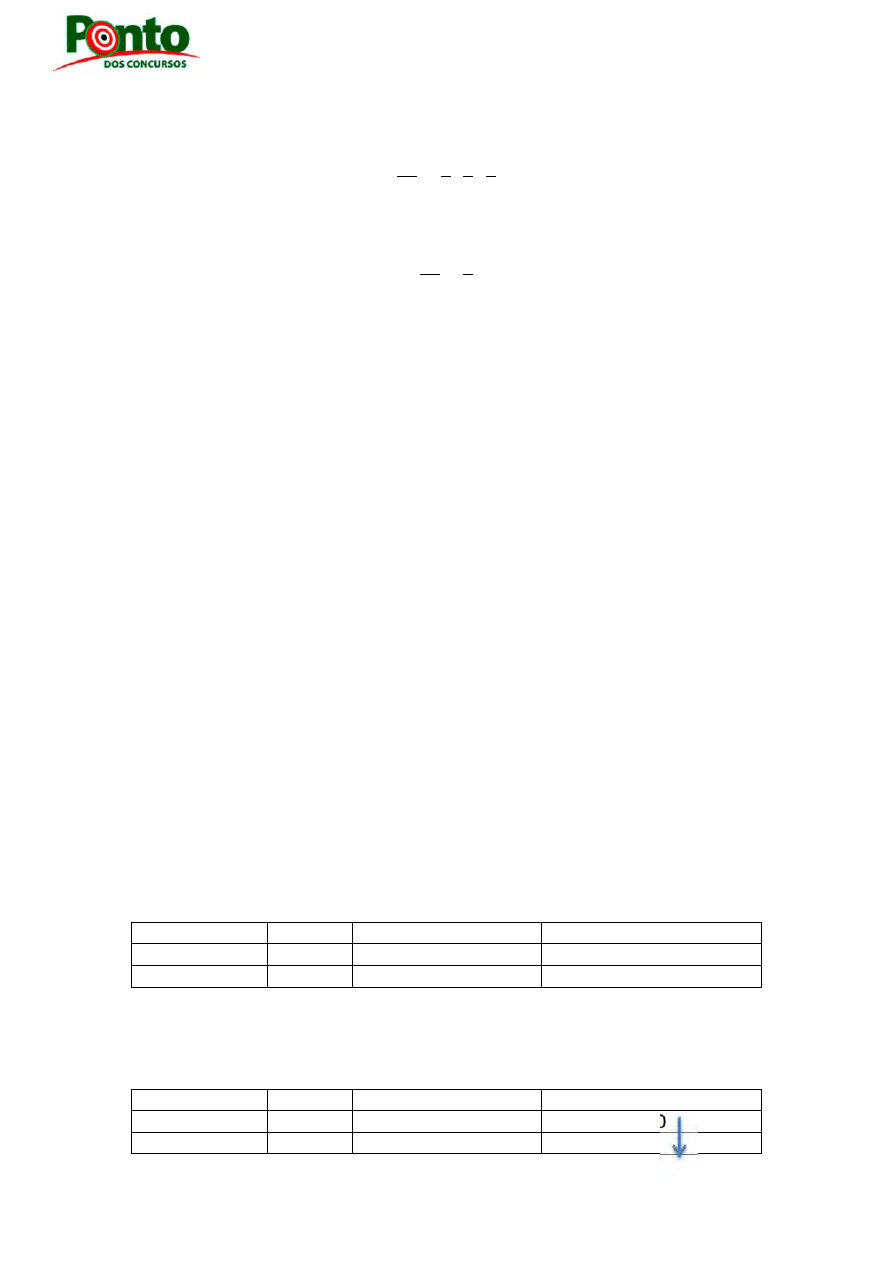
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
66
Vamos agora montar a proporção.
24
/ =
4
5 ∙
5
4 ∙
4
5
As duas últimas frações se cancelam.
24
/ =
4
5
4/ = 120
/ = 30
Letra C
59.
(SMF-RJ 2010/ESAF) Dois trabalhadores, trabalhando 8 horas por dia cada um,
durante 15 dias, colhem juntos 60 sacos de arroz. Três outros trabalhadores, trabalhando
10 horas por dia cada um, colhem juntos 75 sacos de arroz em 10 dias. Em média, quanto
um trabalhador do primeiro grupo é mais ou menos produtivo que um trabalhador do
segundo grupo?
a) O trabalhador do primeiro grupo é 10% menos produtivo.
b) O trabalhador do primeiro grupo é 10% mais produtivo.
c) O trabalhador do primeiro grupo é 25% mais produtivo.
d) As produtividades dos trabalhadores dos dois grupos é a mesma.
e) O trabalhador do primeiro grupo é 25% menos produtivo.
Resolução
Digamos que a produtividade do primeiro grupo seja igual a 100. Vamos calcular a
produtividade do segundo grupo para poder comparar.
Podemos juntar duas grandezas. O primeiro grupo trabalha 8 horas por dia durante 15
dias, ou seja, eles trabalham 8 x 15 = 120 horas.
O segundo grupo trabalha 10 horas por dia durante 10 dias, ou seja, eles trabalham
10x10 = 100 horas.
Trabalhadores
Horas
Sacos de arroz
Produtividade
2
120
60
100
3
100
75
x
Vamos simplificar as colunas. A segunda coluna pode ser simplificada por 20 e a terceira
coluna pode ser simplificada por 15.
Trabalhadores
Horas
Sacos de arroz
Produtividade
2
6
4
100
3
5
5
x
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
67
Vamos comparar as grandezas com a grandeza “produtividade”.
Lembre que quando, por exemplo, eu comparo a grandeza “trabalhadores” com a
grandeza “produtividade”, nós supomos que as outras grandezas são constantes.
Se no segundo grupo eu preciso de mais trabalhadores para efetuar um determinado
serviço, é porque eles são menos produtivos. As grandezas são inversamente
proporcionais e a seta fica voltada para cima.
Se o segundo grupo faz o serviço em menos tempo é porque eles são mais produtivos. As
grandezas são inversamente proporcionais e a seta fica voltada para cima.
Se o segundo grupo colhe mais sacos de arroz é porque eles são mais produtivos. As
grandezas são diretamente proporcionais e a seta fica voltada para baixo.
Trabalhadores
Horas
Sacos de arroz
Produtividade
2
6
4
100
3
5
5
x
Vamos armar a proporção.
100
/ =
3
2 ∙
5
6 ∙
4
5
100
/ =
60
60
/ = 100
A produtividade do segundo grupo também é igual a 100. Isto significa que os dois grupos
têm a mesma produtividade.
Letra D
60.
(Agente Administrativo DNOCS 2010/FCC) Suponha que 8 máquinas de
terraplanagem, todas com a mesma capacidade operacional, sejam capazes de nivelar
uma superfície de 8.000 metros quadrados em 8 dias, se funcionarem ininterruptamente 8
horas por dia. Nas mesmas condições, quantos metros quadrados poderiam ser nivelados
por 16 daquelas máquinas, em 16 dias de trabalho e 16 horas por dia de funcionamento
ininterrupto?
(A) 16 000
(B) 20 000
(C) 64 000
(D) 78 000
(E) 84 000
Resolução

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
68
Trata-se de um enunciado típico de uma questão de regra de três.
Vamos relacionar as grandezas com uma tabela:
Máquinas
Metros quadrados
Dias
Horas por dia
8
8.000
8
8
16
/
16
16
Para facilitas as contas, vamos simplificar as colunas. Cada coluna pode ser simplificada
por 8.
Máquinas
Metros quadrados
Dias
Horas por dia
1
8.000
1
1
2
/
2
2
Devemos comparar cada uma das grandezas conhecidas com a grandeza desconhecida.
Aumentando o número de máquinas, a área a ser nivelada aumenta. As grandezas são
diretamente proporcionais.
Aumentando a quantidade de dias, a área a ser nivelada aumenta. As grandezas são
diretamente proporcionais.
Aumentando a carga horária diária, a área a ser nivelada aumenta. As grandezas são
diretamente proporcionais.
Máquinas
Metros quadrados
Dias
Horas por dia
1
8.000
1
1
2
/
2
2
Vamos armar a proporção:
8.000
/ =
1
2 ∙
1
2 ∙
1
2
8.000
/ =
1
8
/ ∙ 1 = 8.000 ∙ 8
/ = 64.000
Serão nivelados 64.000 metros quadrados.
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
69
Letra C
61.
(Agente de Estação – METRO-SP 2007/FCC) Se um trem leva 2 minutos para
percorrer o trajeto entre duas estações, o esperado é que outro trem, cuja velocidade
média é 80% da velocidade do primeiro, percorra o mesmo trajeto em
(A) 2 minutos e 40 segundos.
(B) 2 minutos e 30 segundos.
(C) 2 minutos e 20 segundos.
(D) 2 minutos e 15 segundos.
(E) 2 minutos e 5 segundos.
Resolução
Vamos considerar que a velocidade do trem na primeira situação é igual a 100. Neste
caso, o trem gasta 2 minutos para percorrer o trajeto. Como a velocidade do outro trem é
igual a 80% da velocidade do primeiro trem, então a sua velocidade será igual a 80. Qual
o tempo gasto por ele?
Vamos armar a regra de três.
Velocidade
Tempo (min)
100
2
80
/
Diminuindo a velocidade, o tempo gasto para percorrer o trajeto aumentará. As grandezas
são inversamente proporcionais. Devemos inverter a coluna das velocidades no momento
de armar a proporção.
Velocidade
Tempo (min)
100
2
80
/
2
/ =
80
100
80 ∙ / = 2 ∙ 100
/ =
200
80 = 2,5 4"38!2,
/ = 2 4"38!2, 30 , .83 2,.
Letra B
62.
(DPE-SP 2010/FCC) Um professor tem de corrigir 48 trabalhos de seus alunos.
Nos primeiros 40 minutos de trabalho ele corrige 6 trabalhos. Se continuar corrigindo no
mesmo ritmo, ele utilizará para corrigir os 48 trabalhos
(A) 5 horas e 20 minutos.
(B) 5 horas e 10 minutos.
(C) 4 horas e 50 minutos.
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
70
(D) 4 horas e 40 minutos.
(E) 4 horas e 30 minutos.
Resolução
Quem já tem um pouquinho mais de experiência pode já seguir o seguinte raciocínio:
Ele gasta 40 minutos para corrigir 6 trabalhos. Para corrigir 48 trabalhos (observe que o
número de trabalhos é 8 vezes maior), gastará 8 vezes mais tempo.
O tempo necessário será igual a
8 ∙ 40 = 320 4"38!2,.
Podemos, alternativamente, armar a tabela da regra de três.
Trabalhos
Tempo (min)
6
40
48
/
A coluna referente ao número de trabalhos pode ser simplificada por 6.
Trabalhos
Tempo (min)
1
40
8
/
Aumentando a quantidade de trabalhos a serem corrigidos, aumenta-se o tempo gasto
para efetuar o serviço. As grandezas são diretamente proporcionais.
40
/ =
1
8
/ ∙ 1 = 40 ∙ 8
/ = 320 4"38!2,
Para transformar esta resposta para “horas e minutos”, devemos dividir o resultado por
60.
320/ 60
20 5 ℎ2*+,
Portanto:
320 4"38!2, = 5 ℎ2*+, 20 4"38!2,
Letra A
63.
(TRF 2ª Região 2007/FCC) Em uma gráfica, foram impressos 1 200 panfletos
referentes à direção defensiva de veículos oficiais. Esse material foi impresso por três
máquinas de igual rendimento, em 2 horas e meia de funcionamento. Para imprimir 5 000
desses panfletos, duas dessas máquinas deveriam funcionar durante 15 horas,
(A) 10 minutos e 40 segundos.

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
71
(B) 24 minutos e 20 segundos.
(C) 37 minutos e 30 segundos.
(D) 42 minutos e 20 segundos.
(E) 58 minutos e 30 segundos.
Resolução
Temos que 1.200 panfletos foram impressos por 3 máquinas em 2 horas e meia de
funcionamento.
Queremos calcular o tempo que duas máquinas gastam para imprimir 5.000 panfletos.
Máquinas
Tempo (h)
Panfletos
3
2,5
1.200
2
/
5.000
Podemos simplificar a coluna dos panfletos. Dividindo 1.200 por 100 e dividindo 5.000 por
100 obtemos 12 e 50, respectivamente.
Máquinas
Tempo (h)
Panfletos
3
2,5
12
2
/
50
Diminuindo a quantidade de máquinas, o tempo gasto para imprimir os panfletos
aumenta. As grandezas são inversamente proporcionais. Portanto, devemos inverter a
coluna das máquinas no momento de armar a proporção.
Aumentando a quantidade de panfletos, aumenta-se o tempo para imprimi-los. As
grandezas são diretamente proporcionais.
Máquinas
Tempo (h)
Panfletos
3
2,5
12
2
/
50
2,5
/ =
2
3 ∙
12
50
2,5
/ =
24
150
24 ∙ / = 150 ∙ 2,5
24/ = 375
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
72
/ =
375
24
Podemos simplificar esta fração por 3.
/ =
375
24 =
125
8 ℎ2*+,
Vamos dividir 125 horas por 8.
125 ℎ2*+,/ 8
5 15 ℎ2*+,
As 5 horas do resto devem ser convertidas para minutos para continuar a divisão. Para
transformar 5 horas em minutos, devemos multiplicar por 60.
5 ℎ2*+, = 5 ∙ 60 4"38!2, = 300 4"38!2,
300 min / 8
4 374"3
Neste momento já podemos marcar a letra C.
Para continuar a divisão, devemos transformar os 4 minutos do resto em segundos. Para
isto, devemos multiplicar 4 por 60 obtendo 240 segundos.
240 ,/ 8
0 30 ,
Portanto, o tempo gasto é igual a 15 horas, 37 minutos e 30 segundos.
Letra C
64.
(MPE-AP 2009/FCC) Em um escritório, três digitadores de produtividade idêntica
realizam a tarefa de digitar 2400 páginas em 20 dias. Para realizar uma tarefa de
digitação de 6000 páginas em 15 dias, o número mínimo de digitadores que devem ser
incorporados à equipe, com a mesma produtividade dos três primeiros é
(A) 6
(B) 7
(C) 8
(D) 9
(E) 10
Resolução
Vamos montar uma tabela para relacionar as grandezas.
Digitadores
Páginas
Dias
3
2.400
20
/
6.000
15
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
73
Vamos simplificar as colunas:
A segunda coluna pode ser simplificar inicialmente por 100. Serão cortados os 2 zeros de
cada um dos números. Ficamos com 24 e 60 que podem ser simplificados por 12. 24
dividido por 12 é igual a 2 e 60 dividido por 12 é igual a 5.
A terceira coluna pode ser simplificada por 5.
Digitadores
Páginas
Dias
3
2
4
/
5
3
Aumentando o número de páginas, deve-se aumentar o número de digitadores. As
grandezas são diretamente proporcionais.
Diminuindo o prazo, devemos aumentar a quantidade de digitadores. As grandezas são
inversamente proporcionais. Devemos inverter a terceira coluna no momento de armar a
proporção.
Digitadores
Páginas
Dias
3
2
4
/
5
3
3
/ =
2
5 ∙
3
4
3
/ =
6
20
6 ∙ / = 3 ∙ 20
6/ = 60 ⇔ / = 10
Como há 3 digitadores, são necessários, no mínimo, 7 digitadores.
Letra B
65.
(SEE-SP 2009/VUNESP) Foi previsto que 6 alunos voluntários, trabalhando 8
horas diárias durante 5 dias, montariam a feira de ciências. Entretanto, só apareceram 4
alunos que, trabalhando 10 horas por dia , com a mesma produtividade, montaram a feira
em
(A) 10 dias.
(B) 9 dias.
(C) 8 dias.
(D) 7 dias.
(E) 6 dias.
Resolução

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
74
Vamos montar uma tabela para resolver a regra de três.
Alunos Horas
Dias
6
8
5
4
10
/
Diminuindo a quantidade de alunos presentes, os alunos gastarão mais dias para
preparar a feira. As grandezas são inversamente proporcionais.
Aumentando a quantidade de horas trabalhadas por dia, a quantidade de dias para
preparar a feira diminuirá. As grandezas são inversamente proporcionais.
Alunos Horas
Dias
6
8
5
4
10
/
5
/ =
4
6 ∙
10
8
5
/ =
40
48
40 ∙ / = 5 ∙ 48
40/ = 240
/ = 6 "+,
Letra E
66.
(SEE-SP 2009/VUNESP) O concessionário de uma cantina escolar compra um
certo tipo de bolacha em pacotes de 2,4 kg e as vende de forma unitária. Para determinar
a quantidade de bolachas em cada pacote, ele verificou que a massa de 15 unidades
retiradas de um pacote era igual a 120 g. Como ele lucra 35 centavos por unidade
vendida, pode-se afirmar que o lucro obtido em cada pacote é igual a
(A) 84 reais.
(B) 88 reais.
(C) 90 reais.
(D) 105 reais.
(E) 126 reais.
Resolução
Vamos calcular a quantidade de bolachas no pacote de 2,4 kg = 2.400 g.
Unidades
Massa (g)
15
120

RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB
PROFESSOR: GUILHERME NEVES
Prof. Guilherme Neves
www.pontodosconcursos.com.br
75
/
2.400
Aumentando a massa, aumenta-se a quantidade de unidades de bolachas. As grandezas
são diretamente proporcionais.
15
/ =
120
2.400
Podemos simplificar a fração do segundo membro por 120.
15
/ =
1
20
/ ∙ 1 = 15 ∙ 20
/ = 300 83" + ,
Isto significa que o pacote de 2,4 kg contém 300 bolachas. Como cada bolacha gera um
lucro de R$ 0,35, então pode-se afirmar que o lucro obtido em cada pacote é igual a
300 × ($ 0,35 = ($ 105,00
Letra D
Wyszukiwarka
Podobne podstrony:
Aula 05 Parte 02
Aula 06 Parte 01 B
Aula 07 Parte 01
Aula 12 Parte 01
Aula 07 Parte 01
Aula 10 Parte 01
Aula 14 Parte 01
Aula 09 Parte 01
Aula 08 Parte 01
Aula 06 Parte 01 A
Aula 06 Parte 01
Aula 15 Parte 01
Aula 05 Parte 02
Aula 06 Parte 01 B
Aula 14 Parte 01
Aula 10 Parte 01
więcej podobnych podstron