
1.Twierdzenie Taylora dla funkcji n zmiennych
Jeżeli funkcja n zmien jest klasy C
2
w otocz O pktu P
0
=(x
1
0
, x
2
0
,
…,x
n
0
)oraz P =(x
1
0
+h
1
, x
2
0
+h
2
,…,x
n
0
+h
n
) є O to istn θ є (0,1)
przyrost f(P) –f(P
0
) = df(P
0
)+1/2 d
2
f(P) [1],a P = (θ
1
0
+ h
1
, θ
2
0
+ h
2
,
…, θ
n
0
+ h
n
) a różniczki df i d
2
f są licz dla przyrostów h
1
, h
2
,…, h
n
DF Składnik nazywamy resztą wzoru Taylora z II- różniczką
stanowi f f(h
1
, h
2
,…, h
n
) gdy mamy tylko h
1
, h
2
to oznacz je
jako h i k i mamy:
f(P) –f(P
0
)=df(P
0
)+1/2 [f
x^2
``
(P) h
2
+ 2 f
xy
``
(P)hk + f
y^2
``
(P) k
2
]
2. Extr f. n zmiennych
f(P) – f.n zmiennych, P(x
1
, x
2
,…, x
n
) w otocz P
0
єR
n
DF:f(P) ma w P
0
max (min) lokal gdy istn takie S(P
0
), że dla
każdego PєS jest spełniona f(P)≤f(P
0
) (f(P) ≥ f(P
0
) )[2], gdy
f(P)<f(P
0
) to extr nazyw właśc.
U: Extr w P
0
jest pojęciem odnosz się do dostat małego otocz
P
0
. Extr nie należy mylić z extr absol, które oznaczają najwię i
najmn wartość dla całej f
3. Wk istn extr f. 2 zmien. Pkt stacj.
Jeżeli f(x,y) ma poch cząst I rz to w P
0
(x
0
, y
0
)i ma w tym pkcie
extr to f `(P
0
)=0 i f `(P
0
)=0 [3]
U: Jeżeli f(x,y) ma w pewnym obsz poch cząstk I rz to może
mieć extr jedynie w tych pktach tego obsz, które są jego
pktami stacj.
4. Ww istn extr (2 zmienne)
Jeżeli f(x,y) klasy C
2
w pewnym otocz P
0
(x
0
, y
0
) i:
1. f`
x
(P
0
) = f`
y
(P
0
) =0
2.W(P)=f
xx
``
(P
0
)*f
yy
``
(P
0
)–[f
xy
``
(P
0
)]
2
>0
to f ma max (min) właśc gdy f
xx
``
(P
0
)<0 (>0)
(W to wyznacznik)
TW Jeżeli jest spełn war 1 oraz W(P
0
)= 0 to w P
0
zarówno
może być extr jak i nie
5. Znajdowanie najwi i najmn warti f (2 zmienne)w obsz
domkn
f(P) i P(x,y) określ w D. Jeżeli w P
0
tego Obsz D f przyjm wart
najwi lub najmn to ma w tym pkcie max (min)
WN: Dla znalezienia wart f w obsz trzeba policz wszystkie max
lok i wybr najwi. Jeżeli f(P) określ w obsz domkn to może
przyjm wart w ext lecz także na brzegu zbioru.
6.całka oznacz
def wzorem
O ile ta gran nie zal od spos
wyboru podz P, ani od spos wyboru x
k
*
I przyjmujemy, że
oraz
7. Interpr całki oznacz
1.Pole trapezu krzywolin
D-trapez krzywolin ogran f. f, osią x, x=a oraz x=b. Pole |D| jest
gran sum pól prostok ∆|D
k
| aproksymujących ten trapez
Obj bryły obrot
V oznacza bryłę ograniczoną powierzchnią powstałą z obrotu
wykresu funkcji f(x) na przedziale [a,b] wokół osi x oraz
płaszczyznami x=a i x=b. Objętość bryły V jest granicą objętości
sumy walców ∆V
k
aproksymujących tę bryłę, gdy średnica
podziału zmierza do zera.
1.
Droga przebyta w ruchu zmiennym
Niech S oznacza drogę przebytą w przedziale czasowym od a
do b ze zmienną prędkością v(t)
Droga S jest granicą sum dróg elementarnych przebytych przez
punkt w czasie t
k
gdy σ(P)->0
8. Warunek wystarczający istnienia całki oznaczonej
Jeżeli f jest ograniczona na przedziale [a,b] i ma na tym
przedziale skończoną liczbę nieciągłości pierwszego rodzaju to
jest ona na nim całkowalna
9. Twierdzenie Newtona-Leibnitza. Liniowość całki
oznaczonej
1.
(tw. Newtona – Leibnitza I) Jeżeli f jest ciągła na
przedziale
[a,b]
to
gdzie F
oznacza dowolną funkcję pierwotną dla funkcji f na tym
przedziale
2.
Jeżeli funkcja f i g są ciągłe w przedziałach [a,b] to
10. Twierdzenia o całkowaniu przez części i przez
podstawienie
1.
Jeżeli f i g mają ciągłe pochodne na przedziale [a,b] to
2.
Jeżeli: f. φ:[a,b] -> [α,β] ma ciągłą pochodną w tym
przedziale [a,b]; φ(a)=α φ(b)=β; f(t) jest ciągła na przedziale
[α,β] to
11. Twierdzenie o równości całek oznaczonych
Niech f będzie całkowalna na przedziale [a,b] oraz g różni się
od f tylko w skończonej liczbie punktów tego przedziału.
Wtedy g także jest całkowalna na tym przedziale oraz
12. Addytywność całki oznaczonej względem przedziałów
całkowania.
Jeśli f. f jest całkowalna na przedziale [a,b] oraz c є (a,b) to f. f
jest całkowana na przedziale [a, c] oraz [c,b] i
∫
a
b
f(x)dx =
∫
a
c
f(x)dx + f(x)dx
13. Zachowanie nierówności i moduł całki oznaczonej.
Jeśli f i g są całkowalne na [a,b] oraz f(x)<=g(x) dla każdego x є
[a,b] to
∫
a
b
f(x)dx <=
∫
a
b
g(x')dx
Wniosek I : Jeśli f jest całkowalna na [a,b] to |
∫
a
b
f(x)dx|
<=
∫
a
b
|f(x')|dx Dla każdego x:
-|f(x)| <= f(x) <= |f(x)|
-
∫
a
b
|f(x)|dx<=
∫
a
b
f(x)dx<=
∫
a
b
|f(x)|dx
Wniosek II : Jeśli f jest całkowalna na [a,b] oraz dla każdego x
є
[a,b] m <= f(x) <= M to m(b-a) <=
∫
a
b
f(x)dx <= M(b-a).
14. Wartość średnia funkcji (w terminach całki oznaczonej).
Interpretacje geometryczna i fizyczna.
Niech f będzie całkowalna na przedziale [a,b]. Jej wartością
średnią na tym przedziale nazywamy liczbę f
śr
=
a
b
−
1
∫
a
b
f(x)dx . Interpr. geom. Jeśli f. f jest ciągła i nieujemna na [a,b]
to jej wart. śr. na tym przedziale jest wysokością prostokąta o
podstawie |ab| , którego pole jest równe polu trapezu
krzywoliniowego ograniczonego wykresem f. f osią X oraz
prostymi x=a i x=b
Wniosek: Interpr. fiz. Jest to szybkość średnia punktu
poruszającego się w przedziale czasu t.
TW Jeśli f jest ciągła na przedziale [a,b] to dla każdego c
є[a,b]
że wart. śr.
f
śr
=
a
b
−
1
∫
a
b
f(x)dx=f(c)
15. Całka oznaczona funkcji parzystej, nieparzystej i
okresowej.
1.Jeśli f jest całkowalna i nieparzysta na [-a,a] to
∫
−
a
a
f(x)dx=0 .Jeśli f jest całkowalna i parzysta na [-a,a] to
∫
−
a
a
f(x)dx=2
∫
a
0
f(x)dx 3. Jeśli f jest okresowa (T) i jest
całkowalna na [0,T] i dla każdego x є R jest całkowalna na [a, a
+T] to
∫
a
aT
f(x)dx=
∫
T
0
f(x)dx
16. Funkcja górnej granicy całkowania. Jej ciągłość.
DF Niech f będzie całkowalna na [a,b] oraz c є [a,b]. F(x) =
∫
c
x
f (t)dt , x є [a,b] – nazywamy tę funkcję funkcją górnej
gr. całkowania.
TW ( o ciągłości f. górnej gr. całkowania): Jeśli f jest całkowalna
na [a,b] to F(x)=
∫
c
x
f (t)dt , c є [a,b] jest ciągła na tym
przedziale.
17. II główne twierdzenie rachunku całkowego (o pochodnej
funkcji górnej granicy całkowania)
Jeśli f jest całkowalna na [a,b] oraz ciągła w x
0
є[a,b] to funkcja
∫
=
x
c
dt
t
f
x
F
)
(
)
(
ma pochodną w x
0
oraz pochodna w x
0
wynosi:
F’(x
0
)=f(x
0
).
(=f(t)?)
18.Długość krzywej.
Niech f ma ciągłą pochodną na [a,b], wtedy długość krzywej
γ
={x,f(x):xє[a,b]}
∫
+
=
b
a
dx
x
f
2
)]
(
'
[
1
|
|
γ
19. Objętość bryły obrotowej. Praca wykonana przez
zmienna siłę
TW. Niech f(x)>=0 na przedziale [a,b] i ciągła na tym
przedziale. Wtedy objętość V powstałej z obrotu funkcji f
wokół osi x wyraża się wzorem
∫
∏
=
b
a
dx
x
f
V
2
)
(
|
|
TW. Niech f będzie ciągła na przedziale [a,b] i a>=0. Niech T
oznacza trapez ograniczony wykresem f, osią x, prostą x=a i
prostą x=b. Wtedy objętość bryły V z obrotu trapezu T wokół
osi y wyraża się wzorem
∫
⋅
∏
=
b
a
dx
x
f
x
V
)
(
2
|
|
TW. Załóżmy, że równolegle do x działa siła zmienna F(x).
Praca wykonana od punktu [a,b] wyraża się wzorem
∫
=
b
a
dx
x
f
W
)
(
|
|
20. Całka niewłaściwa na przedziale nieskończonym.
Definicje.
DF Jeżeli f jest całkowalna w każdym przedziale [a,T], gdzie a<T
oraz istnieje granica skończona To nazywamy ją całką
niewłaściwą funkcji f w przedziale [a,+∞] i oznaczamy
symbolem
∫
∞
a
dx
x
f
)
(
Jeżeli granica skończona (1) nie istnieje to mówimy że całka
niewłaściwa (1) nie istnieje lub jest rozbieżna.
DF Całkę niewłaściwą f na przedziale [-∞,a] określamy wzorem
∫
∫
− ∞
→
∞
−
=
a
T
T
a
dx
x
f
dx
x
f
)
(
)
(
lim
Jeżeli f jest całkowalna w każdym przedziale skończonym to
∫
∫
∫
+ ∞
→
− ∞
→
∞
∞
−
+
=
'
0
0
)
(
)
(
)
(
lim
lim
T
T
T
T
dx
x
f
dx
x
f
dx
x
f
(2)
Całką po lewej stronie równości (2) nazywamy całkę
niewłaściwą f w przedziale (-∞,∞). Mówimy, że całka ta
istnieje (jest zbieżna) jeżeli istnieją obydwie skończone granice
po prawej stronie równości(2)
21.Kryterium porównawcze dla całki niewłaściwej na
przedziale niekończonym
TW. (kryt. porównawcze) Jeśli f i g są określone w przedziale
[a,+∞] całkowalne w każdym przedziale [a,T] oraz f(x)>=g(x)
dla wszystkich x>=a to zbieżność całki
∫
+ ∞
a
dx
x
g )
(
(3) zapewnia
zbieżność całki
∫
+ ∞
a
dx
x
f
)
(
(4). Natomiast rozbieżność całki
(4) zapewnia rozbieżność całki (3)
22. Kryterium całkowe zbieżności szeregów.
Niech f: [n
0
->∞) i nierosnąca. Wtedy Σ(od n=n
0
do ∞) f(n) jest
zbieżny wtedy i tylko wtedy gdy całka niewłaściwa jest
zbieżna:
∫
∞
0
)
(
n
dx
x
f
23. Całka niewłaściwa funkcji nieograniczonej. Definicje.
Niech f(x) określona w [a,b], nieograniczona w lewostronnym
sąsiedztwie pktu b, całkowalna w każdym przedziale [a,b-E],
E>0
Jeśli istnieje granica skończona lim(przy E->0-)
∫
−
E
b
a
dx
x
f )
(
to
nazywamy ją całką niewłaściwą funkcji f w [a,b] i oznaczamy
symbolem całka (od a do b) f(x)dx
24. Podstawowe definicje całki podwójnej w prostokącie.
Jeśli dla każdego ciągu przedziałów prostokąta Π, ciąg sum
całkowych S
n
jest zbieżny do tej samej skończonej granicy,
niezależnie od wyboru pkt P
k
, to te granice nazywamy całką
podwójną z f w prostokącie Π i oznaczamy całka podwójna po
Π f(x,y)dσ
25. Interpretacje geometryczne i fizyczne całki podwójnej w
prostokącie.
Geom: Całka po obszarze równa jest objętości bryły
ograniczonej płaszczyznami tego obszaru i wykresem funkcji
f(x,y)
Fiz: Jeśli ρ(x,y) jest gęstością powierzchniową prostokąta Π to
całka(po Π) z ρ(x,y) przedstawia z definicji masę tego
prostokąta.
26. Własności całki podwójnej w prostokącie. Wartość
średnia. Twierdzenie o wartości średniej.
1) Jeśli f jest całkowalna w prostokącie Π to a*f (a-dowolne)
też jest całkowalna w prostokącie.
2) Jeśli f i g są całkowalne w prostokącie Π to ich suma też jest
całkowalna w prostokącie Π.
3) Jeśli podzielimy prostokąt na 2 (Π
1
i Π
2
) i f jest całkowalna w
prostokącie Π to jest też całkowalna w Π
1
i Π
2
.
Wart. śr.: f
śr
=(całka po Π z f(x,y)dσ):(σ)- to jest po ułamkiem.
TW: Jeśli f jest ciągła w Π to istnieje pkt CєΠ, że wartość
średnia: f
śr
=(całka po Π z f(x,y)dσ):(σ)= f(C)
27. Twierdzenie o zmianie całki podwójnej na całkę
iterowaną.
Całka określona wzorem:
=
to całka iterowana.
Z własności całek iterowanych bezpośrednio wynika, że jeśli D
jest prostokątem danym nierównościami a≤x≤b, c≤y≤d, to:
=
=
A jeśli ponadto funkcja f(x,y)= Φ(x) Ψ(y), to całka podwójna
równa się iloczynowi całek pojedynczych:
=
28. Obszar normalny. Całka podwójna w tym obszarze. Wz
ory do obliczania całki podwójnej w obszarze normalnym.
Zbiór regularny.
DF Zbiór domknięty D określony nierównościami a≤x≤b,
Φ(x)≤y≤ Ψ(x), gdzie Φ(x) i Ψ(x)
są to funkcje ciągłe w przedziale [a,b], nazywamy obszarem
normalnym.
Całkę podwójną f w obszarze normalnym D oznaczamy
symbolem:
i określamy
Powołując się na twierdzenie o zamianie całki podwójnej na
całkę iterowaną:
=
DF Zbiór D określony nierównościami a≤y≤b; Φ(x)≤x≤ Ψ(x),
gdzie Φ(x) i Ψ(x) są to
funkcje ciągłe w przedziale [a,b] nazywamy obszarem
normalnym względem osi Y.
Całkę podwójną z funkcji f(x,y) w obszarze normalnym D
względem osi Y określamy analogicznie:
=
DF Zbiór D nazywamy regularnym jeśli jest on sumą D=D
1
+D
2
+
…
+D
n
obszarów normalnych względem osi X lub osi Y, które nie
mają wspólnych punktów wewnętrznych.
DF Całkę podwójną funkcji f w obszarze regularnym D
określamy jako sumę całek w obszarze normalnym D
1
,D
2 …
D
n.
=
+
+…+
29. Interpretacje geometryczne i fizyczne całki podwójnej w
obszarze normalnym.
Geom. Niech f(x,y) będzie funkcją ciągłą w obszarze
regularnym D, gdzie f(x,y)≥0 dla każdego (x,y)єD.
przedstawia objętość bryły o podstawie D,
ograniczonej powierzchnią będącą wykresem f oraz
powierzchnią walcową utworzoną z prostych równoległych do
z i przechodzących przez brzegi obszaru D.
Fiz.
1.
Jeżeli ρ(x,y) jest gęstością powierzchniową masy
obszaru regularnego D to:
przedstawia masę
m tego obszaru.
2.
= My,
= Mx -
momenty statyczne względem osi X i Y.
30. Zmiana zmiennych w całce podwójnej. Jakobian.
Zmiana zmiennych w całce podwójnej jest ściśle związana z
odwzorowaniem zbioru płaskiego na zbiór płaski za pomocą
pary funkcji dwóch zmiennych.
Jakobian – wyznacznik macierzy zbudowanej z pochodnych
cząstkowych pierwszego rzędu pewnego układu funkcji
rzeczywistych. J(u, v) =
31. Wprowadzenie zmiennych biegunowych w całce
podwójnej.
Przy wprowadzaniu współrzędnych biegunowych: x = ρ cos Φ,
y = ρ sin Φ
Mamy:
=
. Jest to wzór na zmianę
współrzędnych prostokątnych na współrzędne biegunowe w
całce podwójnej.

32. Całka potrójna w prostopadłościanie. Podstawowe
definicje.
Niech Ω będzie obszarem regularnym lub domkniętym
obszarem regularnym a f(x,y,z) funkcją ograniczoną w Ω.
Oznaczmy przez A punkt o współrzędnych (x,y,z). Będziemy
oznaczali funkcję f(x,y,z) krótko przez f(A). Niech P będzie
dowolnym prostopadłościanem (o ścianach równoległych do
płaszczyzn współrzędnych) zawierającym Ω. Niech π
n
oznacza
dowolny rozkład prostopadłościanu na skończoną liczbę m
n
prostopadłościanów częściowych. Niech A
i
oznacza dowolny
punkt obszaru Ω należący do prostopadłościanu.
Jeżeli dla każdego ciągu podziałów {π
n
}, dla którego
n
=0 ciąg jest zbieżny do tej samej liczby bez
względu na wybór punktów A
i,
to mówimy, że funkcja f(x,y,z)
jest całkowalna w obszarze Ω, a wspólną granicę ciągów
nazywamy całką potrójną funkcji f(x,y,z) w obszarze Ω i
oznaczamy symbolem:
lub
Łatwo wykazać, że całkowalność funkcji f(x,y,z) w obszarze Ω i
wartość całki nie zależy od wyboru prostopadłościanu P
(byleby tylko obejmował on obszar Ω). Można wykazać, że
każda funkcja ciągła w obszarze regularnym Ω jest w nim
całkowalna, a nawet że funkcja f(x,y,z) ciągła w obszarze
regularnym Ω z wyjątkiem punktów leżących na skończonej
ilości powierzchni jest całkowalna w Ω. Stale jednak
obowiązuje założenie, że funkcja f(x,y,z) jest ograniczona w
całym obszarze Ω.
33. Interpretacje geometryczne i fizyczne całki potrójnej.
(*)
Geom. Jeśli f(P)=1 to całka (*) przedstawia objętość
prostopadłościanu
Π
.
Fiz. Jeśli f(P) jest gęstością objętościową masy
Π
to całka (*)
przedstawia masę tego prostopadłościanu.
34. Własności całki potrójnej w prostopadłościanie. Wartość
średnia. Twierdzenie o wartości średniej.
Całka potrójna w prostopadłościanie posiada własności
analogiczne do własności całki podwójnej.
DF Niech f będzie całkowalna w prostopadłościanie
Π
o
objętości V, to:
nazywamy wartością średnią
funkcji f w prostopadłościanie
Π
. Oznaczamy F
śr
.
TW (o wartości średniej) Jeśli f jest ciągła w
Π
to istnieje taki
punkt CєΠ dla którego F
śr
równa się wartości funkcji f w tym
punkcie F
śr
= f(C)
35.Twierdzenie o zamianie całki potrójnej na całkę
iterowaną.
Jeśli f jest ciągła w
Π
określonym nierównościami: a≤x≤ b,
c≤y≤d, p≤z≤q to całka potrójna w tym prostopadłościanie
równa
się:
=
36. Całka potrójna w obszarze normalnym. Wzory do
obliczania.
DF Zbiór domknięty (
Ω
) określamy nierównościami
K(x,y)≤z≤
Ψ
(x,y) gdzie punkt (x,y)
∈
D gdzie D jest obszarem
regularnym na płaszczyźnie a funkcje K,
Ψ
są w nim ciągłe
nazywamy obszarem normalnym względem płaszczyzny x, y.
Analogicznie określamy obszar normalny względem
płaszczyzny y,z i x,z.
Wzory:
1.
Do obliczania masy ciała:
=
(*)
Gdy
=
, że dla
∀
z
∈
[p,q] zbiór wszystkich punktów obszaru
Ω
, które mają
trzecią współrzędną z stanowi figurę, której rzutem na
płaszczyznę x,y jest obszar regularny D
2
, wtedy naszą całkę
potrójną można obliczyć korzystając z:
=
Uwaga 1: Jeżeli zbiór
Ω
jest obszarem normalnym względem
płaszczyzny xz lub yz to całkę potrójną w tym obszarze można
obliczyć za pomocą wzoru analogicznego do
Uwaga 2: Jeśli zbiór
Ω
jest sumą skończoną obszarów
normalnych, które nie mają punktów wspólnych
wewnętrznych to całkę z funkcji f w zbiorze
Ω
określamy jako
sumę całek po wszystkich tych obszarach.
37. Zamiana zmiennych w całce potrójnej. Jakobian
Przypuśćmy, że: x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) to
odwzorowuje jednocześnie zbiór
Ω
o w przestrzeni UVW na
zbiór regularny
Ω
w przestrzeni XYZ przy czym każda z funkcji
będzie klasy C1.
Jeżeli funkcja f(x,y,z) jest ciągła w obszarze
Ω
oraz jakobian J
przekształcenia równa się:
J(u,v,w) =
≠ 0, dla każdego (u,v,w)єΩ, to jest
poprawny wzór:
=
38. Współrzędne sferyczne.
x = rcos
ϕ
cos
φ
, y = rsin
ϕ
sin
φ
, z = rcos
φ
, J=r
2
sin
φ
=
39. Współrzędne cylindryczne (walcowe)
x = rcosθ , y = rsinθ, z = z, J(r,θ,z)= r
=
40.
Krzywa,
kierunek
DF Zbiór punktów (x,y) na płaszczyźnie określonych
równościami x=x(t) , y=y(t), tє[α,β] (1)
gdzie x(t) i y(t) funkcje ciągłe, nazywamy krzywą na
płaszczyźnie,
t
to
parametr.
DF Krzywą określoną równaniami (1) nazywamy prostą jeśli t
1
≠
t
2
->(x(t1),
y(t1)
≠(x(t2),
y(t2)).
DF Krzywą nazywamy otwartą jeśli A nierówna się B. (dwa
końce
krzywej)
Kierunek: krzywej o równaniu (1) można nadać kierunek
przypisując A za początek a B za koniec, albo na odwrót. W
pierwszym przypadku kierunek jest zgodny ze wzrostem
parametru.
41. Całka krzywoliniowa skierowana. Podstawowe definicje.
Interpretacja fizyczna.
DF Zbiór pkt (x,y) na płaszczyźnie określonych równościami
x=x(t) , y=y(y), tϵ[α,β) (1) gdzie x(t) i y(t) → f. ciągła i nazywamy
krzywą na płaszczyźnie.
Wartości α, β odpowiadają punkty A=(x(α),y(α)) B=(x(β),y(β))
DF Krzywą nazywamy otwartą, jeśli A ≠ B
DF Krzywą określoną równaniem (1) nazywamy prostą jeśli t
1
≠t
2
→ (x(t
1
),y(t
1
))≠(x(t
2
),y(t
2
))
Krzywej o równaniu (1) można nadać kierunek przyjmując A za
pocz. a B za koniec (albo odwrotnie). W I przyp. kier krzywej
jest zgodny ze wzrostem parametru. W II przyp. kier.
niezgodny.
DF Krzywej której nadano kierunek nazywamy krzywą
skierowaną i oznaczamy AB
Gdy krzywe AB i BAróżnią się tylko kierunkiem to oznaczamy
AB = - BA
Jeśli nie mówimy że przeciwne – krzywa zgodna z parametrem
42. Twierdzenie o zamianie całki krzywoliniowej skierowanej
na całkę oznaczoną.
Jeśli funkcje P(x,y),Q(x,y) są ciągłe na stałej krzywej prostej AB
o wzorze parametrycznym x(t), y(t) → klasy C
1
to istnieje
(4)
=
Fiz.
=
(3)
Jeśli R jest wektorem siły w pkt (x,y) o wspołrz P(x,y) i Q(x,y) to
całka (3) przedstawia prace siły R wzdłuż krzywej AB
Uwaga 1: Jeśli Q = 0 to całka (4) redukuje się do : Całka od AB z
P(x,y)dx (5)
Jeśli P =0 to : Całka od AB z Q(x,y)dy (6)
Uwaga 2: Całka (4) red się do (5) gdy AB jest odcinkiem || do
osi X
Całka (4) redukuje się do (6) gdy AB jest odcinkiem || do osi Y
43. Skierowanie krzywej względem swego wnętrza.
Utwórzmy wektor styczny s skierowany zgodnie z kierunkiem
krzywej oraz wektor n (prostopadły do s) o początku w P
0
i
skierowany od wektora s przeciwnie do wskazówek zegara.
Wtedy: Jeśli wektor n jest skierowany do wnętrza D krzywej to
mówimy że krzywa K jest skierowana dodatnio względem
swego wnętrza. W przeciwnym razie- ujemnie.
44.
Twierdzenie
Greena
Jeżeli funkcje P(x,y) i Q (x,y) są klasy C
1
w obszarze normalnym
D względem osi X lub osi Y, przy czym brzeg K tego obszaru
jest krzywą skierowaną dodatnio względem wnętrza to:
∫
∫∫
−
=
+
K
D
Y
X
dxdy
y
x
P
y
x
Q
dy
y
x
Q
dx
y
x
P
)]
,
(
'
)
,
(
'
[
)
,
(
)
,
(
-wzór Greena
X
Q'
-pochodna względem X,
Y
P'
-pochodna względem Y
45. Twierdzenie o niezależności całki krzywoliniowej
skierowanej od kształtu drogi całkowania. Wnioski.
Jeżeli funkcje P(x,y) i Q (x,y) są klasy C
1
w obszarze
normalnym D to spełnienie równości:
X
Q'
=
Y
P'
(1) jest równoważne temu, że całka
∫
+
B
A
dy
y
x
Q
dx
y
x
P
~
)
,
(
)
,
(
po otwartej krzywej gładkiej
CD
B
A
nie zależy od kształtu tej krzywej, a tylko od punktu
A
i
B
Wniosek
1:
Jeżeli P(x,y) i Q (x,y) są klasy C
1
i spełniają warunek (1) w
obszarze
normalnym
D
to:
∫
=
+
0
)
,
(
)
,
(
dy
y
x
Q
dx
y
x
P
dla każdej
kawałkami gładkiej krzywej zamkniętej C
(2)
Wniosek
2:
Jeżeli P(x,y) i Q (x,y) są klasy C
1
w obszarze normalnym D oraz
dla każdej kawałkami gładkiej krzywej
D
C
⊂
spełniony jest warunek (2) to w każdym punkcie tego obszaru
spełniony
jest
warunek
(1)
46. Warunek istnienia funkcji z danymi pochodnymi
cząstkowymi.
Jej
znalezienie.
Przypuśćmy, że P(x,y) i Q (x,y) są klasy C
1
w prostokącie D, że
a<x<b
i
c<y<d
Sprawdzamy czy istnieje w tym obszarze funkcja U(x,y), która
ma
takie
własności:
P
U
X
=
'
i
Q
U
Y
=
'
(1)
Gdy (1) istnieje, to:
Y
Y
X
XY
P
U
U
'
)'
'
(
''
=
=
i
X
X
Y
YX
Q
U
U
'
)'
'
(
'
=
=
P(x,y) i Q (x,y) są klasy C
1
więc drugie pochodne mieszane są
równe:
YX
XY
U
U
''
''
=
Jeżeli (1) istnieje to warunek
X
Q'
=
Y
P'
jest spełniony.
Warunek
X
Q'
=
Y
P'
jest konieczny, by U spełniała warunek
(1)
Okazuje się, że warunek ten jest także wystarczający
∫
∫
+
=
x
x
y
y
dt
t
x
Q
dt
y
t
P
y
x
U
0
0
)
,
(
)
,
(
)
,
(
0
(6), gdzie
)
,
(
0
0
y
x
- dowolny
punkt
CD
)
,
(
'
y
x
P
U
X
=
)
,
(
)
,
(
'
)
,
(
'
)
,
(
)
,
(
)
,
(
'
0
0
0
0
y
x
Q
y
x
Q
y
x
Q
y
x
Q
y
x
Q
dt
y
t
P
U
x
x
Y
=
+
−
=
+
=
∫
47. Całka krzywoliniowa nieskierowana. Podstawowe
definicje.
Krzywa L –otwarta o równaniach parametrycznych x=x(t) i
y=y(t),
]
,
[
β
α
∈
t
Przypuśćmy, że dla danej krzywej x=x(t) i y=y(t)
1
C
∈
Można udowodnić, że dlugość L-
dt
t
y
t
x
l
∫
+
=
β
α
2
2
)]
(
'
[
)]
(
'
[
.
Przypuścmy, że w każdym punkcie krzywej l określona jest
funkcja
dwóch
zmiennych
)
,
( y
x
f
L
Def. (całki z funkcji
f(x,y)
po krzywej L):
Dzielimy przedział
]
,
[
β
α
:
β
α
=
<
<
<
<
=
n
t
t
t
t
...
2
1
0
Podziałowi temu odpowiada podział krzywej L na części:
n
A
A
A
,...,
,
1
0
(
))
(
),
(
(
0
0
0
t
y
t
x
A
=
)itd.
k
l
∆
-długość części krzywej
k
k
A
A
1
−
k=1,…,n
dt
t
y
t
x
l
k
k
t
t
k
∫
−
+
=
∆
1
2
2
)]
(
'
[
)]
(
'
[
W każdym przedziale
]
,
[
1
k
k
t
t
−
wybieramy punkt k
τ
, taki że
]
,
[
1
k
k
k
t
t
−
∈
τ
Punktowi temu odpowiada na krzywej punkt
)
,
(
))
(
),
(
(
k
k
k
k
k
y
x
y
x
C
=
τ
τ
Utwórzmy sumę
∑
=
∆
=
n
k
k
k
k
n
l
y
x
f
S
1
)
,
(
(1) oraz rozważmy ciąg
normalny
podziału
przedziału
]
,
[
β
α
DEF: Jeżeli dla każdego normalnego ciągu podziału przedziału
]
,
[
β
α
ciąg sum (1) jest zbieżny do tej samej granicy
skończonej niezależnej od wyboru punktu
k
τ
to tę granicę
nazywamy całką krzywoliniową nieskierowaną z funkcji f po
krzywej L i oznaczamy symbolem:
∫
L
dL
y
x
f
)
,
(
∑
∫
=
→
∆
=
n
k
k
k
k
L
l
y
x
f
dL
y
x
f
n
1
0
)
,
(
lim
)
,
(
δ
, gdzie
n
δ
-średnica
podziału
przedziału
na
n
części
48. Interpretacje geometryczne i fizyczne całki
krzywoliniowej
nieskierowanej.
Interpretacja
geometryczna:
1. f(x,y)=1 to
∑
=
∆
=
n
k
k
k
k
n
l
y
x
f
S
1
)
,
(
jest stały i jest równy l więc
∫
L
dL
y
x
f
)
,
(
przedstawia długość krzywej L
2. f(x,y)>0 i jest ciągła to
∫
L
dL
y
x
f
)
,
(
przedstawia pole
powierzchni
Interpretacja
fizyczna:
Jeżeli
)
,
( y
x
ρ
jest gęstością liniową masy krzywej L to
∫
L
dL
y
x )
,
(
ρ
przedstawia masę m tej krzywej
natomiast liczby
m
dL
y
x
x
x
L
∫
=
)
,
(
ρ
i
m
dL
y
x
y
y
L
∫
=
)
,
(
ρ
to
współrzędne
środka
masy
krzywej
L
49. Zamiana całki krzywoliniowej nieskierowanej na całkę
oznaczoną.
Jeżeli f(x,y) jest ciągła na otwartej prostej i gładkiej krzywej L o
przestawieniu parametrycznym x=x(t) i y=y(t)
1
C
∈
, to całka
∫
L
dL
y
x
f
)
,
(
istnieje,
przy
czym:
∫
∫
+
=
L
dt
t
y
t
x
t
y
t
x
f
dL
y
x
f
β
α
2
2
)]
(
'
[
)]
(
'
[
))
(
),
(
(
)
,
(
50. Gładki płat powierzchniowy. Całka powierzchniowa
niezorientowana. Podstawowe definicje.
Gładkim płatem powierzchniowym (względem płaszczyzny xy)
nazywamy wykres funkcji z=f(x,y) gdzie płat (x,y) €D klasy
C1(D) gdzie D- oznacza obszar regularny.
Pow. Stanowiącą zbiór spójny pkt, którą można podzielić na
skończoną liczbę gładkich płatów powierzchniowych
nazywamy pow. regularną.
Rozważmy F określona na płacie: F*(x,y,z)=F(x,y,z) €D a
F*(x,y,z)=0
∉
D
P
k
=P(x
k
,y
k
) punkt należący do prostokąta ∩. A
k
=(x
k
,y
k
,f(x
k
,y
k
))
(x
k
,y
k
)€D a
A
k
=(x
k
,y
k
,0) (x
k
,y
k
)€∩\D.
∆
S
k
-pole tej części płaszczyzny
stycznej do
Ω
w w pkt A
k
która leży nad ∩.
Całka niezorien.-Jeśli dla każdego normalnego ciągu podziału
prostokąta na ∩ (∩ jest prost. Zawierającym interesujący nas
obszar D) ciąg sum S
n
=
∑
=
n
k
F
1
*(A
k
)
∆
S
k
jest zbieżny do tej
samej granicy skończonej niezależnie od wyboru P
k
to te
granice nazywamy całką powierzchniową niezorientowaną z F
po
Ω
.
51. Interpretacje geometryczne i fizyczne całki
powierzchniowej niezorientowanej.
Interpretacja geom. Jeśli F(x,y,z)=1 to całka
∫∫
Ω
1
dS.
przedstawia pole płata gładkiego.
Interpretacja fiz. Jeśli g(x,y,z) jest gęstością powierzchni masy
płata
Ω
to
∫∫
Ω
g
(x,y,z)dS przedstawia masę tego płata.
52. Obliczanie całki powierzchniowej niezorientowanej.
Jeśli F jest ciągłe na gładkim płacie
Ω
to całka ∫∫F(x,y,z)dS
istnieje i można ją obliczyć ze wzoru:
∫∫
Ω
F
(x,y,z)dS=
∫∫
D
F
(x,y,f(x,y))
1
]
'
[
]
'
[
2
2
+
+
y
f
x
f
dxdy
53. Szereg funkcyjny, jego zbieżność. Szereg potęgowy.
Promień zbieżności. Przedział zbieżności. Ich obliczanie.
Szeregiem funkcyjnym nazywamy wyrażenie postaci
f
1
(x)+ f
2
(x)+ f
3
(x)+…=
∑
∞
=
1
n
f
n
(x). Mówimy że ten szereg jest
zbieżny w pkt x
1
gdy szereg liczb
∑
∞
=
1
n
f
n
(x
1
) jest zbieżny.
Szereg potęgowy może być zbieżny lub rozbieżny. Szereg pot.
o środku x
0
i współczynnikach C
n
nazywamy szereg funkcyjny
postaci:
∑
∞
=
0
n
C
n
(x-x
0
)
n
, x€R. Istnieje taka liczba R€[0,∞], że szereg
ten jest zbieżny bezwzględnie w przedziale (x0-R, x
0
+R) i
rozbieżny (-∞,x
0
-R) i (x
0
+R,∞).
Liczby R nazywamy promieniem zbieżności.
Obliczanie: R=
|
|
|
|
lim
1
+
∞
→
n
n
n
C
C
lub R=
n
n
n
C
1
lim
∞
→
54. Szereg Taylora i Maclaurina. Wielomian Taylora. Wzór z
reszta La Grange’a. Tw o rozwijaniu funkcji w szereg Taylora.
Tw o jednoznaczności rozwijania funkcji szereg potęgowy.
Def. szeregów Taylora i Maclaurina. Niech f ma w x
0
pochodną
dowolnego
rzędu.
)
(
!1
)
('
)
(
0
0
0
x
x
x
f
x
f
−
+
...
)
(
!
2
)
(
''
2
0
0
+
−
+
x
x
x
f
=
−
+
n
n
x
x
n
x
f
)
(
!
)
(
...
0
0
n
n
n
x
x
n
x
f
)
(
!
)
(
0
0
0
−
∑
∞
=
Dla x
0
=0 jest to szereg Maclaurina.
Tw. o rozwijaniu funkcji w szereg Taylora 1)Niech f ma poch.
dowolnego rzędu w otoczeniu O(x
0
) punktu x
0
2) dla każdego
C€ O(x
0
)
0
)
(
!
)
(
0
→
−
n
n
x
x
n
c
f
I wtedy dla każdego x€ O(x
0
) zachodzi równość: f(x)=
n
n
n
x
x
n
x
f
)
(
!
)
(
0
0
−
∑
∞
=
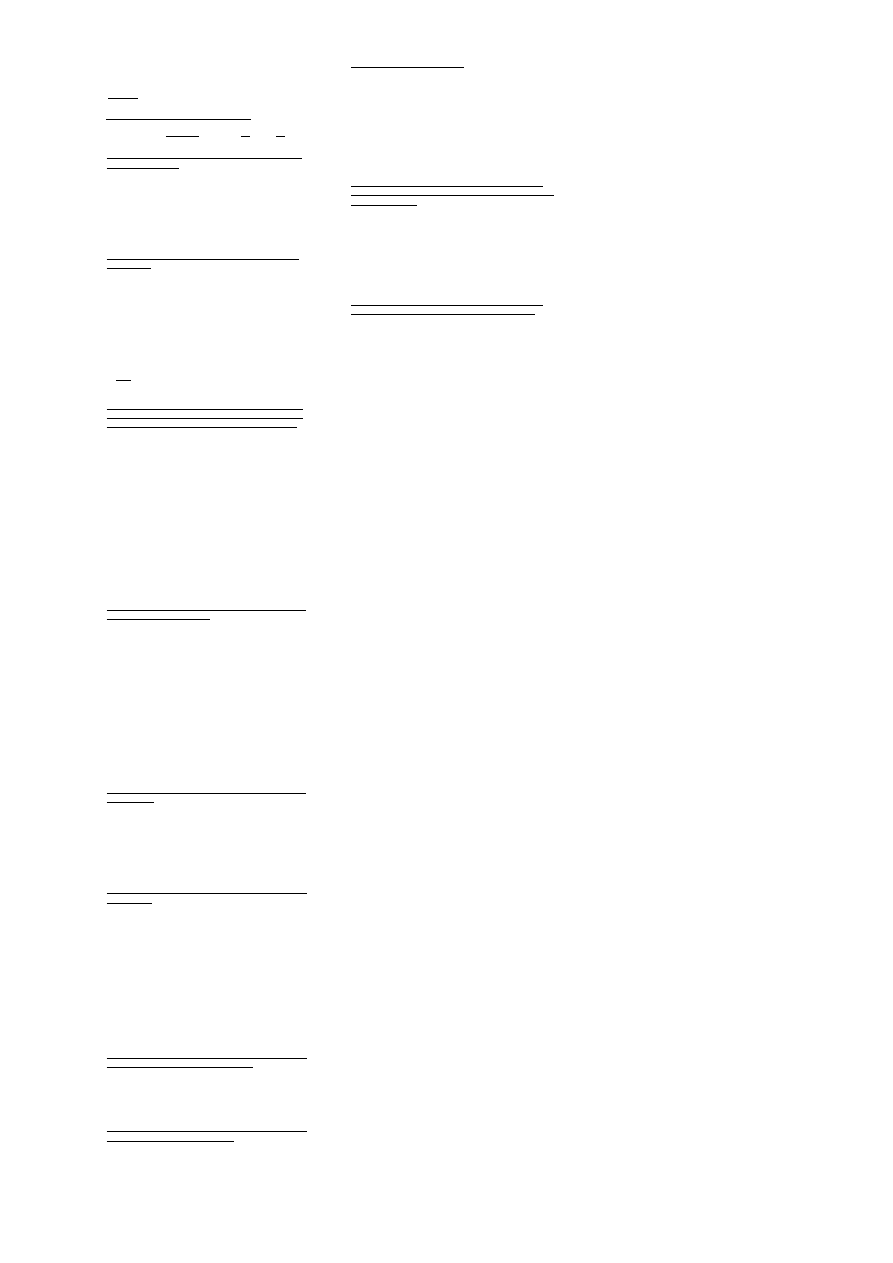
Tw o jednoznaczności rozwinięcia funkcji w szereg potęgowy:
Jeżeli na otoczeniu pkt x
0
funkcja jest sumą szer. Potęgowego
to jest to jej szereg Taylora.
Jeśli f(x)=
n
n
n
x
x
C
)
(
0
−
∑
∞
=
dla każdego x€ O(x
0
) to te liczby C
n
=
!
)
(
0
n
x
f
n
dla każdego n€N
55. Szeregi Maclaurina dla funkcji sinx, cosx ,e
x
sinx=
∑
∞
=
−
−
−
−
1
1
2
1
)!
1
2
(
)
1
(
n
n
n
n
x
cos=
∑
∞
=
−
1
2
!
2
)
1
(
n
n
n
n
x
e
x
=
e
n
x
n
∑
∞
=
0
!
1
56. Twierdzenia o różniczkowaniu szeregu potęgowego.
Przykład zastosowania.
TW: Niech liczba 0<R≤∞ będzie promieniem zbieżności
szeregu potęgowego wtedy ∑
∞
n=1
(nC
n
*X
n-1
) jest zbieżny na
przedziale (-R,R) i (∑
∞
n=0
C
n
*X
n
)’ = ∑
∞
n=1
nC
n
*X
n-1
.
UWAGA! Podobny wzór jest prawdziwy dla postaci: ∑
∞
n=0
C
n
(X-
X
0
)
n
Przykład: Oblicz ∑
∞
n=1
n(0/5)
n-1
Rozpatrzmy szereg (∑
∞
n=0
X
n
)’=(1/(1-x))’=1/(1-x)
2
dla (-1,1),
Korzystamy z TW. (∑
∞
n=0
X
n
)’ = ∑
∞
n=1
nX
n-1
; ∑
∞
n=1
(0,5)
n-1
=1/(1-
0,5)
2
=4
57. Twierdzenie o całowaniu szeregu potęgowego. Przykład
zastosowania.
TW: Niech liczba 0<R≤∞ będzie promieniem zbieżności
szeregu potęgowego ∑
∞
n=0
C
n
*X
n
, x
0
=0 wtedy szereg ∑
∞
n=0
(C
n
/
(n+1))*X
n+1
jest zbieżny dla każdego xє(-R, R), ponadto
∫ ∑
∞
=
x
n
n
n
dt
t
C
0
0
)
(
= ∑
∞
n=
0(C
n
/(n+1))*X
n+1
.
UWAGA! Podobny wzór jest prawdziwy dla postaci: ∑
∞
n=0
C
n
(X-
X
0
)
n
Przykład: ln(1+x)
Wiemy, że szereg geom. 1-t+t
2
-t
3
+…=1/(1+t) jest zbieżny w (-
1,1)
∫
∫
−
+
−
=
+
x
x
dt
t
t
dt
t
0
0
2
...)
1
(
1
1
=x- x
2
/2 + x
3
/3 - …= ∑
∞
n=1
(-
1)
n-1
* X
n
/n w przedziale (-1,1)
58. Równania różniczkowe. Rozwiązywanie szczególne.
Rozwiązanie ogólne. Zagadnienie Cauchy’ego. Warunki
początkowe. Rząd równania różniczkowego. Krzywa całkowa.
DEF. Równaniem różniczkowym zwyczajnym nazywamy
równanie postaci F (x, y, y’, y”, y
(n’)
) = 0 w którym F - funkcja
wiadoma od n+2 zmiennych, y(x) - niewiadoma określona na
przedziale (a, b);
DEF. Liczbę n (w równaniu F (x, y, y’, y”, y
(n’)
) = 0) nazywamy
rzędem równania różniczkowego
DEF. Równaniem ogólnym równania F(x, y, y’, y”, y
(n’)
) = 0
nazywamy zbiór wszystkich rozwiązań tego równania.
DEF. Rozwiązanie, szczególny, równania F(x, y, y’, y”, y
(n’)
) = 0
nazywamy każdą pojedynczą funkcję spełniającą to równanie.
DEF. Wykres każdego rozwiązania szczególnego równania
różniczkowego nazywamy krzywą całkową tego równania.
DEF. Zagadnieniem Cauchy’ego dla równania F(x, y, y’, y”, y
(n’)
)
= 0 nazywamy następujące zagadnienie: „znaleźć rozwiązanie
szczególne danego równania F(x, y, y’, y”, y
(n’)
) = 0 które
spełnia warunki początkowe”: y(x
0
) = y
0
; y’(x
0
) = y
1
; …; y
(n’)
= y
n-
1;
W tych wartościach liczby y
0
, y
1
…y
n-1
są znane i nazywamy
wartościami początkowymi
59. Równanie o zmiennych rozdzielonych. Postać
różniczkowa równania. Przykłady
[ f(x) określ. na (a,b) i g(x) określ. na (c,d) ] są ciągłe g(x)≠0
DEF. Równanie różniczkowe postaci: y’(x)=f(x)/g(y(x)) o f.
niewiadomej y(x) i nazywamy równ. różniczkowym o
zmiennych rozdzielonych.
Jeśli dy/dx = f(x)/g(y) to można to zapisać w postaci
różniczkowej: g(y)dy=f(x)dx
Przykład1: g(y(x))*y’(x)=f(x)
∫ g(y(x))*y’(x)dx=∫f(x)dx
y(x)=y wtedy dy=y’(x)dx, ∫g(y)dy=∫f(x)dx
Jeśli G(y) – jest f. pierwotną dla g(y) i F(x) jest funkcją
pierwotną dla f(x) to mamy
G(y)=F(x)+C; y=G
-1
[F(x)+C] – równanie ogólne
y’(x)=f(x)/g(y(x))
Przykład2: znajdź rozwiązanie szczególne: dy/dx=e
-y
*cos
spełnia w.p. y(0)=0, x=0, y=0
∫e
y
dy = ∫cosxdx; e
y
=sinx + C; e
0
=sin0 + C; 1=C; e
y
=sinx+1
oraz ln(e
y
=ln(sinx+1)
l=ln(sinx+1) rozwiązanie zagadnienia Cauche’go
60. Równanie liniowe rzędu 1-go. Jednorodne i
niejednorodne.
DEF. dy/dx + p(x)y = f(x); p(x), f(x) – f. dane i ciągłe w (a, b);
nazywamy równaniem różniczkowym liniowym rzędu 1-go:
jednorodnym gdy f(x)=0, niejednorodnym f(x)≠0
Przykład: dy/dx –e
xy
=0 – równ. liniowe rzędu 1-go jednorodne
(p(x)=e
x
, f(x)=0)
dy/dx+2sinx*y=cos – równ. liniowe rzędu 2-
go niejednorodne (p(x)=2sinx, f(x)=cos)
dy/dx + y
2
= 0 nie jest równ. liniowym rzędu
1-go
61. Rozwiązanie równania liniowego rzędu 1-go
jednorodnego.
dy/dx + p(x)y=0;
Równanie dy/dx + p(x)y=0 spełnia funkcja y(x)=0; Jeśli y(x)≠0
jest równ. 0 zmiennych rozdzielonych
dy/dx = -p(x)y; p(x) = ∫p(x)dx
∫dy/y = ∫-p(x)dx;
ln|y| = -p(x) + C
1
, C
1
єR;
|y|=e
-p(x)
* e
C1
, C
1
єR
y = e
C1
* e
-p(x)
lub y= - e
C1
* e
-p(x)
c=e
C1
y = c * e
-p(x)
, c≠0
Rozw. ogólne równania dy/dx + p(x)y=0: y = c * e
-p(x)
, cєR
Rozważamy zagadnienie Cauche’go dla tego równania:
y(x
0
)=y
0
; y
0
=c*e
-p(x0)
c=y
0
* e
-p(x0)
W: Jeśli funkcja p(x) jest ciągła w przedziale (a, b) to wzór:” y =
ce
-p(x)
, c є R ” przedstawia rozwiązanie ogólne zadanego
równania. Zagadnienie Cauchy’ego dla zadanego równania ma
dokładnie 1. rozwiązanie.
62. Rozwiązanie równania liniowego rzędu 1-go
niejednorodnego. Metoda uzmienniania stałej.
Metoda polega na tym, że we wzorze: y=ce
-P(x)
, c є R,
zastępujemy stałą c funkcją C(x) i tak dobieramy funkcję, aby
y(x) = C(x)e
-P(x)
była rozwiązaniem ogólnym równania dy/dx –
e
xy
= 0. Czyli, C(x) = ∫f(x)e
P(x)
dx + C
1
jest rozwiązaniem ogólnym,
aby otrzymać rozwiązanie szczególne to musimy z warunku
(wcześniej podanego) obliczyć nasze C
1
.
63. Rozwiązanie równania liniowego rzędu 1-go
niejednorodnego. Metoda przewidywań.
Rozwiązanie ogólne równania niejednorodnego można
zapisać, jako sumę rozwiązanie ogólnego równania
jednorodnego oraz rozwiązania szczególnego. Równanie
szczególnego możemy wyznaczyć metodą przewidywania, tzn.
jeżeli p(x) = const a q(x) jest wielomianem, funkcją
wykładniczą, sinusem, cosinusem lub kombinację
wymienionych to istnieje rozwiązanie szczególne (RS) w tej
samej postaci, ale z innymi współczynnikami, które wyliczamy
po podstawieniu do równania.np.
64. Równanie zupełne. Rozwiązanie.
Niech będą dane funkcje P(x,y) i Q(x,y) klasy C
1
w pewnym
obszarze normalnym D, i niech Q(x,y) będzie różne od zera w
tym obszarze D.
dy/dx = -P(x,y)/Q(x,y)
P(x,y)dx + Q(x,y)dy = 0 (*)
Mówimy, że równanie (*) jest równaniem różniczkowym
zupełnym, gdy istnieje taka funkcja u(x,y) klasy C
2
w obszarze
D, której różniczka zupełna równa się lewej stronie tego
równania.
u'
x
dx + u'
y
dy = P(x,y)dx + Q(x,y)dy, czyli u'
x
= P(x,y) i u'
y
= Q(x,y)
Rozwiązanie: du = 0, czyli u(x,y) = C – jest to rozw. ogólne
równania (*) zapisane w postaci uwikłanej
65. Równanie liniowe rzędu 2-go o stałych współczynnikach,
jednorodne. Rozwiązanie za pomocą równania
charakterystycznego.
y'' + py' + qy = 0, p,qєR jest to równ. różniczkowe liniowe
jednorodne II rzędu o stałych współczynnikach. Jego
równaniem charakterystycznym jest równanie: r
2
+ ar + b = 0
(*). Rozwiązanie równania różniczkowego jest w zależności od
pierwiastków równania (*):
- dwa pierwiastki rzeczywiste (r
1
, r
2
) to rozwiązanie ogólne:
C
1
e
r1x
+ C
2
e
r2x
- jeden pierwiastek rzeczywisty (r
0
) to RO: C
1
e
r0x
+ C
2
xe
r0x
- pierwiastki zespolone (a+bi, a-bi) to RO: C
1
e
ax
cosbx +
C
2
e
ax
sinbx
66. Równanie liniowe rzędu 2-go o stałych współczynnikach,
niejednorodne. Rozwiązanie metodą uzmiennienia stałych.
Równanie różniczkowe liniowe niejednorodne: y'' + ay' + b =
f(x) można rozwiązać metodą uzmiennienia stałych, czyli stałe
C
1
i C
2
zamienić na funkcje C
1
(x), C
2
(x) które będą spełniały
układ równań:
C'
1
(x)y
1
(x) + C'
2
(x)y
2
(x) = 0
C'
1
(x)y'
1
(x) + C'
2
(x)y'
2
(x) = f(x)
z którego wyliczamy algebraicznie C'
1
, C'
2
, a następnie całkując
C
1
, C
2
.
UWAGA!! współczynnik przy y'' musi być 1. Jeśli nie jest
dzielimy obustronnie przez niego równanie.
Wyszukiwarka
Podobne podstrony:
MATMA 2 ściąga teoria
matma ściaga (grupa 1)22
Teoria matma ściąga
Matma - sciaga, bankowość i finanse - pomoce naukowe
Matma ściąga
matma sciaga, Studia, Matematyka wyższa ;p
matma ściąga czerwona, Matematyka
MATMA- ściąga, Studia
MATMA (sciąga - macierze, Technika Rolnicza i Leśna, Semestr 1, Matematyka
matma ściąga
ściąga matma funkcje trygonomertyczne
Sciaga matma
matma zadania ściaga
ściaga matma pochodna ekstrema fun
sciaga wyk matma
sciąga matma
Wyklady z matematyki II sciaga, MATMA, matematyka, Matma, Matma, Stare, I semestr
sciąga z teorii matma(2)
ściąga Matma II sem
więcej podobnych podstron