MECHANIKA BUDOWLI
Architektura sem. II letni
Warunki równowagi: REAKCJE
dr inż. Marek BARTOSZEK
KTKB p.126 WB
22 marzec 2011
Za wszystkie uwagi odnośnie poniższych wykładów z góry dziękuję.
Jeśli ktoś chciałby wykorzystać te materiały to proszę o kontakt.
www.rb.polsl.pl
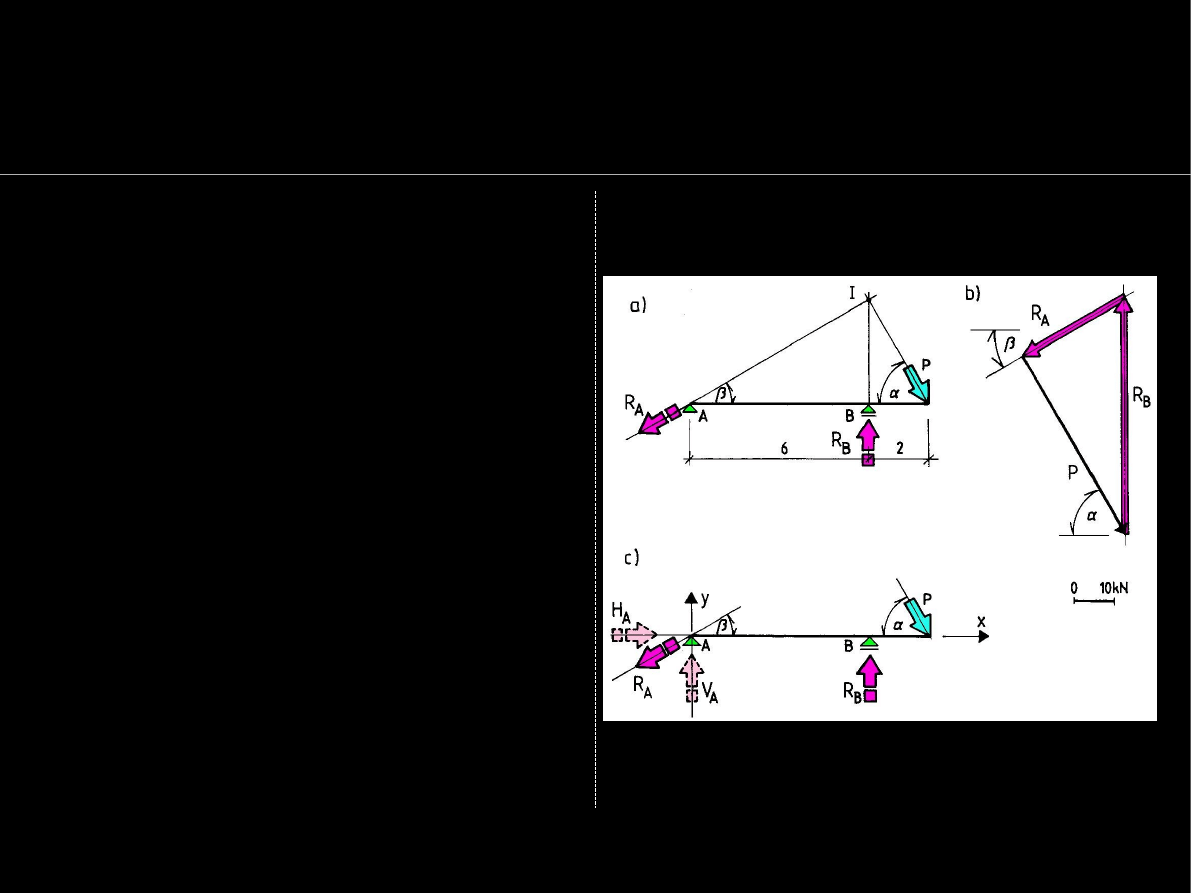
22.03.11
dr inż. Marek Bartoszek
2
Siły działające na konstrukcję
siły czynne i bierne czyli przyczyny i skutki
●
Siły czynne
czyli
obciążenia
działające na
konstrukcję
●
Siły bierne
są to
reakcje
oraz
siły
wewnętrzne
powstające na
skutek działania obciążeń
reakcje
pojawiają się m.in. w
podporach podtrzymujących
konstrukcję
wyznacza się je metodami
mechaniki budowli
22.03.11
dr inż. Marek Bartoszek
3
Równowaga statyczna konstrukcji
●
Statyka
budowli
–
zajmuje się konstrukcjami, na które
– zgodnie z I zasadą
dynamiki Newtona –
działają zrównoważone układy sił
(lub
nie działają żadne siły);
–
takie obiekty pozostają w spoczynku – są
statyczne
(lub
poruszają się ruchem jednostajnym prostoliniowym) .
●
Budowla
– t
o przedmiot inżynierskiej działalności człowieka
na
stale związany z podłożem
(gruntem lub nawet inną budowlą) .
●
Związanie z podłożem
unieruchamia budowlę
odróżniając ją
od
mechanizmów
(Budownictwo nie Wydział Mechaniczny) .
●
Skoro
budowla jest nieruchoma to oznacza, że siły na nią działające
są w równowadze statycznej
, tzn.:
obciążenia zewnętrzne jako siły
czynne są w równowadze z reakcjami podpór, czyli siłami biernymi.
22.03.11
dr inż. Marek Bartoszek
4
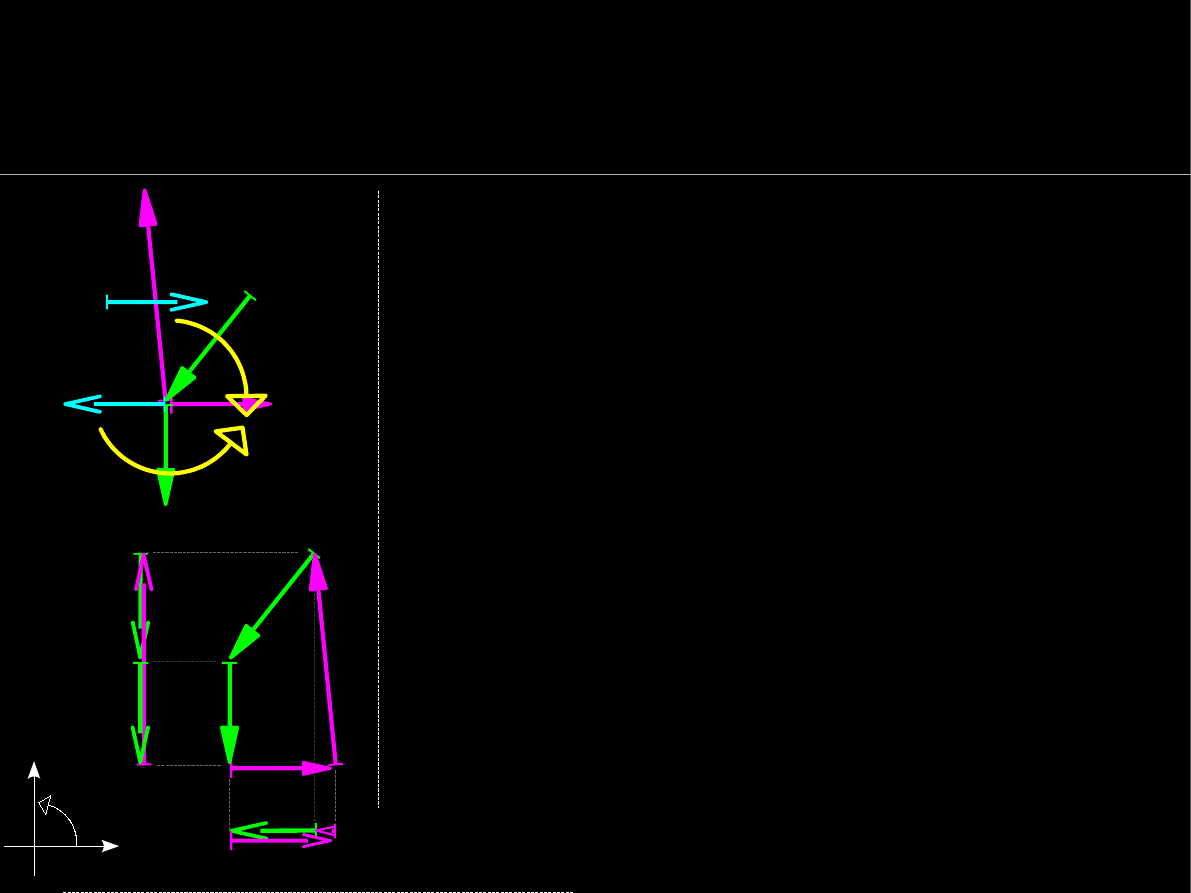
Warunki równowagi statycznej
Rozróżniamy dwa typy warunków równowagi
statycznej sił:
●
Suma rzutów sił na jakiś kierunek, np. oś
OX
„blokująca” możliwość przesuwu ustroju
w danym kierunku. W 2D układa się sumy
rzutów na dwa (np prostopadłe) kierunki.
●
Suma momentów sił względem jakiegoś
punktu, np. punktu A
zapewniająca brak możliwości obrotu
elementu względem tego punktu.
∑
P
y
=
0
∑
M
A
=
0
A
x
y
∑
P
x
=
0
∑
P
y
=
0
22.03.11
dr inż. Marek Bartoszek
5
Warunki równowagi statycznej
Wyznaczanie reakcje podpór
1 element – 3 niewiadome
22.03.11
dr inż. Marek Bartoszek
6
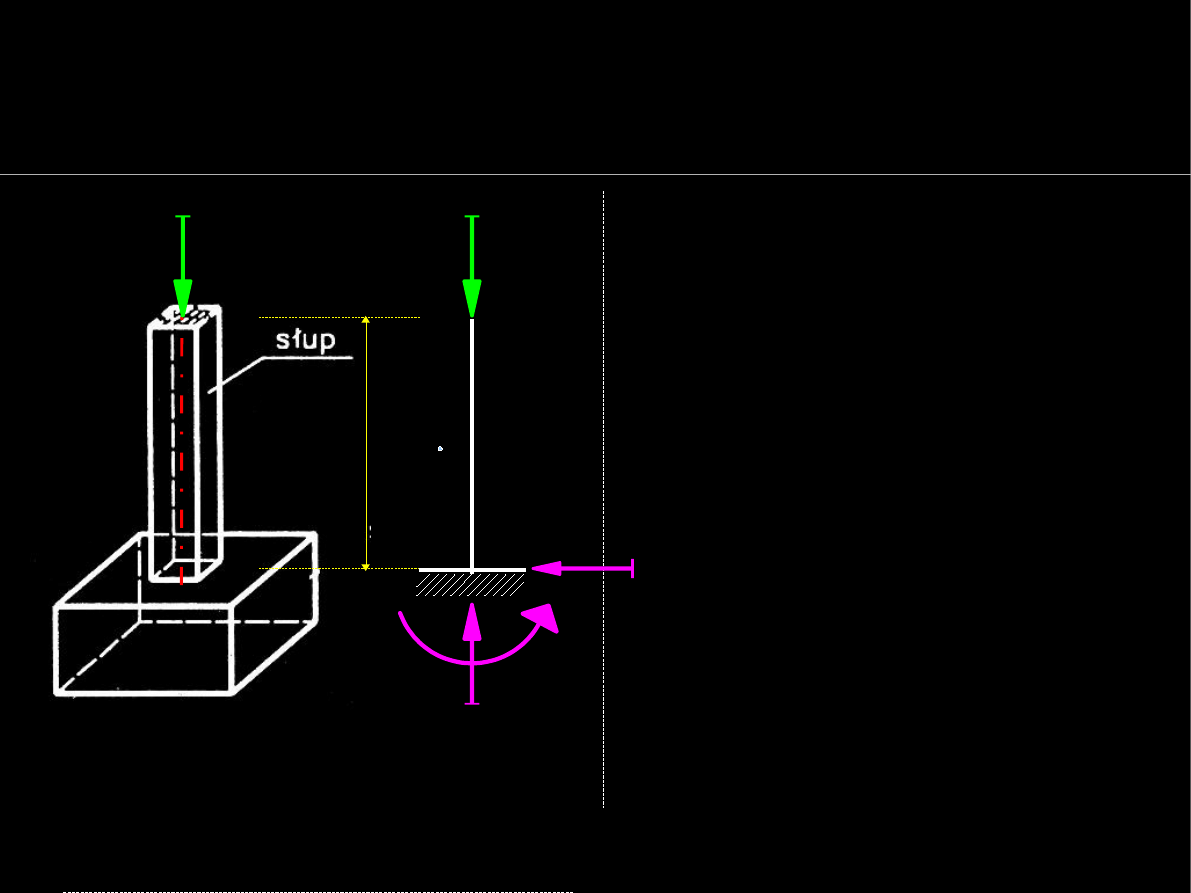
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
P ≈ 2.32 kN
L
P
r=3
H
M
V
A
B
C
Obciążony słup,
zamocowany w
fundamencie i podłożu
Schemat
statyczny z
reakcjami
St. swobody : 1x3=3 st.sw.
Więzy:
r=3
w.zewn.
Równa liczba więzów i stopni
swobody więc można ułożyć
tyle niezależnych równań
równowagi statycznej ile jest
reakcji
podpór. Taki ustrój
nazywamy
statycznie
wyznaczalnym
.
Utwierdzenie w p. A całkowicie
unieruchamia słup więc jest
on też
geometrycznie
niezmienny
.
22.03.11
dr inż. Marek Bartoszek
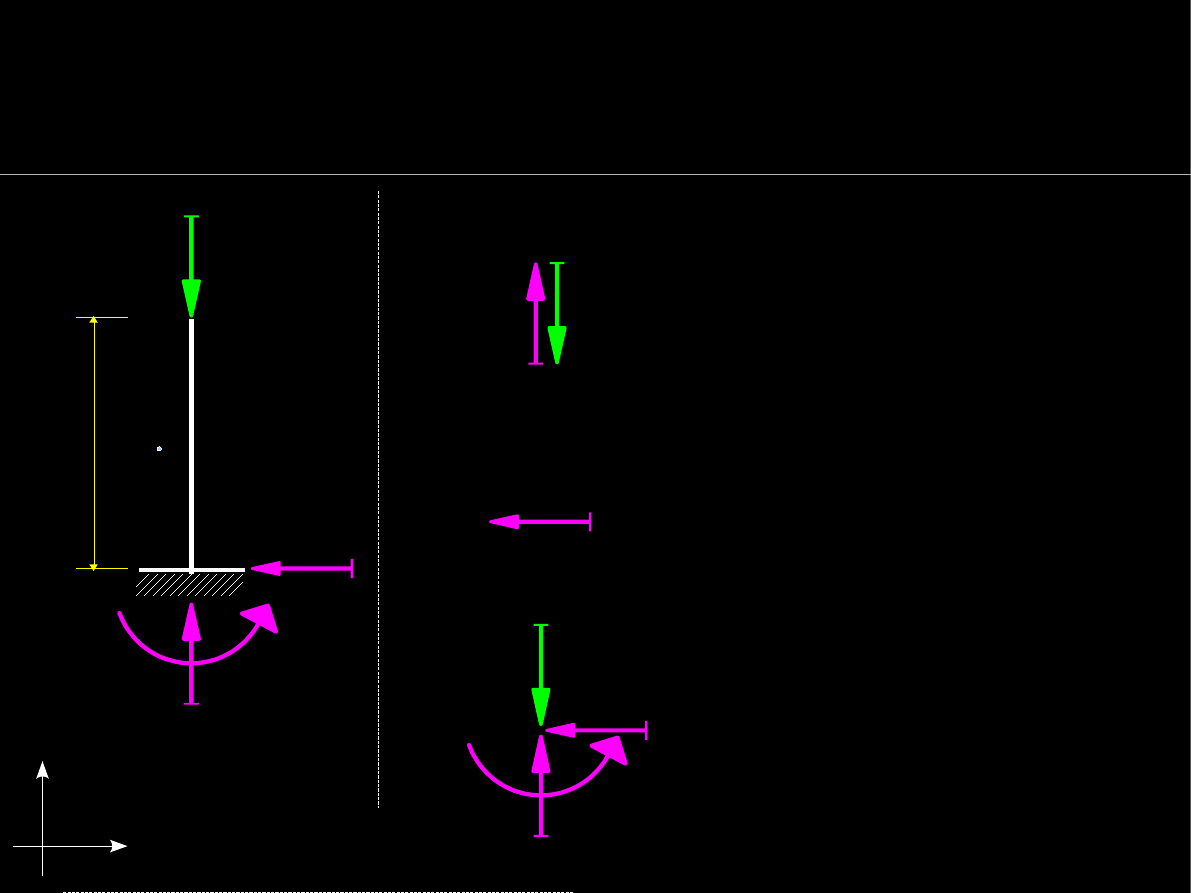
7
●
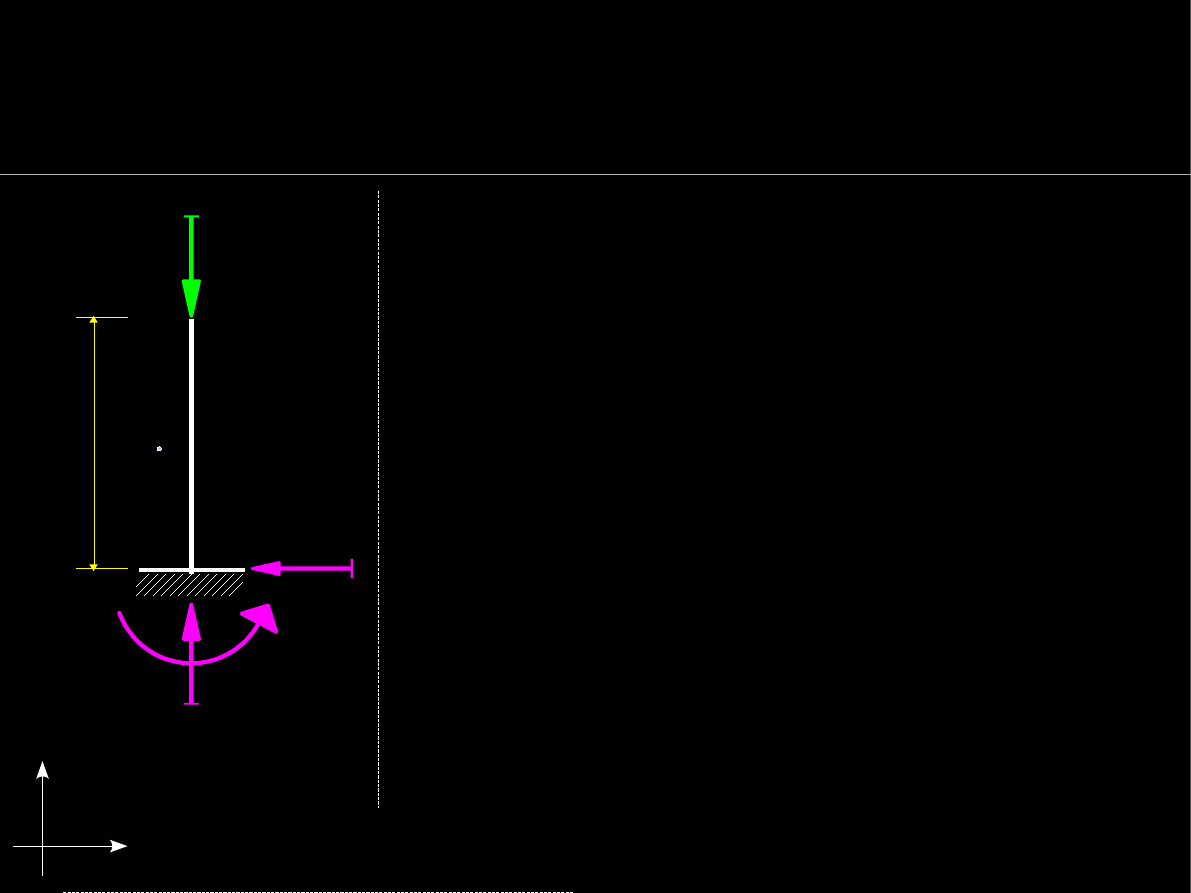
Równowaga w pionie – rzuty sił na OY
(nieruchome
– statyczne w pionie)
V
=
P
●
Równowaga pozioma – rzuty sił na OX
(nieruchome
– statyczne w poziomie)
H
= 0
●
Równowaga momentów względem p. A
(
brak obrotu wokół p. A)
M
= 0
Warunki równowagi statycznej
Równoważenie geometryczne
L
P
r=3
H
M
V
A
B
C
∑
M
A
=
0
x
y
∑
P
y
=
0
∑
P
x
=
0
P
V
H
P
H
M
V
A
22.03.11
dr inż. Marek Bartoszek
8
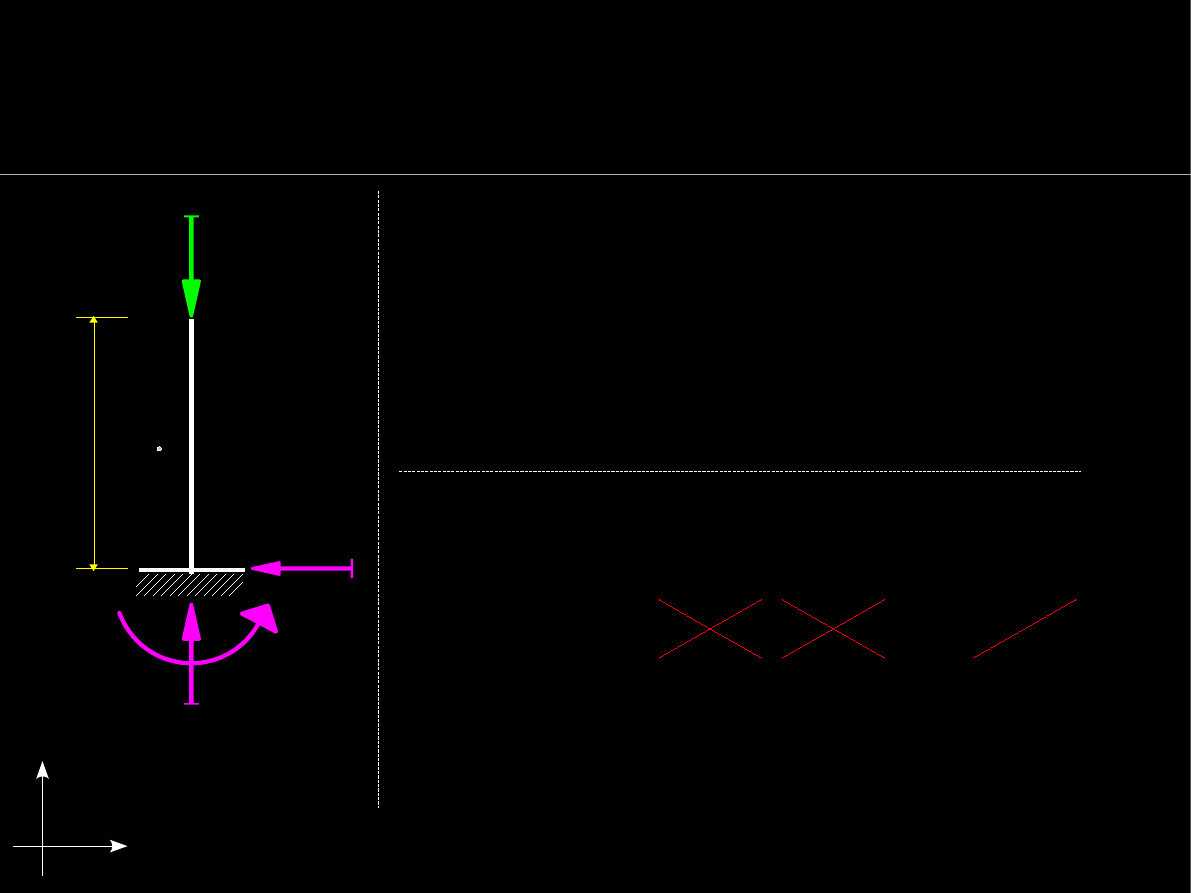
Warunki równowagi statycznej
Wyznaczanie reakcji podpór analitycznie
L
P
r=3
H
M
V
A
B
C
St. swobody : 1x3=3 st. swobody.
Więzy:
r=3
w. zewnętrznych.
Liczba więzów i stopni swobody zgodne!
3 nieznane reakcje więzów
zapewniają
równowagę statyczną sił co do:
●
przesuwu w poziomie – wzdłuż OX
●
przesuwu w pionie – wzdłuż OY
●
Obrotu np. względem punktu A
∑
M
A
=
0
x
y
∑
P
y
=
0
∑
P
x
=
0
22.03.11
dr inż. Marek Bartoszek
9
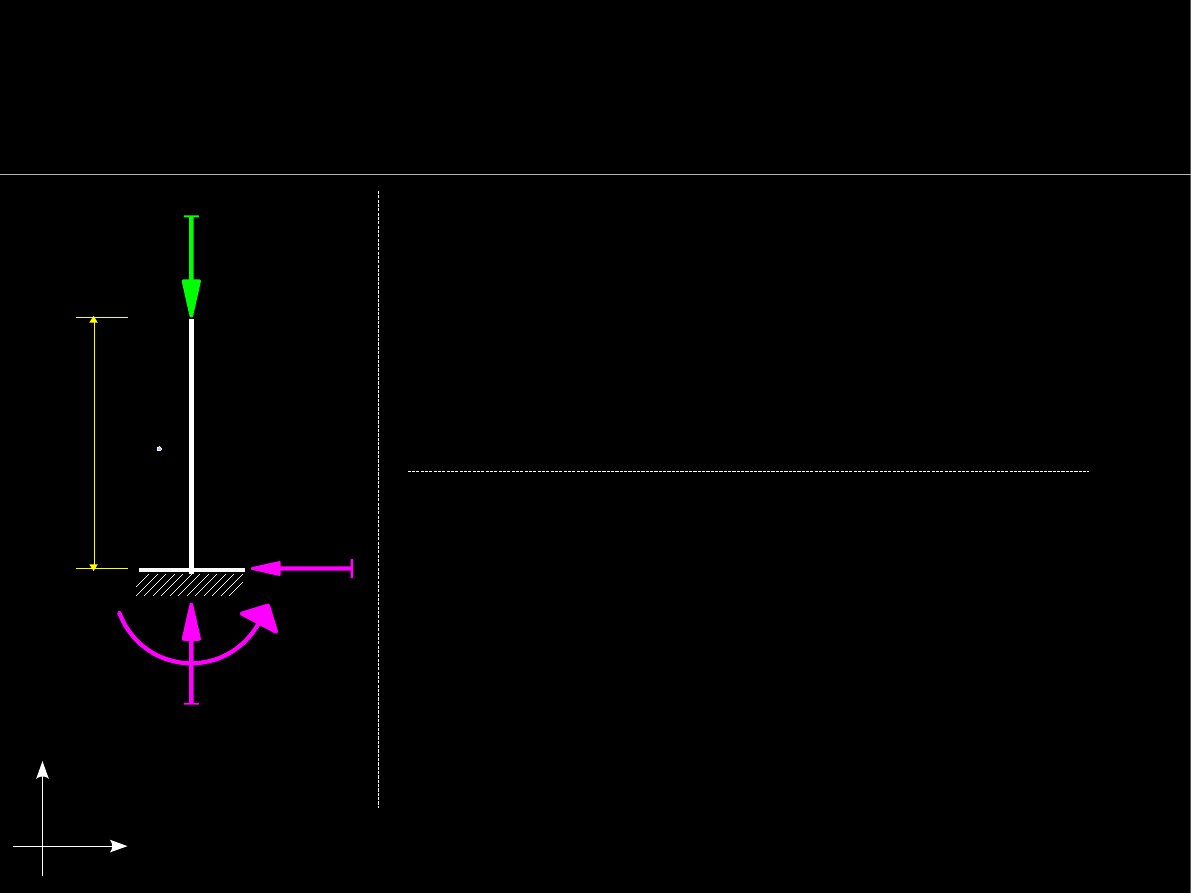
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
Warunek równowagi ze względu na
przesuw w poziomie:
Aby ustrój był w równowadze w poziomie
reakcja
H=0
.
Warunek równowagi ze względu na obrót
względem punktu A:
Aby ustrój nie obracał się moment
podporowy
M=0
.
∑
P
x
=
0:
∑
M
A
=
0 :
−
H =0
H∗0V ∗0M =P∗0
L
P
r=3
H
M
V
A
B
C
x
y
22.03.11
dr inż. Marek Bartoszek
10
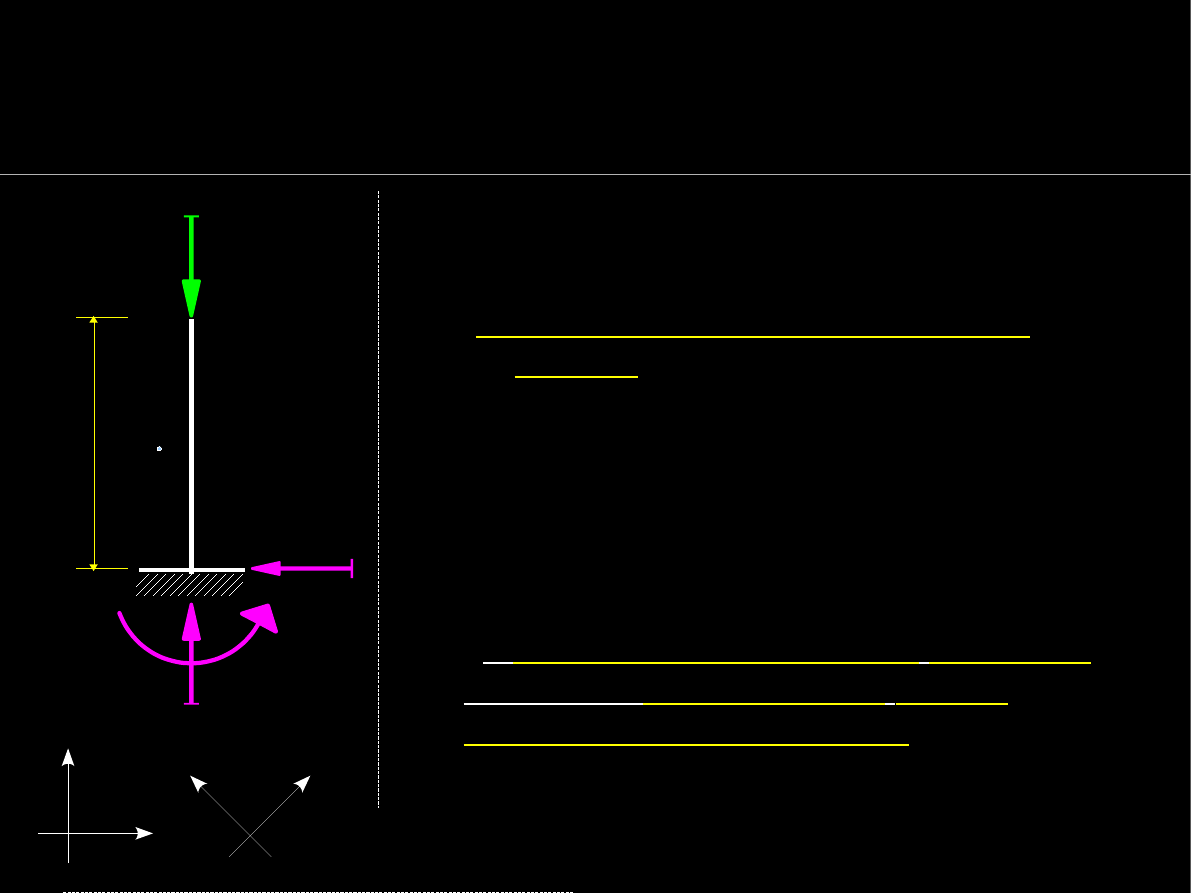
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
Warunek równowagi ze względu na
przesuw w pionie:
Aby ustrój był w równowadze w pionie
reakcja
V=P
.
∑
P
y
=
0 :
V − P=0
H i M zerują się więc mamy
równowagę
dwóch sił
P i V, która zachodzi gdy
zgodnie z II. zasadą statyki dwie siły
:
•
leżą na jednej linii,
•
są równe co do wartości,
•
są przeciwnie skierowane.
L
P
r=3
H
M
V
A
B
C
x
y
22.03.11
dr inż. Marek Bartoszek
11
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
L
P
r=3
H
M
V
A
B
C
Można użyć innych 3 war. równ.
W 2D dla
całego ustroju niezależne są tylko 3
, np.:
●
sumy rzutów sił tylko na 2 dowolne
kierunki
oraz sumę momentów :
lub 2 sumy momentów oraz sumę rzutów
sił na jakiś jeden kierunek
lub 3
warunki sumy momentów
względem
dowolnych
trzech punktów
ale nie
leżących na jednej prostej
.
O wyborze decyduje prostota rozwiązania.
∑
P
=
0 ∑ P
=
0 ∑ M
C
=
0
∑
M
A
=
0 ∑ M
C
=
0 ∑ P
y
=
0
x
y
∑
M
A
=
0 ∑ M
B
=
0 ∑ M
C
=
0
ξ
η
22.03.11
dr inż. Marek Bartoszek
12
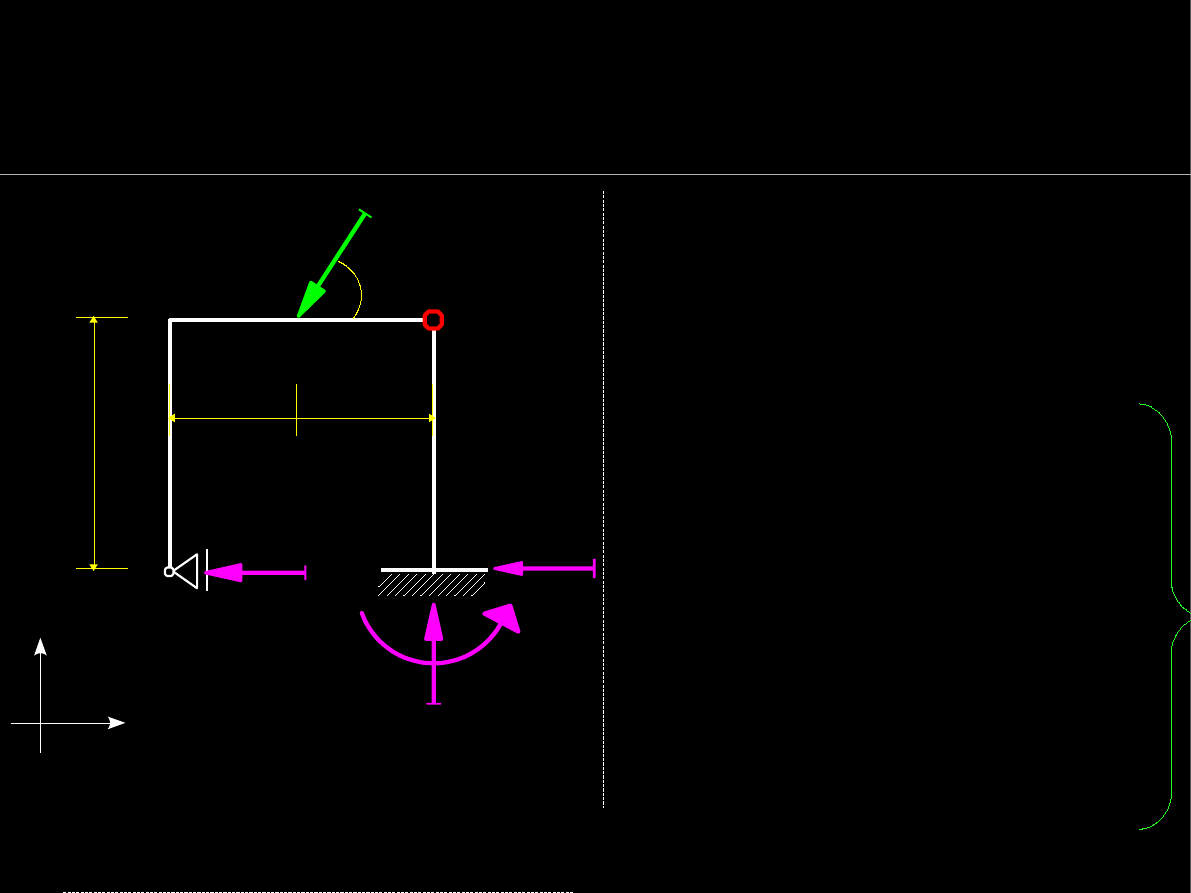
Warunki równowagi statycznej
Wyznaczanie reakcje podpór
2 elementy – 4 niewiadome
22.03.11
dr inż. Marek Bartoszek
13
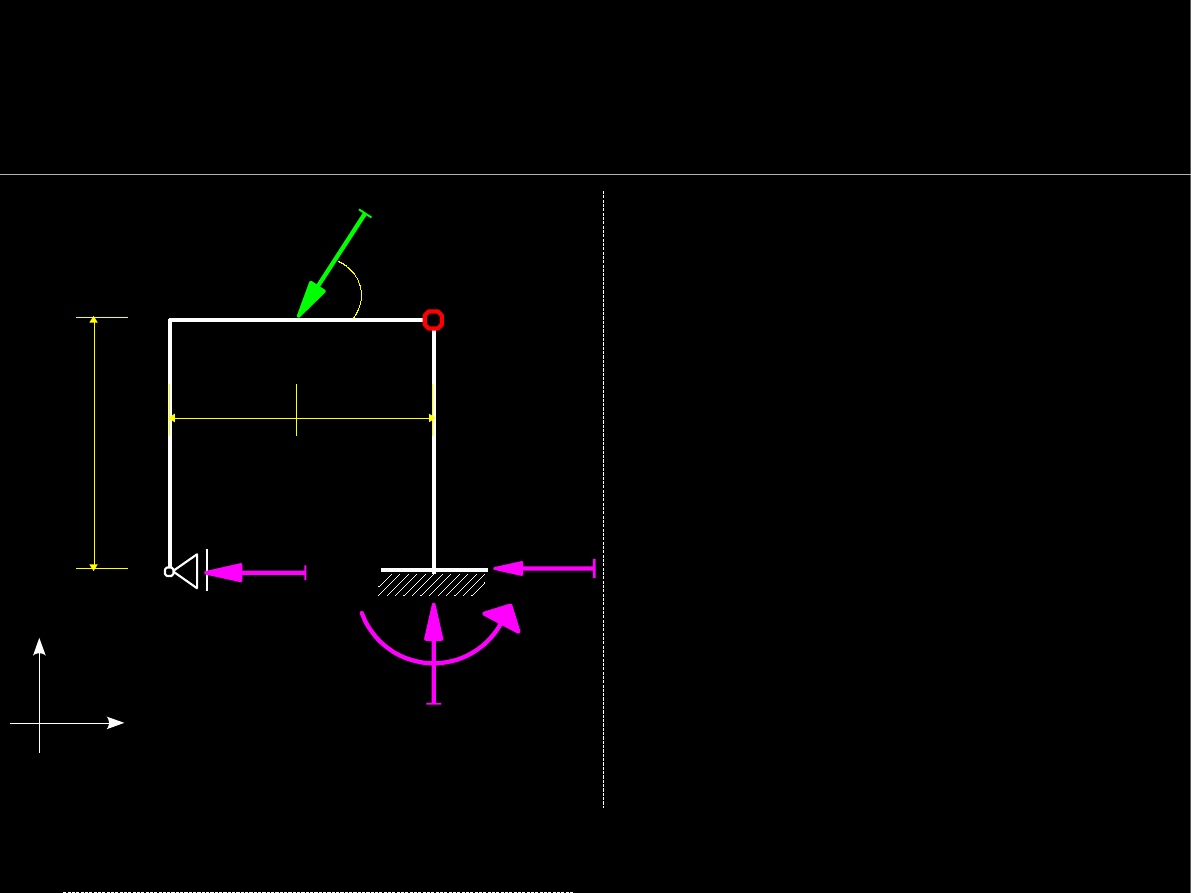
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
Schemat statyczny ramy
statycznie
wyznaczalnej
i
geom. niezmiennej
W=3*e-(
2*p
+
r
)=3*2-(
2*1
+
4
)=0
Warunek konieczny
statycznej
wyznaczalności
spełniony:
zgodna liczba więzów i stopni swobody
.
Słup AB
jest
sztywno
zamocowany
w podporze
A
więc jest
geom. niezmienny
.
Element BCD
jest oparty na
nieruchomym słupie
(
przegub B -
2 więzy
) a
możliwość obrotu wokół
p. B
blokuje trzeci więz
w
podporze przesuwnej
D
=>
element
geom. niezmienny
.
L
P
r=3
H
A
M
V
A
B
C
D
H
D
r=1
p=1
L/2
L/2
e2
e1
α
x
y
22.03.11
dr inż. Marek Bartoszek
14
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
Schemat statyczny ramy
statycznie
wyznaczalnej
i
geom. niezmiennej
Ustrój ma
4 nieznane reakcje
więzów zewn., które można
wyznaczyć
z
war
unków
rów
nowagi
statycznej
.
Dla
całej konstrukcji są zawsze
tylko 3 niezależne warunki
równowagi.
Skąd czwarty?
Przegub
umożliwia obrót
jednego elementu względem
drugiego. Jeśli ustrój ma być
w równowadze statycznej, to
nie może dojść do obrotu!
Stąd
dodatkowy warunek sumy
momentów dla części ustroju
względem
przegubu B
.
L
P
r=3
H
A
M
V
A
B
C
D
H
D
r=1
p=1
L/2
L/2
e2
e1
α
x
y
22.03.11
dr inż. Marek Bartoszek
15
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
Schemat statyczny ramy
statycznie
wyznaczalnej
i
geom. niezmiennej
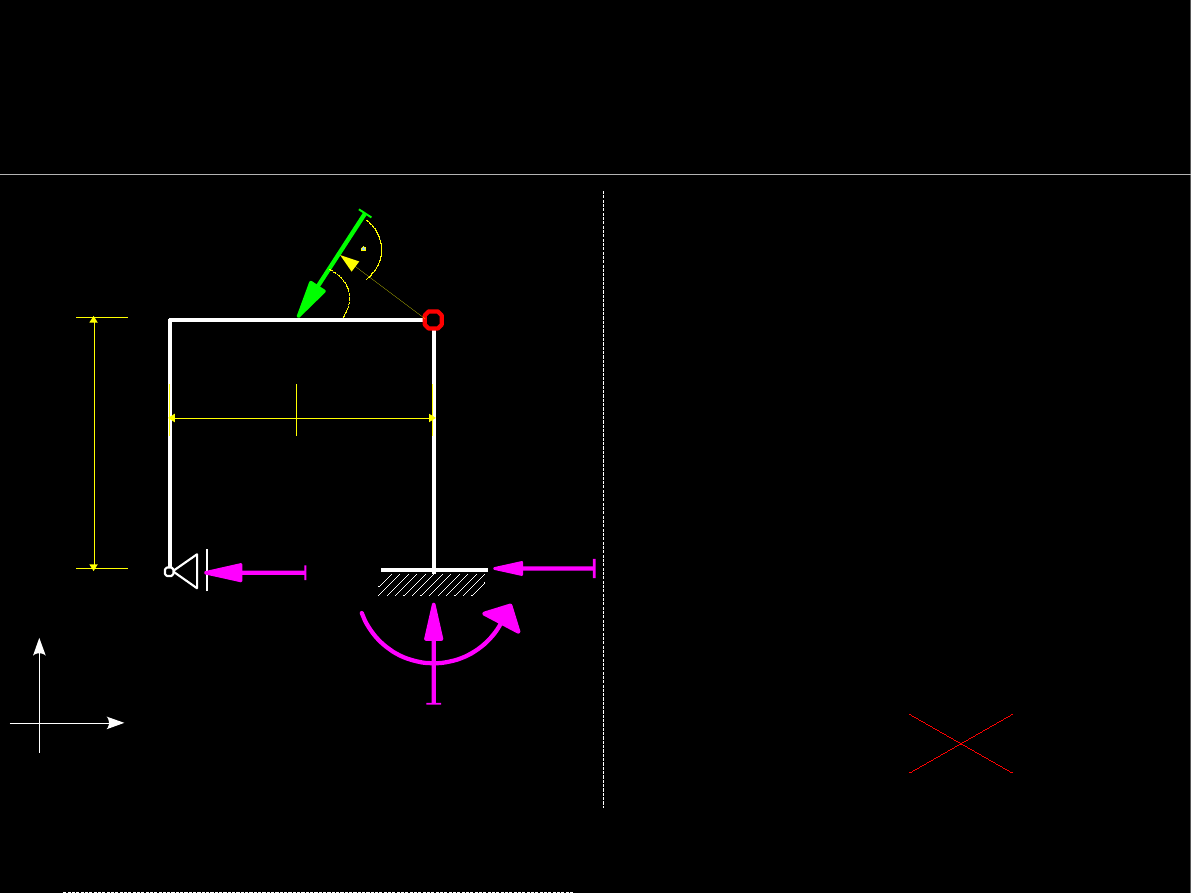
Jak ułożyć
warunek sumy
momentów dla części ustroju
względem
przegubu B
?
Przegub musi dzielić ustrój na
dwie, oddzielne części.
Zapisujemy warunek sumy
momentów względem punktu
B ale
bierzemy pod uwagę
tylko siły po jednej ze stron
od przegubu
- np.:
●
(od strony A)
(od strony C)
L
P
r=3
H
A
M
V
A
B
C
D
H
D
r=1
p=1
r
α
L/2
L/2
e2
e1
4 reakcje
nieznane
x
y
∑
M
B
A
=
0 :
H
A
∗
L−V ∗0−M =0
∑
M
B
C
=
0 :
H
D
∗
L−P∗r=0
22.03.11
dr inż. Marek Bartoszek
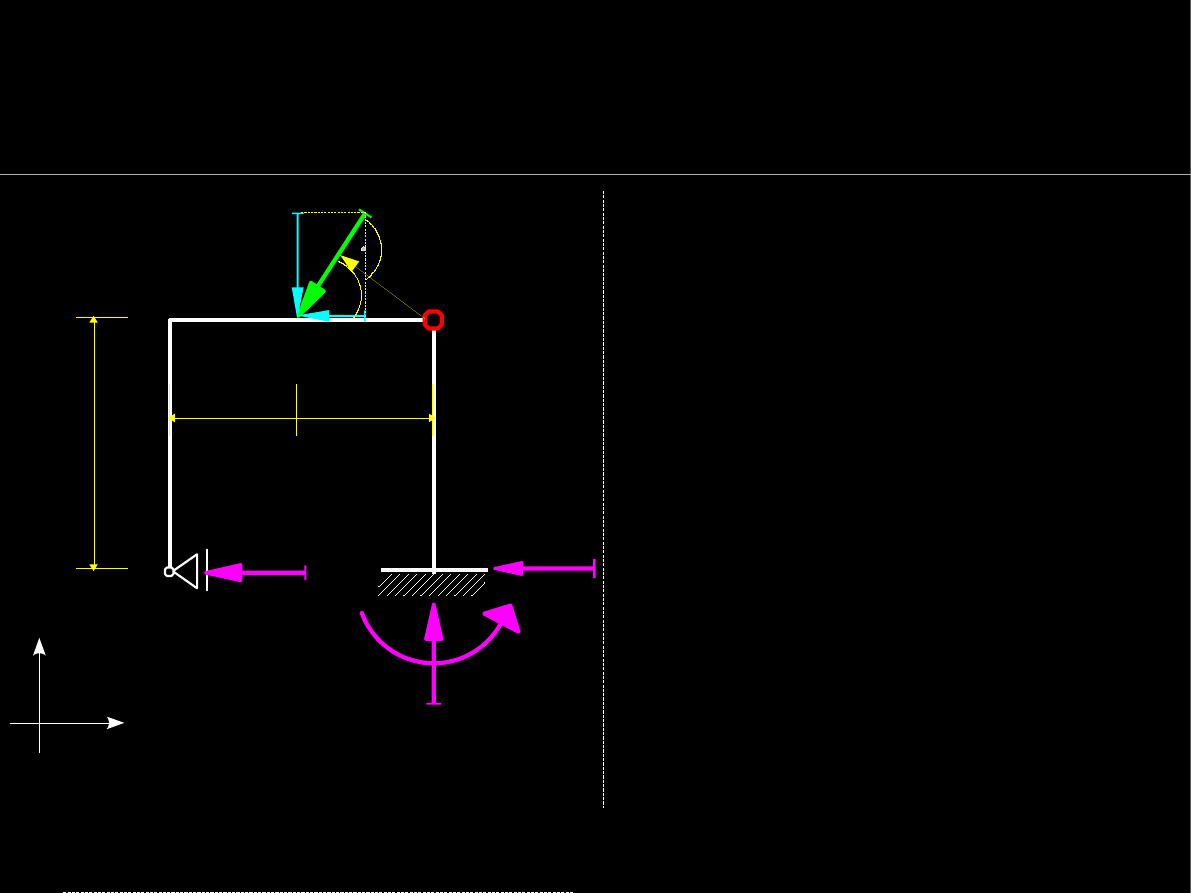
16
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
Schemat statyczny ramy
statycznie
wyznaczalnej
i
geom. niezmiennej
Mamy do wyboru dwa warunki:
wybierzmy drugi, w którym
mamy tylko 1 nieznaną
reakcję
H
D
.
Pierwszy warunek można
później będzie użyć np. do
wyznaczenia
M
, ale wtedy
nie będzie można już użyć
3-go war-ku sumy
momentów
dla całej ramy
wzgl.
p. B
!
L
P
r=3
H
A
M
V
A
B
C
D
H
D
r=1
p=1
r
α
L/2
L/2
e2
e1
4 reakcje
nieznane
x
y
∑
M
B
A
=
0 :
H
A
∗
L−V ∗0−M =0
∑
M
B
C
=
0 :
H
D
∗
L−P∗r=0
22.03.11
dr inż. Marek Bartoszek
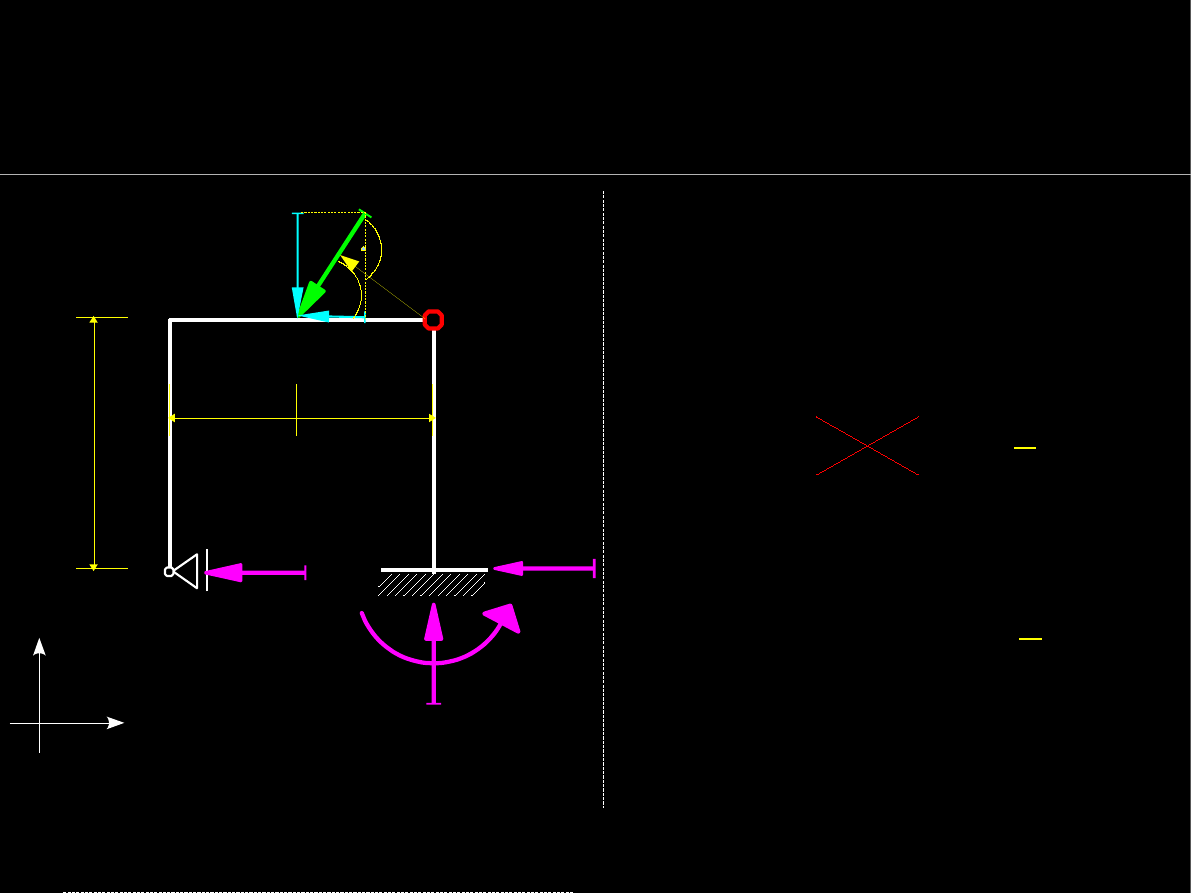
17
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
Schemat statyczny ramy
statycznie
wyznaczalnej
i
geom. niezmiennej
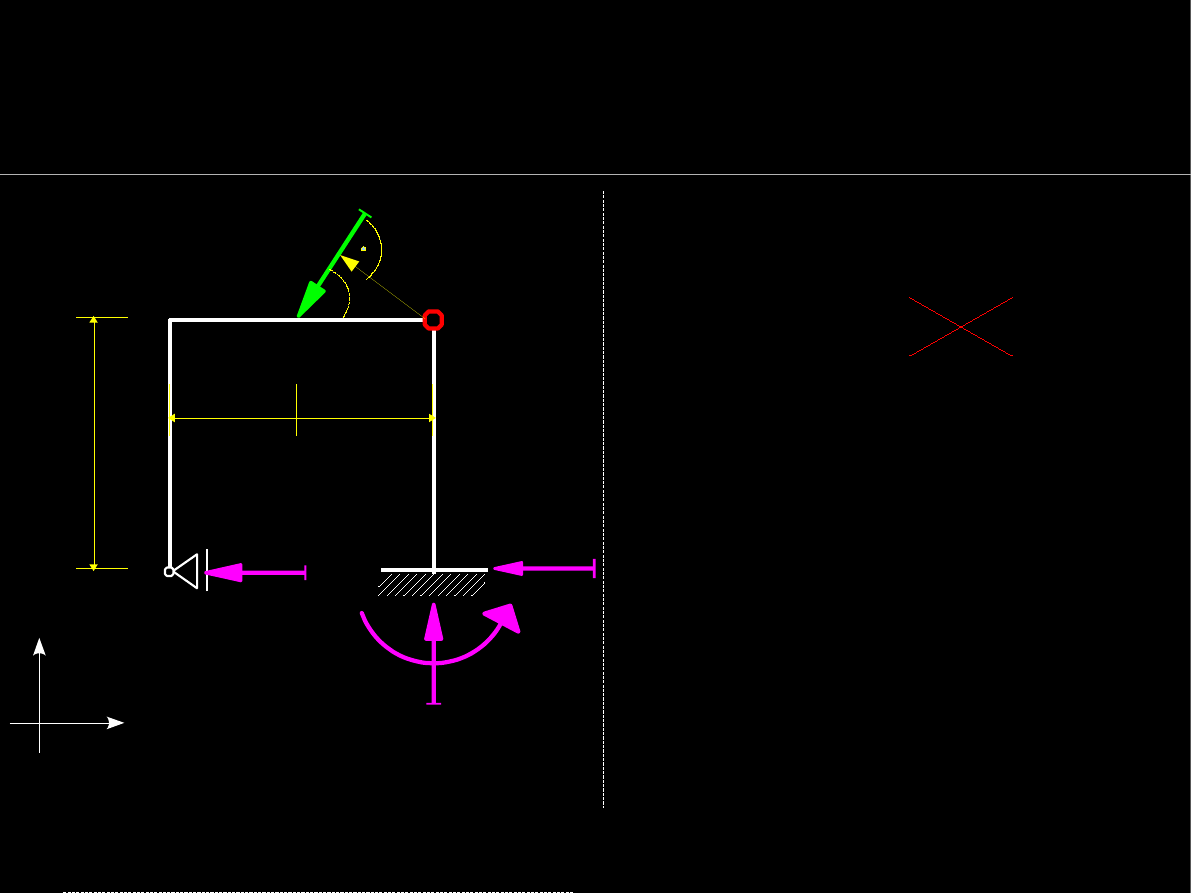
W wybranym warunku sumy M
występuje odległość punktu
B
od siły
P
– promień r
:
Możemy obliczyć „r” albo
rozłożyć siłę P na
składowe
P
x
i P
y
korzystając z
I zasady
statyki (zas.równoległoboku):
Dowolne dwie siły
przechodzące przez jeden
punkt są składowymi ich
wypadkowej
działającej na
ten sam punkt, będącej
sumą
ich wektorów
(wektorową)
.
L
P
r=3
H
A
M
V
A
B
C
D
H
D
P
y
P
x
r=1
p=1
r
L/2
L/2
e2
e1
α
4 reakcje
nieznane
x
y
∑
M
B
C
=
0 :
H
D
∗
L−P∗
r
=
0
22.03.11
dr inż. Marek Bartoszek
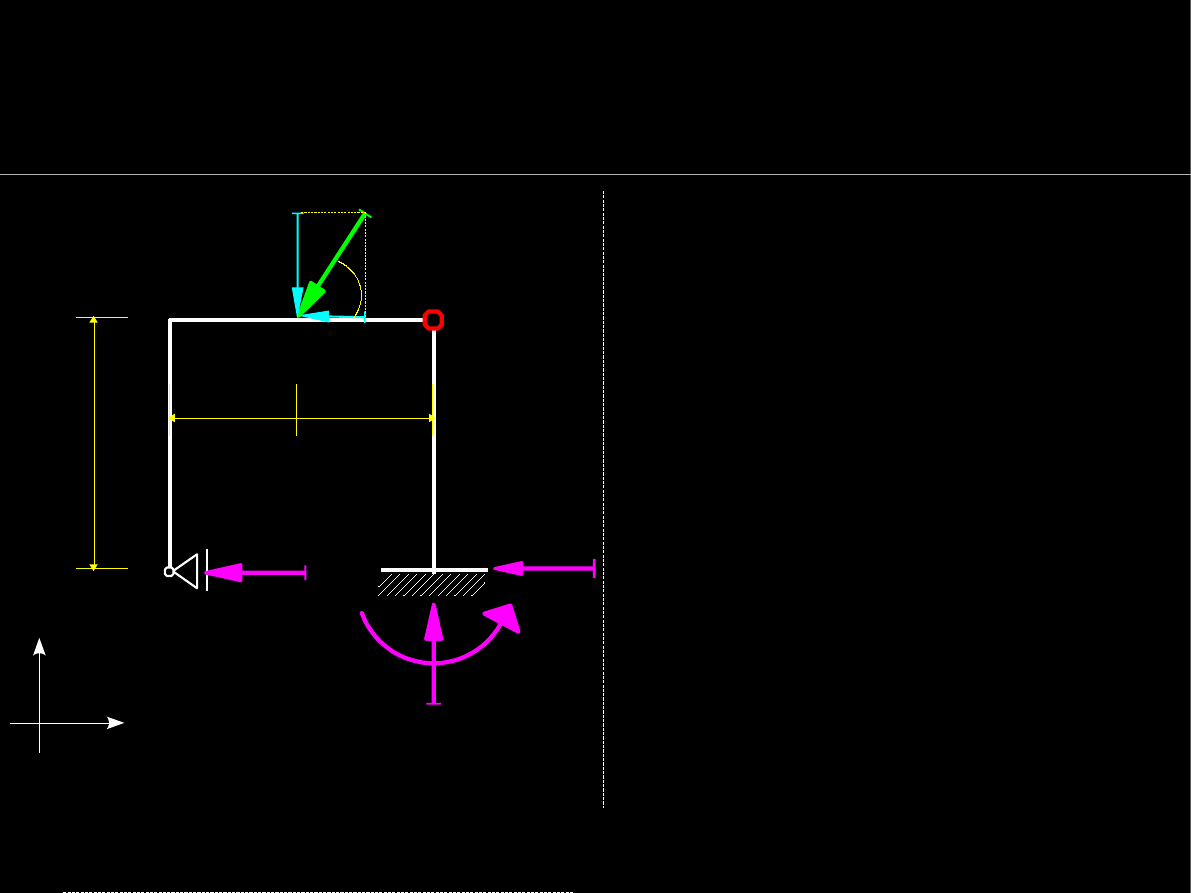
18
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
Schemat statyczny ramy
statycznie
wyznaczalnej
i
geom. niezmiennej
Równanie
można więc zapisać w
alternatywnej postaci :
Podstawiając
P
y
lub r otrzymamy
to samo równanie:
Teraz należy ułożyć brakujące
trzy równania, aby oprócz
H
D
wyznaczyć także pozostałe
niewiadome:
H
A
, M, V
.
L
P
r=3
H
A
M
V
A
B
C
D
H
D
P
y
P
x
r=1
p=1
r
L/2
L/2
e2
e1
α
4 reakcje
nieznane
x
y
∑
M
B
C
=
0 :
H
D
∗
L−P∗
r
=
0
H
D
∗
L−P
x
∗
0−P
y
∗
L
2
=
0
H
D
∗
L−P∗sin ∗
L
2
=
0
22.03.11
dr inż. Marek Bartoszek
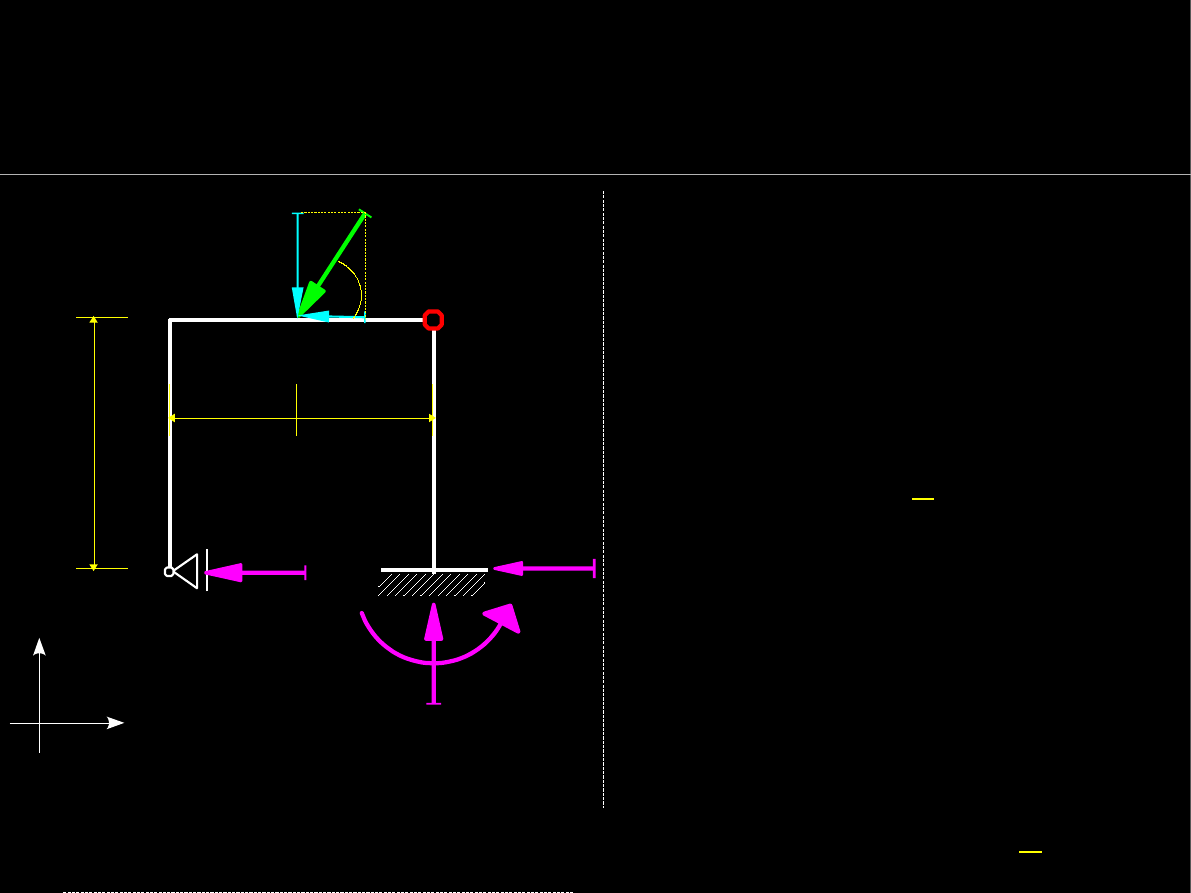
19
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
Schemat statyczny ramy
statycznie
wyznaczalnej
i
geom. niezmiennej
Unikając układu 4 równań z 4
niewiadomymi szukamy
prostych równań z jedną
niewiadomą :
(
M
i
H
A
)
(
M
i
H
A
,
H
D
, P)
(
M
, P)
(
!
)
(
H
A
i
H
D
, P
x
)
(
?
)
(
V
, P
y
)
(
!
)
L
P
r=3
H
A
M
V
A
B
C
D
H
D
P
y
P
x
r=1
p=1
L/2
L/2
e2
e1
α
4 reakcje
nieznane
x
y
∑
M
B
A
=
0 :
∑
M
B
=
0 :
∑
M
A
=
0 :
∑
P
x
=
0:
∑
P
y
=
0 :
22.03.11
dr inż. Marek Bartoszek
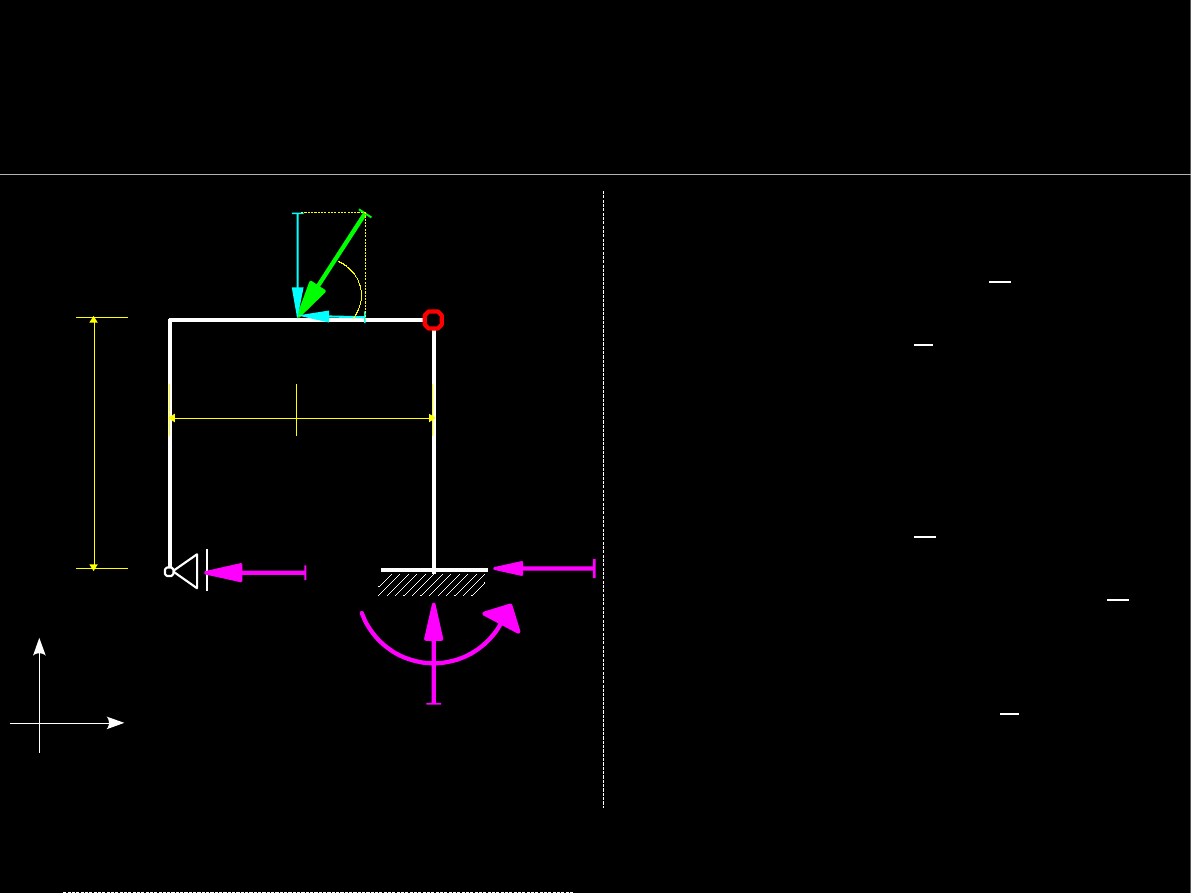
20
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
Schemat statyczny ramy
statycznie
wyznaczalnej
i
geom. niezmiennej
Równania z jedną niewiadomą
i/lub najprostsze:
oraz wybrana suma momentów
dla części ustroju:
L
P
r=3
H
A
M
V
A
B
C
D
H
D
P
y
P
x
r=1
p=1
L/2
L/2
e2
e1
α
4 reakcje
nieznane
x
y
V −P
y
=
0 ⇒ V =P
y
∑
M
A
=
0 :
∑
P
x
=
0:
∑
P
y
=
0 :
P
x
∗
LP
y
∗
L
2
M =0
H
D
H
A
−
P
x
=
0
∑
M
B
C
=
0 :
H
D
∗
L−P∗sin ∗
L
2
=
0
22.03.11
dr inż. Marek Bartoszek
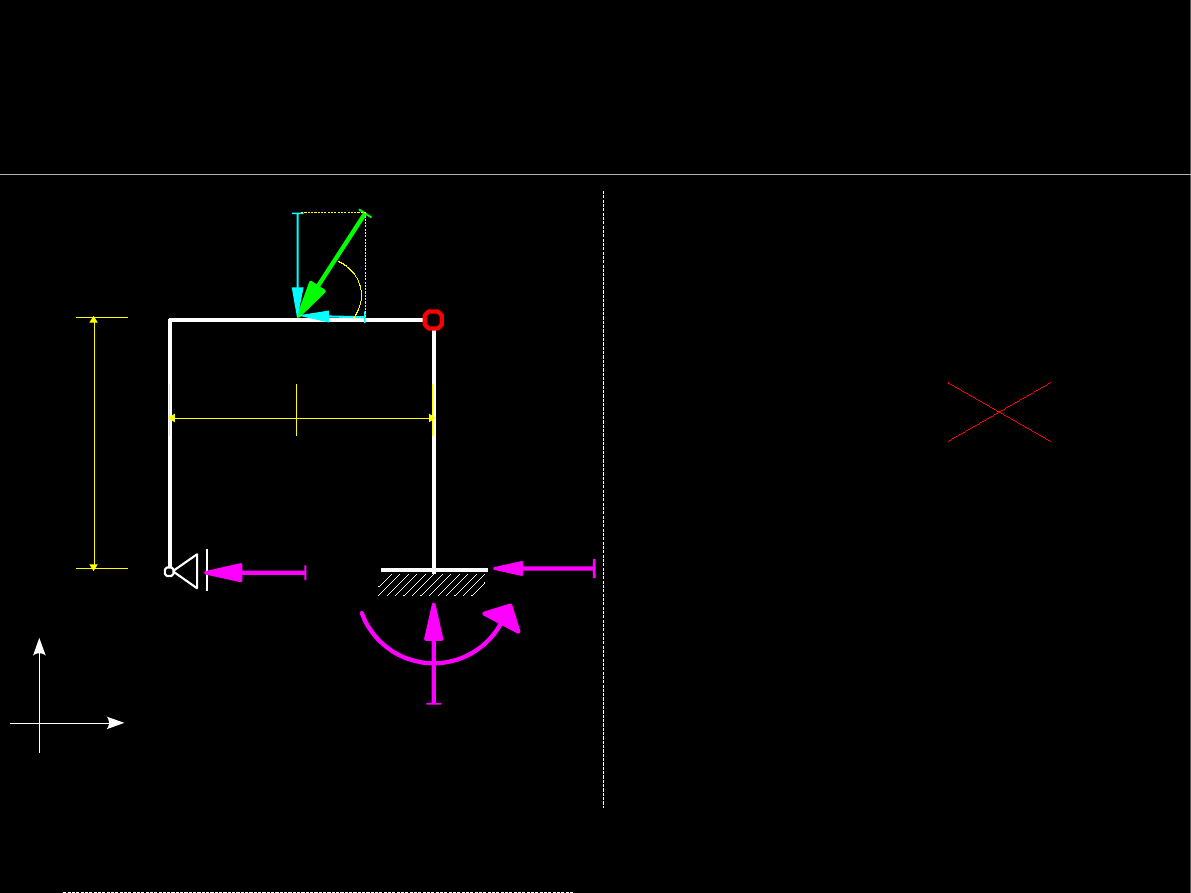
21
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
Schemat statyczny ramy
statycznie
wyznaczalnej
i
geom. niezmiennej
Wyznaczmy reakcje:
L
P
r=3
H
A
M
V
A
B
C
D
H
D
P
y
P
x
r=1
p=1
L/2
L/2
e2
e1
α
x
y
V −P
y
=
0 ⇒ V =P
y
P
x
∗
LP
y
∗
L
2
M =0
P∗cos∗LP∗sin ∗
L
2
M =0
M =−P∗L∗[cos
1
2
∗
sin ]
H
D
H
A
−
P
x
=
0 ⇒
H
A
=
P
x
−
H
D
V −P
y
=
0 ⇒ V =P
y
H
D
∗
L−P∗sin ∗
L
2
=
0 ⇒
⇒
H
D
=
P∗
1
2
∗
sin
22.03.11
dr inż. Marek Bartoszek
22
Warunki równowagi statycznej
Wyznaczanie reakcji podpór
Schemat statyczny ramy
statycznie
wyznaczalnej
i
geom. niezmiennej
Sprawdzenie równaniami nie
wykorzystanymi – np. :
Są one zależne od poprzed-ich.
Można też podstawić wyliczone
reakcje do równań, z których
je otrzymaliśmy. Jednak w
ten sposób nie sprawdzimy
poprawności ułożonych
równań tylko dalsze ich
przekształcenia.
L
P
r=3
H
A
M
V
A
B
C
D
H
D
P
y
P
x
r=1
p=1
L/2
L/2
e2
e1
α
x
y
∑
M
B
A
=
0 :
H
A
∗
L−M V ∗0=0
22.03.11
dr inż. Marek Bartoszek
23
DZIEKUJĘ ZA UWAGĘ
KONIEC wykładu