Metody Numeryczne cz.4

1

METODY NUMERYCZNE

część 4

Dr inż. Ziemowit Ostrowski

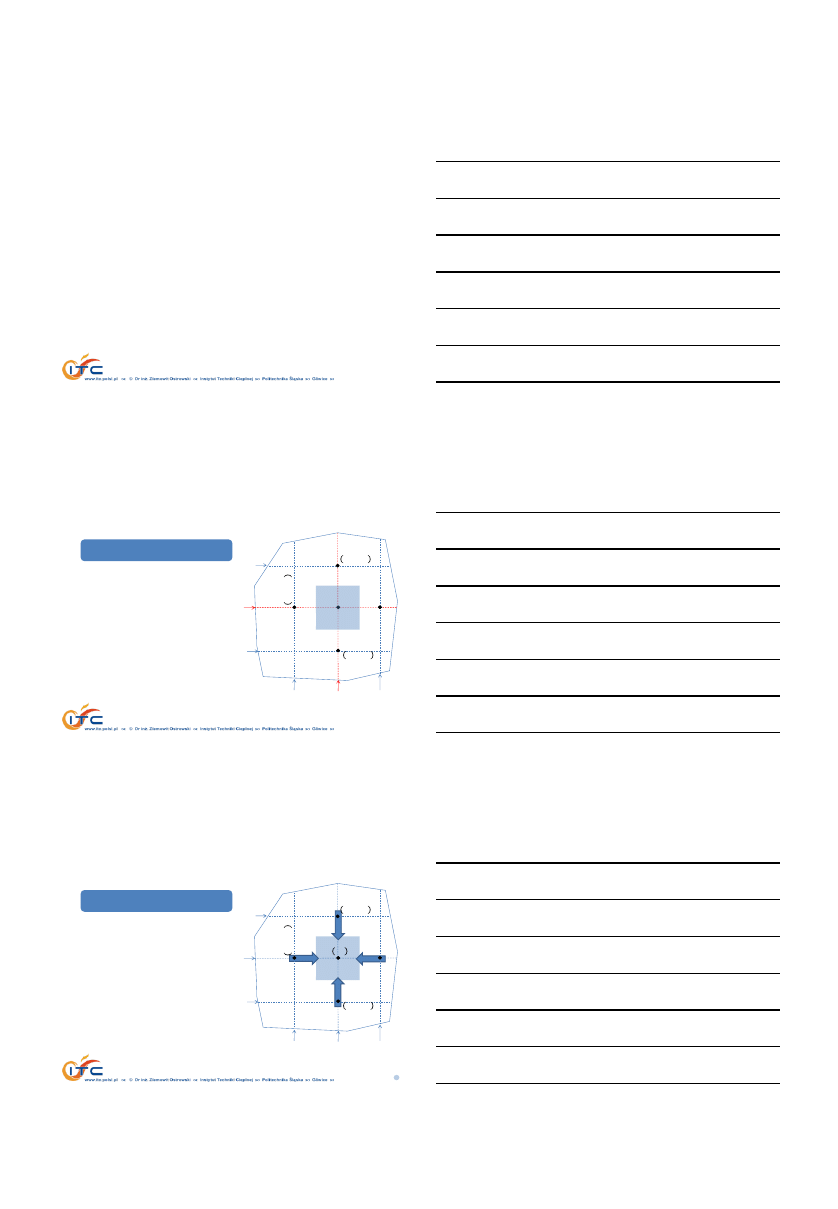
METODA BILANSÓW ELEMENTARNYCH

Bilans energii, 2D

dla objętości związanej z

𝑖

,j

−tym węzłem

𝑖 − 1

𝑖

𝑖 + 1

𝑗 + 1

𝑗

𝑗 − 1

2𝐷, 𝜆, 𝑞

𝑣

𝑖, 𝑗 + 1

𝑖−

1,

𝑗

(𝑖

+

1,

𝑗)

𝑖, 𝑗 − 1

𝑄

𝜆,𝑃

METODA BILANSÓW ELEMENTARNYCH

𝑖, 𝑗

𝑖 − 1 𝑖 𝑖 + 1

𝑖, 𝑗 + 1

𝑗 + 1

𝑗

𝑗 − 1

2𝐷, 𝜆, 𝑞

𝑣

𝑄

𝜆,𝐿

Bilans energii, 2D

dla objętości związanej z
𝑖, 𝑗−tym węzłem

𝑞

𝑣

𝑖−

1,

𝑗

(𝑖

+

1,

𝑗)

𝑖, 𝑗 − 1

𝑄

𝜆,𝐺

𝑄

𝜆,𝐷

Metody Numeryczne cz.4

2

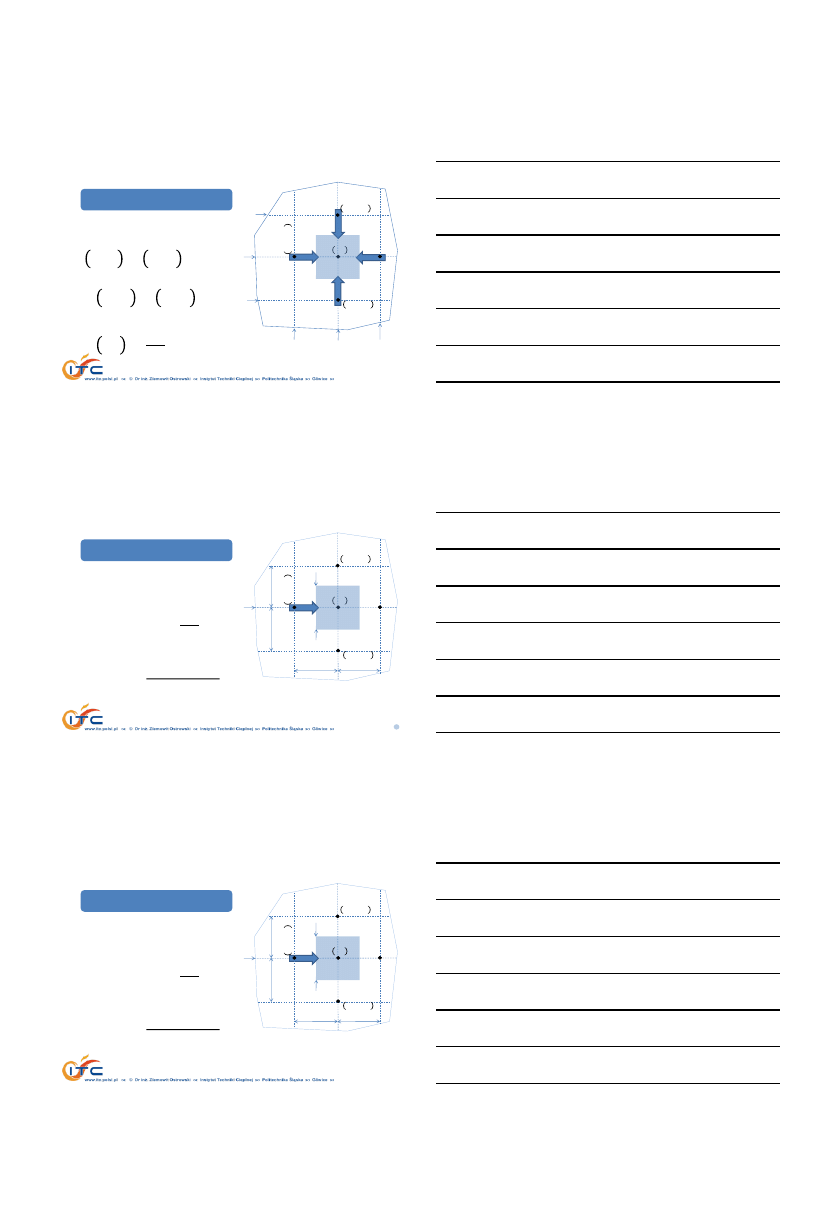
METODA BILANSÓW ELEMENTARNYCH

dla objętości związanej z
𝑖, 𝑗−tym węzłem

Bilans energii, 2D

𝑄

𝜆,𝐿

+ 𝑄

𝜆,𝑃

+

+ 𝑄

𝜆,𝐺

+ 𝑄

𝜆,𝐷

+

+ 𝑄

𝑣

=

Δ𝐸

Δ𝜏

= 0

𝑖, 𝑗

𝑖 − 1 𝑖 𝑖 + 1

𝑖, 𝑗 + 1

𝑗 + 1

𝑗

𝑗 − 1

2𝐷, 𝜆, 𝑞

𝑣

𝑄

𝜆,𝐿

𝑞

𝑣

𝑖−

1,

𝑗

(𝑖

+

1,

𝑗)

𝑖, 𝑗 − 1

𝑄

𝜆,𝐺

𝑄

𝜆,𝐷

𝑄

𝜆,𝑃

(stan ustalony)

METODA BILANSÓW ELEMENTARNYCH

Bilans energii, 2D

dla objętości związanej z
𝑖,j−tym węzłem

𝑄

𝜆,𝐿

= 𝜆

𝐴

𝐿

∆𝑇

∆𝑥

=

= 𝜆

∆𝑦

𝑇

𝑖−1,𝑗

− 𝑇

𝑖,𝑗

∆𝑥

𝑖, 𝑗

𝑖, 𝑗 + 1

2𝐷, 𝜆, 𝑞

𝑣

𝑄

𝜆,𝐿

𝑞

𝑣

𝑖−

1,

𝑗

(𝑖

+

1,

𝑗)

𝑖, 𝑗 − 1

∆𝑦

∆𝑦

∆𝑦

∆𝑥

∆𝑥

𝑗

METODA BILANSÓW ELEMENTARNYCH

Bilans energii, 2D

dla objętości związanej z
𝑖,j−tym węzłem

𝑄

𝜆,𝐿

= 𝜆

𝐴

𝐿

∆𝑇

∆𝑥

=

= 𝜆

∆𝑦

𝑇

𝑖−1

,𝑗

− 𝑇

𝑖

,𝑗

∆𝑥

𝑖

, 𝑗

𝑖, 𝑗 + 1

2𝐷, 𝜆, 𝑞

𝑣

𝑄

𝜆,𝐿

𝑞

𝑣

𝑖−

1,

𝑗

(𝑖

+

1,

𝑗)

𝑖, 𝑗 − 1

∆𝑦

∆𝑦

∆𝑦

∆𝑥

∆𝑥

𝑗

Metody Numeryczne cz.4

3

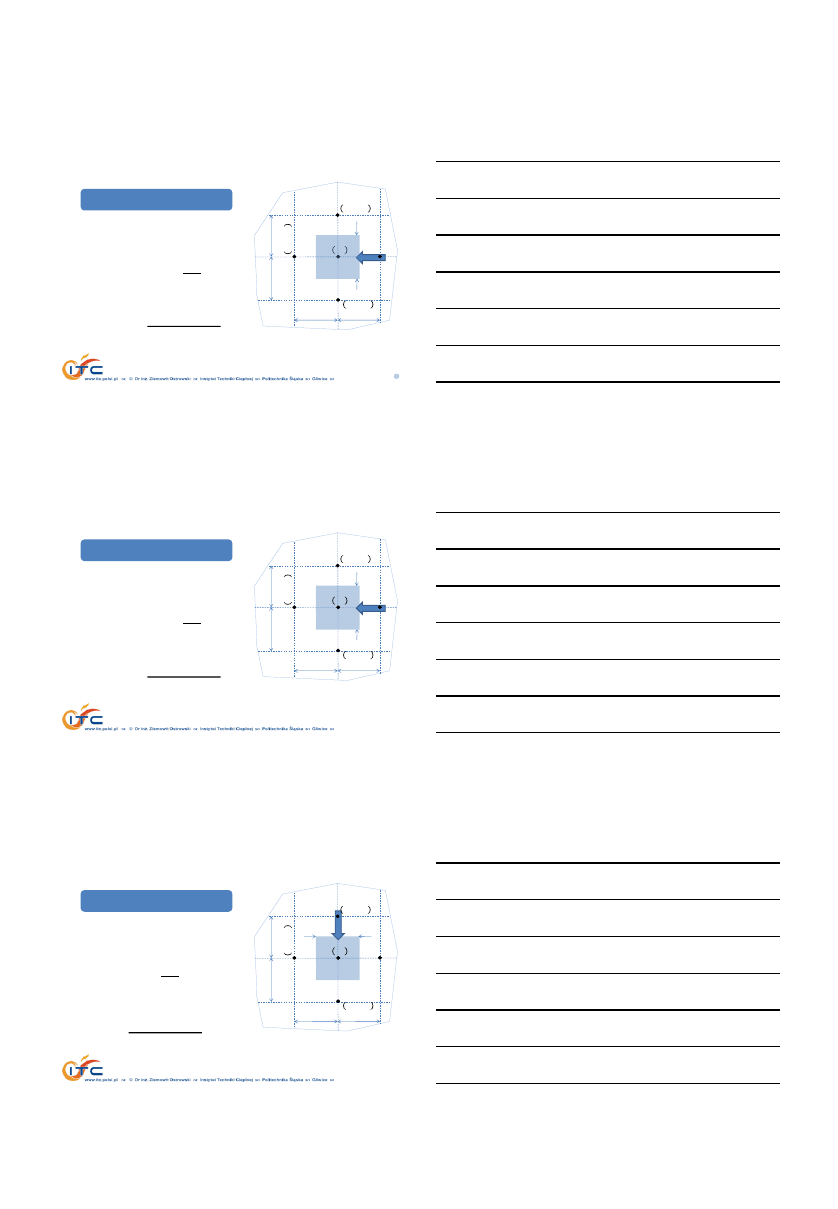
METODA BILANSÓW ELEMENTARNYCH

Bilans energii, 2D

dla objętości związanej z
𝑖,j−tym węzłem

𝑄

𝜆,𝑃

= 𝜆

𝐴

𝑃

∆𝑇
∆𝑥

=

= 𝜆

∆𝑦

𝑇

𝑖+1,𝑗

− 𝑇

𝑖,𝑗

∆𝑥

𝑖, 𝑗

𝑖, 𝑗 + 1

2𝐷, 𝜆, 𝑞

𝑣

𝑞

𝑣

𝑖−

1,

𝑗

(𝑖

+

1,

𝑗)

𝑖, 𝑗 − 1

∆𝑦

𝑄

𝜆,𝑃

∆𝑦

∆𝑦

∆𝑥

∆𝑥

METODA BILANSÓW ELEMENTARNYCH

Bilans energii, 2D

dla objętości związanej z
𝑖,j−tym węzłem

𝑄

𝜆,𝑃

= 𝜆

𝐴

𝑃

∆𝑇
∆𝑥

=

= 𝜆

∆𝑦

𝑇

𝑖+1,

𝑗

− 𝑇

𝑖

,𝑗

∆𝑥

𝑖

, 𝑗

𝑖, 𝑗 + 1

2𝐷, 𝜆, 𝑞

𝑣

𝑞

𝑣

𝑖−

1,

𝑗

(

𝑖+

1,

𝑗)

𝑖, 𝑗 − 1

∆𝑦

𝑄

𝜆,𝑃

∆𝑦

∆𝑦

∆𝑥

∆𝑥

METODA BILANSÓW ELEMENTARNYCH

Bilans energii, 2D

dla objętości związanej z
𝑖,j−tym węzłem

𝑄

𝜆,𝐺

= 𝜆

𝐴

𝐺

∆𝑇
∆𝑦

=

= 𝜆

∆𝑥

𝑇

𝑖,

𝑗+1

− 𝑇

𝑖,

𝑗

∆𝑦

𝑄

𝜆,𝐺

𝑖,

𝑗

∆𝑦

∆𝑦

𝑖,

𝑗 + 1

2𝐷, 𝜆, 𝑞

𝑣

𝑞

𝑣

𝑖−

1,

𝑗

(𝑖

+

1,

𝑗)

𝑖, 𝑗 − 1

∆𝑥

∆𝑥

∆𝑥

Metody Numeryczne cz.4

4

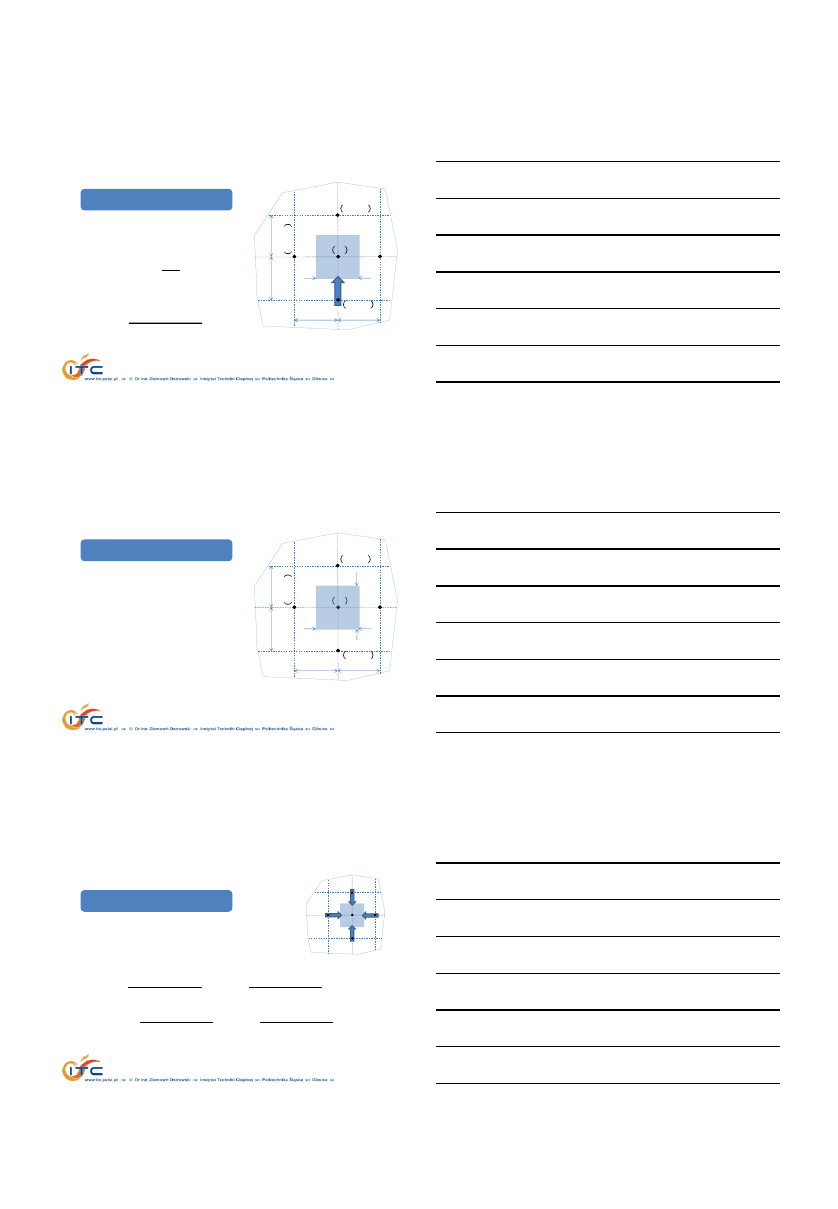
METODA BILANSÓW ELEMENTARNYCH

Bilans energii, 2D

dla objętości związanej z
𝑖, 𝑗−tym węzłem

𝑄

𝜆,𝐷

= 𝜆

𝐴

𝐷

∆𝑇

∆𝑥

=

= 𝜆

∆𝑥

𝑇

𝑖,

𝑗−1

− 𝑇

𝑖,

𝑗

∆𝑦

𝑖,

𝑗

∆𝑦

∆𝑦

𝑖, 𝑗 + 1

2𝐷, 𝜆, 𝑞

𝑣

𝑞

𝑣

𝑖−

1,

𝑗

(𝑖

+

1,

𝑗)

𝑖,

𝑗 − 1

∆𝑥

∆𝑥

∆𝑥

𝑄

𝜆,𝐷

METODA BILANSÓW ELEMENTARNYCH

Bilans energii, 2D

dla objętości związanej z
𝑖, 𝑗−tym węzłem

𝑄

𝑣

= 𝑞

𝑣

𝑉 =

𝑞

𝑣

∆𝑥 ∆𝑦

𝑖, 𝑗

∆𝑦

∆𝑦

𝑖, 𝑗 + 1

2𝐷, 𝜆, 𝑞

𝑣

𝑞

𝑣

𝑖−

1,

𝑗

(𝑖

+

1,

𝑗)

𝑖, 𝑗 − 1

∆𝑥

∆𝑥

∆𝑥

∆𝑦

METODA BILANSÓW ELEMENTARNYCH

Bilans energii, 2D

dla objętości związanej z
𝑖,j−tym węzłem

𝑞

𝑣

𝜆∆𝑦

𝑇

𝑖−1

,𝑗

− 𝑇

𝑖,𝑗

∆𝑥

+ 𝜆∆𝑦

𝑇

𝑖+1

,𝑗

− 𝑇

𝑖,𝑗

∆𝑥

+

+𝜆∆𝑥

𝑇

𝑖,

𝑗+1

− 𝑇

𝑖,𝑗

∆𝑦

+ 𝜆∆𝑥

𝑇

𝑖,

𝑗−1

− 𝑇

𝑖,𝑗

∆𝑦

+

+𝑞

𝑣

∆𝑥 ∆𝑥=0

Metody Numeryczne cz.4

5

METODA BILANSÓW ELEMENTARNYCH

Bilans energii, 2D

po uproszczeniu ≡

≡ numeryczną
aproksymacją r. różn.
przewodzenia ciepła 2D !!!

𝑞

𝑣

𝑇

𝑖−1,𝑗

− 2𝑇

𝑖,𝑗

+ 𝑇

𝑖+1,𝑗

∆𝑥

2

+

+

𝑇

𝑖,𝑗−1

− 2𝑇

𝑖,𝑗

+ 𝑇

𝑖,𝑗+1

∆𝑦

2

+

𝑞

𝑣

𝜆

= 0

METODA BILANSÓW ELEMENTARNYCH

Bilans energii, 2D

Dla siatki regularnej
kwadratowej
tj.

Δ𝑥 = Δ𝑦 = 𝑙

𝑞

𝑣

𝑇

𝑖−1,

𝑗

+

𝑇

𝑖+1,

𝑗

+ 𝑇

𝑖,𝑗−1

+ 𝑇

𝑖,𝑗+1

− 4𝑇

𝑖,𝑗

+

𝑞

𝑣(𝑖,𝑗)

𝑙

2

𝜆

= 0

𝑇

𝐿

+

𝑇

𝑃

+ 𝑇

𝐺

+ 𝑇

𝐷

− 4𝑇

𝐶

+

𝑞

𝑣

𝑙

2

𝜆

= 0

METODA BILANSÓW ELEMENTARNYCH

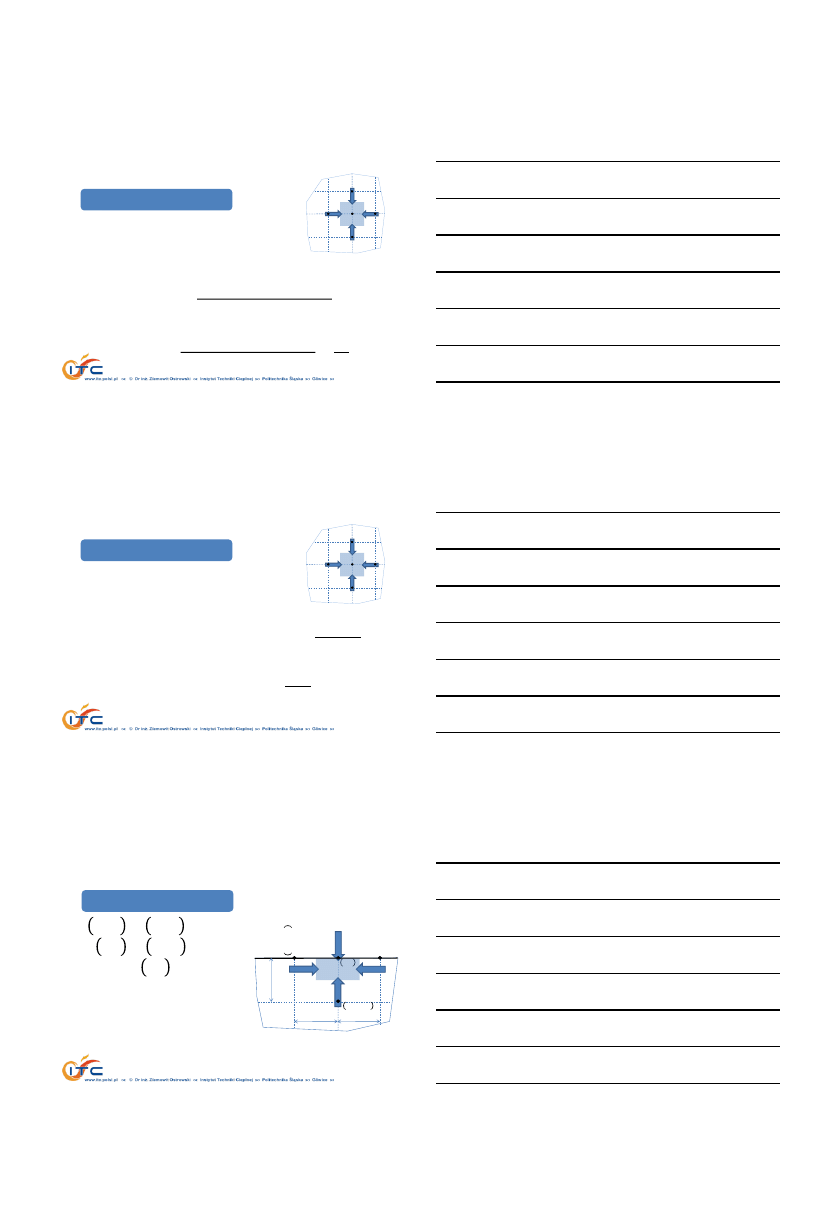
Warunki brzegowe

𝑄

𝜆,𝑃

𝑖, 𝑗

𝑄

𝜆,𝐿

𝑞

𝑣

𝑖−

1,

𝑗

(𝑖

+

1,

𝑗)

𝑖, 𝑗 − 1

𝑄

𝐺

𝑄

𝜆,𝐷

∆𝑦

∆𝑥

∆𝑥

𝑄

𝜆,𝐿

+ 𝑄

𝜆,𝑃

+

+

𝑄

𝐺

+ 𝑄

𝜆,𝐷

+

+ 𝑄

𝑣

= 0

𝑄

Γ

+ 𝑞

𝑣

𝑉 = 0

Γ –wszystkie brzegi