1

Inżynierskie zastosowania statystyki – ćwiczenia

Temat 5: Wybrane typy rozkładów, rozkłady wielowymiarowe

Zadania do rozwiązania:

1. Czas (w minutach) między kolejnymi zgłoszeniami w pewnej centrali abonenckiej jest

zmienną losową o rozkładzie wykładniczym z parametrem λ = 2. Wyznacz:

a. średni czas pomiędzy kolejnymi zgłoszeniami,
b. prawdopodobieostwo, że przed upływem 3 minut nastąpi zgłoszenie.

2. Narysuj wykres funkcji gęstości prawdopodobieostwa dla rozkładu: jednomodalnego,

wielomodalnego, antymodalnego, o asymetrii lewej, o asymetrii prawej, mającego
przedział *a, b+ median.

3. Fabryka produkuje odważniki 10-gramowe. Błędy pomiarów masy odważników mają

rozkład normalny o wartości przeciętnej μ=0 g oraz odchyleniu standardowym
σ=0,01. Znajdź prawdopodobieostwo tego, że pomiar masy będzie przeprowadzony z
błędem nie przekraczającym 0,02 g.

4. Prawdopodobieostwo nieprzekroczenia przez fabrykę dobowego limitu zużycia

energii wynosi p=0,8. Niech K oznacza liczbę dni w ciągu tygodnia pracy (5-
dniowego), w których nie nastąpiło przekroczenie limitu. Wyznacz:

a. funkcję prawdopodobieostwo zmiennej losowej K i jej histogram,
b. dystrybuantę i jej wykres,
c. prawdopodobieostwo, że co najmniej w trzech dniach limit nie zostanie

przekroczony,

d. najbardziej prawdopodobną liczbę dni, w których limit nie zostanie

przekroczony i prawdopodobieostwo takiej liczby dni,

e. wartośd przeciętna i wariancję zmiennej losowej K,
f. współczynnik asymetrii rozkładu.

5. Doświadczenie polega na losowaniu 1 karty z talii 52 kart. Zmienna losowa X

przyjmuje wartości równe liczbie wylosowanych asów. Zmienna losowa Y przyjmuje
wartości równe liczbie wylosowanych pików. Wyznacz rozkład prawdopodobieostwa
dwuwymiarowej zmiennej losowej (X, Y).

6. W fabryce produkowane jest urządzenie składające się między innymi z dwóch kół

zębatych: dużego i małego. Przy produkcji każdego koła może wystąpid dodatnie i
ujemne odchylenie grubości zębów od wartości nominalnej. Urządzenie nie będzie
działało prawidłowo, jeżeli do jego montażu zostaną użyte dwa koła zębate o
dodatnim odchyleniu grubości zębów. Montażysta losuje z partii produkcyjnej koło
duże i koło małe. Zmienna losowa X przyjmuje wartośd 1, jeżeli montażysta wylosuje
duże koło z odchyleniem dodatnim, natomiast 0, jeżeli montażysta wylosuje duże
koło z odchyleniem ujemnym. Analogiczne wartości przyjmuje zmienna losowa Y dla
koła małego.

a. Wyznacz i naszkicuj dystrybuantę zmiennej losowej (X, Y)

2

b. Jakie jest prawdopodobieostwo, że urządzenie nie będzie działało

prawidłowo?

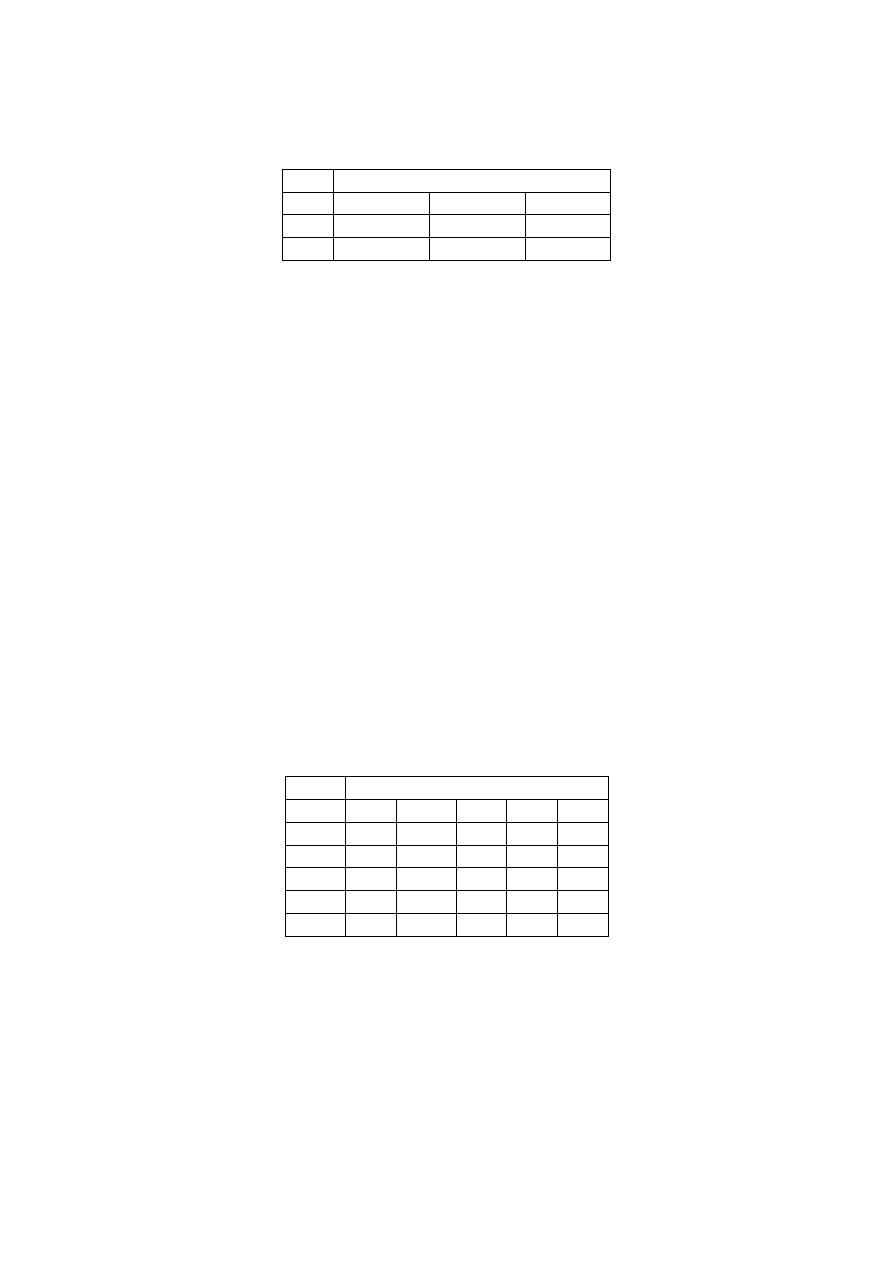
7. Rozważamy dwuwymiarową zmienną losową (X, Y) o rozkładzie określonym w tabeli:

x

i

y

k

1

2

3

2

0,2

0,2

0,1

4

0,1

0,3

0,1

a. Wyznacz dystrybuantę rozkładu brzegowego zmiennej losowej Y
b. Wyznacz dystrybuantę rozkładu brzegowego zmiennej losowej X

8. Dla następującej funkcji:



















przypadkow

h

pozostalyc

dla

0

1

0

2

0

dla

)

,

(

y

x

cxy

y

x

f

a. dobierz stałą c, aby funkcja f(x,y) była gęstością dwuwymiarowej zmiennej

losowej (X, Y)

b. wyznacz i narysuj jej dystrybuantę

9. Doświadczenie losowe polega na rzucie symetryczną sześciościenną kostką do gry.

Zmienna losowa X przyjmuje wartośd 0, gdy wyrzucimy parzystą liczbę oczek oraz
wartośd 1, gdy wyrzucimy nieparzystą liczbę oczek. Zmienna losowa Y przyjmuje
wartośd 1, gdy liczba oczek jest podzielna przez 3 oraz wartośd 2, gdy liczba oczek nie
jest podzielna przez 3. Zbadaj niezależnośd zmiennych losowych X i Y.

10. Zmienna losowa X jest oceną z kolokwium z Inżynierskich Zastosowań Statystyki

losowo wybranego studenta pewnej specjalności. Zmienna losowa Y jest oceną z
kolokwium z Metod numerycznych. Dwuwymiarowa zmienna losowa (X, Y) ma
rozkład określony w tabeli.

x

k

y

k

2

3

3,5

4

5

2

3/35 2/35

1/35 0

0

3

1/35 10/35 2/35 1/35 0

3,5

0

1/35

5/35 1/35 1/35

4

0

0

0

3/35 2/35

5

0

0

0

1/35 1/35

a) Wyznacz dystrybuantę rozkładu brzegowego zmiennej losowej Y.
b) Wyznacz rozkład warunkowy zmiennej losowej Y pod warunkiem, że X = 4.

Wyznacz dystrybuantę tego rozkładu.