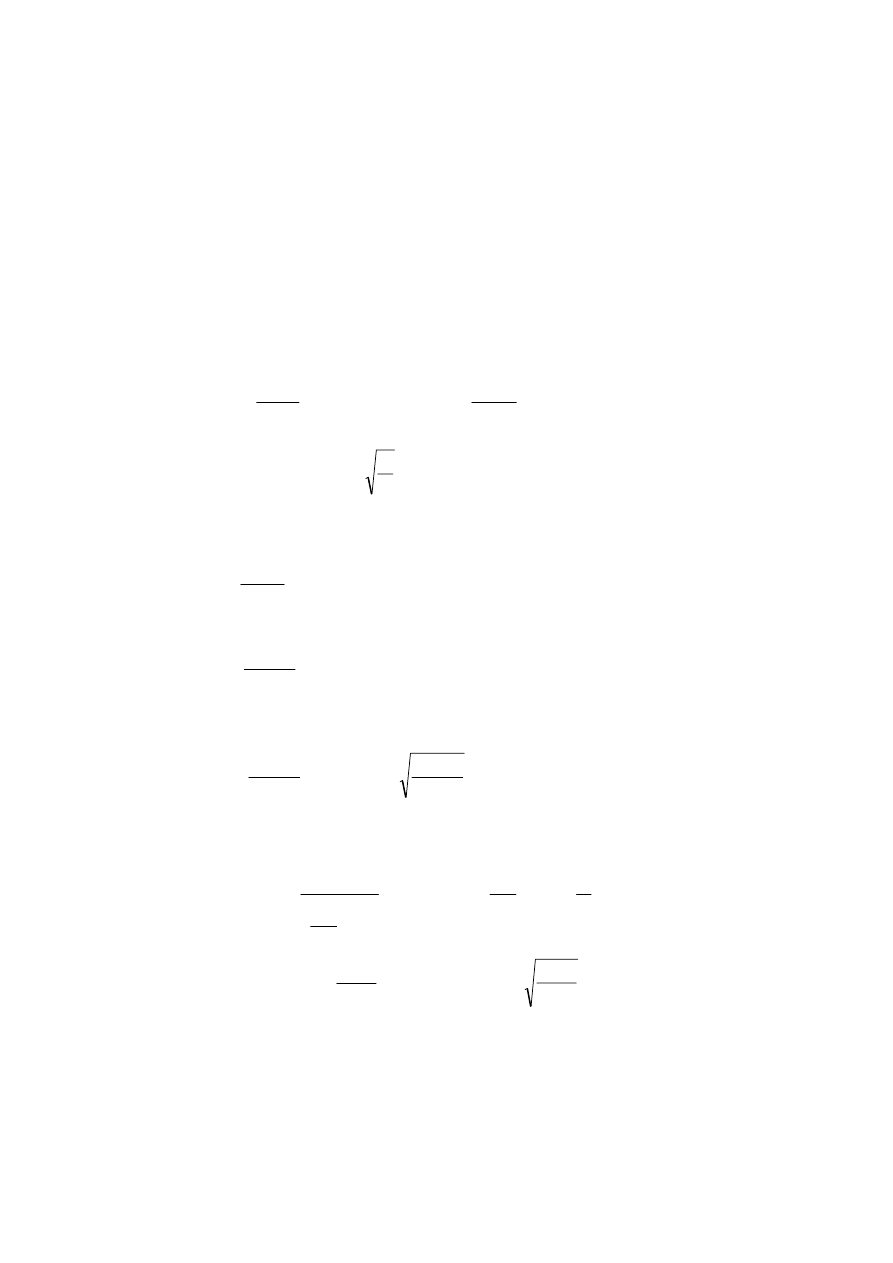
Zadanie 2.
Wszystkie te zadanka opierają się na analizie: CO MAMY => CO CHCEMY DOSTAĆ
Ważne jest by wszystkie wartości przeliczyć na cm! (dotyczy: e, f, E)
Zawsze podaje nam wartość E (moduł Young’a) jest on różny dla różnych materiałów, ale on
ZAWSZE daje tą samą wartość 2,1·10

5

MPa = 2,1·10

6

kG·cm

-2

Literkę „I” na kartce powinno się pisać tak: „

I” ja będę pisał: I.

Zatem mamy:

E = 2,1·10

6

kG·cm

-2

l – choć na ostatnim terminie podał stosunek l do d

Wszystkie wzorki:

1) Jeśli podał nam Q, a nie podał m:

m

=

Q/g

[kG·s

2

·cm

-1

]

gdzie g = 10 m/s

2

= 1000 cm/s

2

,

2) zawsze podaje albo n

w

albo n

kr

, dla obu używa się wzoru:

30

w

w

n

⋅

=

π

ω

30

kr

kr

n

⋅

=

π

ω

3)

Jeśli mamy m i ω

kr

to liczymy:

To piszemy:

m

k

kr

=

ω

=>

[kG·cm

m

k

kr

⋅

=

2

ω

-1

]

Podstawiamy

m i ω

kr

i otrzymujemy k

4) Jeśli mamy d (choć zazwyczaj go nie mamy):

I =

64

d

⋅

π

4

5)

jeśli mamy I oraz l, a nie mogliśmy wcześniej obliczyć k to liczymy:

3

48

l

I

E

k

⋅

=

6) analogicznie, jeśli mamy k oraz I obliczamy l:

k

I

E

l

⋅

=

48

3

=>

3

48

k

I

E

l

⋅

=

7) Wiedząc w jakim zakresie pracujemy (nad- czy podkrytycznym) oraz mając:

e, f, ω

w

obliczamy ω

kr

Dla stanu nadkrytycznego:

1

2

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

w

kr

e

f

ω

ω

=>

f

e

w

kr

=

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

1

2

ω

ω

=>

=>

2

2

w

kr

f

f

e

ω

ω

⋅

+

=

=>

w

kr

f

f

e

ω

ω

⋅

+

=

Podstawiamy i obliczamy na kalkulatorku.

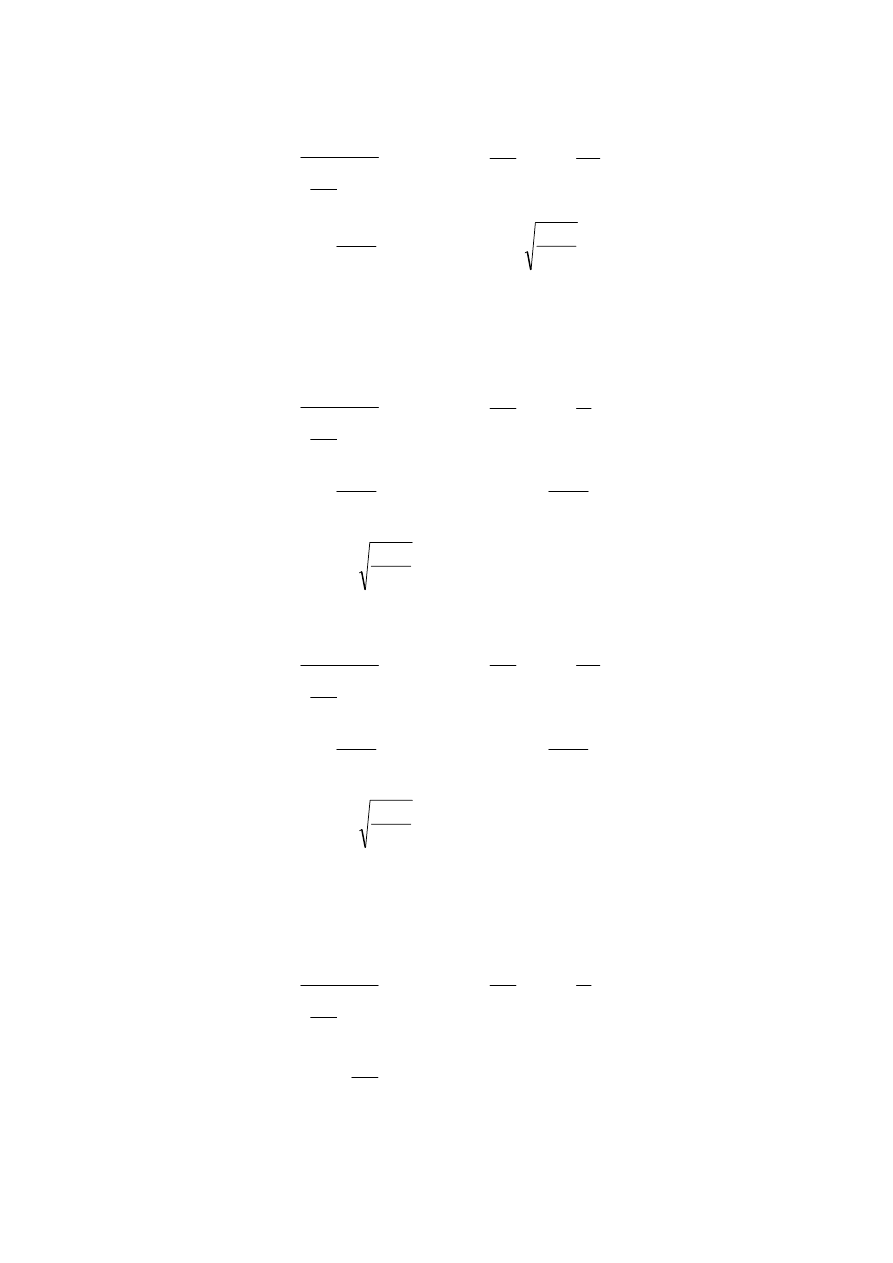
Dla stanu podkrytycznego:

1

2

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

w

kr

e

f

ω

ω

=>

f

e

w

kr

−

=

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

1

2

ω

ω

=>

=>

2

2

w

kr

f

e

f

ω

ω

⋅

−

=

=>

w

kr

f

e

f

ω

ω

⋅

−

=

Podstawiamy i obliczamy na kalkulatorku.

8) Wiedząc w jakim zakresie pracujemy (nad- czy podkrytycznym) oraz mając:

e, f, ω

kr

obliczamy ω

w

Dla stanu nadkrytycznego:

1

2

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

w

kr

e

f

ω

ω

=>

f

e

w

kr

=

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

1

2

ω

ω

=>

=>

2

2

w

kr

f

f

e

ω

ω

⋅

+

=

=>

f

e

f

kr

w

+

=

2

2

ω

ω

=>

=>

f

e

f

kr

w

+

=

ω

ω

Podstawiamy i obliczamy na kalkulatorku.

Dla stanu podkrytycznego:

1

2

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

w

kr

e

f

ω

ω

=>

f

e

w

kr

−

=

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

1

2

ω

ω

=>

=>

2

2

w

kr

f

e

f

ω

ω

⋅

−

=

=>

e

f

f

kr

w

−

=

2

2

ω

ω

=>

=>

e

f

f

kr

w

−

=

ω

ω

Podstawiamy i obliczamy na kalkulatorku.

9) Wiedząc w jakim zakresie pracujemy (nad- czy podkrytycznym) oraz mając:

ω

w

, f, ω

kr

obliczamy e: (taka sytuacja chyba jeszcze się nie zdarzyła)

Dla stanu nadkrytycznego:

1

2

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

w

kr

e

f

ω

ω

=>

f

e

w

kr

=

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

1

2

ω

ω

=>

=>

f

f

e

w

kr

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

=

2

ω

ω

Podstawiamy i obliczamy na kalkulatorku.

Dla stanu podkrytycznego:

1

2

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

w

kr

e

f

ω

ω

=>

f

e

w

kr

−

=

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

1

2

ω

ω

=>

=>

f

f

e

w

kr

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

=

−

2

ω

ω

=>

2

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

−

=

w

kr

f

f

e

ω

ω

Podstawiamy i obliczamy na kalkulatorku.

10) Wiedząc w jakim zakresie pracujemy (nad- czy podkrytycznym) oraz mając:

ω

w

, e, ω

kr

obliczamy f:

Dla stanu nadkrytycznego:

1

2

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

w

kr

e

f

ω

ω

Podstawiamy i obliczamy na kalkulatorku.

Dla stanu podkrytycznego:

1

2

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

w

kr

e

f

ω

ω

Podstawiamy i obliczamy na kalkulatorku.

11) Chyba nie pominąłem nic, więc mamy już wszystko, zostaje tylko naprężenie
gnące:

(α zawsze przyjmujemy równe ¼)

3

3

3

8

32

4

1

32

d

l

f

k

d

l

f

k

d

l

P

W

M

x

g

g

π

π

π

α

ϑ

⋅

⋅

⋅

=

⋅

⋅

⋅

=

⋅

⋅

=

=

Mające te wzory nie ma szans nie zrobić tego typu zadań, gdy daje stosunek coś w
rodzaju tego stosunku l/d trzeba tylko zobaczyć w jakim wzorze jest l/d lub d/l i
podstawić.

Pamiętajcie o jednostkach:

⎥⎦

⎤

⎢⎣

⎡

=

s

1

ω

⎥⎦

⎤

⎢⎣

⎡

⋅

=

2

s

cm

kg

g

ϑ

⎥⎦

⎤

⎢⎣

⎡

=

min

obr

n