Są to układy, wykonujące operacje arytmetycznych na

liczbach, przedstawionych w zapisie dwójkowym.

Ponieważ wszystkie podstawowe działania arytmetyczne:

dodawanie, odejmowanie, mnożenie i dzielenie, a także

wszystkie inne operacje matematyczne, wykonać można

przy zastosowaniu odpowiednich algorytmów

za pomocą

jednego tylko działania arytmetycznego - dodawania

,

podstawowym układem arytmetycznym jest

układ,

realizujący dodawanie

, nazywany

sumatorem

.

Do układów arytmetycznych zalicza się ponadto

układy do

porównywania dwu liczb

, nazywane

komparatorami

oraz

uniwersalne układy arytmetyczno - logiczne, realizujące

różne operacje arytmetyczne i logiczne.

1

8.5. Układy arytmetyczne

ETR 8.5

Opracował dr inż. Grzegorz Stępień

1. Sumatory

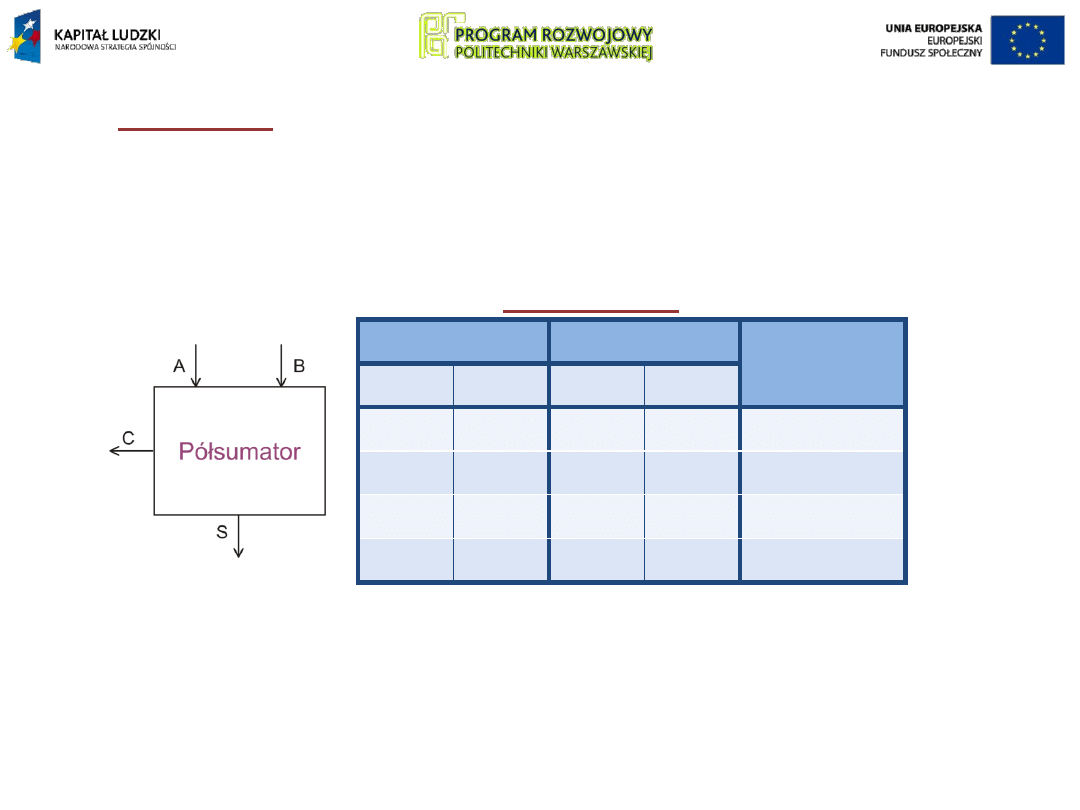
Sumatory to układy wykonujące dodawanie liczb,

przedstawionych w zapisie dwójkowym. Podstawowy układ

do dodawania dwóch jednobitowych liczb dwójkowych A i B

to tzw.

półsumator

.

Reguły sumowania przedstawia tabela.

Wynik

dodawania

musi być

przedstawiony przy użyciu dwóch bitów

. Młodszy

bit wyniku wyprowadzany jest na wyjście S, starszy bit

wyniku na wyjście C.

Wejścia

Wyjścia

Suma

dziesiętnie

B

A

C

S

0

0

0

0

(0)

0

1

0

1

(1)

1

0

0

1

(1)

1

1

1

0

(2)

2

ETR 8.5

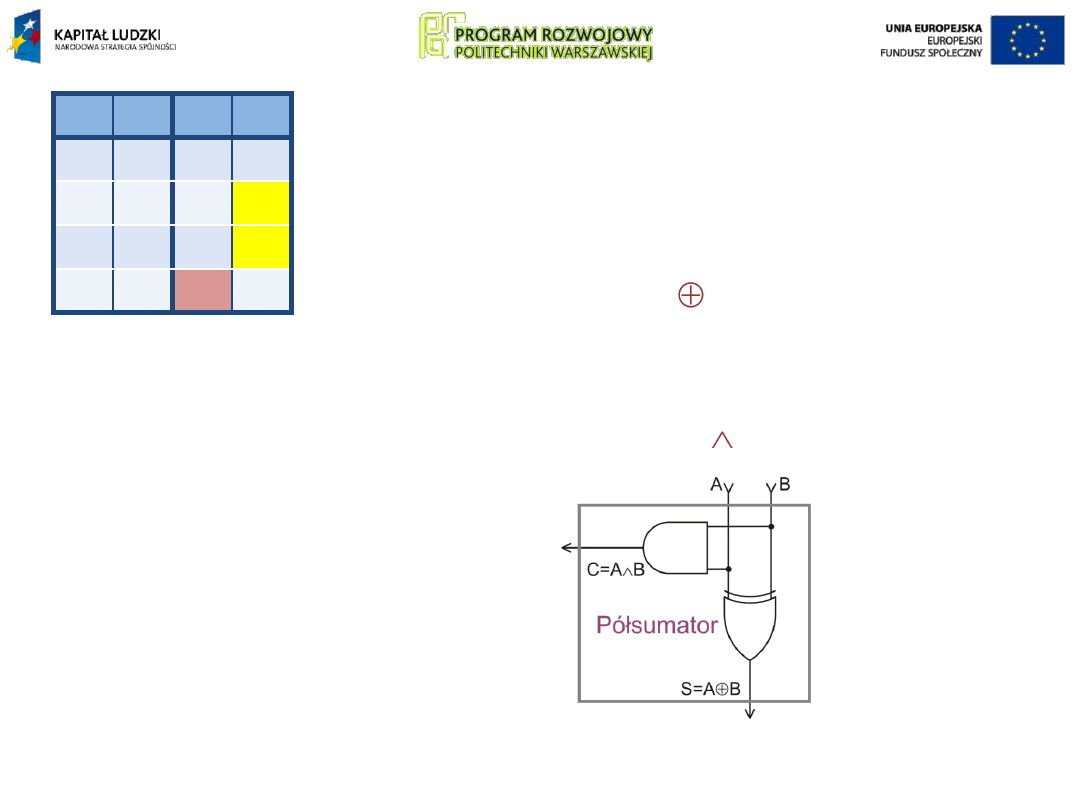
Wyjście S znajduje się w stanie 1 gdy jedno

z wejść (A lub B) znajduje się w stanie 0 a

drugie w stanie 1. Wyjście S związane jest

zatem z wejściami A i B funkcją XOR:

S = A

B

Układ do dodawania dwóch

jednobitowych liczb

dwójkowych można zatem

zrealizować przy użyciu

jednej bramki Exlusive OR i

jednej bramki AND:

3

ETR 8.5

Na wyjściu C pojawia się 1 gdy jednocześnie A i B jest

równe 1, wyjście C realizuje zatem funkcję iloczynu

logicznego (AND):

C = A B

B

A

C

S

0

0

0

0

0

1

0

1

1

0

0

1

1

1

1

0

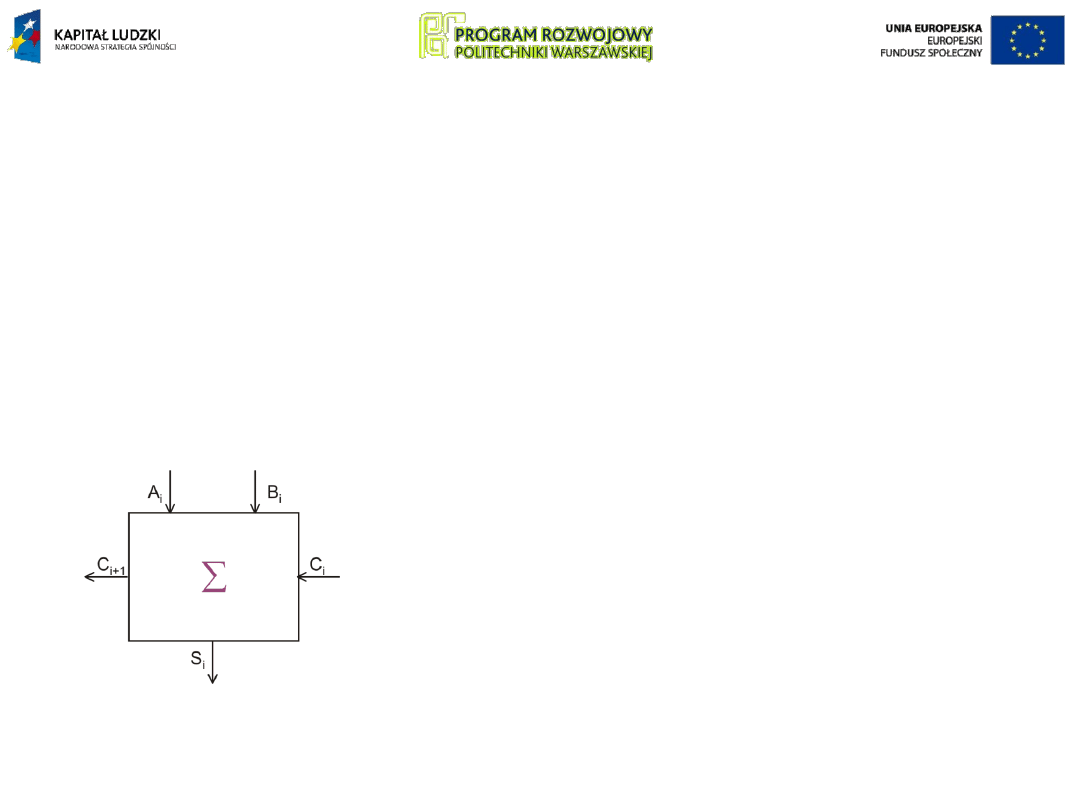
W przypadku dodawania liczb o większej liczbie bitów

wartość wyprowadzana przez wyjście C układu do

sumowania liczb jednobitowych musi być dodana do bitów

na wyższej pozycji (przeniesiona do wyższej pozycji).

Wyjście C jest w związku z tym nazywane

wyjściem

przeniesienia

(ang. Carry

). Sumowanie bitów na pozycji i

wymaga dodania wartości i-tych bitów liczb A i B oraz

przeniesienia z niższej pozycji:

A

i

+ B

i

+C

i

a układ realizujący takie dodawanie,

zwany

jednobitowym sumatorem

pełnym

, musi zawierać dodatkowe

wejście, wprowadzające przeniesienie C

i

4

ETR 8.5

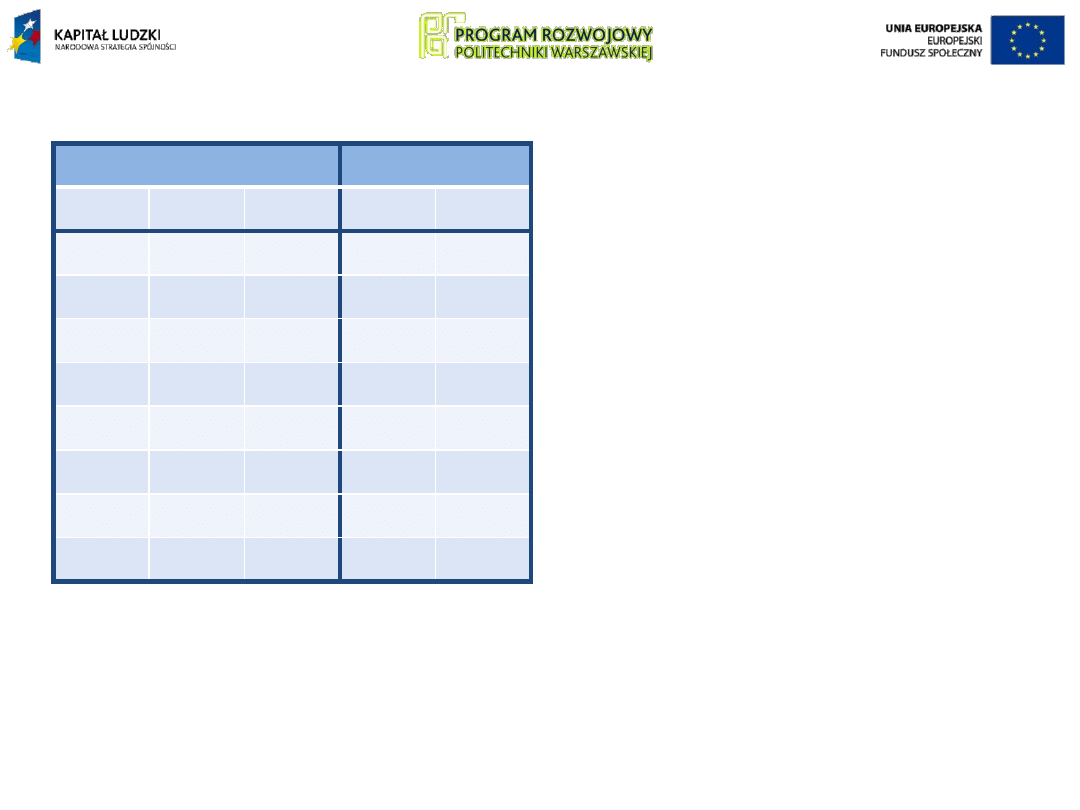
Tabela przedstawia sumowanie A

i

+ B

i

+C

i

:

mają wartość „1” (suma 2) lub wszystkie 3 wejścia mają

wartość „1” (suma równa 3):

C

i+1

= A

i

B

i

C

i

+

A

i

B

i

C

i

+A

i

B

i

C

i

+A

i

B

i

C

i

;

Wyjście S

i

przyjmuje

wartość „1” gdy tylko jedno

z wejść C

i

, A

i

lub B

i

równa

się 1 (suma równa 1) lub

wszystkie 3 wejścia mają

wartość „1” (suma równa 3):

S

i

=

A

i

B

i

C

i

+A

i

B

i

C

i

+

A

i

B

i

C

i

+A

i

B

i

C

i

;

Wyjście C

i+1

jest równe „1”,

gdy dwa z wejść C

i

, A

i

lub B

i

5

ETR 8.5

Wejścia

Wyjścia

B

i

A

i

C

i

C

i+1

S

i

0

0

0

0

0

0

0

1

0

1

0

1

0

0

1

0

1

1

1

0

1

0

0

0

1

1

0

1

1

0

1

1

0

1

0

1

1

1

1

1

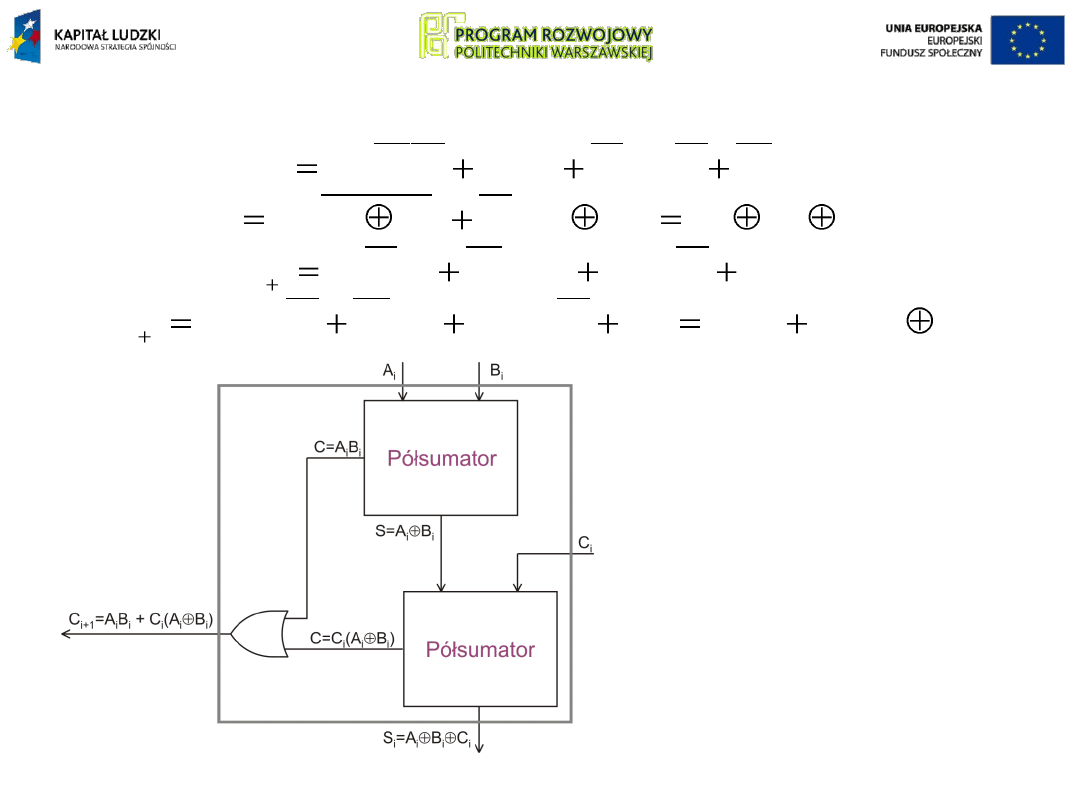
Po przekształceniach:

Jednobitowy sumator

pełny realizuje się przy

użyciu dwóch

półsumatorów i

dodatkowej bramki

sumy logicznej (OR),

sumującej

przeniesienia obydwu

półsumatorów.

6

ETR 8.5

)

B

A

B

(A

C

)

B

A

B

A

(

C

S

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

C

B

A

)

B

A

(

C

)

B

A

(

C

S

i

i

i

i

i

i

i

i

i

i

i

i

1

i

C

B

A

C

B

A

C

B

A

C

B

A

C

)

B

A

(

C

B

A

)

C

C

(

B

A

)

B

A

B

A

(

C

C

i

i

i

i

i

i

i

i

i

i

i

i

i

i

1

i

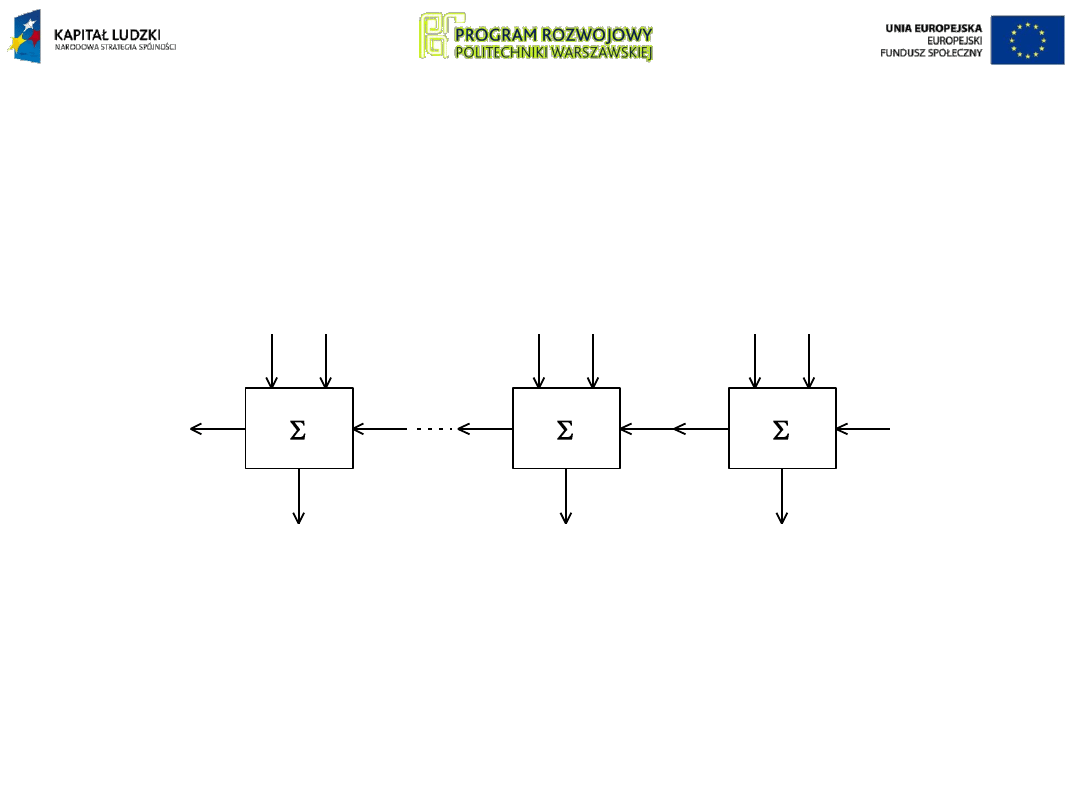
W celu dodawania liczb wielobitowych sumatory

jednobitowe łączy się w większe zespoły. W najprostszym

przypadku tworzy się kaskadę sumatorów z szeregowo

połączonymi wejściami i wyjściami przeniesień (z tzw.

przeniesieniami szeregowymi

).

7

ETR 8.5

Wadą takiego połączenia jest ustalanie wyniku n-tego

sumatora dopiero po ustaleniu kolejnych stanów

wszystkich poprzedzających sumatorów, co opóźnia

otrzymanie wyniku.

C

n+1

C

n

B

n

A

n

S

n

C

2

C

1

B

1

A

1

S

1

C

1

C

0

B

0

A

0

S

0

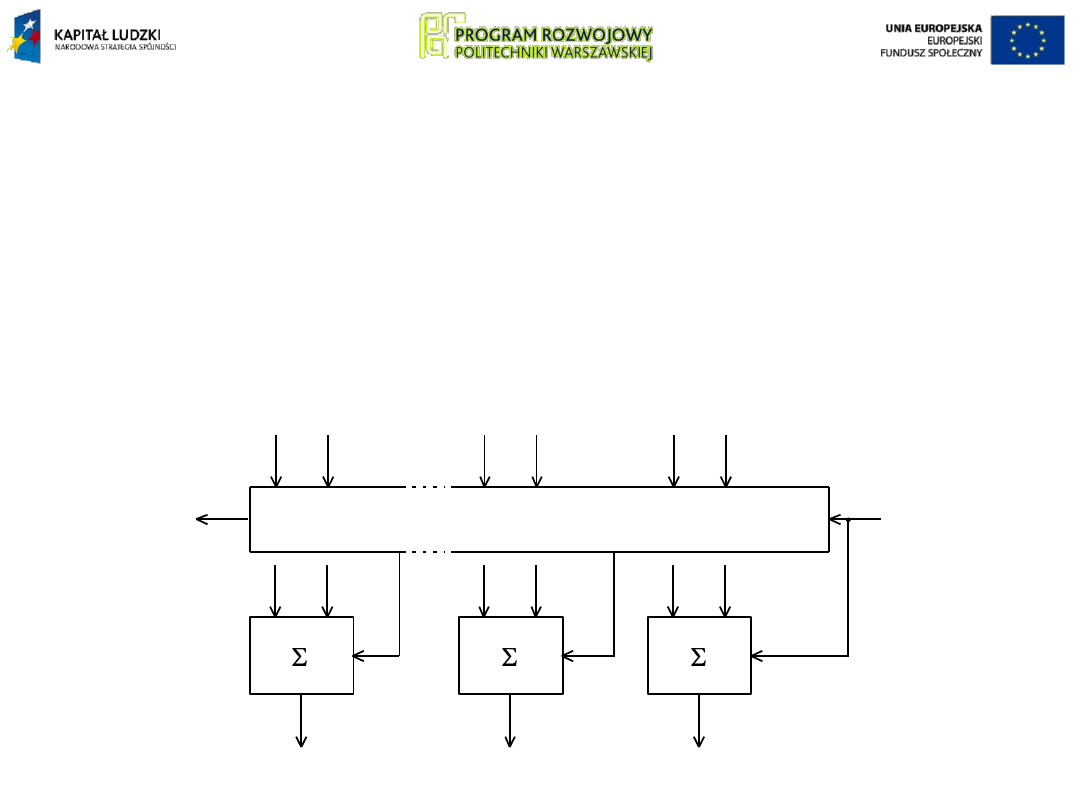
Lepszym rozwiązaniem jest wstępne wyznaczenie

wszystkich przeniesień na podstawie wartości liczb

wejściowych A i B przez tzw.

blok generacji przeniesień

i

następnie jednoczesne dodanie bitów na wszystkich

pozycjach przez zespół sumatorów. Układy takie nazywane

są

sumatorami z przeniesieniami równoległymi

(ang. look

ahead).

8

ETR 8.5

C

n+1

C

n

B

n

A

n

S

n

C

1

B

1

A

1

S

1

C

0

B

0

A

0

S

0

B

n

A

n

B

1

A

1

B

0

A

0

C

0

blok generacji przeniesień

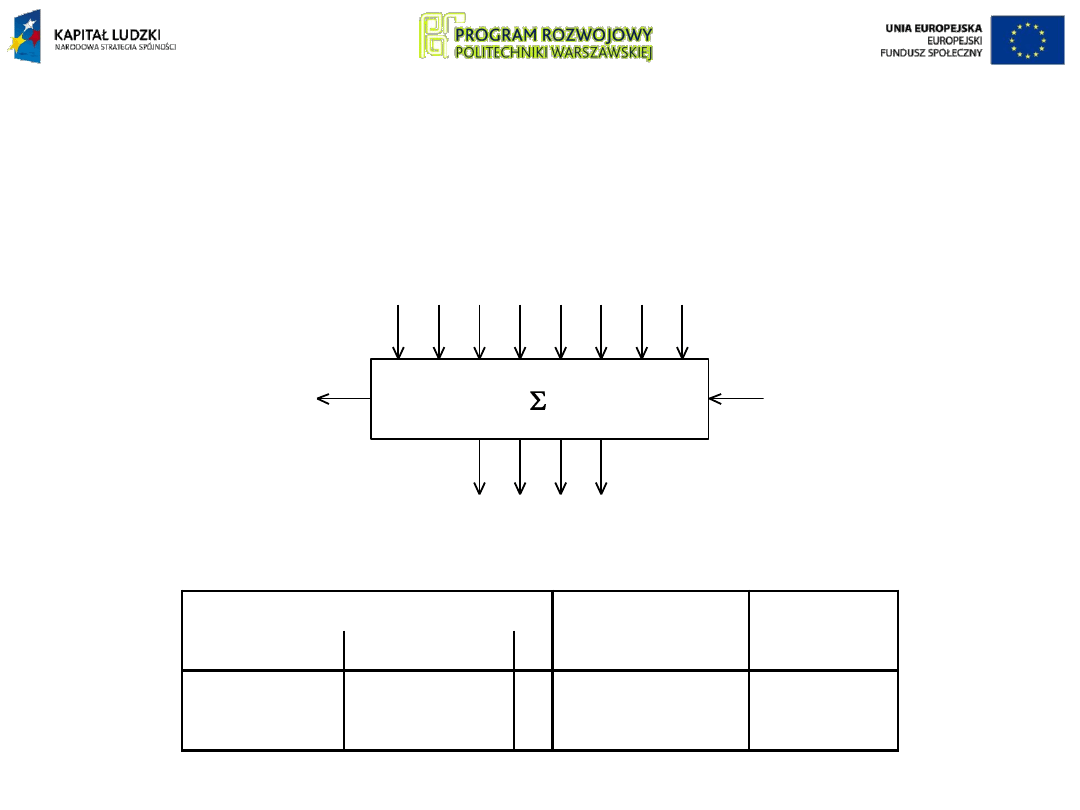
W rodzinie układów scalonych TTL i TTL LS dostępne są

sumatory dwójkowe 4-bitowe: 7483 (starego typu, z

przeniesieniami szeregowymi) oraz 7483A, 74LS83A i

74LS283 (z przeniesieniami równoległymi):

Fragment tabeli stanów sumatora 7483…74LS283:

9

ETR 8.5

Wejścia

Wyjścia

działanie

B

3

B

2

B

1

B

0

A

3

A

2

A

1

A

0

C

I

C

O

S

3

S

2

S

1

S

0

1

0

0

1

1

0

1

0

0

1

0

0

1

1

10+9=19

0

1

1

0

0

1

0

1

1

0

1

1

0

0

C

I

+5+6=12

S

2

B

3

A

3

C

I

B

2

A

2

B

1

A

1

B

0

A

0

S

1

S

0

S

3

C

O

2. Komparatory

Są to układy do porównywania liczb, przedstawionych w

zapisie dwójkowym.

Informację o równości

dwóch liczb jednobitowych a i b

uzyskać można za pomocą funkcji:

która przyjmuje wartość 1 wtedy, gdy a=b=1 lub a=b=0.

Funkcją taką jest negacja funkcji ALBO (Exclusive OR).

Układ do badania równości liczb wielobitowych zbudować

można z realizujących powyższą funkcję dwuwejściowych

bramek Exclusive

NOR, badających równość

poszczególnych bitów i wielowejściowej bramki iloczynu

logicznego AND, zbierającej wyniki tych badań.

10

ETR 8.5

b

a

b

a

b

a

)

b

a

(

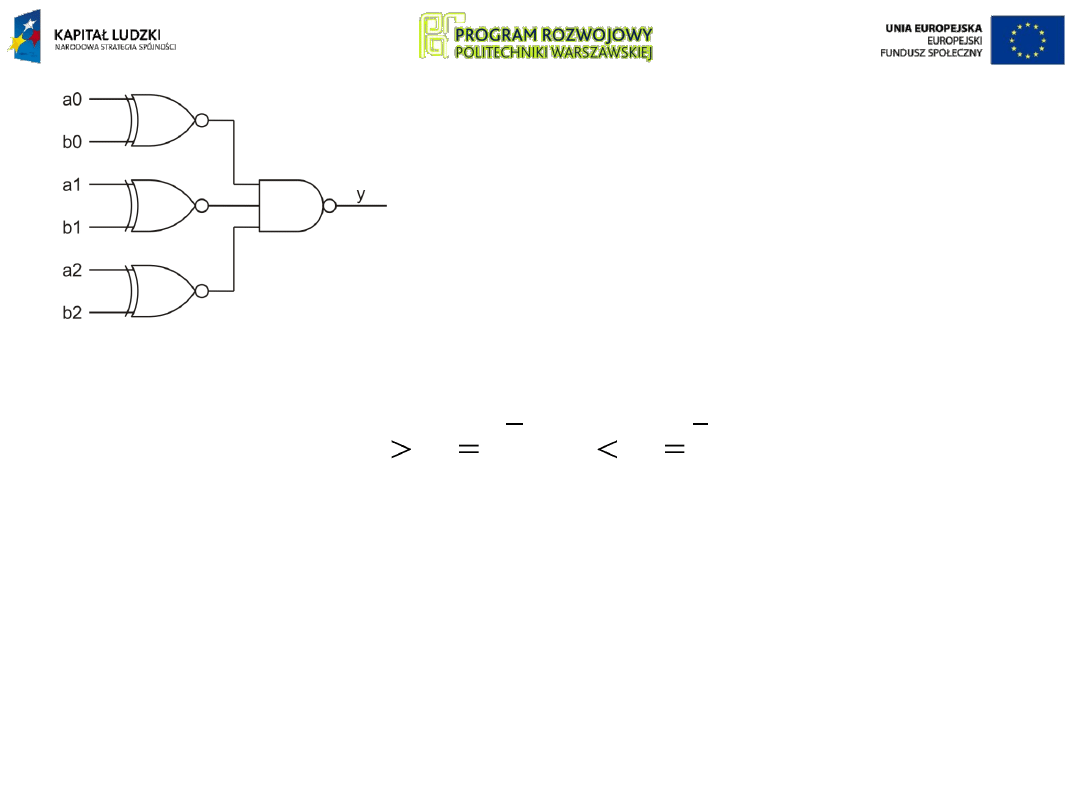
Na wyjściach bramek Ex NOR

uzyskuje się 1 gdy bit a

i

= b

i

. Na

wyjściu y występuje 1 gdy bity na

wszystkich pozycjach są sobie równe.

Informację o relacjach a>b lub a<b dwóch liczb

jednobitowych uzyskać można za pomocą funkcji:

gdyż jednobitowa liczba a jest większa od jednobitowej

liczby b tylko wtedy, gdy a=1 a b=0. Funkcje takie można

zrealizować przy użyciu dwuwejściowej bramki AND i

negacji. Relacje A>B lub A<B liczb wielobitowych określają

relacje a>b lub a<b między bitami na najwyższej pozycji,

na której wartości bitów są różne. Relacje między bitami

niższych pozycji są nieistotne.

11

ETR 8.5

b

a

)

b

a

(

b

a

)

b

a

(

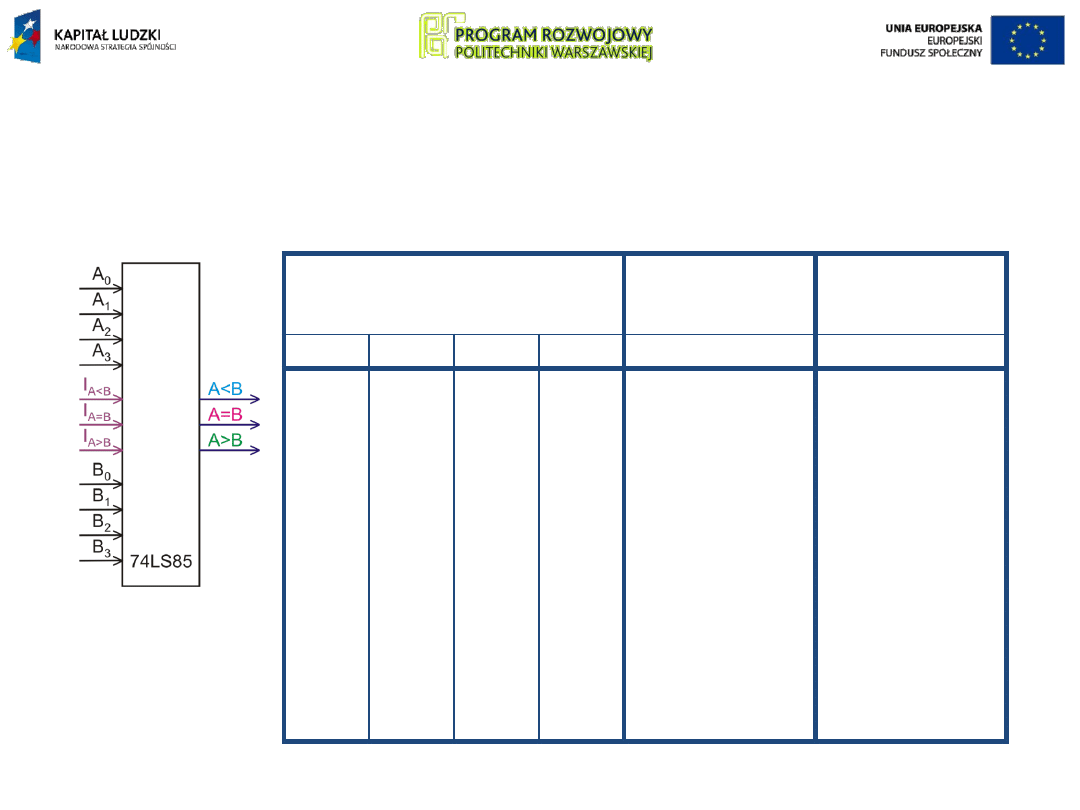
Scalonym komparatorem, wyznaczającym relacje:

A<B, A=B lub A>B

dla dwóch 4-bitowych liczb A i B jest układ 74LS85

12

ETR 8.5

Wejścia komparacyjne

Wejścia do

połączeń

kaskadowych

Wyjścia

A

3

, B

3

A

2

, B

2

A

1

, B

1

A

0

, B

0

A<B A=B A>B A<B A=B A>B

A

3

<B

3

x

x

x

x

x

x

1

0

0

A

3

>B

3

x

x

x

x

x

x

0

0

1

A

3

=B

3

A

2

<B

2

x

x

x

x

x

1

0

0

A

3

=B

3

A

2

>B

2

x

x

x

x

x

0

0

1

A

3

=B

3

A

2

=B

2

A

1

<B

1

x

x

x

x

1

0

0

A

3

=B

3

A

2

=B

2

A

1

>B

1

x

x

x

x

0

0

1

A

3

=B

3

A

2

=B

2

A

1

=B

1

A

0

<B

0

x

x

x

1

0

0

A

3

=B

3

A

2

=B

2

A

1

=B

1

A

0

>B

0

x

x

x

0

0

1

A

3

=B

3

A

2

=B

2

A

1

=B

1

A

0

=B

0

1

0

0

1

0

0

A

3

=B

3

A

2

=B

2

A

1

=B

1

A

0

=B

0

0

1

0

0

1

0

A

3

=B

3

A

2

=B

2

A

1

=B

1

A

0

=B

0

0

0

1

0

0

1

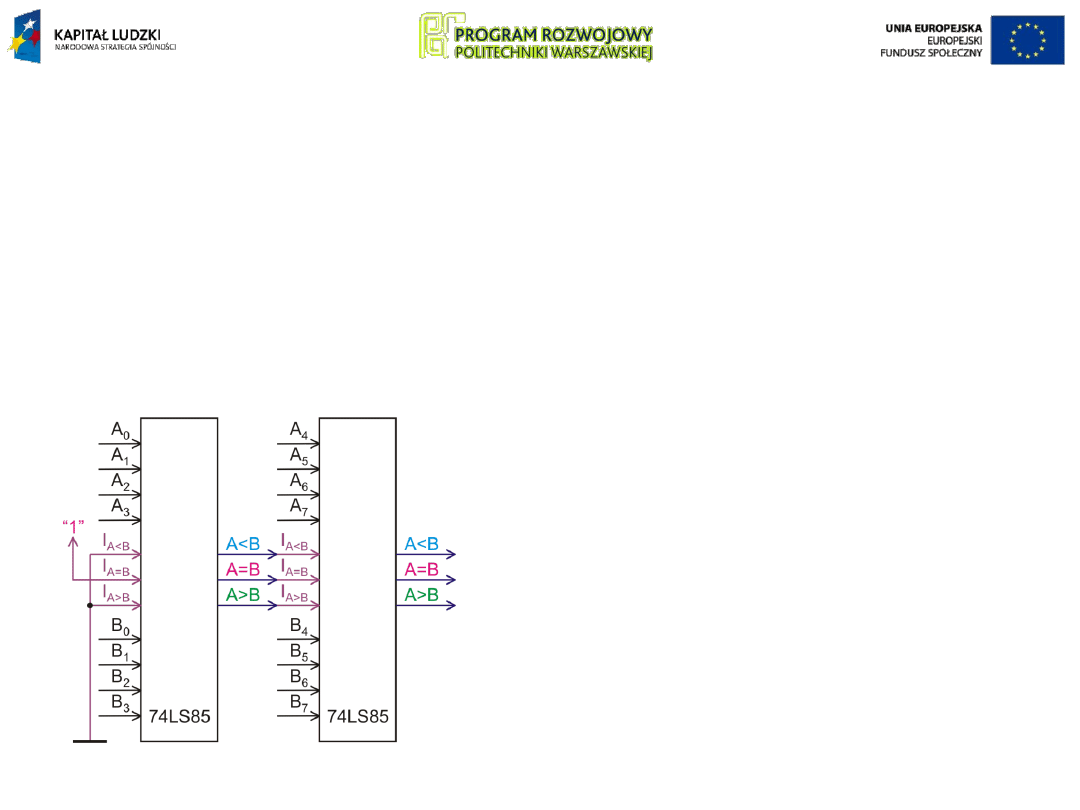
Wynik porównania znaczony jest stanem 1 na jednym z

trzech osobnych wyjść. Układ wyposażony jest w wejścia

I

A<B

, I

A=B

, I

A>B

, umożliwiające

kaskadowe łączenie

kilku

komparatorów w celu porównywania liczb o większej liczbie

bitów. Wejścia te łączy się z odpowiednimi wyjściami

poprzedzającego komparatora, porównującego mniej

znaczące bity liczb.

W komparatorze porównującym

bity na najniższych pozycjach

wejścia te ustawia się na stałe w

stan:

I

A<B

=0, I

A=B

=1, I

A>B

=0,

co neutralizuje wpływ tych wejść

na wynik porównania.

13

ETR 8.5

Stan wejść I

A<B

, I

A=B

, I

A>B

,

wpływa na stan wyjść

komparatora

tylko gdy

porównywane przez komparator

4-bitowe

części liczb są równe

. Stan tych wejść jest

wówczas po prostu przenoszony na wyjścia. W przypadku

A<B lub A>B

wynik porównania mniej znaczącej części

liczb przez poprzedzający komparator nie ma znaczenia.

14

ETR 8.5

3. Uniwersalna jednostka arytmetyczno-logiczna (ALU)

W rodzinie układów scalonych TTL i TTL LS produkowana

jest uniwersalna jednostka arytmetyczno-logiczna 74LS181

(74181), zwana ALU (ang. Arythmetic Logic Unit).

Jednostka taka umożliwia wykonywanie różnorodnych

operacji arytmetycznych i logicznych na dwóch 4-bitowych

liczbach dwójkowych.

Liczby, na których wykonywane są
operacje doprowadza się do wejść

A

3

..A

0

i B

3

..B

0.

Rodzaj operacji programuje się za

pomocą wejść M i S

3

..S

0

.

15

ETR 8.5

Przy M=1 wykonywane są

operacje logiczne

, przy M=0

wykonywane są

operacje arytmetyczne

. Rodzaj operacji

określa stan wejść S

3

..S

0

. Cztery linie wejściowe S

3

..S

0

umożliwiają wybór 16-tu różnych funkcji. Układ wykonuje

zatem

16 różnych funkcji logicznych

i

16 różnych funkcji

arytmetycznych

(łącznie 32 różne funkcje). Wynik operacji

ustawiany jest na wyjściach F

3

..F

0

i wyjściu przeniesienia C

o

.

F

2

B

3

A

3

ALU

74LS181

B

2

A

2

B

1

A

1

B

0

A

0

F

1

F

0

F

3

C

O

A=B

G
P

C

i

M
S

3

S

2

S

1

S

0

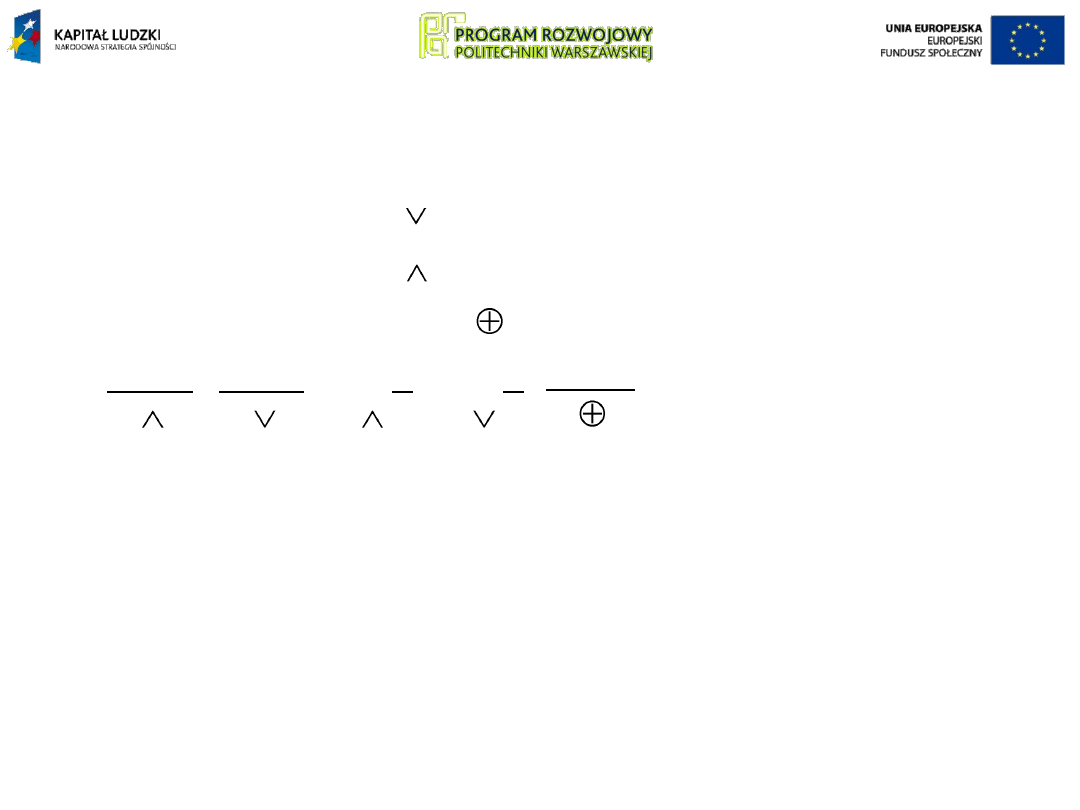
Podstawowe wykonywane

funkcje logiczne

to:

• negacja

A

lub

B

• suma logiczna
• iloczyn logiczny
• różnica symetryczna
• różne funkcje kombinowane:

itp.

Funkcje logiczne wykonywane są na pojedynczych bitach,

tzn. każda funkcja wykonywana jest niezależnie i
równolegle na wszystkich bitach A

i

i B

i

(i = [0,3]).

16

ETR 8.5

B

A

B

A

B

A

A

B A

B A

B A

B A

B

Podstawowe

wykonywane funkcje arytmetyczne

to:

• suma arytmetyczna

A+B

• różnica arytmetyczna

A-B-1

oraz mieszane funkcje logiczno-arytmetyczne:

itp.

Przy funkcjach arytmetycznych uwzględniany jest stan

wejścia przeniesienia

C

i

, a zatem funkcje te realizowane

są jako

A+B+

C

i

lub

A-B-1+

C

i

. Za pomocą funkcji

A-B-1+

C

i

można uzyskać bezpośrednio wynik

A-B

przy

ustawieniu na wejściu przeniesienia (

C

i

) stanu 0.

Wyjście A=B ustawiane jest w stan 1 przy F

3

F

2

F

1

F

0

= 1111.

Można to wykorzystać do porównywania liczb A i B za
pomocą funkcji

A-B-1

. Przy wykorzystaniu wyjścia

C

o

za

pomocą tej samej funkcji można ustalić zależności A>B i
A<B.

17

ETR 8.5

);

B

A

(

A

;

A

)

B

A

(

Układ 74LS181 zaopatrzony jest w

blok generacji

przeniesień równoległych

, w związku z czym jest bardzo

szybki. Do operacji na liczbach o większej liczbie bitów

można łączyć kaskadowo kilka układów tego typu. W

najprostszym przypadku wejście przeniesienia

C

i

układu

operującego na starszych czterech bitach liczby łączy się z

wyjściem

C

o

układu operującego na młodszych czterech

bitach liczby. Przeniesienia między każdą czwórką bitów są

przekazywane szeregowo. Można zastosować równoległą

generację przeniesień między kolejnymi czwórkami bitów za

pomocą

specjalnych układów generacji przeniesień

równoległych 74LS182

. Do połączenia z tymi układami służą

wyjścia G i P. Również wyjścia A=B (z otwartym kolektorem),

łączy się równolegle do wspólnego rezystora, otrzymując

sygnalizację stanu A = B liczb o długości większej niż 4 bity.

18

ETR 8.5

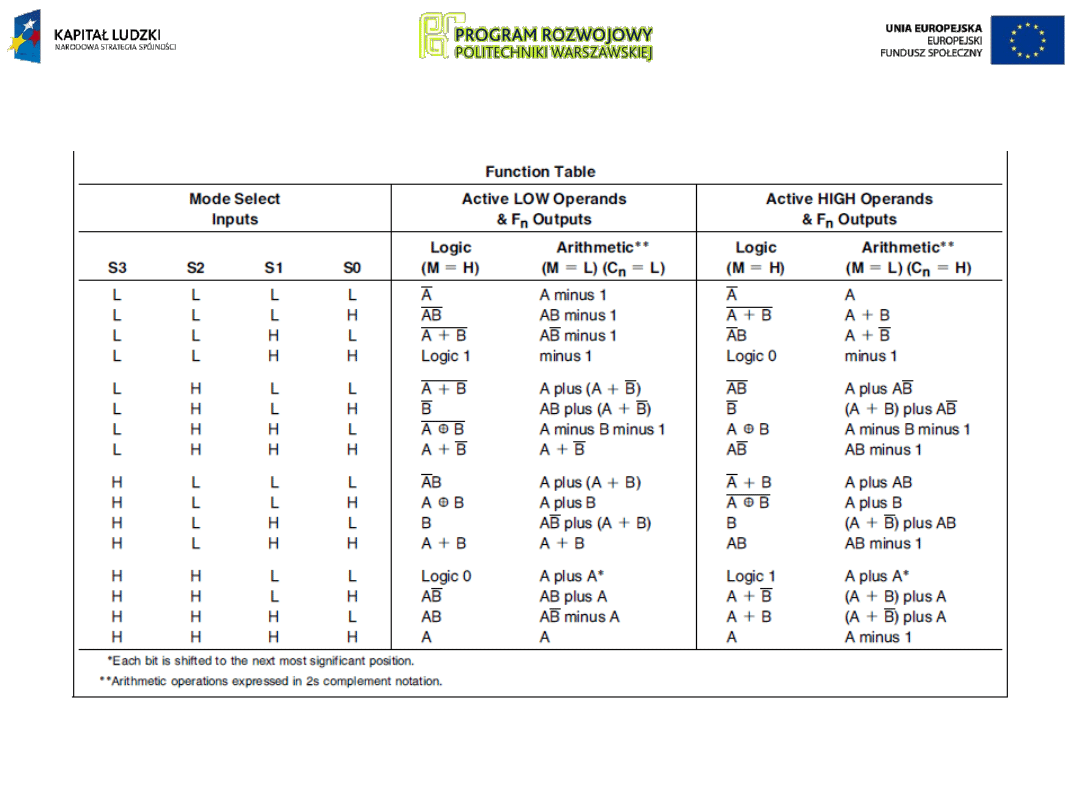
Pełna lista wykonywanych funkcji 74LS181:

19

ETR 8.5