W
W
Y
Y
K
K
Ł
Ł
A
A
D
D
1
1
1
1
W
W
Z
Z
Ó
Ó
R
R
H
H
A
A
G
G
E
E
N
N
A
A
-
-
P
P
O
O
I
I
S
S
E
E
U
U
I
I
L
L
L
L
E
E
’
’
A
A
,
,
D
D
O
O
Ś
Ś
W
W
I
I
A
A
D
D
C
C
Z
Z
E
E
N
N
I
I
E
E
R
R
E
E
Y
Y
N
N
O
O
L
L
D
D
S
S
A
A
,
,
R
R
Ó
Ó
W
W
N
N
A
A
N
N
I
I
A
A
B
B
E
E
Z
Z
W
W
Y
Y
M
M
I
I
A
A
R
R
O
O
W
W
E
E
“Gallery of Fluid Motion”-M. Samimy, K.S. Breuer
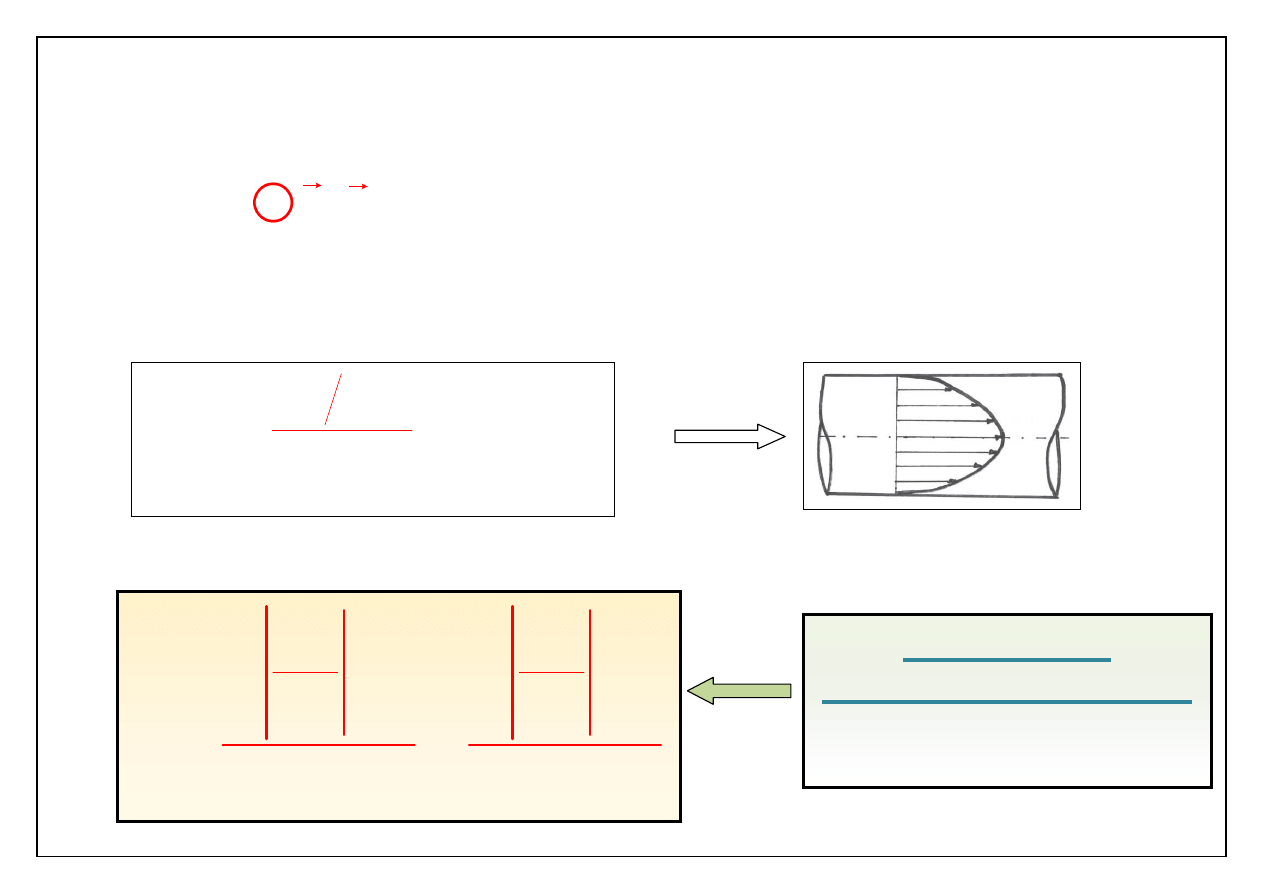
Policzmy wydatek płynący rurą
Wiemy, że prędkość w rurze wyraża się wzorem:
Podstawiając to wyrażenie pod całkę dostajemy:
2
R
1
A
0 0
Q
n v dA
v dA
dA
rdr d
4
4
p
p
R
D
x
x
Q
8
128
Jest to wzór
Hagena - Poiseiu
ille’a
D
– oznacza średnicę rury.
2
2
1
1
dp dx
v
R
r
4
D
D
O
O
Ś
Ś
W
W
I
I
A
A
D
D
C
C
Z
Z
E
E
N
N
I
I
E
E
R
R
E
E
Y
Y
N
N
O
O
L
L
D
D
S
S
A
A
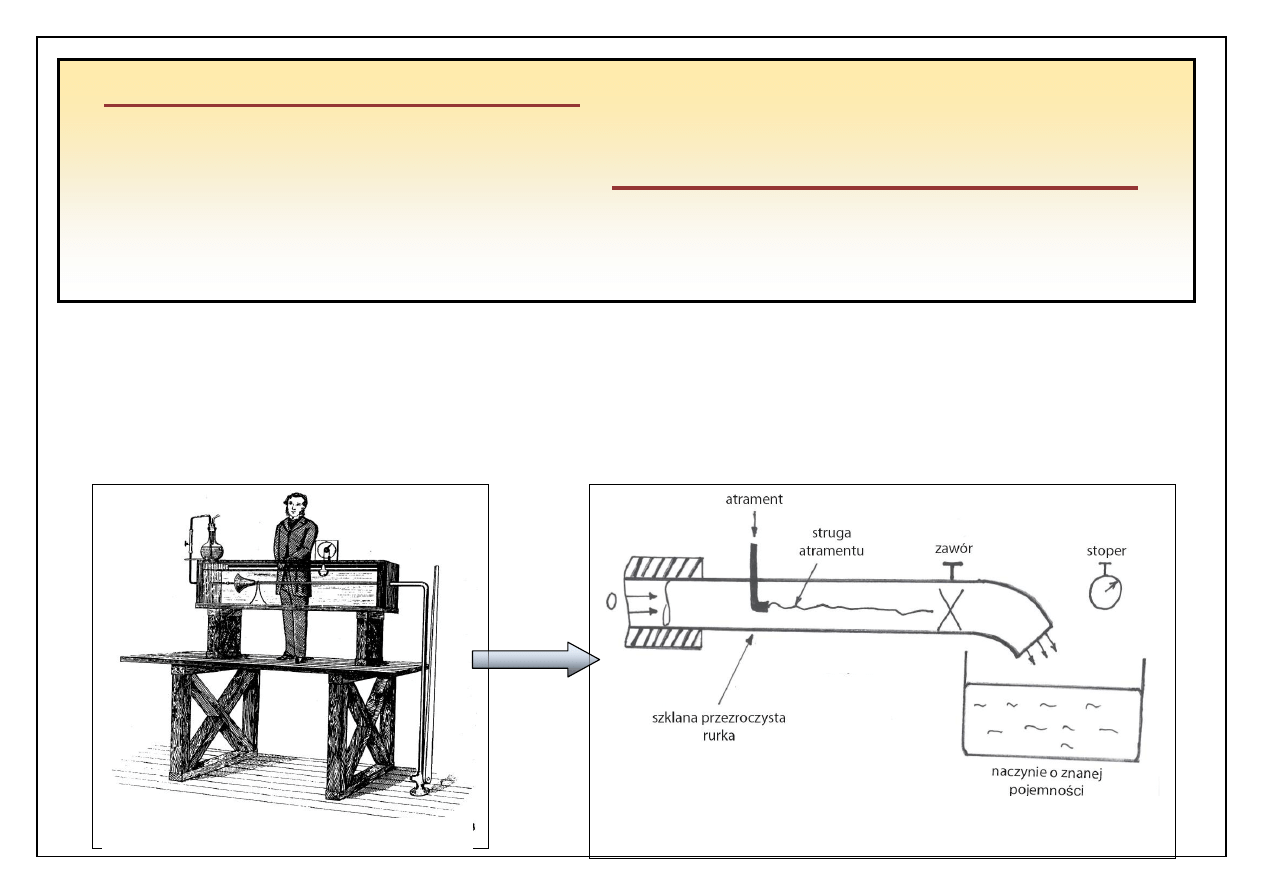
Osborne Reynolds wykonał elementarne doświadczenie: do
szkalnej rury wprowadził strugę barwnika.
Wzór Hagena – Poiseiuille’a określa wydatek w zależności od
spadku ciśnienia, rodzaju cieczy i geometrii przewodu.
Wzór ten jest poprawny tylko dla ruchów bardzo powolnych!
Dla ruchów szybkich, przy dużych wydatkach pomiary i
obliczenia dają radykalnie różne wyniki
http://misclab.umeoce.maine.edu/boss/classes/SMS_491_2003/Week_5.htm
1.
Małe wydatki – ruch powolny. Pole prędkości jest
parabolo
idalne, występuje tylko składowa wzdłużna.
2. Ruch szybszy. Pole
prędkości ma składowe poprzeczne,
zależy też od składowej wzdłużnej.
http://www.uic.edu/classes/me/me536/gallery.html
http://www.uic.edu/classes/me/me536/gallery.html
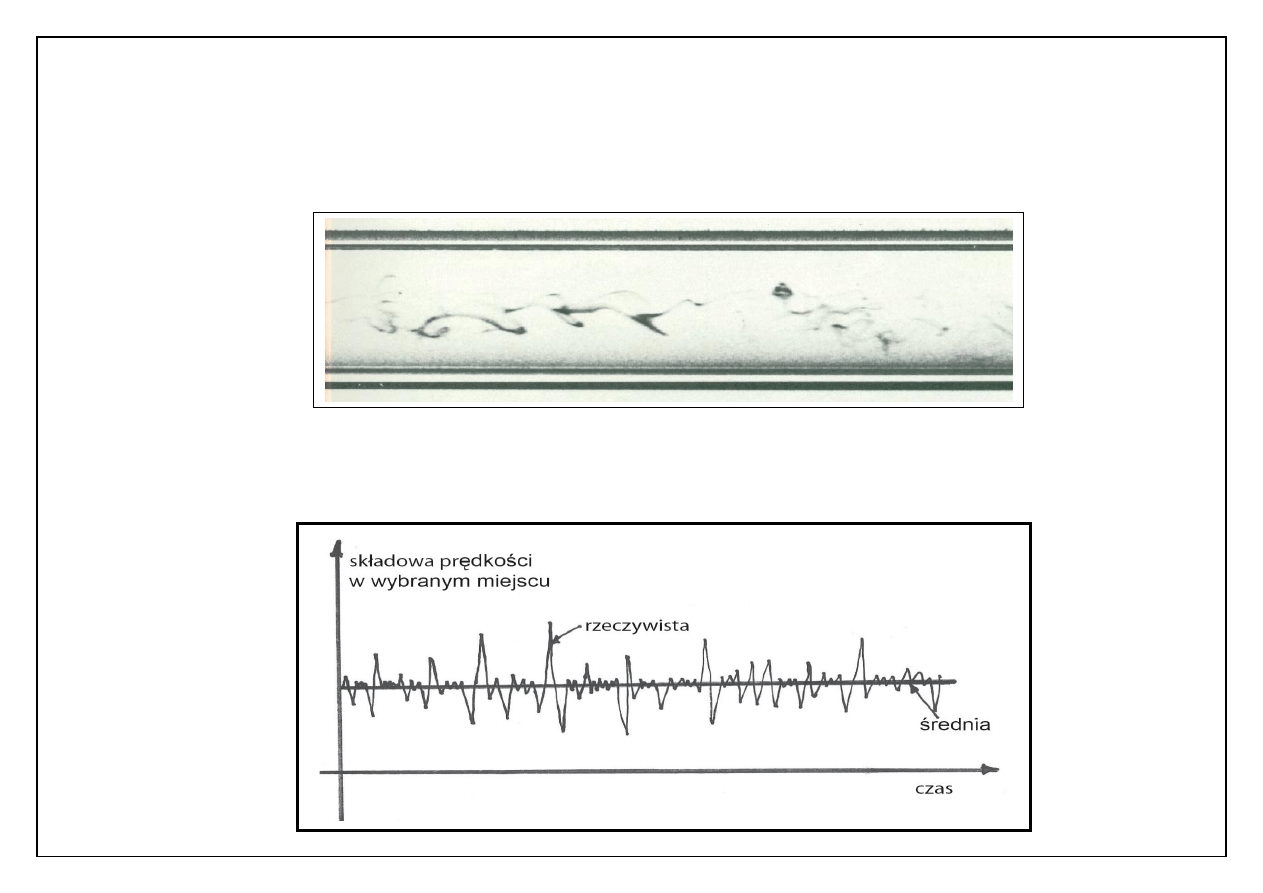
3. Ruch szybki.
Cząstki atramentu zachowują się podobnie
do cząstek dyfundującego gazu.
Zachodzą znaczące losowe zmiany prędkości
http://www.uic.edu/classes/me/me536/gallery.html
R
R
U
U
C
C
H
H
L
L
A
A
M
M
I
I
N
N
A
A
R
R
N
N
Y
Y
I
I
T
T
U
U
R
R
B
B
U
U
L
L
E
E
N
N
T
T
N
N
Y
Y
Profil prędkości średniej w rurze dla ruchu
turbulentnego
Ruch powolny, bez pulsacji
prędkości nazywa się
ruchem laminarnym.
W ruch
u tym wymiana masy, pędu i energii zachodzi
na drodze molekularnej.
Dla takiego ruchu w rurze
możemy korzystać ze wzoru
Hagena
– Poiseiuille’a.
Ruch szybki, dla którego zachodzą znaczące losowe
zmiany prędkości, a między sąsiednimi warstwami
płynu zachodzi wymiana masy, pędu i energii na
drodze wymiany elementów płynu to ruch turbulentny
R
R
Ó
Ó
W
W
N
N
A
A
N
N
I
I
A
A
B
B
E
E
Z
Z
W
W
Y
Y
M
M
I
I
A
A
R
R
O
O
W
W
E
E
I
I
P
P
O
O
D
D
O
O
B
B
I
I
E
E
Ń
Ń
S
S
T
T
W
W
O
O
T
– skala czasu,
L
-
skala długości,
p
0
– skala ciśnienia,
U
– skala prędkości.
Wielkości promowane nie mają wymiaru.
Wstawmy p
odane zależności do równania ciągłości.
'
'
k
k
0
k
k
t
T t ',
x
Lx ,
p
p p ',
v
Uv
'
'
k
k
k
'
'
k
k
k
Uv
v
v
U
diw v
0
x
L
x
Lx
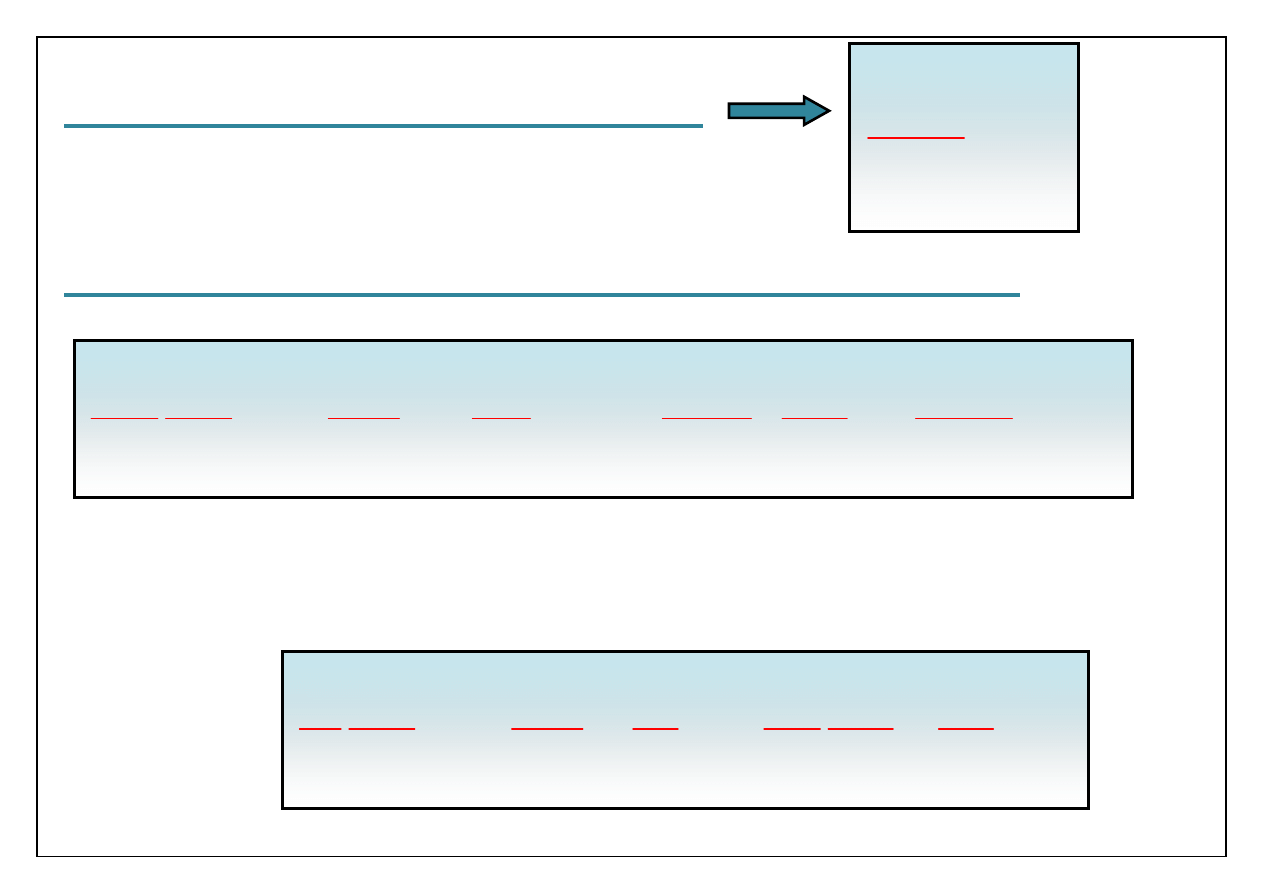
Bezwymiarowe równanie ciągłości
:
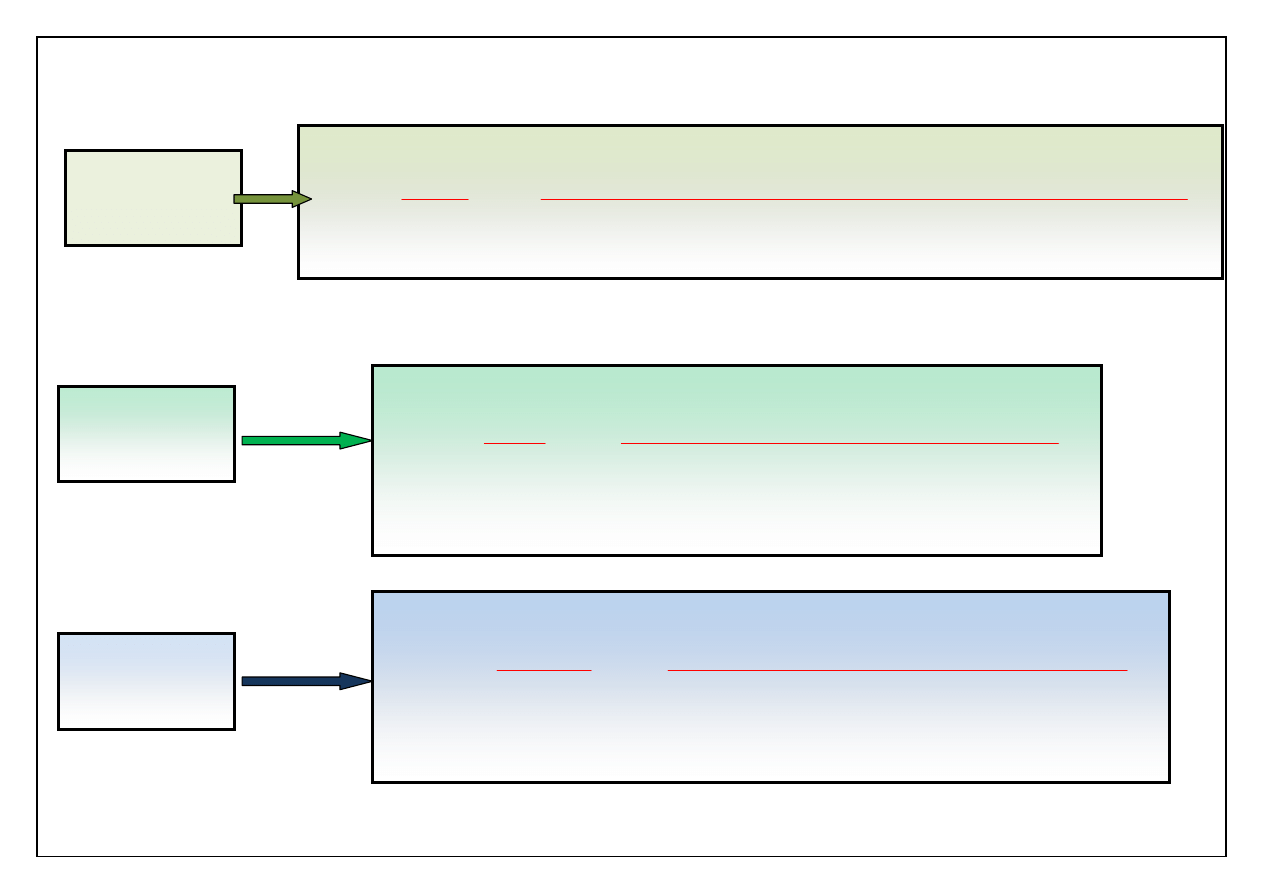
Bezwymiarowe równanie ruchu dla j – tej składowej
Zapiszmy to równanie używając pewnych liczb bezwymiarowych:
'
k
'
k
v
0
x
'
'
'
j
j
'
'
'
'
k
j
j
'
'
k
j
v
v
1
1
1
p
1
v
F
v
St
t
x
Fr
Eu x
Re
'
'
'
j
j
'
'
'
'
0
k
j
j
'
2
2
'
k
j
v
v
p
L
gL
p
v
F
v
UT
t
x
U
U
x
UL
L
L
I
I
C
C
Z
Z
B
B
Y
Y
P
P
O
O
D
D
O
O
B
B
I
I
E
E
Ń
Ń
S
S
T
T
W
W
A
A
UT
skala sil bezwladnosci
St
L
skala sil przyspieszenia loka ln ego
Liczba
Strouhala
Liczba
Froude’a
2
U
skala sil bezwladnosci
Fr
gL
skala sil masowych
Liczba
Eulera
2
0
U
skala sil bezwladnosci
Eu
p
skala sil cisnieniowych
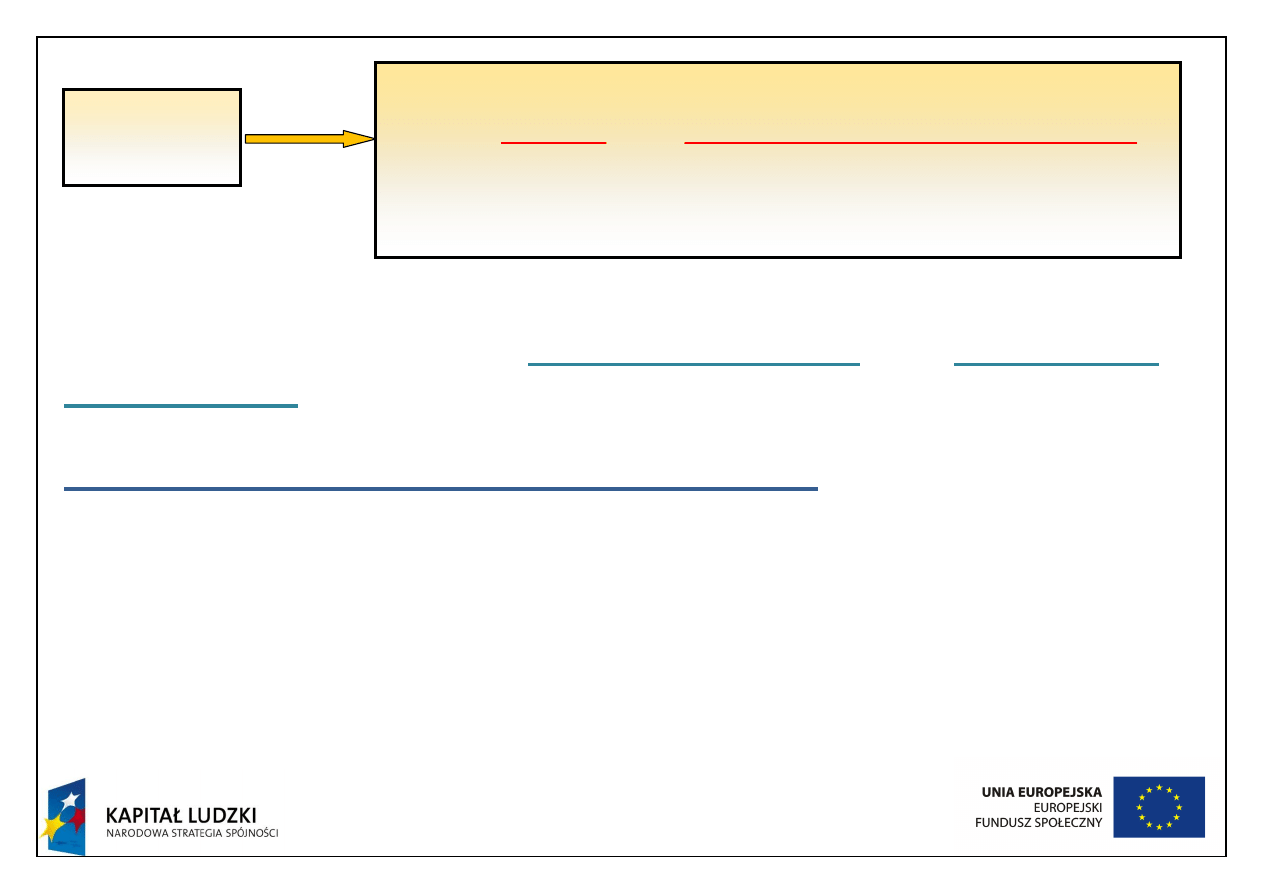
Liczby - Strouhala, Frouda, Eulera i Reynoldsa, czyli odpowiednio
St, Fr, Eu, Re noszą nazwę
liczb
podobieństwa
albo
parametrów
kryterialnych.
Dwa zjawiska są podobne dynamicznie gdy:
obszary ruchu są podobne geometrycznie
liczby podobie
ństwa są takie same
bezwymiarowe warunki brzegowe i bezwymiarowe warunki
początkowe są identyczne
Liczba
Reynoldsa
UL
skala sil bezwladnosci
Re
skala sil lepkosci