1

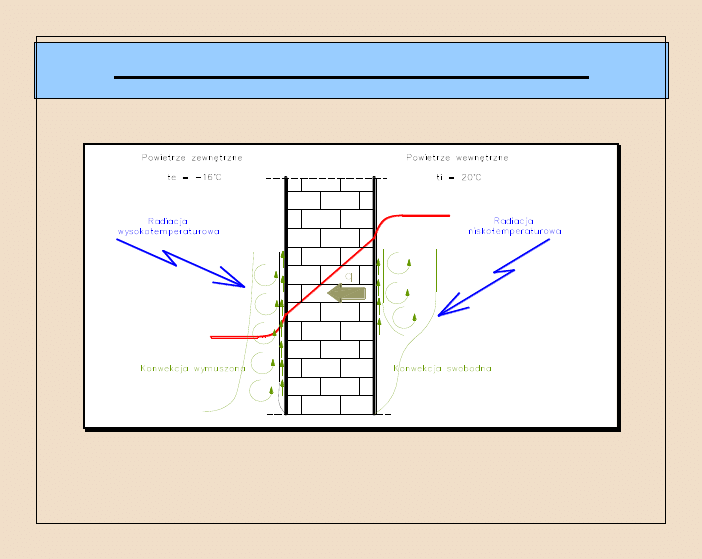
Wymiana ciepła przez przewodzenie.

Proces wymiany ciepła przez przegrodę jednowarstwową

2

POZ.
NADCIĄG

0,00=112,87

+

-

112,85

POZ. 4.3.1

POZ. 4.5

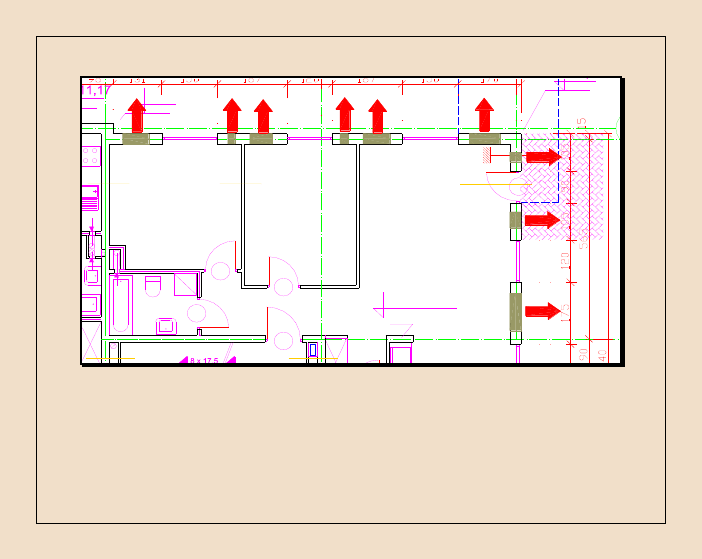
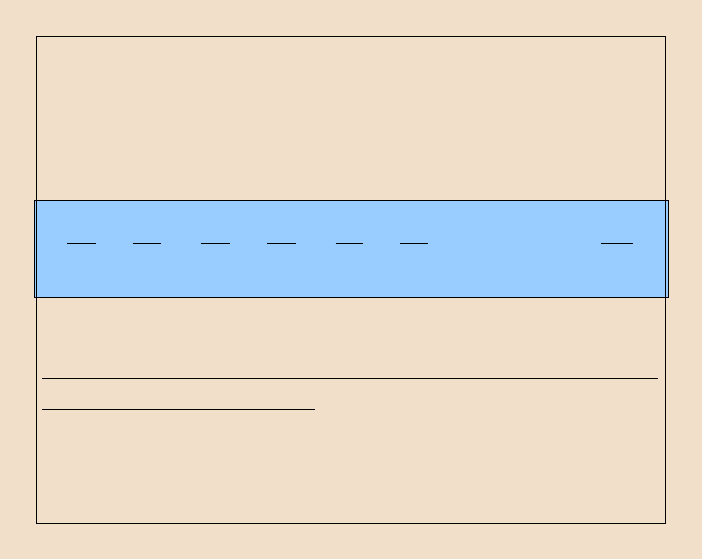
Obszary jednokierunkowego przepływu ciepła w budynku

3

Przepływ ciepła przez obszary zaburzeń geometrii przegrody.

4

Przewodzenie ciepła w ciałach stałych w sposób ilościowy opisuje empiryczne

prawo Fouriera:

q = -



grad t

,

gdzie:

q - wektor gęstości strumienia cieplnego,



- współczynnik przewodzenia ciepła ,

t - temperatura .

5

W ogólnym przypadku , w kartezjańskim układzie współrzędnych, wektor q ma

trzy składowe, q

x

, q

y

i q

z

, przy czym :

x

t

q

x











y

t

q

y











z

t

q

z











6

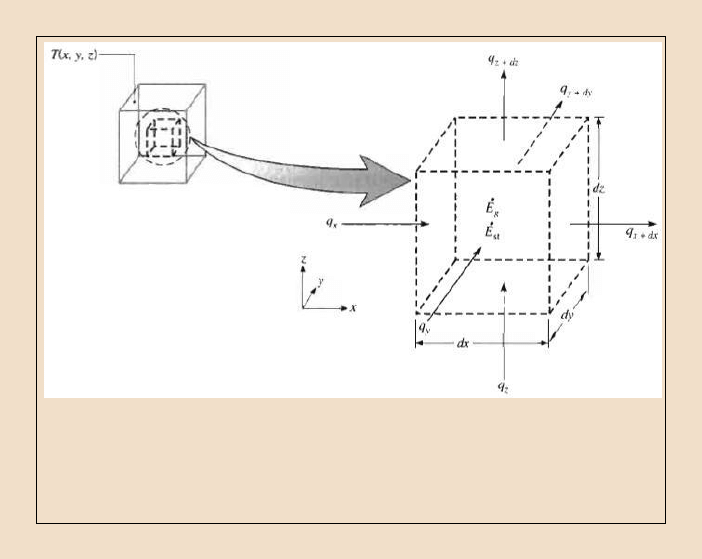
Przewodzenie ciepła przez elementarny prostopadłościan ciała stałego.

7

Przez powierzchnię odległą o x od początku układu współrzędnych dopływa do

elementu, w czasie d



, ilość ciepła:

przez powierzchnię zaś odległą o x + dx odpływa ciepło:



d

dz

dy

dx

q

q

dQ

x

x

x

x





















''

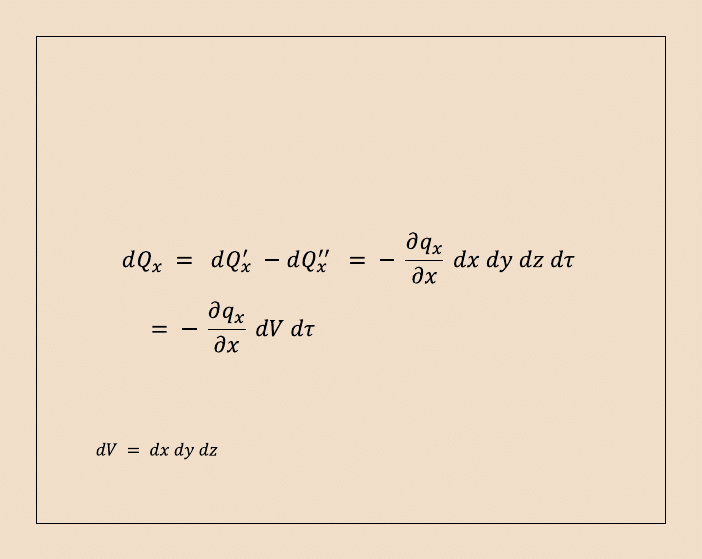
8

Różnica między ilością ciepła dopływającego a ilością ciepła odpływającego z

elementu w kierunku osi OX układu współrzędnych, wynosi:

gdzie:

jest objętością rozpatrywanego prostopadłościanu.

9

Podobnie, różnica pomiędzy ilością ciepła doprowadzonego a ilością ciepła

odprowadzonego z elementu w kierunku osi OY układu współrzędnych wynosi :

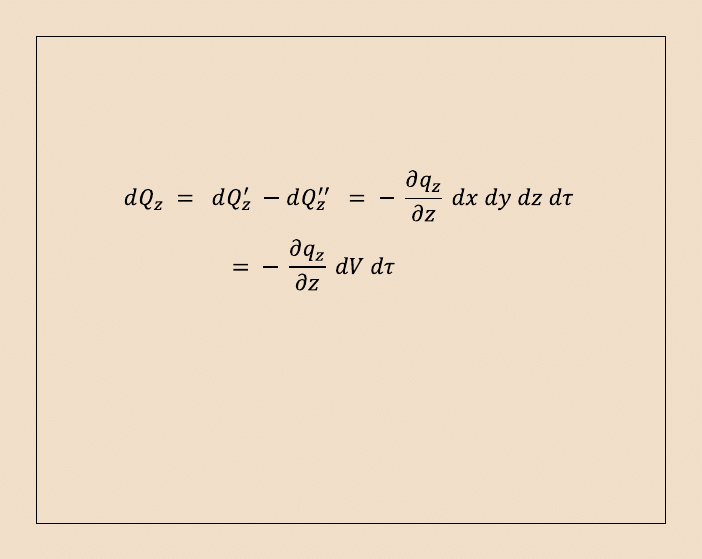
10

i odpowiednio w kierunku osi OZ układu współrzędnych :

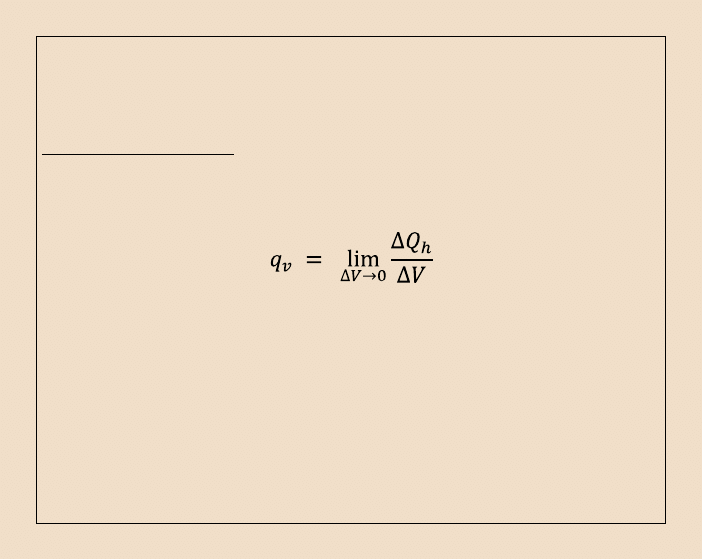
11

Miarą natężenia wydzielania się energii wewnętrznego źródła jest tzw.

wydajność żródła ciepła q

v ,

która jest równa:

gdzie:



Q

h

- ciepło wydzielające w ciągu jednostki czasu w objętości



V rozważanego układu.

12

Bilans energetyczny prostopadłościanu odniesiony do okresu czasu d



z

uwzględnieniem możliwości wewnętrznego wydzielania się ciepła można wyrazić

opisowo w następujący sposób:

ciepło doprowadzone do prostopadłościanu – ciepło

odprowadzone z prostopadłościanu + ciepło wydzielone w

elemencie =

= przyrost energii wewnętrznej prostopadłościanu + praca

zewnętrzna.

13

Matematycznym wyrażeniem bilansu energetycznego jest więc równanie:

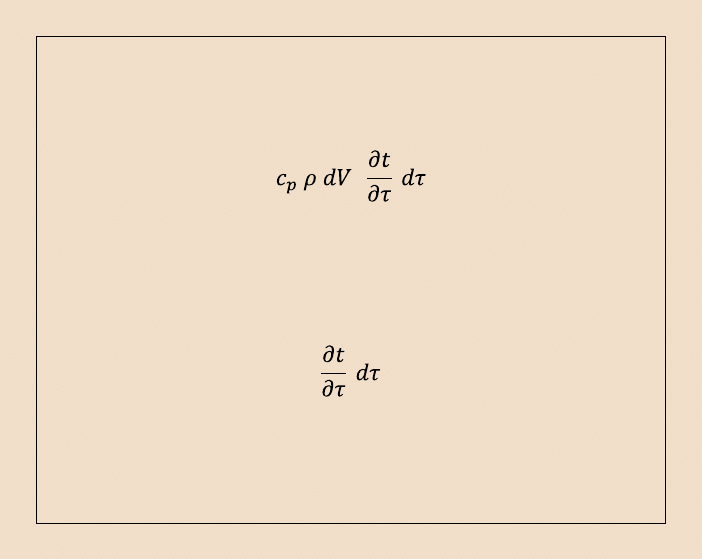
14

Człon równania bilansu cieplnego:

oznacza przyrost entalpii prostopadłościanu w czasie d



, gdyż jego temperatura

ulegnie wówczas zmianie o:

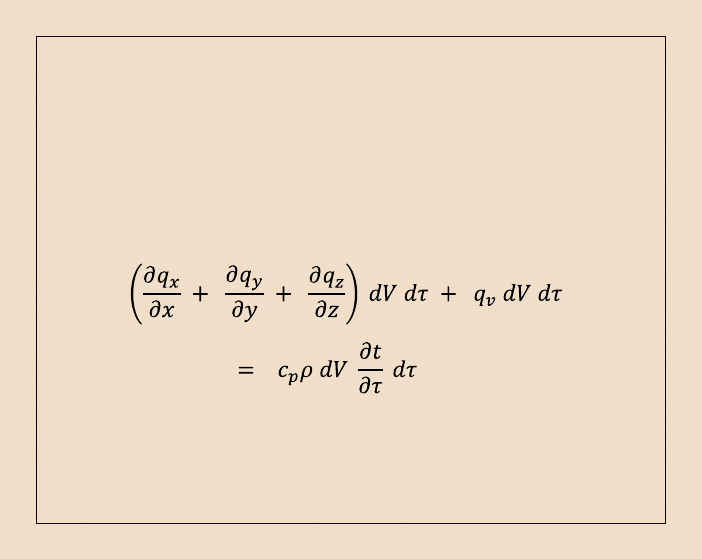
15

Podstawiając poprzednio otrzymane wyrażenie na różnice ilości ciepła dQ

’

x

- dQ

”

x

,

dla poszczególnych kierunków głównych układu współrzędnych, równanie bilansu

można przedstawić w następującej postaci:

16

Skracając całe równanie przez dV d



oraz podstawiając wartości q

x

, q

y

i q

z

otrzymuje się:











































































t

c

q

z

t

z

y

t

y

x

t

x

p

v

Jest to ogólne równanie przewodzenia ciepła w ciele izotropowym z uwzględnieniem

wewnętrznego wydzielania się ciepła.

17

W większości przypadków praktycznych można założyć, że przynajmniej w pewnym

obszarze zmienności temperatur, wartość przewodności cieplnej nie zależy od

temperatury i jest stała.

 

const

t





18

Przyjęcie warunku



(t) = const pozwala sprowadzić równanie przewodnictwa

cieplnego do równania liniowego o postaci :



















t

c

q

t

c

p

v

p

2

,

gdzie:

2

2

2

2

2

2

2

z

y

x





















, jest symbolem laplasjanu drugiego rzędu

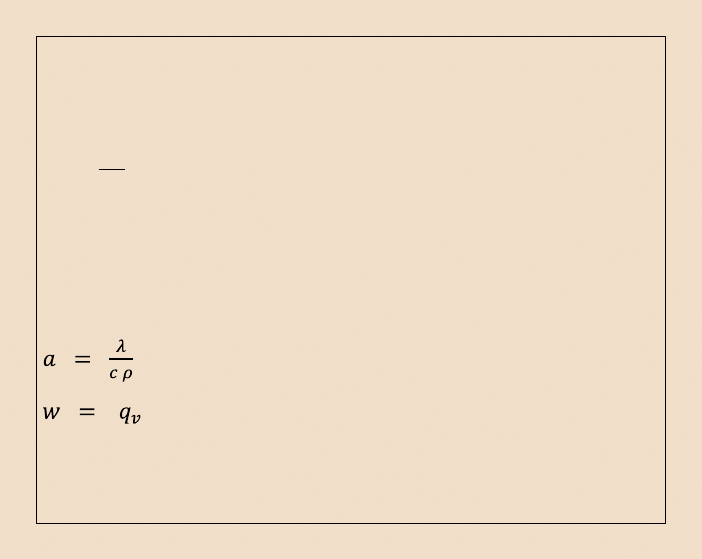
19

W większości zagadnień fizyki budowli można przyjąć z dostateczną dokładnością,

że ciepło właściwe materiału nie zależy od temperatury:

0







t

c

,

Oznaczając:

- tzw. współczynnik wyrównywania temperatury oraz

- natężenie źródeł cieplnych na jednostkę objętości i jednostkę

czasu ,

20

Można równanie przewodnictwa cieplnego zapisać w powszechnie stosowanej

postaci:

t

a

t

2











równania przewodnictwa cieplnego bez źródeł, oraz w postaci:





p

c

w

t

a

t











2

,

tzw. równania dyfuzji lub przewodnictwa cieplnego ze źródłami.

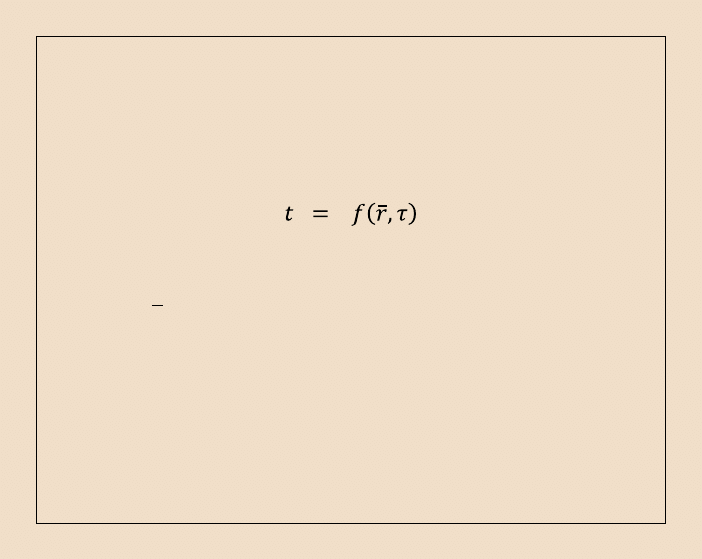
21

Rozwiązanie równania różniczkowego przewodnictwa cieplnego w dowolnym ciele

stałym lub układzie ciał polega na określeniu pola temperatury, tj. podania zależności

funkcyjnej temperatury od współrzędnych przestrzennych i czasu w postaci:

gdzie:

r

- wektor określający położenie punktu w wybranym

układzie współrzędnych.

22

Jeżeli temperatura zależy od czasu, to pole temperatury nosi nazwę nieustalonego

(lub niestacjonarnego).

Jeżeli temperatura w każdym punkcie jest stała w czasie:

0

)

,

,

,

(











z

y

x

f

to pole temperatury nazywa się jako ustalone lub stacjonarne.

23

Ustalone pole rozkładu temperatury uzyskuje się je jako rozwiązanie równania

przewodnictwa , w którym temperatura nie zależy od czasu:

0

2





t

- równanie Laplace

’

a

lub

0

2









w

t

równanie Poissona.

24

Prowadząc dalej rozważania zmierzające do uproszczenia modelu matematycznego

przewodzenia ciepła, można przyjąć założenie , że dla licznych zagadnień

temperatura elementów budowli zmienia się wzdłuż tylko jednej osi układu

współrzędnych, a wzdłuż pozostałych nie odbywa się przepływ ciepła:

0













z

t

y

t

,

i stąd:

Pole temperatury opisane powyższym równaniem nazywamy jednowymiarowym.

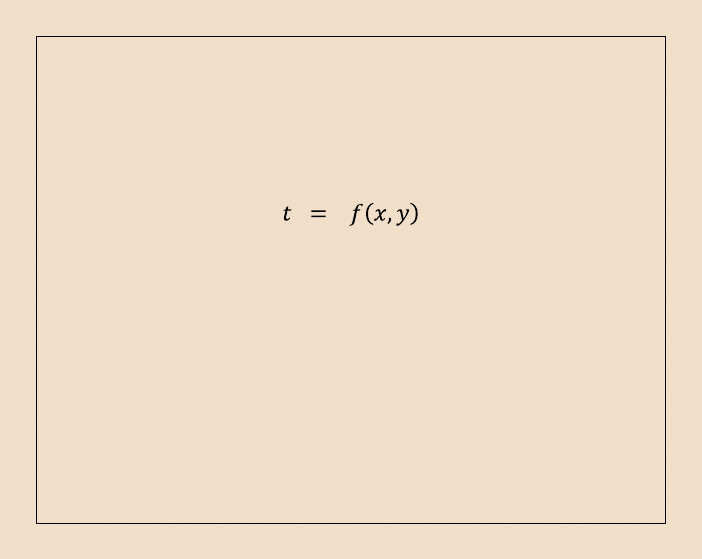
25

W miejscach zaburzeń geometrii elementu (np. w narożach pomieszczeń) lub

miejscach niejednorodnej budowy elementów często jest konieczne jest

rozpatrywanie dwuwymiarowego pola temperatury, najczęściej ustalonego, postaci:

W ogólnym przypadku, gdy przepływ ciepła ma charakter trójwymiarowy i

niestacjonarny, rozwiązanie równania przewodnictwa cieplnego wymaga określenia

warunku początkowego.

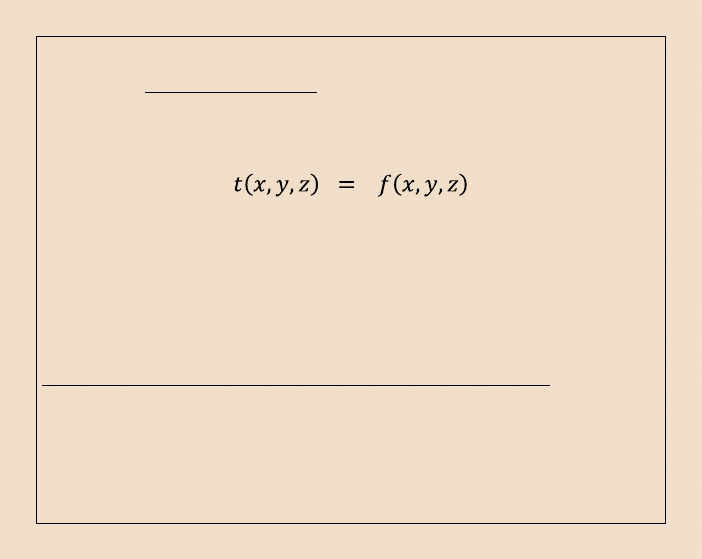
26

Pod pojęciem warunku początkowego należy rozumieć pole rozkładu temperatury w

rozpatrywanym obszarze w chwili



= 0 :

Poza warunkiem początkowym, rozwiązanie szczególne niestacjonarnego równania

przewodnictwa cieplnego wymaga określenia warunków jednoznaczności

rozwiązania, które nazywamy warunkami brzegowymi.

Warunki brzegowe opisują sposób wymiany ciepła na granicy obszaru o

jednorodnych cechach cieplnych , w którym przewodzenie ciepła jest opisane

jednym równaniem.

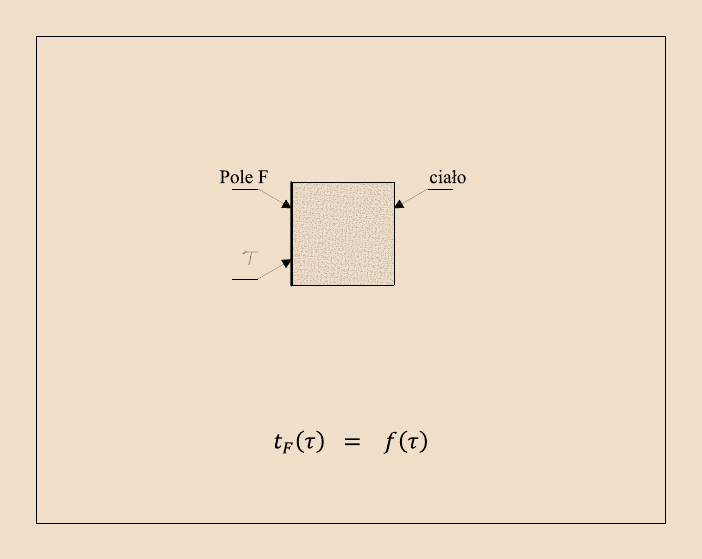
27

W pracach podstawowych na temat teorii przewodnictwa cieplnego wyróżnia się

następujące przypadki warunków brzegowych:

-

warunek brzegowy I rodzaju

stałe

t

F

( )

ma miejsce gdy znany jest rozkład temperatury na brzegu obszaru w

dowolnej chwili :

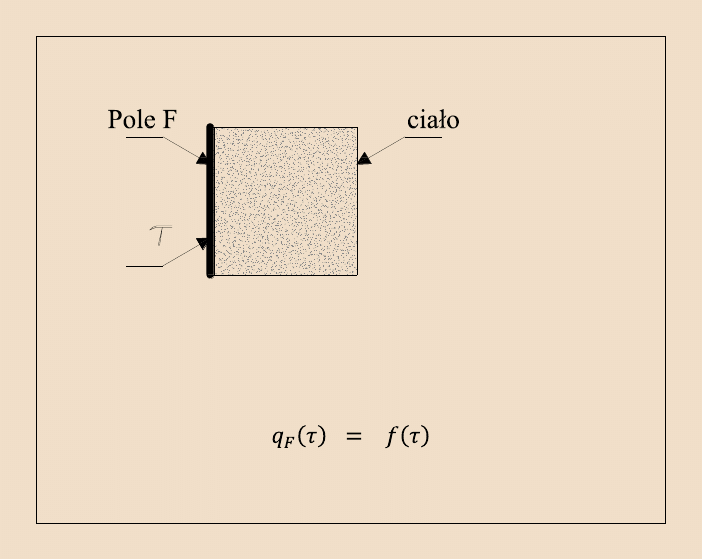
28

-

warunek brzegowy II rodzaju

stałe

q

F

( )

ma miejsce gdy znany jest rozkład gęstości strumienia cieplnego

na brzegu obszaru w dowolnej chwili:

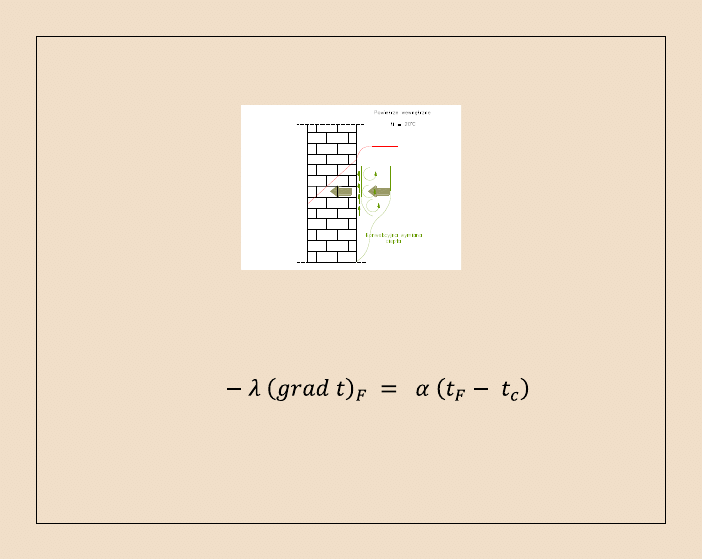
29

-

warunek brzegowy III rodzaju

q

p

q

k

ma miejsce gdy wymiana ciepła na brzegu obszaru odbywa się według

prawa Newtona :

gdzie:

t

c

- temperatura otaczającego ośrodka;

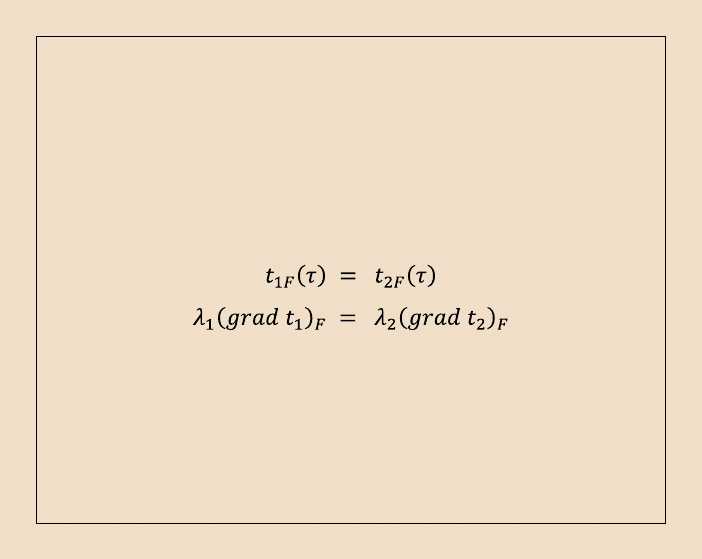
30

-

warunek brzegowy IV rodzaju

obejmuje warunki ciągłości temperatury i gęstości strumienia cieplnego na

brzegu wspólnym dla obszarów, w których przewodzenie ciepła jest opisane

różnymi równaniami np. wskutek różnych właściwości cieplnych materiałów:

31

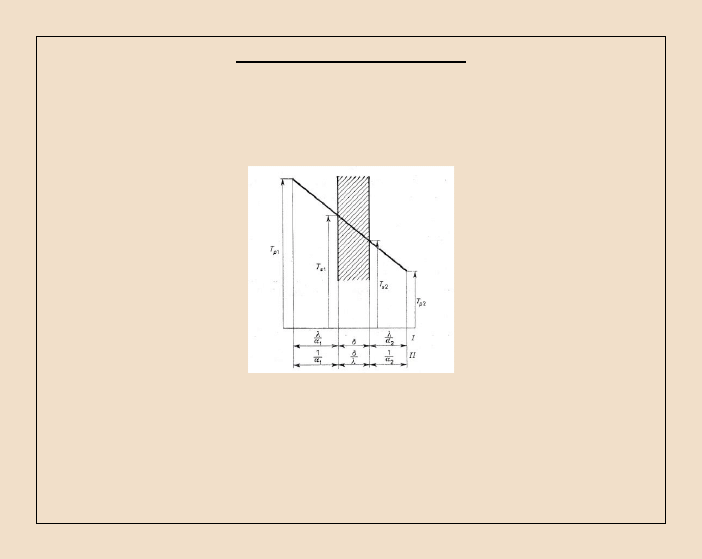
Ustalone przewodzenie ciepła.

Rozważmy przypadek przewodzenia ciepła przez warstwę materiału ograniczoną

dwiema równoległymi płaszczyznami, przy czym przepływ ciepła odbywa się w

kierunku wyłącznie prostopadłym do płaszczyzn ograniczających tę warstwę.

Rozkład temperatury na grubości jednorodnej warstwy

materiału przy warunkach brzegowych I rodzaju.

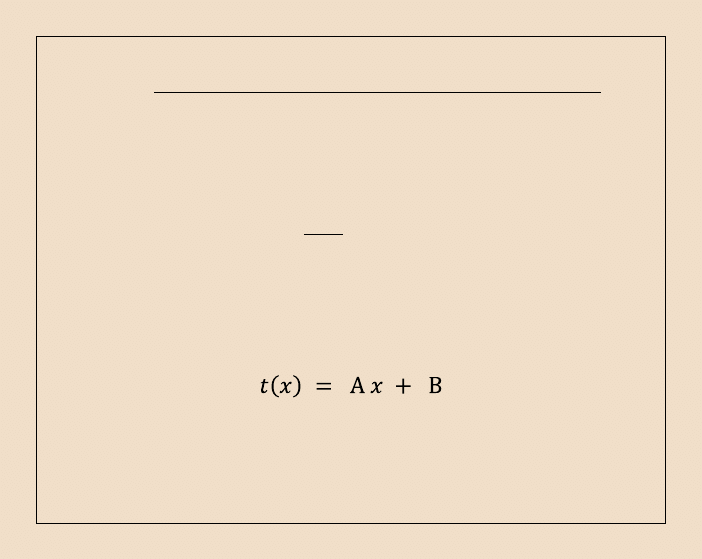
32

Zakłada się, że współczynnik przewodzenia ciepła jest stały na całej grubości

warstwy. W takim przypadku równanie ustalonego przepływu ciepła ( równanie

Laplace

,

a) sprowadza się do postaci:

0

2

2



dx

t

d

,

i ma rozwiązanie ogólne, wyznaczone przez dwukrotne całkowanie:

Postać stałych A i B zależy od typu warunków brzegowych.

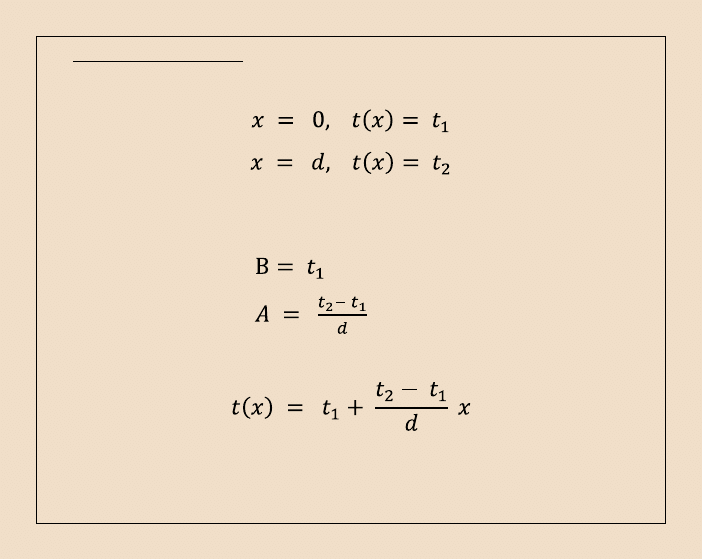
33

Dla warunku brzegowego I rodzaju na powierzchniach granicznych, w postaci:

stałe całkowania są równe :

Stąd rozwiązanie dane jest wzorem:

34

Dla warunku brzegowego III rodzaju na obu powierzchniach granicznych w

postaci:

x = 0,

 





0

1

1

t

t

dx

dt











x = d,

 





2

2

t

d

t

dx

dt











gdzie:

t

1

, t

2

- temperatury ośrodków rozdzielonych ścianką ,



1 ,



2

- współczynniki przejmowania ciepła na

powierzchniach ,

35

stałe całkowania są równe:

U

t

t

t

1

1

2

1

B









U

t

t



1

2

A





gdzie:

2

1

1

1

1













d

U

Wielkość U, która opisana jest powyższym wzorem, nazywamy współczynnikiem

przenikania ciepła.

36

Podstawiając stałe całkowania do rozwiązania ogólnego, można przedstawić postać

rozwiązania szczególnego równania przewodnictwa cieplnego dla przyjętych

założeń:

Ux

t

t

U

t

t

t

x

t





1

2

1

1

2

1

)

(











Opierając się na prawie Fouriera , można obliczyć gęstość strumienia cieplnego,

przepływającego przez warstwę w omówionych warunkach:

-

dla warunków brzegowych I rodzaju na powierzchniach granicznych:

37

R

t

t

dx

dt

q

1

2











gdzie:



d

R



- opór przewodzenia ciepła ,

- dla warunków brzegowych III rodzaju na powierzchniach

granicznych





k

R

t

t

t

t

U

q

1

2

1

2









gdzie:

U

R

k

1



- opór przewodzenia ciepła.

38

Współczynnik przenikania ciepła U charakteryzuje statyczną pracę przegród

zewnętrznych. W rzeczywistości przegrody, na skutek zmiennych w czasie

wymuszeń zewnętrznych (takich jak temperatura powietrza zewnętrznego i

wewnętrznego , prędkość wiatru współczynnik przejmowania ciepła ) „pracują” jako

układy dynamiczne. W pewnych warunkach może doprowadzić do wystąpienia

bardzo dużych błędów w ocenie termoizolacyjności przegrody.

39

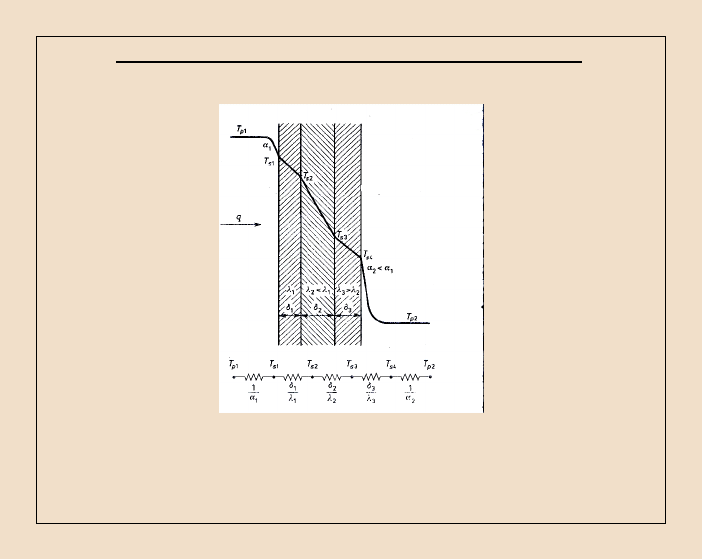
Ustalone przewodzenie ciepła przez ściankę wielowarstwową.

Rozkład temperatury na grubości ścianki wielowarstwowej.

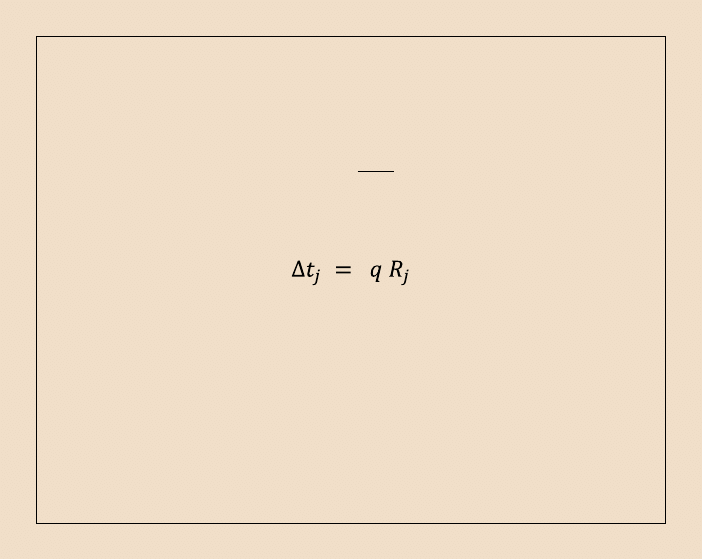
40

W każdej z warstw gęstość strumienia ciepła określona jest wzorem:

j

j

R

t

q





stąd różnicę temperatury na powierzchniach ścianki wyznaczamy jako:

a różnicę temperatury na powierzchniach ścianki wielowarstwowej













j

j

j

j

R

q

t

t

41

W związku z powyższą zależnością, dla ścianki wielowarstwowej opór

przewodzenia ciepła jest sumą oporów poszczególnych warstw, jak i – co łatwo

udowodnić – oporów cieplnych szczelin powietrznych.

Stąd też współczynnik przenikania ciepła dla ścianki wielowarstwowej wyraża się

wzorem:









j

j

R

U

2

1

1

1

1





Powyższe wyprowadzenie wzoru opisującego przewodzenie ciepła można

przeprowadzić również inaczej ( będzie ono nawet bardziej poprawne z

matematycznego punktu widzenia).

42

Rozwiązanie można osiągnąć poprzez rozwiązanie układu równań Laplace

’

a:



























0

.....

..........

..........

0

0

2

2

2

2

2

2

1

2

dx

t

d

dx

t

d

dx

t

d

n

gdzie:

n - numer warstwowy.

43

Warunkami jednoznaczności rozwiązania są warunki brzegowe trzeciego rodzaju na

brzegach ścianki:

x = 0 ,





)

0

(

1

1

t

t

dx

dt











,

x = d ,





n

n

t

d

t

dx

dt







)

(





,

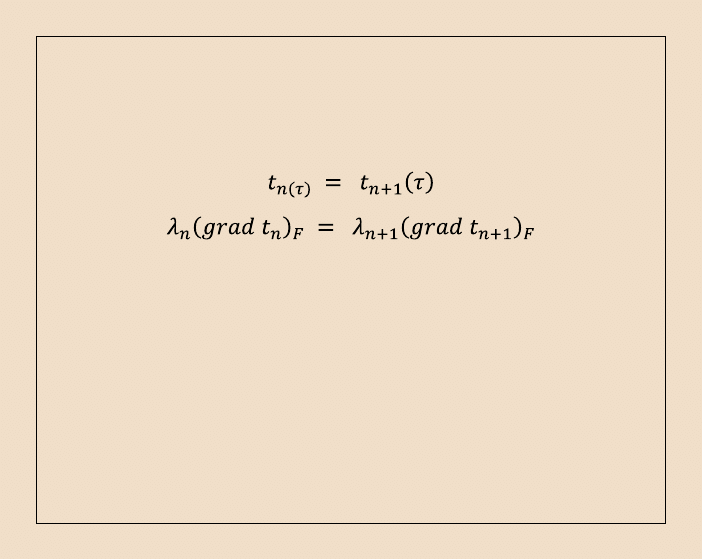
44

Na powierzchniach styku między poszczególnymi warstwami należy przyjąć

warunki brzegowe czwartego rodzaju:

Współczynnik przenikania ciepła U przeważnie oblicza się dla przegród

zewnętrznych , oddzielających powietrze wewnętrzne o temperaturze t

i

od

zewnętrznego o temperaturze t

e

.

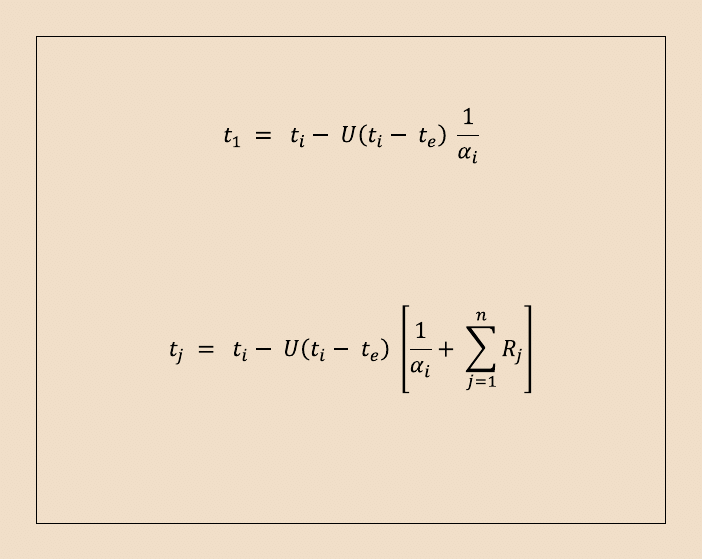
45

Temperaturę powierzchni wewnętrznej ( od strony napływu ciepła ) można wyliczyć

ze wzoru:

a na styku j – tej i j + 1 warstwy ( numerując warstwy od strony napływu ciepła )

obliczamy ze wzoru: