Finanse – materiały do studiowania nr 7

Instrumenty finansowe – analiza i wycena

Problem 1. W dniu 19 maja 2007 roku bank centralny zawarł z bankiem komercyjnym transakcję repo na 125 000
szt. papierów wartościowych po cenie zakupu 93 zł. Bank komercyjny zobowiązał się je odkupić po cenie 93,10 zł w
dniu 26 maja 2007 roku. Jakie było oprocentowanie transakcji?

Oprocentowanie transakcji repo: i = (cena odsprzedaży – cena zakupu) / cena zakupu * 360 /t

i = (93,1 – 93) / 93 * 360 / 7 = 5,53%.

Odp. Oprocentowanie tej transakcji w skali roku wynosiło 5,53%.



Problem 2. Bank komercyjny poszukuje środków finansowych na poprawę płynności. Ustal czy powinien
zaciągnąć pożyczkę w banku centralnym, według stopy z problemu 1, czy tez na rynku międzybankowym – WIBOR
– 5,3%.

Odp. Oprocentowanie środków na rynku międzybankowym jest niższe, a więc powinien tam poszukiwać
krótkoterminowego kapitału.



Problem 3.
Bank otrzymał do dyskonta weksel pochodzący z obrotu gospodarczego w wysokości 100 000 zł, płatny za 3
miesiące.

1)

Wyjaśnij, co to jest weksel i czym się różni weksel własny od trasowanego.

2)

Jaką kwotę bank wypłaci klientowi przy stopie dyskontowej 12% (prowizja za usługę wynosi 0,5%, nie mniej
niż 100 zł).

Korzystamy ze wzoru na dyskonto wekslowe:

365

*

*

t

d

Sw

D

=

, gdzie:

D - wartość dyskonta,
Sw – suma wekslowa,
d – stopa kredytu dyskontowego,
t – czas pozostały do wykupu weksla
365 – liczba dni w roku.

D = 100 000 zł * 0,12 * 90 dni / 365 dni = 2 958,9 zł.
P = 100 000 zł *0,005 = 500 zł.
Kwota wypłacona klientowi: 100 000 – 2 958,9 – 500 = 96 541,1 zł.

Odp. Bank wypłaci klientowi 96 541,1 zł, tj. 96,5% sumy wekslowej.



Problem 4.
Spółka Komtech, sp. z o.o. w dniu 17 maja 2005 roku jako zapłatę za towar wręczyła spółce Kwiatkowski Druk,
spółka jawna z siedzibą w Olsztynie, weksel płatny w 136 dni po dacie wystawienia. W imieniu wystawcy weksel
wypełniła Ćwiklińska, wystawiając go w Ostródzie, wskazując jako domicyliata Bank Śląski, O/Ostróda. Weksel
został wystawiony na sumę 34 576 zł. Dnia 14 czerwca 2005 r. spółka Kwiatkowski Druk przeniosła za pomocą
indosu prawa z tego weksla na spółkę ALMA S.A., wręczając ten weksel jako zapłatę za zakupione materiały
drukarskie (w imieniu spółki Kwiatkowski Druk podpisali się Kwiatkowski i Kwiatkowska).
Spółka ALMA dnia 28 czerwca 2005 r. przedstawiła ten weksel do dyskonta w Banku Złoty Interes. Stopa dyskonta
weksli, wynosiła 8% w skali roku, a bank za tę operację pobierał prowizję w wysokości 0,2% sumy wekslowej, nie
mniej niż 40 zł.
W dniu 14 lipca 2005 r. weksel ten został przyjęty przez Narodowy Bank Polski do redyskonta. Stopa redyskonta
wynosiła 5,5%.
Na podstawie powyższych informacji ustal nominalny zysk Banku Złoty Interes SA na tym instrumencie
finansowym.

Termin płatności weksla: 17.05.2005 r. + 136 dni, tj. 14 + 30 + 31 +31 +30, czyli 30 września 2005 roku.

Finanse – materiały do studiowania nr 7

Dyskonto weksla przez Bank Złoty Interes w dniu 28.06, czyli 136 – 14 – 28 = 94 dni przed terminem płatności.
Korzystam ze wzoru na dyskonto wekslowe:

365

*

*

t

d

Sw

D

=

,

D = 34 576 zł * 0,08 * 94 dni / 365 dni = 712,36 zł,
P = 34 576 zł * 0,002 = 69,15 zł
Bank Złoty Interes zapłaci spółce ALMA: 34 576 – 712,36 – 69,15 = 33 794,49 zł.

Redyskonto weksla przez NBP w dniu 14.07, czyli 17 +31 +30 = 78 dni przed terminem płatności:
Korzystam ze wzoru na dyskonto wekslowe:

365

*

*

t

d

Sw

D

=

,

RD = 34576 zł * 0,055 * 78 dni / 365 dni = 408,39 zł
Bank Złoty Interes otrzyma: 34 576 – 408,39 = 34 167,61 zł

Nominalny zysk: 34 167,61 – 33 794,49 = 373,12 zł.

Stopa zwrotu z inwestycji (16-dniowa) = 373,12 / 33 794,49 = 1,1%
Stopa zwrotu z inwestycji (roczna) = 1,1% * 365 / 16 = 25,18%.

Odp. Bank Złoty Interes zarobi na tej transakcji 373,12 złotych w okresie 16 dni.



Problem 5.
Bank centralny, wykonując operację bezwarunkowego zakupu bonów skarbowych 180-dniowych, kupił je po cenach
odpowiadających 90% ich wartości nominalnej. Wartość nominalna to 10 000 zł.

1)

Wymień znane Tobie instrumenty rynku pieniężnego.

2)

Scharakteryzuj bony skarbowe.

3)

Oblicz, jakie oprocentowanie (stopę zwrotu) w skali roku dla lokat 180-dniowych chce uzyskać bank
centralny na powyższej operacji.

100

×

=

kapitału

anego

zainwestow

wartość

(netto)

korzyści

ch

osiągnięty

suma

zwrotu

Stopa

Dyskonto (korzyść): 10 000 zł * (1-0,9) = 1 000 zł.
Kwota zainwestowana: 10 000 zł – 1 000 zł = 9 000 zł.
Stopa zwrotu (za 180 dni): 1 000 / 9 000 * 100 = 11,11%.
Roczna stopa zwrotu: 11,11% * 365 / 180 = 22,53%

Odp. Bank centralny wykonując operację bezwarunkowego zakupu 180-dniowych bonów skarbowych chce
uzyskać 22,53% stopę zwrotu w skali roku.



Problem 6.
Oblicz, jaką cenę za bon pieniężny o wartości nominalnej 10 000 zł z 28-dniowym terminem wykupu musi
zaoferować emitent, aby uzyskać stopę dochodowości na poziomie nie niższym niż 10% w skali roku.
Scharakteryzuj ten instrument finansowy.

Stopa zwrotu >= 10%
Stopa zwrotu = (cena nominalna – cena rynkowa zakupu = dyskonto) / (cena rynkowa zakupu) *100% * 365 dni /
termin wykupu instrumentu, czyli:

(10 000 zł – Cr)/Cr *100 % * 365/28 >= 10%

(10 000 zł – Cr)/Cr >= 0,1 * 28/365

10 000 zł >= Cr * 0,1 * 28/365 + Cr

Cr <= 10 000 / (1 + 0,1 * 28/365)

Cr <= 9 923,87 zł.

Odp. Emitent musi zaoferować cenę nie wyższą niż 9923,87 zł, aby potencjalny nabywca osiągnął co najmniej
10% stopę rentowności.

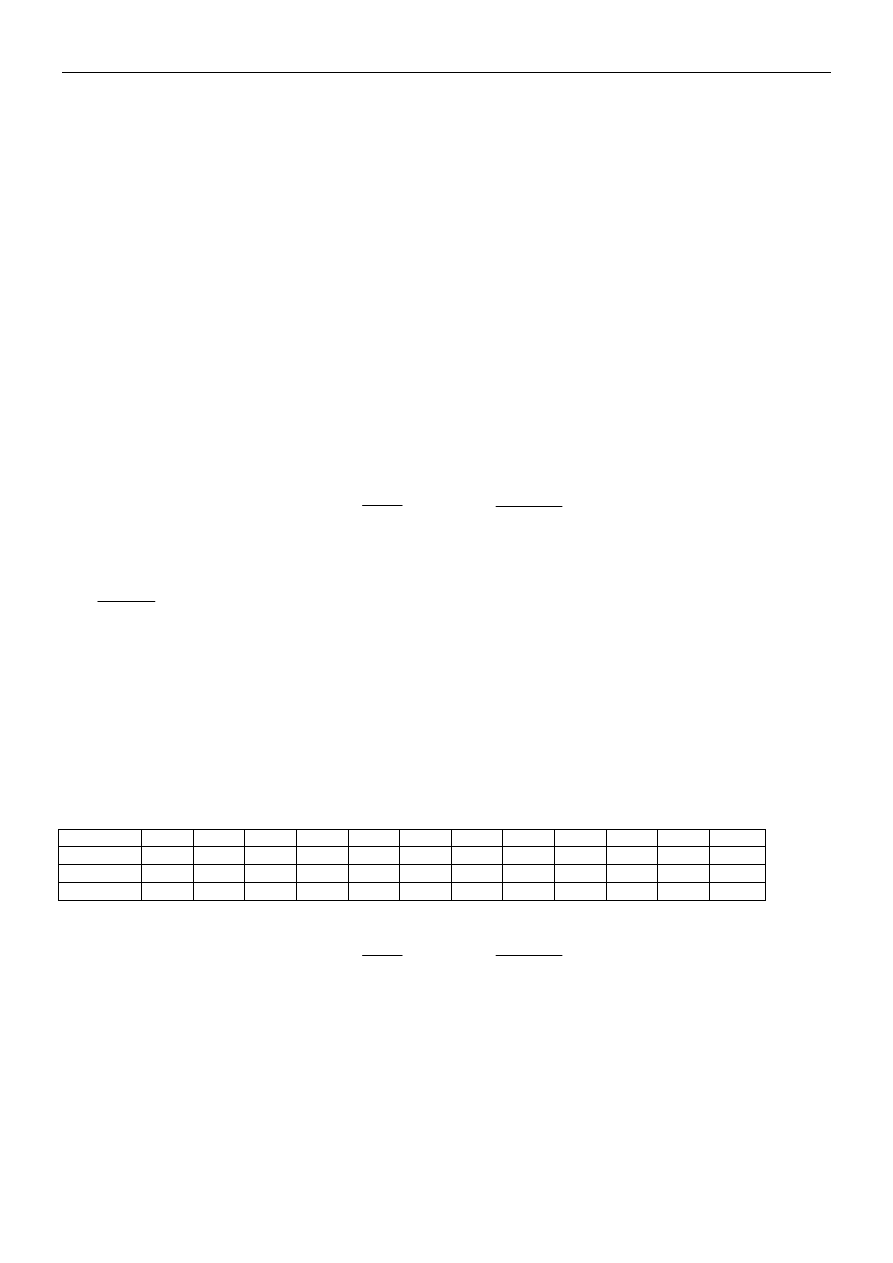
Finanse – materiały do studiowania nr 7

Problem 7. Uszereguj niżej wymienione inwestycje finansowe według stopy zwrotu oraz według stopnia ryzyka:
-

obligacje skarbowe oprocentowane 5,75% w skali roku,

-

akcje przedsiębiorstwa „X” – stopa dywidendy 7%, zakładany wzrost wartości akcji 4% rocznie,

-

obligacje przedsiębiorstwa „Y” – kupon – 9%,

-

obligacje komunalne oprocentowane 6% w skali roku.

Odpowiedź:
Uwzględniając stopę zwrotu najwięcej zarobię na akcjach, dalej na obligacjach przedsiębiorstwa, obligacjach
komunalnych i skarbowych.
Uwzględniając ryzyko: największe ryzyko wiążę się z inwestycją w akcje, następnie w obligacje
przedsiębiorstwa, komunalne i skarbowe.



Problem 8.
Spółka SUP będzie osiągać zyski w wysokości 1 mln zł rocznie. Na dywidendy planuje się przeznaczyć 5% zysków i
firma zamierza zwiększyć zysk o 1% rocznie. Rynkowa stopa zwrotu wynosi 10%, a wyemitowano 100 000 akcji tej
spółki. Oblicz ile są warte akcje tej spółki, przy danej rynkowej stopie zwrotu. Wskaż, po jakiej cenie opłaca się je
nabyć na giełdzie w chwili obecnej.

Przez następne lata wartość dywidendy będzie wzrastać o 1% rocznie, więc wartość tych korzyści będzie
równoważna cenie akcji na koniec 10 roku, którą możemy obliczyć korzystając z modelu Gordona, gdyż ks > g:

P

D

k

g

0

1

s

=

−

,

lub

P

D

(1 g)

k

g

0

0

s

=

⋅ +

−

Wartość dywidendy = 1 000 000 zł * 0,05 = 50 000 zł
Planowana dywidenda na jedną akcję = 50 000 zł / 100 000 = 0,5 zł/ akcję.

56

,

5

01

,

0

1

,

0

0,5

P

0

=

−

=

zł.

Odp. Aktualnie akcje są warte nie więcej niż 5,56 zł, a więc opłaca się je nabyć jeżeli ich cena będzie niższa od 5,56
zł.


Problem 9. Akcje firmy COMP S.A. założonej 5 lat temu znajdują się na giełdzie. W ostatnich trzech latach firma
wypłacała swoim akcjonariuszom dywidendę w wysokości 2 zł; 2,5 zł; 3,125 zł na akcję. Zakładając, że tempo
wzrostu firmy przez 10 kolejnych lat będzie takie samo, a następnie ustabilizuje się na poziomie 5% rocznie, wskaż
ile jesteś skłonny/a zapłacić za akcje, jeśli chcesz zarobić 20% rocznie?

Ustalamy wartość zdyskontowanych dywidend w ciągu pierwszych 10 lat, uwzględniając ich 25% wzrost w każdym
roku.
Wyszcz.

D0

D1

D2

D3

D4

D5

D6

D7

D8

D9

D10

Razem

dywidenda 3,125

3,91

4,88

6,10

7,63

9,54

11,92 14,90 18,63 23,28 29,10 -

wsp.dysk.

x

0,833 0,694 0,579 0,482 0,402 0,335 0,279 0,233 0,194 0,162 -

PV (zł)

x

3,26

3,39

3,53

3,68

3,83

3,99

4,16

4,33

4,51

4,70 39,39

Przez następne lata wartość dywidendy będzie wzrastać o 5% rocznie, więc wartość tych korzyści będzie
równoważna cenie akcji na koniec 10 roku, którą możemy obliczyć korzystając z modelu Gordona, gdyż ks > g:

P

D

k

g

0

1

s

=

−

,

lub

P

D

(1 g)

k

g

0

0

s

=

⋅ +

−

gdzie:
P

0

- cena akcji,

D

1

- wartość dywidendy,

k

s

- oczekiwana stopa zwrotu z kapitału,

g - planowana stopa wzrostu,
D

0

- wartość wypłaconej dywidendy w okresie t

0

,

k

s

- oczekiwana stopa zwrotu.

Wartość dożywotniej renty dywidendowej:
P

(10)

= 29,10 (1+0,05) / (0,2-0,05) = 203,70 zł

PV (P10) = 203,70 / 1,20^10 = 32,90 zł

Finanse – materiały do studiowania nr 7

Łączna wartość korzyści z posiadania akcji: 39,39 + 32,90 = 72,29 zł

Odp. Za akcje firmy COMP nie należy płacić więcej niż 72,29 zł, jeżeli chcemy osiągnąć 20% stopę zwrotu z tego
instrumentu.



Problem 10. Jeden z inwestorów na giełdzie papierów wartościowych zakłada, że spółka, w którą zainwestował,
wypłaci za rok 70 zł, a za dwa lata 100 zł dywidendy. Według inwestora cena akcji za dwa lata będzie wynosiła
165 zł.

1)

Wyjaśnij pojęcie dywidendy i źródła jej powstawania.

2)

Na podstawie powyższych danych wskaż, czy przy dzisiejszej cenie akcji równej 200 zł inwestor powinien
zainwestować w akcje tej spółki, czy też kapitał powinien ulokować w banku na 5 % rocznie?

Lokata kapitału w banku: FV = 200 zł (1+0,05)(1+0,05) = 220,5 zł

Inwestycja w akcje:
Korzyści z inwestycji to dywidenda po 1. roku (70 zł) oraz dywidenda i przychody ze sprzedaży akcji po 2. roku (100
+ 165 = 265 zł), stąd
FV = 70 zł (1+0,05) + 265 zł = 338,5 zł.

Odp. Inwestor powinien zainwestować w akcje, gdyż mimo spadku ich wartości na przestrzeni dwóch lat
otrzyma on wysokie dywidendy rekompensujące utratę wartości akcji, w rezultacie jego zarobek będzie o ponad
100 zł wyższy na jednej akcji.



Problem 11.
Oprocentowanie pewnej obligacji o wartości nominalnej 10 000 zł jest stałe i wynosi 9% rocznie, jest ono wypłacane
regularnie na koniec każdego roku. Do momentu wykupu obligacji pozostały 3 lata. Obecnie obligacja ta jest
oferowana na rynku po 9 900 zł. Inwestor oczekuje 12% stopy zwrotu z inwestycji, a więc stopa dyskontowa w
najbliższych latach będzie wynosiła 12% rocznie.
Czy warto dziś kupić tę obligację na rynku?

Obligacja oferuje 9% kupon, co nie spełnia oczekiwań inwestora (12%). Można ją co prawda nabyć z 1% dyskontem,
ale łączne korzyści nie przewyższą oczekiwanej stopy zwrotu. Dla sprawdzenia można obliczyć bieżącą wartość
obligacji.

Oprocentowanie 10 000 zł * 0,09 = 900 zł
WB = 900/1,12 + 900/1,12*1,12 + 10900/1,12*1,12*1,12 = 9 279,45 zł.

Odp. Nie warto wydawać 9 900 zła na instrument finansowy, który jest dla nas warty mniej, bo nie osiągniemy
spodziewanych zysków. Daje on tylko stopę zwrotu na poziomie 8,66%.



Problem 12. Oblicz dzisiejszą wartość obligacji o nominale 100 zł, z terminem wykupu przypadającym za 3 lata,
jeżeli od obligacji na koniec każdego roku są wypłacane odsetki, a jej oprocentowanie jest wyższe od wskaźnika
inflacji o 5 punktów procentowych? Inflacja w pierwszym roku wyniesie 4%, w drugim 3%, w trzecim 2,5%, a
oczekiwana stopa zwrotu jest wyższa od stopy inflacji o 4 punkty procentowe.

Wyszczególnienie

Rok 1

Rok 2

Rok 3

Inflacja

4%

3%

2,5%

Oprocentowanie obligacji

4% + 5 % = 9%

3% + 5 % = 8%

2,5% + 5 % = 7,5%

Oczekiwana stopa zwrotu

4% + 4 % = 8%

3% + 4 % = 7%

2,5% + 4 % = 6,5%

Korzystam z wzoru na wartość bieżącą korzyści związanych z posiadaniem obligacji:

n

n

t

t

r

y

WN

y

O

WR

)

1

(

)

1

(

1

+

+

+

=

∑

=

, gdzie:

WR - wartość obligacji
y - stopa dochodu w terminie do wykupu (w tym przypadku stopa jest zmienna)
O

r

- odsetki w skali roku

WN - wartość nominalna

Finanse – materiały do studiowania nr 7

=

+

+

+

+

+

+

+

+

+

+

+

+

=

)

06

,

0

1

)(

07

,

0

1

)(

065

,

0

1

(

100

)

06

,

0

1

)(

07

,

0

1

)(

065

,

0

1

(

075

,

0

*

100

)

08

,

0

1

)(

07

,

0

1

(

08

,

0

*

100

08

,

0

1

09

,

0

*

100

PV

= 102,60

zł.

Odp. Wartość dzisiejsza obligacji wynosi 102,60 zł, a więc gdyby była ona dziś sprzedawana po cenie nominalnej,
to jej zakup byłby opłacalny.



Problem 13.
Transakcja z kontrahentem zagranicznym opiewa na 30 tys. euro, tj. na dzień dzisiejszy 129 000 zł. Eksporter chce
zabezpieczyć kurs sprzedaży 30.000 euro na datę waluty za miesiąc. Kurs opcyjny opcji put ustalono na poziomie
4,30. Koszt opcji wynosi 4200 PLN. Za miesiąc możliwe są dwa scenariusze:

a)

złotówka się umocniła i kurs wynosi 3,90 zł za euro,

b)

złotówka się osłabiła i kurs wynosi 4,85 zł za euro.

Oszacuj korzyści z tej transakcji. Sprawdź co by się stało, gdyby nie była ona związana ze sprzedażą.

Przypadek A:
Kurs jest niższy niż zakładany w opcji sprzedaży, a więc posiadacz opcji korzysta z prawa sprzedaży waluty po
ustalonym kursie. Następuje rozliczenie opcji:
Dostarcza bankowi 30000 euro, a otrzymuje w zamian 129 000 zł, a więc do dyspozycji ma kwotę 129 000 – 4200
= 125 800 zł. Przy kursie rynkowym bez zabezpieczenia opcyjnego otrzymałby tylko 117 000 zł. Tak więc poniósłby
stratę rzędu 12 000 zł.

Przypadek B
Kurs jest wyższy niż zakładany, a więc posiadacz opcji sprzedaży nie wykonuje jej i godzi się ze stratą 4200 zł. W
zamian sprzedaje walutę na rynku walutowym 30 000 * 4,85 = 145 500 zł. A więc uwzględniając koszty opcji jego
korzyści są następujące (145 500 – 129 000) – 4 200 = 12 300 zł.

Odp. W przypadku opcji typu put nic, a właściwe poniesie stratę w wysokości ceny opcji. Przy niezadowalającej
zmianie kursu walutowego opcja nie będzie realizowana. To nie tłumaczy problemów polskich firm z
transakcjami opcyjnymi. Polskie przedsiębiorstwa korzystały ze złożonych instrumentów opcyjnych łączących
opcje put na określoną kwotę z opcją call na kwotę dwa razy większą, przy czym były to opcje bezkosztowe (nie
trzeba było płacić premii). W rezultacie całe ryzyko zostało przeniesione z wystawcy opcji (banku) na nabywcę
(przedsiębiorstwo).