1

Analiza wariancji

Cel analizy wariancji to porównanie średnich w kilku populacjach. Analiza wariancji została

wymyślona w ramach nauk eksperymentalnych (rolniczych). Tam była wykorzystywane do

oceny, czy zastosowany czynnik (np. nawóz w odpowiednich porcjach) zmieniał wielkość

wyników (plonów). W ekonomii analiza wariancji może być stosowana do porównywania

choćby efektów różnych strategii marketingowych.

Model jednoczynnikowy ANOVA

W podstawowym przypadku zakładamy, że u próby analizowanych w badaniu pochodzi z

rozkładów normalnych N(

µ

i

,

σ

2

) o być może różnych średnich (to będzie przedmiotem testu)

ale o takich samych wariancjach. Liczebność poszczególnych prób wynosi

i

n i zakładamy,

ż

e

n

n

r

i

i

=

∑

=

1

.

Hipotez zerowa w teście przyjmuje postać:

µ

µ

µ

µ

=

=

=

=

u

H

...

:

2

1

0

Hipoteza alternatywna powiada, że conajmniej dwie z pośród r średnich są różne.

j

i

że

t

j

i

j

i

H

µ

µ

≠

≠

∃

.

,

:

1

Oznaczmy przez y

ki

obserwację o numerze k z i-tej próby. Przyjmiemy, że obserwacje są

generowane następującym modelem:

r

s

n

i

dla

y

i

si

s

si

,...,

2

,

1

;

,...,

2

,

1

=

=

+

+

=

ξ

α

µ

,

gdzie:

µ

- stała wartość, identyczna dla wszystkich grup,

α

s

- nieznana stała opisująca wpływ i-tego poziomu czynnika na wartość zmiennej Y,

ξ

si

- zmienna losowa opisująca łączny wpływ innych czynników o charakterze losowym na

wartość zmiennej Y.

Suma

s

α

µ

+

jest wartością średniej w s-tej populacji. Jeśli prawdziwa jest hipoteza zerowa,

czyli równe są wszystkie średnie, wówczas równe są również wszystkie

α

s

.

2

W ramach testu zakładamy, że składniki losowe modelu w poszczególnych populacjach mają

rozkłady normalne o średniej równej zero, takiej samej wariancji (N(0;

σ

) ) i nie są ze sobą

skorelowane tj.

(

)

0

,

cov

'

,'

=

i

k

ki

ξ

ξ

dla wszystkich

k, i, k’, i’, przy czym k

≠

k’.

Przy powyższych założeniach i oznaczeniach możemy (podobnie jak w przypadku regresji

linowej) rozpisać zmienność (całkowitą) zmiennej Y. Zmienność całkowita jest sumą dwóch

składników sumy objaśnionej zmieniającym się czynnikiem (modelem) oraz zmiennością

resztową.

(

)

(

)

(

)

(

)

∑∑

∑∑

∑∑

∑

=

=

=

=

=

=

=

+

=

−

=

−

+

−

=

−

=

r

i

n

k

ki

r

i

n

k

r

i

n

k

r

i

i

i

i

ki

ki

i

i

i

SSB

SSE

y

y

SST

y

y

n

y

y

y

y

SST

1

1

2

1

1

1

1

1

2

2

2

gdzie:

Ś

rednia ogólna:

∑

∑ ∑

=

=

=

=

=

r

i

i

i

r

i

n

k

ki

n

y

n

y

n

y

i

1

1

1

1

1

Ś

rednia grupowa:

∑

=

=

i

n

k

ki

i

i

y

n

y

1

1

SST – całkowita zmienność zmiennej Y,

SSE – zmienność wewnątrzgrupowa,

SSB – zmienność międzygrupowa.

Jeśli hipoteza zerowa jest prawdziwa, wówczas zmienność międzygrupowa powinna być

niewielka w porównaniu do zmienności całkowitej – albo równoważnie do zmienności

wewnątrzgrupowej.

Statystyka

:

MSE

MSB

F

=

gdzie:

r

n

SSE

MSE

oraz

r

SSB

MSB

−

=

−

=

1

3

Ma przy założeniu słuszności hipotezy zerowej rozkład F-Snedecora o stopniach swobody

(licznika i mianownika) odpowiednio r-1 oraz n-r.

W przypadku, gdy średnie w porównywanych populacjach różnią się od siebie, wówczas

liczniki w statystyce testowej F będzie znacznie większy od mianownika, statystyka będzie

przyjmować wartości znacznie większe od 1.

Obszar krytyczny wyznaczony jest z zależności:

{

}

α

α

=

≥

F

F

P

Uwaga. Analiza wariancji jest dość wrażliwa na naruszenie założeń związanych z równością

wariancji. Konieczne jest sprawdzenie, czy wariancje w poszczególnych populacjach są takie

same. Służy do tego np. test Bartletta, Cochrana, Hartleya. Niewielkie odstępstwa od

normalności rozkładów nie wpływają znacząco na rozkład statystyki F.

Test Bartletta, test Hartleya (równość wariancji w populacjach)

Służy do badania: HOMOSKEDASTYCZNOŚĆI (jednorodności wariancji w grupach)

Hipoteza zerowa:

2

2

1

2

1

.....

:

r

o

H

σ

σ

σ

=

=

=

Hipoteza alternatywna:

j

i

.

,

:

2

2

1

≠

≠

∃

j

i

że

t

j

i

H

σ

σ

Sprawdzianem hipotezy zerowej jest statystyka:

]

1

)

1

(

1

[

)

1

(

3

1

1

10

ln

1

r

n

n

r

M

r

i

i

−

−

−

−

+

⋅

=

∑

=

λ

przy czym:

4

∑

=

−

−

−

=

r

i

i

i

s

n

MSE

r

n

M

1

2

log

)

1

(

log

)

(

gdzie:

r

– liczba poziomów czynnika,

n

– liczba replikacji (obserwacji) ogółem

i

n

– liczba replikacji przy i-tym poziomie czynnika

2

i

s

– wariancja przy i-tym poziomie czynnika (w każdej z grup)

Jeśli prawdziwa jest hipoteza zerowa, wówczas rozkład statystyki

λ

zmierza do rozkładu Chi

kwadrat z r-1 stopniami swobody.

Wartość krytyczna

2

α

χ

wyznacza prawostronny obszar krytyczny tj.

α

χ

λ

α

=

≥

)

(

2

P

. W

przypadku, gdy

2

α

χ

λ

≥

odrzucamy hipotezę zerową. Wówczas nie możemy korzystać z

analizy wariancji.

Jeśli wylosowane próby są równoliczne

r

n

n

n

=

=

=

....

2

1

i ponadto, spełnione są założenia

jak w teście Bartleta, wtedy możemy zastosować test Hartleya. Postać hipotez: zerowej i

alternatywnej są takie same jak poprzednio. Statystyka testowa ma postać:

( )

( )

2

2

min

max

i

i

i

i

S

S

H

=

Wartości krytyczne testu Hartleya są dostępne w programach statystycznych. Obszar

krytyczny jest prawostronny.

Testy post hoc.

Odrzucenie hipotezy zerowej w teście analizy wariancji oznacza stwierdzenie, że niektóre z

pośród badanych populacji różnią się średnimi. Nie mniej jednak nie wiadomo, które z pośród

średnich są statystycznie od siebie różne. Testy post hoc służą do wskazania tych par średnich,

które istotnie się od siebie różnią.

Hipoteza zerowa w teście ma postać:

'

0

:

s

s

H

µ

µ

=

Statystyka testowa ma postać:

5

__

'

__

__

n

MSE

y

y

HSD

s

s

−

=

Gdzie

__

n to średnia harmoniczna liczebności przypadającej na każdy badany czynnik (każdą

populację). Jeśli prawdziwa jest hipoteza zerowa, statystyka HSD ma rozkłada Tukeya. Jest on

tablicowany. Zależy od liczby stopni swobody r oraz n-r.

Przykład anova

Pewna korporacja finansowa celem poprawy wyników postanowiła przeszkolić doradców

finansowych. Zaproponowano 4 rodzaje szkoleń i na każde z nich skierowano po 11

pracowników. W ciągu kolejnego miesiąca po kursie postanowiono zweryfikować wyniki

poszczególnych przeszkolonych grup. Zebrano dane opisujące wartość aktywów klientów

pozyskanych przez doradców. Zostały one zestawione w tabeli:

I szkolenie

28,2 ,36.1,26.8,28,25.1,27.8,33.3,26.5,31.6,32.4,29

II szkolenie

29.6,27.1,34.7,24.3,29.6,33.9,26.9,33.2,32.3,24.9,31.8

III szkolenie

30.9,24.5,37.4,29.6,27.4,29.1,33,28.6,31.1,27.4,27.7

IV szkolenie

30.8,29.6,35.4,34.9,50,28.5,32.5,30.6,37.5,35.8,39.9

Dane znajdują się w pliku: dane_kurs1

Ocenić czy wszystkie rodzaje kursów dają takie same efekty.

Rozwiązanie:

1.

Szkicujemy wykres pudełkowy dla poszczególnych kategorii (ocenimy poziom oraz

zmienność poszczególnych grup)

2.

Naszkicujemy wykresy kwanty-kwantyl (ocenimy normalność rozkładów wyników w

grupach)

3.

Przeprowadzamy formalne testy: normalności Shapiro-Wilka, oraz na

heteroskedastyczność

4.

Jeśli spełnione są założenia przeprowadzamy test ANOVA

5.

Jeśli odrzucimy hipotezę zerową przeprowadzamy testy post hoc. Oceniamy, które

średnie się różnią.

6

Dwuczynnikowa analiza wariancji MANOVA

Dwuczynnikowa analiza wariancji.

Należy zbadać wpływ dwóch czynników A oraz B, o charakterze jakościowym na poziom

zmiennej Y. Pierwszy czynnik przyjmuje u poziomów, drugi przyjmuje p poziomów. Daje to

razem up grup zbiorowości. Z każdej zbiorowości pobieramy próbę o liczebności k – obserwacji,

Interakcje:

Jeżeli zmiana średniej wynikająca ze zmiany jednego czynnika zależy od poziomu drugiego

czynnika – mówimy, że między czynnikami zachodzi interakcja.

Przykład: zarobki w grupach zawodowych w wybranych regionach.

Dane w plikach:

Zarobki 1

Zarobki 2.

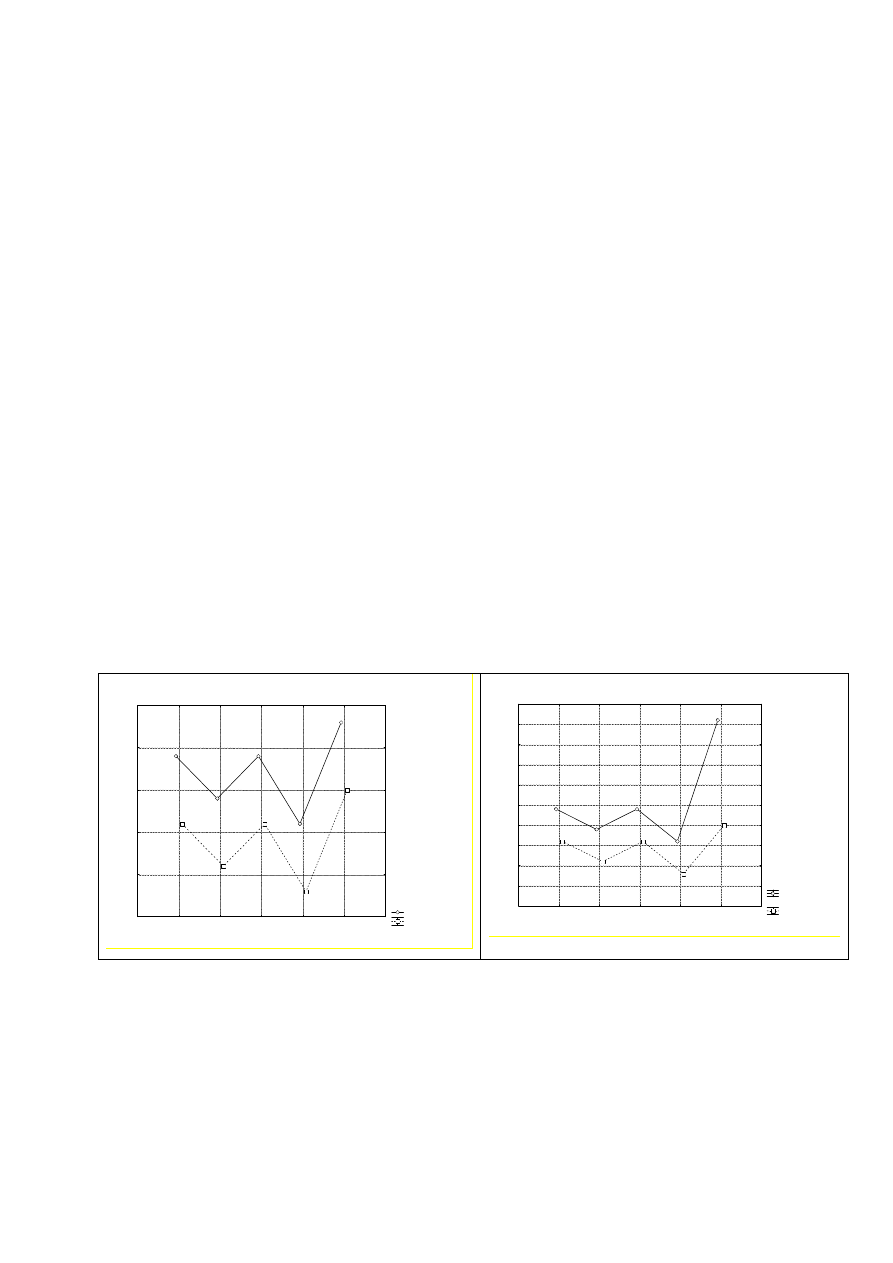
Narysować wykresy interakcji i zinterpretować je.

Wykres

ś

rednich i przedz. ufno

ś

ci (95,00%)

Zmn8

region

ś

rodkowy

region północny

mat-inf

biol

fiz

soc

in

ż

Zmn6

45

50

55

60

65

70

W

a

rt

o

ś

c

i

Wykres

ś

rednich i przedz. ufno

ś

ci (95,00%)

Zmn8

Zmn7
region

ś

rodkowy

Zmn7
region północny

mat

biol

fiz

soc

in

ż

Zmn6

40

45

50

55

60

65

70

75

80

85

90

W

a

rt

o

ś

c

i

W przypadku, gdy występują interakcje nie ma sensu sprawdzać jak wpływa poziom

wybranego czynnika na średnią. W takiej sytuacji wpływ ten nie jest stały i zależy od

poziomu drugiego czynnika.

7

Przypadek 1. (k=1) Brak interakcji

Rozważany model:

p

r

u

s

dla

y

sr

r

s

sr

,...,

2

,

1

;

,...,

2

,

1

=

=

+

+

+

=

ξ

β

α

µ

gdzie:

µ

- stała wartość, identyczna dla wszystkich grup,

α

s

- nieznana stała opisująca wpływ i-tego

poziomu czynnika A na wartość zmiennej Y,

r

β

-

wpływ r-tego poziomu czynnika B,

ξ

sr

-

zmienna losowa opisująca łączny

wpływ innych czynników o charakterze losowym na wartość

zmiennej Y.

Rozważane hipotezy – oceniane osobno:

)

...,

,

1

(

0

:

0

u

s

H

s

A

=

=

α

)

...,

,

1

(

0

:

0

p

r

H

r

B

=

=

β

Suma

s

α

µ

+

jest wartością średniej w s-tej populacji. Jeśli prawdziwa jest hipoteza zerowa,

czyli równe są wszystkie średnie, wówczas równe są również wszystkie

α

s

W przypadku tego modelu całkowita zmienność zmiennej Y tj. SST rozkłada się na sumę

trzech składników:

STT = SSB

A

+ SSB

B

+ SSE

Gdzie: SSB

A

to zmienność międzygrupowa czynnika A, SSB

B

– zmienność międzygrupowa

czynnika B, SSE – zmienność międzygrupowa

Statystyka testowa służąca weryfikacji pierwszej z hipotez ma postać:

MSE

MSB

F

A

=

gdzie:

)

1

)(

1

(

1

−

−

=

−

=

p

u

SSE

MSE

oraz

u

SSB

MSB

A

A

Jeśli prawdziwa jest hipoteza zerowa statystyka ta ma rozkład F z (u-1) oraz (u-1)(p-1)

stopniami swobody.

Zweryfikujemy drugą z hipotez przy pomocy statystyki:

8

MSE

MSB

F

B

=

gdzie:

)

1

)(

1

(

1

−

−

=

−

=

p

u

SSE

MSE

oraz

p

SSB

MSB

B

B

Jeśli prawdziwa jest hipoteza zerowa statystyka ta ma rozkład F z (p-1) oraz (u-1)(p-1)

stopniami swobody.

Zbiory krytyczne w obu przypadkach są prawostronne. Odrzucamy hipotezę zerową, jeśli F

testowe jest większe od wartości krytycznej

α

F .

Przykład „Czas wykonania” lub szkolenia

9

Przypadek 2. (k>1)

Zakładamy teraz, że w każdej podklasie znajduje się k obserwacji (k>1). Łącznie

dysponujemy puk obserwacjami.

Rozważany model może być zapisany następująco:

sri

sr

r

s

sri

X

ξ

γ

β

α

µ

+

+

+

+

=

Gdzie:

µ

- stała wartość, identyczna dla wszystkich grup,

α

s

- nieznana stała opisująca wpływ

i-tego poziomu czynnika A na wartość zmiennej Y,

r

β

-

wpływ r-tego poziomu czynnika B,

sr

γ

określa wspólny wpływ zmiennej A na poziomie s oraz zmiennej B na poziomie r

ξ

sr

-

zmienna losowa opisująca łączny

wpływ innych czynników o charakterze losowym na wartość

zmiennej Y.

Hipotezy zerowe przyjmują postać:

)

...,

,

1

(

0

:

0

u

s

H

s

A

=

=

α

)

...,

,

1

(

0

:

0

p

r

H

r

B

=

=

β

)

...,

,

1

;

..,

,

1

(

0

:

)

(

0

p

r

u

s

H

sr

AxB

=

=

=

γ

Wszystkie hipotezy weryfikujemy oddzielnie.

Statystyki testowe uzyskamy po rozłożeniu zmienności całkowitej SST na składowe:

STT = SSB

A

+ SSB

B

+ SSB

AB

+SSE

gdzie: SSB

A

to zmienność między poziomami czynnika A, SSB

B

– zmienność między

poziomami czynnika B, SSB

AB

zmienność wynikająca z interakcji między czynnikami, SSE –

zmienność wewnątrzgrupowa (suma kwadratów reszt).

„Statystyka dla interakcji”

(

)(

)

1

1

)

(

2

1

1

−

−

+

−

−

=

=

=

−

=

−

−

∑ ∑

p

u

y

y

y

y

k

MSB

r

i

oj

s

j

io

ij

AxB

I dalej:

MSE

MSB

F

AxB

=

10

Która to statystyka, przy założeniu prawdziwości hipotezy zerowej ma rozkład F Snedecora o

(u-1)(p-1) oraz up(k-1).

Statystyka dla

A

H

0

MSE

MSB

F

A

=

,

gdzie:

1

)

(

1

2

__

−

−

=

∑

=

−

•

•

u

y

y

pk

MSB

u

s

s

A

,

)

1

(

)

(

1

1

1

2

__

−

−

=

∑∑∑

=

=

=

•

k

up

y

y

MSE

u

s

p

r

k

i

sr

sri

Ma przy założeniu hipotezy zerowej ma rozkład F Snedecora o (u-1) oraz up(k-1) stopniach

swobody.

Statystyka dla

B

H

0

MSE

MSB

F

B

=

,

gdzie:

1

)

(

1

2

__

−

−

=

∑

=

−

•

•

u

y

y

uk

MSB

p

r

r

B

,

)

1

(

)

(

1

1

1

2

__

−

−

=

∑∑∑

=

=

=

•

k

up

y

y

MSE

u

s

p

r

k

i

sr

sri

Ma przy założeniu hipotezy zerowej ma rozkład F Snedecora o (p-1) oraz up(k-1) stopniach

swobody.

Przykład

W pliku dane_kurs 2 sprawdzić wpływ zmiennych jakościowych na wyniki kursu.

Ocenić interakcję pomiędzy zmiennymi jakościowymi.

Sprawdzić założenia testu.

Przykład

W pliku toxic sprawdzić wpływ rodzaju substancji toksycznej oraz zakładu na wyniki

wydolności oddechowej.

Ocenić wpływ czynników głównych oraz interakcję pomiędzy nimi.

Ocenić założenia testu

11

Analiza kontrastów

W ramach ANOVA porównujemy średnie we wszystkich populacjach. Hipoteza zerowa

powiada, że wszystkie średnie są takie same.

Jeśli chcemy analizować inne hipotezy (np. czy średnie w populacji 2 i 3 są takie same jak w

populacji 4 i 5 albo czy w trzech pierwszych populacjach średnie są takie same) możemy je

zapisać w postaci kontrastów.

Kontrast dla k średnich w populacji

k

µ

µ

µ

...,

,

,

2

1

nazywamy każdą liniową funkcję :

∑

=

=

k

i

i

i

c

L

1

µ

, gdzie

∑

=

=

k

i

i

c

1

0

Przykładowe kontrasty (dla średnich w 4 populacjach):

(

)

3

2

1

4

1

0

2

1

µ

µ

µ

µ

⋅

+

+

−

=

L

albo

(

)

3

2

1

4

1

0

2

µ

µ

µ

µ

⋅

+

+

−

=

L

3

3

2

1

3

1

2

0

0

µ

µ

µ

µ

µ

µ

⋅

+

−

⋅

−

=

−

=

L

4

3

2

1

3

3

µ

µ

µ

µ

−

+

−

−

=

L

Uwaga. Posługując się kontrastami, będziemy zapisywać wartości parametrów

i

c , które

pokażą o jaki kontrast chodzi. Wyżej przedstawione kontrasty mogą być symbolicznie

zapisane w postaci ciągów (-1, -1, 0, 2), (1, 0, -1, 0), (-1, -1, 3, -1)

Przykład.

Otworzyć plik Toxic,

1.

Wywołać analizę ANOVA dla układów czynnikowych (opcja szybkie definiowanie)

2.

Wybrać zmienne: zależną (FEV – ocena wydolności oddechowej – wyższa ocena –

lepszy wynik) oraz obie pozostałe zmienne jako predykatory jakościowe

3.

Sprawdzić założenia analizy (normalność rozkładów, jednorodność wariancji)

4.

Ocenić istotność efektów głównych oraz interakcji pomiędzy efektami głównymi

5.

Sprawdzić za pomocą kontrastów czy:

a)

W zakładzie drugim, substancja C jest bardziej szkodliwa od substancji A i B?

b)

W zakładzie I, II, III substancja A i B jest tak samo szkodliwa?

12