2011-10-11

1

Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec

Analiza krańcowa –
przypomnienie



poziom aktywności a

– ilość zasobów, czasu itp. poświęconych na dane działanie



korzyść netto NB

(ang. net benefit)

– różnica między korzyścią całkowitą z danej czynności a jej kosztem

całkowitym:

NB = TB

– TC



korzyść krańcowa MB

(ang. marginal benefit)

– przyrost korzyści całkowitej TB, spowodowany zwiększeniem

poziomu aktywności a o jednostkę:

MB = TB'(a)



koszt krańcowy MC

(ang. marginal cost)

– przyrost kosztu całkowitego TC, spowodowany zwiększeniem

poziomu aktywności a o jednostkę:

MC = TC'(a)



cel:

zmaksymalizowanie korzyści netto NB(a)



przykład: w przypadku firmy produkującej i sprzedającej dobra:



a:

wielkość produkcji sprzedanej,



TB:

utarg ze sprzedaży,



MB:

utarg krańcowy,



TC:

łączny koszt produkcji,



MC:

krańcowy koszt produkcji,



NB:

zysk

poziom

aktywności a

korzyść całkowita

(total benefit) TB(a)

koszt całkowity (total

cost) TC(a)

korzyść netto

(net benefit)

NB(a)

α

β

TC (a)

TB (a)

Korzyść
całkowita

Koszt
całkowity

Poziom aktywności

a

TC(a)-TB(a) = NB(a)
 maks.

Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec

Analiza krańcowa
– przypomnienie

1. warunek

NB

’ = 0

(TB

– TC)’ = 0

TB

’ – TC’ = 0

MB

– MC = 0

MB = MC

2. warunek

NB

” < 0

(TB

– TC)” < 0

TB

” – TC” < 0

MB

’ – MC’ < 0

MB

’ < MC’

Korzyść netto NB jest maksymalizowana, gdy spełnione są
dwa warunki:
1. pierwsza pochodna funkcji NB jest zerowa: NB' = 0,
2. druga pochodna funkcji NB jest ujemna: NB" < 0:

Należy zwiększać poziom aktywności tak długo, aż
korzyść krańcowa MB zrówna się z kosztem krańcowym MC
(przy zachowaniu warunku MB' < MC')

α

β

TC(a)

TB(a)

Korzyść
całkowita

Koszt
całkowity

Poziom aktywności

a

MC(a)

MB(a)

Korzyść
krańcowa

koszt
krańcowy

Poziom aktywności

a

NB (a)

Korzyść
netto

Poziom aktywności

a

przykład: w przypadku przedsiębiorstwa produkującego i
sprzedającego dobra:

a:

wielkość produkcji sprzedanej,

TB:

utarg ze sprzedaży,

MB:

utarg krańcowy,

TC:

łączny koszt produkcji,

MC:

krańcowy koszt produkcji,

NB: zysk

Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec

α

β

TC(Q)

TB(Q)

Korzyść
całkowita

Koszt
całkowity

Poziom produkcji

Q

X

MC(Q)

MB(Q)

Korzyść
krańcowa

koszt
krańcowy

Poziom produkcji

Q

X

NB (Q)

Korzyść
netto

Poziom produkcji

Q

X

Analiza krańcowa –

przypomnienie

Korzyść całkowita i koszt całkowity



utarg całkowity i koszt całkowity

Korzyść krańcowa i koszt krańcowy



utarg krańcowy i koszt krańcowy

Korzyść netto



zysk (różnica między utargiem a kosztami)

Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec

MC(Q)

MB(Q)

Korzyść
krańcowa

koszt
krańcowy

Poziom produkcji

Q

X

NB(Q)

Korzyść
netto

Poziom produkcji

Q

X

dNB(Q)/dQ

Krańcowa
korzyść
netto

Poziom produkcji

0

Q

X

Analiza krańcowa –

przypomnienie

Korzyść krańcowa i koszt krańcowy



utarg krańcowy i koszt krańcowy

Korzyść netto



zysk (różnica między utargiem a kosztami)

Korzyść krańcowa netto



zysk krańcowy

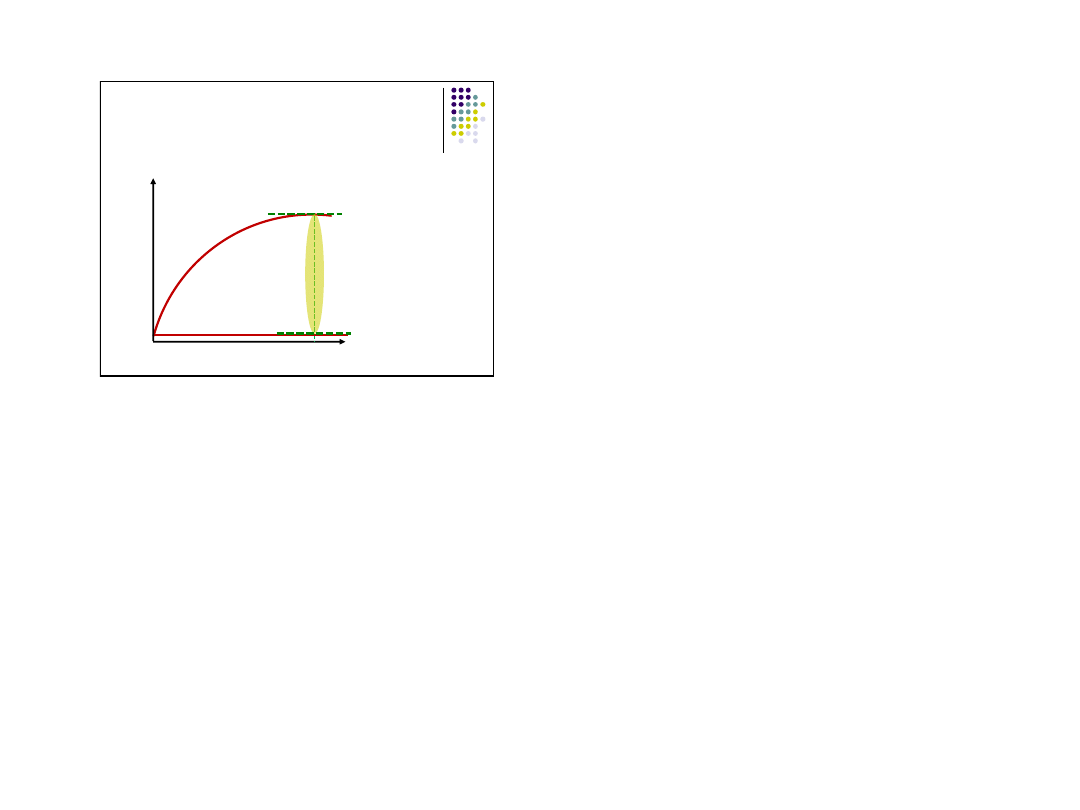
2011-10-11

2

Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec
Tomasz Tylec Tomasz Tylec

TC

TR

Utarg
całkowita

Koszt
całkowity

Poziom
produkcji

Q

X

Analiza krańcowa –
przypomnienie

znajdujemy takie Q,
dla którego TR jest
maksymalne (tak jak dla
korzyści netto: NB’ = 0),
co przy wszystkich
kosztach stałych
oznacza maksymalizację
zysku:

1) MR = 0;

2) MR''(Q) < 0

W takim przypadku maksymalizacja zysku jest
jednocześnie maksymalizacją utargu, dlatego
też: