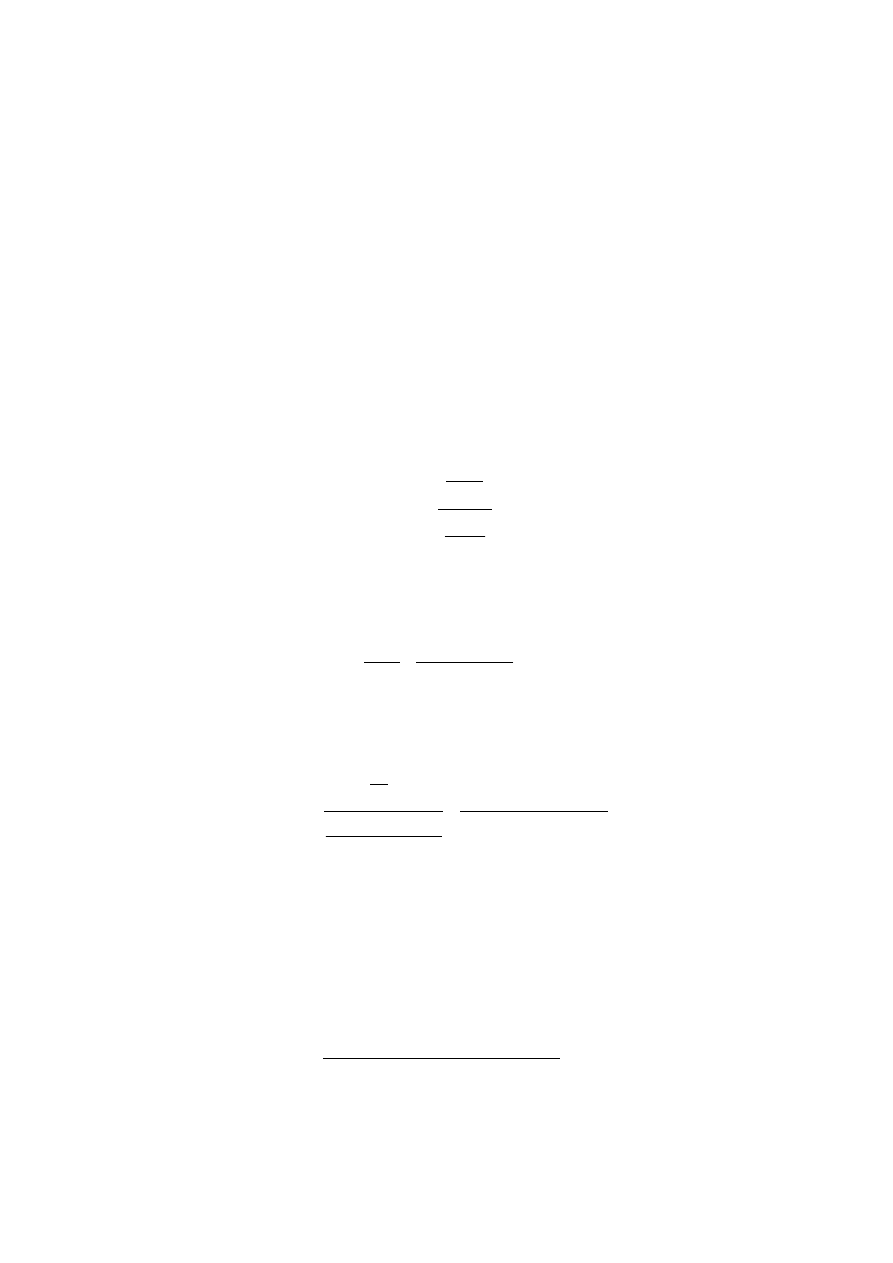
3. RÓWNOWAGA CHEMICZNA

Zadania przykładowe

3.1.

Do naczynia o objętości 2

⋅10

-2

m

3

wprowadzono 0,1 mola gazowego N

2

O

4

w temperaturze

298 K. Sumaryczne ciśnienie mieszaniny równowagowej wynosi 1,425

⋅10

5

Pa. Obliczyć ciśnieniową

stałą równowagi reakcji rozpadu N

2

O

4

do NO

2

oraz prężności cząstkowe reagentów w stanie

równowagi.

Rozwiązanie
Rozpad

N

2

O

4

do NO

2

zachodzi zgodnie z reakcją:

N

2

O

4

= 2NO

2

Ciśnieniowa stała równowagi tej reakcji dana jest zależnością:

K

P

P

P

P

p

NO

s

N O

s

=











2

2

4

2

gdzie:

P

i P

NO

N O

2

2 4

- to równowagowe ciśnienia odpowiednio NO

2

i N

2

O

4

,

P

s

jest ciśnieniem standardowym.

Obliczamy początkowe ciśnienie (P

p

) wprowadzonego N

2

O

4

.

P N O

nRT

V

Pa

p

(

)

,

,

,

2

4

3

5

01 8 314 298

2 10

1 239 10

=

=

⋅

⋅

⋅

=

⋅

−

Jeżeli przyjmiemy, że równowagowe ciśnienie NO

2

wynosi x, to ze stechiometrii reakcji wynika,

że ciśnienie N

2

O

4

w stanie równowagi wynosi P

p

(N

2

O

4

) - 0,5x. Stałą równowagi możemy zatem

zapisać w postaci zależności:

(

)

K

x

P

P N O

x

P

x

P N O

x P

p

s

p

s

p

s

=













−

=

−

⋅

2

2

4

2

2

4

0 5

0 5

(

)

,

(

,

Prężność sumaryczna w stanie równowagi wynosi 1,425

.

10

5

Pa i jest równa sumie prężności

cząstkowych reagentów

1,425

⋅ 10

5

= (P

p

(N

2

O

4

) - 0,5x) + x

Ponieważ ciśnienie początkowe N

2

O

4

wynosi 1,239

⋅10

5

Pa, zatem

1,425

⋅ 10

5

= (1,239

⋅ 10

5

- 0,5x) + x

stąd

x

=

0,372

⋅ 10

5

Pa

Po podstawieniu tej wartości do wzoru na stałą równowagi otrzymujemy

(

)

(

)

K

p

=

⋅

⋅

−

⋅

⋅

⋅

=

0 372 10

1239 10

0 5 0 372 10

10

0131

5 2

5

5

5

,

,

.

,

,

Prężności cząstkowe w stanie równowagi wynoszą:
P(NO

2

) = x = 0,372

⋅ 10

5

Pa

P(N

2

O

4

) = P

p

(N

2

O

4

) - 0,5x = 1,239

⋅ 10

5

- 0.5

⋅ 0,372 ⋅ 10

5

=1,053

⋅ 10

5

Pa

3.2.

W stanie równowagi mieszanina reakcyjna znajdująca się w naczyniu o objętości 10

-2

m

3

w

temp. 500 K zawiera 4 mole Br

2

, 2,5 mola H

2

i 1 mol HBr. Obliczyć stałą równowagi reakcji: 2HBr =

H

2

+ Br

2

.

W innym doświadczeniu prowadzonym w tych samych warunkach do pustego naczynia

wprowadzono pewną ilość HBr. Po ustaleniu się stanu równowagi okazało się, że w mieszaninie
znajduje się 8 moli bromu. Wyznaczyć liczby moli poszczególnych reagentów w stanie równowagi, a
także liczbę moli wprowadzonego na początku bromowodoru.

Rozwiązanie
Wyrażamy stałą K

p

za pomocą K

n

K

K

P

P N

p

n

s

n

=











∆

gdzie:

K

n

- jest równowagowym ilorazem liczby moli reagentów; K

n

nie jest stałą równowagi,

ponieważ wielkość ta jest zależna od ciśnienia i sumarycznej liczby moli reagentów,

P - sumaryczne ciśnienie równowagowe,

N - sumaryczna liczba moli reagentów w stanie równowagi,

∆n - różnica liczby moli gazowych produktów i substratów

reakcji

(zgodnie z zapisem reakcji).

Wobec faktu, że

∆n dla powyższej reakcji równe jest zeru, zatem K

p

= K

n

.

Stąd

(

)

K

K

n

n

n

p

n

H

Br

HBr

=

=

⋅

=

⋅

=

2

2

2

2

2 5 4

1

10

,

Stała równowagi jest oczywiście równa 10 także dla drugiego doświadczenia, ponieważ temperatura
jest ta sama.

Z zapisu reakcji wynika, że jeżeli w stanie równowagi mamy 8 moli bromu, to w naczyniu musi

się znajdować także 8 moli wodoru, gdyż do naczynia wprowadzono jedynie bromowodór.
Liczbę moli bromowodoru w stanie równowagi obliczymy z wyrażenia na stałą równowagi

(

)

10

8 8

2

=

⋅

n

HBr

skąd:

n

HBr

=

2,53 mola

Obliczając liczbę moli HBr wprowadzonego na początku do naczynia, musimy uwzględnić liczbę moli
HBr znajdującą się w naczyniu w stanie równowagi oraz liczbę moli HBr, która musiała
przereagować, aby powstało 8 moli Br

2

. Ze stechiometrii reakcji wynika, że musiało przereagować 16

moli HBr. Liczba moli HBr wprowadzonego na początku do naczynia wynosi zatem n

HBr

= 2,53 + 16

= 18,53 moli.

3.3.

Wyznaczyć stopień dysocjacji gazowego PCl

5

w temperaturze 550 K. Równowagowe

ciśnienie sumaryczne wynosi 2

.

10

5

Pa, a stała równowagi reakcji dysocjacji PCl

5

= PCl

3

+ Cl

2

wynosi

w tych warunkach K

p

= 1,98.

Rozwiązanie
Wyrazimy

stałą dysocjacji K

p

za pomocą K

n

.

K

n

n

n

P

P N

p

PCl

Cl

PCl

s

n

=

⋅











3

∆

Jeżeli stopień dysocjacji oznaczymy jako

α , to w stanie równowagi liczba moli Cl

2

i PCl

3

będzie

równa iloczynowi liczby moli wprowadzonego PCl

5

i stopnia dysocjacji, czyli w tym przypadku n

o

α.

Liczba moli PCl

5

w stanie równowagi jest równa n

o

(1 -

α).

Sumaryczna liczba moli w stanie równowagi będzie równa

N = n

o

α + n

o

α + n

o

(1 − α) = n

o

(1 + α)

Różnica liczby moli gazowych produktów i substratów reakcji wynosi w tym przypadku 1. Po
podstawieniu do równania na stałą równowagi otrzymujemy:

K

p

=

−

⋅

+









 =

−

α

α

α

α

α

2

5

5

1

2

2

1

2 10

10 1

2

1

(

)

Zwróćmy uwagę, że początkowa liczba moli PCl

5

(n

o

) nie występuje w wyrażeniu na stałą równowagi.

Po podstawieniu za K

p

wartości 1,98 otrzymujemy

198

2

1

2

2

,

=

−

α

α

stąd

α = 0,70

3.4.

Stała równowagi K

p

dla reakcji N

2

+ 3H

2

= 2NH

3

w temperaturze 400

o

C wynosi 1,64

⋅10

-4

.

Czy mieszanina, w której prężności cząstkowe wszystkich reagentów wynoszą po 2

⋅10

5

Pa

przereaguje w kierunku tworzenia amoniaku?

Rozwiązanie
Informację o kierunku przebiegu reakcji otrzymamy określając zmianę entalpii swobodnej (

∆G) .

Jeżeli

∆G < 0 , to reakcja przebiega zgodnie z zapisem, jeżeli ∆G > 0, to w kierunku odwrotnym.

Korzystamy z równania izotermy Van't Hoffa, które dla podanej reakcji przyjmuje postać:

∆

∆

G

G

RT

P NH

P

P H

P

P N

P

o

s

s

s

=

+

























ln

(

)

(

)

(

)

3

2

2

3

2

gdzie prężności reagentów występujące w równaniu nie są prężnościami równo-wagowymi , a
aktualnymi.

Ponieważ

∆G

o

= -RT lnK

p

, to:

∆G

RT

K

RT

P NH

P

P H

P N

p

s

= −

+

⋅

⋅

ln

ln

(

)

(

)

(

)

2

3

2

3

2

2

(

) ( )

(

)

∆G

J

= −

⋅

⋅

+

⋅

⋅

⋅

⋅ ⋅

=

−

8 314 673

164 10

8 314 673

2 10

10

2 10

2 10

41010

4

5 2

5 2

5 3

5

,

ln ,

,

ln

Wartość

∆G jest dodatnia, zatem reakcja przebiega w przeciwnym kierunku do zapisu, czyli w

kierunku rozpadu amoniaku. Odpowiedź: nie.

3.5.

Wyznaczyć równowagowe ciśnienia H

2

i H

2

S w temperaturze 298 K, jeżeli sumaryczne

ciśnienie mieszaniny równowagowej wynosi 10

5

Pa. Czy ze wzrostem temperatury zawartość H

2

w

mieszaninie równowagowej wzrośnie, zmaleje, czy też pozostanie bez zmian?
Dane potrzebne do obliczeń należy znaleźć w literaturze.

Rozwiązanie

Gazowy wodór i siarkowodór będą współistniały w temperaturze 298 K w obecności stałej

siarki rombowej, co możemy przedstawić równaniem reakcji:

H

2

+ S(s) = H

2

S.

Ciśnieniową stałą równowagi tej reakcji (K

p

) przedstawia równanie:

K

P H S

P

P H

P

P H S

P H

p

s

s

=

=

(

)

(

)

(

)

(

)

2

2

2

2

W zapisie stałej równowagi nie uwzględniono oczywiście siarki (faza stała). Stałą równowagi
obliczymy z zależności:

∆G

o

= -RT ln K

p

.

Wartość standardowej entalpii swobodnej wyliczymy korzystając ze wzoru:
∆G

o

=

∆H

o

- T

∆S

o

. Wartości

∆H

o

i S

o

reagentów w temp. 298 K znajdujemy w tablicach

termochemicznych.

Reagent

∆H

o

[

kJ

⋅mol

-

1

]

S

o

[J

⋅mol

-

1

⋅K

-1

]

H

2

0

130,6

S(r) 0 31,88
H

2

S -20,15

205,64

∆

∆

∆

∆

H

H

H S

H

H

H

S

kJ

o

o

o

o

298

298

2

298

2

298

2015

=

−

−

= −

(

)

(

)

( )

,

( )

(

)

∆S

S

H S

S

H

S

S r

J K

o

o

o

o

298

298

2

298

2

298

205 64 130 6 3188 4316

=

−

−

=

−

−

=

(

)

(

)

,

,

,

,

/

∆

∆

∆

G

H

T S

J

kJ

o

o

o

298

298

298

20150 298 4316

330116

33 01

=

−

= −

−

⋅

= −

=

,

,

,

∆G

RT

K

o

p

298

= −

ln

stąd:

ln

,

,

,

K

G

RT

K

p

o

p

=

−

=

⋅

=

⇒

=

⋅

∆

298

5

33010

8 314 298

13 324

6114 10

Ciśnienie sumaryczne w stanie równowagi wynosi 10

5

Pa, zatem P(H

2

S)+P(H

2

) = 10

5

Pa, z

kolei wartość stałej równowagi daje nam wartość stosunku P(H

2

S)/P(H

2

) = 6,114

.

10

5

.

Rozwiązujemy układ dwóch równań:

P(H

2

S) + P(H

2

) = 10

5

suma ciśnień równowagowych H

2

i H

2

S

wynosi 10

5

Pa

P(H

2

S)/P(H

2

) = 6,114

.

10

5

stosunek ciśnień H

2

S do H

2

równy jest

wartości stałej równowagi

stąd: P(H

2

) = 0,163 Pa, P(H

2

S)

≈ 10

5

Pa

Ponieważ reakcja jest egzotermiczna (

∆H < 0), zatem ze wzrostem temperatury stała równowagi

zmaleje i tym samym, co wynika ze wzoru na stałą równowagi, zwiększy się ilość H

2

.

3.6.

Dla reakcji CO +

1
2

O

2

= CO

2

zależność stałej równowagi od temperatury dana jest

zależnością:

ln

,

K

T

p

=

−

34015

10 45

Obliczyć wartość

∆H

o

i

∆S

o

reakcji w temperaturze 298 K.

Rozwiązanie

Zapiszmy równanie izobary Van’t Hoffa.

d

K

dT

H

RT

p

o

ln

=

∆

2

Po scałkowaniu powyższego równania, przy założeniu, że

∆H

o

nie jest funkcją temperatury,

otrzymujemy:

ln K

H

RT

B

p

o

= −

+

∆

gdzie: B - jest stałą całkowania.
Porównując uzyskane równanie z podanym w treści zadania dochodzimy do wniosku, że -

∆H

o

/R =

34015, stąd

∆H

o

= -34015

.

8,314 = -282800 J = -282,8 kJ

∆S

o

reakcji znajdujemy z zależności:

∆G

o

=

∆H

o

- T

∆S

o

(

*

)

W tym celu musimy znaleźć wartość standardowej entalpii swobodnej (

∆G

o

), której związek ze stałą

równowagi K

p

ma postać:

∆G

o

= -RT lnK

p

Po podstawieniu do równania zależności podanej w zadaniu otrzymamy:

∆G

RT

T

R

RT

o

= −

−









 = − ⋅

+

⋅

34015

10 45

34015

10 45

,

,

Porównując uzyskane równanie z równaniem opatrzonym gwiazdką (

*

) otrzymujemy

∆S

o

= -R

.

10,45 = -86,88 J

⋅K

-1

3.7.

W temperaturze 1000 K w stanie równowagi w naczyniu zawierającym stały węgiel

znajduje się równomolowa mieszanina CO

2

i CO. Ciśnienie sumaryczne wynosi 1,4

.

10

6

Pa. W jakiej

temperaturze, przy tym samym ciśnieniu sumarycznym, stosunek ciśnień P(CO)/P(CO

2

) wyniesie 4?

Dla reakcji:

CO

2

+ C(s) = 2CO

∆H

o

wynosi 170 kJ i nie zależy od temperatury.

Rozwiązanie
Stała równowagi reakcji K

p

dana jest zależnością:

K

P CO

P

P CO

P

P CO

P CO

P

p

s

s

s

=













=

⋅

(

)

(

)

(

)

(

)

2

2

2

2

Ciśnienia cząstkowe CO i CO

2

w stanie równowagi dane są zależnościami:

P(CO) = x(CO) P

r

oraz P(CO

2

) = x(CO

2

) P

r

gdzie:

x - oznacza ułamek molowy w mieszaninie równowagowej,

P

r

- jest równowagowym ciśnieniem sumarycznym.

Obliczamy teraz K

p

w temp. 1000 K. Ponieważ mamy mieszaninę równomolową, to x(CO) = x(CO

2

)

= 0,5. Prężności cząstkowe CO

2

i CO wynoszą zatem:

P(CO) = P(CO

2

) = 0,5

.

1,4

.

10

6

= 0,7

.

10

6

Pa

Po podstawieniu do wyrażenia na K

p

otrzymujemy:

(

)

K

K

p

(

)

,

,

1000

0 7 10

0 7 10 10

7

6 2

6

5

=

⋅

⋅

⋅

=

Obliczamy wartość K

p

w poszukiwanej temperaturze T. Skoro stosunek prężności cząstkowych CO i

CO

2

wynosi 4, to odpowiada to także stosunkowi molowemu n(CO)/n(CO

2

) = 4. Zatem na n moli CO

2

przypada 4n moli CO. Ułamki molowe CO i CO

2

wynoszą:

x CO

n CO

n CO

n CO

n

n n

(

)

(

)

(

)

(

)

,

=

+

=

+

=

2

4

4

0 8

oraz

x CO

n CO

n CO

n CO

n

n n

(

)

(

)

(

)

(

)

,

2

2

2

4

0 2

=

+

=

+

=

Stąd prężności cząstkowe w temperaturze T wyniosą:

P(CO) = 0,8

⋅ 1,4

.

10

6

Pa

P(CO

2

) = 0,2

⋅ 1,4

.

10

6

Pa

Po podstawieniu prężności do wyrażenia na K

p

otrzymujemy:

(

)

K

p

=

⋅ ⋅

⋅ ⋅

⋅

=

0 8 14 10

0 2 14 10 10

40

6 2

6

5

,

,

,

,

Obliczamy temperaturę, w której stała równowagi K

p

wynosi 40, korzystając z zależności:

ln

( )
( )

K T

K T

H

R

T

T

o

2

2

1

1

1

2

1

1

=

−











∆

otrzymanej przez całkowanie równania izobary Van’t Hoffa w granicach od T

1

do T

2

przy założeniu,

że

∆H

o

reakcji nie jest funkcją temperatury. Po podstawieniu danych otrzymujemy:

ln

,

40

7

170000

8 314

1

1000

1

2

=

−











T

stąd: T

2

= 1093 K

ZADANIA

3.1.

Dla reakcji:

PCl

5

= PCl

3

+ Cl

2

w temperaturze 550 K,

∆G

o

= -3,123 kJ i

∆S

o

= 173 J

⋅K

-1

.

a) Obliczyć stopień dysocjacji gazowego PCl

5

w temperaturze 550 K, jeżeli 1 mol tego związku

umieścimy w naczyniu o pojemności V. Równowagowe ciśnienie sumaryczne wynosi 2

⋅10

5

Pa.

b) Czy stopień dysocjacji wzrośnie, zmaleje, czy też pozostanie bez zmian, gdy objętość naczynia
zmniejszymy o połowę?
c) Jak wpłynie wzrost temperatury na stałą równowagi reakcji?

3.2.

Ile moli PCl

5

należy wprowadzić do pustego naczynia o objętości 1 dm

3

, aby

równowagowe stężenie chloru wynosiło w temperaturze 327

o

C

0,1 mol

⋅dm

-3

? K

p

reakcji dysocjacji PCl

5

wynosi w tych warunkach 2.

3.3.

W naczyniu o pojemności 0,5 dm

3

w temperaturze 25

o

C początkowo znajduje się

1,588 g N

2

O

4

. Po ustaleniu się stanu równowagi ciśnienie mieszaniny gazowej składającej się z NO

2

i

N

2

O

4

wynosi 10

5

Pa. Obliczyć stopień dysocjacji N

2

O

4

oraz stałą równowagi K

p

. Czy stopień

dysocjacji zmaleje, wzrośnie, czy pozostanie bez zmian, jeżeli ciśnienie równowagowe wyniesie 2

⋅10

5

Pa?

3.4.

W temperaturze 523 K pod ciśnieniem 1,013

⋅10

5

Pa stopień dysocjacji fosgenu (COCl

2

)

na tlenek węgla i chlor wynosi 0,7. Obliczyć stałą równowagi K

p

oraz równowagowy iloraz liczby

moli reagentów K

n

, jeżeli do opróżnionego naczynia wprowadzono 1 mol fosgenu w tej temperaturze.

Do obliczenia której z ww. wielkości potrzebna jest informacja o początkowej liczbie moli fosgenu?

3.5.

W stanie równowagi w temperaturze T w naczyniu o objętości V znajdują się wodór,

chlor i chlorowodór , których prężności cząstkowe wynoszą 10

5

Pa,

∆H

o

reakcji wynosi -92,3 kJ.

a) Obliczyć stałą równowagi K

p

reakcji H

2

+ Cl

2

= 2HCl(g).

b) W którą stronę przesunie się położenie równowagi, jeżeli objętość naczynia dwukrotnie
zwiększymy?
c) Czy stała równowagi wzrośnie, zmaleje, czy pozostanie bez zmian, jeżeli temperaturę podwoimy?

3.6

.

Ile moli CO

2

należy dodać do naczynia zawierającego stały CaO, aby w temperaturze

1200 K otrzymać 1 mol stałego CaCO

3

? Skorzystać z tablic.

a) Odpowiedź podać w postaci zależności liczby moli od objętości naczynia.
b) Wykonać obliczenia dla objętości naczynia równej 1 dm

3

.

3.7.

Dla reakcji:

2NO + O

2

= 2NO

2

stała równowagi K

p

w temperaturze 298 K wynosi 4,6

⋅10

23

,

∆S

o

298

= -170 J

⋅K

-1

, a

∆C

p

= 0. Obliczyć

∆G

o

i K

p

reakcji w temperaturze 700 K.

3.8.

Znaleźć zależność stałej równowagi od temperatury dla reakcji:

SO

2

+

1
2

O

2

= SO

3

wiedząc, że

∆H

o

298

i

∆S

o

298

dla powyższej reakcji wynoszą odpowiednio: -98,3 kJ oraz -94,38 J

⋅K

-1

.

Zakładamy, że

∆C

p

= 0.

3.9.

Wyznaczyć prężność CO

2

nad tlenkiem baru w temperaturze 800 K korzystając z danych

tablicowych zakładając, że dla reakcji rozkładu węglanu baru

∆C

p

= 0. Jak wpłynie wzrost

temperatury na prężność CO

2

?

3.10.

Wyznaczyć

∆H

o

,

∆S

o

oraz stałą równowagi K

p

reakcji

FeO(s) + CO

2

= FeCO

3

(s)

w temperaturze 298 K wykorzystując dane tablicowe. Obliczyć także stałą równowagi tej reakcji w
temperaturze 1000 K zakładając, że ciepło reakcji jest niezależne od temperatury.

3.11.

Stała równowagi K

p

reakcji:

FeO(s) + CO(g) = Fe(s) + CO

2

wynosi 0,871 w temperaturze 600

o

C oraz 0,403 w temperaturze 1000

o

C. Obliczyć

∆H

o

reakcji oraz

stałą równowagi w temperaturze 1000 K.
Zakładamy, że

∆C

p

= 0.

3.12.

Dla reakcji:

C + 2H

2

(g) = CH

4

(g)

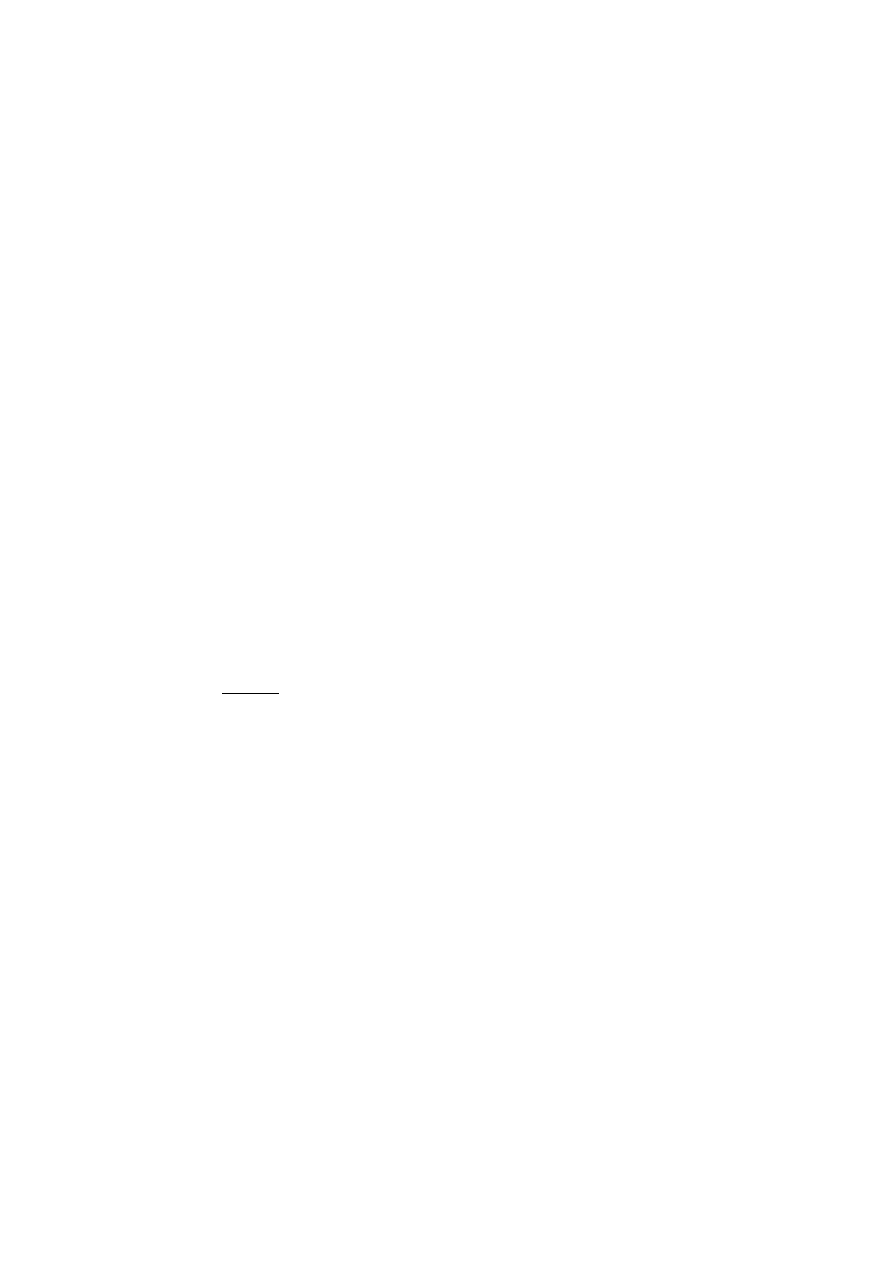
zależność stałej równowagi od temperatury ma postać: lnK

p

= 9000,5/T - 9,712. Obliczyć

∆H

o

i

∆S

o

reakcji.

3.13.

Czy mieszanina zawierająca NO

2

o ciśnieniu P = 10

5

Pa oraz N

2

O

4

o ciśnieniu P = 10

6

Pa w

temperaturze 25

o

C będzie reagować w kierunku tworzenia N

2

O

4

? Dla reakcji: 2NO

2

= N

2

O

4

standardowa zmiana entalpii swobodnej

∆G

o

wynosi -4860 J.

3.14.

Obliczyć stałą równowagi reakcji:

NiO(s) + CO(g) = Ni(s) + CO

2

(g)

w temperaturze 298 oraz 500 K korzystając z danych tablicowych. Zakładamy, że

∆C

p

reakcji wynosi

0.

ODPOWIEDZI DO ZADAŃ

3.1.

a)

α = 0,70;

b)

α zmaleje;

c)

stała równowagi wzrośnie.

3.2.

0,35 mola PCl

5

.

3.3.

α = 0,169; K

p

= 0,1184;

α zmaleje.

3.4.

K

p

= 0,961; K

n

= 1,633; Znajomość początkowej liczby moli fosgenu jest potrzebna do

obliczenia K

n

.

3.5.

a) K

p

= 1;

b)

położenie równowagi nie zmieni się (

∆n = 0);

c)

K

p

zmaleje.

3.6.

a) n = 1 + 46,608

⋅ V;

b) n = 1,047 mola CO

2

.

3.7.

∆G

o

700

= -66,651 kJ; K

p

= 9,41

⋅10

4

.

3.8.

ln

,

,

K

T

p

=

−

11823 4

1135

.

3.9.

P(CO

2

) = 3,37

⋅10

-3

Pa; ze wzrostem temperatury prężność CO

2

wzrośnie.

3.10.

∆H

o

298

= -90,49 kJ;

∆S

o

298

= -179,51 J

⋅K

-1

; K

p

(298 K) = 3,05

⋅10

6

; K

p

(1000 K) = 2,23

⋅10

-5

.

3.11.

∆H

o

= -17,82 kJ; K

p

(1000 K) = 0,637.

3.12.

∆H

o

= -74,83 kJ;

∆S

o

= -80,75 J

⋅K

-1

.

3.13.

∆G = 844,8 J > 0; nie.

3.14.

K

p

(298 K) = 1,02

⋅10

8

; K

p

(500 K) = 8,75

⋅10

4

.

4. ELEKTROCHEMIA

Zadania przykładowe

4.1.

W naczyńku konduktometrycznym elektrody o powierzchni 1 cm

2

są umieszczone w

odległości 2 cm. Zmierzona w tym naczyńku rezystancja (R) roztworu HCl o stężeniu 0,01 mol

⋅dm

-3

wynosi 487,8

Ω.

a) Obliczyć przewodnictwo właściwe i równoważnikowe roztworu HCl.
b) Ile wyniosłaby rezystancja roztworu NaOH o stężeniu 0,01 mol

⋅dm

-3

w tym naczyńku?

Przewodnictwo molowe roztworu NaOH o stężeniu 0,01mol

⋅dm

-3

wynosi 240 S

⋅cm

2

⋅mol

-1

.

Rozwiązanie
Stała naczyńka konduktometrycznego dana jest zależnością:

k

l

s

cm

= = =

−

2
1

2

1

gdzie:

l - odległość pomiędzy elektrodami

s - powierzchnia elektrody

a) Przewodnictwo właściwe obliczamy z zależności:

κ =

=

=

⋅

⋅

−

−

k

R

S cm

2

487 8

410 10

3

1

,

,

Natomiast przewodnictwo równoważnikowe, równe w przypadku elektrolitu
1,1-wartościowościowego przewodnictwu molowemu, wyliczamy ze wzoru:

Λ

r

c

S cm

=

=

⋅

⋅

=

⋅

−

1000

1000 410 10

0 01

410

3

2

κ

,

,

⋅ równ.

-1

b) Ze wzoru definiującego przewodnictwo równoważnikowe wynika, że

κ =

=

k

R

c

Λ

1000

Stąd:

R

k

c

=

⋅

⋅

=

⋅

⋅

=

1000

1000 2

240 0 01

833 33

Λ

Ω

,

,

4.2.

Rezystancja (R) roztworu zawierającego 0,871 g K

2

SO

4

w 1 dm

3

roztworu, zmierzona w

naczyńku konduktometrycznym o stałej równej 150 m

- 1

, wynosi 1000

Ω. Obliczyć przewodnictwo

właściwe, molowe i równoważnikowe roztworu K

2

SO

4

. M (K

2

SO

4

) = 174,2 g

⋅mol

-1

.

Rozwiązanie

Przewodnictwo

właściwe roztworu obliczamy z zależności:

κ =

k

R

gdzie:

κ - przewodnictwo właściwe,

k - stała naczyńka,

R - rezystancja roztworu.

Po podstawieniu

κ =

=

⋅

−

150

1000

015

1

, S m

Aby znaleźć przewodnictwo molowe i równoważnikowe, obliczamy stężenie roztworu K

2

SO

4

w

molach

⋅ m

-3

.

c

n
v

m

M

v

m

mol m

K SO

=

=

=

=

⋅

−

−

2

4

0 871

174 2

10

5

3

3

3

,

,

Przewodnictwo molowe obliczamy z zależności:

(

)

Λ K SO

c

S m mol

2

4

2

1

015

5

0 03

= =

=

⋅

⋅

−

κ

,

,

Przewodnictwo równoważnikowe, czyli przewodnictwo połowy mola K

2

SO

4

, obliczamy z zależności:

Λ

1
2

2

015

2 5

0 015

2

4

2

K SO

c

S m









 =

=

⋅

=

⋅

κ

,

,

⋅

równ

.

-1

Należy zwrócić uwagę na to, że w większości podręczników i tablic podaje się wartości
przewodnictw równoważnikowych w S

⋅cm

2

⋅równ.

-1

, a przewodnictw właściwych w S

⋅cm

-1

, i tymi

jednostkami będziemy się posługiwać w tym skrypcie. Stała naczyńka k po zmianie jednostek wynosi
1,5 cm

-1

, przewodnictwo właściwe równe jest zatem

κ =

=

=

⋅

⋅

−

−

k

R

S cm

15

1000

15 10

3

1

,

,

Przewodnictwo molowe obliczamy z zależności:

(

)

Λ K SO

c

S cm mol

2

4

3

3

2

1

1000

1000 15 10

5 10

300

=

=

⋅

⋅

⋅

=

⋅

⋅

−

−

−

κ

,

gdzie

κ wyrażone jest w S⋅cm

-1

, a stężenie w molach

⋅dm

-3

.

Przewodnictwo równoważnikowe jest równe odpowiednio:

Λ

1
2

1000 15 10

2 5 10

150

2

4

3

3

2

K SO

S cm









 =

⋅

⋅

⋅ ⋅

=

⋅

⋅

−

−

,

równ.

-1

4.3.

100 cm

3

roztworu NaOH miareczkowano za pomocą 0,5 molowego roztworu H

2

SO

4

.

Przewodnictwo mierzono stosując zanurzeniowe naczyńko konduktometryczne o stałej równej
0,2 cm

-1

. Wiedząc, że w punkcie równoważnikowym rezystancja roztworu wynosi 153,85

Ω, obliczyć

ilość moli NaOH zawartą w roztworze oraz jego stężenie przed miareczkowaniem. Przewodnictwa
równoważnikowe jonów Na

+

i SO

4

-

wynoszą odpowiednio: 50 i 80 S

⋅cm

2

⋅równ.

-1

. Efekt

rozcieńczania należy pominąć.

Rozwiązanie

Podczas miareczkowania roztworu NaOH za pomocą roztworu H

2

SO

4

zachodzi reakcja:

2NaOH + H

2

SO

4

= Na

2

SO

4

+ 2H

2

O

W punkcie równoważnikowym znajduje się w roztworze jedynie siarczan sodowy, którego stężenie
molowe obliczamy wykorzystując zależności:

(

)

(

)

κ

κ

Na SO

k

R

Na SO

Na SO

c

2

4

2

4

2

4

1
2

1000

2

=









 =

⋅

⋅

Λ

Połączenie obu równań daje wyrażenie:

(

)

c Na SO

k

R

Na SO

2

4

2

4

1000

2

1
2

=

⋅

⋅ ⋅











Λ

gdzie:

(

)

Λ

1
2

1
2

50 80 130

2

4

4

2

2

Na SO

Na

SO

S cm









 =

+









 =

+

=

⋅

⋅

+

−

λ

λ

równ.

-1

Po podstawieniu danych otrzymujemy:

(

)

c Na SO

mol dm

2

4

3

3

1000 0 2

2 153 85 130

5 10

=

⋅

⋅

⋅

= ⋅

⋅

−

−

,

,

Zatem w 100 cm

3

roztworu (pomijamy efekt rozcieńczania) znajduje się

5

⋅10

-3

mol

⋅dm

-3

⋅0,1 dm

3

= 5

⋅10

-4

mola Na

2

SO

4

Z zapisanej reakcji wynika, że dla powstania 1 mola Na

2

SO

4

muszą przereagować 2 mole NaOH. Stąd

w wyjściowym roztworze musiało znajdować się 2

⋅5⋅10

-4

= 1

⋅10

-3

mola NaOH.

Stężenie wyjściowego roztworu NaOH wynosiło:

c

n
v

mol dm

=

=

= ⋅

⋅

−

−

−

−

10
10

1 10

3

1

2

3

4.4.

Przewodnictwo właściwe roztworu HCl o stężeniu 0,1 mol

⋅dm

-3

wynosi 4,10

⋅10

-2

S

⋅cm

-1

.

Jeżeli do tego roztworu zostanie dodana identyczna objętość roztworu KOH o stężeniu 0,1 mol

⋅dm

-3

,

to przewodnictwo zmaleje do wartości 6,25

⋅10

-3

S

⋅cm

-1

. Dodanie drugiej, takiej samej objętości

roztworu KOH o stężeniu 0,1 mol

⋅dm

-3

powoduje z kolei wzrost przewodnictwa właściwego roztworu

do wartości 1,204

⋅10

-2

S

⋅cm

-1

. Obliczyć:

a) przewodnictwo równoważnikowe HCl,
b) przewodnictwo równoważnikowe KCl,
c) przewodnictwo równoważnikowe KOH,
d) sumę przewodnictw jonowych H

+

i OH

-

.

Rozwiązanie
a) Przewodnictwo równoważnikowe HCl obliczamy z zależności:

(

)

Λ HCl

c

S cm

=

⋅

=

⋅

⋅

=

⋅

⋅

−

1000

410 10

1000

01

410

2

2

κ

,

,

równ.

-1

b) Po dodaniu do roztworu HCl o stężeniu 0,1 mol

⋅dm

-3

identycznej objętości roztworu KOH o

stężeniu 0,1 mol

⋅dm

-3

otrzymamy zgodnie z reakcją:

HCl + KOH = KCl + H

2

O

wodny roztwór KCl o stężeniu równym połowie stężeń wyjściowych, czyli 0,05 mol

⋅dm

-3

.

Zatem

(

)

Λ KCl

S cm

=

⋅

⋅

=

⋅

⋅

−

1000 6 25 10

0 05

125

3

2

,

,

równ.

-1

c) Jeżeli do roztworu otrzymanego w punkcie b) dodamy kolejną, identyczną objętość roztworu KOH
o stężeniu 0,01 mol

⋅dm

-3

, to w uzyskanej mieszaninie znajdzie się KCl o stężeniu 0,033 mol

⋅dm

-3

(objętość roztworu KCl zwiększona została o 1/3) oraz KOH o stężeniu 0,033 mol

⋅dm

-3

(jedną

objętość roztworu KOH dodano do dwóch objętości).
Przewodnictwo

właściwe mieszaniny równe jest sumie przewodnictw KCl i KOH.

(

)

(

)

κ κ

κ

=

+

K Cl

K OH

Po podstawieniu w miejsce

κ wyrażenia

Λ ⋅ c

1000

otrzymujemy:

(

) (

)

(

) (

)

κ =

⋅

+

⋅

Λ

Λ

KCl c KCl

KOH c KOH

1000

1000

gdzie

niewiadomą jest poszukiwana wartość przewodnictwa równoważnikowego KOH.

Wstawiając dane otrzymamy:

(

)

1204 10

125 0 033

1000

0 033

1000

2

,

,

,

⋅

=

⋅

+

⋅

−

Λ KOH

Stąd

Λ(KOH) = 240,0 S⋅cm

2

⋅równ.

-1

.

d) Aby obliczyć sumę przewodnictw jonowych H

+

i OH

-

, skorzystamy z prawa niezależnej wędrówki

jonów Kohlrauscha.

( ) (

)

( ) ( ) ( ) ( ) ( ) (

)

(

)

(

)

(

)

λ

λ

λ

λ

λ

λ

λ

λ

H

OH

H

Cl

K

Cl

K

OH

HCl

KCl

KOH

+

−

+

−

+

−

+

−

+

=

+

−

−

+

+

↓

↓

↓

Λ

Λ

Λ

Po podstawieniu danych otrzymujemy:

( ) (

)

λ

λ

H

OH

S cm

+

−

+

=

−

+

=

⋅

⋅

410 125 240 525

2

równ.

-1

4.5

.

Miareczkując konduktometrycznie 100 cm

3

pewnego roztworu HCl za pomocą

roztworuNaOH o stężeniu 0,5 mol

⋅dm

-3

uzyskano następujące wyniki:

NaOH [cm

3

]

0 2,0 4,0 6,0 8,0 10,0

κ⋅10

3

[S

⋅cm

-1

]

20,0 14,3 8,75 7,35 9,95 12,5

Obliczyć liczbę moli HCl zawartą w wyjściowym roztworze oraz jego stężenie.

Rozwiązanie

Podczas miareczkowania roztworu HCl roztworem NaOH zachodzi reakcja:

H

+

+ Cl

-

+ Na

+

+ OH

-

= Na

+

+ Cl

-

+ H

2

O

Celem wyznaczenia punktu równoważnikowego wykonuje się wykres zależności przewodnictwa
właściwego roztworu w funkcji objętości dodawanego roztworu NaOH. Przez punkty
eksperymentalne prowadzimy linie proste, których przecięcie wyznaczy punkt równoważnikowy. Z
pokazanego rysunku wynika, że punkt równoważnikowy osiągamy po dodaniu 5 cm

3

roztworu

NaOH o stężeniu 0,5 mol

⋅dm

-3

, co odpowiada 5

⋅10

-3

dm

3

⋅ 0,5 mol⋅dm

-3

= 2,5

⋅10

-3

mola NaOH.

Z reakcji wynika, że liczba moli HCl zawarta w wyjściowym roztworze jest równa liczbie moli

zużytego NaOH, czyli wynosi 2,5

⋅10

-3

moli.

Ponieważ 2,5

⋅10

-3

moli HCl znajdowało się w 100 cm

3

roztworu, zatem stężenie wyjściowe

roztworu HCl wynosiło:

c HCl

n

V

mol dm

(

)

,

,

,

=

=

⋅

=

⋅

−

−

2 5 10

01

0 025

3

3

V [cm ]

10 S cm

0

5

10

15

20

0

5

10

Krzywa miareczkowania konduktometrycznego roztworu HCl roztworem NaOH

4.6.

W aparacie Hittorfa o platynowych elektrodach znajduje się roztwór NaOH o stężeniu 0,10

mol

⋅dm

-3

. Po przepłynięciu przez roztwór ładunku 5

⋅10

-3

F do przestrzeni katodowej przybyło 1

⋅10

-3

mola NaOH. Obliczyć liczbę przenoszenia jonu OH

-

w tym roztworze oraz końcowe stężenie NaOH w

przestrzeni katodowej i anodowej. W obu przestrzeniach znajduje się po 100 cm

3

roztworu.

Rozwiązanie

Na elektrodach platynowych zajdą następujące reakcje elektrodowe:

katoda: H

2

O + e =

1
2

H

2

+ OH

-

anoda:

1
2

H

2

O =

1
4

O

2

+ H

+

+ e

Wykonujemy bilans materiałowy dla obu przestrzeni przy przepływie ładunku 1 F:
Przestrzeń katodowa: wskutek reakcji elektrodowej przybywa 1 gR OH

-

wskutek wędrówki jonów

przybywa t gR Na

ubywa t gR OH

+

+

−

−







____________________________

po podsumowaniu:

1 gR OH

-

+ t

+

gR Na

+

- t

-

gR OH

-

Uwzględniając, że 1 - t

-

= t

+

, otrzymujemy: + t

+

gR NaOH

Przestrzeń anodowa: wskutek reakcji elektrodowej przybywa 1 gR H

+

wskutek wędrówki jonów

przybywa t gR OH

ubywa

t

gR Na

−

−

+

+







__________________________

po podsumowaniu:

1 gR H

+

+ t

-

gR OH

-

- t

+

gR Na

+

Zastępując t

-

gR OH

-

przez (1 - t

+

) gR OH

-

otrzymujemy:

1gR H

+

+ 1gR OH

-

- t

+

gR OH

-

+ t

+

gRNa

+

,

a ponieważ jony H

+

z jonami OH

-

utworzą cząsteczkę H

2

O otrzymamy ostatecznie 1 gR H

2

O - t

+

gR

NaOH.
Z bilansu przestrzeni katodowej wynika, że ze zmian liczby moli NaOH w tej przestrzeni możemy
wyliczyć liczbę przenoszenia jonu Na

+

z zależności:

(

)

t Na

n

Q

+

=

∆

∆ n = 1⋅10

-3

mola, Q = 5

⋅10

-3

F.

Po podstawieniu otrzymamy:

(

)

t Na

+

−

−

=

⋅

⋅

=

1 10
5 10

0 20

3

3

,

stąd

(

)

(

)

t OH

t Na

−

+

= −

= −

=

1

1 0 2 0 8

,

,

Obliczamy stężenie końcowe NaOH w przestrzeni katodowej. W 100 cm

3

roztworu NaOH o stężeniu

0,10 znajduje się 0,010 mola NaOH. Ponieważ przybyło 1

⋅10

-3

mola NaOH, zatem po elektrolizie w

przestrzeni katodowej znajduje się 0,011 mola NaOH w 100cm

3

, co odpowiada stężeniu 0,11mol

⋅dm

-3

.

W przestrzeni anodowej mamy do czynienia z ubytkiem 1

⋅10

-3

mola NaOH. Po elektrolizie w

przestrzeni anodowej znajduje się 0,010 - 0,001 = 0,0099 mola NaOH, co odpowiada stężeniu 0,099
mol

⋅dm

-3

.

4.7.

W aparacie Hittorfa, w którym katoda jest platynowa, a anoda chlorosrebrna, znajduje się

roztwór KCl o stężeniu 0,10 mol

⋅dm

-3

. Po przepuszczeniu przez roztwór ładunku 1

⋅10

-2

F z

przestrzeni anodowej ubyło 4,9

⋅10

-3

mola KCl. Obliczyć liczbę przenoszenia jonu Cl

-

w tym roztworze

oraz końcowe stężenie KCl w przestrzeniach katodowej i anodowej. W obu przestrzeniach znajduje
się po 100 cm

3

roztworu.

Rozwiązanie
Reakcja

zachodząca na anodzie jest reakcją utleniania

Ag + Cl

-

= AgCl + e

Bilans przestrzeni anodowej przy przepływie ładunku 1F:
wskutek reakcji elektrodowej z przestrzeni anodowej ubywa -1 gR Cl

-

wskutek wędrówki

jonów

przybywa t

gR Cl

ubywa

t

gR K

−

−

+

+







____________________________________
Po podsumowaniu:

-1 gR Cl

-

- t

+

gR K

+

+ t

-

gR Cl

-

= -t

+

gR KCl.

Zatem ze zmian liczby moli KCl w przestrzeni anodowej można obliczyć liczbę przenoszenia jonu
t(K

+

). Korzystamy z zależności:

( )

t K

n

Q

+

=

∆

gdzie:

∆n = 4,9⋅10

-3

, a Q = 1

⋅10

-2

F.

Po podstawieniu otrzymamy:

( )

t K

+

−

−

=

⋅

=

4 9 10

10

0 49

3

2

,

,

stąd

( )

( )

t Cl

t K

−

+

= −

= −

=

1

1 0 49 0 51

,

,

.

Stężenie końcowe KCl w przestrzeni anodowej:
w 100 cm

3

znajdowało się 0,010 mola KCl, ubyło 4,9

⋅10

-3

mola KCl, zatem pozostało 5,1

⋅10

-3

mola

KCl w 100 cm

3

, czyli stężenie wynosi 0,051 mol

⋅dm

-3

.

W przestrzeni katodowej:
na platynowej katodzie zachodzi rozkład wody z wydzieleniem wodoru

H

2

O + e =

1
2

H

2

+ OH

-

Bilans materiałowy dla tej przestrzeni przy przepływie 1 F:

wskutek reakcji elektrodowej

przybywa 1 gR OH

-

wskutek wędrówki jonów

przybywa

ubywa

t

gR Cl

t

+

gR K+

−

−









___________________________

Po podsumowaniu:

1 gR OH

-

+ t

+

gR K

+

- t

-

gR Cl

-

.

Po zastąpieniu t

+

(K

+

) przez (1 - t

-

)(K

+

) otrzymujemy:

1

1

1

gR OH

gR K

t gR K

t gR KCl

gR K OH t gR K Cl

−

+

−

+

−

−

+

−

−

=

−

Z przestrzeni katodowej ubywa t

-

gR KCl. Ubytek liczby moli KCl z przestrzeni katodowej obliczymy

z zależności:

( )

∆ n Q t Cl

mola

= ⋅

= ⋅

⋅

=

⋅

−

−

−

1 10

0 51 51 10

2

3

,

,

W 100 cm

3

roztworu katodowego znajdowało się 0 010 mola KCl, ubyło 5,1

⋅10

-3

mola, pozostało

zatem 0,0049 mola KCl. Stężenie końcowe KCl w roztworze katodowym wynosi 0,049 mol

⋅dm

-3

.

4.8.

Przed elektrolizą przestrzeń anodowa aparatu Hittorfa zawierała 10,42g CdSO

4

w 1 kg

wody. Przepuszczono ładunek 1,5

⋅10

-3

F. Liczba przenoszenia jonu Cd

2+

w CdSO

4

wynosi 0,37.

M(CdSO

4

) = 208,4 g

⋅mol

-1

.

Zapisać bilans materiałowy i obliczyć molalność siarczanu kadmu w przestrzeni anodowej
zawierającej 50 g H

2

O w przypadku, gdy:

a) anoda jest platynowa,
b) anoda jest kadmowa.

Rozwiązanie
a) Reakcja zachodząca podczas elektrolizy CdSO

4

na anodzie platynowej jest reakcją rozkładu wody z

wydzieleniem tlenu.

1
2

H

2

O

→

1
4

O

2

+ H

+

+ e

Bilans materiałowy dla przestrzeni anodowej przy przepływie 1 F ładunku przedstawia się
następująco:
wskutek reakcji elektrodowej do przestrzeni anodowej przybywa 1 gR H

+

wskutek wędrówki jonów

przybywa t

gR SO

ubywa

t

gR Cd

−

+

−

+







4

2

2

___________________________

Po podsumowaniu:

1 gR H

+

+ t

-

gR SO

4

2-

- t

+

gR Cd

2+

Zastępując t

-

przez 1 - t

+

otrzymujemy:

1

1

1

4

2

2

4

2

2

4

4

gR H

gR SO

t gR Cd

t gR SO

gR H SO

t gR CdSO

+

−

+

+

+

−

+

+

−

−

=

−

Z

przeprowadzonego bilansu wynika, że ze zmiany liczby gramorównoważników CdSO

4

w przestrzeni

anodowej możemy obliczyć liczbę przenoszenia jonów Cd

2+

. Liczba przenoszenia jonów Cd

2+

dana

jest zależnością:

(

)

t Cd

n

Q

2

+

=

∆

gdzie:

∆ n - ubytek CdSO

4

wyrażony w gramorównoważnikach,

Q - ładunek, który przepłynął przez roztwór.

Ponieważ znana jest liczba przenoszenia jonu Cd

2+

oraz ładunek, możemy obliczyć

∆ n.

(

)

∆ n Q t Cd

gR CdSO

= ⋅

=

⋅

⋅

=

⋅

+

−

−

2

3

4

4

15 10

0 37 5 55 10

,

,

,

co odpowiada 2,775

⋅10

-4

mola CdSO

4

.

Obliczamy początkową zawartość CdSO

4

w 50 g H

2

O.

W 1kg H

2

O znajdowało się

10 42

208 4

0 05

,

,

,

=

mola CdSO

4

W 50 g H

2

O znajdowało się

0 05

20

0 0025

,

,

=

mola CdSO

4

.

Wskutek elektrolizy ubyło 2,775

⋅10

-4

mola CdSO

4

, stąd po elektrolizie w 50 g H

2

O znajduje się

2,5

⋅10

-3

- 0,2775

⋅10

-3

= 2,2225

⋅10

-3

mola CdSO

4

. W 1000 g H

2

O po elektrolizie znajduje się 0,04445

mola CdSO

4

.

b) Reakcja zachodząca na kadmowej anodzie jest reakcją utleniania kadmu do jonów Cd

2+

:

1
2

Cd

→

1
2

Cd

2+

+ e

Bilans materiałowy przestrzeni anodowej.
Wskutek reakcji elektrodowej przybywa 1 gR Cd

2+

Wskutek wędrówki jonów

przybywa

gR SO

ubywa

gR Cd

t

t

−

−

+

+







4

2

2

Po uwzględnieniu, że 1 gR Cd

2+

- t

+

gR Cd

2+

= +t

-

gR Cd

2+

, okazuje się, że do przestrzeni anodowej

przybyło t

-

gR CdSO

4

.

W tym przypadku słuszna będzie zależność:

(

)

t SO

n

Q

4

2

−

=

∆

Ponieważ t(SO

4

2-

) = 1 - t(Cd

2+

) = 1 - 0,37 = 0,63, zatem

∆n (przybytek liczby gramorównoważników

CdSO

4

) wynosi 0,63

⋅1,5⋅10

-3

= 0,945

⋅10

-3

gR CdSO

4

, czyli 0,4725

⋅ 10

-3

moli CdSO

4

.

Uwzględniając obliczenia wykonane w punkcie a) otrzymujemy, że liczba moli CdSO

4

w 50 g H

2

O

po elektrolizie wynosi 2,5

⋅ 10

-3

+ 0,4725

⋅ 10

-3

= 2,9725

⋅10

-3

moli, co odpowiada zawartości 0,05945

mola w 1000 g H

2

O.

4.9.

Zapisać reakcję zachodzącą w ogniwie:

Ag | AgCl

(s) | HCl(aq) | H

2

(1,013

⋅10

5

Pa) |Pt

oraz obliczyć jej stałą równowagi w temperaturze 298 K korzystając z danych literaturowych.

Rozwiązanie
Według zalecanej przez UIPAC (International Union of Pure and Applied Chemistry)
konwencji półogniwo umieszczone po stronie lewej stanowi anodę, a półogniwo umieszczone po
stronie prawej katodę ogniwa. Na anodzie zachodzi reakcja utleniania, a na katodzie reakcja redukcji.

Reakcje elektrodowe:

Katoda:

H

+

+ e =

1
2

H

2

Anoda:

Ag

+

Cl

-

= AgCl(s) + e

_____________________________________________

Reakcja sumaryczna: Ag + H

+

+ Cl

-

=

1
2

H

2

+ AgCl

Stałą równowagi reakcji zachodzącej w ogniwie obliczamy, wykorzystując związki pomiędzy
standardową entalpią swobodną (

∆G

o

) a standardową siłą elektromotoryczną (E

o

)

∆G

o

= -zFE

o

gdzie:

z - liczba wymienionych elektronów podczas reakcji,
F - stała Faradaya równa 96500 C,

oraz związek pomiędzy standardową entalpią swobodną a stałą równowagi reakcji (K)

∆G

o

= - RT lnK

gdzie:

T - temperatura w Kelwinach,

R - stała gazowa.

Porównanie lewych stron obu równań daje zależność:

ln K

zF

RT

E

o

=

Standardową siłę elektromotoryczną ogniwa obliczamy zgodnie ze stosowaną konwencją jako różnicę
potencjałów standardowych półogniwa prawego i lewego.

E

o

= E

o

p

- E

o

l

= E

o

(H

+

| H

2

|Pt) - E

o

(Ag | AgCl | Cl

-

)

Wartości potencjałów standardowych półogniw w Poradniku fizykochemicznym wynoszą:

E

o

298K

(H

+

|H

2

) = 0 V i E

o

298K

(Ag | AgCl | Cl

-

) = 0,222 V

stąd standardowa

siła elektromotoryczna ogniwa wynosi:

E

o

298K

= 0 - 0,222 = -0,222 V

Po wstawieniu tej wartości do wzoru na stałą równowagi otrzymujemy:

(

)

ln

,

,

,

K

=

⋅

⋅

⋅ −

= −

1 96500

8 314 298

0 222

8 647

Stała równowagi reakcji zachodzącej w ogniwie wynosi K = 1,76

⋅10

-4

.

4.10

.

Obliczyć iloczyn rozpuszczalności PbSO

4

w temperaturze 298 K mając dane:

E

o

298

(Pb

2+

| Pb) = -0,126 V,

E

o

298

(Pb | PbSO

4

|SO

4

2-

) = -0,359 V.

Rozwiązanie
Iloczyn

rozpuszczalności (I

r

), czyli stała równowagi reakcji

PbSO

4

(s) = Pb

2+

+ SO

4

2-

(4.10.1)

związana jest ze zmianą entalpii swobodnej reakcji zależnością:

∆G

o

1

= - RT ln I

r

Zapisujemy reakcje elektrodowe półogniw i odpowiadające im wartości

∆G

o

w ten sposób, aby po ich

dodaniu otrzymać reakcję (4.10.1).

PbSO

4

+ 2e = Pb + SO

4

2-

(4.10.2)

∆G

o

2

= -2FE

o

(Pb | PbSO

4

| SO

4

2-

) = -2F(-0,359)

Pb = Pb

2+

+ 2e (4.10.3)

∆G

o

3

= -2F(-E

o

(Pb

2+

| Pb)) = -2F

⋅0,126

Ponieważ reakcję elektrodową zapisano jak reakcję utleniania, a potencjały standardowe są
potencjałami dla reakcji redukcji, zmieniono zatem znak potencjału standardowego półogniwa.
Dodanie reakcji (4.10.2) i (4.10.3) daje reakcję (4.10.1), zatem:

∆G

o

1

=

∆G

o

2

+

∆G

o

3

.

Po podstawieniu:

-RT ln I

r

= +2F

⋅0,359 - 2F⋅0,126 ⇒ I

r

= 1,31

⋅10

-8

4.11.

Zamierzamy wyznaczyć potencjometrycznie stężenie jonów Sn

4+

w roztworze. Dobierz

czynnik miareczkujący i uzasadnij jego wybór. Do dyspozycji mamy następujące układy utleniająco-
redukujące:
a) Cr

3+

| Cr

2+

⇒ E

o

298

= -0,58 V

b) Cu

2+

| Cu

+

⇒ E

o

298

= 0,15 V

c) Fe

3+

| Fe

2+

⇒ E

o

298

= 0,771 V

Potencjał standardowy półogniwa Sn

4+

| Sn

2+

= 0,15 V.

Rozwiązanie

Podczas miareczkowania potencjometrycznego jony Sn

4+

mają być redukowane do Sn

2+

.

Zatem czynnik miareczkujący powinien charakteryzować się silnymi własnościami redukującymi.
Własności redukujące półogniw są tym większe, im niższy jest potencjał standardowy półogniwa. W
tym przypadku półogniwem o najniższym potencjale jest półogniwo Cr

3+

| Cr

2+

.

Podczas miareczkowania potencjometrycznego będzie zachodziła reakcja:

Sn

4+

+ 2Cr

2+

= Sn

2+

+ 2Cr

3+

Wyznaczenie punktu równoważnikowego miareczkowania będzie tym łatwiejsze, im większa będzie
różnica między potencjałami standardowymi obu użytych układów utleniająco-redukujących, a wobec
zależności

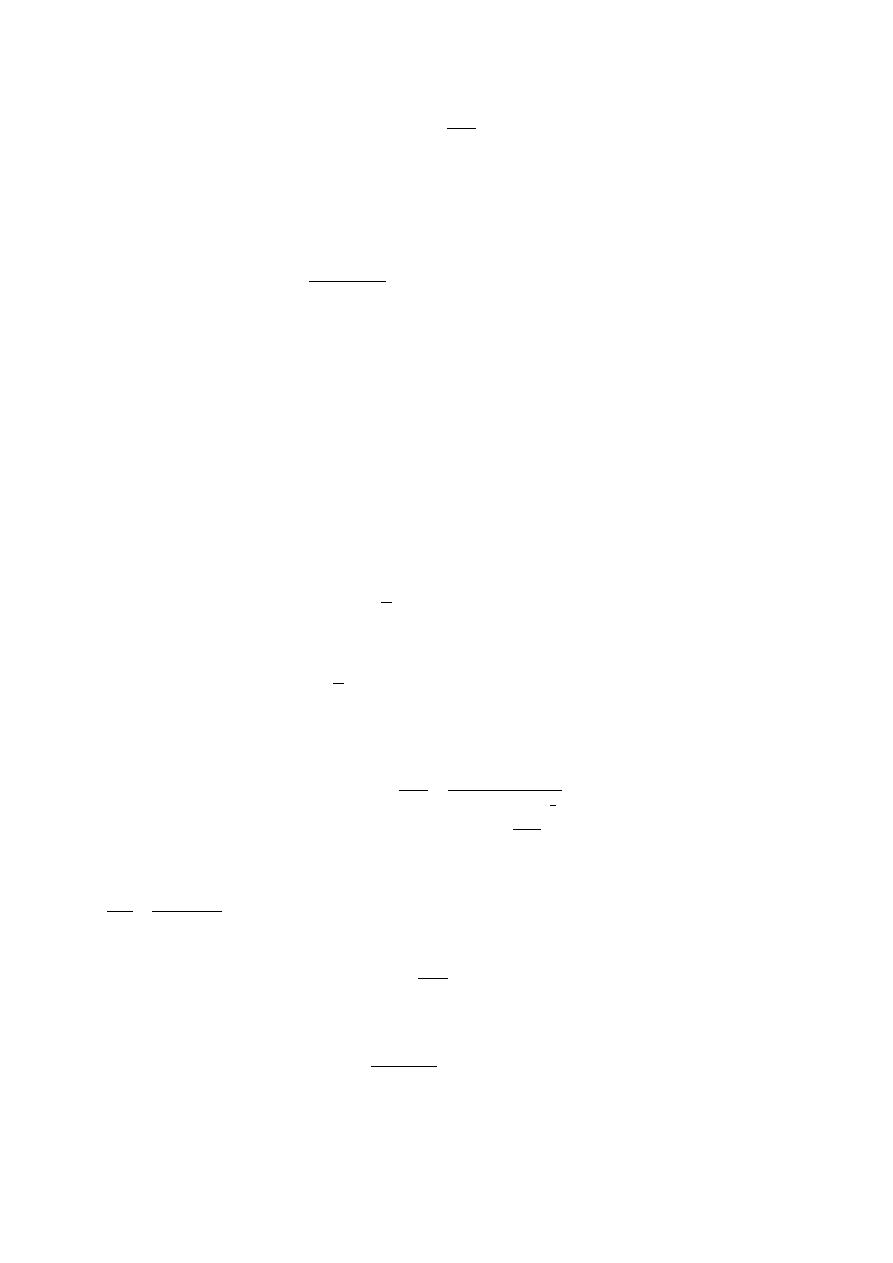
ln K

zF

RT

E

o

=

im większa będzie stała równowagi reakcji.
Różnica potencjałów standardowych będzie równa różnicy potencjału katody (zachodzi na niej reakcja
redukcji) i anody (reakcja utleniania).
Stąd E

o

= E

o

(Sn

4+

| Sn

2+

) - E

o

(Cr

3+

| Cr

2+

) = 0,15 - (-0,58) = 0,73 V.

Po podstawieniu wartości E

o

do wzoru na stałą równowagi otrzymamy:

ln

,

,

,

,

K

K

=

⋅

⋅

⋅

=

⇒

=

⋅

2 96500

8 314 298

0 73 56 87

4 97 10

24

Ta bardzo duża wartość stałej równowagi wskazuje, że w punkcie równoważnikowym, czyli w stanie
równowagi, zdecydowanie dominują produkty reakcji, czyli praktycznie występują tylko jony Sn

2+

.

4.12.

Mamy ogniwo:

Pt | H

2

(1,013

⋅10

5

Pa) | HBr(0,01 mol

⋅kg

-1

) | AgBr(s) | Ag

a) Zapisać reakcję zachodzącą w ogniwie.
b) Obliczyć siłę elektromotoryczną ogniwa w temperaturze 298 K.
c) Obliczyć

∆G, ∆H i ∆S reakcji zachodzącej w ogniwie wiedząc, że

dE/dT = 0,002 V

⋅K

-1

.

Potencjał standardowy półogniwa Ag | AgBr | Br

-

wynosi 0,071V w temperaturze 298 K.

Rozwiązanie
a) W ogniwie przebiegają następujące reakcje:

anoda:

1
2

H

2

= H

+

(m) + e

katoda:

AgBr(s) + e = Ag + Br

-

(m)

______________________________________________________

reakcja sumaryczna

1
2

H

2

+ AgBr(s) = H

+

(m) + Br

-

(m) + Ag

b) Równanie Nernsta dla danego przypadku ma postać:

[ ][ ]

[ ]

[

]

E E

RT

F

H

Br

Ag

AgBr

P

P

o

H

s

=

−

⋅











+

−

1

2

1
2

ln

Wziąwszy pod uwagę, że stężenia faz stałych przyjmujemy jako równe 1, a wyrażenie

P

P

H

s

2

1013 10
1013 10

1

5

5

=

⋅
⋅

=

,
,

, otrzymujemy ostatecznie zależność:

[ ][ ]

E E

RT

F

H

Br

o

=

−

⋅

+

−

1

ln

gdzie:

E

o

= E

o

p

- E

o

l

=E

o

(Ag | AgBr | Br

-

) - E

o

(H

2

| H

+

) = 0,071 - 0 = 0,071 V.

Stąd

(

)

E

V

=

−

⋅

⋅

⋅

=

0 071

8 31 298

1 96500

0 01 0 01

0 307

,

,

ln ,

,

,

c) Związek między zmianą entalpii swobodnej a siłą elektromotoryczną ogniwa ma postać:

∆G

zFE

= −

Po

podstawieniu:

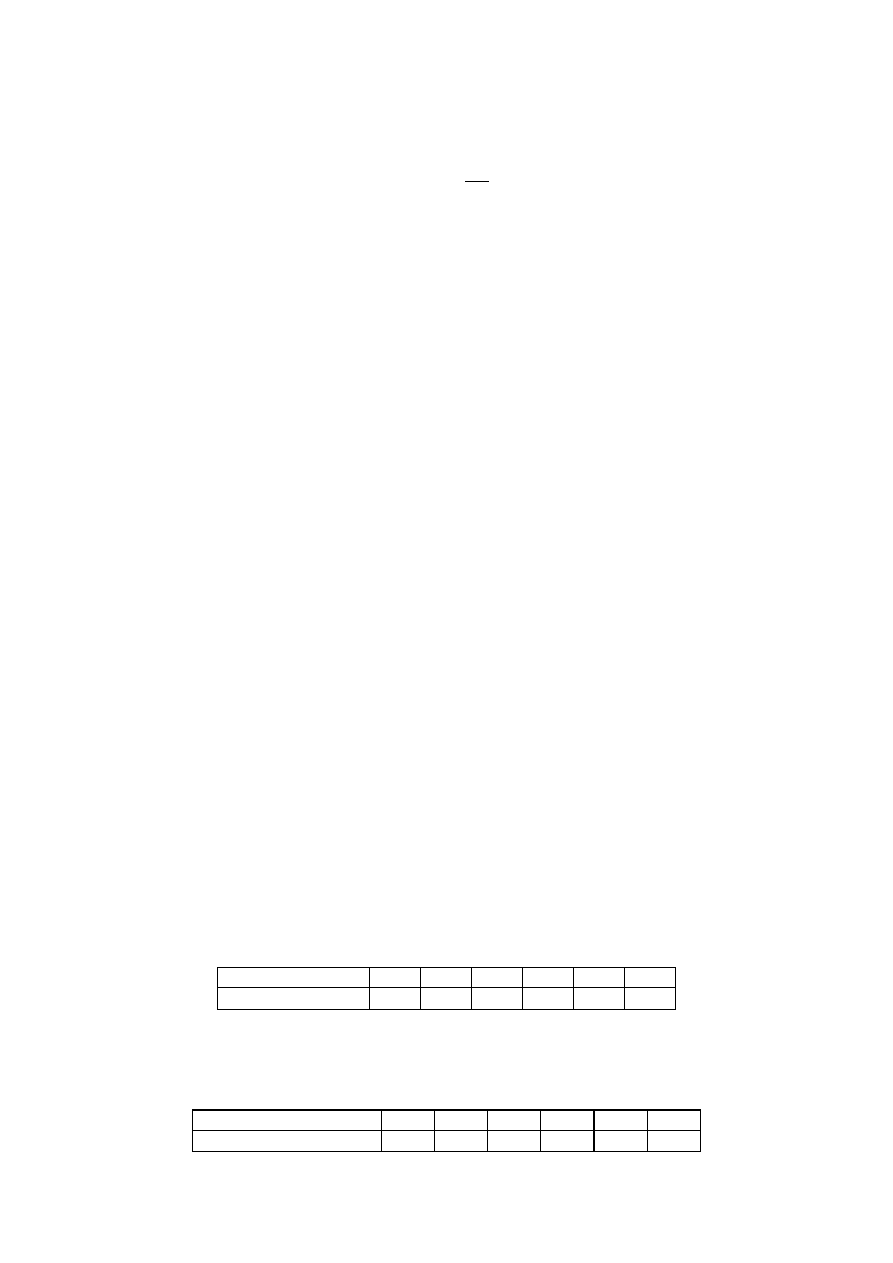
∆G

J

kJ

= − ⋅

⋅

= −

= −

1 96500 0 307

29625

29 625

,

,

Zmiana entropii reakcji zachodzącej w ogniwie dana jest wyrażeniem:

∆S zF

dE
dT

=

po podstawieniu otrzymujemy:

∆S

J K

= ⋅

⋅

=

⋅

−

1 96500 0 002 193

1

,

Zmianę entalpii reakcji znajdziemy z zależności:

∆G = ∆H - T∆S

stąd

∆H = ∆G + Τ∆S

Po podstawieniu:

∆H = -29625 + 298 ⋅ 193 = 27889 J

ZADANIA

4.1.

Obliczyć graniczne przewodnictwo równoważnikowe AgNO

3

na podstawie znanych

granicznych przewodnictw równoważnikowych AgIO

3

, KIO

3

i KNO

3

, równych w 298K odpowiednio:

102,7; 114,3 i 144,9 S

⋅cm

2

⋅mol

-1

.

4.2.

Wiedząc, że

Λ

o

(AgNO

3

) = 133,3,

λ

o

(K

+

) = 73,5 S

⋅cm

2

⋅mol

-1

oraz t

o

(Ag

+

) = 0,464, obliczyć:

a) graniczne przewodnictwa równoważnikowe jonów Ag

+

i NO

3

-

,

b) liczbę przenoszenia jonu K

+

w bardzo rozcieńczonym roztworze KNO

3

.

4.3.

Zmieszano 100 cm

3

wodnego roztworu NaCl o stężeniu 0,01 mol

⋅dm

-3

i 100 cm

3

roztworu

HCl o stężeniu 0,01 mol

⋅dm

-3

. Przewodnictwa równoważnikowe jonów Na

+

, H

+

i Cl

-

wynoszą

odpowiednio: 45; 330 i 70 S

⋅cm

2

⋅mol

-1

.

Obliczyć:
a) przewodnictwo właściwe otrzymanego roztworu,
b) liczbę przenoszenia jonu Cl

-

w tym roztworze.

4.4.

Zmieszano 200 cm

3

roztworu AgNO

3

o stężeniu 0,03 mol

⋅dm

-3

oraz 100 cm

3

NaCl o

stężeniu 0,06 mol

⋅dm

-3

. Przewodnictwa równoważnikowe jonów Na

+

i NO

3

-

wynoszą odpowiednio: 45

i 65 S

⋅cm

2

⋅mol

-1

.

Obliczyć:
a) przewodnictwo właściwe otrzymanego roztworu,
b) liczbę przenoszenia jonu Na

+

w tym roztworze.

4.5.

Miareczkując konduktometrycznie 200 cm

3

roztworu NH

4

OH za po-mocą roztworu HCl o

stężeniu 0,5 mol

⋅dm

-3

otrzymano następujące wyniki:

HCl [cm

3

]

0 2,0 4,0 6,0 8,0 10,0

κ⋅10

3

[S

⋅cm

-1

]

0,41 2,65 4,86 7,09 14,0 21,3

Obliczyć liczbę moli NH

4

OH zawartą w roztworze wyjściowym oraz jego stężenie.

4.6.

Miareczkując konduktometrycznie 50 cm

3

roztworu kwasu octowego (CH

3

COOH)

roztworem NH

4

OH o stężeniu 1 mol

⋅dm

-3

otrzymano następujące wyniki:

NH

4

OH [cm

3

]

0 2,0 4,0 6,0 8,0 10,0

Rezystancja roztworu [

Ω] 97,0 74,0 51,5 40,5 41,0 42,5

Obliczyć liczbę moli CH

3

COOH zawartą w roztworze wyjściowym oraz jego stężenie.

4.7.

Podczas elektrolizy roztworu CuSO

4

przyrost masy platynowej katody wyniósł 0,6354 g.

Obliczyć:
a) Jaki ładunek przepłynął przez roztwór?
b) Jak zmieniła się masa miedzianej anody?
c) Jak zmieniłaby się masa platynowej katody, gdyby ten sam ładunek przepłynął przez roztwór
AgNO

3

?

M(Cu) = 63,54, M(Ag) = 107,9g

⋅mol

-1

.

4.8.

Podczas elektrolizy wodnego roztworu Na

2

SO

4

na elektrodach platynowych w naczyniu, w

którym przestrzenie anodowa i katodowa są rozdzielone, zebrano znad przestrzeni katodowej gaz,
który w warunkach normalnych zajmuje objętość 44,8 cm

3

.

a) Określić, jaki to gaz oraz jaki ładunek przepłynął przez roztwór.
b) Jaka substancja i w jakiej ilości wydzieli się w tych warunkach na anodzie?

4.9.

W naczyniu Hittorfa znajduje się roztwór AgNO

3

o stężeniu 0,2 mol

⋅dm

3

, a elektrody

wykonane są z platyny. Po elektrolizie okazało się, że roztwór katodowy, którego było 100 cm

3

,

zawiera AgNO

3

o stężeniu 0,1894 mol

⋅dm

-3

. Przestrzeń anodowa o objętości 100 cm

3

zawierała po

elektrolizie kwas azotowy o stężeniu 0,02 mol

⋅dm

-3

Napisać reakcje elektrodowe oraz bilanse materiałowe dla przestrzeni katodowej i anodowej
przy przepływie ładunku 1 F . Obliczyć liczbę przenoszenia jonu Ag

+

w AgNO

3

.

4.10.

W aparacie Hittorfa, w którym katoda i anoda są miedziane, znajduje się roztwór CuSO

4

o

stężeniu 0,05 mol

⋅dm

-3

. Po przepłynięciu ładunku 4

⋅10

-3

F do przestrzeni anodowej wskutek reakcji

elektrodowej i wędrówki jonów przybyło 1,2

⋅10

-3

mola CuSO

4

. Obliczyć liczbę przenoszenia jonu

Cu

2+

w tym roztworze oraz końcowe stężenia CuSO

4

w przestrzeniach katodowej i anodowej. W obu

przestrzeniach znajdowało się po 200 cm

3

roztworu.

4.11.

W aparacie Hittorfa o platynowych elektrodach poddano elektrolizie wodne roztwory

HNO

3

, NaOH i ZnSO

4

.

Zapisać reakcje elektrodowe oraz bilanse materiałowe dla przestrzeni katodowej i anodowej przy
przepływie ładunku 1 F. Wskazać, którą z liczb przenoszenia można wyznaczyć na podstawie zmian
ilościowych elektrolitu w przestrzeni katodowej, spowodowanych elektrolizą.

4.12.

Zapisać reakcje zachodzące w ogniwach oraz obliczyć wartości standardowych sił

elektromotorycznych korzystając z danych literaturowych.
a) Pb | PbSO

4

(s) | H

2

SO

4

(aq) | H

2

| Pt

b) Zn | ZnSO

4

||CuSO

4

| Cu

c) Pt | H

2

| HBr

(aq) | AgBr(s) | Ag

d) Pt |SnCl

4

, SnCl

2

||FeCl

2

, FeCl

3

| Pt

4.13.

Zapisać ogniwa, w których zachodzą następujące reakcje:

a) AgCl +

1
2

H

2

= Ag + HCl

b) Pb + H

2

SO

4

= PbSO

4

(s) + H

2

c) FeCl

2

+

1
2

Hg

2

Cl

2

= FeCl

3

+ Hg

4.14.

Mamy ogniwo:

Cu | CuBr

2

(aq) | AgBr(s) | Ag

.

Potencjały standardowe półogniw wynoszą odpowiednio:

E

o

298

(Cu

2+

| Cu) = 0,340 V,

E

o

298

(Ag | AgBr(s) | Br

-

) = 0,071 V.

a) Zapisz reakcję zachodzącą w ogniwie.
b) Oblicz E

o

298

tego ogniwa.

c) Co można powiedzieć o kierunku przebiegu reakcji w czasie pracy ogniwa? Przy jakim stężeniu
CuBr

2

nastąpi odwrócenie kierunku reakcji?

4.15.

Standardowa siła elektromotoryczna ogniwa :

Pb | PbSO

4

(s) | H

2

SO

4

(0,01 mol

⋅kg

-1

) | H

2

(1,015

⋅10

5

Pa)

| Pt

wynosi 0,359 V.
a) Zapisać reakcję zachodzącą w ogniwie.
b) Obliczyć siłę elektromotoryczną ogniwa w temperaturze 298 K.
c) Obliczyć

∆G

o

,

∆H

o

i

∆S

o

reakcji zachodzącej w ogniwie w temperaturze 298 K wiedząc, że

współczynnik dE

o

/dT = 0,002 V

⋅K

-1

.

4.16

.

W ogniwie:

Sn | Sn

2+

(m

1

)||Pb

2+

(m

2

) | Pb

m

1

= 0,01 mol

⋅kg

-1

, m

2

= 0,02 mol

⋅kg

-1

,

potencjały standardowe półogniw wynoszą odpowiednio:

E

o

298

(Sn

2+

| Sn) = -0,136 V,

E

o

298

(Pb

2+

| Pb) = - 0,126 V.

a) Obliczyć siłę elektromotoryczną ogniwa w temperaturze 298 K i wskazać kierunek biegu reakcji
zachodzącej w ogniwie.
b) Czy kierunek biegu reakcji zmieni się, gdy stężenie m

1

zwiększymy dziesięć razy

(m

1

= 0,1 mol

⋅kg

-1

)?

4.17.

Zapisać reakcję zachodzącą w ogniwie

Ag | Ag

2

SO

4

(s)|H

2

SO

4

| H

2

| Pt

oraz obliczyć wartość jej stałej równowagi w temperaturze 298 K korzystając z danych literaturowych.

4.18.

W ogniwie

Zn | ZnSO

4

(m

1

)||FeSO

4

(m

2

) | Fe

m

1

= 0,02 mol

⋅kg

-1

, m

2

= 0,01 mol

⋅kg

-1

,

potencjały standardowe półogniw wynoszą odpowiednio:

E

o

298

(Zn

2+

| Zn) = -0,763 V,

E

o

298

(Fe

2+

| Fe) = -0,440 V.

a) Zapisać reakcję zachodzącą w ogniwie.
b) Obliczyć siłę elektromotoryczną ogniwa w temperaturze 298 K i wskazać

kie

runek biegu reakcji

zachodzącej w ogniwie.
c) Czy kierunek biegu reakcji zachodzącej w ogniwie zmieni się, gdy zwiększymy
dziesięciokrotnie stężenie ZnSO

4

(m

1

= 0,2 mol

⋅kg

-1

)?

4.19.

Obliczyć standardowy potencjał półogniwa Ag | AgI | I

-

mając dane:

E

o

298

(Ag

+

| Ag) = 0,800 V oraz iloczyn rozpuszczalności AgI; I

r

= 8,1

⋅10

-17

.

4.20.

Spośród podanych niżej układów utleniająco-redukujących wybrać układ mogący posłużyć

do oznaczenia stężenia jonów V

2+

na drodze miareczkowania potencjometrycznego.

a) Cr

3+

| Cr

2+

⇒ E

o

298

(Cr

3+

| Cr

2+

| Pt) = -0,58 V,

b) Cu

2+

| Cu

+

⇒ E

o

298

(Cu

2+

| Cu

+

| Pt) = 0,15 V,

c) Sn

4+

| Sn

2+

⇒ E

o

298

(Sn

4+

| Sn

2+

| Pt) = 0,15 V.

Potencjał standardowy półogniwa V

3+

| V

2+

wynosi -0,225 V. Odpowiedź uzasadnić.

4.21.

Czy można oznaczyć stężenie jonów Fe

3+

na drodze miareczkowania potencjometrycznego,

redukując je jonami Sn

2+

? Odpowiedź uzasadnić, np. przez wyznaczenie stałej równowagi

zachodzącej reakcji. Wykorzystać wartości potencjałów elektrodowych podanych w zadaniu
przykładowym nr 4.11.

ODPOWIEDZI DO ZADAŃ

4.1.

Λ

o

(AgNO

3

) = 133,3 S

⋅cm

2

⋅mol

-1

4.2.

a)

λ

ο

(Ag

+

) = 61,85 S

⋅cm

2

⋅mol

-1

;

λ

o

(NO

3

-

) = 71,45 S

⋅cm⋅mol

-1

;

b) t (K

+

) = 0,507.

4.3.

κ = 2,575⋅10

-3

S

⋅cm

-1

; t (Cl

-

) = 0,272.

4.4.

a)

κ = 2,2⋅10

-3

S

⋅cm

-1

;

b) t (Na

+

) = 0,41.

4.5.

3

⋅10

-3

mola; c = 0,015 mol

⋅dm

-3

.

4.6.

5

⋅10

-3

mola; c = 0,1 mol

⋅dm

-3

.

4.7.

a) Q = 2

⋅10

-3

F;

b) masa anody zmniejszyła się o 0,6354 g;

c) przyrost masy wyniósłby 0,2158 g Ag.

4.8.

a) H

2

; Q = 4

⋅10

-3

F;

b)

O

2

; 22,4 cm

3

.

4.9.

t (Ag

+

) = 0,470.

4.10.

t (Cu

2+

) = 0,40; przestrzeń anodowa c(CuSO

4

) = 0,056 mol

⋅dm

-3

;

przestrzeń katodowa c(CuSO

4

) = 0,044 mol

⋅dm

-3

.

4.11.

Roztwór HNO

3

⇒ t (NO

3

-

); roztwór NaOH

⇒ t (Na

+

); roztwór ZnSO

4

⇒ t (SO

4

2-

).

4.12.

a) 0,359 V;

b) 1,10 V;

c) 0,017 V;

d) 0,621 V.

4.14.

a) Cu + 2AgBr = 2Ag + Cu

2+

+ 2Br

-

;

b)

E

o

= -0,269 V;

c) ponieważ E

o

< 0, reakcja przebiega w kierunku tworzenia metalicznej miedzi i

bromku srebra. Zmiana kierunku reakcji nastąpi, gdy E zmieni znak na dodatni, czyli
dla

m

(CuBr

2

) < 5,83

⋅10

-4

mol

⋅kg

-1

.

4.15.

b) E = 0,199 V;

c)

∆G

o

298

= -69,287 kJ;

∆S

o

298

= 386 J

⋅K

-1

;

∆H

o

298

= 45,74 kJ.

4.16.

a) E = 0,019; ponieważ E > 0, to

∆G < 0, zatem reakcja zachodzi w kierunku redukcji

jonów Pb

2+

do Pb;

b) E = -0,107 V; w tym przypadku

∆G > 0, zatem reakcja w ogniwie przebiega w

kierunku przeciwnym, to znaczy w kierunku redukcji jonów Sn

2+

do Sn.

4.17.

K = 7,5

⋅10

-23

.

4.18.

b) E = 0,314 V

⇒ ∆G < 0, reakcja biegnie w kierunku redukcji jonów Fe

2+

do Fe;

c) E = 0,284 V

⇒ ∆G < 0, kierunek reakcji jak w punkcie b).

4.19.

E

o

298

(Ag | AgI (s)| I

-

) = -0,151 V.

4.20.

b) K = 2,2

⋅10

6

lub c) K = 4,86

⋅10

12

.

4.21.

Można, stała równowagi redukcji jonów Fe

3+

jonami Sn

2+

wynosi 10

21

.

LITERATURA

1. Poradnik fizykochemiczny. Praca zbiorowa. Warszawa: WNT 1974.
2. Miszczenko K.P., Rawdiel A.A.: Zbiór wielkości fizykochemicznych. Warszawa: PWN 1974.
3. Mizerski W.: Tablice chemiczne. Warszawa: Wydawnictwo Adamantan 1993.
4. Adamson A.W.: Zadania z chemii fizycznej. Warszawa: PWN 1978.
5. Zbiór zadań z chemii fizycznej. Praca zbiorowa. Gdańsk: Wydawnictwo Politechniki Gdańskiej 1985.