1

1

2. RÓWNOWAGI FAZOWE

Zadania przykładowe

2.1.

Obliczyć wyrażenia dT/dP dla procesu parowania wody i topnienia

lodu, jeżeli ciepło parowania wody w temperaturze 100

o

C wynosi 40,66 kJ

⋅mol

-1

, a ciepło topnienia lodu wynosi 6,0 kJ

⋅mol

-1

w temperaturze 0

o

C. Gęstości lodu i

wody w temp. 0

o

C wynoszą odpowiednio 0,920 g

⋅cm

-3

i 0,999 g

⋅cm

-3

.

Rozwiązanie

Równanie Clausiusa-Clapeyrona dla przemiany ciało stałe - ciecz można

zapisać następująco:

(

)

dP

dT

H

T V

V

t

c

s

=

−

∆

(2.1.1)

gdzie:

∆H

t

- molowe ciepło topnienia lodu,

V

s

i V

c

- odpowiednio objętości molowe wody stałej i ciekłej.

( )

V

M H O

d H O

cm mol

m mol

s

s

=

=

=

=

⋅

−

−

−

(

)

(

)

,

,

,

2

2

3

1

6

3

1

18

0 920

19 565

19 565 10

(

)

V

M H O

d H O c

cm mol

m mol

c

=

=

=

=

⋅

−

−

−

(

)

( )

,

,

,

2

2

3

1

6

3

1

18

0 999

18 018

18 018 10

Przekształcamy równanie (2.1.1) i podstawiamy dane.

(

)

(

)

dT

dP

T V

V

H

K Pa

c

s

t

=

−

=

⋅

−

⋅

= −

⋅

−

−

−

−

∆

273 18 018 10

19 565 10

6000

7 04 10

6

6

8

1

,

,

,

Do obliczenia wartości dT/dP, słusznej dla zakresu temperatur bliskich tempe-
raturze wrzenia wody, skorzystamy ze zmodyfikowanego równania Clausiusa-
Clapeyrona

dP

dT

P H

RT

p

=

∆

2

st¹d

2

2

dT

dP

RT

P H

K Pa

p

=

=

⋅

⋅

⋅

=

⋅

⋅

−

−

2

2

5

4

1

8 314 373

1013 10 40660

2 81 10

∆

,

,

,

Jak widać, wpływ ciśnienia zewnętrznego na temperaturę wrzenia jest około 4
rzędy większy niż na temperaturę topnienia.

2.2.

Wyznaczyć współrzędne punktu potrójnego benzenu, jeżeli w

temp.10

o

C prężność par nad ciekłym benzenem wynosi 6170 Pa, natomiast w

temp. 0

o

C prężność par nad stałym benzenem wynosi 3330 Pa.Ciepło topnienia

benzenu wynosi 10,6 kJ

⋅mol

-1

, natomiast ciepło sublimacji 43,9 kJ

⋅mol

-1

.

Rozwiązanie

Skorzystamy z równania Clausiusa-Clapeyrona w postaci:

lg

,

P

P

H

R T

T

2

1

1

2

2 3

1

1

=

−











∆

gdzie:

∆H - jest odpowiednio ciepłem parowania lub sublimacji

.

Równanie to jest słuszne dla przemian ciecz-para i ciało stałe-para przy zało-
żeniach:
a) ciepło parowania lub sublimacji nie jest funkcją temperatury,
b) objętości fazy stałej i ciekłej są do pominięcia wobec objętości fazy gazowej,
c) pary substancji zachowują się jak gazy doskonałe.

W temperaturze punktu potrójnego (T

pp

) prężność par nad ciekłym i stałym

benzenem będzie taka sama (P

pp

).

Zapiszmy powyższe równanie dla procesu parowania i sublimacji zastępując P

1

i T

1

współrzędnymi punktu potrójnego.

lg

,

lg

,

P

P

H

R T

T

i

P

P

H

R T

T

s

pp

s

pp

s

c

pp

p

pp

c

=

−













=

−













∆

∆

2 3

1

1

2 3

1

1

Po podstawieniu danych otrzymujemy:

lg

,

lg

,

3330 43900

2 3

1

1

273

6170 33300

2 3

1

1

283

P

R T

i

P

R T

pp

pp

pp

pp

=

−













=

−













Ciepło parowania obliczamy z zależności:

∆H

p

=

∆H

s

-

∆H

t

= 43,9 - 10,6 = 33,3 kJ

⋅ mol

-1

Po rozwiązaniu układu równań otrzymujemy:

T

pp

= 278,86 K

P

pp

= 5

.

10

3

Pa

3

3

2.3.

Prężność par nad stałym VF

6

dana jest równaniem:

lg

,

,

P

T

s

=

−

⋅

12 763 25591

1

(2.3.1)

a nad ciekłym:

lg

,

,

P

T

c

=

−

⋅

9 678 15113

1

(2.3.2)

Wyznaczyć temperaturę i ciśnienie odpowiadające punktowi potrójnemu oraz
obliczyć ciepło parowania i topnienia VF

6

.

Rozwiązanie

W punkcie potrójnym prężność par nad stałym i ciekłym VF

6

jest taka

sama. Porównując zatem prawe strony przedstawionych zależności otrzymamy:

12 763 25591

1

9 678 15113

1

,

,

,

,

−

⋅

=

−

⋅

T

T

pp

pp

stąd

T

pp

=339,6 K

Podstawienie wyznaczonej temperatury punktu potrójnego do dowolnego z
równań daje nam wartość ciśnienia w punkcie potrójnym

P

pp

= 1,68

.

10

5

Pa

Zależność prężności pary nad cieczą lub fazą stałą od temperatury przy
założeniu, że ciepło parowania lub sublimacji nie zależy od temperatury, dana
jest równaniem:

ln P

H

RT

const

= −

+

∆

(2.3.3)

Zamieniając logarytm dziesiętny w równaniu (2.3.1) na naturalny otrzymujemy:

ln

,

,

,

,

P

T

s

= −

⋅

+

⋅

2 3 25591

2 3 12 763

(2.3.4)

z porównania równania (2.3.3) z równaniem (2.3.4) wynika, że

∆H

R

s

=

⋅

2 3 25591

,

,

stąd

∆H

s

= 48935 J

⋅mol

-1

= 48,94 kJ

⋅mol

-1

Postępując podobnie z równaniem (2.3.2) otrzymamy:

∆H

R

p

=

⋅

2 3 15113

,

,

stąd

∆H

p

= 28899 J

⋅mol

-1

= 28,90 kJ

⋅mol

-1

Wiadomo, że ciepło sublimacji równe jest sumie ciepeł topnienia i parowania
zatem:

∆H

t

=

∆H

s

-

∆H

p

= 48,94 - 28,90 = 20,04 kJ

⋅mol

-1

4

4

2.4.

Obliczyć ciepło parowania eteru dietylowego w normalnej

temperaturze wrzenia 307,9 K, jeżeli dP/dT = 3,53

⋅10

3

Pa

⋅

K

-1

. Obliczyć także

temperaturę wrzenia eteru dietylowego pod ciśnieniem 1020 hPa.

Rozwiązanie
Przy

założeniu, że pary eteru dietylowego zachowują się jak gaz doskonały,

i przy pominięciu objętości cieczy zmodyfikowane równanie Clausiusa-
Clapeyrona można zapisać w postaci:

dP

dT

P H

RT

p

=

∆

2

st¹d

∆H

RT

P

dP

dT

kJ mol

p

=

⋅

=

⋅

⋅

⋅

⋅

=

⋅

−

2

2

5

3

1

8 314 307 9

1013 10

3 53 10

27 47

,

,

,

,

,

Do obliczenia temperatury wrzenia eteru dietylowego pod ciśnieniem 1020 hPa
= 1,02

⋅

10

5

Pa potrzebna nam jest zależność dT/dP, a więc zmiana temperatury

wrzenia ze zmianą ciśnienia o 1 Pa.:

dP/dT = 3,53

⋅

10

3

Pa K

-1

; dT/dP = 2,832

⋅

10

-4

K

⋅Pa

-1

Poszukiwaną temperaturę wrzenia pod ciśnieniem 1,02

⋅

10

5

Pa obliczymy ze

wzoru:

T

w

(P=1,02

⋅

10

5

) = T

w

(1,013

⋅

10

5

) + (dT/dP)

⋅

∆P

zatem

T = 307,9 + 2,832

⋅

10

-4

(1,02

⋅

10

5

- 1,013

⋅

10

5

) = 308,1 K

2.5.

Ciecze A i B tworzą roztwór doskonały. Prężności par nad czystymi

składnikami wynoszą P

o

A

= 6

⋅

10

4

Pa i P

o

B

= 4

⋅

10

4

Pa w temperaturze 310 K.

Obliczyć sumaryczne ciśnienie nad roztworem, w którym ułamek molowy
składnika A wynosi 0,5 w temperaturze 310 K oraz skład par nad tym
roztworem.

Rozwiązanie
Sumaryczna

prężność par nad roztworem równa jest sumie prężności

cząstkowych składników

P = P

A

+ P

B

Prężności cząstkowe znajdziemy z prawa Raoulta

P

i

= P

o

i

⋅

X

i

5

5

gdzie:

P

o

i

- prężność pary nad czystym składnikiem,

X

i

- ułamek molowy składnika w roztworze.

Zatem:

P = P

o

A

⋅

X

A

+ P

o

B

⋅

X

B

Suma ułamków molowych składników roztworu równa jest oczywiście jedności.
Stąd:

X

B

= 1 - X

A

= 1 - 0,5 = 0,5

Po podstawieniu otrzymujemy:

P = 6

⋅

10

4

.

0,5 + 4

⋅

10

4

.

0,5 =5

⋅10

4

Pa

Ułamek molowy składnika mieszaniny gazowej (para) dany jest równaniem:

Y

A

= (P

A

/ P)

P

A

wyrazimy za pomocą znanej już zależności P

A

= P

o

A

⋅ X

A

st¹d:

Y

P

X

P

A

A

o

A

=

⋅

=

⋅

⋅

⋅

=

6 10 0 5

5 10

0 6

4

4

,

,

Y

B

= 1 - Y

A

= 0,4

2.6.

Prężność par nad roztworem doskonałym zawierającym 3 mole

składnika A i 7 moli składnika B wynosi 1

⋅

10

5

Pa w temperaturze 338 K. Do-

datek 4 moli składnika A do tego roztworu powoduje wzrost prężności par do
1,2

⋅

10

5

Pa w tej samej temperaturze. Obliczyć P

o

A

i P

o

B

oraz skład par znajdu-

jących się w równowadze z pierwszym roztworem w temperaturze 338 K.

Rozwiązanie

Ułamek molowy składnika roztworu dany jest zależnością:

X

n

n

i

i

i

=

∑

gdzie:

n

i

- oznacza liczbę moli danego składnika,

n

i

∑

- sumaryczną liczbę moli wszystkich składników roztworu.

Dla pierwszego roztworu

X

X

A

B

=

+

=

⇒

= −

=

3

3 7

0 3

1 0 3 0 7

,

,

,

dla drugiego roztworu

X

X

A

B

=

+

=

⇒

= −

=

3 4

14

0 5

1 0 5 0 5

,

,

,

6

6

Napiszmy dla obu roztworów równania na sumaryczną prężność par nad
roztworem:

10

5

= P

o

A

.

0,3 + P

o

B

.

0,7

1,2

.

10

5

= P

o

A

.

0,5 + P

o

B

.

0,5

Rozwiązanie układu równań daje:

P

o

A

= 1,7

⋅

10

5

Pa

P

o

B

= 7

⋅

10

4

Pa

Skład par znajdujących się w równowadze z pierwszym roztworem (X

A

=0,3)

znajdziemy z zależności:

Y

P

P

P X

A

A

A

o

A

=

=

⋅

=

⋅

⋅

=

10

1 7 10 0 3

10

0 51

5

5

5

,

,

,

Y

B

= 0 49

,

2.7.

Ciecze A i B tworzą roztwór doskonały. Roztwór zawierający

początkowo 0,3 mola A i 0,7 mola B poddano destylacji. Po osiągnięciu tempe-
ratury 80

o

C okazało się, że ułamek molowy składnika B w pozostałości (X’

B

) wynosi 0,6, natomiast w destylacie (Y

B

) 0,8. Obliczyć liczbę moli destylatu i

cieczy pozostałej.

Rozwiązanie
Bilans

materiałowy składnika B w układzie przedstawia równanie:

n

⋅

X

B

= n

p

⋅

Y

B

+ n

c

⋅

X'

B

(2.7.1)

gdzie:

n - sumaryczna liczba moli,

n

p

- liczba moli pary,

n

c

- liczba moli pozostałej cieczy,

zatem: n

⋅ X

B

- liczba moli składnika B w układzie,

n

p

⋅Y

B

- liczba moli składnika B w destylacie,

n

c

⋅X'

B

- liczba moli składnika B w pozostałości po destylacji.

Jeżeli równanie (2.7.1) uzupełnimy zależnością

n = n

p

+ n

c

to otrzymamy układ równań, który zastosujemy do obliczenia szukanych
wielkości.

(n

p

+ n

c

)

⋅ 0,7 = n

p

⋅

0,8 + n

c

⋅ 0,6

n

p

+ n

c

= 1

Rozwiązując ten układ równań otrzymamy liczbę moli destylatu: n

p

= 0,5 mola i

cieczy pozostałej n

c

= 0,5 mola.

7

7

2.8.

Obliczyć prężność pary w temperaturze 100

o

C nad roztworem zawie-

rającym 51,35 g sacharozy (M=342 g

⋅mol

-1

) w 1000 g H

2

O. Jaka jest tempe-

ratura wrzenia pod ciśnieniem normalnym tego roztworu, jeżeli stała ebulio-
skopowa wody wynosi 0,516 K

⋅kg⋅mol

-1

? Zakładamy, że roztwór sacharozy w

wodzie jest roztworem doskonałym.

Rozwiązanie
Aby

obliczyć prężność pary nad roztworem, skorzystamy ze wzoru:

P

P

P

X

o

o

−

=

2

(2.8.1)

gdzie:

P

o

- prężność pary czystego rozpuszczalnika (woda),

P - prężność pary nad roztworem,

X

2

- ułamek molowy substancji rozpuszczonej.

Wszystkie wielkości odnoszą się do tej samej temperatury.
Obliczamy ułamek molowy sacharozy w wodzie (X

2

)

X

n

n

n

m

M

m

M

m

M

s

s

w

s

s

s

s

w

w

2

=

+

=

+

gdzie:

n, m i M - oznaczają odpowiednio liczbę moli, masę i molową masę cząsteczkową.

Po podstawieniu otrzymujemy:

X

2

3

5135

342

5135

342

1000

18

2 695 10

=

+

=

⋅

−

,

,

,

Po podstawieniu otrzymanej wartości do równania (2.8.1) mamy:

1013 10

1013 10

2 695 10

5

5

3

,

,

,

⋅

−

⋅

=

⋅

−

P

Stąd szukana prężność pary wynosi 1,010

⋅

10

5

Pa.

Temperaturę wrzenia tego roztworu znajdziemy wykorzystując zależność

∆T = K

e

⋅

m

(2.8.2)

gdzie:

∆T - jest różnicą temperatur wrzenia roztworu i czystego rozpuszczalnika,

K

e

- stałą ebulioskopową rozpuszczalnika (woda),

m - molalnością.

8

8

Równanie (2.8.2) jest słuszne dla roztworów rozcieńczonych, a ponadto
spełniane jest wyłącznie przez substancje nie dysocjujące i nie asocjujące w
roztworze.
Obliczamy molalność, czyli liczbę moli substancji rozpuszczonej w 1000 g
wody.

m

mol kg

=

=

⋅

−

5135

342

0150

1

,

,

Obliczamy podwyższenie temperatury wrzenia

∆T = K

e

⋅

m = 0,516

⋅

0,150 = 0,0774 K

Zatem temperatura wrzenia roztworu wynosi 100,077

o

C

≈ 100,08

o

C.

2.9.

Obliczyć obniżenie temperatury krzepnięcia wodnych roztworów

zawierających w 1000 g H

2

O:

a) 0,6006 g mocznika (nieelektrolit) (NH

2

)

2

CO,

b) 0,5845 g chlorku sodowego (mocny elektrolit),
c) 0,6006 g mocznika i 0,5845 g chlorku sodowego.
Stała krioskopowa wody wynosi 1,86 K

⋅kg⋅mol

-1

.

Rozwiązanie

Skorzystamy z zależności na obniżenie temperatury krzepnięcia.

∆T = K

k

⋅

m

⋅ i

gdzie:

K

k

- stała krioskopowa rozpuszczalnika,

m - molalność substancji rozpuszczonej,

i - współczynnik izotoniczny równy:

i = 1 +

α(ν - 1), przy czym α jest stopniem dysocjacji, a ν liczbą jonów , na które dyso-

cjuje substancja rozpuszczona. Współczynnik izotoniczny przyjmuje wartość od 1, gdy

substancja rozpuszczona jest nieelektrolitem, do

ν w sytuacji, gdy α = 1.

a) Mocznik jest nieelektrolitem (

α = 0) zatem i = 1.

Molalnoœć wynosi:

m

mol kg

=

=

⋅

−

0 6006

60 06

0 01

1

,

,

,

st¹d

∆T = K

k

⋅ m = 1,86 ⋅ 0,01 = 0,0186 K

b) Chlorek sodowy dysocjuje na dwa jony i jeżeli

α = 1, to i = 2.

Molalność chlorku sodowego wynosi:

m

mol kg

=

=

⋅

−

0 5845

58 45

0 01

1

,

,

,

9

9

st¹d

∆T = K

k

⋅ m ⋅ i

= 1,86

⋅ 0,01 ⋅ 2 = 0,0372 K

c) Obniżenie temperatury krzepnięcia mieszaniny będzie sumą wartości
otrzymanych w punkcie a) i b).

∆T = 0,0186 + 0,0372 = 0,0558 K

2.10

.

Rozpuszczono 3 g nieznanej substancji w 100 g wody. Stwierdzono,

że roztwór krzepnie w temperaturze -0,401

o

C, a wrze w 100,111

o

C. Obliczyć

molową masę cząsteczkową nieznanej substancji oraz ciepło topnienia i paro-
wania wody, jeżeli ciepło sublimacji wody wynosi 46,4 kJ

⋅

mol

-1

.

Przyjmujemy, że czysta woda krzepnie w warunkach zadania w 0,0

o

C, a wrze w

100,0

o

C.

Rozwiązanie

Mamy tu do czynienia z obniżeniem temperatury krzepnięcia oraz

podwyższeniem temperatury wrzenia. Jeżeli przyjmiemy, że roztwór jest
rozcieńczony, to słuszne są zależności:

∆T

k

= K

k

⋅ m ,

∆T

e

= K

e

⋅ m

gdzie: stała krioskopowa K

k

i ebulioskopowa K

e

dane są zależnościami:

K

RT M

H

k

k

t

=

⇒

2

1000

186

∆

,

oraz

K

RT M

H

e

w

p

=

2

1000

∆

T

k

i T

w

są odpowiednio równe temperaturom krzepnięcia i wrzenia rozpusz-

czalnika.

∆H

p

i

∆H

t

są molowymi ciepłami parowania i topnienia rozpusz-

czalnika. M jest masą molową rozpuszczalnika.

Po podstawieniu do równań na obniżenie temperatury krzepnięcia i

podwyższenie temperatury wrzenia wyrażeń na stałą krioskopową i
ebulioskopową uzyskamy zależności:

∆

∆

T

RT M

H

m

k

k

t

=

⋅

⋅

2

1000

oraz

∆

∆

T

RT M

H

m

e

w

p

=

⋅

⋅

2

1000

Po podzieleniu równań stronami przez siebie otrzymujemy:

∆

∆

∆

∆

∆

∆

∆

∆

T

T

T

H

T

H

H

H

T

T

T

T

k

e

k

p

w

t

p

t

k

e

w

k

=

⋅

⋅

⇒

=

⋅

2

2

2

2

st¹d

∆

∆

H

H

p

t

=

⋅

⋅

=

0 401 373

0111 273

6 74

2

2

,

,

,

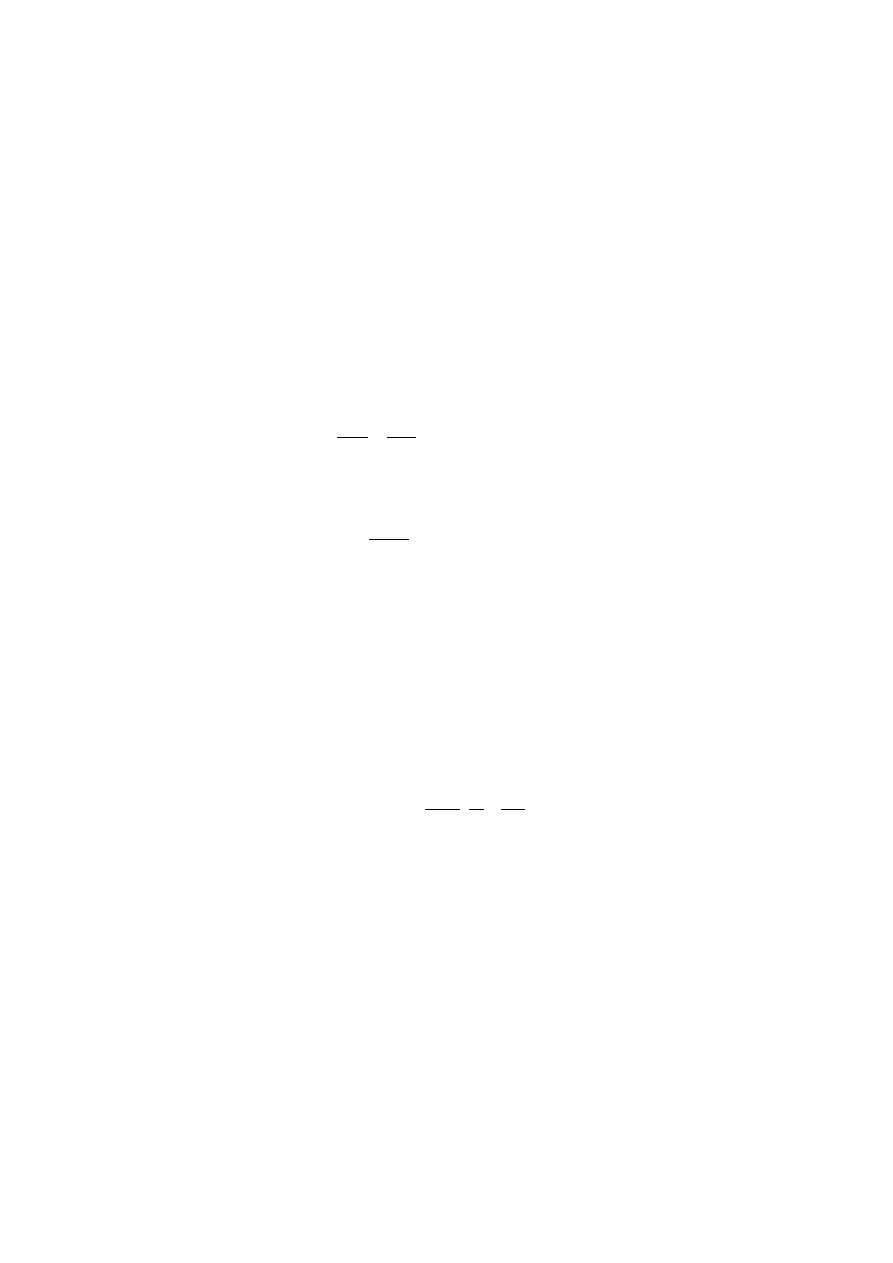
10

10

Ponieważ suma ciepeł topnienia i parowania równa jest wartości ciepła sublima-
cji, możemy zapisać układ równań:

∆H

p

= 6,74

.

∆H

t

;

∆H

p

+

∆H

t

= 46,4

st¹d: H

t

= 6,0 kJ

H

p

= 40,44 kJ

⋅mol

-1

Aby obliczyć masę molową nieznanej substancji, skorzystać możemy z jednej z
podanych uprzednio zależności, np.

∆T

t

=K

k

⋅ m. Wyliczona stała krioskopowa

ma wartość 1,86, stąd molalność

m

T

K

mol kg H O

t

k

=

=

=

⋅

−

∆

0 4

186

0 215

1

2

,

,

,

Jak wynika z treści zadania, 3 g substancji rozpuszczono w 100 g H

2

O, zatem w

1000 g H

2

O jest jej 30 g, co stanowi 0,215 mola. Masa jednego mola wynosi:

30

0 215

139 5

1

,

,

=

⋅

−

g mol

2.11.

Temperatura topnienia naftalenu wynosi 80

o

C, a molowe ciepło

topnienia 18,8 kJ

⋅

mol

-1

. Wyznaczyć rozpuszczalność naftalenu w chloroformie

w procentach wagowych w temperaturze 50

o

C zakładając, że naftalen w

chloroformie tworzy roztwór doskonały. Molowe masy cząsteczkowe naftalenu i
chloroformu wynoszą odpowiednio: 128 i 119,5 g

⋅mol

-1

.

Rozwiązanie

Równanie na obniżenie temperatury krzepnięcia ma postać:

−

=

−











ln X

H

R

T

T

t

t

o

∆

1

1

gdzie:

X - ułamek molowy składnika znajdującego się w obu fazach, czyli wydzielającego się

z

roztworu (rozpuszczalnik),

∆H

t

- molowe ciepło topnienia substancji o ułamku molowym X,

T

o

t

- normalna temperatura topnienia czystej substancji,

T - temperatura krzepnięcia składnika o ułamku molowym X w roztworze.

Równanie powyższe jest słuszne w całym zakresie zmienności ułamków
molowych pod warunkiem, że roztwór jest roztworem doskonałym.
Poszukujemy

ułamka molowego naftalenu (N), przy którym zaczyna on

wydzielać się z roztworu w temperaturze 323 K.

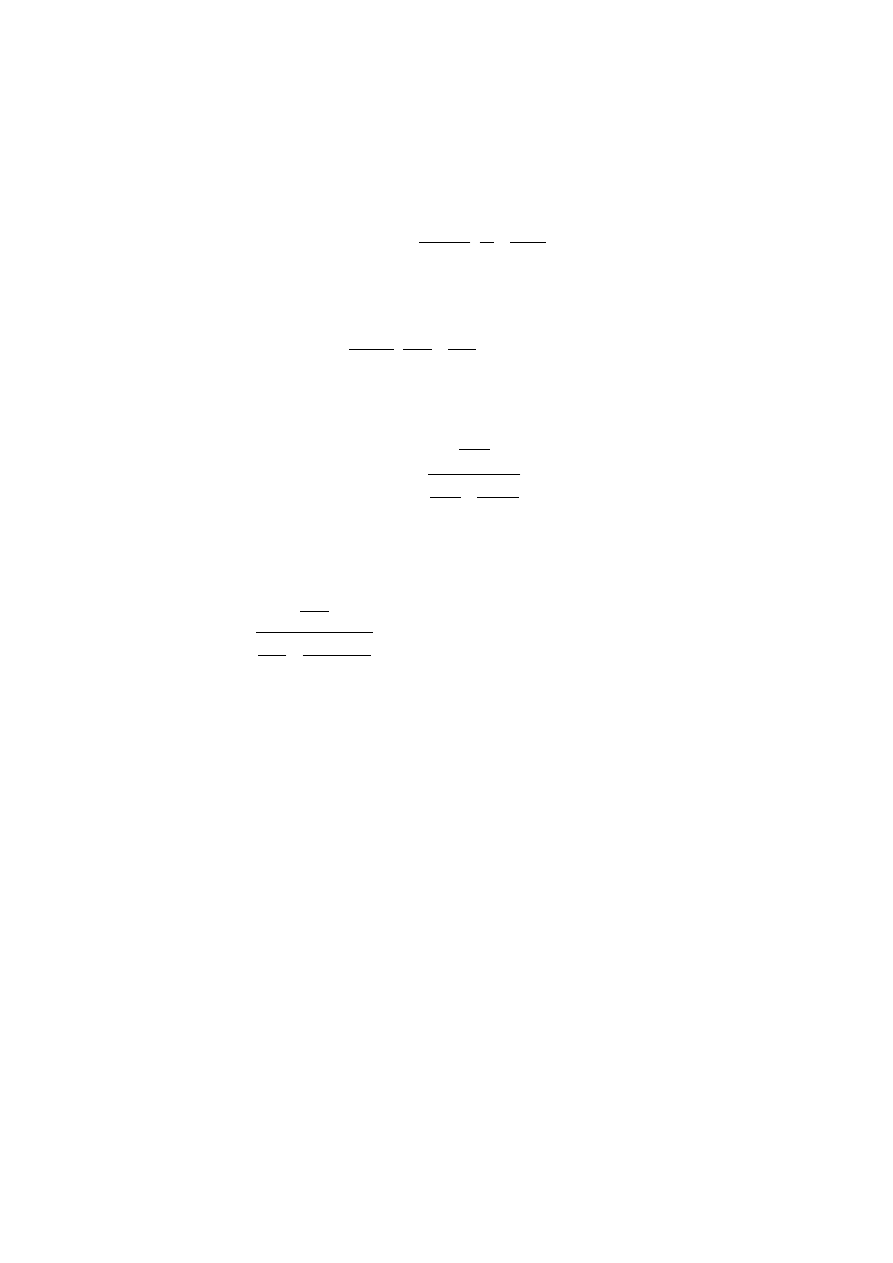
11

11

( )

( )

−

=

−













ln X

H

R

T T

N

t N

t N

o

∆

1

1

Po podstawieniu danych otrzymujemy:

−

=

−









 ⇒

=

ln

,

,

X

X

N

N

18800

8 314

1

323

1

353

0 552

Dokonujemy przeliczenia ułamka molowego na procent wagowy. Z definicji
ułamka molowego otrzymujemy:

X

m

M

m

M

m

M

N

N

N

N

N

Chl

Chl

=

+

.

.

Przyjmując, że masa roztworu wynosi 100 g, czyli m

N

+ m

Chl.

= 100,

otrzymamy:

0 552

128

128

100

119 5

56 9

56 9%

,

,

,

,

=

+

−

⇒

=

⇒

m

m

m

m

g

wagowych

N

N

N

N

.

ZADANIA

2.1.

Czy można w tyglu o pojemności 1,4 dm

3

stopić 10 kg cyny, jeżeli jej

ciepło topnienia wynosi 59,400 kJ

⋅

kg

-1

w temperaturze topnienia 232

o

C, gęstość

stałej cyny wynosi 7,18 kg

⋅

dm

-3

, a współczynnik (dT/dP) = 3,27

⋅

10

-8

K

⋅

Pa

-1

?

2.2.

Temperatura topnienia bizmutu pod normalnym ciśnieniem wynosi

271,0

o

C. W tych warunkach gęstość bizmutu ciekłego wynosi 10g

⋅

cm

-3

, nato-

miast temperatura obniża się o 3,49

⋅

10

-8

K, gdy ciśnienie wzrasta o 1 Pa. Obli-

czyć gęstość stałego bizmutu, jeżeli ciepło topnienia bizmutu w tych warunkach
wynosi 11,0 kJ

⋅

mol

-1

. (M(Bi) = 209g

⋅mol

-1

)

.

12

12

2.3.

Przemiana jodku rtęci(II) czerwonego w żółty odbywa się w

temperaturze 127

o

C. Obliczyć ciepło przemiany, jeżeli zmiana objętości

molowej jest równa 5,4 cm

3

⋅

mol

-1

, przy czym gęstość odmiany czerwonej jest

mniejsza (dT/dP = - 1,73

⋅

10

-6

K

⋅

Pa

-1

).

2.4

.

Prężność par chloru nad stałym chlorem wynosi 348 Pa w

temperaturze -112

o

C oraz 34 Pa w temperaturze -126,5

o

C. Obliczyć ciepło

sublimacji i parowania chloru, jeżeli ciepło topnienia chloru wynosi 9,1

kJ

⋅mol

-1

.

2.5.

Obliczyć ciepło topnienia srebra, jeżeli ciepło parowania srebra

wynosi 254,3 kJ

⋅

mol

-1

, a zależność prężności pary nad stałym srebrem od

temperatury dana jest równaniem:

ln

,

,

P

T

s

=

−

⋅

31952

3 225 10

4

2.6.

Obliczyć ciepło sublimacji srebra, jeżeli ciepło topnienia srebra

wynosi 13,83 kJ

⋅

mol

-1

, a zależność prężności par nad ciekłym srebrem od

temperatury dana jest równaniem:

lg

,

,

P

T

c

=

−

⋅

13 347

133 10

4

2.7.

Obliczyć ciepło parowania oraz normalną temperaturę wrzenia cyja-

nowodoru, jeżeli zależność prężności pary od temperatury nad ciekłym cyjano-
wodorem dana jest zależnością:

lg

,

P

T

=

−

916

1237

2.8.

Prężność par chloru nad ciekłym chlorem wynosi 1567 Pa w tem-

peraturze -100

o

C oraz 7841 Pa w temperaturze -80

o

C. Obliczyć ciepło

parowania i topnienia chloru, jeżeli ciepło sublimacji chloru wynosi
31,45kJ

⋅

mol

-1

.

2.9.

Normalna temperatura wrzenia acetonu wynosi 56,13

o

C. Obliczyć

temperaturę wrzenia acetonu pod ciśnieniem 1,0266

⋅

10

5

Pa, jeżeli ciepło

parowania acetonu wynosi 29,09 kJ

⋅

mol

-1

w normalnej temperaturze wrzenia.

2.10.

Normalna temperatura wrzenia roztworu doskonałego zawierającego

0,3 mola składnika A i 0,7 mola składnika B wynosi 70

o

C. W tej temperaturze

13

13

P

o

A

= 2 P

o

B

. Obliczyć P

o

A

i P

o

B

w temperaturze 70

o

C. Obliczyć także sumaryczne

ciśnienie nad roztworem zawierającym 0,8 mola składnika A i 1,2 mola
składnika B oraz skład par nad tym roztworem.

2.11.

Ciecze A i B tworzą roztwór doskonały. Zależność ciśnienia

całkowi-tego nad roztworem od ułamka molowego substancji B w temperaturze
300

K dana jest zależnością:

[ ]

P

X

Pa

B

= ⋅

+ ⋅

3 10

4 10

4

4

Obliczyć P

o

A

i P

o

B

w temperaturze 300 K oraz skład pary pozostającej w

równowadze z roztworem, w którym ułamek molowy składnika A wynosi 0,8.

2.12.

Prężności par czystych cieczy A i B w temperaturze 340 K są równe.

Obliczyć stosunek prężności par cieczy A i B w temperaturze 360 K, jeżeli
ciepło parowania wynosi 20 kJ

⋅

mol

-1

dla cieczy A i 30 kJ

⋅

mol

-1

dla cieczy B.

2.13.

Prężność par czystego etanolu wynosi 6,0

⋅

10

3

Pa, a metanolu

1,2

⋅

10

4

Pa w temperaturze 20

o

C. Wyznaczyć sumaryczną prężność par nad roz-

tworem zawierającym 60% wagowych etanolu oraz obliczyć skład fazy gazowej
w procentach wagowych. M(CH

3

OH) = 32 g

⋅

mol

-1

, M(C

2

H

5

OH)= 46 g

⋅

mol

-1

.

2.14.

Ciecze A i B tworzą roztwór doskonały. Roztwór zawierający 20%

molowych cieczy A pozostaje w równowadze z parami zawierającymi 40%
molowych cieczy A w temperaturze 60

o

C. Obliczyć stosunek prężności pary

czystej cieczy B do prężności pary czystej cieczy A w temperaturze 60

o

C.

2.15.

Stosunek prężności par czystych cieczy A i B wynosi 3 w tempe-

raturze 27

o

C. Ile wynosi ten stosunek w temperaturze 77

o

C, jeżeli ciepła paro-

wania wynoszą 30 kJ

⋅

mol

-1

dla cieczy A oraz 20 kJ

⋅

mol

-1

dla cieczy B?

2.16.

0,4 mola roztworu o składzie X

B

= 0,645 umieszczono w

zamkniętym naczyniu o pojemności 4

⋅

10

-3

m

3

w temperaturze 25

o

C. Ciecz

paruje do osiągnięcia stanu równowagi, w którym skład cieczy wynosi X'

B

=

0,600, natomiast ciśnienie w naczyniu wynosi 5

⋅

10

4

Pa. Obliczyć liczbę moli

pary oraz skład pary. Objętość cieczy w stanie równowagi można pominąć, a
parę potraktować jak gaz doskonały.

2.17.

W temperaturze 315 K prężności par dichloroetanu i benzenu

wynoszą odpowiednio: 2,066

⋅

10

4

oraz 2,433

⋅

10

4

Pa.

a) ZnaleYć skład mieszaniny, która będzie wrzeć pod ciśnieniem 2,267

⋅

10

4

Pa w

temperaturze 315 K.

14

14

b) Pod jakim ciśnieniem będzie wrzeć mieszanina zawierająca 50% molowych
benzenu?

2.18.

Mieszaninę zawierającą 1 mol alkoholu etylowego i 1 mol dichloro-

etanu destylowano do momentu, gdy normalna temperatura wrzenia osiągnęła
70

o

C. Przez cały czas destylacji pary skraplano i destylat gromadzono w

odbieralniku. Prężność par kondensatu w temperaturze 70

o

C wyniosła 1,30

⋅

10

5

Pa. Prężności par alkoholu etylowego i dichloroetanu wynoszą w tej
temperaturze odpowiednio: 7

⋅

10

4

Pa i 1,5

⋅

10

5

Pa. Zakładając, że roztwór jest

doskonały, obliczyć:

a) ułamek molowy dichloroetanu w cieczy pozostałej w kolbie destylacyjnej,
b) ułamek molowy dichloroetanu w destylacie,
c) liczbę moli dichloroetanu, która znajduje się w destylacie.

2.19

.

W stanie równowagi znajdują się 3 mole cieczy A oraz pewna ilość

cieczy B. Prężność równowagowa wynosi 7,321

⋅10

4

Pa w temperaturze 350 K.

Prężności par czystych cieczy A i B wynoszą odpowiednio: 4,666

⋅10

4

i 1,013

⋅10

5

Pa w temperaturze 350 K. Obliczyć ułamek molowy cieczy A w

roztworze, liczbę moli cieczy B w roztworze oraz ułamek molowy składnika B
w parze.

2.20

.

Obliczyć rozpuszczalność sacharozy w wodzie (w molach na 1000 g

H

2

O) w temperaturze 25

o

C, wiedząc, że temperatura topnienia sacharozy wynosi

200

o

C, a jej ciepło topnienia 15,1 kJ

⋅mol

-1

. Molowa masa cząsteczkowa sacharo-

zy wynosi 342 g. Zakładamy, że roztwór sacharozy w wodzie jest roztworem
doskonałym.

2.21

.

Obliczyć podwyższenie temperatury wrzenia wodnych roztworów

zawierających w 100 g H

2

O:

a) 1,20 g mocznika (nieelektrolit),
b) 0,7455 g chlorku potasowego (mocny elektrolit),
c) 1,20 g mocznika oraz 0,7455 g chlorku potasowego.
Stała ebulioskopowa wody wynosi 0,516 K

⋅kg⋅mol

-1

.

2.22

.

Prężność pary nad roztworem zawierającym 11,1 g CaCl

2

w 1000 g

H

2

O w temperaturze 20

o

C wynosi 2,328

⋅10

3

Pa. Czysta woda ma w tej tempe-

raturze prężność pary 2,338

⋅10

3

Pa. Obliczyć stopień dysocjacji CaCl

2

w tym

roz-tworze. Molowa masa cząsteczkowa CaCl

2

wynosi 111 g.

15

15

2.23

.

Pewna substancja rozpuszczona w 100 g benzenu powoduje

obniżenie temperatury krzepnięcia o 1,28

o

C, a ta sama ilość tej substancji

rozpuszczona w 100 g H

2

O powoduje obniżenie temperatury krzepnięcia o

1,395

o

C. Obliczyć, na ile jonów dysocjuje substancja w wodzie zakładając, że w

benzenie znajduje się ona w postaci cząsteczkowej, a w wodzie jest w pełni
zdysocjowana. Stałe krioskopowe dla wody i benzenu wynoszą odpowiednio:
1,86 i 5,12 K

⋅kg⋅mol

-1

.

2.24

.

Prężność pary CCl

4

w temperaturze 20

o

C wynosi 1,140

⋅10

4

Pa, a

prężność par nad roztworem zawierającym 0,550 g substancji A w 25 g CCl

4

w

tej samej temperaturze wynosi 1,105

⋅10

4

Pa. Obliczyć molową masę cząstecz-

kową substancji A.

2.25.

Prężność par nad roztworem zawierającym 5,48 g aniliny w 50 g ete-

ru etylowego wynosi 4,4255

⋅10

4

Pa w temperaturze 15,3

o

C. Normalna

temperatura wrzenia eteru etylowego wynosi 35

o

C, a jego ciepło parowania

27,82 kJ

⋅mol

-1

. Obliczyć molową masę cząsteczkową aniliny.

2.26.

Obliczyć stopień dysocjacji Ba(NO

3

)

2

w roztworze wodnym

zawierającym 9,261 g Ba(NO

3

)

2

w 100 g H

2

O. Temperatura wrzenia tego

roztworu pod ciśnieniem normalnym wynosi 100,381

o

C. Stała ebulioskopowa

wody wynosi 0,516 K

⋅kg⋅mol

-1

.

2.27.

Dla benzenu stała krioskopowa wynosi 5,16 K

⋅kg⋅mol

-1

, a stała

ebulioskopowa 2,61 K

⋅kg⋅mol

-1

. Obliczyć ciepło parowania i topnienia benzenu,

jeżeli ciepło sublimacji benzenu wynosi 41,14 kJ

⋅mol

-1

. Temperatury wrzenia i

topnienia benzenu wynoszą odpowiednio: 80

o

C i 5,5

o

C.

ODPOWIEDZI DO ZADAŃ

2.1.

Nie mo?na; V

c

= 1,431 dm

3

;

2.2.

d = 9,67 g

⋅cm

-3

.

2.3.

∆H = 1249 J.

2.4.

∆H

s

= 31,45 kJ

⋅mol

-1

;

∆H

p

= 22,35 kJ

⋅mol

-1

.

2.5.

∆H

t

= 13,83 kJ

⋅mol

-1

.

2.6.

∆H

s

= 268,13 kJ

⋅mol

-1

.

2.7.

T = 298 K;

∆H

p

= 23,65 kJ

⋅mol

-1

.

2.8.

H

t

= 9,10 kJ

⋅mol

-1

.

2.9.

t = 56,55

o

C.

2.10.

P

o

A

= 1,538

⋅10

5

Pa; P

o

B

= 7,69

⋅10

4

Pa; P

ca3k.

= 1,077

⋅10

5

Pa; Y

A

= 0,571.

2.11.

P

o

A

= 3

⋅10

4

Pa; P

o

B

= 7

⋅10

4

Pa; Y

A

= 0,631.

16

16

2.12.

P

B

/P

A

= 1,217.

2.13.

P = 8,93

⋅10

3

Pa; 57,13% wagowych metanolu.

2.14.

P

o

A

/P

o

B

= 2,67;

2.15.

P

A

/P

B

= 5,32.

2.16.

n

p

= 0,08 mola; Y

B

= 0,825.

2.17.

a) X(dichloroetanu) = 0,452;

b) P = 2,2495

⋅10

4

Pa.

2.18.

a) X'(dichloroetanu) = 0,375;

b) Y(dichloroetanu) = 0,75;

c) n = 0,5 mola.

2.19.

X

A

= 0,514; n

B

= 2,84 moli; Y

B

= 0,672.

2.20.

6,52 moli w 1000 g H

2

O.

2.21.

a)

∆T = 0,103 K:

b) 0,103 K;

c)

∆T = 0,206 K.

2.22.

α = 0,688.

2.23.

3 jony.

2.24.

M

A

= 107 g.

2.25.

M = 90 g.

2.26.

α = 0,54.

2.27.

∆H

p

= 31,29 kJ

⋅mol

-1

;

∆H

t

= 9,85 kJ

⋅mol

-1

.