Wykłady z Elektrotechniki

Wykłady z Elektrotechniki

teoretycznej

teoretycznej

Wykład 16

Wykład 16

a. Indukcyjność własna i wzajemna cewek, zjawiska

występujące przy sprzężeniu magnetycznym

b. Połączenie szeregowe elementów sprzężonych

magnetycznie

c. Połączenie równoległe elementów sprzężonych

magnetycznie

d. Metody analizy obwodów magnetycznych sprzężonych

MENU

EXIT

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

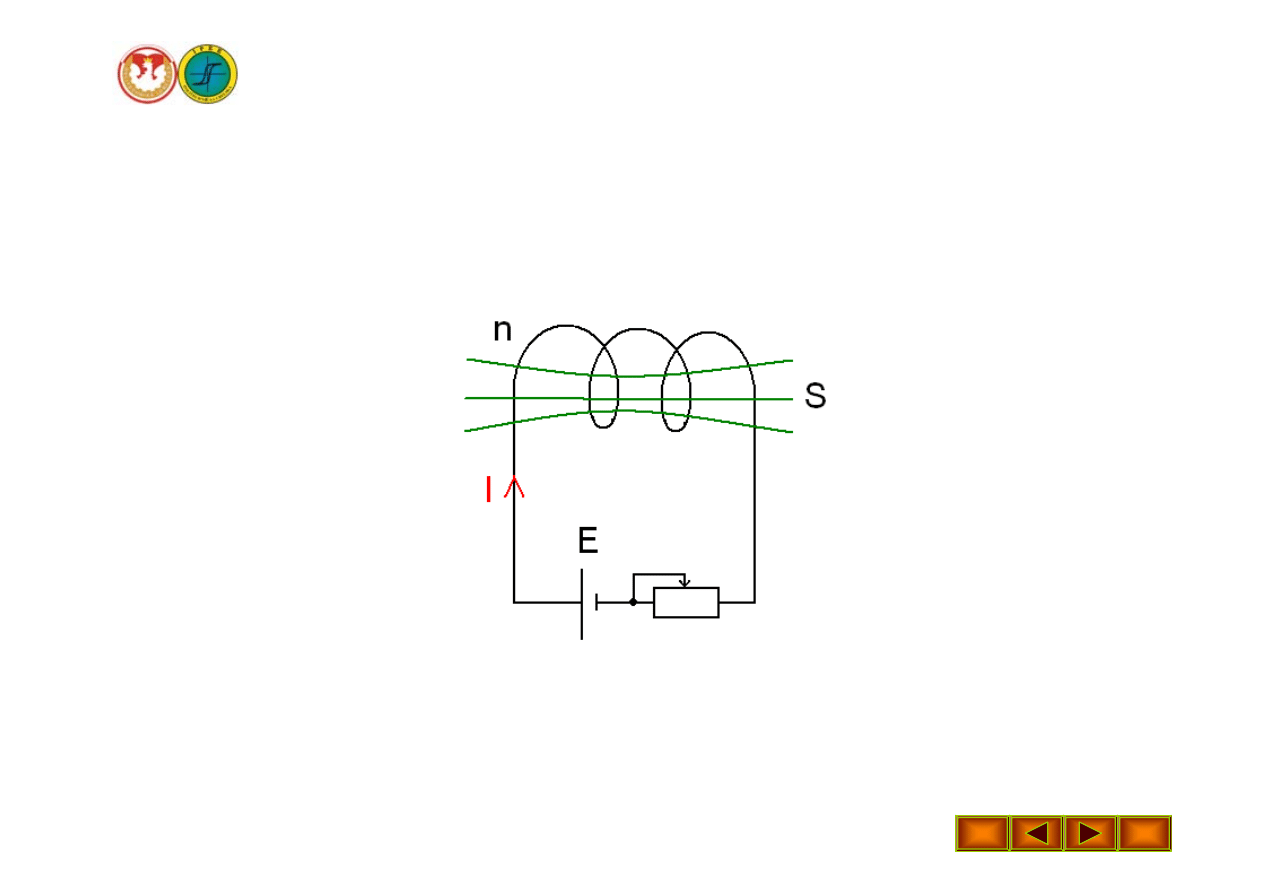
Indukcyjność własna

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Indukcyjnością własną

cewki nazywamy stosunek

strumienia skojarzonego z cewką

Ψ

do prądu

I

płynącego

przez cewkę.

I

L

Ψ

=

Indukcyjność własną oznaczamy przez

L

. Jednostką

indukcyjności jest jeden henr (1H).

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Zmiany natężenia prądu i w obwodzie powodują zmianę strumienia
indukcji, a w konsekwencji powstanie siły elektromotorycznej

ε

.

dt

di

L

dt

d

ji

samoindukc

−

=

φ

−

=

ε

Znak minus reprezentuje regułę Lenza:

"

powstająca siła elektromotoryczna przeciwdziała zmianom prądu

"

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Indukcyjność własna cewki zależy od liczby zwojów , gęstości

nawinięcia, rozmiarów geometrycznych i kształtu. Dla cewki o

długości

l

,

liczbie zwojów na jednostkę długości

n

i powierzchni

przekroju

S

, w próżni indukcyjność własną określa zależność:

l

S

n

µ

L

2

0

=

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

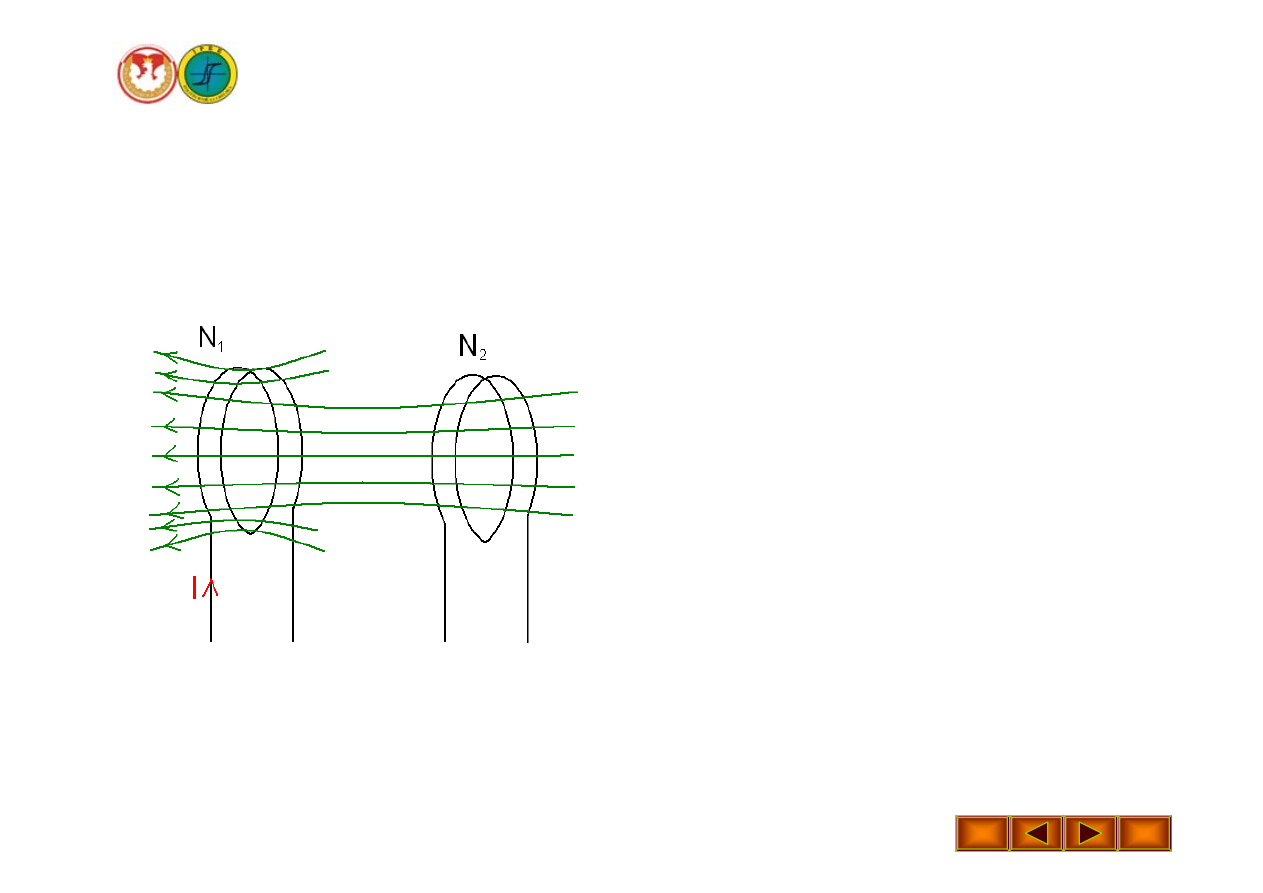
Sprzężenie magnetyczne

Dwa elementy usytuowane względem

siebie w taki sposób, że pole

magnetyczne jednego z nich przenika,

choćby częściowo, element drugi

nazywamy elementami

sprzężonymi

magnetycznie

.

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

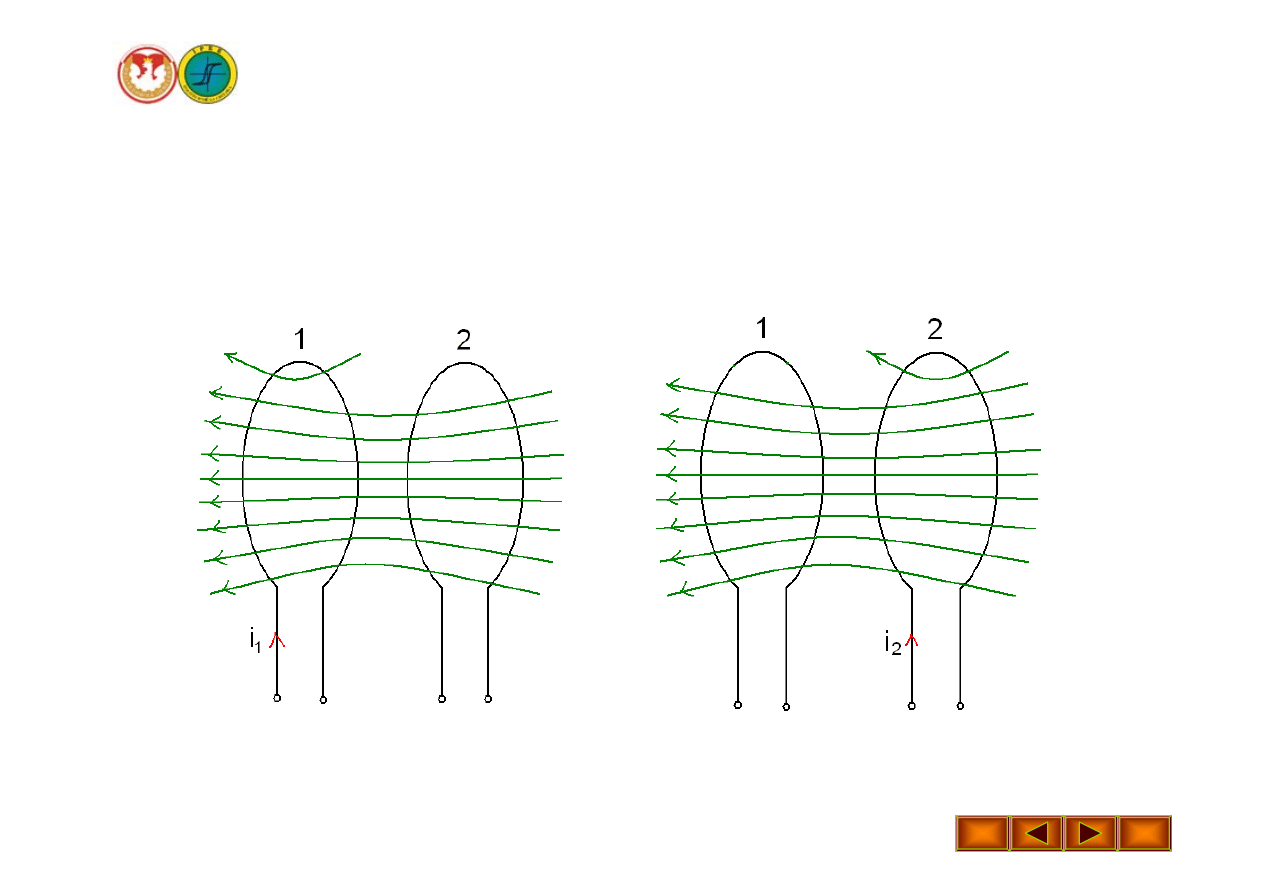
Elementy sprzężone magnetycznie

Φ

11

Φ

22

Φ

g1

Φ

g2

Φ

s1

Φ

s2

Prąd przepływa przez element 1

Prąd przepływa przez element 2

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Strumień główny i rozproszenia

Przy przepływie prądu i

1

powstaje strumień magnetyczny

Φ

11

. Strumień ten obejmuje element 1 a jego część którą

oznaczamy

Φ

g1

nazywamy

strumieniem głównym

cewki

1 obejmuje element 2. Pozostałą część strumienia

Φ

11

która nie dochodzi do cewki 2 nazywamy

strumieniem

rozproszenia

i oznaczamy przez

Φ

s1

.

Φ

11

= Φ

g1

+ Φ

s1

i analogicznie dla cewki 2:

Φ

22

= Φ

g2

+ Φ

s2

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Strumień skojarzony

Jeśli elementy indukcyjne mają odpowiednio

n

1

i

n

2

zwojów i przez każdy zwój przenika taki sam strumień, to

strumienie skojarzone

od poszczególnych strumieni

wynoszą:

Ψ

11

= n

1

Φ

11

Ψ

22

= n

2

Φ

22

Ψ

12

= n

2

Φ

g1

Ψ

21

= n

1

Φ

g2

Ψ

g1

= n

1

Φ

g1

Ψ

g2

= n

2

Φ

g2

Ψ

s1

= n

1

Φ

s1

Ψ

s2

= n

2

Φ

s2

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Indukcyjność wzajemna

Stosunek strumienia magnetycznego wytworzonego w cewce
pierwszej 1 i skojarzonego z cewką drugą 2, do prądu płynącego w
cewce pierwszej nazywamy

indukcyjnością wzajemną

cewki

pierwszej z drugą i oznaczamy przez

M

12

.

1

12

12

i

M

Ψ

=

Między indukcyjnościami własnymi cewek a indukcyjnością
wzajemną zachodzi zależność:

2

1

L

L

k

M

=

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Indukcyjności własne i wzajemne elementów

- indukcyjności własne:

- indukcyjności wzajemne:

1

11

1

1

11

1

i

n

i

L

φ

=

Ψ

=

2

22

2

2

22

2

i

n

i

L

φ

=

Ψ

=

1

1

2

1

12

12

i

n

i

M

g

φ

=

Ψ

=

2

2

1

2

21

21

i

n

i

M

g

φ

=

Ψ

=

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

- indukcyjności główne

2

2

2

2

2

2

i

n

i

L

g

g

g

φ

=

Ψ

=

1

1

1

1

1

1

i

n

i

L

g

g

g

φ

=

Ψ

=

- indukcyjności rozproszenia

2

2

2

2

2

2

i

n

i

L

s

s

s

φ

=

Ψ

=

1

1

1

1

1

1

i

n

i

L

s

s

s

φ

=

Ψ

=

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Współczynnik sprzężenia

Współczynnikiem sprzężenia

cewki pierwszej z drugą (drugiej z

pierwszą) nazywamy stosunek sprzężenia magnetycznego głównego
cewki pierwszej (drugiej) do strumienia całkowitego tej cewki.

11

1

1

φ

φ

g

k

=

22

2

2

φ

φ

g

k

=

Współczynnik sprzężenia obu cewek

:

2

1

* k

k

k

=

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Współczynnik rozproszenia

Współczynnikiem rozproszenia

nazywamy stosunek strumienia

magnetycznego rozproszenia do strumienia całkowitego.

22

2

2

φ

φ

σ

s

=

11

1

1

φ

φ

σ

s

=

Współczynnik sprzężenia i rozproszenia dopełniają się do jedności:

k

2

+ σ

2

= 1

k

1

+ σ

1

= 1

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

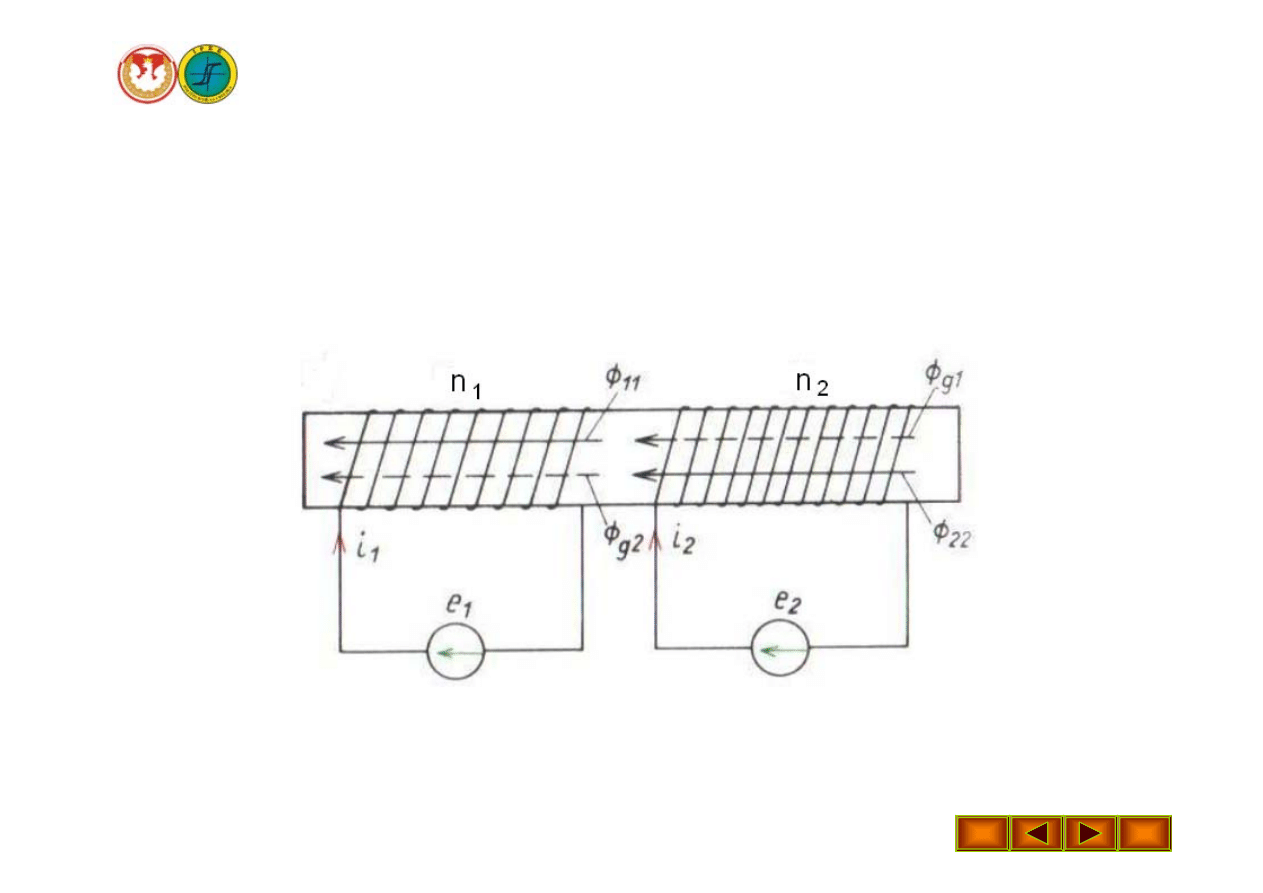
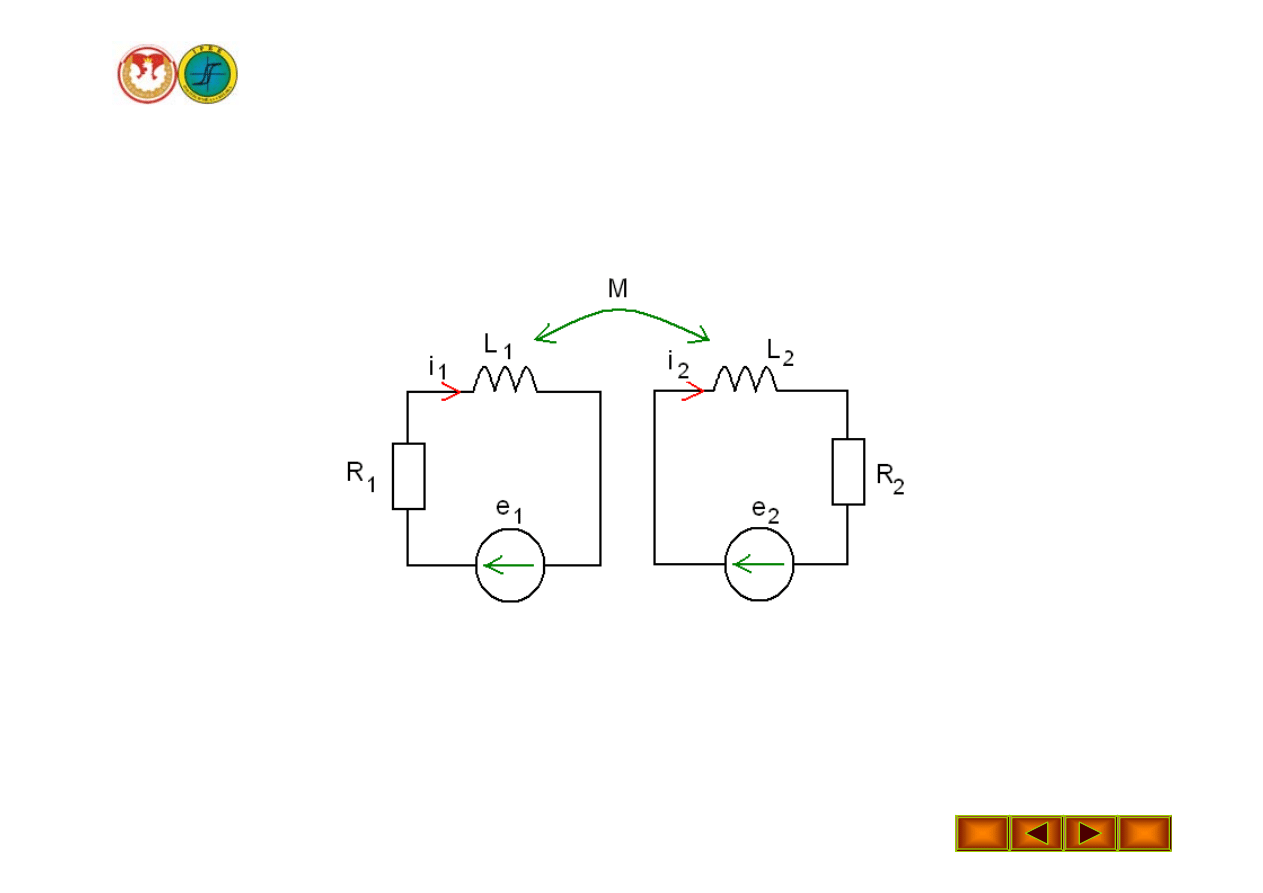
Dwie cewki sprzężone magnetycznie nawinięte na

wspólnym rdzeniu, każda zasilana napięciem

sinusoidalnym.

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Schemat zastępczy.

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Całkowity strumień magnetyczny

Skojarzony z cewką pierwszą

Ψ

1

= n

1

(Φ

11

+ Φ

g2

) = Ψ

11

+ Ψ

21

Skojarzony z cewką drugą

Ψ

1

= n

2

(Φ

22

+ Φ

g1

) = Ψ

22

+ Ψ

12

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Równanie bilansu napięć chwilowych

dt

d

dt

d

i

R

dt

d

i

R

e

21

11

1

1

1

1

1

1

Ψ

Ψ

Ψ

+

+

=

+

=

dt

d

dt

d

i

R

dt

d

i

R

e

12

22

2

2

2

2

2

2

Ψ

Ψ

Ψ

+

+

=

+

=

dt

di

M

dt

di

L

i

R

e

2

1

1

1

1

1

+

+

=

dt

di

M

dt

di

L

i

R

e

1

2

2

2

2

2

+

+

=

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Napięcie indukcji własnej

dt

di

L

u

L

2

2

2

=

dt

di

L

u

L

1

1

1

=

Napięcie indukcji wzajemnej

dt

di

M

u

M

2

2

=

dt

di

M

u

M

1

1

=

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Wartość skuteczna napięcia indukcji własnej

U

L1

= ωL

1

I

1

U

L2

= ωL

2

I

2

Wartość skuteczna napięcia indukcji wzajemnej

U

M1

= ωMI

1

U

M2

= ωMI

2

EXIT

MENU

Wykład 16 – Indukcyjność własna i wzajemna cewek, zjawiska występujące przy sprzężeni

magnetycznym

Równania w postaci zespolonej

e

1

= u

R1

+ u

L1

+ u

M2

e

2

= u

R2

+ u

L2

+ u

M1

E

1

= R

1

I

1

+ jX

L1

I

1

+jX

M

I

2

E

2

= R

2

I

2

+ jX

L2

I

2

+jX

M

I

1

EXIT

MENU

Wykład 16 – Połączenie szeregowe elementów sprzężonych magnetycznie

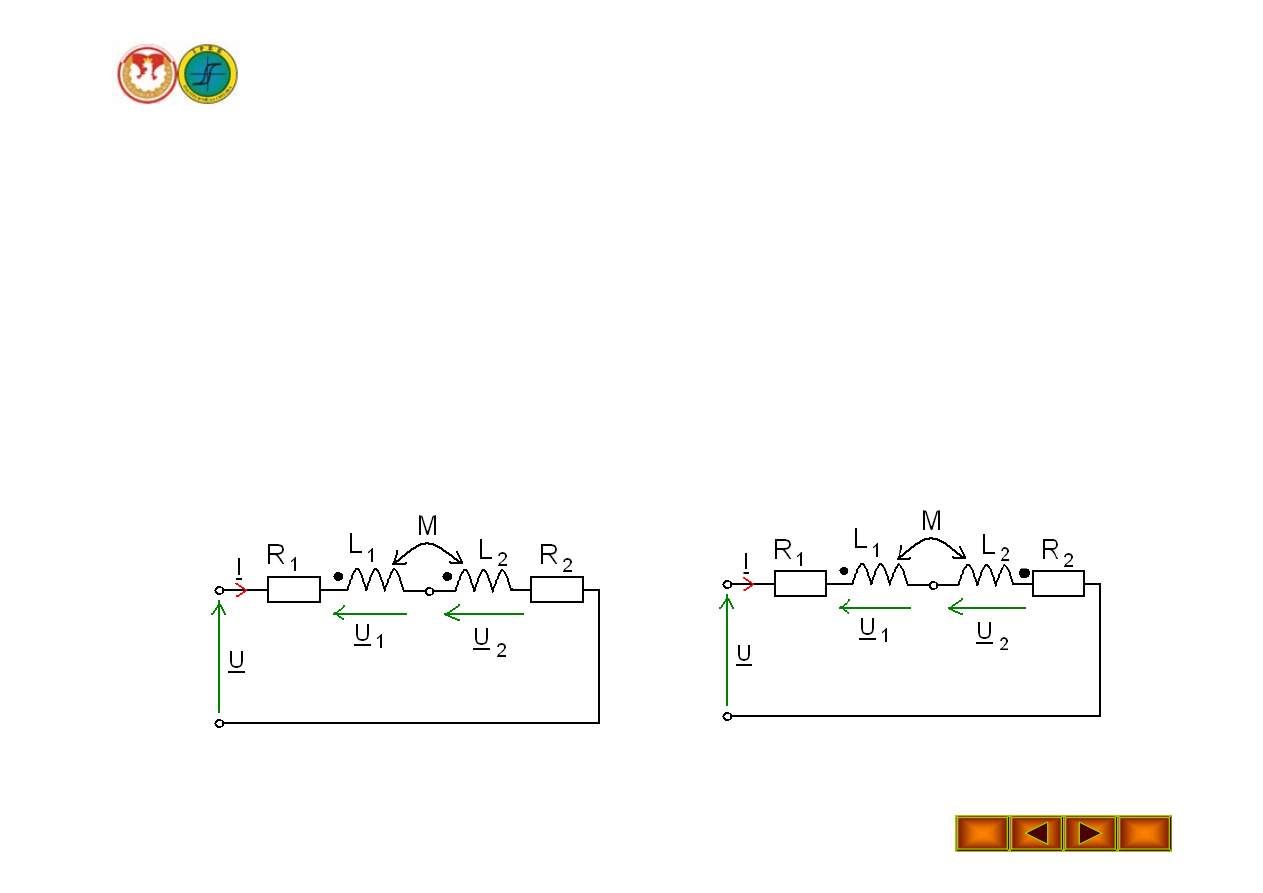
Połączenie szeregowe elementów

sprzężonych magnetycznie

Istnieją dwa sposoby połączenia cewek:

- zgodne

- przeciwne

EXIT

MENU

Wykład 16 – Połączenie szeregowe elementów sprzężonych magnetycznie

Połączenie zgodne

Przy połączeniu zgodnym prądy w obu cewkach mają jednakowe
zwroty względem zacisków jednoimiennych. Strumienie indukcji
własnej i wzajemnej w każdej cewce dodają się i napięcie indukcji
wzajemnej ma znak plus( + ).

Wartości chwilowe napięć na elementach

dt

di

M

dt

di

L

i

R

u

+

+

=

1

1

1

dt

di

M

dt

di

L

i

R

u

+

+

=

2

2

2

EXIT

MENU

Wykład 16 – Połączenie szeregowe elementów sprzężonych magnetycznie

Napięcie w postaci zespolonej

U

1

= R

1

I + jωL

1

I + jωMI

U

2

= R

2

I + jωL

2

I + jωMI

Napięcie całkowite na zaciskach układu cewek połączonych

szeregowo zgodnie:

U = U

1

+U

2

= [R

1

+R

2

+jω(L

1

+L

2

+2M) ]*I = Z

zg

*I

Z

zg

=R

1

+R

2

+jω(L

1

+L

2

+2M)

EXIT

MENU

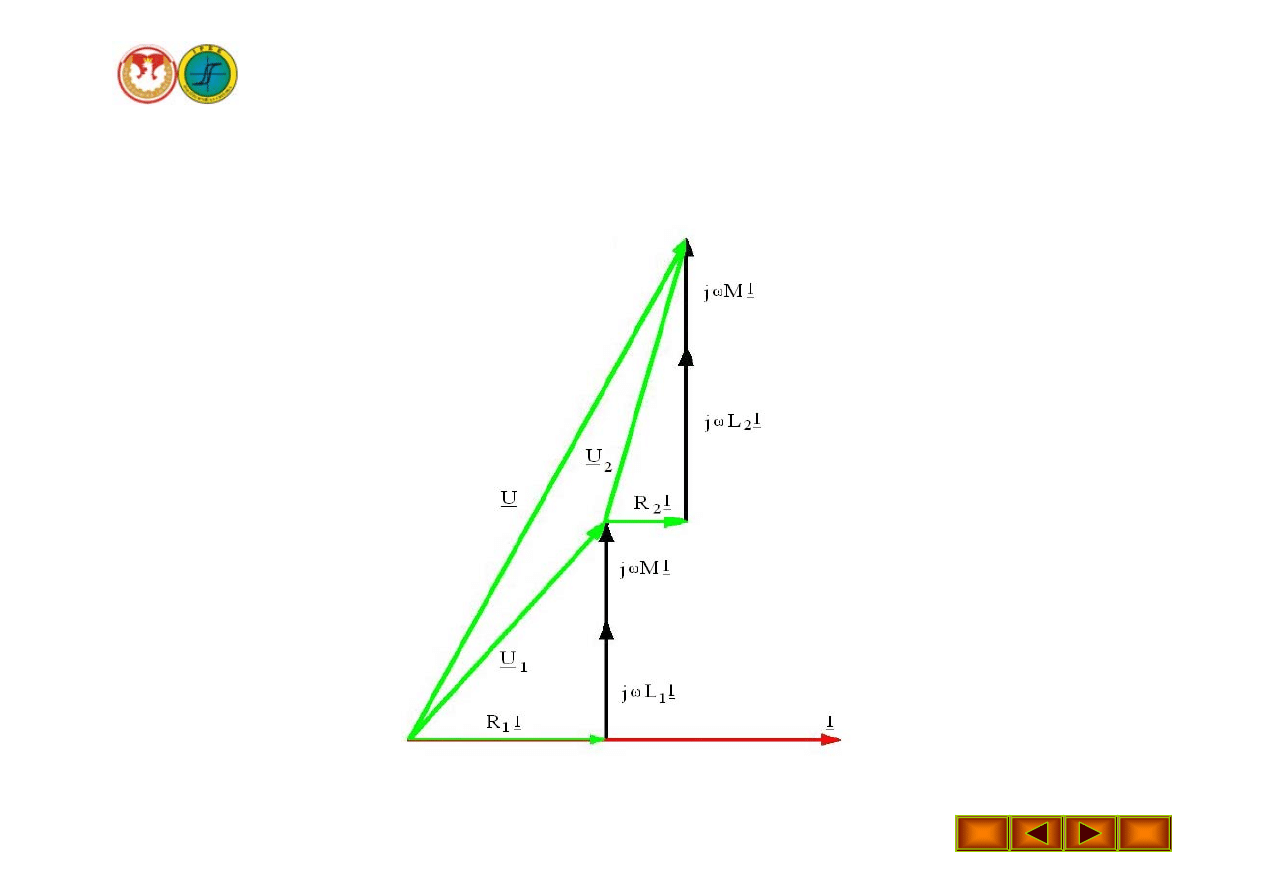
Wykład 16 – Połączenie szeregowe elementów sprzężonych magnetycznie

Wykres wektorowy

EXIT

MENU

Wykład 16 – Połączenie szeregowe elementów sprzężonych magnetycznie

Połączenie przeciwne

Przy połączeniu przeciwnym prądy w obu cewkach mają różne zwroty

względem zacisków jednoimiennych. Strumień indukcji własnej i

wzajemnej w każdej cewce odejmuje się i napięcie indukcji wzajemnej

ma znak minus( - ).

Wartości chwilowe napięć na elementach

dt

di

M

dt

di

L

i

R

u

−

+

=

2

2

2

dt

di

M

dt

di

L

i

R

u

−

+

=

1

1

1

EXIT

MENU

Wykład 16 – Połączenie szeregowe elementów sprzężonych magnetycznie

Napięcie w postaci zespolonej

U

1

= R

1

I + jωL

1

I - jωMI

U

2

= R

2

I + jωL

2

I - jωMI

Napięcie całkowite na zaciskach układu cewek połączonych

szeregowo przeciwnie:

U = U

1

+U

2

= [R

1

+R

2

+jω(L

1

+L

2

-2M) ]*I = Z

p

*I

Z

p

=R

1

+R

2

+jω(L

1

+L

2

-2M)

EXIT

MENU

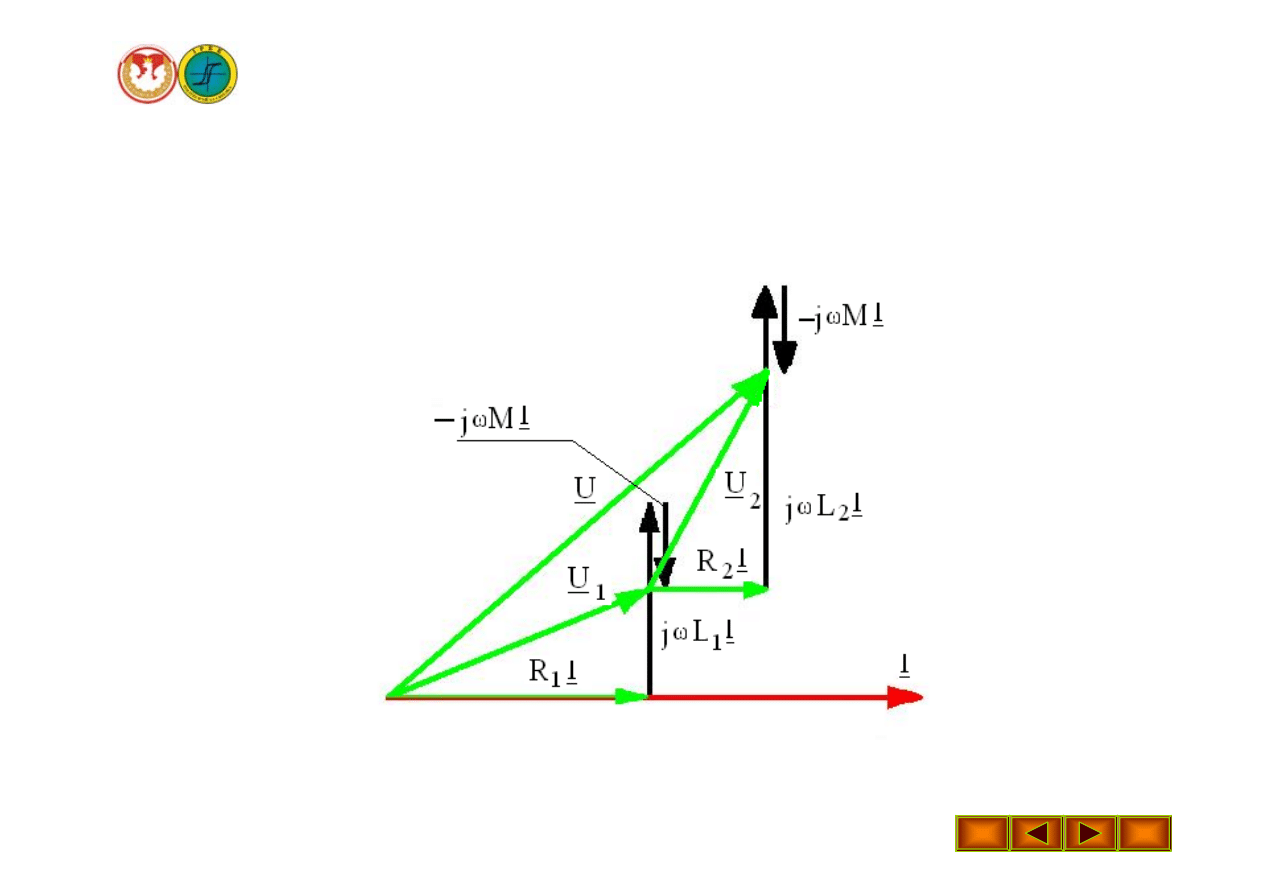
Wykład 16 – Połączenie szeregowe elementów sprzężonych magnetycznie

Wykres wektorowy

EXIT

MENU

Wykład 16 – Połączenie szeregowe elementów sprzężonych magnetycznie

Na podstawie pomiaru impedancji zastępczej przy
połączeniu szeregowym zgodnym i przeciwnym
można wyznaczyć indukcyjność wzajemną M:

EXIT

MENU

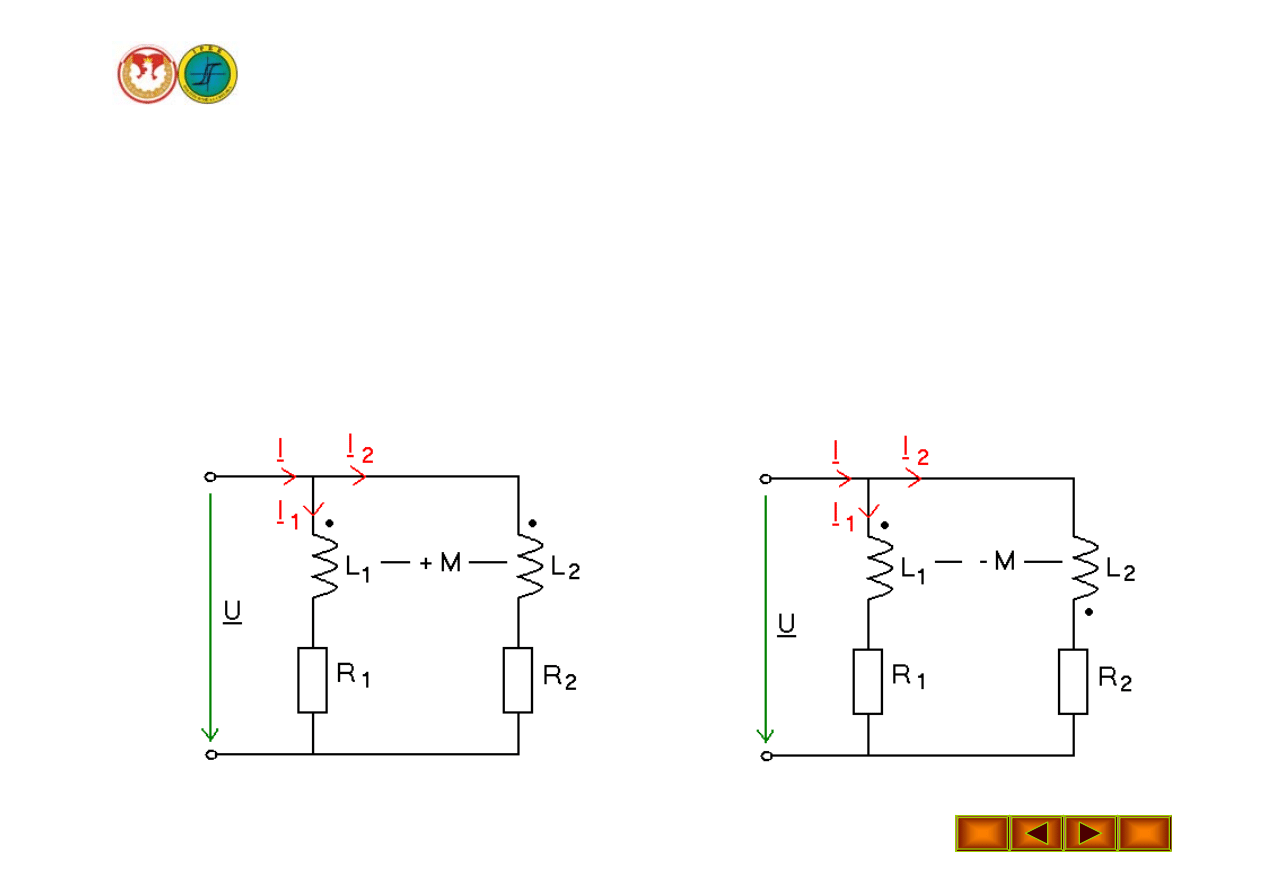
Wykład 16 – Połączenie równoległe elementów sprzężonych magnetycznie

Połączenie równoległe elementów

sprzężonych magnetycznie

- zgodne

- przeciwne

EXIT

MENU

Wykład 16 – Połączenie równoległe elementów sprzężonych magnetycznie

Połączenie równoległe zgodne

Równania:

I = I

1

+ I

2

(R

1

+ jωL

1

)*I

1

+ jωMI

2

= U

(R

2

+ jωL

2

)*I

2

+ jωMI

1

= U

Oznaczmy:

Z

1

= R

1

+ jωL

1

Z

2

= R

2

+ jωL

2

Z

M

= jωM

EXIT

MENU

Wykład 16 – Połączenie równoległe elementów sprzężonych magnetycznie

Prąd dopływający do połączenia

EXIT

MENU

Wykład 16 – Połączenie równoległe elementów sprzężonych magnetycznie

Połączenie równoległe przeciwne

Równania:

I = I

1

+ I

2

(R

1

+ jωL

1

)*I

1

+ jω(-M)I

2

= U

(R

2

+ jωL

2

)*I

2

+ jω(-M)I

1

= U

Oznaczmy:

Z

1

= R

1

+ jωL

1

Z

2

= R

2

+ jωL

2

Z

M

= jω(-M)

EXIT

MENU

Wykład 16 – Połączenie równoległe elementów sprzężonych magnetycznie

Prąd dopływający do połączenia

EXIT

MENU

Wykład 16 – Metody analizy obwodów magnetycznych sprzężonych

Metody analizy obwodów magnetycznych

Prawa Kirchhoffa

Przy analizie obwodów zawierających cewki magnetycznie sprzężone
wygodnie jest przedstawić II prawo Kirchhoffa w następującej postaci:

∑

∑

∑

=

+

k

k

n

k

kn

k

k

e

dt

di

M

u

∑

k

k

u

dt

di

M

n

k

kn

∑

∑

k

k

e

Suma algebraiczna sum elektromotorycznych działających w obwodzie

Suma algebraiczna napięć na elementach z wyłączeniem napięć indukowanych

w cewkach sprzężonych magnetycznie

Suma algebraiczna napięć indukowanych w wyniku indukcji wzajemnej

EXIT

MENU

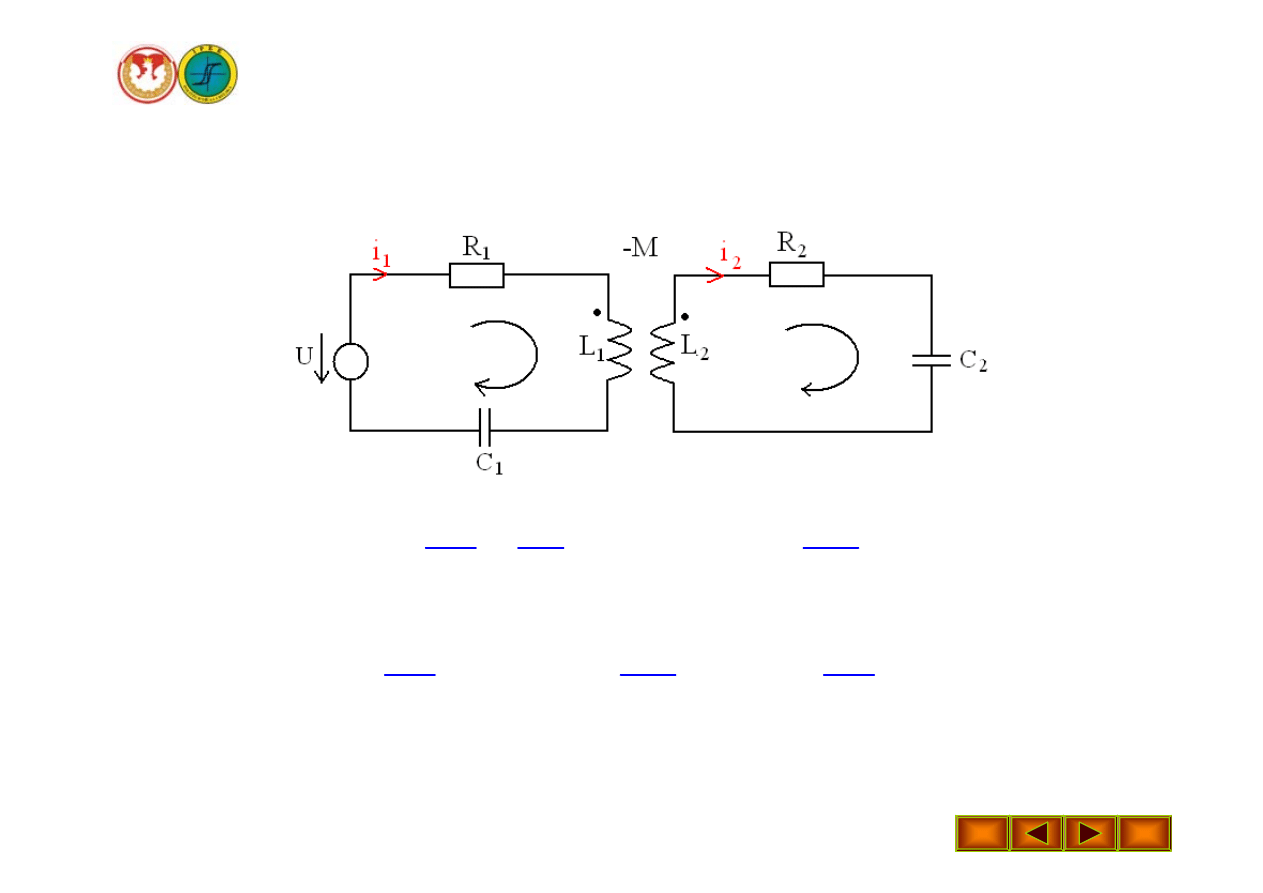
Wykład 16 – Metody analizy obwodów magnetycznych sprzężonych

Przykład

0

)

(

1

2

1

1

1

1

1

1

=

−

−

+

+

+

∫

U

dt

di

M

dt

i

C

dt

di

L

i

R

0

)

(

1

1

2

2

2

2

2

2

=

−

+

+

+

∫

dt

di

M

dt

di

L

dt

i

C

i

R

EXIT

MENU

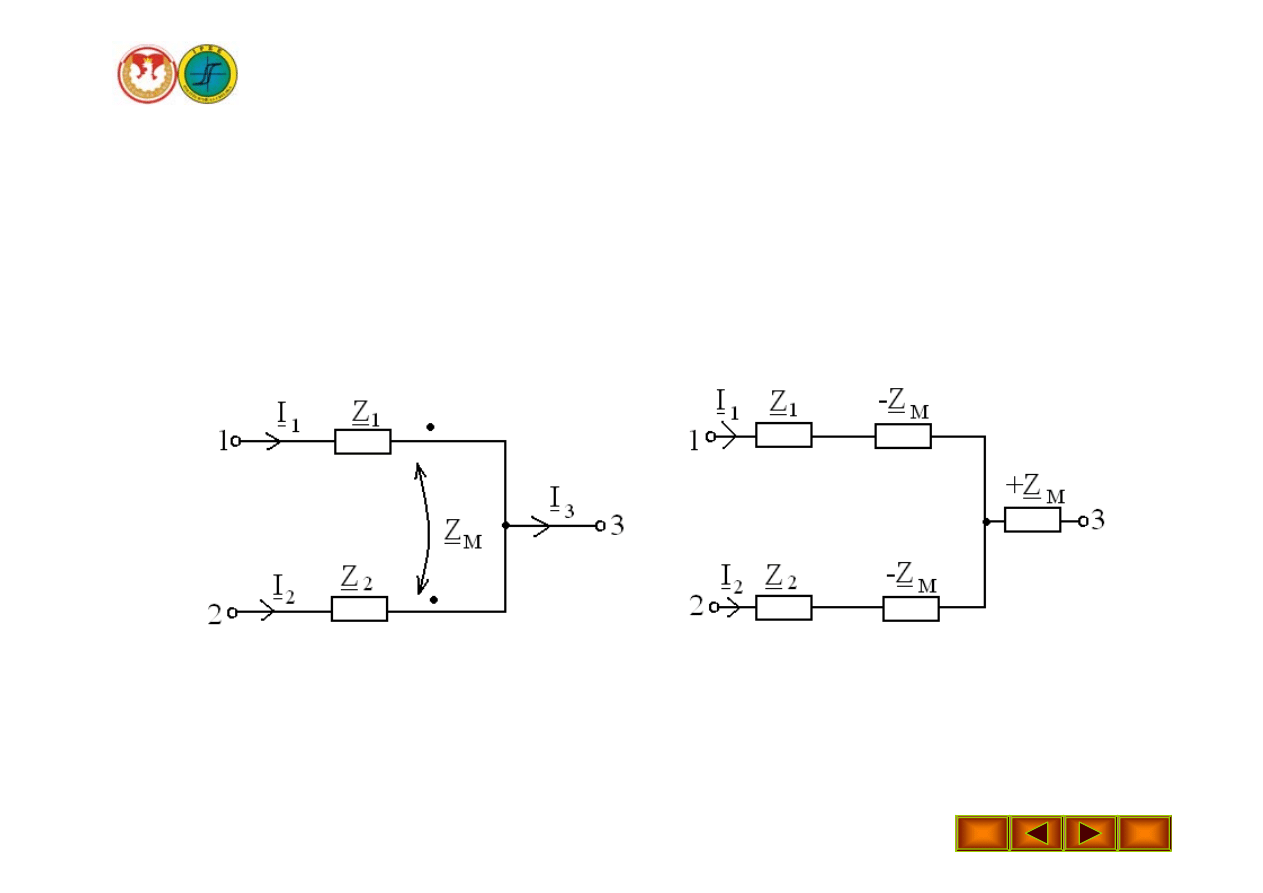
Wykład 16 – Metody analizy obwodów magnetycznych sprzężonych

Zastąpienie układu ze sprzężeniem układem bez sprzężenia

Cewki dołączone do węzła zaciskami jednoimiennymi

EXIT

MENU

Wykład 16 – Metody analizy obwodów magnetycznych sprzężonych

Równania dla powyższego układu są następujące:

EXIT

MENU

Wykład 16 – Metody analizy obwodów magnetycznych sprzężonych

Po odpowiednim podstawieniu otrzymujemy:

EXIT

MENU

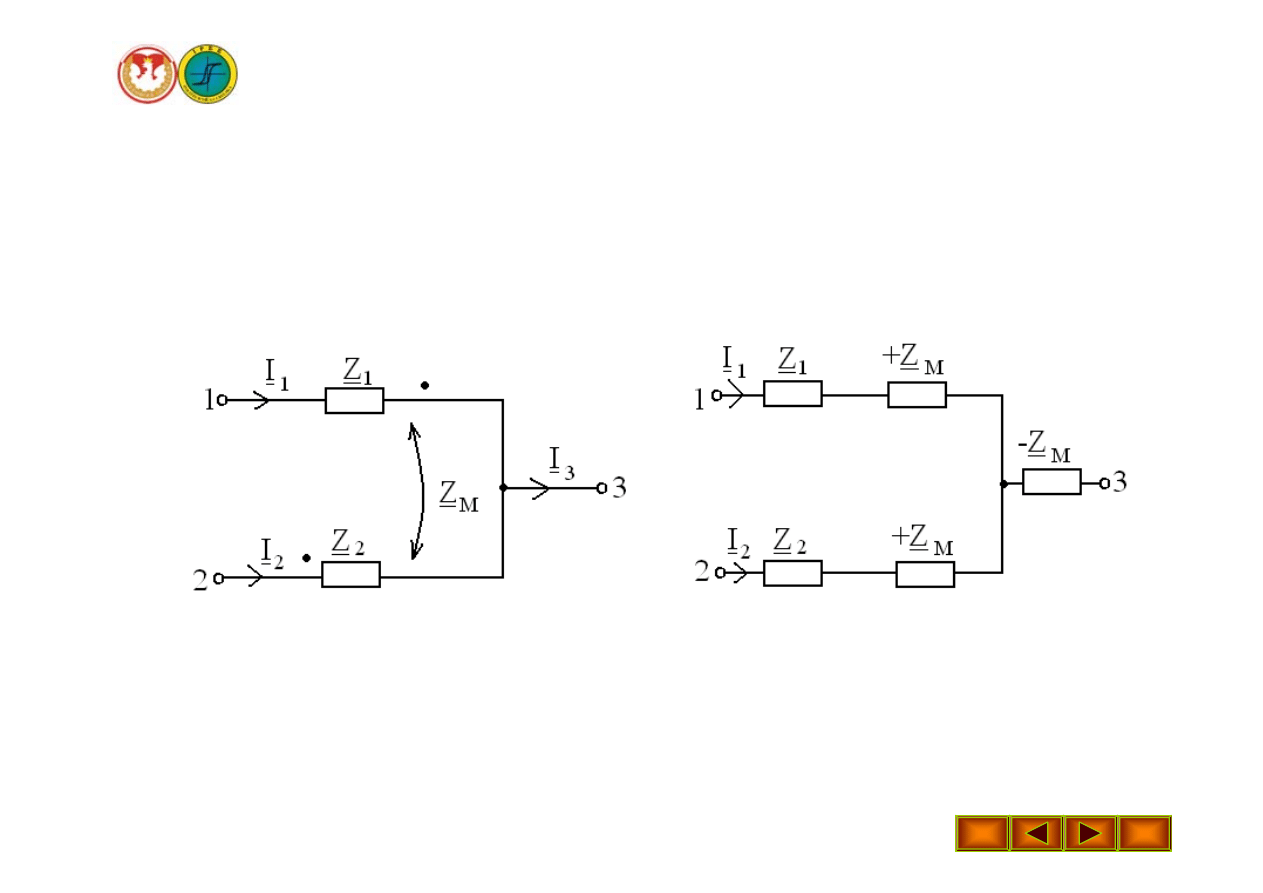
Wykład 16 – Metody analizy obwodów magnetycznych sprzężonych

Cewki dołączone do węzła zaciskami różnoimiennymi

EXIT

MENU

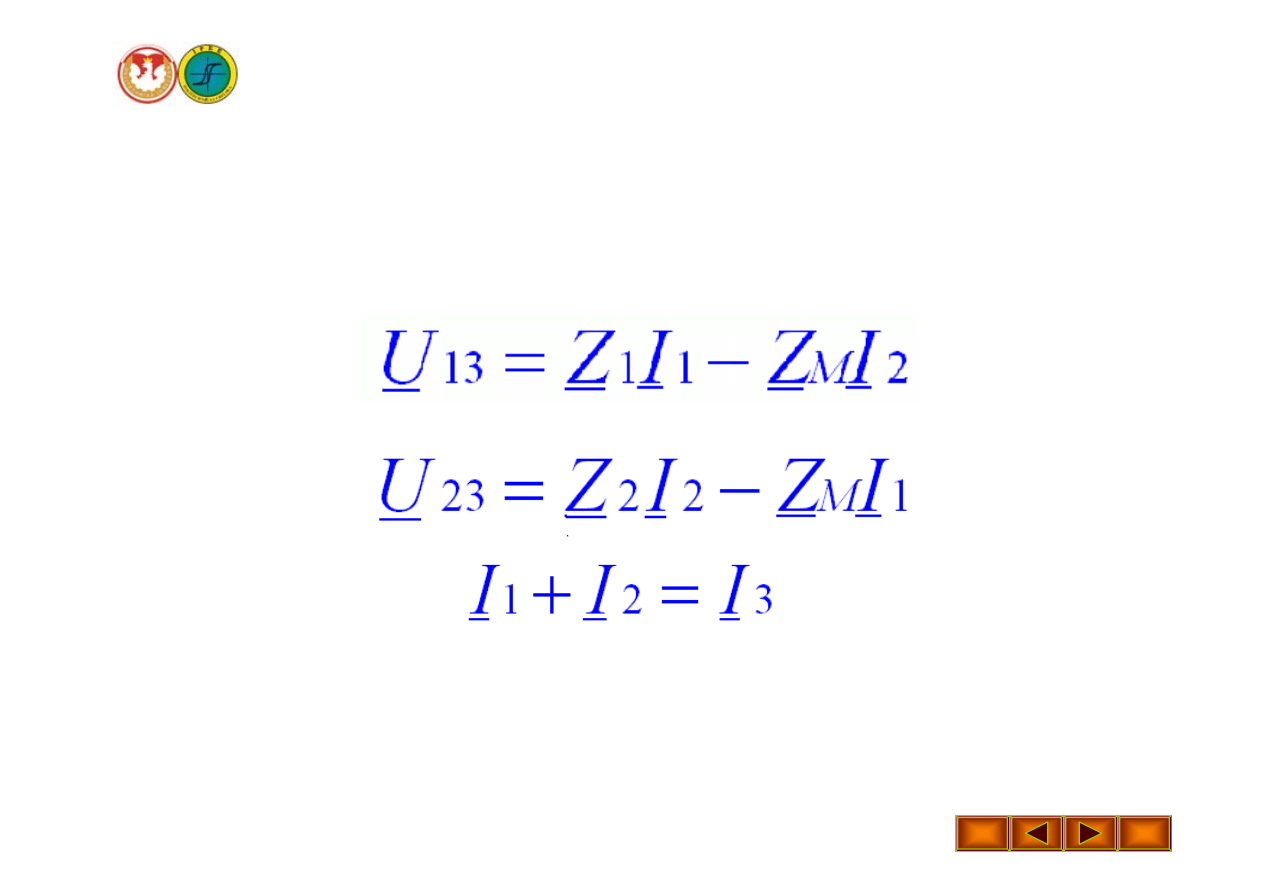
Wykład 16 – Metody analizy obwodów magnetycznych sprzężonych

Równania dla powyższego układu są następujące:

EXIT

MENU

Wykład 16 – Metody analizy obwodów magnetycznych sprzężonych

Po odpowiednim podstawieniu otrzymujemy:

EXIT

MENU