POLITECHNIKA POZNAŃSKA

INSTYTUT ELEKTROTECHNIKI PRZEMYSŁOWEJ

Zakład Podstaw Elektrotechniki

Laboratorium Elektrotechniki Teoretycznej

Ćwiczenie nr 4

Temat: Obwody sprzężone m agnetycznie – indukcja elektro m agnetyczna

Rok akademicki:2005/2006

Wykonawcy:

Data

Wydział Elektryczny

1. Maciej Medycki

Wykonania
ćwiczenia

Oddania
sprawozdania

Studia dzienne magisterskie

2. Artur Ośka
3. Łuksz Olszewski

14.03.06

28.03.06

Nr grupy: E-4

Ocena:

Uwagi:

1. Wiadomości teoretyczne
Zjawisko samoindukcji – prąd i płynący w obwodzie zamkniętym wytwarza pole magnetyczne,
którego linie przenikają wnętrze tego obwodu. Wobec tego z rozpatrywanym obwodem skojarzony
jest strumień Ψ. Przypuśćmy, że prąd jest wielkością zmienną w czasie, wówczas zarówno pole
magnetyczne wytworzone przez ten prąd, jak i strumień zmieniają się w czasie, a więc w obwodzie
indukuje się siła elektromotoryczna. Zjawisko indukowania się siły elektromotorycznej w obwodzie
w skutek przepływu zmiennego prądu w tym samym obwodzie nazywamy indukcją własną.
Załóżmy, że w otocznieu tozpatrywanego obwodu nie ma żadnychciał ferromagmetycznych,
wówczasindukcja magnetyczna B w każdym punkcie pola jest proporcjonalna do prądu. Na tej
podstawie wnioskujemy, że strumień skojarzony obwodu jest proporcjonalny do prądu płynącego w
tym obwodzie, wobec tego

Wielkość L nazywa się indukcyjnością własną lub indukcyjnością obwodu. Indukcyjność ta jest
wielkością stałaą , gdy w otocznieu nie ma żadnych ciał ferromagnetycznych. Jednostką główną
indukcyjności w układzie SI jest henr [H].

Indukcja wzajemna.

=

L⋅i

1

2

I

I

B

B

2

1

2

1

Rozpatrujemy dwa obwody 1,2 zawierające odpowiednie z

1

, z

2

zwojów i znajdujące się blisko

siebie w jednorodnym iztropowym środowisku.
Zakładamy, że w obwodzie 1 płynie prąd i

1

, natomiast obwód 2 jest rozwarty, wobec tego i

2

= 0.

Prąd i

1

w obwodzie 1 wytwarza pole magnetyczne, przy czym część linii tego pola przenika obwód

2.
Otrzymujemy

Teraz zakładamy, że obwód 1 jest rozwarty, czyli i

1

= 0, natomiast w obwodzie 2 płynie prąd i

1

. W

tym przypadku część linii pola magnetycznego wytworzonego przez prąd i

1

przenika obwód 1.

Otrzymujemy

Ponieważ: M

12

=

M

21

=

M

Wzory na strumienie skojarzone przybierają postać 

12

=

M⋅i

2

; 

21

=

M⋅i

1

Czyli:

Wielkość M określoną powyższym wzorem nazywa się indukcyjnością wzajemną. Jednostka
główną w indukcyjności wzajemnej w układzie Si jest henr [H]

Strumienie: główny, rozproszenia, skojarzenia.

Pod wpływem prądu I płynącego w uzwojeniu powstaje w rdzeniu pole magnetyczne. Część linii
pola przebiega całkowicie w rdzeniu tworząc strumien główny Φ;strumień główny koncentruje się
zatem całkowicie w rdzeniu. Pozostała część linii pola przebiega częściowo w rdzeniu, częściowo
zaś w otaczającym środowisku; te linie tworzą strumień rozproszenia Φ

0

.

Strumieniem skojarzonym Ψ cewki nazywamy sumę strumieni magnetycznych przenikających
poszczególne zwoje, czyli:

Współczynnik sprzężenia magnetycznego
Sprzężenie magnetyczne dwóch cewek charakteryzuje współczynnik sprzężenia:

Przy czym 0 k 1 . Wartość k=0 otrzymuje się wtedy gdy między cewkami nie ma sprzężenia
magnetycznego, tzn. Gdy strumień magnetyczny wytworzony przez prąd płynący w jednej cewce
nie przenika drugiej cewki. Wartość k=1 otrzymuje się w przpadku sprzężenia idealnego, gdy cały
strumieć magnetyczny wytworzony przez prąd płynący e jedenej cewce przenika drugą cewkę.

(Zjawisko samoindukcji, indukcja wzajemna, magnesowanie zgodne i przeciwne, sposoby
wyznaczania
indukcyjności wzajemnej, cewki powietrzne, cewki na rdzeniu ferromagnetycznym, indukcyjność
własna,
wzajemna, strumień główny, rozproszenia, strumienie skojarzone, współczynnik sprzężenia
magnetycznego).



21

=

Z

2

⋅

21



21

=

M

21

⋅

i

1



12

=

Z

1

⋅

12



12

=

M

12

⋅

i

2

M =



12

i

2

=



21

i

1

=

1



2



...

z

k =

∣

M∣



L

1

L

2

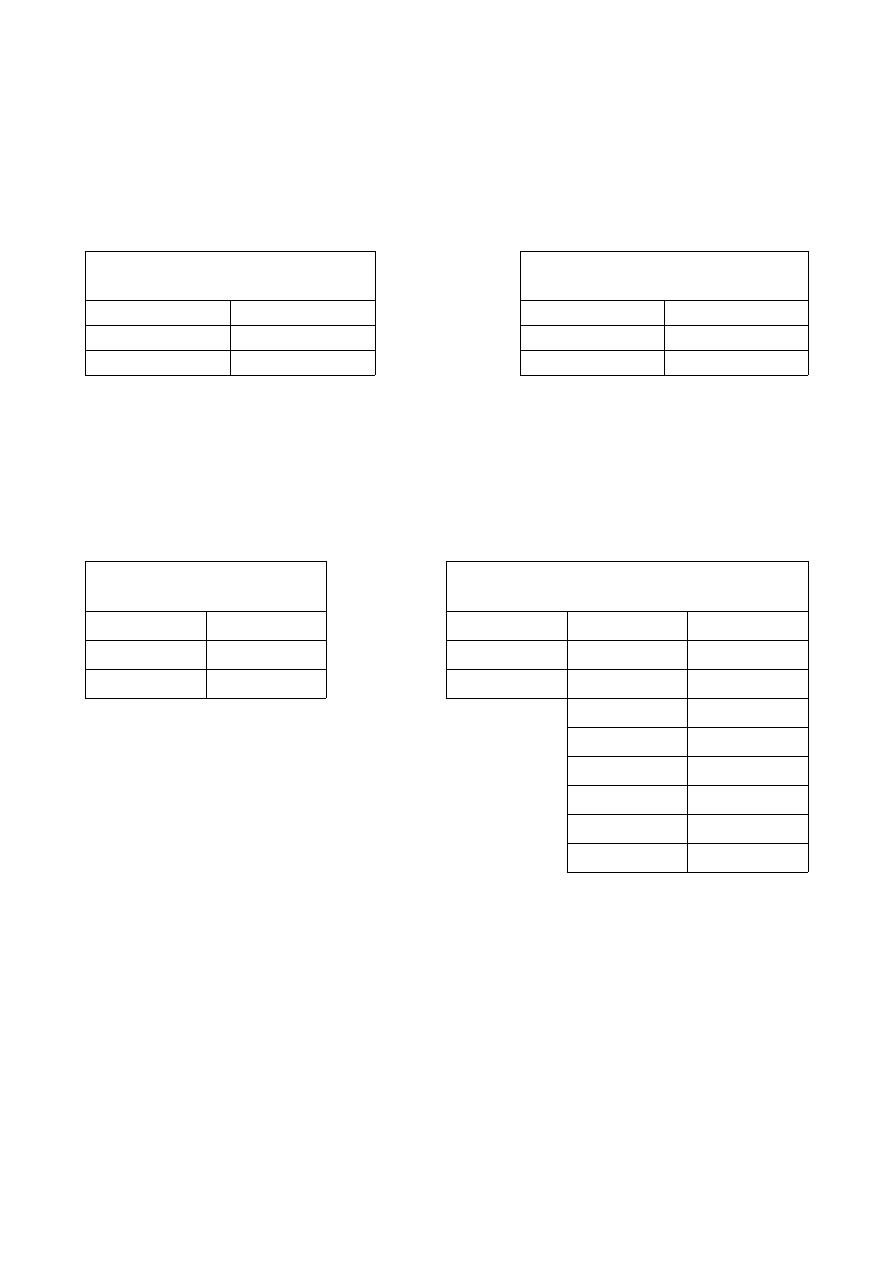
2. Przebieg ćwiczenia

2.1. Pomiar rezystancji i indukcyjności własnej cewek powietrznych i cewek na rdzeniu

ferromagnetycznym AB i CD miernikami

2.1.1.Pomiar rezystancji cewek AB i CD mostkiem Thomsona

Cewki

powietrzne

Cewki na rdzeniu

ferromagnetycznym

R

AB

R

CD

R

AB

R

CD

[Ω]

[Ω]

[Ω]

[Ω]

1,65

2,28

1,65

2,28

2.1.2. Pomiar indukcyjności własnej cewek AB i CD mostkiem LCR
(częstotliwość źródła napięcia wewnętrznego f = 1 kHz). Dla cewki CD na rdzeniu
ferromagnetycznym pomiary należy wykonać w funkcji położenia na rdzeniu.

Cewki

powietrzne

Cewki na rdzeniu

ferromagnetycznym

L

AB

L

CD

L

AB

d

L

CD

[mH]

[mH]

[mH]

[mm]

[mH]

0,07

0,142

0,556

0

1,28

5

1,335

10

1,364

15

1,344

20

1,281

25

1,164

30

1,084

2.2. Pomiar indukcyjności własnej cewek powietrznych i cewek na rdzeniu

ferromagnetycznym

2.2.1.Schemat połączeń

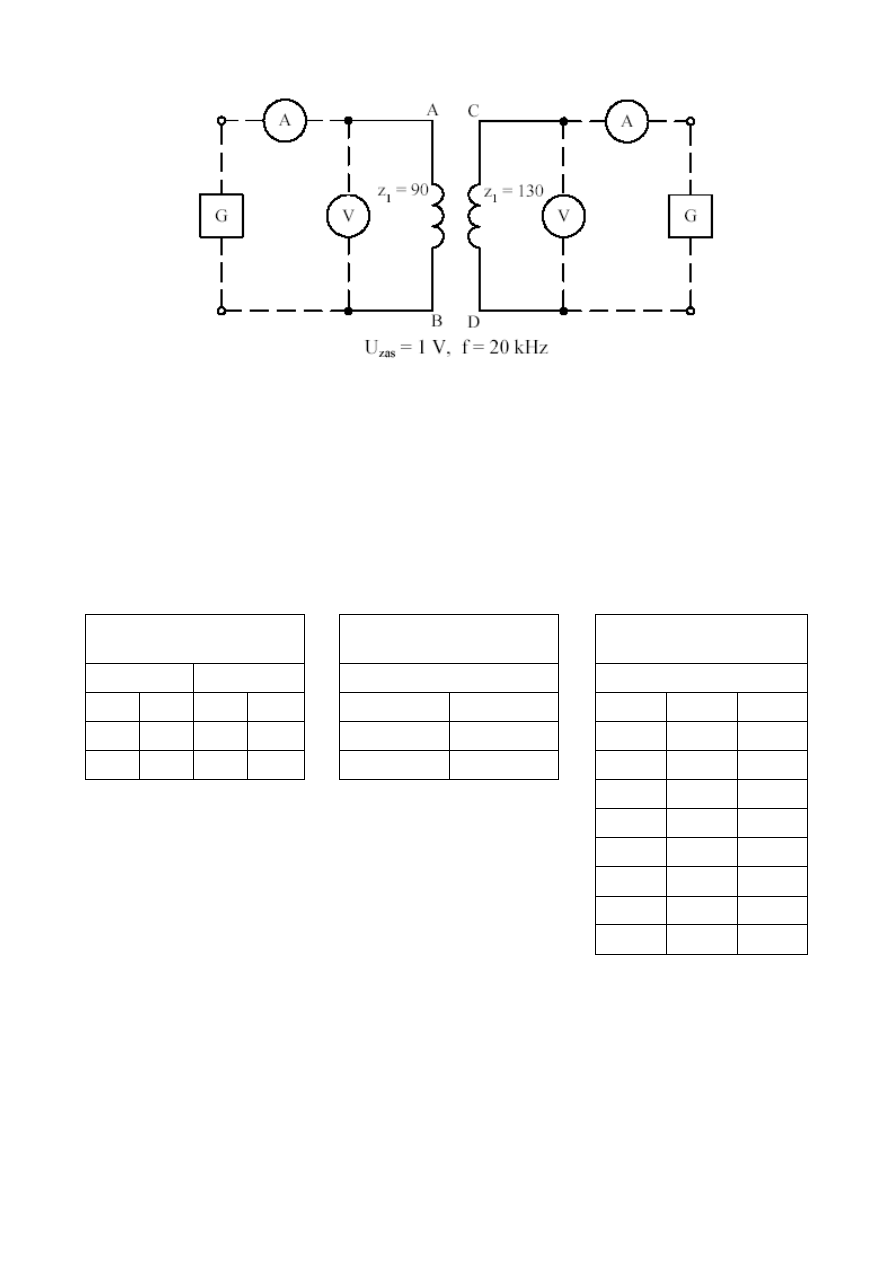
2.2.2.Zestawić układ przedstawiony w punkcie 2.2.1

Dokonać pomiarów U i I zasilając z generatora napięcia sinusoidalnie zmiennego przy
częstotliwości f = 20 kHz i napięciu ok. 1 V kolejno cewki powietrzne AB i CD w ich skrajnym
położeniu oraz cewkę na rdzeniu ferromagnetycznym AB (skrajne dolne położenie). Dla cewki CD
wykonać pomiary U, I w funkcji położenia na rdzeniu, a wyniki zapisać w odpowiednich tabelach
a, b, c.
a) b) c)

Cewki

powietrzne

Cewki na rdzeniu

ferromagnetycznym

Cewki na rdzeniu

ferromagnetycznym

AB

CD

AB

CD

U

AB

I

AB

U

CD

I

CD

U

AB

I

AB

U

CD

I

CD

d

[V]

[mA]

[V]

[mA]

1,02 119,4 1,004 56,84

[V]

[mA]

1,006

15,31

[V]

[mA]

[mm]

1,009

6,492

0

1,016

6,234

5

1,019

6,157

10

1,019

6,23

15

1,014

6,42

20

1,004
0,981

6,842
7,626

25
30

2.3. Pomiar indukcyjności wzajemnej cewek powietrznych i cewek na rdzeniu
ferromagnetycznym w funkcji odległości przy f = 20 kHz

2.3.1. Cewki powietrzne

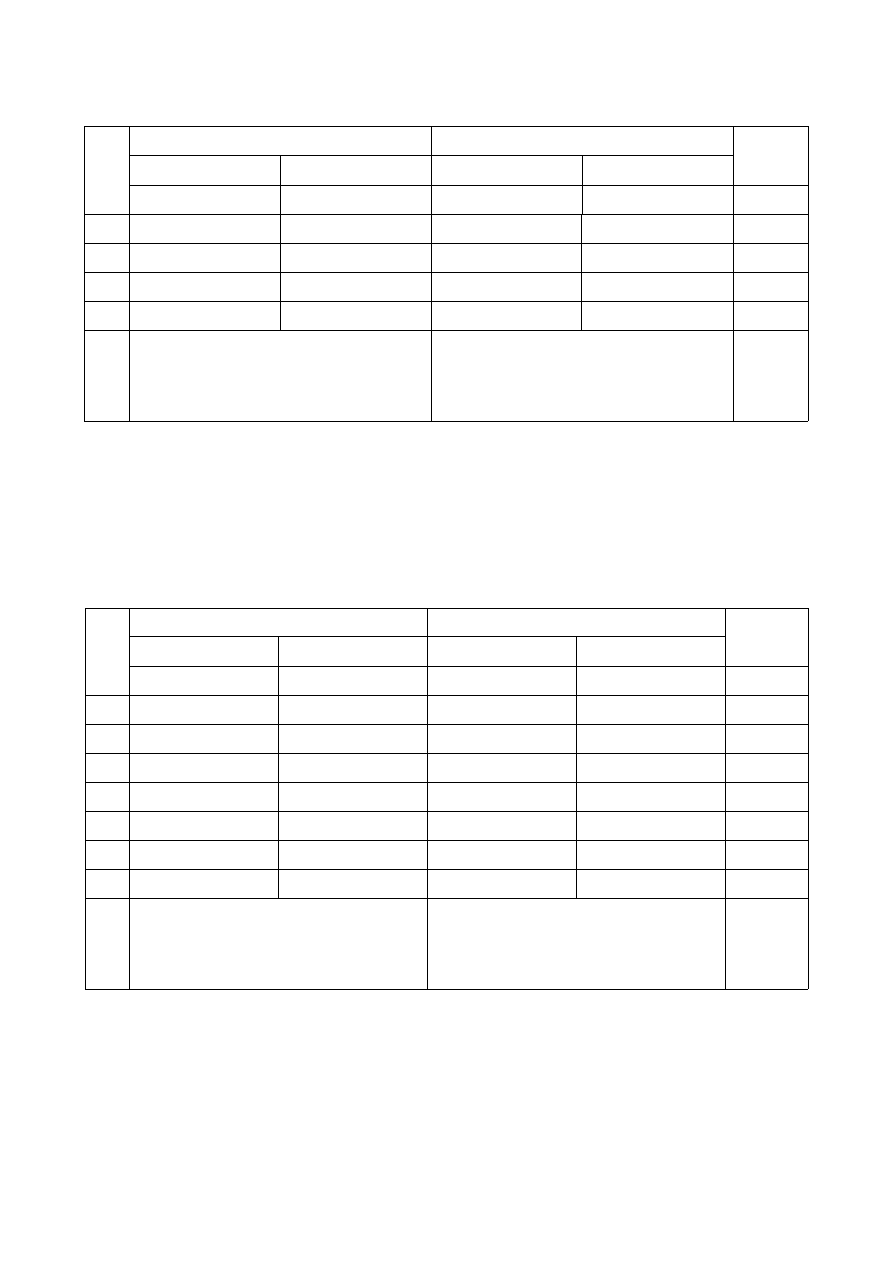
Zestawić odpowiednio układ pomiarowy wg schematu z pkt. 2.2.1, a wyniki pomiarów zamieścić w
tabeli.

Lp

Cewka AB

U

CD

I

AB

[V]

[mA]

Cewka CD

U

AB

I

CD

[V]

[mA]

d

[mm]

1

240

116,08

126,9

55,8

0

2

50

116,07

42,2

55,96

5

3

6

116,03

13,6

56,05

10

4

2,6

116,08

5,16

56,08

15

Zasilana jest cewka AB, która

położona jest w dolnym

skrajnym położeniu, oddalamy

cewkę CD

Zasilana jest cewka CD, która

położona jest w dolnym

skrajnym położeniu, oddalamy

cewkę AB

2.3.2. Cewki na rdzeniu ferromagnetycznym

Zestawić odpowiednio układ pomiarowy wg schematu z pkt. 2.2.1, a wyniki pomiarów zamieścić w
tabeli.

Lp

Cewka AB

U

CD

I

AB

[V]

[mA]

Cewka CD

U

AB

I

CD

[V]

[mA]

d

[mm]

1

1,07

15

0,451

6,36

0

2

0,89

15

0,333

6,07

5

3

0,746

15

0,278

6,03

10

4

0,616

15

0,254

6,09

15

5

0,507

15

0,211

6,36

20

6

0,396

15

0,189

6,71

25

7

0,310

15

0,162

7,44

30

Zasilana jest cewka AB, która

położona jest w dolnym

skrajnym położeniu, oddalamy

cewkę CD

Zasilana jest cewka CD, która

położona jest w dolnym

skrajnym położeniu, oddalamy

cewkę AB

2.4. Wyznaczanie zacisków jednakoimiennych cewek sprzężonych magnetycznie

2.4.1. Układ pomiarowy
a) b)

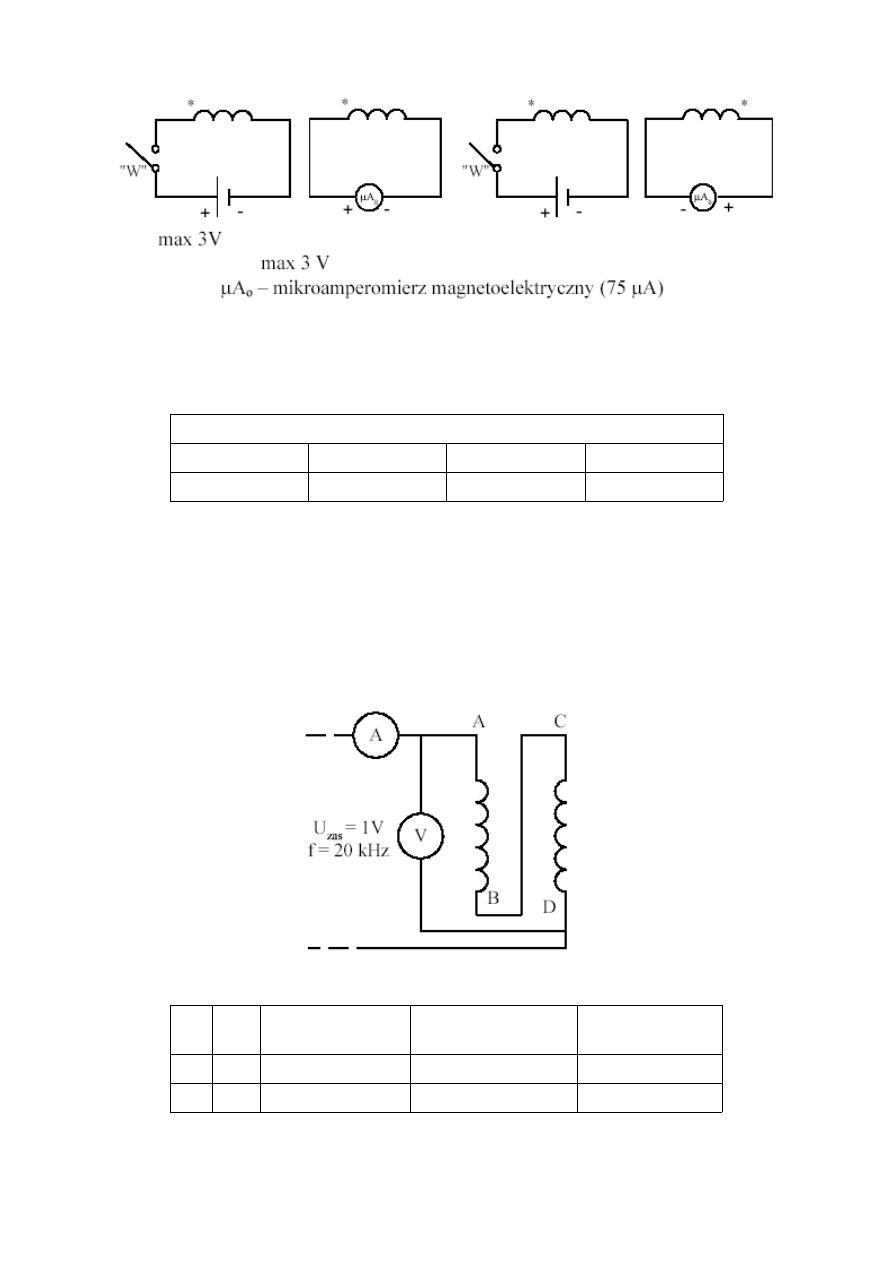
Po zamknięciu wyłącznika „W” obserwować kierunek wychylenia woltomierza, aby określić
zaciski jednakoimienne.

2.4.2. Tabela oznaczeń
Na podstawie wykonanych obserwacji w tabeli zanotować zaciski jednakoimienne.

Cewki

A

B

C

D

*

*

2.5. Wyznaczanie indukcyjności zastępczej cewek połączonych szeregowo i równolegle przy
magnesowaniu zgodnym, przeciwnym i braku sprzężenia

2.5.1. Połączenie szeregowe

a) Układ pomiarowy
Wykorzystując układ z pkt. 2.2.1 połączyć cewki AB, CD szeregowo wg schematu przy
magnesowaniu zgodnym, przeciwnym (maksymalne sprzężenie) i braku sprzężenia.

b) Tabela pomiarów

Maksymalne

sprzężenie zgodne

Maksymalne

sprzężenie przeciwne

Brak sprzężenia

U

[V]

1,039

1,007

1,028

I

[mA]

2,753

13,99

39,06

2.5.2. Połączenie równoległe

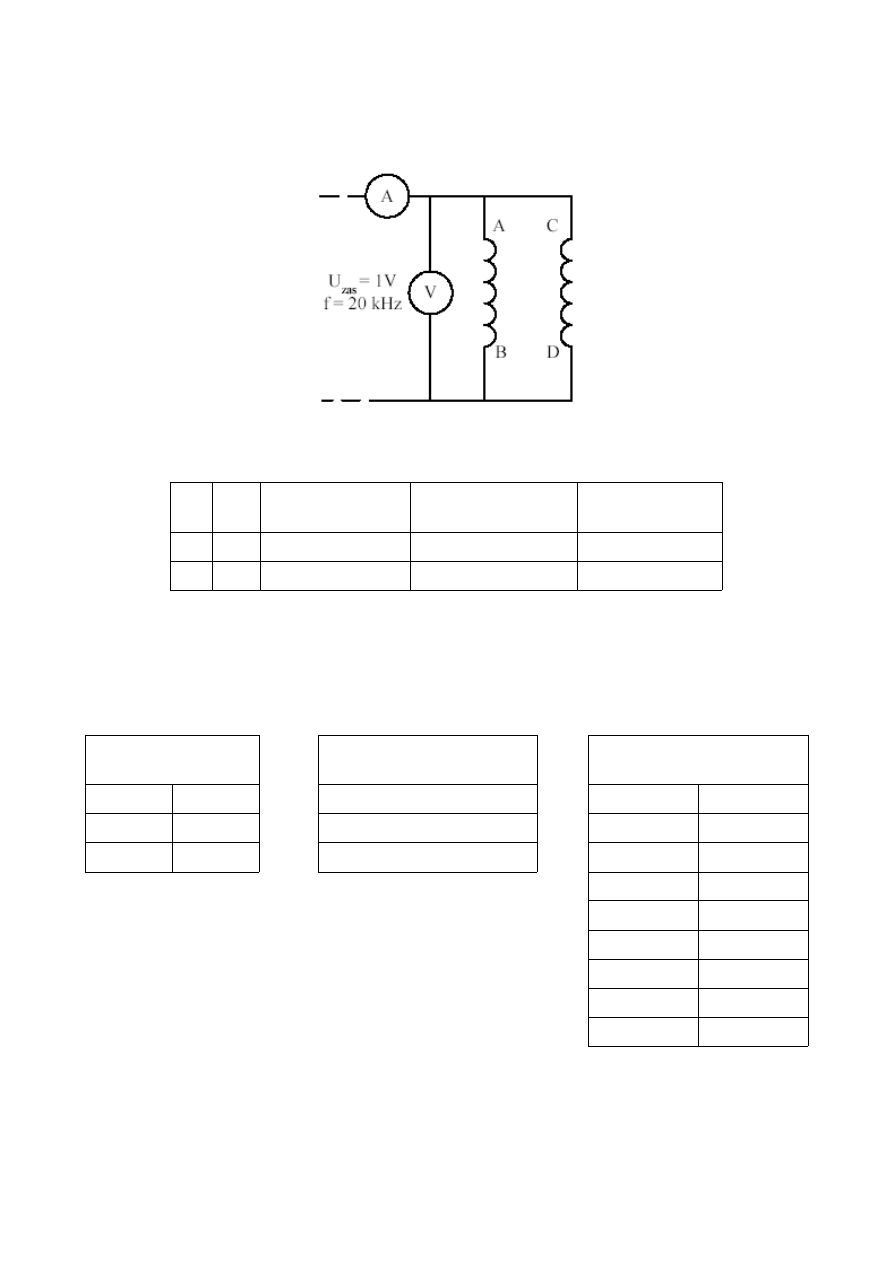
a) Układ pomiarowy
Wykorzystując układ z pkt. 2.2.1 połączyć cewki AB, CD równolegle wg schematu przy
magnesowaniu zgodnym, przeciwnym (maksymalne sprzężenie) i braku sprzężenia.

b) Tabela pomiarów

Maksymalne

sprzężenie zgodne

Maksymalne

sprzężenie przeciwne

Brak sprzężenia

U

[V]

1,012

1,01

0,754

I

[mA]

15,62

74,58

130,95

3. Obliczenia

Na podstawie uzyskanych pomiarów należy obliczyć:
a) Indukcyjności własne cewek powietrznych i cewek na rdzeniu ferromagnetycznym (pkt. 2.2.2).
Wyniki obliczeń zamieścić w tabelach

Cewki

powietrzne

Cewki na rdzeniu

ferromagnetycznym AB

Cewki na rdzeniu

ferromagnetycznym CD

L

AB

L

CD

L

AB

L

CD

d

[µH]

[µH]

[µH]

[µH]

[mm]

66,7

138,8

522,7

1237

0

1297

5

1317

10

1301

15

1257

20

1168
1024

25
30

Przykłądowe obliczenia:

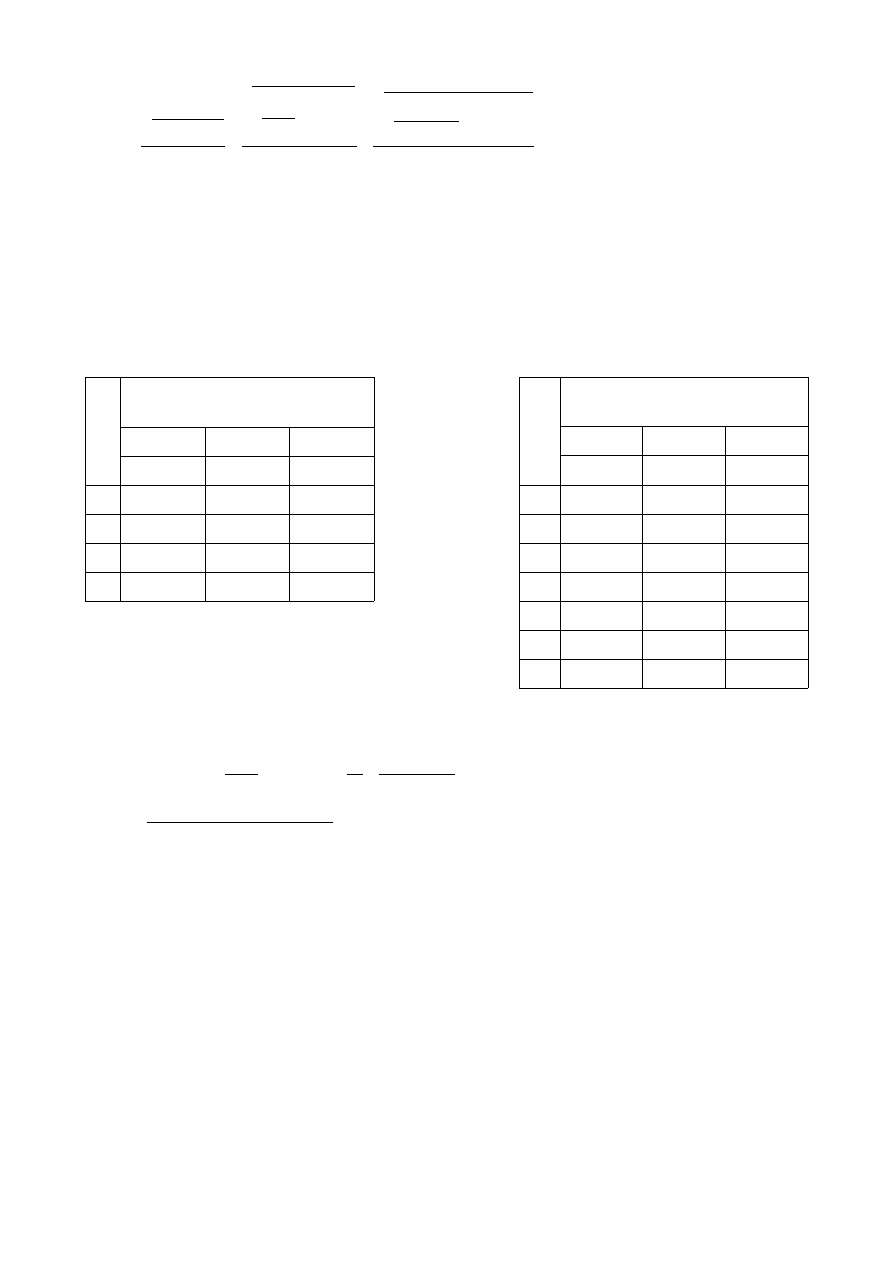
L

CD

=



Z

CD

2

−

R

CD

2

2 ⋅⋅f

=





U

CD

I

CD



2

−

R

CD

2

2 ⋅⋅f

=





1,004

0,05684



2

−

2,28

2

2 ⋅⋅20000

=

0,0001388 =138,8  F

Wyniki otrzymane z obliczeń są bardzo zbliżone do wartości zmierzonych mostkiem pomiarowym.
Niewielkie rozbieżności między pomiarami i wynikami z obliczeń są spowodowane
niedokładnościąa pomiarów, stratami na łączeniach i przewodach, małymi błędami ustawienia
częstitliwości.

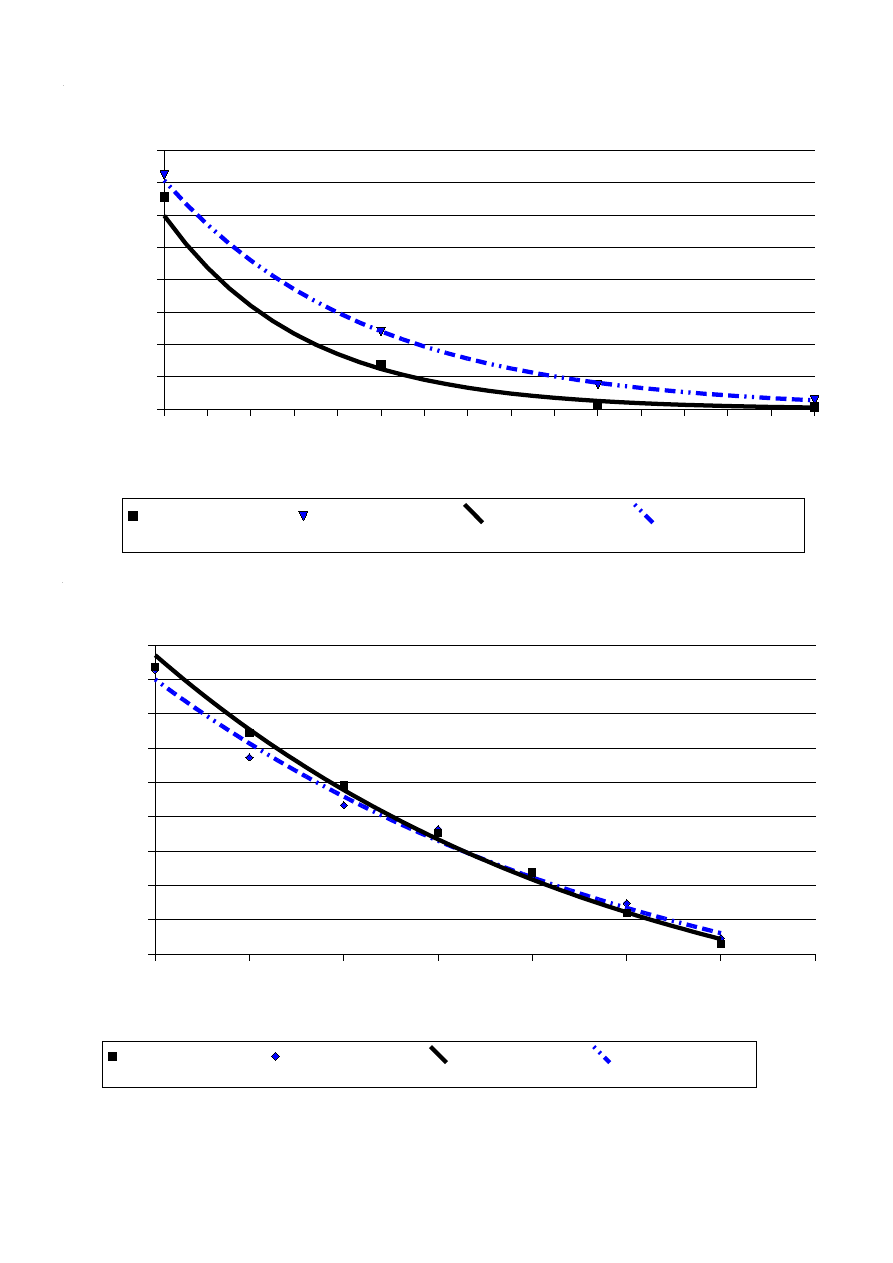
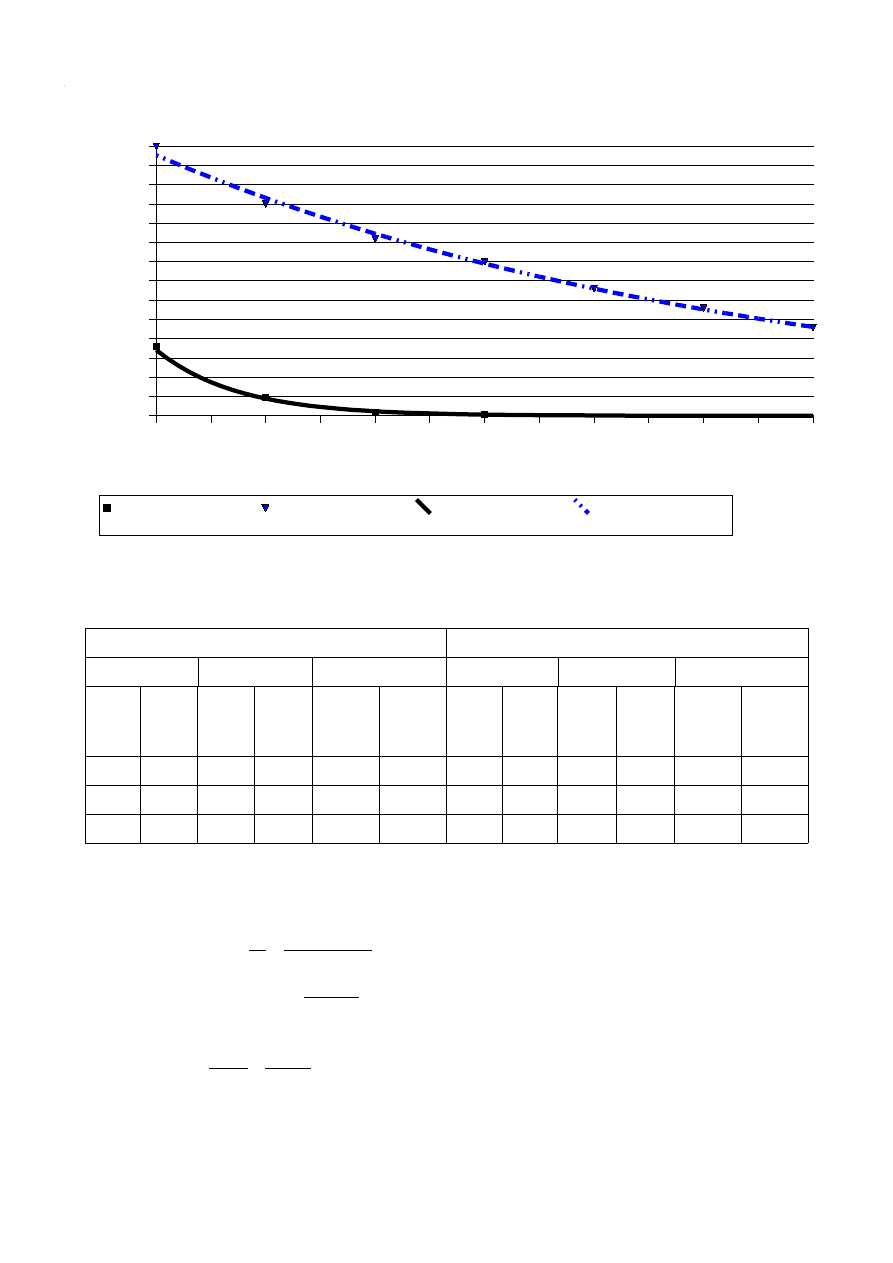
b) Indukcyjności wzajemne cewek powietrznych i na rdzeniu ferromagnetycznym (pomiary w pkt.
2.3.1 i 2.3.2 ) i narysować wykresy M

12

, M

21

= f(d).

Lp

Cewki powietrzne

d

M

12

M

21

[mm]

[µH]

[µH]

Lp

Cewki na rdzeniu

ferromagnetycznym

d

M

12

M

21

[mm]

[µH]

[µH]

1

0

16,4

18,1

1

0

567,6

564,3

2

5

3,43

6

2

5

472,2

436,6

3

10

0,41

1,93

3

10

395,8

366,9

4

15

0,18

0,73

4

15

326,8

331,9

5

20

268,9

264,1

6

25

210,1

224,1

7

30

164,5

173,3

Przykładowe obliczenia:

X

M

=

Z =

U

CD

I

AB

M

12

=

Z



=

U

CD

I

AB

⋅

2  f

M

12

=

240 ⋅10

−

3

116,08 ⋅10

−

3

⋅

2  20000

=

0,0000164 =16,4  H

c) Obliczyć współczynnik sprzężenia magnetycznego k cewek powietrznych i cewek na rdzeniu

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

0

2,5

5

7,5

10

12,5

15

17,5

20

Cewki powietrzne M12, M21 = f(d)

M12

M21

Regresja wy-
kładnicza, M12

Regresja wy-
kładnicza, M21

d

M

[

u

H

]

0

5

10

15

20

25

30

35

150

200

250

300

350

400

450

500

550

600

Cewki ferromagnetyczne M12, M21 = f(d)

M12

M21

Regresja wykład-
nicza, M12

Regresja wykład-
nicza, M21

d [mm]

M

[u

H

]

ferromagnetycznym, oraz określić jakiego rodzaju jest to sprzężenie. Narysować wykresy k = f(d)

Lp

Cewki powietrzne

d

k

[mm]

-

Rodzaj

sprzężenia

Lp

Cewki na rdzeniu

ferromagnetycznym

d

k

[mm]

-

Rodzaj

sprzężenia

1

0

0,18

Silne

1

0

0,7

B. mocne

2

5

0,047

Słabe

2

5

0,55

Mocne

3

10

0,009

Słabe

3

10

0,46

Mocne

4

15

0,0036

B. słabe

4

15

0,4

Mocne

5

20

0,33

Mocne

6

25

0,28

Mocne

7

30

0,23

Mocne

Przykładowe obliczenia dla cewek powietrznych:

k

1

=

M

12



L

AB

⋅

L

CD

=

16,4 ⋅10

−

6



66,7 ⋅10

−

6

⋅

138,8 ⋅10

−

6

=

0,17

k

2

=

M

21



L

AB

⋅

L

CD

=

18,1 ⋅10

−

6



66,7 ⋅10

−

6

⋅

138,8 ⋅10

−

6

=

0,19

k =



k

1

⋅

k

2

=



0,17 ⋅0,19=0,18

Przykładowe obliczenia dla cewek na rdzeniu ferromagnetycznym dla d=0:

k

1

=

M

12



L

AB

⋅

L

CD

=

567,6 ⋅10

−

6



522,7 ⋅10

−

6

⋅

1237 ⋅10

−

6

=

0,71

k

2

=

M

21



L

AB

⋅

L

CD

=

564,3 ⋅10

−

6



522,7 ⋅10

−

6

⋅

1237 ⋅10

−

6

=

0,7

k =



k

1

⋅

k

2

=



0,17 ⋅0,19=0,7

d) Indukcyjność zastępczą cewek połączonych szeregowo i równolegle (2.5.1 i 2.5.2)

Połączenie szeregowe

Połączenie równoległe

zgodne

przeciwne

brak sprzężenia

zgodne

przeciwne

brak sprzężenia

z
pomia
rów

spraw

dzenie

z

pomia

rów

spraw

dzenie

z

pomiar

ów

sprawd

zenie

z

pomia

rów

spraw

dzenie

z

pomia

rów

spraw

dzenie

z

pomiar

ów

sprawd

zenie

Lzas

L’zas

Lzas

L’zas

Lzas

L’zas

Lzas L’zas

Lzas

L’zas

Lzas

L’zas

[µH]

[µH]

[µH]

[µH]

[µH]

[µH]

[µH]

[µH]

[µH]

[µH]

[µH]

[µH]

3003

2892

572

628

208

205

515

520

103

113

33,5

45

Indukcyjność zastępcza cewek połączonych szeregowo zgodnie:

R=R

AB



R

CD

=

1,65 2,28 =3,93 

Z=

U

I

=

1,039

2,753 ⋅10

−

3

=

377 

X

Lzas

=



Z

2

−

R

2

=

377,4

L zas=

X

Lzas



=

377,4

2  f

=

3003  H

f =20kHz

L ' zas=L

AB



L

CD



2M=522,7 1237 2 ⋅565,95 =2892  H

Indukcyjność zastępcza cewek połączonych szeregowo przeciwnie:

0

2,5

5

7,5

10

12,5

15

17,5

20

22,5

25

27,5

30

0

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

0,5

0,55

0,6

0,65

0,7

k = f(d)

Powietrze

Ferromagnetyk

Regresja wykładnicza,
Powietrze

Regresja wykładnicza,
Ferromagnetyk

d[mm]

k

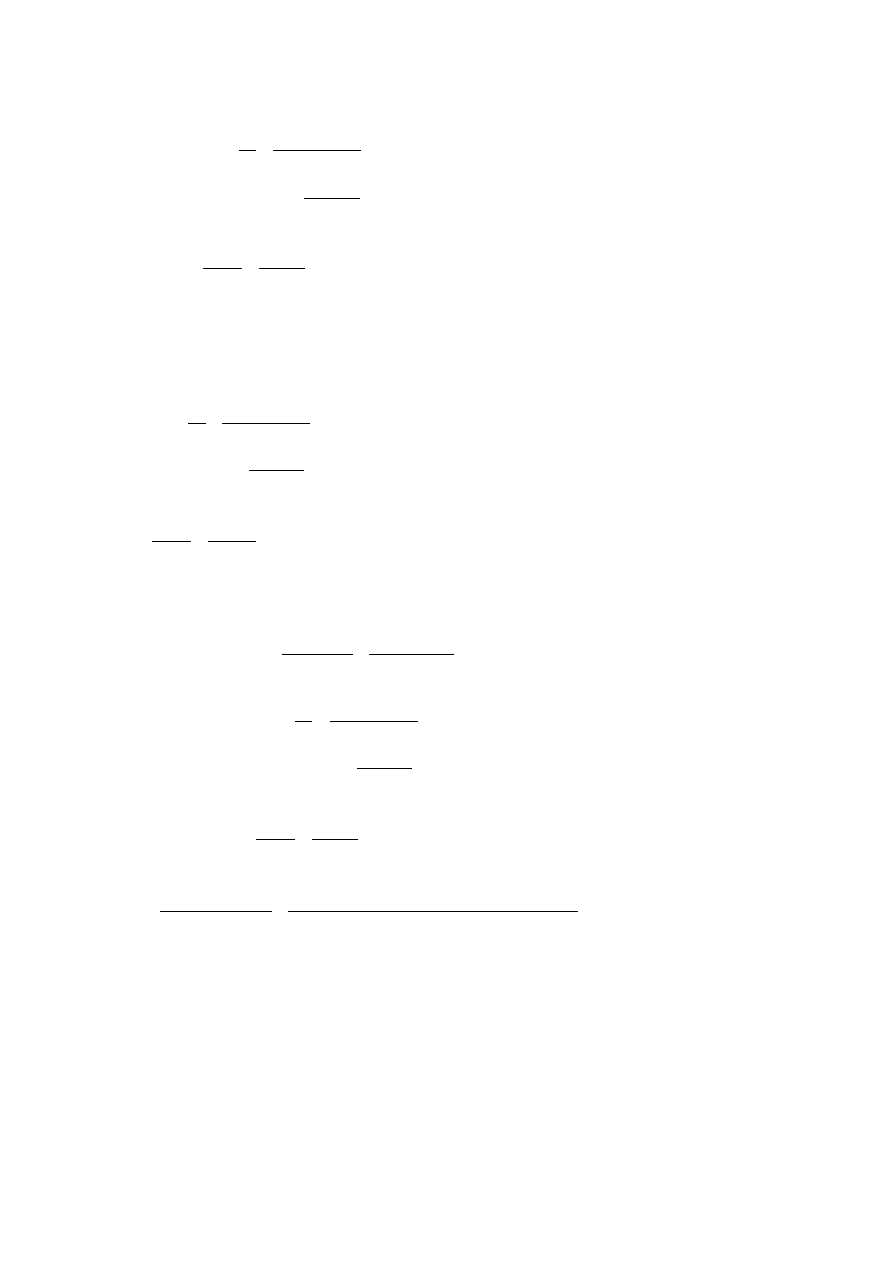
R=R

AB



R

CD

=

1,65 2,28 =3,93 

Z =

U

I

=

1,01

13,99 ⋅10

−

3

=

71,98 

X

Lzas

=



Z

2

−

R

2

=

71,9

L zas=

X

Lzas



=

71,9

2  f

=

571,9  H

f =20kHz

L ' zas=L

AB



L

CD

−

2M=522,7 1237 −2 ⋅565,95 =628  H

Indukcyjność zastępcza cewek połączonych szeregowo bez sprzężenia:

R=R

AB



R

CD

=

1,65 2,28 =3,93 

Z =

U

I

=

1,03

39,06 ⋅10

−

3

=

26,32 

X

Lzas

=



Z

2

−

R

2

=

26,02

L zas=

X

Lzas



=

26,02

2  f

=

207,9  H

f =20kHz

L ' zas=L

AB



L

CD

=

66,7 138,8 =205,5  H

Indukcyjność zastępcza cewek połączonych równolegle zgodnie:

R=

R

AB

⋅

R

CD

R

AB



R

CD

=

1,65 ⋅2,28

1,65 2,28

=

1 

Z =

U

I

=

1,01

15,62 ⋅10

−

3

=

64,8 

X

Lzas

=



Z

2

−

R

2

=

64,7

L zas=

X

Lzas



=

64,7

2  f

=

514,6  H

f =20kHz

L ' zas=

L

AB

⋅

L

CD

−

M

2

L

AB



L

CD

−

2M

=

523 ⋅10

−

6

⋅

1237 ⋅10

−

6

−

566 ⋅10

−

6



2

523 ⋅10

−

6



1237 ⋅10

−

6

−

2 566 ⋅10

−

6



=

520  H

Indukcyjność zastępcza cewek połączonych równolegle przeciwnie:

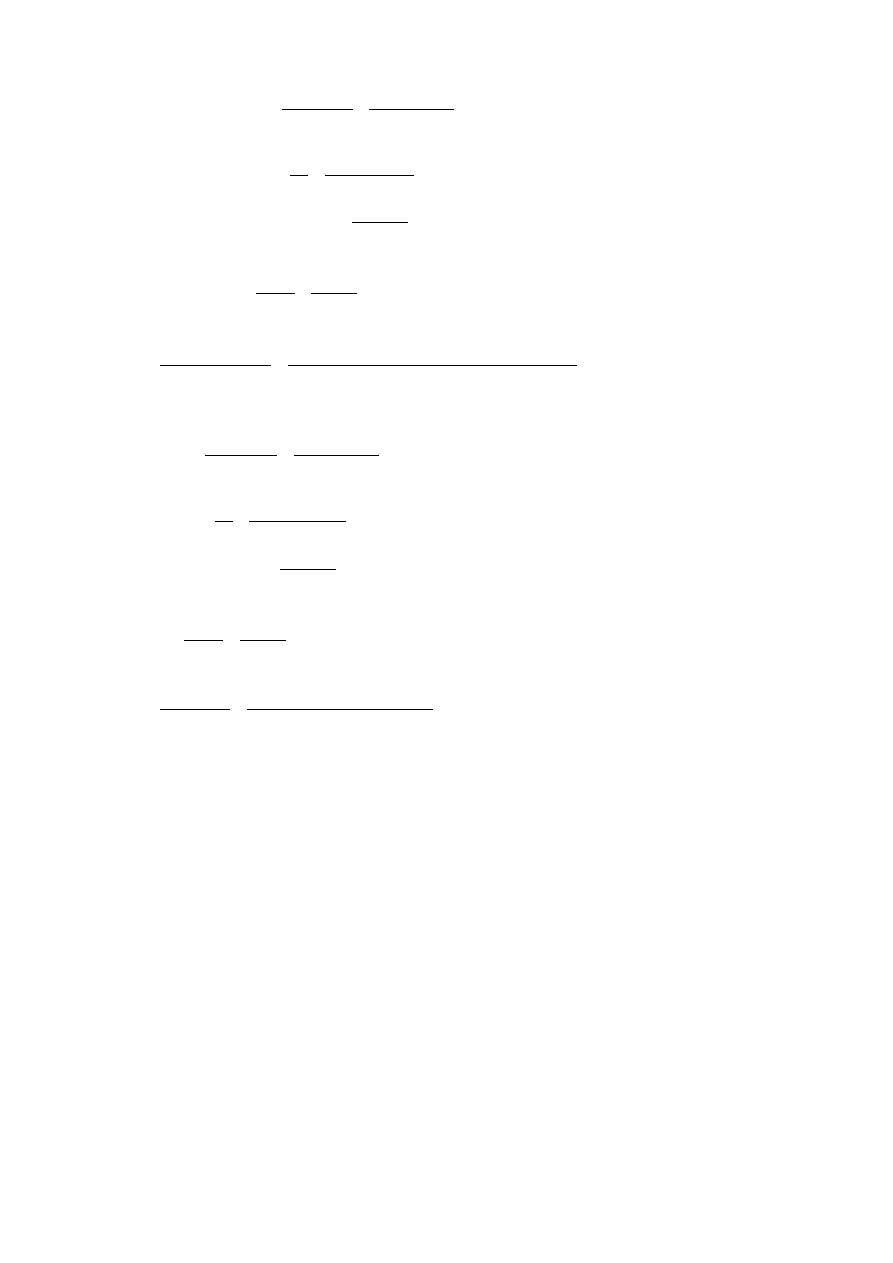
R=

R

AB

⋅

R

CD

R

AB



R

CD

=

1,65 ⋅2,28

1,65 2,28

=

1 

Z=

U

I

=

1,01

74,58 ⋅10

−

3

=

13,54 

X

Lzas

=



Z

2

−

R

2

=

12,96

L zas=

X

Lzas



=

12,96

2  f

=

103,1  H

f =20kHz

L ' zas=

L

AB

⋅

L

CD

−

M

2

L

AB



L

CD



2M

=

523 ⋅10

−

6

⋅

1237 ⋅10

−

6

−

566 ⋅10

−

6



2

523 ⋅10

−

6



1237 ⋅10

−

6



2 566 ⋅10

−

6



=

113  H

Indukcyjność zastępcza cewek połączonych równolegle bez sprzężenia:

R=

R

AB

⋅

R

CD

R

AB



R

CD

=

1,65 ⋅2,28

1,65 2,28

=

1 

Z =

U

I

=

0,75

130,95 ⋅10

−

3

=

5,76 

X

Lzas

=



Z

2

−

R

2

=

4,21

L zas=

X

Lzas



=

4,21

2  f

=

33,5  H

f =20kHz

L ' zas=

L

AB

⋅

L

CD

L

AB



L

CD

=

66,7 ⋅10

−

6

⋅

138,8 ⋅10

−

6

66,7 ⋅10

−

6



138,8 ⋅10

−

6

=

45  H

4. Uwagi końcowe i wnioski
Z obliczeń indukcyjności własnej cewek możemy wywnioskować, że w cewkach z rdzeniem
ferromagntycznym ich indukcyjność własna maleje wraz ze wzrostem odległości. Indukcyjność
wzajemna cewek zarówno powietrznych jak i na rdzeniu ferromagntycznym również maleje wraz
ze wzrostem odległości między nimi. Można zauważyć, że w cewkach powietrzynch indukcja
wzajemna zanika przy dużo mniejszej odległości niż w przypadku cewek na rdzeniu. Podobna
sytuacja zachodzi w przypadku współczynnika sprzężenia magnetycznego. Ostatnim parametrem
jaki badaliśmy była indukcyjność zastępcza dla połączenia seregowego i równoległego dwóch
cewek Do pomiarów maksymalnych sprzężeń używaliśmy cewek na rdzeniu ferromagnetycznym
położonych jak najbliżej siebie,natomiast przy braku sprzężeń cewek powietrzynch maksymalnie
oddalonych od siebie. Wyniki otrzymane z pomiarów są bardzo zbliżone do wartości
wyznaczonych na podstawie obliczeń. Otrzymane wyniki i przebiegi wszystkich charakterystyk
wskazują na poprawne wykonanie ćwiczenia. Wszystkie niedokładności i odchylenia od
książkowych przykładów i teorii spowodowane mogą być niedokładnością przyrządów
pomiarowych, nieuwzględnienia rezystancji przewodów oraz małymi błędami przy nastawianiu
częstotliwości.

5. Parametry i dane znamionowe zastosowanych urządzeń i mierników
- multimetr BM857 x3

- generator FG-506
- płytka “obwody sprzężone magnetycznie” x2
- miliamperomierz
- mostek techniczny Thomsona
- mostek LCR
- generator PS 3005

6. Literatura
1. Atabiekow G., Teoria liniowych obwodów elektrycznych, WNT, Warszawa 1964.
2. Bolkowski S., Elektrotechnika teoretyczna, Wyd. 6, WNT, Warszawa 2001.
3. Cholewicki T., Elektrotechnika teoretyczna t. 1 WNT, Warszawa 1973.
4. Krakowski M., Elektrotechnika teoretyczna t. 1, PWN, Warszawa 1995.
5. Kurdziel R., Podstawy elektrotechniki, WNT, Warszawa 1972.