1
Beata Jędrys
doradca metodyczny matematyki
PCDZN Puławy
KONSPEKT LEKCJI OTWARTEJ Z MATEMATYKI
w klasie II gimnazjum
Temat: Przed nami powtórki materiału – działania na potęgach
i pierwiastkach
Cele ogólne:
rozwijanie umiejętności czytania ze zrozumieniem tekstu
matematycznego
nauczanie dobrej organizacji pracy, systematyczności, wytrwałości
i pracowitości
przyzwyczajanie ucznia do korzystania z definicji i twierdzeo
nabycie sprawności wykonywania obliczeo na liczbach wymiernych,
potęgach i pierwiastkach,
Cele szczegółowe:
Uczeo:
oblicza potęgi liczb i pierwiastki liczb;
zapisuje w postaci jednej potęgi: iloczyny i ilorazy potęg o takich samych
podstawach, iloczyny i ilorazy potęg o takich samych wykładnikach oraz
potęgę potęgi (przy wykładnikach naturalnych);
zamienia potęgi o wykładnikach całkowitych ujemnych na odpowiednie
potęgi o wykładnikach naturalnych;
2
stosuje własności potęg i pierwiastków przy obliczaniu wartości wyrażeo
arytmetycznych;
zbiera i analizuje informacje zawarte w tekście oraz rozwiązuje zadania
z treścią.
Metody nauczania – eksponująca, burza mózgów, dwiczeniowa
Formy pracy na lekcji – indywidualna, grupowa, zbiorowa
Środki dydaktyczne – plansze pomocnicze, załączniki do lekcji, przygotowane
zadania dla uczniów
Przebieg lekcji:
A. Część wstępna
1. Powitanie uczestników lekcji.
2. Wstępna organizacja i przygotowanie do lekcji.
3. Powtórzenie wiadomości dotyczących własności działao na potęgach
i pierwiastkach.
- uczniowie na przygotowanym przez nauczyciela arkuszu papieru
wypisują znane im definicje dotyczące potęg i pierwiastków oraz
własności działao na nich
B. Część podstawowa
1. Podanie tematu lekcji.
2. Zapoznanie uczniów z celem lekcji.
3. Uczniowie analizują treśd zadania przygotowanego przez nauczyciela
(załącznik 1) – wydrukowane zadanie wisi na tablicy. Jeden z uczniów
przedstawia sposób rozwiązania i formułuje wniosek. Nauczyciel
3
koryguje w razie potrzeby odpowiedź ucznia, czuwa nad poprawnością
języka matematycznego.
4. Każdy uczeo otrzymuje inne zadanie do rozwiązania – każdemu
otrzymanemu wynikowi jest przyporządkowana odpowiednia litera
(karta pracy z przykładami dla uczniów – załącznik 2) oraz jednakowy
szablon z zaszyfrowanym hasłem (szablon do hasła – załącznik 3).
Uczniowie rozwiązują otrzymane zadanie w zeszytach, następnie wybrani
uczniowie przedstawiają rozwiązania na tablicy i swoją literkę wpisują
w tabeli wiszącej na tablicy pod odpowiednim wynikiem. Wspólna praca
owocuje odczytaniem hasła:
„Dajcie mi punkt podparcia, a sam jeden poruszę z posad Ziemię”
Nauczyciel podaje, że powyższa myśl jest autorstwa Archimedesa.
5. Dwójka uczniów przedstawia przygotowane przez nich informacje z życia
Archimedesa (krótki życiorys, osiągnięcia, anegdoty, portret uczonego).
6. Uczniowie zapoznają się z treścią zadania (załącznik 4). Na podstawie
tekstu źródłowego analizują w parach zadanie a następnie jeden
z uczniów omawia sposób rozwiązania i przedstawia go na tablicy.
C. Część końcowa
1. Podsumowanie pracy na lekcji, ocena aktywności uczniów.
2. Refleksje uczniów po zakooczonej lekcji.
Załącznik 1
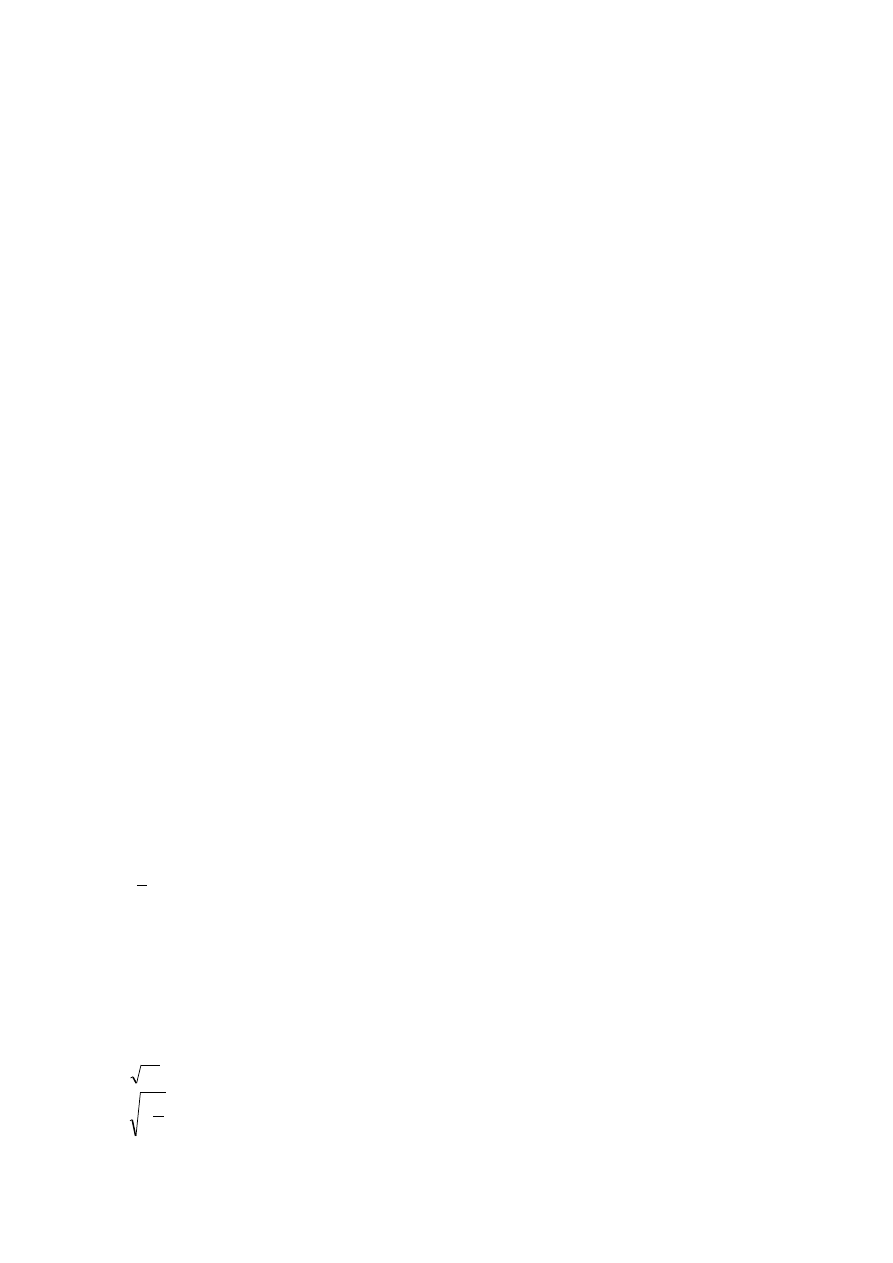
4
Na gałązce świerku każdego roku wyrastają z jednego pąka 3 nowe pędy
zakooczone pąkiem. Ile pąków będzie miała po siedmiu latach świerkowa
gałązka, która wyrosła z jednego pąka?
A) 3 * 7;
B) 3 + 7
C) 7
3
;
D) 3
7
.
Załącznik 2
Zapisz w postaci potęgi:
D. 3*3*3*3 =
A. 7
4
*7
3
=
J. 5
11
: 5
7
=
C. (4
2
)
3
=
Oblicz:
I. 3
2
=
E. (-2)
4
=
M. 2
-3
=
P. (
6
5
)
-2
=
Zapisz w postaci potęgi i oblicz:
U. (-0,2)
7
*5
7
=
N. (4
5
: 4
-2
)*(4
-2
)
3
=
Znajdź pierwiastki kwadratowe i sześcienne z liczb:
K.
36
=
T.
4
1
2
=
5
O.
3
8
=
Usuo niewymiernośd z mianownika:
R.
3
3
2
=
Wyłącz czynnik przed znak pierwiastka:
S.
20
=
Z.
3
24
=
Ę. Znajdź liczbę dodatnią, której podwojony kwadrat jest równy 200.
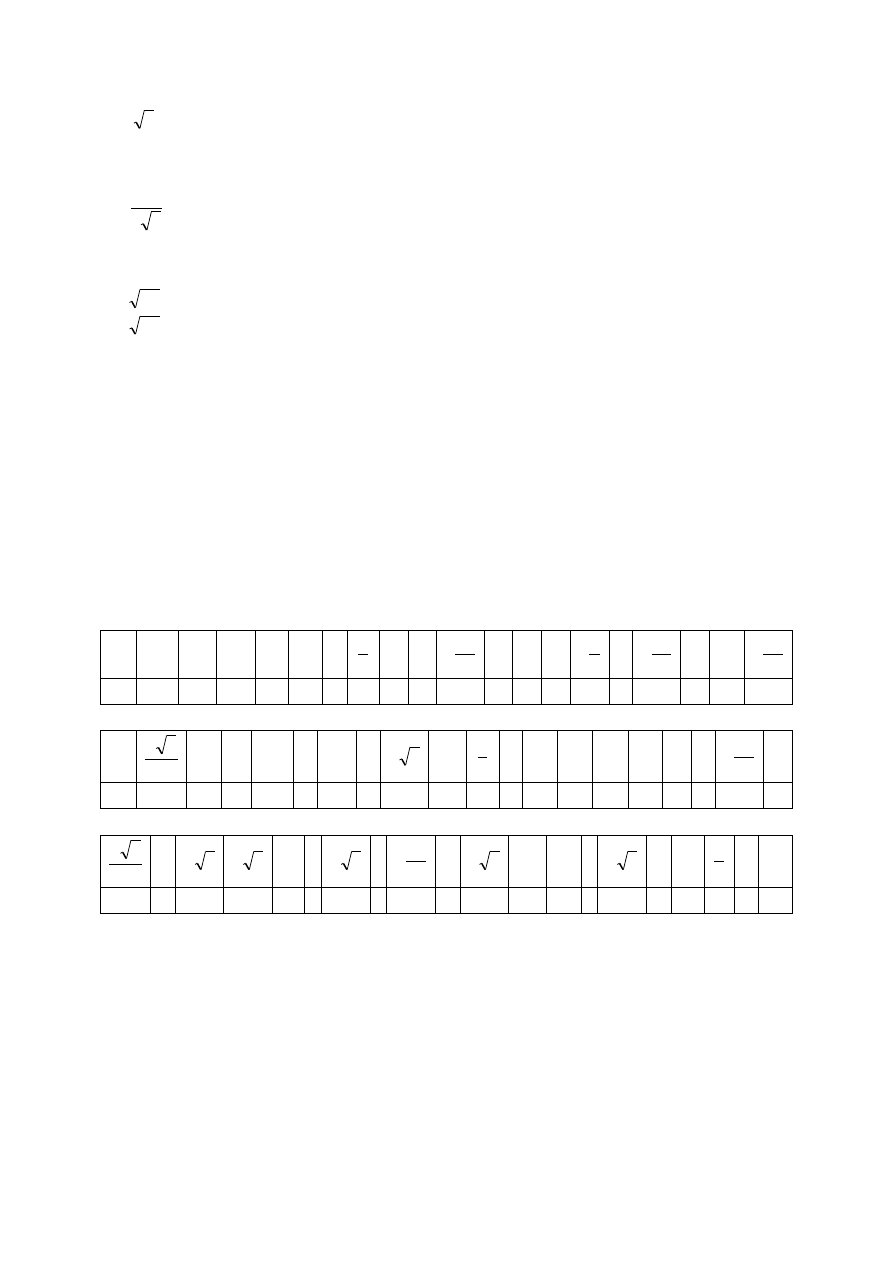
Załącznik 3
SZABLON DO HASŁA Z SZYFREM
3
4
7
7
5
4
4
6
9 16
8
1
9 1
25
11
-1 4 6 1
2
1
1
25
11
2 3
4
1
25
11
7
7
3
3
2
4
6
9 7
7
7
7
2
5
7
7
8
1
5
4
16 3
4
16 4 1
25
11
2
3
3
2
-
1
2
5
2
3
3
10 2
3
3
1
25
11
2 2
5
7
7
3
4
2
3
3
9 16
8
1
9 10
Załącznik 4
Zadanie 3
Przeczytaj poniższy tekst:
6
„Wielkimi liczbami posługiwała się już Archimedes. Oprócz znanej
Grekom liczby miriada (10000) wprowadził liczbę miriada miriad. W swoim
dziele „Rachmistrz piasku” szacował, ile ziaren piasku jest na plaży. Obliczał
także, ile ziaren piasku wypełniłoby wszechświat. Wynik, jaki otrzymał
Archimedes, dzisiaj zapisalibyśmy jako 10
52
.”
Odpowiedz na pytanie: Do jakiej potęgi należy podnieśd liczbę miriada, aby
otrzymad liczbę 10
52
?