Zakład Podstaw Elektrotechniki i Informatyki

METODY NUMERYCZNE – PROJEKT

Częś

ć

Temat

1/2

Interpolacja wielomianowa Lagrange’a

Opracowali

Rok / gr. lab.

Data wyk. ćw.

1. Paweł Lewicki

2. Piotr Lembryk

1EF-DI / L08

14.05.2012

Streszczenie

Praca przedstawia omówienie interpolacji wielomianowej, nazywanej interpolacją Lagrange’a

wraz z przedstawieniem jej implementacji w języku Turbo Pascal, której działanie zostało następnie
porównane z funkcją „polyfit” programu GNU Octave . Dobór przykładów nie jest przypadkowy i ma
na celu uwypuklenie cech charakterystycznych obu metod, zamieszczonych kolejno we wnioskach.

1.Interpolacja Lagrange’a

Interpolacja wielomianowa, nazywana też interpolacją Lagrange'a, od nazwiska pioniera badań

nad interpolacją Josepha Lagrange'a, lub po prostu interpolacją jest metodą numeryczną przybliżania
funkcji tzw. wielomianem Lagrange'a stopnia n, przyjmującym w n+1 punktach, zwanych węzłami
interpolacji wartości takie same jak przybliżana funkcja.

Interpolacja jest często stosowana w naukach doświadczalnych, gdzie dysponuje się zazwyczaj

skończoną liczbą danych do określenia zależności między wielkościami.

Zgodnie z twierdzeniem Weierstrassa dowolną funkcję y=f(x) ciągłą na przedziale domkniętym

można dowolnie przybliżyć za pomocą wielomianu odpowiednio wysokiego stopnia.

Interpolacja liniowa

Jest przypadkiem interpolacji wielomianowej dla dwóch punktów pomiarowych

i

, dla

których można utworzyć funkcję liniową, której wykres przechodzi przez punkty

i

.

Ogólna metoda

Metoda interpolacji polega na:

wybraniu

punktów

należących do dziedziny , dla których

znane są wartości

znalezieniu wielomianu

stopnia co najwyżej takiego, że

.

Interpretacja geometryczna – dla danych

punktów na wykresie szuka się wielomianu

stopnia co najwyżej , którego wykres przechodzi przez dane punkty

Znajdowanie odpowiedniego wielomianu

Wielomian przyjmujący zadane wartości w konkretnych punktach można zbudować w ten
sposób:

Dla pierwszego węzła o wartości

znajduje się wielomian, który w tym punkcie

przyjmuje wartość

, a w pozostałych węzłach

wartość zero.

Dla kolejnego węzła znajduje sie podobny wielomian, który w drugim węźle
przyjmuje wartość

, a w pozostałych węzłach

wartość zero.

Dodaje się wartość ostatnio obliczonego wielomianu do wartości poprzedniego

Dla każdego z pozostałych węzłów znajduje się podobny wielomian, za każdym
razem dodając go do wielomianu wynikowego

Wielomian będący sumą wielomianów obliczonych dla poszczególnych węzłów jest
wielomianem interpolującym

Dowód ostatniego punktu i dokładny sposób tworzenia poszczególnych wielomianów opisany
jest poniżej w dowodzie istnienia wielomianu interpolującego będącego podstawą algorytmu
odnajdowania tego wielomianu.

Dowód istnienia wielomianu interpolującego

Niech

będą węzłami interpolacji funkcji takimi, że znane są wartości

Można zdefiniować funkcję:

,

taką, że dla

jest wielomianem stopnia (mianownik jest

liczbą, a licznik iloczynem wyrazów postaci

)

Gdy

i

:

Gdy

i

:

(licznik = 0 ponieważ występuje element

)

Niech

będzie wielomianem stopnia co najwyżej , określonym jako:

Dla

Wszystkie składniki sumy o indeksach różnych od są równe zeru (ponieważ dla

, składnik o indeksie jest równy:

.

A więc

z czego wynika, że

jest wielomianem interpolującym funkcję

w punktach

.

2.Implementacje w języku Turbo Pascal

2.1 Interaktywny program

Poniżej znajduje się kod programu wykorzystującego funkcję „lagrange.pas” daną w
ramach materiałów pomocniczych projektu użytą w prostym programie interaktywnym:

program zastosowanie_funkcji_lagrange_interaktywny;
function Lagrange (n : Integer;
var x,f : array of Extended;
xx : Extended;
var st : Integer) : Extended;
var i,k : Integer;
fx,p : Extended;
begin
if n<0
then st:=1
else begin
st:=0;
if n>0
then begin
i:=-1;
repeat
i:=i+1;
for k:=i+1 to n do
if x[i]=x[k]
then st:=2
until (i=n-1) or (st=2)
end;
if st=0
then begin
fx:=0;
for i:=0 to n do
begin
p:=1;
for k:=0 to n do
if k<>i then p:=p*(xx-x[k])/(x[i]-x[k]);
fx:=fx+f[i]*p
end;
Lagrange:=fx
end
end
end;
var
global_n, global_st: integer;
global_x, global_f: array[1..20] of Extended;

global_xx: Extended;

i: Integer;

begin
write('podaj liczbe wezlow n : '); readln(global_n);
writeln('podaj ',global_n,' par "wezel wartosc_funkcji" oddzielonych enterem');
for i:=1 to global_n do readln(global_x[i], global_f[i]);
writeln;
writeln('teraz dla kazdego danego x podana zostanie wartosc wielomianu interpolacyjnego, x=100 -> KONIEC');
repeat
read(global_xx);
writeln(Lagrange(global_n, global_x, global_f, global_xx, global_st));
until global_xx = 100;
end.

Przykładowe działanie:

podaj liczbe wezlow n : 5
podaj 5 par "wezel wartosc_funkcji" oddzielonych enterem
1 2
3 3.3
4 2.55
5 7.2
7 11

teraz dla kazdego danego x podana zostanie wartosc wielomianu interpolacyjnego,x=100 -> KONIEC
1
2.0000000000000000E+0000
3
3.3000000000000000E+0000
4
2.5500000000000000E+0000
4.5
4.0669921875000000E+0000
5
7.2000000000000000E+0000
5.6
1.2327380266666667E+0001
8
-4.4166666666666667E+0001
10
-6.1435000000000000E+0002
55
-2.3604310085714286E+0007
100
-5.3809269796428571E+0008

2.2 Program „automatyczny”, wypisujący wartości interpolującego wielomianu dla

zadanego przedziału z zadaną rozdzielczością:

program zastosowanie_funkcji_lagrange_automatyczny;
function Lagrange (n : Integer;
var x,f : array of Extended;
xx : Extended;
var st : Integer) : Extended;
var i,k : Integer;
fx,p : Extended;
begin
if n<0
then st:=1
else begin
st:=0;
if n>0
then begin
i:=-1;
repeat
i:=i+1;
for k:=i+1 to n do
if x[i]=x[k]
then st:=2
until (i=n-1) or (st=2)
end;
if st=0
then begin
fx:=0;

for i:=0 to n do
begin
p:=1;
for k:=0 to n do
if k<>i then p:=p*(xx-x[k])/(x[i]-x[k]);
fx:=fx+f[i]*p
end;
Lagrange:=fx
end
end
end;
var
global_x, global_f: array[1..20] of Extended;
global_xx, global_n, global_st, i: integer;
j, rozdzielczosc: extended;
begin
write('podaj liczbe wezlow n : '); readln(global_n);
writeln('podaj ',global_n,' par "wezel wartosc_funkcji" oddzielonych enterem');
for i:=1 to global_n do readln(global_x[i], global_f[i]);
writeln;
j:=global_x[1]-3;
rozdzielczosc:=0.1;
repeat
writeln(j:5:2,' ', Lagrange(global_n, global_x, global_f, j, global_st):8:5);
j:=j + rozdzielczosc;
until j>global_x[global_n]+3 ;
end.

Przykładowe działanie(dla zakresu <pierwszy_węzeł-3;ostatni_węzeł+3) i rozdzielczości 0.1 ustalonych w
kodzie:

podaj liczbe wezlow n : 4
podaj 4 par "wezel wartosc_funkcji" oddzielonych enterem
2 4.54
3 8.543
8 -2
10 15

-1.00 7.43341
-0.90 6.17306
-0.80 5.04376
-0.70 4.03923
-0.60 3.15333
-0.50 2.38002
-0.40 1.71340
-0.30 1.14768
-0.20 0.67721
-0.10 0.29646
0.00 -0.00000
0.10 -0.21744
0.20 -0.36102
0.30 -0.43579
0.40 -0.44666
0.50 -0.39842
0.60 -0.29573
0.70 -0.14315
0.80 0.05492
0.90 0.29418
1.00 0.57045
1.10 0.87969
1.20 1.21798
1.30 1.58151
1.40 1.96661
1.50 2.36973
1.60 2.78745
1.70 3.21645
1.80 3.65356
1.90 4.09572
2.00 4.54000
2.10 4.98359
2.20 5.42382
2.30 5.85811
2.40 6.28403
2.50 6.69927
2.60 7.10164
2.70 7.48908

2.80 7.85964
2.90 8.21151
3.00 8.54300
3.10 8.85253
3.20 9.13867
3.30 9.40009
3.40 9.63559
3.50 9.84410
3.60 10.02467
3.70 10.17648
3.80 10.29882
3.90 10.39111
4.00 10.45291
4.10 10.48389
4.20 10.48383
4.30 10.45265
4.40 10.39040
4.50 10.29724
4.60 10.17347
4.70 10.01949
4.80 9.83584
4.90 9.62319
5.00 9.38232
5.10 9.11414
5.20 8.81968
5.30 8.50010
5.40 8.15669
5.50 7.79084
5.60 7.40408
5.70 6.99807
5.80 6.57459
5.90 6.13553
6.00 5.68291
6.10 5.21890
6.20 4.74576
6.30 4.26588
6.40 3.78179
6.50 3.29613
6.60 2.81167
6.70 2.33130
6.80 1.85803
6.90 1.39501
7.00 0.94550
7.10 0.51289
7.20 0.10068
7.30 -0.28748
7.40 -0.64784
7.50 -0.97651
7.60 -1.26949
7.70 -1.52265
7.80 -1.73172
7.90 -1.89234
8.00 -2.00000
8.10 -2.05007
8.20 -2.03780
8.30 -1.95832
8.40 -1.80663
8.50 -1.57761
8.60 -1.26601
8.70 -0.86646
8.80 -0.37346
8.90 0.21859
9.00 0.91545
9.10 1.72298
9.20 2.64716
9.30 3.69412
9.40 4.87009
9.50 6.18143
9.60 7.63462
9.70 9.23628
9.80 10.99314
9.90 12.91205
10.00 15.00000
10.10 17.26409
10.20 19.71155
10.30 22.34974

10.40 25.18612
10.50 28.22830
10.60 31.48401
10.70 34.96109
10.80 38.66752
10.90 42.61139
11.00 46.80091
11.10 51.24445
11.20 55.95045
11.30 60.92752
11.40 66.18438
11.50 71.72985
11.60 77.57290
11.70 83.72263
11.80 90.18824
11.90 96.97907
12.00 104.10457
12.10 111.57434
12.20 119.39807
12.30 127.58560
12.40 136.14688
12.50 145.09199
12.60 154.43114
12.70 164.17465
12.80 174.33297
12.90 184.91667

3. Zestawienie z działaniem funkcji „polyfit”

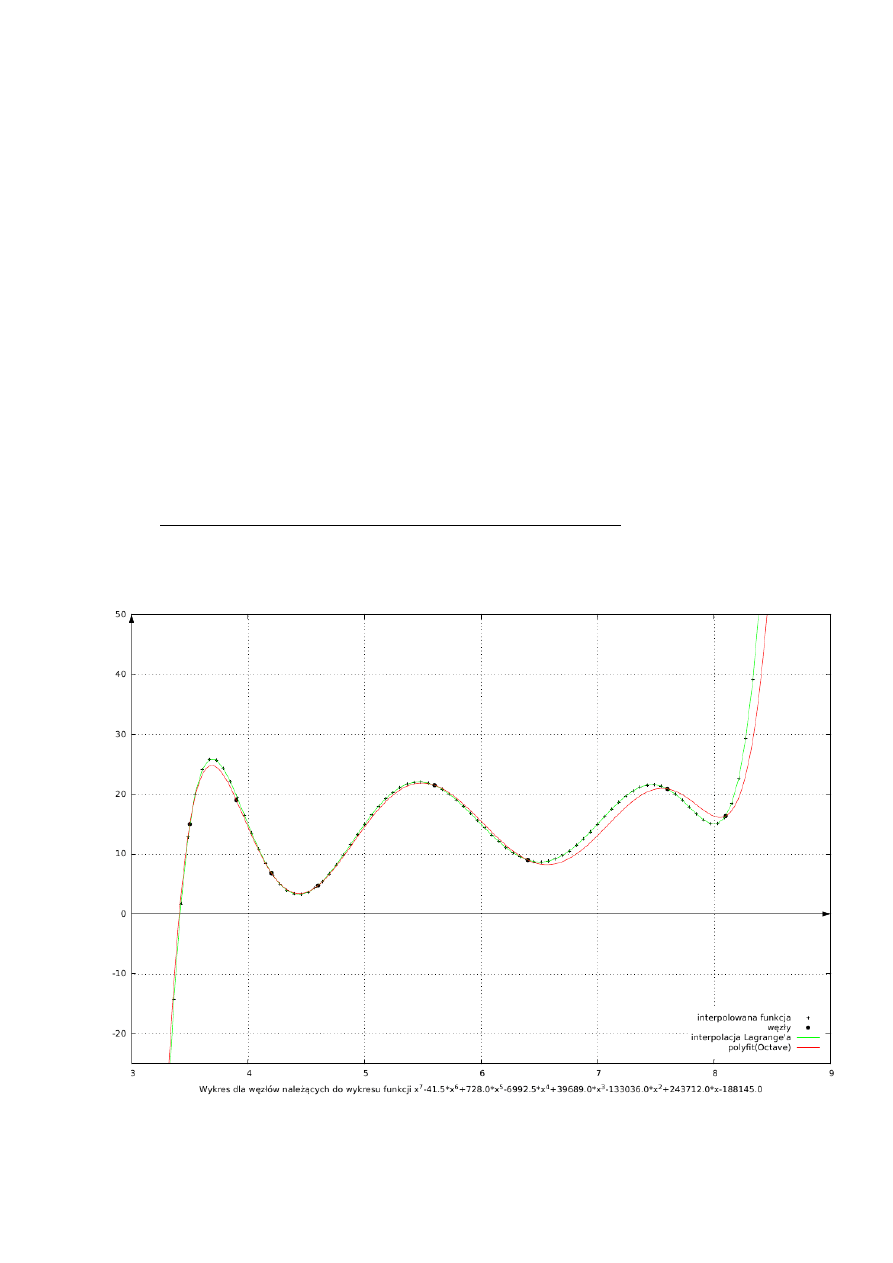
3.1 Osiem węzłów należących do wykresu funkcji x^7-41,5x^6+728x^5-

6992,5x^4+39689x^3-133036x^2+243712x-188145

n=7
węzły:

x[0]=3,5 x[1]=3,9 x[2]=4,2

x[3]=4,6

x[4]=5,6

x[5]=6,4 x[6]=7,6

x[7]=8,1

f[0]=15 f[1]=19 f[2]=6,8489 f[3]=4,7458 f[4]=21,503 f[5]=9,0135 f[6]=20,895 f[7]=16,35

wynik lagrange: funkcja wyjściowa będąca wielomianem(z założenia)
wynik polyfit: 0.85307x^7-35.623x^6+628.58x^5-6070.9x^4+34633x^3-116630x^2+214540x-
166230

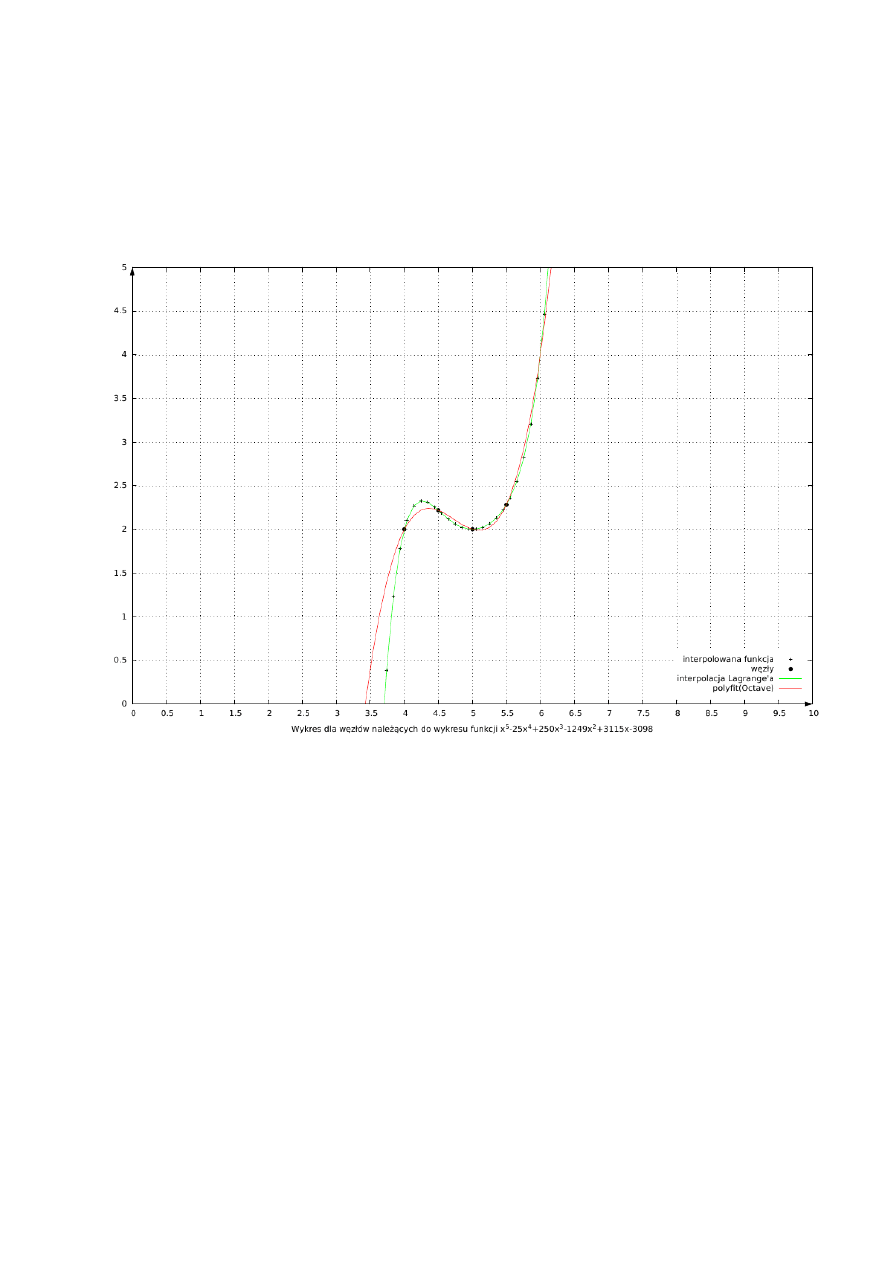
3.2 Cztery węzły należące do funkcji: x^5-25x^4+250x^3-1249x^2+3115x-3098

n=3
węzły:
x[0]=4

x[1]=4,5

x[2]=5 x[3]=5,5

f[0]=2

f[1]=2,21875 f[2]=2 f[3]=2,28125

funkcja: x^5-25x^4+250x^3-1249x^2+3115x-3098
lagrange: funkcja wyjściowa będąca wielomianem(z założenia)
polyfit: 1,25x^3-17,75x^2+83,5x-128

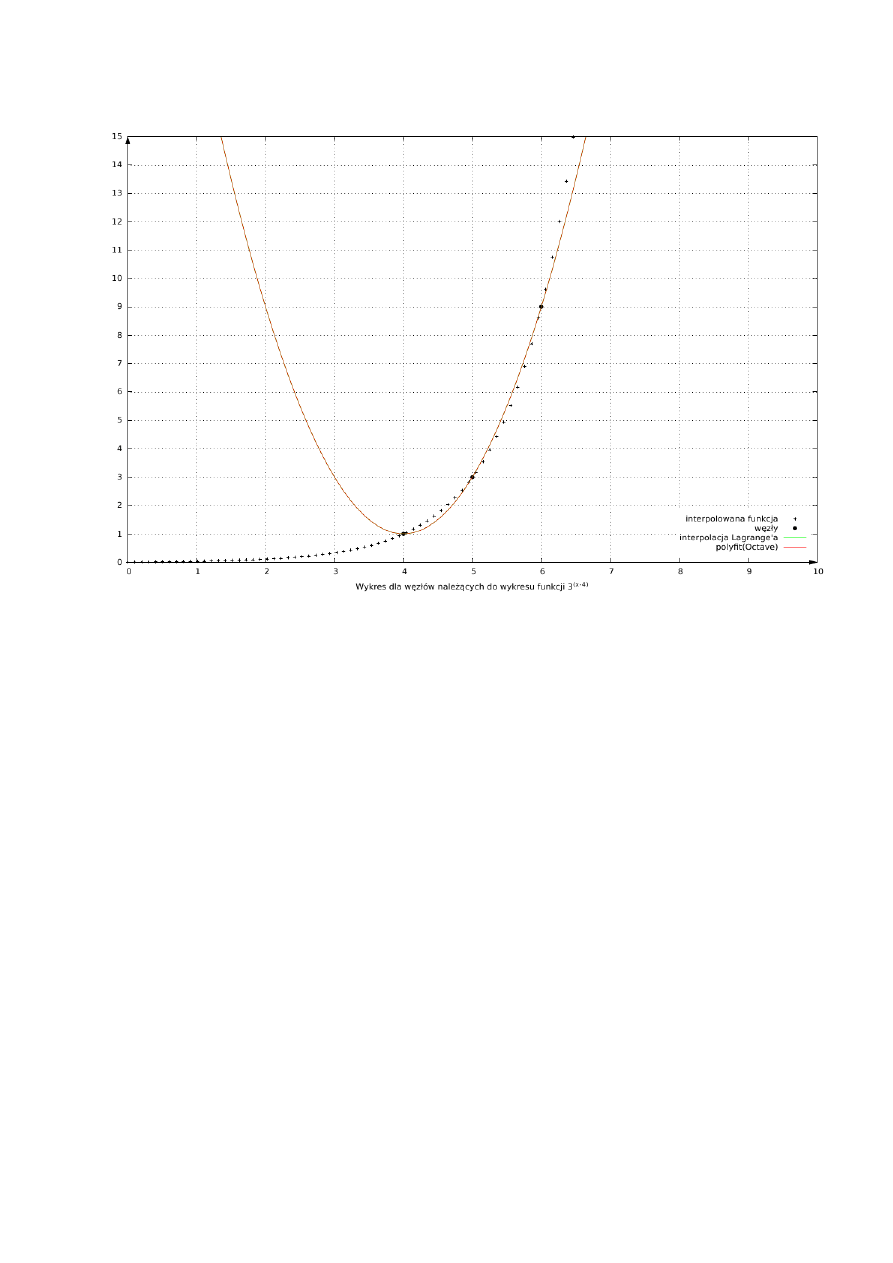
3.3 Trzy węzły należące do wykresu funkcji 3^(x-4)

n=2
węzły:
x[0]=4 x[1]=5 x[2]=6
f[0]=1 f[1]=3 f[2]=9
funkcja: 3^(x-4)
lagrange:

2x^2-16x+33

polyfit:

2x^2-16x+33

komentarz:

- wykresy interpolacji polyfit i lagrange nakładają się na siebie
- jak wydać wielomian nie przybliża przebiegu danej funkcji dla x<4

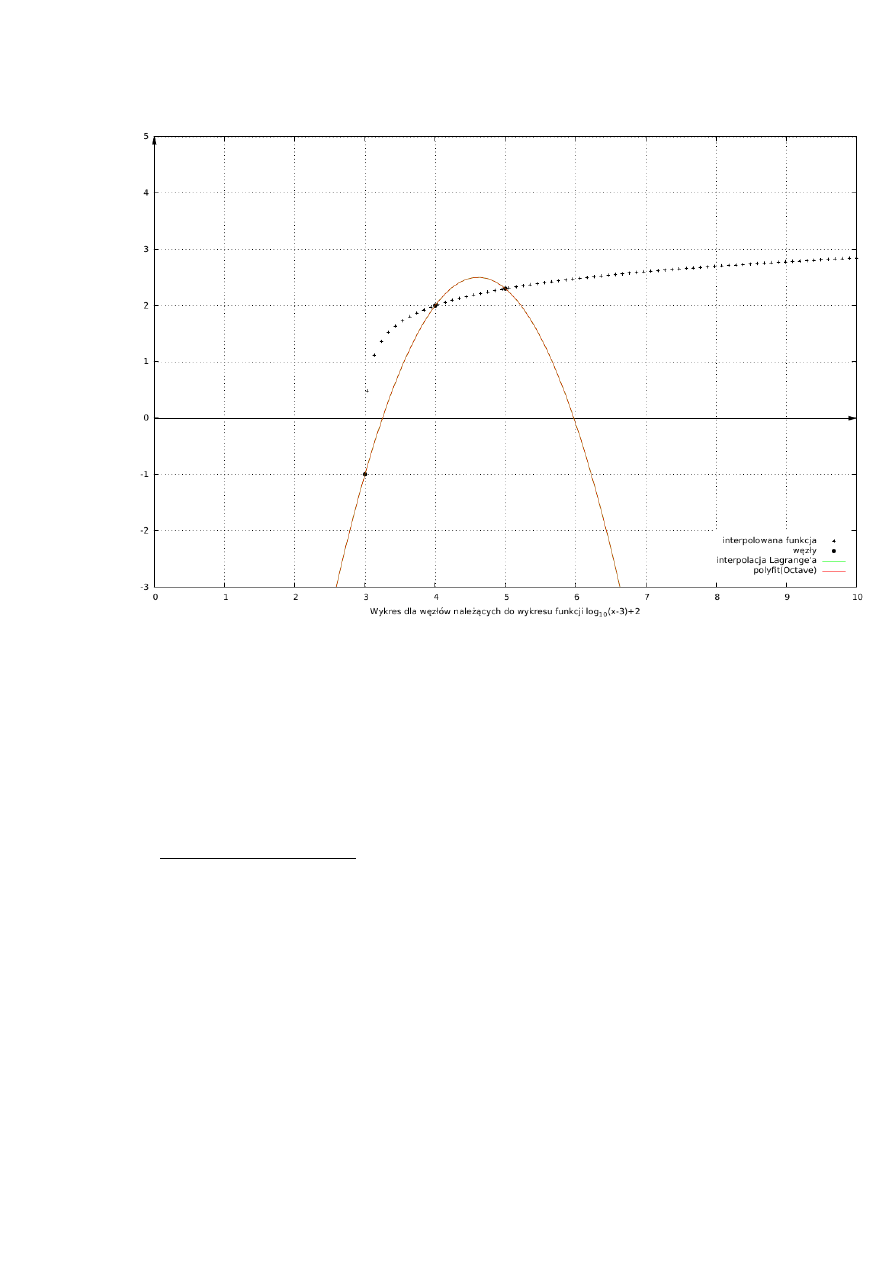
4.4 Trzy węzły należące do wykresu funkcji log10(x-3)+2

n=2
węzły:
x[0]=2,999 x[1]=4 x[2]=5
f[0]=-1

f[1]=2,301

f[2]=2,47712

funkcja: log10(x-3)+2
polyfit: -1,3473x^2+12,4269x-26,1505
lagrange: prawie ta sama co polyfit ( z różnica na 5 miejscu miejscu rozwinięcia dziesiętnego)
komentarz: wykresy interpolacji polyfit i lagrange nakładają się na siebie

4. Wnioski końcowe

- funkcja „lagrange” interpoluje wielomianem który dla punktów węzłowych przyjmuje dokładnie
wartości funkcji interpolowanej, jest nawet w stanie odwzorować całą funkcję interpolowaną o ile
jest ona wielomianem stopnia n+1 gdzie n to liczba węzłów
- przetwarzanie z poziomu kodu Pascala jest szybsze od interpretowanego w Octave
- wraz ze wzrostem stopnia interpolowanego wielomianu błąd rośnie w wypadku Octave
- procedury interpolacji charakteryzujące się mniejszym błędem są zwykle obliczeniowo bardziej
kosztowne
- podobnie ceną dokładności interpolacji metody lagrange’a jest jej złożoność obliczeniowa
- w wypadku interpolacji lagrange'a o ile format zmiennych nie ogranicza precyzji obliczeń błąd
dla węzłów jest zerowy
- lepiej było użyć dużych liczb by uwidocznić błędy, lub ukazując ja jako względne
- algorytm z którego korzysta funkcja polyfit to "metoda najmniejszych kwadratów"

- metoda najmniejszych kwadratów w przeciwieństwie do lagrange’a nie wskazuje najmniejszego
stopnia wielomianu potrzebnego by przeciąć wszystkie wezly, gdyz jej założeniem jest możliwie
dokładne ustalenie wielomianu o stopniu s<=n
- dokładność procedury polyfit zależy jednocześnie od rozmieszczenia punktów węzłowych
względem siebie oraz zadanego stopnia wynikowego wielomianu,
- przebieg wielomianu wynikowego w znacznej mierze zależy od rozmieszczenia względem siebie
węzłów
- charakterystyka działania funkcji lagrange’a pozwala jaj na zerowy błąd w węzłach i
odwzorowanie tej samej funkcji jeżeli węzły należą do wielomianu(bo bazuje na twierdzeniu
Weierstrassa)
- jeśli węzły byłyby punktami przegięcia funkcji której wykresem jest wielomian, funkcja polyfit
mogłaby odwzorować jego przebieg z zerowym błędem – tak jak robi to funkcja „lagrange” bez
względu na to czy węzły są jednocześnie punktami przegięcia