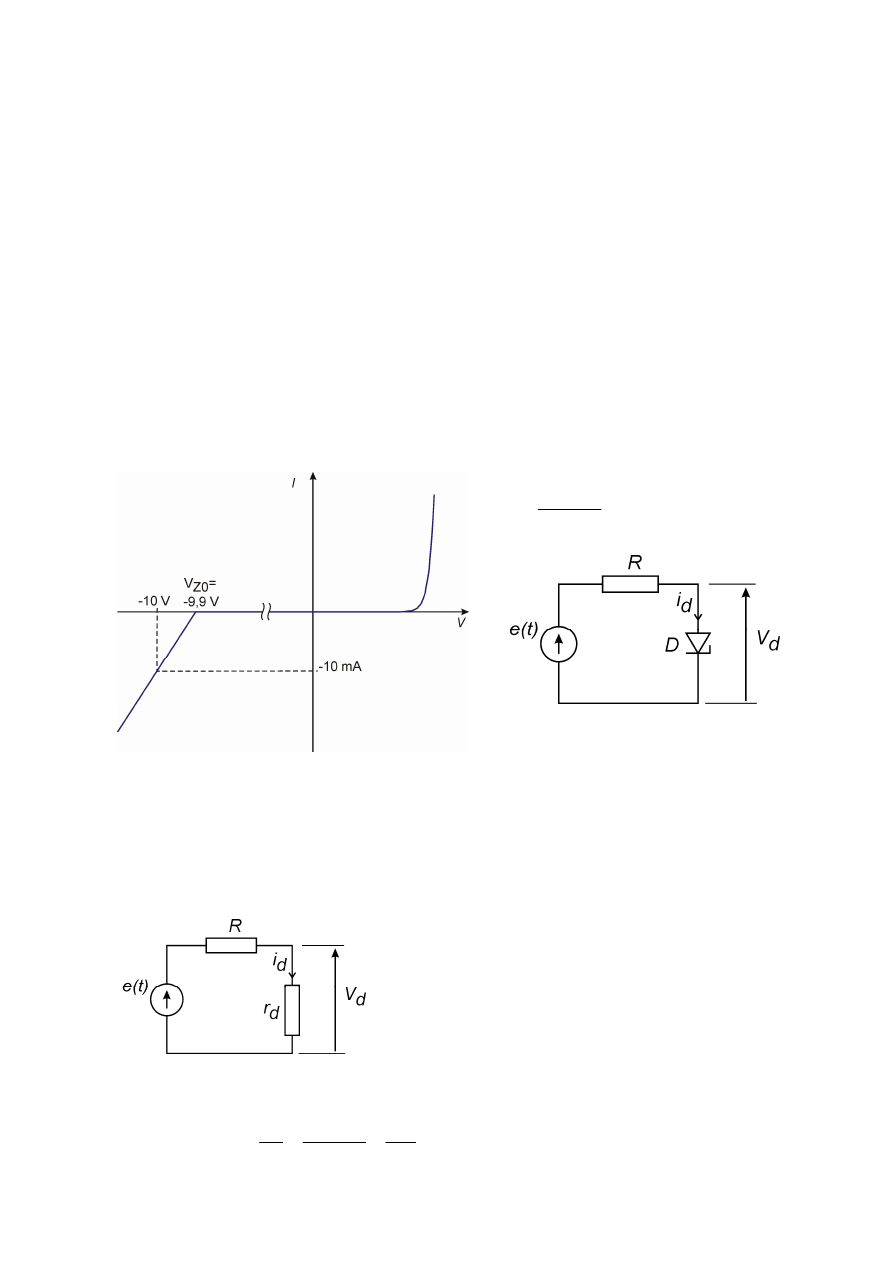
- 1 -

ZADANIA DO ĆWICZEŃ Z ELEMENTÓW ELEKTRONICZNYCH

temat: Diody

2009.11.30 – 12.04

Piotr Płotka, [e-mail], tel. [phone], pok. 301

konsultacje: środa 8:00 – 9:00, 13:00 – 14:00

ZADANIE 1. (Zad. 2.32 ze skryptu W. Janke, W. J. Stepowicz, D. Tollik, L. Tomczak,
"Zadania Z Elementów Elektronowych", Wyd. Politechniki Gdańskiej, wyd. III, 1983)
Dioda o danej charakterystyce I(V), jak na rys. 1.1 pracuje w układzie jak na rys. 1.2.
Wyznaczyć składową stałą i amplitudę składowej zmiennej napięcia na diodzie dla wartości
napięcia zasilania: (a) E

0

= 20 V oraz (b) E

0

= -20 V. Dane: e(t) = E

0

+ E

m

· sin(

ω

t), E

m

= 1

V, I

S

= 1·10

-12

A, R = 1 k

Ω

, T = 300 K.

Rozwiązanie:
(a) Kierunek przewodzenia. Składową stałą liczymy metodą kolejnych przybliżeń:

I

D0

= I

Dmax

= E/R = 20 mA, V

D0

= V

T

ln(I

D0

/I

S

) = 612 mV,

(1.1)

gdzie V

T

= k

B

T/q , k

B

≈

1,38·10

-23

J/K = 8,62·10

-5

eV/K , q

≈

1,6·10

-19

C , V

T

≈

25 mV

przy T = 300 K.
I

D1

= I

Dmax

= (E - V

D0

)/R = 19,4 mA, stąd V

D1

= 611 mV.

(1.2)

Składową zmienną wyznaczamy zkorzystając z małosygnałowego schematu zastępczego
przedstawionego na rys. 1.3, gdzie

(1.3)

Rys. 1.1

Ddc

T

s

Ddc

T

D

D

I

V

I

I

V

g

r

≈

+

=

=

1

Rys. 1.2

Rys. 1.3













−













⋅

≈

1

exp

T

k

n

qV

I

I

B

ideal

s

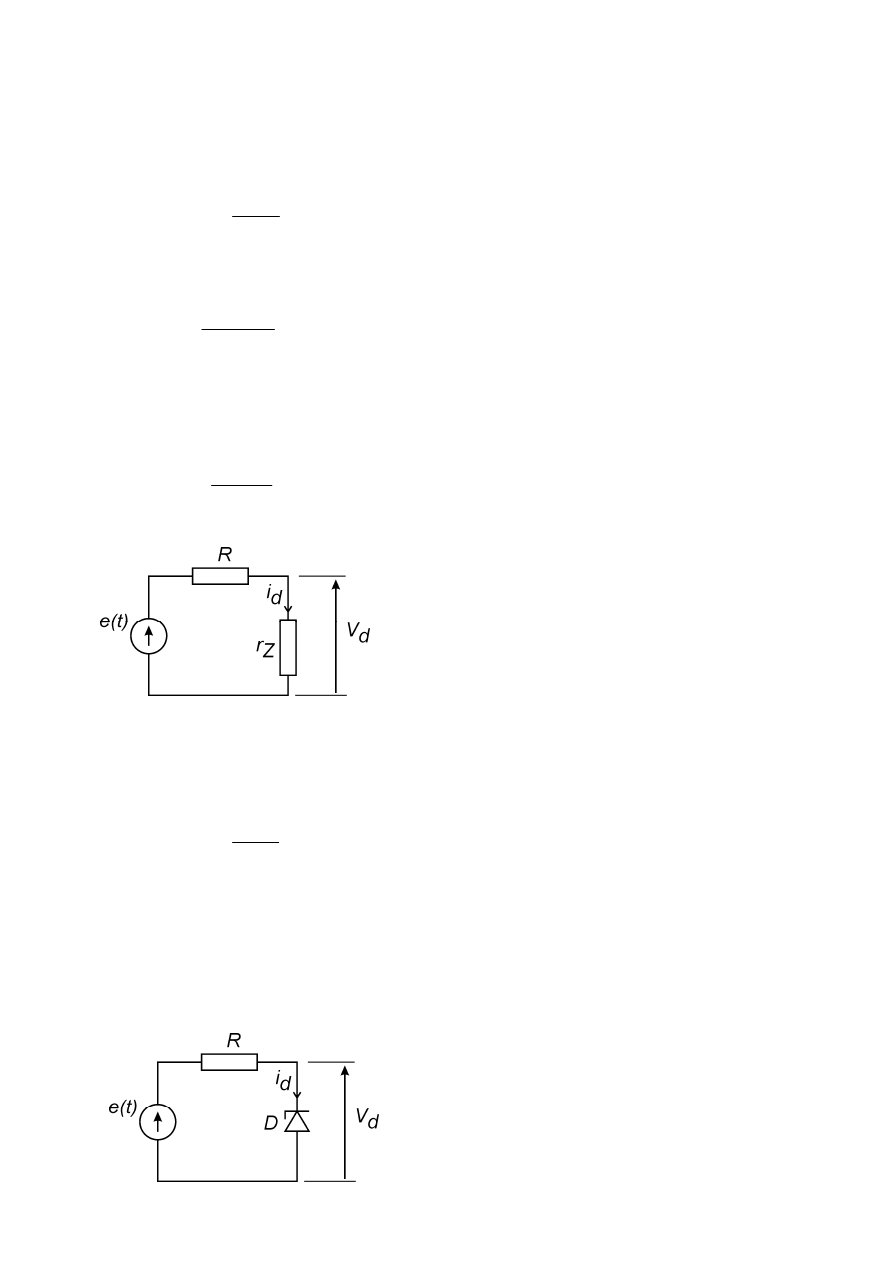
- 2 -

obliczamy r

D

= 1,33

Ω

, więc amplituda składowej zmiennej

mV

33

,

1

≈

+

⋅

=

R

r

r

E

V

D

D

m

d

(1.4)

(b) Kierunek zaporowy.
Charakterystykę statyczna diody dla napięć V

D

< -|V

Z0

| zapisujemy jako:

Z

Z

D

D

r

V

V

I

|

|

0

+

≈

(1.5)

gdzie V

Z0

oraz r

Z

wyznaczone są z rys. 1.1

V

Z0

= -9,9 V , r

Z

=

∆

v/

∆

i = 10

Ω

(1.6)

Aby znaleźć składową stałą rozwiązujemy to równanie wraz z równaniem opisującym prąd
płynący przez rezystor R:

R

V

E

I

Ddc

Ddc

−

=

(1.7)

Otrzymujemy V

Ddc

= -10 V.

Amplitudę składowej zmiennej wyznaczamy z dzielnika napięciowego:

mV

9

,

9

=

+

⋅

=

R

r

r

E

V

Z

Z

m

d

(1.8)

ZADANIE 2. (Zad. 2.42 ze skryptu W. Janke, W. J. Stepowicz, D. Tollik, L. Tomczak,
"Zadania Z Elementów Elektronowych", Wyd. Politechniki Gdańskiej, wyd. III, 1983)

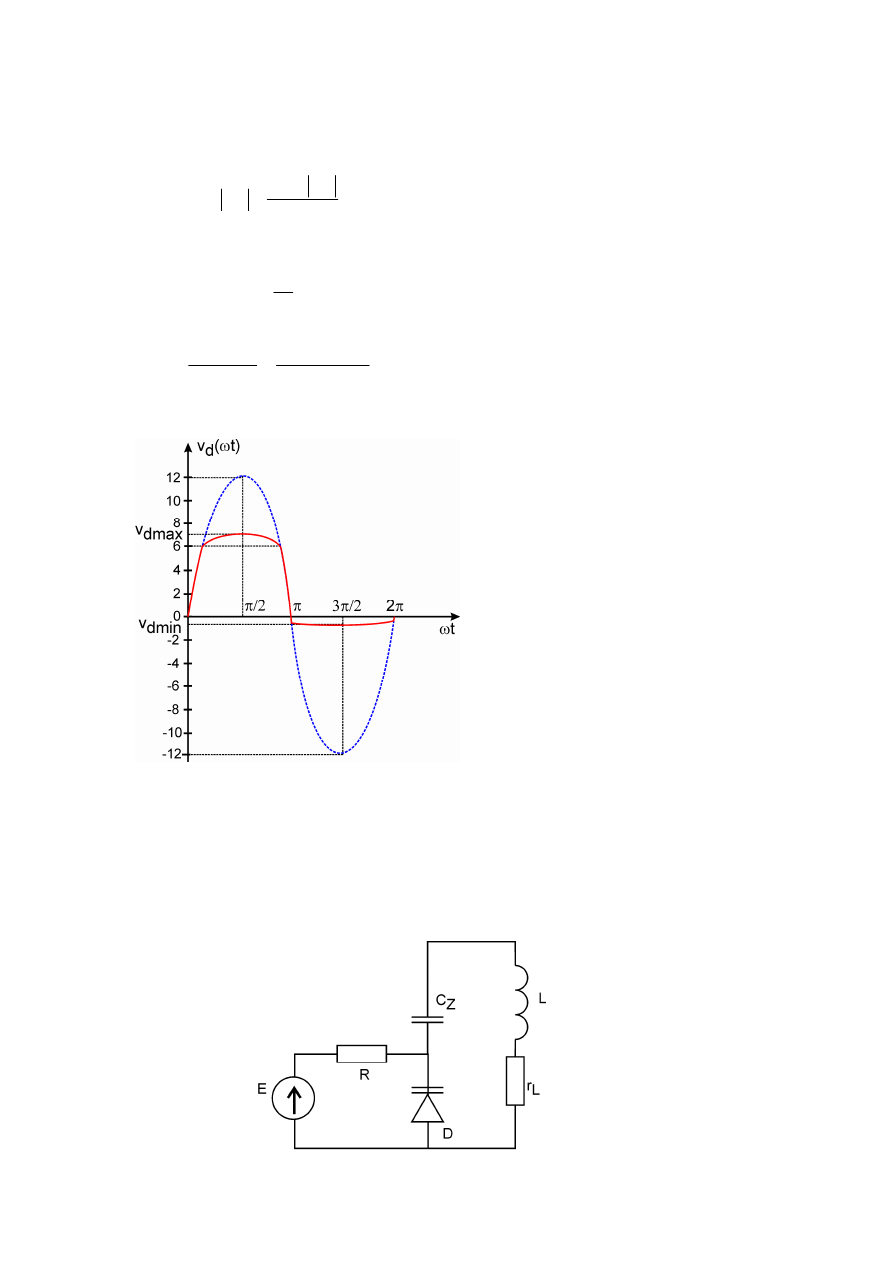
Wyznaczyć i naszkicować przebieg zależności v

D

(

ω

t

) w układzie jak na rys. 2.1, dla zakresu

0

≤

ω

t

≤

2

π

. Obliczyć wartości ekstremalne przebiegu v

D

(

ω

t

). Dane: I

S

= 1·10

-12

A, |V

Z0

| = 6

V, r

Z

= 50

Ω

, rezystancja szeregowa r

s

= 0

Ω,

R

= 200

Ω,

e(t)

= 12 V · sin(

ω

t), T = 300 K.

Rys. 2.1

Rys. 1.4

- 3 -

Rozwiązanie:
Dla diody spolaryzowanej zaporowo otrzymujemy wartość ekstremalną przebiegu v(

ω

t

):

V

2

,

7

0

0

max

=

+

−

+

=

Z

Z

Z

m

Z

d

r

r

R

V

E

V

v

(2.1)

zaś dla kierunku przewodzenia:

S

T

d

I

i

V

v

ln

min

⋅

−

=

(2.2)

gdzie

mA

57

200

V

6

,

0

V

12

=

Ω

−

=

−

≈

R

V

E

i

DF

m

(2.3)

czyli v

dmin

= -639 mV. Wykres v(

ω

t) przedstawiono na rys. 2.2.

ZADANIE 3.
Dioda D o pojemności 40 pF przy V

R

= 3 V oraz o pojemności 15 pF przy V

R

= 30 V

wykorzystana została do przestrajania obwodu rezonansowego jak na rys. 3.1. Obliczyć
minimalną i maksymalną częstotliwość rezonansową obwodu, gdy: R = 100 k

Ω

, L = 100 nH,

r

L

= 1

Ω

, zaś E zmienia się w przedziale [0 V, 30 V]. Przyjąć wartość napięcia wbudowanego

V

j

= 0,7 V oraz, że pojemność C

Z

stanowi zwarcie dla składowej zmiennej.

Rys. 2.2

Rys. 3.1

- 4 -

Rozwiązanie:

Zależność pojemności złączowej C diody od napięcia polaryzującego V można
aproksymować zależnością

0

,

1

)

0

(

)

(

≤















−

=

=

V

dla

V

V

V

C

V

C

m

j

(3.1)

gdzie V

j

jest wartością napięcia wbudowanego. Nie znamy wartości C(V =0), ani m. Wartość

współczynnika m możemy wyznaczyć posługując się znanymi wartościami C dla dwóch
znanych napięć polaryzujących V

R1

oraz V

R2

:

m

j

R

m

j

R

R

R

V

V

V

V

V

C

V

C















−

−















−

−

=

1

2

2

2

1

1

1

1

)

(

)

(

(3.2)

co w wyniku logarytmowania daje:















+

+













=

1

2

2

2

1

1

ln

)

(

)

(

ln

R

j

R

j

R

R

V

V

V

V

V

C

V

C

m

(3.3)

Przyjmując, że V

R1

= 3 V oraz V

R1

= 30 V otrzymujemy m

≈

0,46, to jest wartość bliską

wartości m dla złącza skokowego.

Wartość C(V=0) wyznaczamy z Zal. (3.1) jako:

m

j

R

R

V

V

V

C

V

C















−

−

⋅

=

=

1

1

1

)

(

)

0

(

(3.4)

czyli C(V=0)

≈

86 pF.

Częstotliwości rezonansowe obwodu wyznaczamy zgodnie z zależnością

)

0

(

2

1

min

=

=

V

LC

f

π

(3.5)

oraz

)

30

(

2

1

max

V

V

LC

f

=

=

π

(3.6)

otrzymując f

min

≈

54 MHz oraz f

max

≈

130 MHz.