- 1 -

ZADANIA DO ĆWICZEŃ Z ELEMENTÓW ELEKTRONICZNYCH

temat: Tranzystory MOS – cz. 2

2009.12.14 – 2009.12.18

prowadzący – Piotr Płotka, [e-mail], tel. [phone], pok. 301

konsultacje: środa 8:00 – 9:00, 13:00 – 14:00

ZADANIE 1.

a) Jakiej najwyższej wartości częstotliwości granicznej f

T

można spodziewać się dla

tranzystora MOS z kanałem typu n, o długości bramki L = 50 nm? Przyjąć, że
długość ścieżki przepływu elektronów wynosi l

n

= 100 nm, a prędkość unoszenia

elektronów w polu elektrycznym równa jest prędkości nasycenia v

sat

= 10

7

cm/s =

10

5

m/s.

b) Jakiej wartości f

T

można by się spodziewać, gdyby ścieżka przepływu elektronów

miała długość bramki L , a ich prędkość unoszenia wynosiła v

driftn

= µ

n

E, gdzie µ

n

=

1000 cm

2

/V·s. Przyjąć wartość nadwyżki napięcia bramka-źródło nad napięciem

progowym V

GS

- V

Tn

= 1 V. Założyć, że tranzystor pracuje w obszarze nasycenia

(pentodowym).

Rozwiązanie:

a) Obliczamy czas przelotu elektronów:

m/s

10

nm

100

5

=

=

sat

n

tn

v

l

t

(1.1)

t

tn

= 10

-12

s.

Szacujemy

częstotliwość graniczną f

T

:

GHz

160

s

10

28

,

6

1

2

1

12

≈

⋅

≈

<

−

tn

T

t

f

π

(1.2)

Uwaga: Długość ścieżki przepływu elektronów l

n

jest około dwukrotnie większa niż

długość bramki L ponieważ części wysoko domieszkowanych obszarów n

+

drenu i

źródła są w znacznym stopniu opróżnione z elektronów przy polaryzacji w zakresie
nasycenia (pentodowym).

b)

Szacujemy częstotliwość graniczną f

T

:

[

]

(

)

L

W

C

V

V

L

W

C

C

C

g

f

ox

Tn

GS

ox

n

gd

gs

m

T

⋅

⋅

⋅

−

⋅

⋅

=

+

<

π

μ

π

2

2

(1.3)

Po

uproszczeniu

(

)

2

2

L

V

V

f

Tn

GS

n

T

⋅

−

⋅

<

π

μ

(1.4)

Podstawiamy

wartości,

(

)

Hz

25

28

,

6

10

Hz

10

25

2π

0,1

nm

50

2π

1V

/Vs

cm

1000

15

16

2

2

⋅

≈

⋅

⋅

≈

⋅

⋅

<

−

T

f

(1.5)

- 2 -

Ostatecznie

f

T

< 6,4·10

12

Hz = 6,4 THz

(1.6)

Komentarz: Oszacowana w ten sposób wielkość f

T

jest wielokrotnie większa od wartości

mierzonej dla tranzystorów z bramkami o długości 50 nm, Mierzone wartości są podobne do
wartości otrzymanej w punkcie a). Błąd szacowania w punkcie b) wynika z przyjęcia
nierealnego założenia, że prędkość unoszenia elektronów jest wprost proporcjonalna do
natężenia pola elektrycznego v

driftn

= µ

n

E. W tranzystorach o najkrótszych produkowanych

dziś długościach kanałów L wartości natężeń pola elektrycznego |

E| są tak duże, że dochodzi

do nasycenia prędkości unoszenia elektronów, jak przyjęto w punkcie a) zadania.


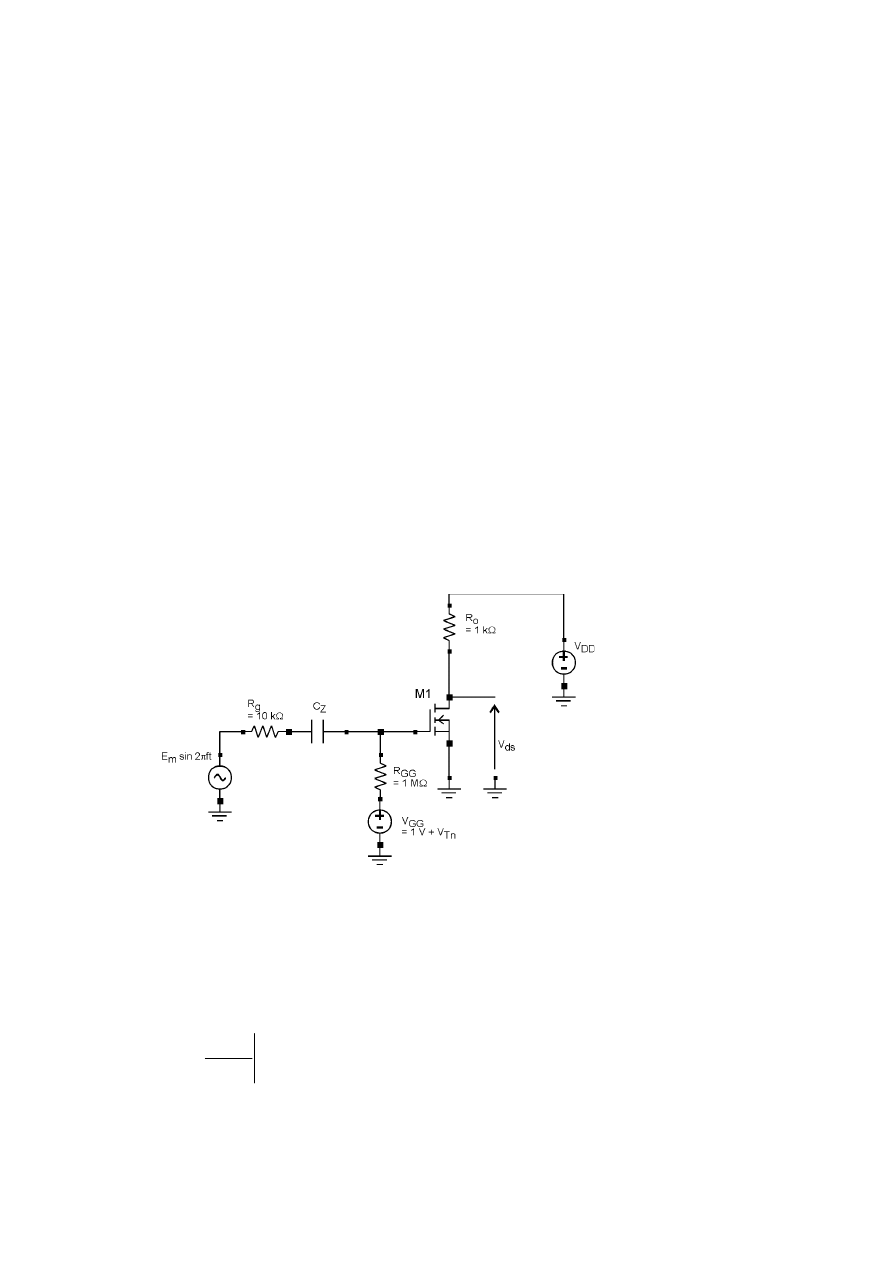
ZADANIE 2.
Dla układu jak na rysunku wyznaczyć górną częstotliwość f

0

pasma przenoszenia

wzmocnienia napięciowego K

V

= V

ds

/E

m

, gdzie V

ds

oraz E

m

są amplitudami napięć

zmiennych. Przyjąć, że C

GG

stanowi zwarcie, a R

GG

stanowi rozwarcie dla składowej

zmiennej. Przyjąć, że tranzystor pracuje w obszarze nasycenia (pentodowym), a elektrony w
kanale poruszaja się z prędkością nasycenia v

sat

= 10

7

cm/s = 10

5

m/s. Pojemność

charakterystyczna C

ox

= 25 fF/µm

2

= 25·10

-3

F/m

2

. Szerokość kanału W = 400 nm, długość

L = 100 nm. Przyjąć, że pojemność tworzona przez przewodzącą elektrodę nad dielektrykiem
bramki dzieli się między źródło a dren w następujący sposób:

C

gs

= 2·L·W·C

ox

/3

(2.1)

C

gd

= L·W·C

ox

/3

(2.2)

Rozwiązanie:
Gdy elektrony poruszają się z prędkością nasycenia natężenie prądu drenu w obszarze
nasycenia można wyrazić zależnością:

I

Ddc

= v

sat

· C

ox

·W·(V

GSdc

- V

Tn

)

(2.3)

Różniczkując tę zależność względem V

GSdc

otrzymujemy wielkość transkonduktancji g

m

W

C

v

V

I

g

ox

sat

const

V

GSdc

Ddc

m

DSdc

⋅

⋅

=

=

=

.

d

d

(2.4)

Po podstawieniu danych

g

m

= 10

5

m/s ·25·10

-3

F/m

2

·400·10

-9

m = 10

-3

A/V = 1 mS

(2.5)

Rys. 2.1

- 3 -

Dla wyznaczenia elementów małosygnałowego schematu zastępczego tranzystora MOS
pozostaje obliczenie wartości pojemności C

gs

oraz C

gd

według zal. 2.1 i zal. 2.2:

C

gs

= 0,66·10

-15

F

(2.6)

C

gd

= 0,33·10

-15

F

(2.7)

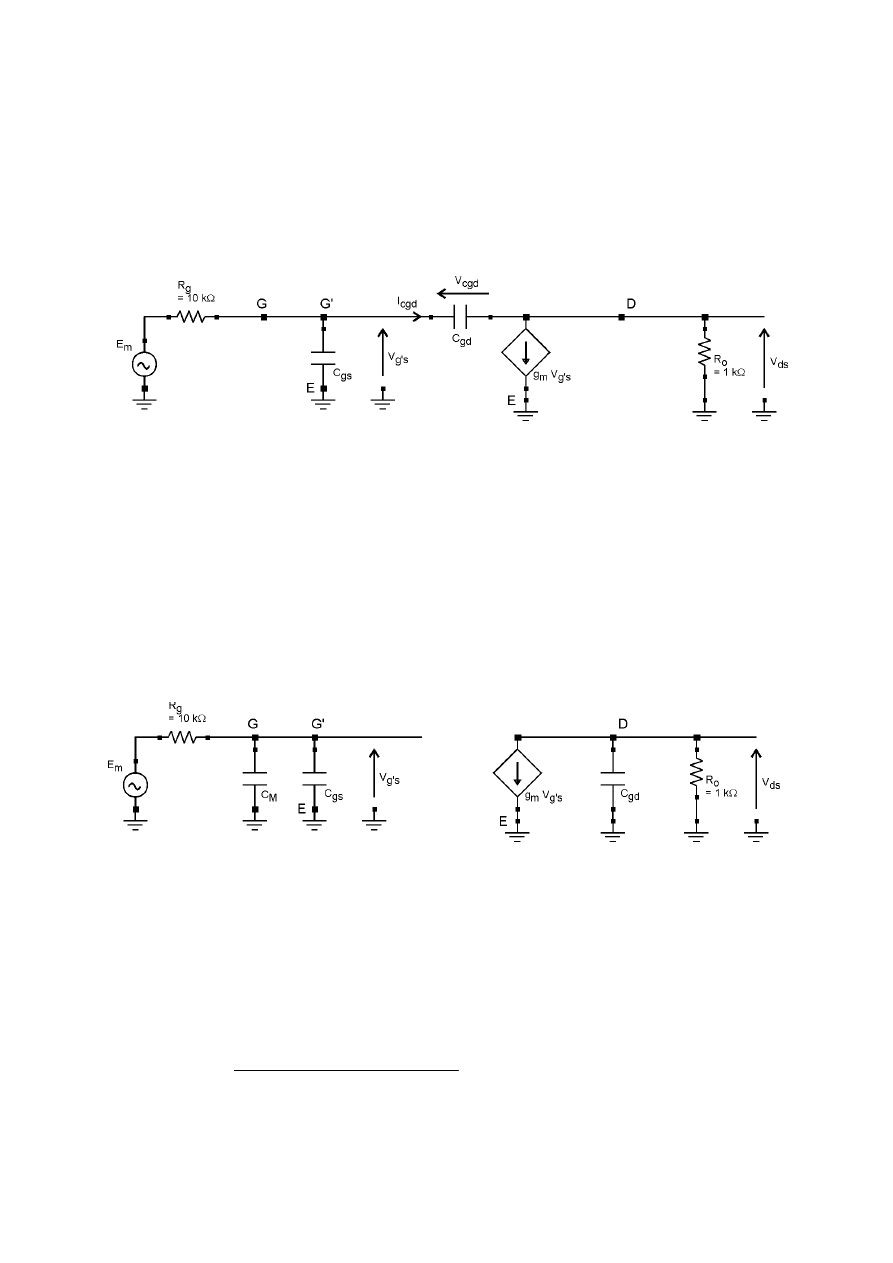
Pamiętając, że pojemność C

Z

oraz źródła napięć stałych stanowią zwarcia dla składowych

zmiennych, R

GG

- rozwarcie, otrzymujemy małosygnałowy schemat zastępczy naszego

układu jak na rys. 2.2.

W układzie z rys. 2.2 znamy wartości wszystkich elementów. Możemy zatem wyznaczyć
funkcję przenoszenia K

V

= V

ds

/E

m

w zależności od częstotliwości, czyli również żądaną

wartość częstotliwości bieguna f

0

. J.M. Miller w 1920 r. zaproponował prostszą metodę

obliczania wartości f

0

. W tym celu zauważył, że przy częstotliwości f

0

moduł wzmocnienia

napięciowego pomiędzy punktami G' oraz D jest tylko około 1,41 razy mniejszy niż dla
małych częstotliwości. Dla celu obliczenia prądu I

cgd

płynącego przez pojemność C

gd

Miller

przyjął zatem, że wartość amplitudy napięcia V

ds

jest taka sama, jak dla małych

częstotliwości:

I

cgd

= V

g'd

·C

gd

= (V

g's

- V

ds

) ·C

gd

= j

ω(1+ g

m

·R

o

) ·C

gd

·V

g's

(2.8)

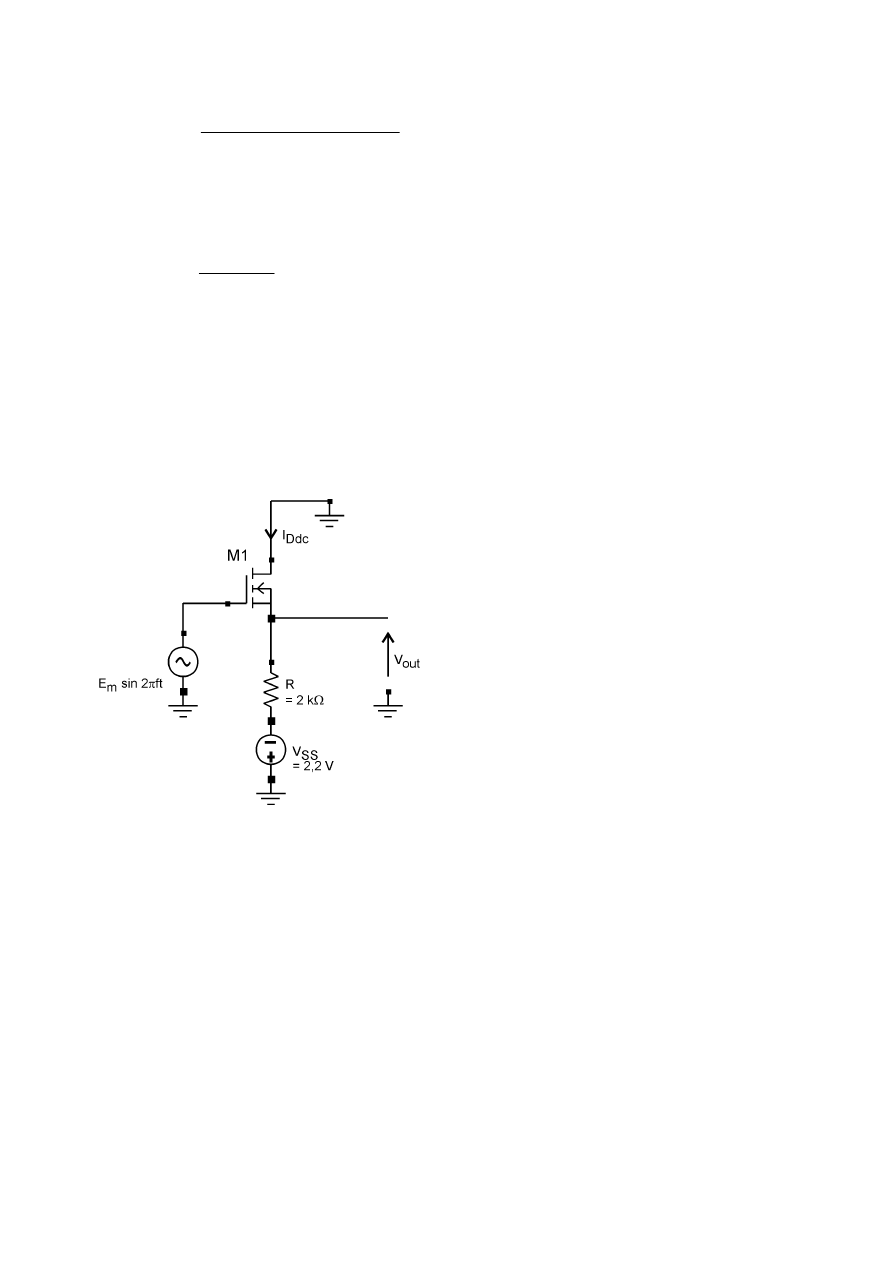
Wartość prądu przedstawionego w zal. (2.8) jest taka sama, jak wartość prądu płynącego
przez pojemność C

M

w układzie przedstawionym na rys.2.3

gdzie

C

M

= (1+ g

m

·R

o

) · C

gd

(2.9)

W układzie przedstawionym na rys. 2.3 obwód wejściowy jest niezależny od obwodu
wyjściowego. Łatwo wyznaczyć częstotliwość bieguna dominującego f

0

analizując obwód

wejściowy.

(

)

[

]

gs

gd

o

m

g

m

s

g

C

C

R

g

R

j

E

V

+

+

⋅

+

=

1

1

)

(

'

ϖ

ω

(2.10)

Stąd wartość częstotliwości bieguna dominującego f

0

Rys. 2.2

Rys. 2.3

- 4 -

(

)

[

]

gs

gd

o

m

g

C

C

R

g

R

f

+

+

⋅

=

1

2

1

0

π

(2.11)

Po podstawieniu danych otrzymujemy
GHz

7

,

3

0

≈

f

(2.12)

Należy jeszcze sprawdzić czy częstotliwość bieguna związanego z obwodem wyjściowym
nie jest mniejsza:

GHz

48

2

1

1

≈

⋅

=

gd

o

C

R

f

π

(2.13)

Widzimy, że nie jest
GHz

48

GHz

7

,

3

0

≈

<

≈

1

f

f

(2.14)

ZADANIE 3.
Tranzystor MOS z indukowanym kanałem typu n pracuje w układzie jak na rys. 3.1. Dla
wartości R = 2 k

Ω, V

SS

= 2,2 V, V

Tn

= 0,2 V oraz

β

n

= µ

n

·C

ox

·W/L = 1 mA/V

2

oblicz

wartości I

Ddc

, V

outdc

oraz amplitudy V

out

.

Rozwiązanie:
Stałoprądowy punkt pracy
Źródło napięcia zmiennego E

m

sin2

πft stanowi zwarcie dla składowej stałej:

V

GSdc

+ I

Sdc

·R – V

SS

= 0

(3.1)

Ale w tranzystorze MOS składowe stałe prądów źródła i drenu są równe

I

Sdc

= I

Ddc

(3.2)

Zatem

V

GSdc

+ I

Ddc

·R – V

SS

= 0

(3.3)

Napięcie V

SS

jest większe niż V

Tn

, więc tranzystor na pewno nie jest odcięty – pracuje w

zakresie nasycenia lub triodowym. Możemy to rozstrzygnąć dostrzegając, że potencjały
bramki i drenu są równe potencjałowi masy, czyli:

V

DGdc

= 0

(3.4)

Rys. 3.1

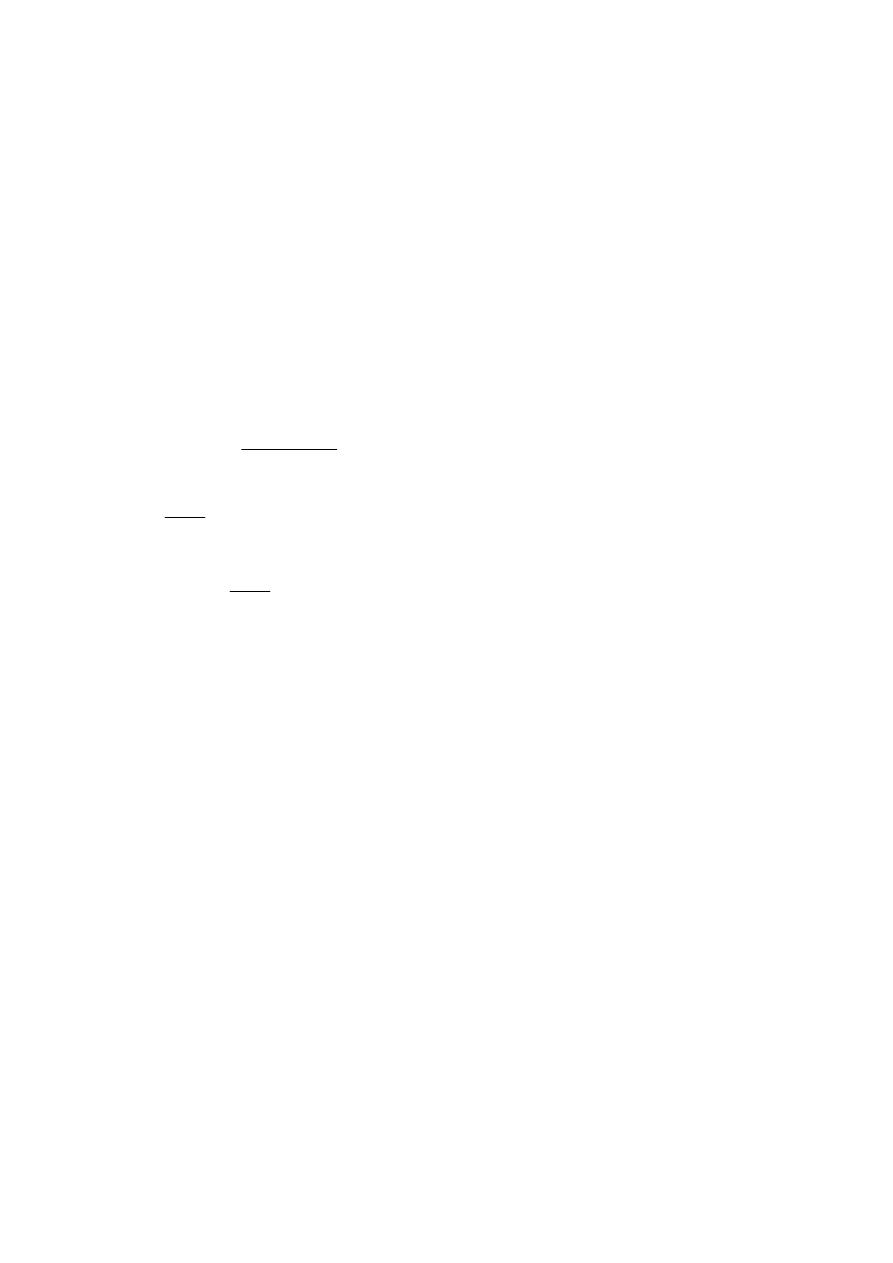
- 5 -

W warunku pracy tranzystora MOS w obszarze nasycenia

V

DSdc

≥

V

GSdc

- V

Tn

(3.5)

możemy dokonać podstawienia

V

DSdc

= V

GDdc

+ V

GSdc

(3.6)

otrzymując

V

GDdc

+ V

GSdc

≥

V

GSdc

- V

Tn

(3.7)

Przy uwzględnieniu zal. 3.4 dla naszego układu otrzymujemy warunek pracy w obszrze
nasycenia w postaci:
0

+

V

GSdc

≥

V

GSdc

- V

Tn

(3.8)

czyli
0

≥

- V

Tn

(3.9)

Ale dla tranzystora MOS z indukowanym kanałem typu n wartość V

Tn

jest dodatnia, czyli

nierówność w zal. 3.9 jest spełniona. Stąd wniosek, że w układzie z rys. 3.1 tranzystor MOS
z indukowanym kanałem typu n pracuje w obszarze nasycenia o ile tylko V

SS

jest większe niż

V

Tn

, co jest spełnione w naszym przypadku. Prąd drenu można zatem przedstawić jako:

(

)

2

2

Tn

GSdc

n

Ddc

V

V

I

−

⋅

=

β

(3.10)

Z zal. 3.10 i zal. 3.3 otrzymujemy

(

)

2

2

R

I

V

V

I

Ddc

Tn

SS

n

Ddc

−

−

=

β

(3.11)

czyli

(

)

(

)

0

2

2

2

2

2

=

−

+

−

−

−

Tn

SS

Ddc

Tn

SS

n

Ddc

Ddc

V

V

I

V

V

R

I

R

I

β

(3.12)

Rozwiązując to równanie otrzymujemy. Z dwóch rozwiązań tego równania poprawne jest

I

Ddc

=

0,5

mA

(3.13)

Drugie rozwiązanie, 2 mA, odrzucamy ponieważ z zal. 3.1 przy uwzględnieniu zal. 3.2
wynikałoby, ze dla tego rozwiązania V

GSdc

< V

Tn

.

Napięcie wyjściowe

V

out

= -V

GSdc

(3.14)

To napięcie wyznaczamy z zal. 3.1 przy uwzględnieniu zal. 3.2:

V

GSdc

=

1,2

V

(3.15)

V

out

= -V

GSdc

= -1,2 V

(3.16)

Amplituda V

out

Wiedząc, że tranzystor pracuje w obszarze nasycenia i znając wartość V

GSdc

, możemy

wyznaczyć wartość

(

)

Tn

GSdc

n

m

V

V

g

−

=

β

(3.17)

g

m

= 1 mS

(3.18)

i narysować małosygnałowy schemat zastępczy dla małych częstotliwości jak na rys. 3.2.

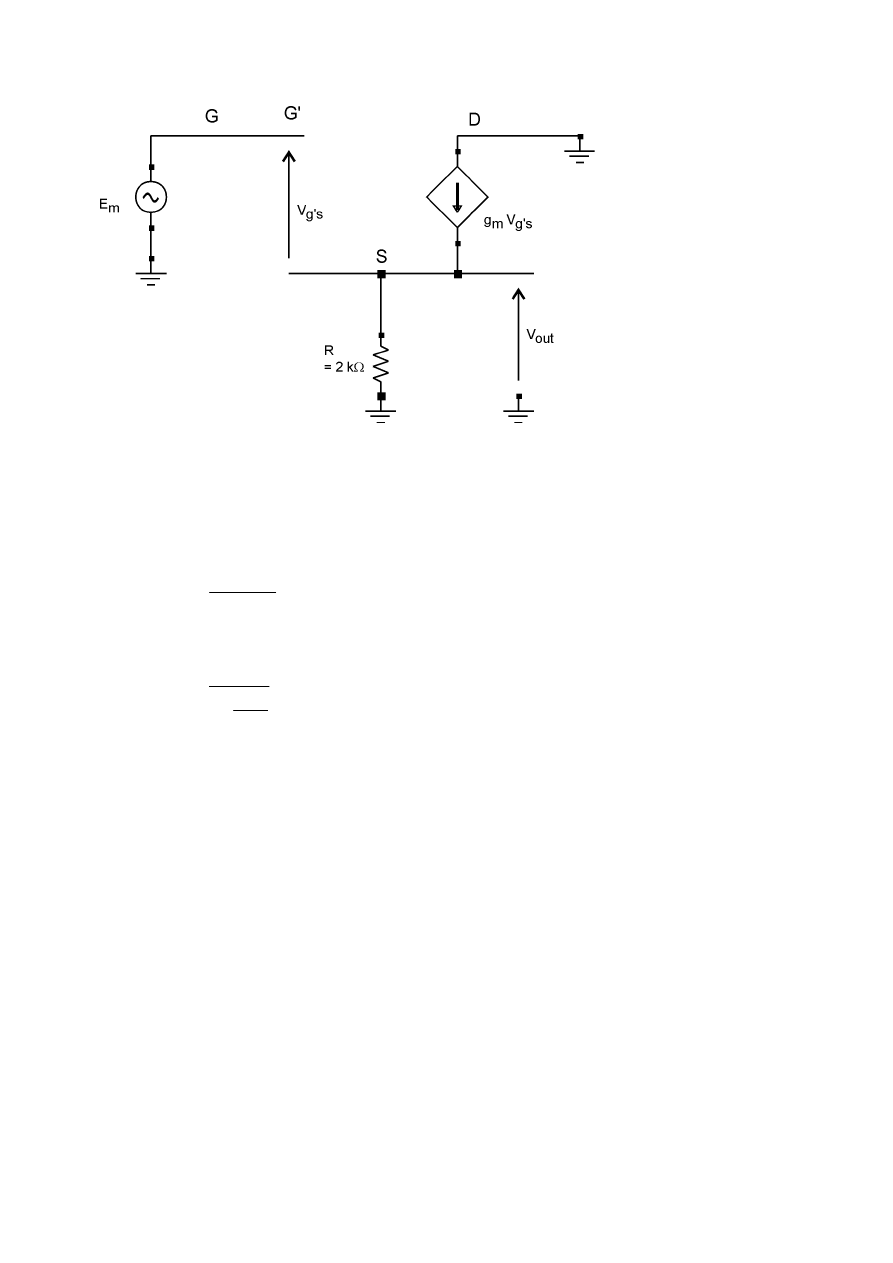
- 6 -

Napięcie V

out

wyrażamy jako

V

out

= g

m

·R·V

g's

(3.19)

Dla oczka obwodu wejściowego

E

m

= V

g's

+ V

out

(3.20)

Z zal. 3.19 i zal. 3.20 otrzymujemy ostatecznie

R

g

E

R

g

V

m

m

m

out

+

⋅

=

1

(3.21)

co można przedstawić jako

R

g

E

V

m

m

out

1

1

+

=

(3.22)

Rys. 3.2