- 1 -

ZADANIA DO ĆWICZEŃ Z ELEMENTÓW ELEKTRONICZNYCH

temat: Tranzystory BPT

2010.01.11 – 2010.01.15

prowadzący – Piotr Płotka, [e-mail], tel. [phone], pok. 301

konsultacje: środa 8:00 – 9:00, 13:00 – 14:00

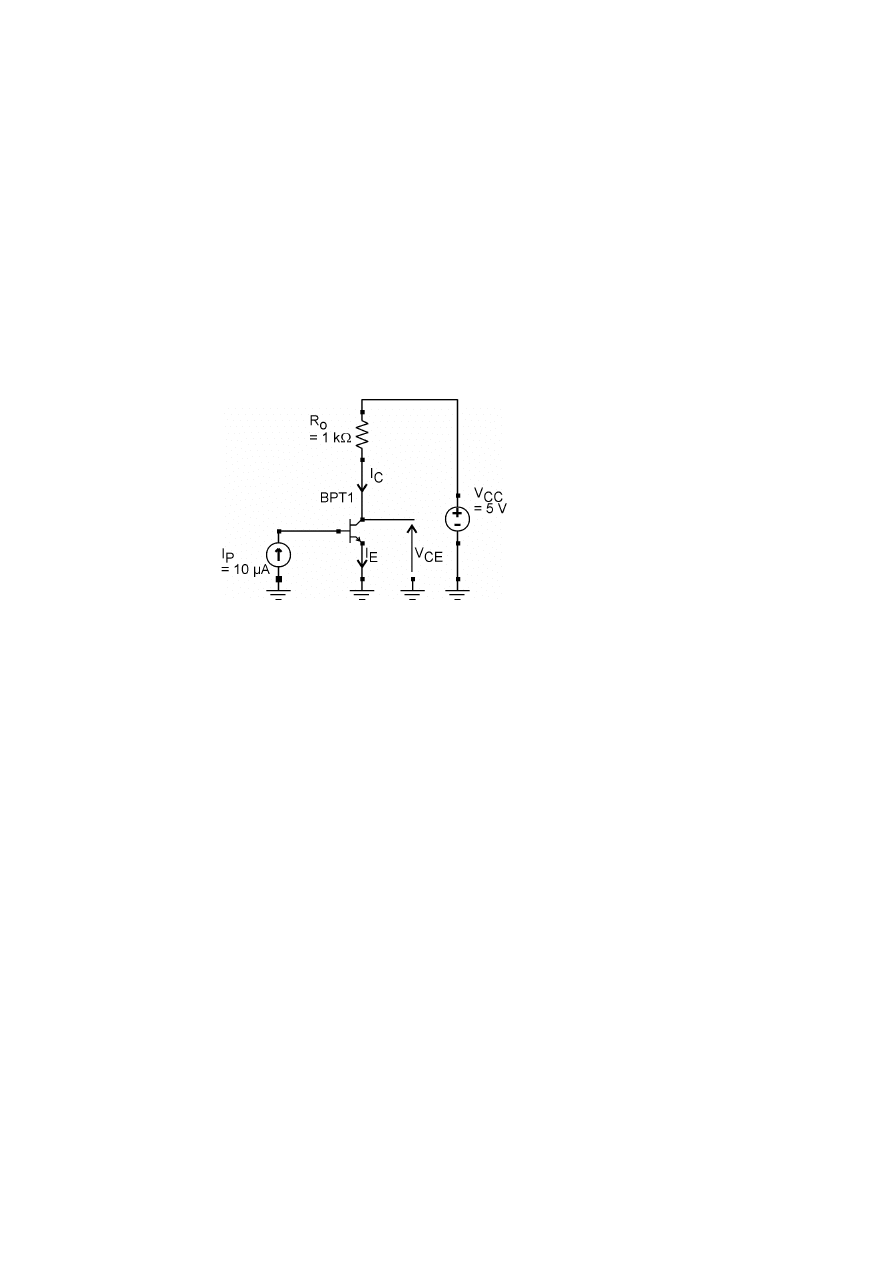
ZADANIE 1.
W układzie jak na rysunku wyznaczyć wielkości V

CEdc

, I

Cdc

, I

Edc

oraz I

Bdc

. Przyjąć, że

β

N

=

100 oraz I

P

= 10 µA.

Rozwiązanie:
Widzimy, że

I

Bdc

= I

P

(1.1)

Prąd ten polaryzuje przewodząco złącze baza-emiter. Z zadawalającym inżynierskim
przybliżeniem można zatem przyjąć, że

V

BEdc

=

0,7

V

(1.2)

Załóżmy, że tranzystor pracuje w obszarze aktywnym normalnym, to znaczy że złącze baza-
emiter jest spolaryzowane przewodząco, a baza-kolektor jest spolaryzowane zaporowo. W
takim razie

I

Cdc

=

β

N

· I

Bdc

(1.3)

Uwzględniając Zal. 1.1 mamy

I

Cdc

=

β

N

· I

P

= 100 · 10 µA = 1 mA

(1.4)

Wartość I

Edc

musi być oczywiście równa sumie I

Cdc

oraz I

Bdc

I

Edc

= I

Cdc

+ I

Bdc

= (

β

N

+ 1) · I

Bdc

= (1+1/

β

N

) · I

Cdc

(1.5)

czyli

I

Edc

= (

β

N

+ 1) · I

P

=

1,01

mA

(1.6)

Równanie oczkowe

V

CC

= V

CEdc

+ I

Cdc

·R

o

(1.7)

pozwala nam wyliczyć

V

CEdc

= V

CC

- I

Cdc

·R

o

(1.8)

V

CEdc

= 5 V – 1,01 mA · 1 k

Ω = 3,99 V

(1.9)

Możemy teraz sprawdzić czy tranzystor rzeczywiście pracuje w obszarze aktywnym
normalnym. W tym celu pozostaje do sprawdzenia czy

V

BCdc

<

0

V

(1.10)

Rys. 1.1

- 2 -

Napięcie V

BCdc

przedstawiamy jako

V

BCdc

= V

BEdc

- V

CEdc

(1.11)

czyli

V

BCdc

= 0,7 V – 3,99 V = -3,29 V < 0 V

(1.12)

Złącze baza-kolektor jest spolaryzowane zaporowo, a złącze baza-emiter - przewodząco.
Tranzystor pracuje rzeczywiście w obszarze aktywnym normalnym.


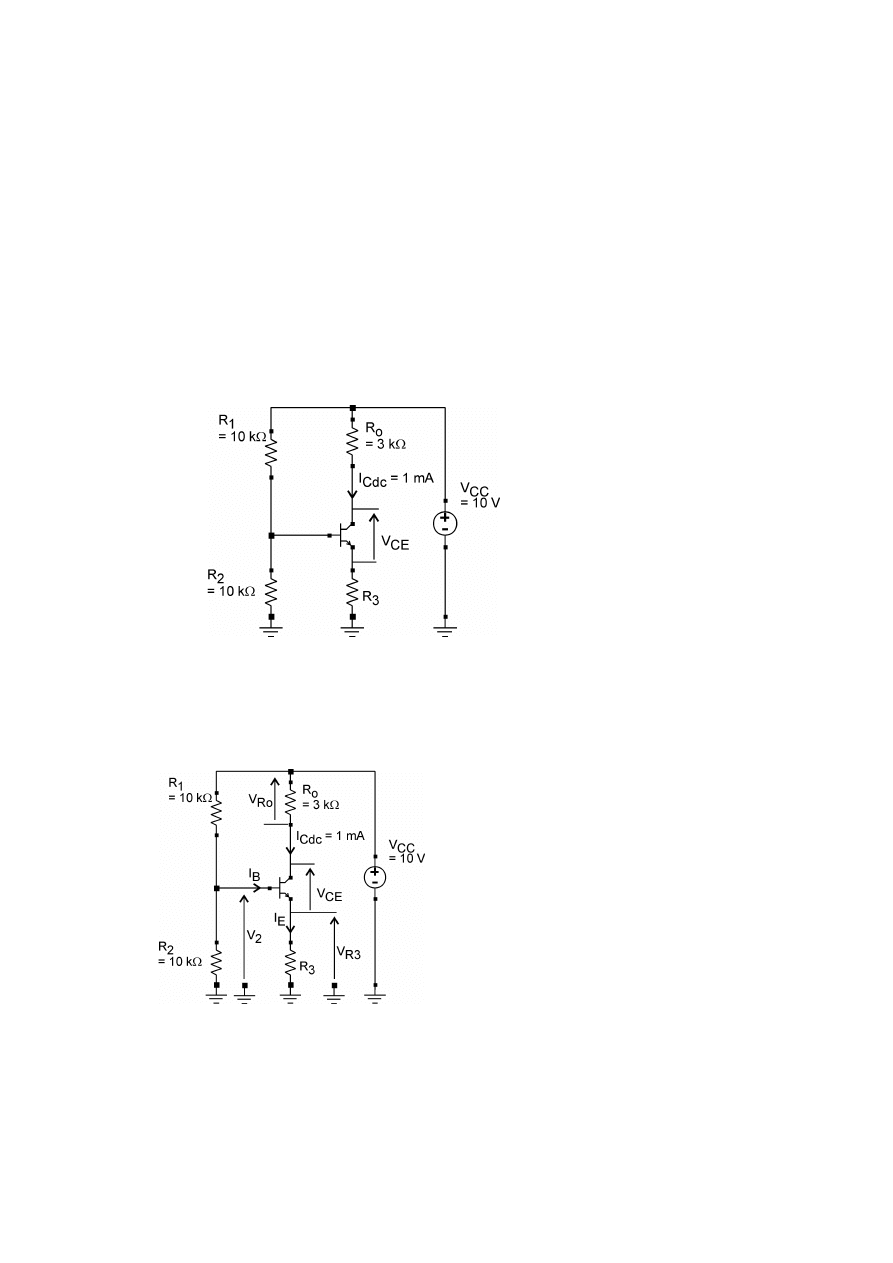
ZADANIE 2.
W układzie jak na rysunku wyznaczyć wielkości V

CEdc

, R

3dc

oraz V

R3dc

. Przyjąć, że I

Bdc

jest

pomijalnie mały w porównaniu z prądami płynącymi przez rezystory R

1

oraz R

2

. Przyjąć, że

β

N

= 100.

Rozwiązanie:

Prąd I

Bdc

jest pomijalnie mały w porównaniu z prądami płynącymi przez rezystory R

1

oraz R

2 ,

więc wartość V

2

wyznaczamy z dzielnika napięciowego R

1

, R

2

.

V

2

≈

V

CC

·R

2

/( R

1

+ R

2

) (2.1)

V

2

≈

5

V (2.2)

Rys. 2.1

Rys. 2.2

- 3 -

Wartość V

2

jest dodatnia i większa niż 0,7 V, więc złącze baza-emiter tranzystora jest

spolaryzowane przewodząco, a jego przybliżona wartość wynosi

V

BEdc

=

0,7

V

(2.3)

Zakładamy, że tranzystor pracuje w obszarze aktywnym normalnym.
Podobnie jak w zad.1

I

Edc

= (1+1/

β

N

) · I

Cdc

(2.4)

I

Edc

= (1+1/

100) · 1 mA = 1,01 mA

(2.5)

Wartość V

2

jest sumą

V

2

= V

BEdc

+ V

R3dc

(2.6)

Gdzie spadek napięcia na rezystorze R

3

V

R3dc

= I

Edc

·R

3

(2.7)

Postawiając zal. 2.4 otrzymujemy

V

R3

= (1+1/

β

N

) ·R

3

·I

Cdc

(2.8)

Uwzględniając zal. 2.6 wyznaczamy

V

2

- V

BEdc

= (1+1/

β

N

) ·R

3

·I

Cdc

(2.9)

Stąd

R

3

= (V

2

- V

BEdc

) / [(1+1/

β

N

) ·I

Cdc

]

(2.10)

R

3

≈

(5 V – 0,7 V) / (1,01 ·1 mA)

≈

4,3 k

Ω

(2.11)

Z zal. 2.8 obliczamy wartość V

R3

:

V

R3dc

≈

4,3

V

(2.12)

Wartość V

CEdc

wyznaczamy z równania oczkowego:

V

CEdc

= V

CC

- I

Cdc

·R

o

- V

R3

(2.13)

V

CEdc

= V

CC

- I

Cdc

·R

o

- I

Edc

·R

3

(2.14)

V

CEdc

= V

CC

- I

Cdc

·[R

o

+ (1+1/

β

N

) ·R

3

]

(2.15)

otrzymując:

V

CEdc

≈

2,7

V

(2.16)

Możemy teraz sprawdzić czy tranzystor rzeczywiście pracuje w obszarze aktywnym
normalnym. Pozostaje do sprawdzenia czy zachodzi zal. 1.10. Przy uwzględnieniu zal. 1.11.
otrzymujemy

V

BCdc

≈

0,7 V – 2,7 V = -2 V < 0 V

(2.17)

Złącze baza-kolektor jest spolaryzowane zaporowo, a złącze baza-emiter - przewodząco.
Tranzystor pracuje rzeczywiście w obszarze aktywnym normalnym.






ZADANIE 3.
W układzie jak na rysunku wartość wzmocnienia napięciowego dla małych częstotliwości

K

V0

= V

o

/E

m

=

-100

(3.1)

gdzie V

o

oraz E

m

są amplitudami małych napięć zmiennych. Wyznaczyć wartość R

3

. Przyjąć,

że I

Bdc

jest pomijalnie mały w porównaniu z prądami płynącymi przez rezystory R

1

oraz R

2

.

Przyjąć, że

β

N

= 100. Wartości pojemności C

1

oraz C

2

są tak duże, że kondensatory można

traktować jako zwarcia dla małych sygnałów zmiennych.

- 4 -

Rozwiązanie:
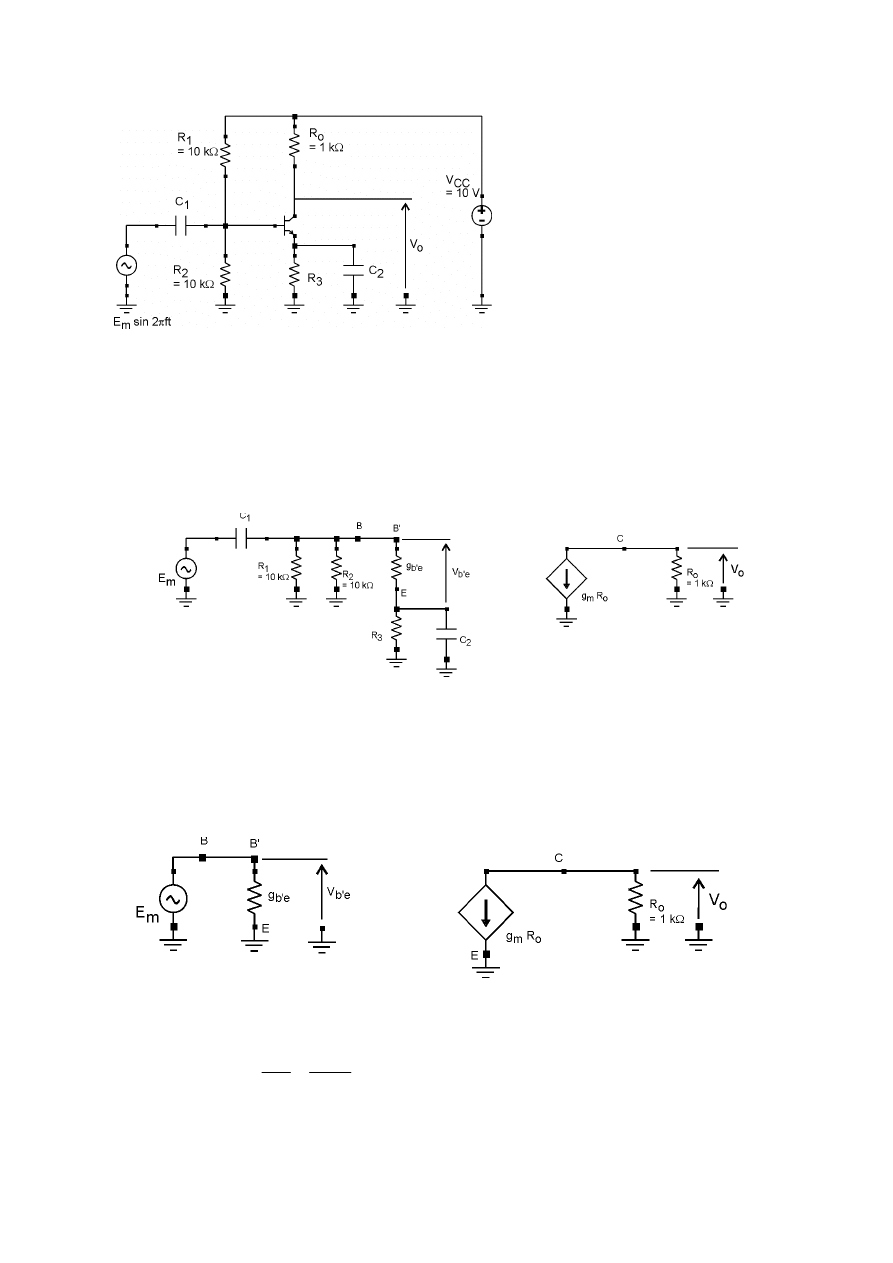
Zakładamy, że tranzystor pracuje w obszarze aktywnym normalnym. Schemat zastępczy
układu z rys. 3.1 dla małych sygnałów, małej częstotliwości przedstawia rys. 3.2.

Zauważmy, że pojemności C

1

oraz C

2

zwierają sygnał zmienny, a rezystancje R

1

oraz R

2

obciążają bezpośrednio źródło napięciowe E

m

. Dla obliczenia wzmocnienia napieciowego

schemat zastępczy można więc uprościć do postaci przedstawionej na rys. 3.3.

Konduktancję g

b'e

oraz transkonduktancję g

m

wyznaczamy ze składowych stałych prądów

kolektora lub bazy:

T

Cdc

T

Bdc

e

b

V

I

V

I

g

⋅

=

=

β

'

(3.1)

Rys. 3.1

Rys. 3.2

Rys. 3.3

- 5 -

T

Cdc

m

V

I

g

=

(3.2)

Amplituda

V

o

równa jest

V

o

=

g

m

·

R

o

(3.3)

Uwzględniając równość

V

b'e

=

E

m

(3.4)

Wzmocnienie napięciowe

K

V0

wyznaczamy jako:

T

o

Cdc

o

m

m

o

V

V

R

I

R

g

E

V

K

−

=

−

=

=

0

(3.5)

Znając wartość

K

V0

możemy wyznaczyć nieznaną wartość

I

Cdc

o

T

V

Cdc

R

V

K

I

0

−

=

(3.6)

po podstawieniu danych otrzymujemy

I

Cdc

=

2,5

mA

(3.7)

Znając wartość

I

Cdc

możemy rozważyć stałoprądowe działanie naszego układu. Jest ono

identyczne jak w zad. 2. Metodą użytą do rozwiazania zad. 2, dla danych z zad. 3
otrzymujemy:

V

R3dc

≈

4,3

V

(3.8)

R

3

≈

(5 V – 0,7 V) / (1,01 ·2,5 mA)

≈

1,7 k

Ω

(3.9)

Podobnie, jak w zad. 2 sprawdzamy na końcu czy tranzystor rzeczywiście pracuje w obszarze
aktywnym normalnym. W tym celu obliczamy

V

CEdc

V

CEdc

=

V

CC

-

I

Cdc

·[

R

o

+ (1+1/

β

N

) ·

R

3

]

(3.10)

Otrzymujemy:

V

CEdc

≈

3,25

V

(3.11)

Stąd:

V

BCdc

=

V

BEdc

-

V

CEdc

≈

0,7 V – 3,25 V = -2,55 V < 0 V

(3.12)

Złącze baza-kolektor jest spolaryzowane zaporowo, a złącze baza-emiter - przewodząco.
Tranzystor pracuje rzeczywiście w obszarze aktywnym normalnym.



ZADANIE 4.
Wartość częstotliwości granicznej wzmocnienia prądowego tranzystora bipolarnego wynosi
f

T

= 50 GHz. Tranzystor pracuje w obszarze aktywnym normalnym. Prąd kolektora ma

wartość

I

Cdc

= 1 mA. Wyznaczyć wartości czasu przelotu elektronów

t

tn

oraz pojemności

C

E

=

C

difE

+

C

jE

+

C

jC

(4.1)

gdzie

C

difE

– pojemność dyfuzyjna baza-emiter,

C

jE

- pojemność złączowa baza-emiter,

C

jC

-

pojemność złączowa baza-kolektor.

Rozwiązanie:
Wartość częstotliwości granicznej wzmocnienia prądowego tranzystora bipolarnego

f

T

związana jest z czasem przelotu nośników

t

tn

w obszarze aktywnym normalnym:

- 6 -

tn

T

t

f

π

2

1

=

(4.1)

Inaczej można tę samą zależność przedstawić jako

(

)

jC

jE

difE

m

T

C

C

C

g

f

+

+

≈

π

2

(4.2)

Z zal. 4.1 otrzymujemy

T

tn

f

t

π

2

1

=

(4.3)

Po podstawieniu danych:

t

tn

= 3,2·10

-12

s

=

3,2

ps (4.4)

Z zal. 4.2 otrzymujemy

T

T

Cdc

jC

jE

difE

E

f

V

I

C

C

C

C

π

2

≈

+

+

=

(4.5)

Po podstawieniu danych:

C

E

= C

difE

+ C

jE

+ C

jC

≈

0,13·10

-12

F

≈

0,13 pF

(4.6)

ZADANIE 5.
Tranzystor bipolarny npn o wartości częstotliwości granicznej f

T

= 50 GHz, jak w zadaniu 4,

został wykorzystany w układzie wzmacniacza ze wspólnym emiterem, podobnego do układu
z do zad. 3. Tranzystor pracuje w obszarze aktywnym normalnym przy I

Cdc

= 1 mA, a

rezystancja obciążenia ma wartość R

o

= 1 k

Ω. Rezystancja szeregowa generatora sygnału

zmiennego ma wartość R

g

= 50

Ω. Rezystancja szeregowa bazy tranzystora R

bb'

= 10

Ω,

pojemność złączowa baza-kolektor C

jC

= 0,05·10

-12

F, a współczynnik wzmocnienia

prądowego

β

N

= 100. Wyznaczyć wartości wzmocnienia napięciowego dla małych

częstotliwości K

V0

oraz górnej częstotliwości granicznej pasma przenoszenia f

0

.

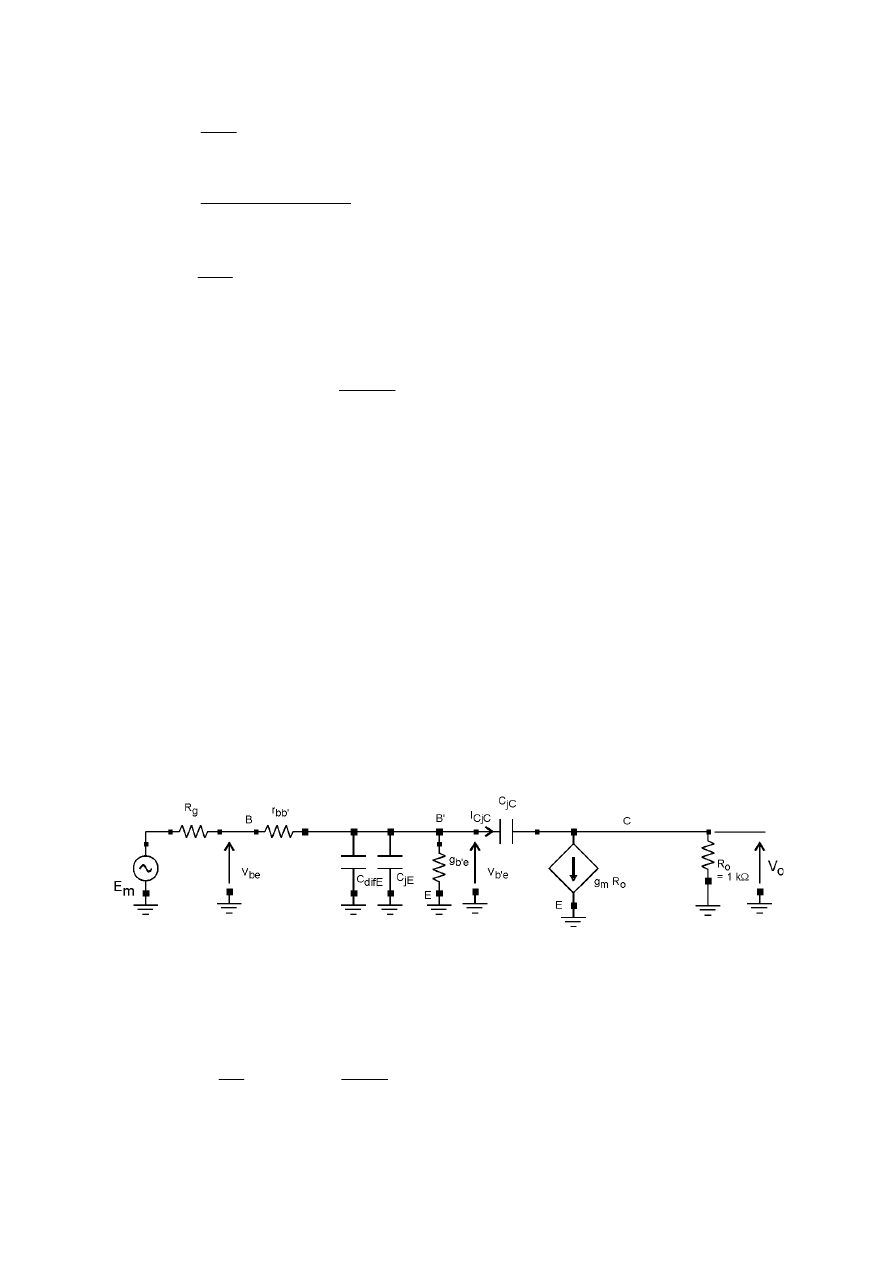
Rozwiązanie:
Przy uwzględnieniu R

g

, R

bb'

oraz pojemności tranzystora schemat małosygnałowy naszego

wzmacniacza ma postać jak na rys. 5.1.

Wzmocnienie napięciowe K

V0

Dla małych częstotliwości można pominąć pojemności w schemacie zastępczym. Widać, że
dla małych częstotliwości zależność amplitudy V

o

od aplitudy V

b'e

jest taka sama, jak zad. 3:

T

o

Cdc

o

m

e

b

o

V

R

I

R

g

V

V

−

=

−

=

'

(5.1)

Wartość wzmocnienie napięciowe K

V0

można przedstawić jako:

Rys. 5.1

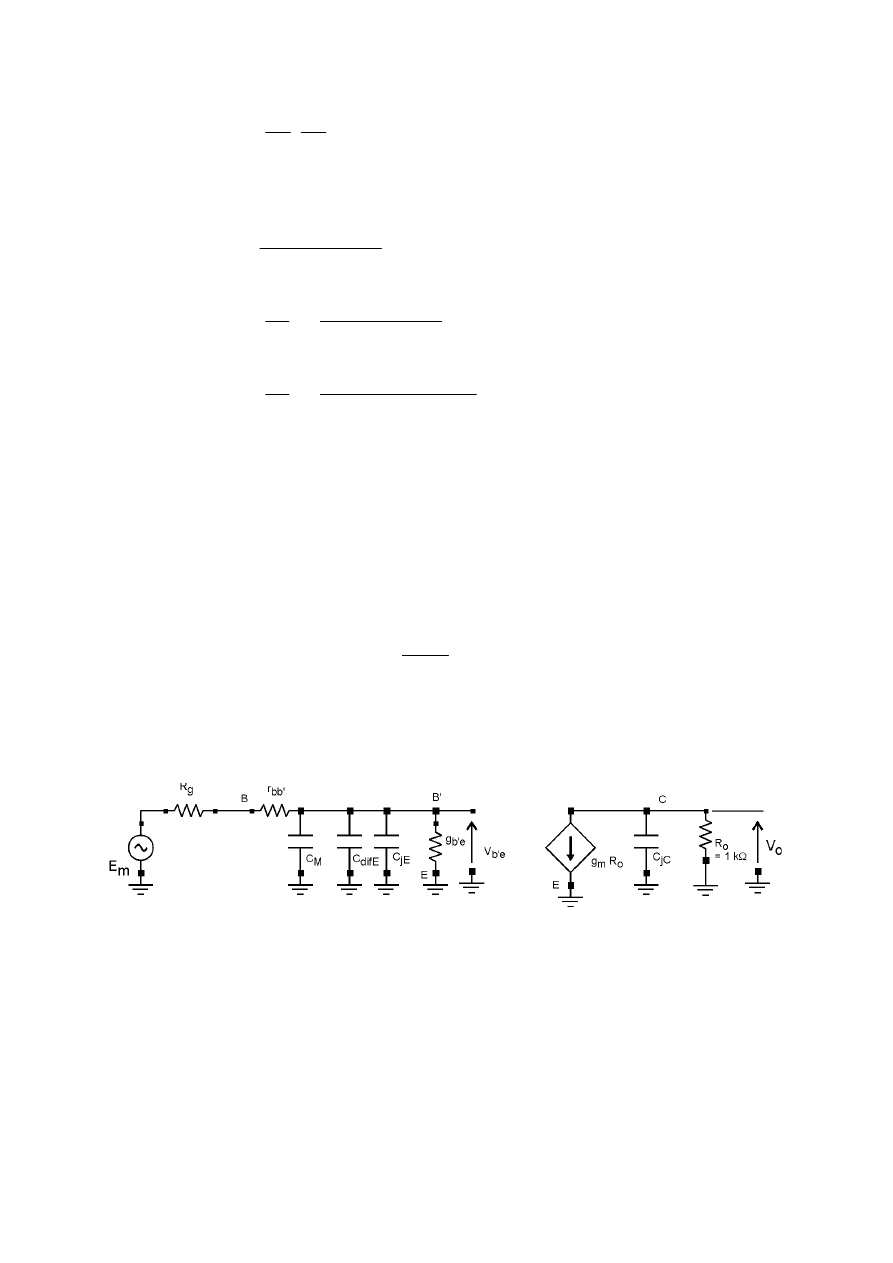
- 7 -

m

e

b

e

b

o

V

E

V

V

V

K

'

'

0

⋅

=

(5.2)

Ze schematu na rys. 5.1 wynika, że dla małych częstotliwości wartość V

b'e

można wyznaczyć

z dzielnika napięciowego tworzonego przez r

g

, r

bb'

oraz g

b'e

:

e

b

bb

g

g

e

b

g

r

r

E

V

'

'

'

)

(

1

⋅

+

+

=

(5.3)

Z zal. 5.1 – zal. 5.3 otrzymujemy:

e

b

bb

g

o

m

m

o

V

g

r

r

R

g

E

V

K

'

'

0

)

(

1

⋅

+

+

−

=

=

(5.4)

czyli

[

]

e

b

bb

g

T

Cdc

o

m

o

V

g

r

r

V

I

R

E

V

K

'

'

0

)

(

1

⋅

+

+

⋅

−

=

=

(5.5)

Korzystając z danych i zal. 3.1 oraz zal. 3.2 otrzymujemy dla małych częstotliwości, to jest
kiedy można zaniedbać pojemności tranzystora

K

V0

= V

o

/E

m

= -39.1

(5.6)

Częstotliwość graniczna f

0

Zauważmy, że wartość amplitudy prądu I

cjc

w układzie z rys. 5.1 wynosi

I

cjc

= j

ωC

jC

(V

b'e

- V

ce

)

(5.7)

Dla częstotliwości takich, że wzmocnienie napięciowe niewiele odbiega od wartości K

V0

amplitudę napięcia V

o

można przybliżyć zależnością

e

b

T

o

Cdc

e

b

o

m

o

ce

V

V

R

I

V

R

g

V

V

'

'

⋅

−

=

⋅

−

≈

=

(5.8)

Podstawiając zal. 5.8 do zal. 5.7 otrzymujemy

I

cjc

= j

ω(1+ g

m

·R

o

) ·C

jC

·V

b'e

(5.9)

Wartość prądu przedstawionego w zal. (5.9) jest taka sama, jak wartość prądu płynącego
przez pojemność C

M

w układzie przedstawionym na rys. 5.2.

gdzie

C

M

= (1+ g

m

·R

o

) ·C

jC

(5.9)

W układzie przedstawionym na rys. 5.2 obwód wejściowy jest niezależny od obwodu
wyjściowego. Łatwo wyznaczyć częstotliwość bieguna dominującego f

0

jako częstotliwość

bieguna funkcji przenoszenia V

b'e

/E

m

, jak zrobił to J.M. Miller w 1920 r.

Rys. 5.2

- 8 -

(

)

[

]

jC

o

m

jC

jE

difE

e

b

bb

g

m

e

b

C

R

g

C

C

C

j

g

R

R

E

V

+

+

+

⋅

+

⋅

+

+

=

ω

ω

'

'

'

)

(

1

)

(

(5.10)

stąd

(

)

jC

o

m

jC

jE

difE

bb

g

e

b

bb

g

C

R

g

C

C

C

R

R

g

R

R

f

+

+

+

⋅

+

⋅

⋅

+

+

=

)

(

2

)

(

1

'

'

'

0

π

(5.11)

Sumę pojemności

C

E

= C

difE

+ C

jE

+ C

jC

(5.12)

wyliczamy według zal. 4.5. Transkonduktancję g

m

i konduktancję g

b'e

obliczamy według zal.

(3.1) i zal. (3.2). Pozostałe wielkości są dane.