1. Na podstawie danych dot. projektu inwestycyjnego przedstawionych w tabeli, oblicz jego

NPV. Stopa dyskontowa wynosi 10%. Co się stanie z wartością NPV, jeśli wzrosną wymagania
inwestora, względem projektu? Zilustruj tę sytuację odpowiednim wykresem i dokonaj jego
opisu.

T0

T1

T2

T3

T4

T5

CF

-1000

220

395

325

400

250

NPV = -1000 * (1/1,1^0) +220 *(1/1,1^1) + 395 * (1/1,1^2) + 325 * (1/1,1^3) + 400 * (1/1,1^4) +
250 * (1/1,1^5) = 199, 06

Im większa stopa dyskonta (inwestora) tym wartość NPV spada.

2. Na podstawie danych dot. projektu inwestycyjnego przedstawionych w tabeli, oblicz jego IRR.

Wskazówka: NPV dla stopy dyskonta 18% jest ujemna i wynosi -16,48

T0

T1

T2

T3

T4

T5

CF

-1000

220

395

325

400

250

Procedury obliczania IRR:
1. Wyznaczamy taką stopę dyskonta k

1

, przy której obliczona wartość NPV jest bliska 0, ale

dodatnia. Obliczoną wartość NPV oznaczamy jako PV.

2. Wyznaczamy stopę dyskonta k

2

, która przy obliczeniu wartości NPV daje wartość bliską 0, ale

ujemną i oznaczamy ją jako NV.

3. Stopy dyskonta k

1

i k

2

nie mogą różnić się między sobą nie więcej niż 2 punkty procentowe.

4. Korzystamy ze wzoru:

𝑰𝑹𝑹 = 𝒌

𝟏

+

𝑷𝑽 ∗ (𝒌

𝟐

− 𝒌

𝟏

)

𝑷𝑽 + |𝑵𝑽|

-2

-1

0

1

2

3

4

5

6

7

8

9

10

0

2

4

6

8

10

12

NP

V

k

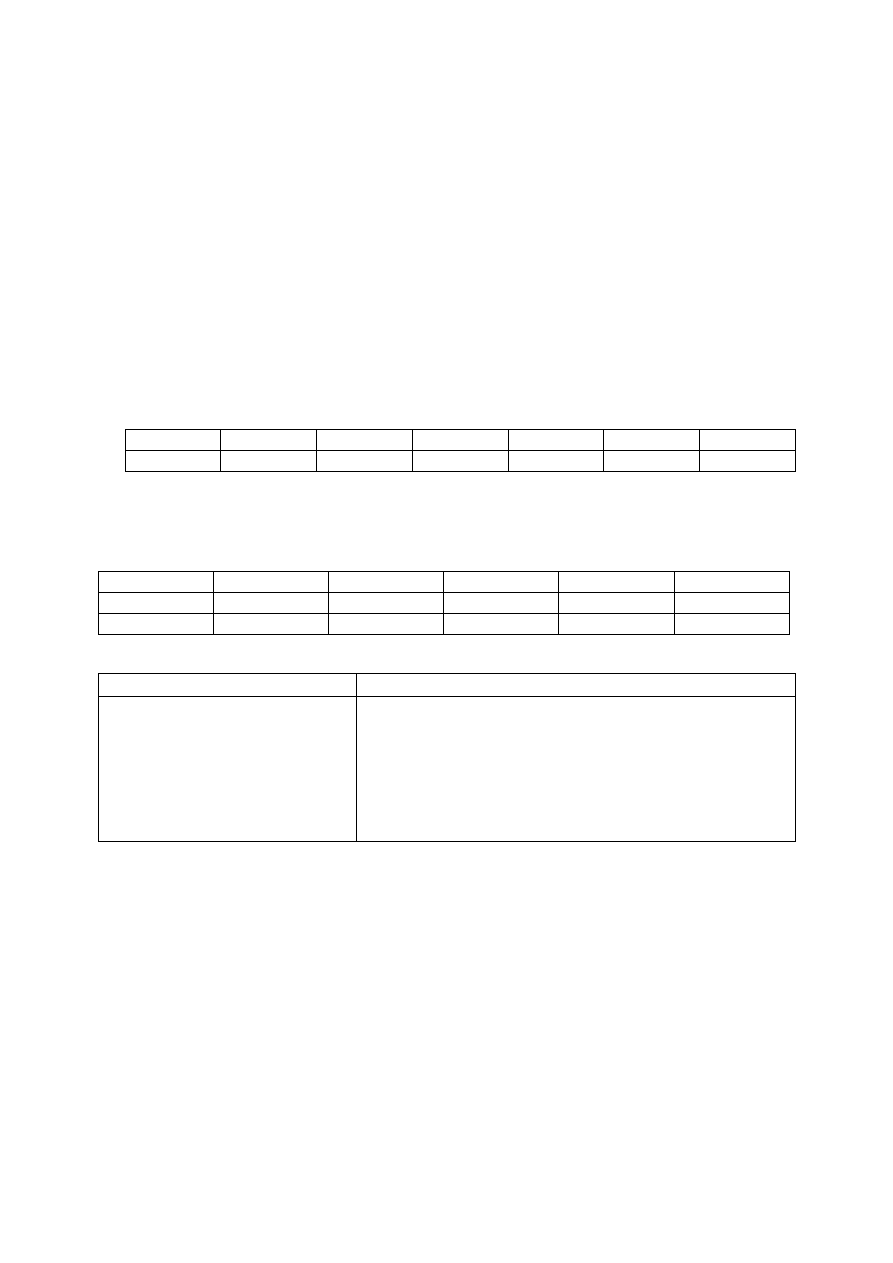
Mamy NV = -16,48 i mamy k2= 18%
Szukamy PV i k1
Wybrałam k1 = 17% (dlatego 1,17) i PV= 7

NVP= -1000 *(1/1,17^0) + 220 *(1/1,17^1) + 395 * (1/1,17^2) + 325 * (1/1,17^3) + 400 *
(1/1,17^4) + 250 * (1/1,17^5) = 7

Podstawiamy pod wzór tj. 17% + 7* (18%-17%) / 7 + 16,48 = 17,30 %

3. Na podstawie danych dot. projektu inwestycyjnego przedstawionych w tabeli, oblicz jego

okres spłaty, a następie wskaż wady i zalety okresu spłaty jako oceny opłacalności projektów
inwestycyjnych.

T0

T1

T2

T3

T4

T5

CF

-1000

220

395

325

400

250

PP = 3 + 60/400 = 3 lata i 1,8 miesiąca

T0

T1

T2

T3

T4

T5

-1000

220

395

325

400

250

-1000

-780

-385

-60

+…

+…

Zalety

Wady



prostota, zrozumiałość i to że
względnie łatwo ją zastosować



zbyt ogólna



nie uwzględnia przepływów pieniężnych generowanych po
okresie spłaty



posługuje się wartościami nominalnymi a nie realnymi



nie uwzględnia czynnika czasu



nie uwzględnia rozłożenia w czasie przepływów pieniężnych



arbitralny sposób ustalania okresu spłaty przez inwestora