Walidacja drzew decyzji

(A. Dąbrowski:

O teorii informacji.

WSiP, Warszawa 1974)

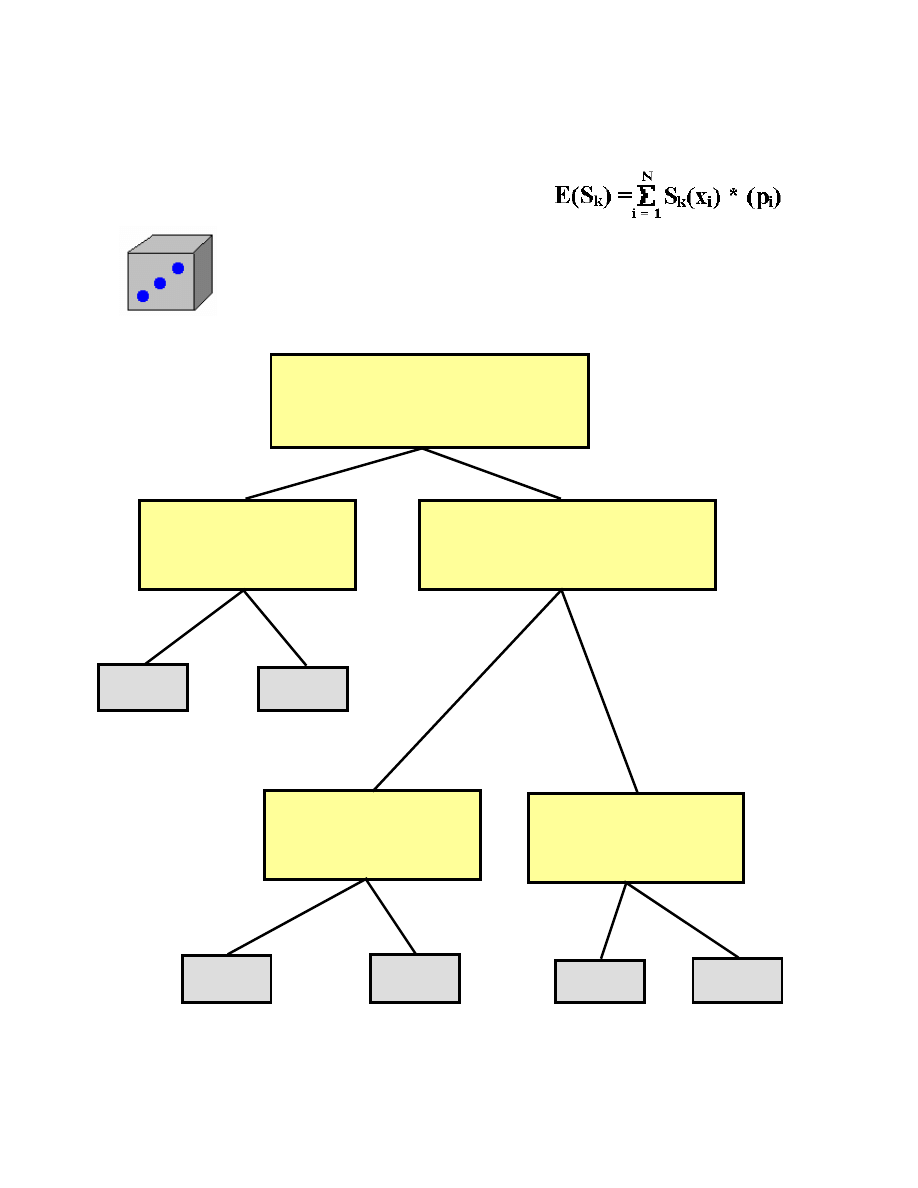
System identyfikacyjny S

1

T N

Y N

T N

T N

T N T N

2*(1/6) + 2*(1/6) + 3*(1/6) + 3*(1/6) +3*(1/6) + 3*(1/6) = 1/3 + 1/3 +

+ 1/2 + 1/2 + 1/2 + 1/2 = 2.66

Czy rzucono 1 or 2 ?

Czy rzucono 1 ?

Czy rzucono 3 lub 4 ?

Czy rzucono 3 ?

1

Czy rzucono 5 ?

2

3

4

5

6

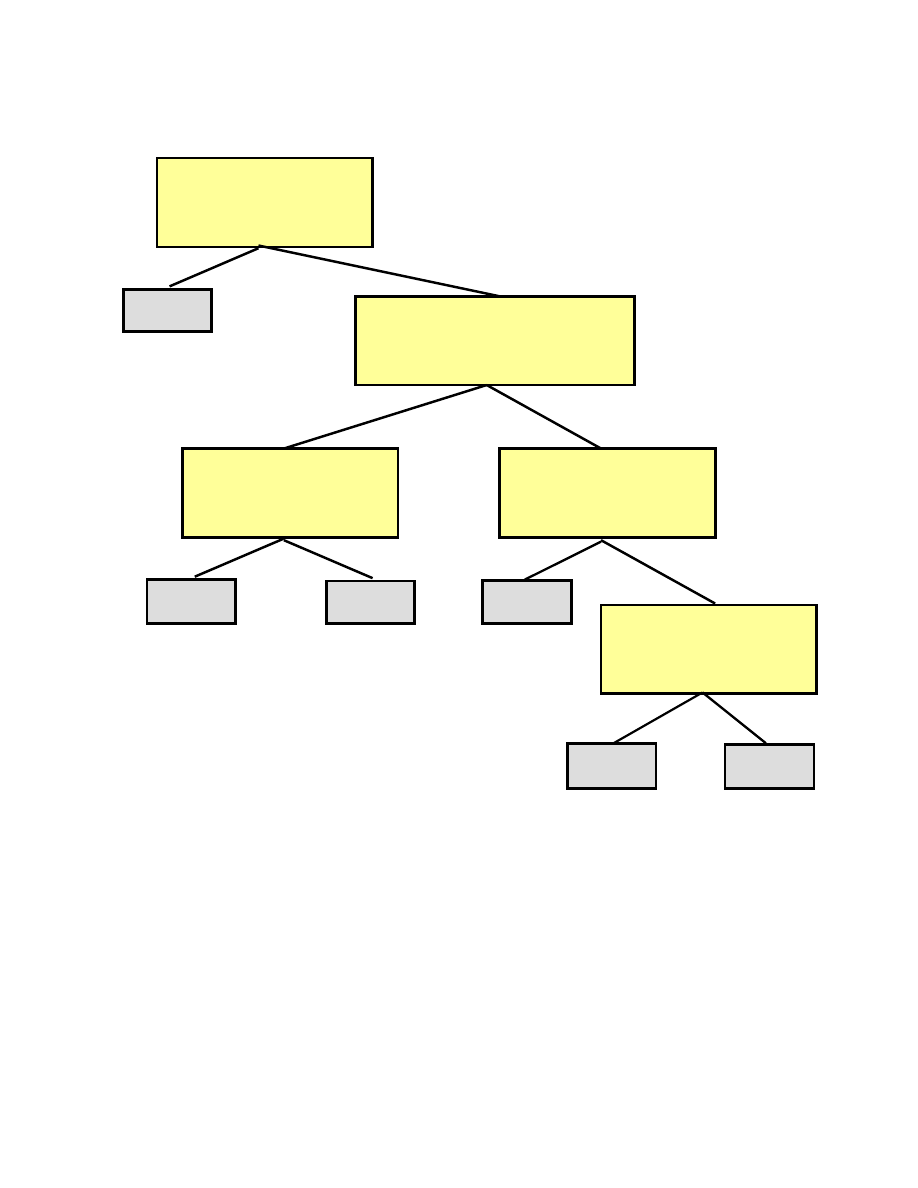
System identyfikacyjny S

2

1*(1/6) + 2*(1/6) + 2*(1/6) + 3*(1/6) +4*(1/6) + 4*(1/6) = 1/6 + 1/3 +

+ 1/3 + 1/2 + 2/3 + 2/3 = 3.00

dla X = {x

1

, x

2

, x

3

, . . . x

N

} P{x

i

} = p

i

(i = 1, 2, 3, . . . N)

E(S

1

) = 2.66 E(S

2

) = 3.00

S

1

jest

lepszy od

S

2

ponieważ: E(S

1

) < E(S

2

)

1

Czy rzucono 3 lub 4 ?

Czy rzucono 3 ?

3

4

2

Czy rzucono 5 ?

5

6

Czy rzucono 2 ?

Czy rzucono 1 ?

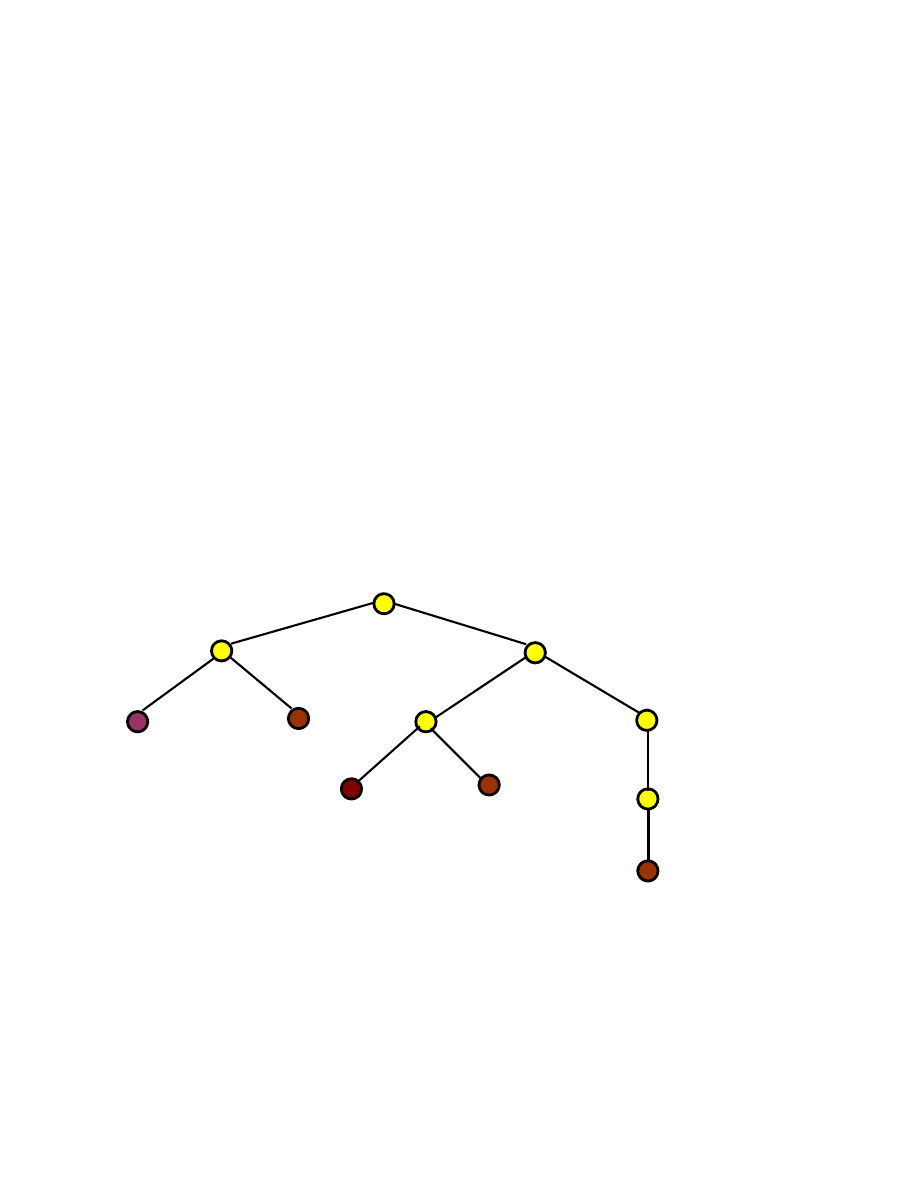
System identyfikacyjny S

3

X = {x

1

, x

2

, x

3

, . . . x

N

} p

1

= 0.95, p

2

, p

3

, p

4

, p

5

, p

6

, = 0.01

E(S

3

) = 1.12

Obecnie rozstrzygniemy kolejne zagadnienie

– możliwości ut-

worzenia optymalnego

drzewa pytań

.

Mamy zbiór liczb, które mogą być rzędami węzłów terminal-
nych w takim drzewie:

S(x

1

) = 2

S(x

3

) = 3

S(x

5

) = 4

S(x

2

) = 2

S(x

4

) = 3

x

1

x

2

x

3

x

4

x

5

Gdy wszystkie alternatywy (obiekty, przypadki) mają to same
prawdopodobieństwo, np.

p

1

= p

2

= p

3

= p

4

= p

5

= 0.20, wtedy E(S

E

) =

2.80

Jednakże gdy prawdopodobieństwa są różne, np.:

p

1

= 0.5, p

2

= 0.2, p

3

= p

4

= p

5

= 0.1

to średnia liczba pytań w tym samym systemie identyfikacyj-
nym, E(S

D

), wynosi

2.40

. Co spowodowało, że rozpatrywany

system stał się lepszy? Zjawisko to zostalo spowodowane po-
przez umiejscowienie (losowe) alternatyw bardziej prawdopo-
dobnych w węzłąch niższych rzędów (tj. węzłów osiągalnych
przy mniejszej liczbie pytań). Stąd, zgodnie ze znaną ogólną re-
gułą (znaną pod nazwą reguły Huffmanna) konstruowania op-
tymalnych systemów identyfikacyjnych, należy alternatywy o
największym prawdopodobieństwie lokować w

drzewie pytań

w

węzłach możliwie najniższego rzędu.

Sciśle mówiąc można utworzyć wiele różnych drzew, posiada-
jących węzły terminalne określonego rzędu. Jednak identyfika-
cyjne odpowiadające tym drzewom, nie muszą być takie same,
a równoważne. Musimy bowiem pamiętać, że nie każda sek-
wencja liczb n

1

, n

2

, n

3

, . . . , n

N

może reprezentować rzędy węz-

łów terminalnych. Na przykład, liczby 1, 1, 1 nie mogą być rzę-
dami liści w jakimkolwiek binarnym drzewie, ponieważ nie
więcej niż dwa węzły mogą być rzędu pierwszego. Zatem, inte-
resująca może być odpowiedź na ogólne pytanie:

Jakie warunki muszą spełniać liczby n

1

, n

2

, n

3

, . . n

N

, aby istnia-

ło drzewo binarne, którego węzły terminalne mają odpowiednio
rząd

S(x

1

) = n

1

, S(x

2

) = n

2

, S(x

3

) = n

3

, . . . , S(x

N

) = n

N

?

Odpowiedzią na powyższe pytanie jest nierowność Krafta. Li-
czby

n

1

, n

2

, n

3

, . . . n

N

mogą być rzędami węzłów w pewnym drzewie wtedy i tylko
wtedy, gdy spełniają tę nierówność:

W naszym przypadku nierównośc Krafta jest spełniona (0.25 +
0.25 + 0.125 + 0.125 + 0.0625 = 0.8125), zatem liczby 2, 2, 3, 3
oraz 4 mogą być rzędami węzłów terminalnych binarnego drze-
wa uprzednio pokazanego.

Porównanie średniej liczby pytań dla dwu (lub więcej) syste-
mów identyfikujących ten sam zbiór przypadków umożliwia
stwierdzenie, który z rozpatrywanych systemów jest lepszy. Na-
leży jednak postawić pytanie, czy (i kiedy?) dane drzewo jest
optymalne, tzn. czy reprezentuje najlepszy system? Odpowiedź
na to pytanie można uzyskać przyjmując założenie, że dla zbio-
ru przypadków (alternatyw) X istnieje liczba, która jest dolną
granicą wartości średniej liczby pytań wszystkich systemów iden-
tyfikacyjnych tego zbioru X. Jeżeli

E(S

k

)

jest równe tej liczbie

(dla pewnego systemu) wtedy wiemy na pewno, że jest to naj-
lepszy system identyfikacyjny danego zbioru alternatyw. Do-
kładny zapis wspomniaego założenia jest następujący:

Niech X = {x

1

, x

2

, x

3

, . . . x

N

} będzie zbiorem alternatyw, zaś

liczby P{x

i

} = p

i

(dla i = 1, 2, 3, . . . N) prawdopodobieństwem

elementów zbioru X. Wtedy dla każdego systemu identyfika-
cyjnego S zachodzi nierówność:

E(S) >= H(X)

gdzie

jest ilością informacji potrzebnej do identyfikacji elemetów z-
bioru X, lub krócej - iloscią informacji zawartej w zbiorze X.

H(X) [bitów] może byc zatem uznane za średnią liczbę pytań w
pewnym idealnym systemie rozpoznającym elementy zbioru X.

Niech, na przykład X = {x

1

, x

2

, x

3

, x

4

},

P{x

1

} = 0.5

P{x

2

} = 0.25 P{x

3

} = P{x

4

} = 0.125

S(x

1

) = 1,

S(x

2

) = 2,

S(x

3

) = S(x

4

) = 3

E(S) = 0.5*1 + 0.25*2 + 0.125*3 + 0.125*3 = 7/4

H(X)

= – 0.5*log

2

0.5 – 0.25*log

2

0.25 – 2*(0.125*log

2

0.125) = 7/4

Nasuwa się pytanie, dla jakich zbiorów X oraz odpowiednich
systemów identyfikacyjnych S

k

, jest ważna (prawdziwa) zależ-

ność E(S) = H(X)? Inaczej mówiąc, jesteśmy zainteresowani
problemem, czy dla danego zbioru przypadków istnieje taki sy-
stem identyfikacyjny, który spełnia tę ogólną zależność? Moż-
liwość udzielenia odpowiedzi na to pytanie, może oszczędzić
mnóstwo niepotrzebnego wysiłku. Użytecznym w rozstrzygnię-
ciu postawionego problemu jest teoremat stwierdzający, że aby
istniał system S identyfikujący elementy zbióru X, koniecznym
i wystarczającym jest aby dla każdego i = 1, 2, 3, . . . N, log

2

p

i

był liczbą człkowitą. Narzuca to wniosek, że jedynie niektóre
zbiory alternatyw mogą mieć absolutnie najlepszy system iden-
tyfikacyjny [tzn. E(S) = H(X)]. Wszystkie inne zbiory przypad-
ków (alternatyw) wykazują taką właściwość, że zawsze istnieje
system identyfikacyjny, w którym średnia liczba pytań różni się
od wartości H(X) o nie więcej niż jeden,

tzn.

H(X) < E(S) < H(X) + 1

.

Wróćmy do przykładu rozważanego poprzednio (system E(S

D

)).

Mamy E(S

D

) = 2.4 (dla nierówno rozdzielonych prawdopodo-

bieństw poszczególnych przypadków), podczas gdy:

H(X) = – 0.5*log

2

0.5 – 0.2*log

2

0.2– 3(0.1*log

2

0.1) = 1.961

Zatem E(S

D

) > H(X), a to oznacza, że E(S

D

) nie jest optymalnym

systemem identyfikacji alternatyw zbioru X. W rozpatrywa-
nym przypadku jedynie można przypuszczać, że może istnieć
taki system identyfikacji przypadków ze zbioru X, dla którego
średnia liczba pytań jest bliższa wartości H(X); w przypadku
systemu doskonałego E(S

D

) będzie równe H(X). Musimy jednak

sprawdzić, czy będzie to możliwe? Okazuje się, że dla rozpatry-
wanego zbioru alternatyw (z przypisanymi wartościami praw-
dopodobieństwa) nie można zaprojektować optymalnego syste-
mu, ponieważ log

2

0.2 oraz log

2

0.1 nie są liczbami całkowitymi.

Z tego więc względu, średnia liczba pytań jest liczbą z przedzia-
łu

E(S

D

) ∈

∈

∈

∈ <1.961, 2.961>

[Być może należy przypomnieć definicję logarytmu:

log

B

N = Z

B

Z

= N

(np. log

10

2 = 0.3010, ponieważ 10

0.3010

= 2)

log

2

N = Z, więc 2

Z

= N

Z ln 2 = ln N

Z = ln N/ln 2 = ln N/0.6931

]