TTTTTTTT

AAAAA

TTTTTTT

C

TTTT

AAA

#6 Metody wiarygodnościowe

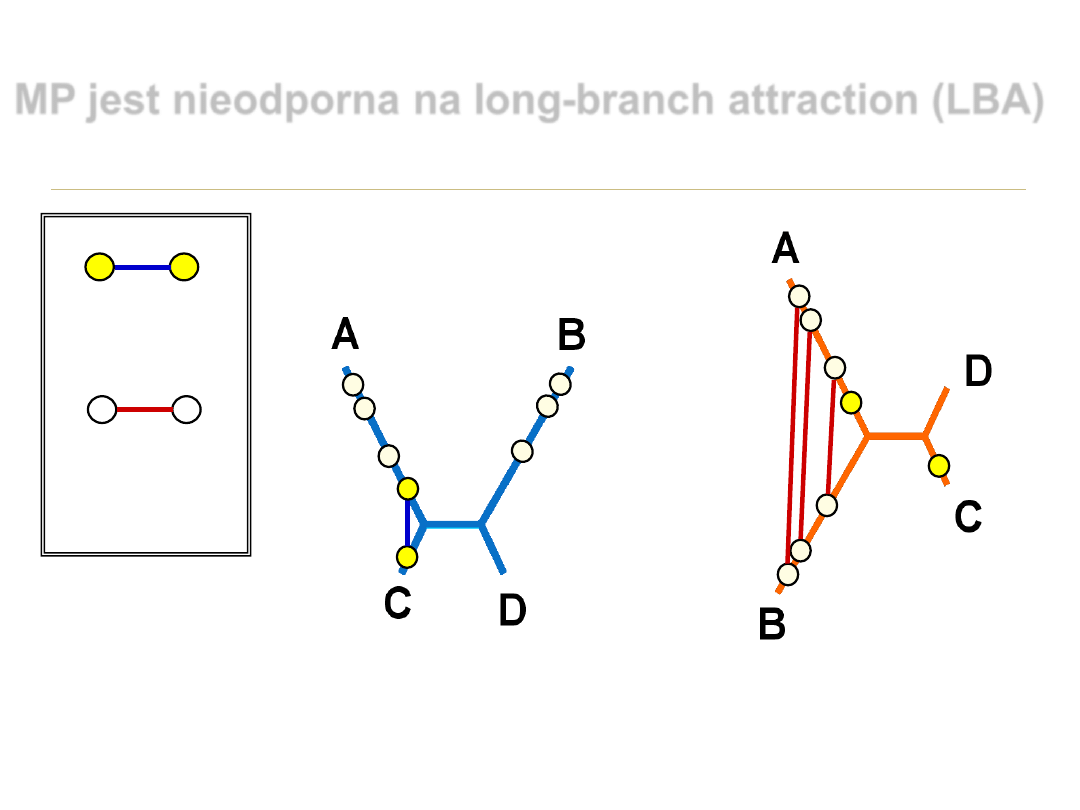
błędne drzewo z LBA

prawdziwe drzewo

MP jest nieodporna na long-branch attraction (LBA)

synapomorfia

homoplazja

– pozorna

synapomorfia

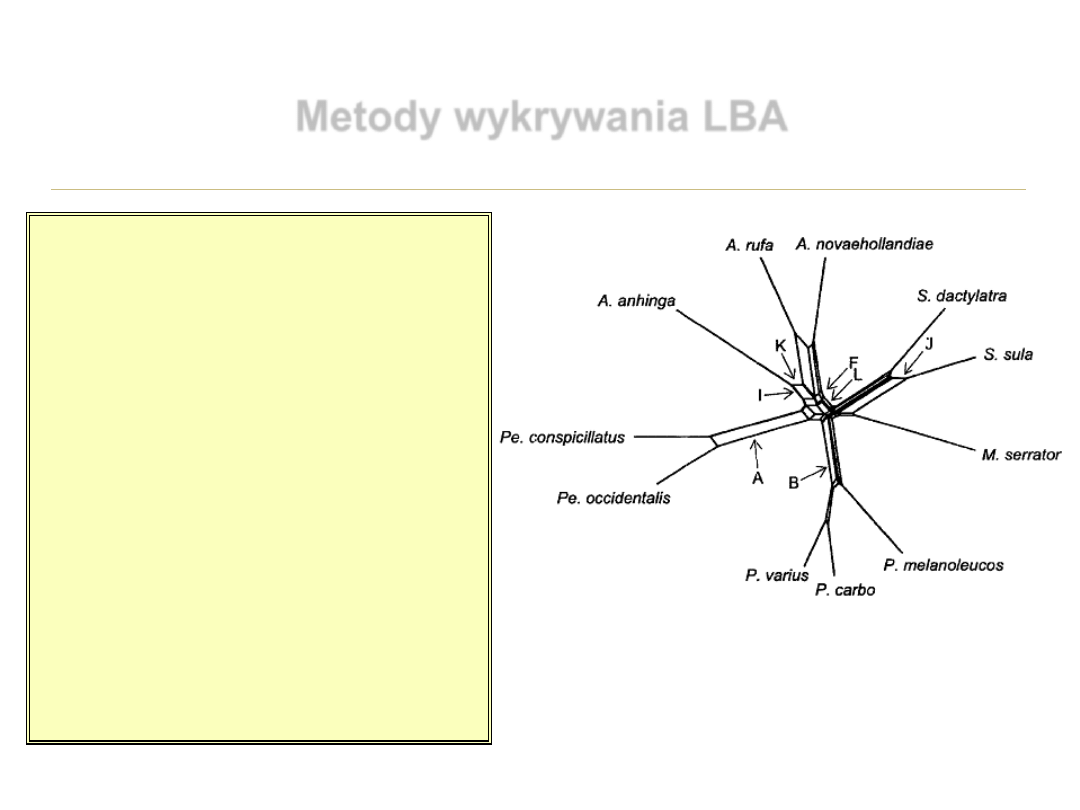
Metody wykrywania LBA

Neighbor-nests generowane
przez SplitTree4

1.

Osobne analizy partycji

2.

Usuwanie potencjalnych

długich gałęzi

3.

Dobór grup zewnętrznych

4.

Symulacje parametryczne
(bootstrap)

5.

Split decomposition +
analiza spektralna

6.

Niezgodność wyników z

różnych metod

7.

Porównanie z filogenią

morfologiczną

Jak uniknąć wpadnięcia w „strefę

Felsensteina”

1.

Wyłączanie pewnych fragmentów
sekwencji np. 3-cia pozycja kodonu,
fragmenty hiperzmienne

2. Dodawanie nowych taksonów (?)
3.

Dodawanie nowych źródeł danych i
analiza total evidence

4.

Zastosowanie metod biorących pod

uwagę długość gałęzi

1.

Wyłączanie pewnych fragmentów
sekwencji np. 3-cia pozycja kodonu,
fragmenty hiperzmienne

2. Dodawanie nowych taksonów
3.

Dodawanie nowych źródeł danych i
analiza total evidence

4.

Zastosowanie metod biorących pod

uwagę długość gałęzi

Metody wiarygodnościowe

są najbardziej odporne na ten problem,

jeśli zostanie zastosowany odpowiedni

model substytucji

Modele ewolucji sekwencji

•

Modele mogą dotyczyć różnych aspektów ewolucji
sekwencji:

–

Różnorodnego stosunku transwersji do tranzycji.

– Odmiennej frekwencji nukleotydów.

–

Różnorodnego tempa ewolucji w poszczególnych
miejscach sekwencji.

–

Różnorodnego tempa ewolucji (=substytucji) w

ramach linii (poszczególnych taksonów) czy całych
partii drzewa.

Modele ewolucji sekwencji

• Bogactwo parametrów modeli ma pozytywne i

negatywne strony:





im więcej parametrów do testowania tym lepiej można

dopasować model do konkretnych danych.





im więcej parametrów do testowania tym wyższa

wariancja oszacowania.

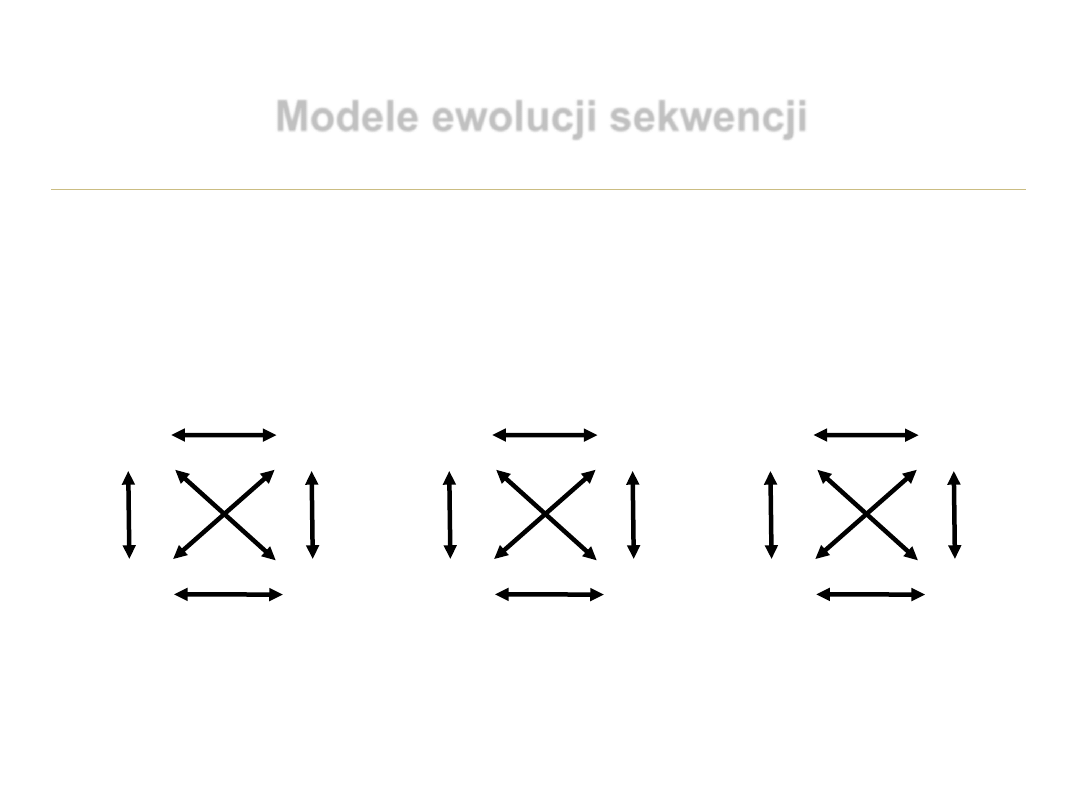
Modele ewolucji sekwencji

T

C

A

G

a

a

a

a

a

a

Jukes-Cantor

T

C

A

G

a

f

e

b

c

d

Generalny

T

C

A

G

2α

α

α

Kimura 2 parametrowy

2α

2α

2α

Metody wiarygodnościowe

1. Maximum Likelihood (ML, metoda

maksymalnej wiarygodności)

2. Bayesian Phylogenetic Inference +

Markov Chain Monte Carlo (BPI+ MCMC,

wnioskowanie Bayesowkie z łańcuchem
Markowa Monte Carlo)

Metody wiarygodnościowe

 Zalety metod:

–

Dobrze pracują z danymi zawierającymi zarówno odlegle
spokrewnione sekwencje jak i bliskie sobie gatunki – najbardziej
uniwersalne

–

Wykorzystują wszystkie dane – zmienne i niezmienne, informatywne
parsymonicznie i nieinformatywne

–

Dobrze sprawują się przy niejednorodnym tempie substytucji (biorą

pod uwagę długość gałęzi) i w związku z tym są najbardziej odporne

na LBA spośród wszystkich metod filogenetycznych

–

Mogą stosować szeroką gamę modeli ewolucji sekwencji (DNA i
aminokwasy), a nawet modele ewolucji cech morfologicznych

 Wady metod:

–

Czułe na źle dobrany model ewolucji cech

–

Bardzo powolne i wymagają dużej mocy obliczeniowej komputera

Metoda maksymalnej wiarygodności

(Maximum Likelihood, ML)

•

Metoda do szacowania parametrów w statystyce: najlepszą

estymacją parametru jest wartość, która najbardziej
prawdopodobnie wygeneruje obserwowane dane

•

Zaaplikowana do filogenetyki molekularnej przez Joe Felsensteina
(1981)

•

ML

zakłada określony, niekiedy złożony model ewolucji sekwencji.

•

Celem analizy ML

jest odpowiedź na pytanie:

Jakie jest prawdopodobieństwo P powstania obserwowanych
danych D (w tym wypadku alignmentu wielu sekwencji) dla danej
topologii drzewa filogenetycznego T

przy określonym modelu

ewolucji ME?

Jak działa ML?

1.

Warunkiem wstępnym analizy jest otrzymanie
odpowiedniego modelu ewolucji sekwencji ME (np.
Modeltest).

2.

Dla każdej pozycji j w alignmencie generowane są

wszystkie możliwe topologie drzewa dla danej liczby
taksonów (sekwencji).

3.

Opierając się na modelu ewolucji ME obliczamy

prawdopodobieństwo układu nukleotydów L(j) dla

każdego z tych drzew w pozycji j i je sumujemy.

4.

Obliczamy prawdopodobieństwo całkowite powstania
obserwowanego alignmentu dla topologii L poprzez

iloczyn wszystkich prawdopodobieństw z
poszczególnych pozycji.

Przykładowa analiza MJ dla przypadku 4 taksonów

1 j N

---------------------------------------

Takson 1:

A... C G C G C T G G G ... C

Takson 2:

A... C G C G C T G G G ... C

Takson 3:

A... C G C A A T G A A ... C

Takson 4:

A... C A C A G G G A A ... C

Wybieramy dowolną cechę j = pozycję w alignmencie

1 2 3 4

C C A G

j

----

1:

C

2:

C

3:

A

4:

G

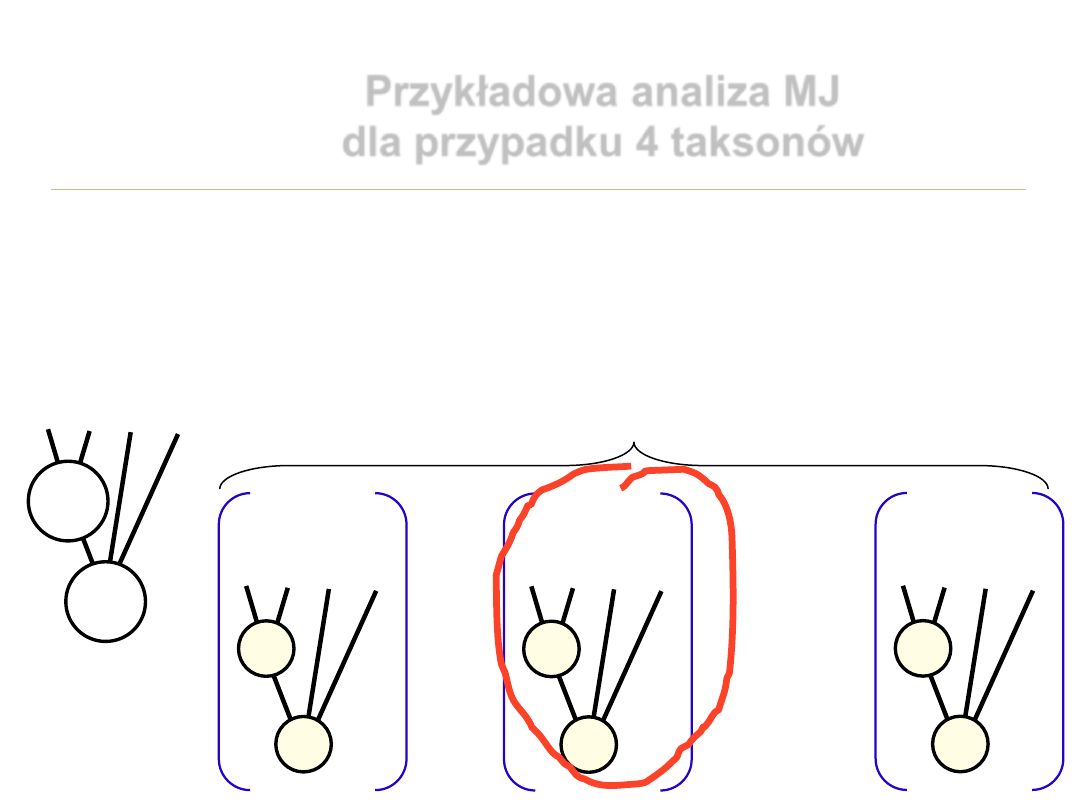
Przykładowa analiza MJ

dla przypadku 4 taksonów

Wyszukujemy wszystkie ukorzenione

topologie dla 4 taksonów i dodatko-

wo oznaczamy liście stanem cechy j

1 2 3 4

C C A G

1 3 2 4

C A C G

2 3 1 4

C A C G

1 4 2 3

C G C A

2 4 1 3

C G C A

3 4 1 2

A G C C

1 2 3 4

C C A G

1 2 4 3

C C G A

3 4 1 2

A G C C

2 3 4 1

C A G C

1 2 3 4

C C A G

1 4 3 2

C G A C

1 3 2 4

C A C G

1 2 3 4

C C A G

1 3 2 4

C A C G

1 4 2 3

C G C A

2 1 3 4

C C A G

2 3 1 4

C A C G

2 4 1 3

C G C A

3 1 2 4

A C C G

3 2 1 4

A C C G

3 4 1 2

A G C C

4 1 2 3

G C C A

4 2 1 3

G C C A

4 3 2 1

G A C C

1 węzeł – 1

2 węzły – 10

3 węzły – 15
-----------

26

j

----

1:

C

2:

C

3:

A

4:

G

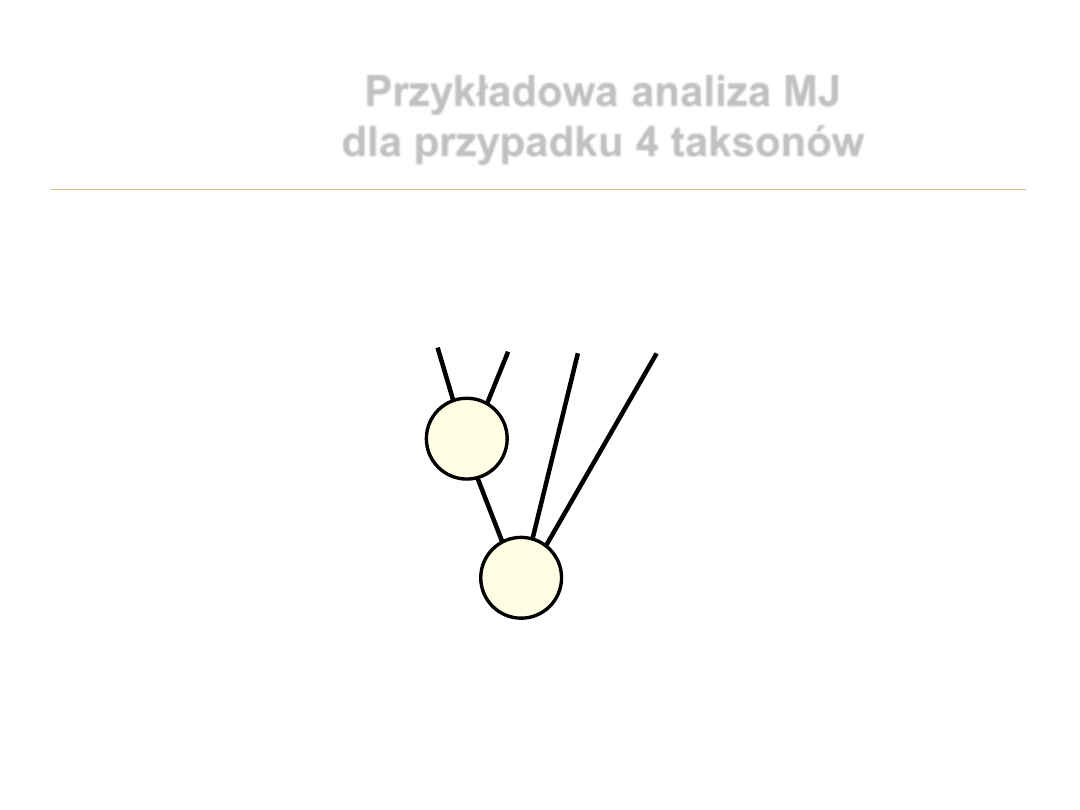
Przykładowa analiza MJ

dla przypadku 4 taksonów

Dla każdego z tych drzew obliczamy prawdopodobieństwo L

(j)

układu

nukleotydów w pozycji j alignmentu

jako sumę prawdopodobieństw

wszystkich możliwych pośrednich stanów cechy prowadzących do tej

topologii przy założonym modelu ewolucji sekwencji ME.

1 2 3 4

C C A G

L(j) = P

(1)

+ P

(2)

+ ... + P

(16)

1 2 3 4

C C A G

A

A

1 2 3 4

C C A G

A

C

1 2 3 4

C C A G

T

G

Liczba aranżacji k= 4 dla danej
topologii o n

węzłach

n

AC

GT

AC

GT

j

----

1:

C

2:

C

3:

A

4:

G

Przykładowa analiza MJ

dla przypadku 4 taksonów

P

(i)

= P

A-C(5)

x P

C-C(1)

x P

C-C(2)

x P

A-A(3)

x P

A-G(4)

1 2 3 4

C C A G

A

C

5

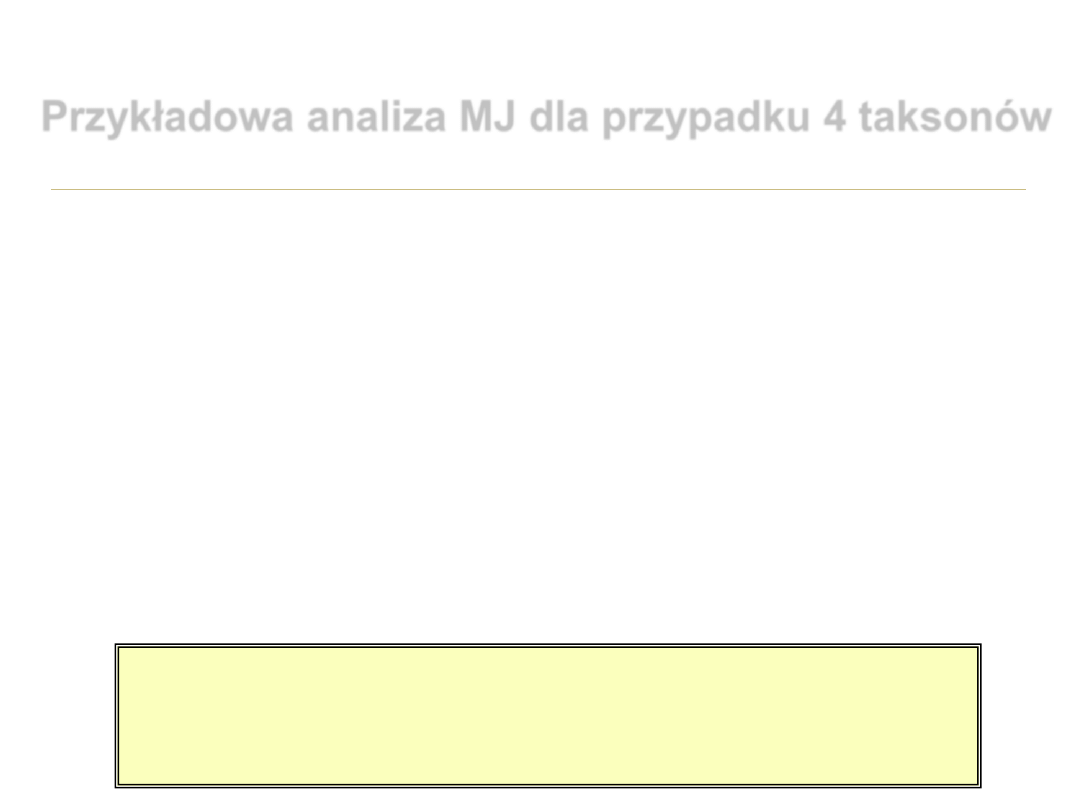
Obliczanie prawdopodobieństwa końcowego dla danej
topologii drzewa

Przykładowa analiza MJ dla przypadku 4 taksonów

Ponieważ L jest bardzo małą wartością przedstawia się je w
postaci logarytmu naturalnego:

Preferowane jest drzewo o największej wartości

prawdopodobieństwa L (Maximum Likelihood)
albo najmniejszej –lnL.

L=L

(1)

× L

(2)

× .... × L

(N)

=

∏

=

N

j

L

(j)

1

∑

=

N

j 1

lnL

(j)

lnL=lnL

(1)

+ lnL

(2)

+ ... + lnL

(N)

=

∑

=

N

j 1

lnL

(j)

lnL=lnL

(1)

+ lnL

(2)

+ ... + lnL

(N)

=

Wnioskowanie bayesowskie (BPI, Bayesian

inference)

• Jedna z najstarszych metod statystycznych – 1790,

Thomas Bayes, zastosowana do filogenetyki od 1968.

•

Metoda zbliżona koncepcyjnie do ML

• Celem analizy BI

jest odpowiedź na pytanie:

Jakie jest prawdopodobieństwo P, że dana topologia
drzewa T

przy określonym modelu ewolucji jest

prawdziwa dla obserwowanych danych D (w tym
wypadku alignmentu wielu sekwencji)?

ML: P(D/T)

BPI: P (T/D)

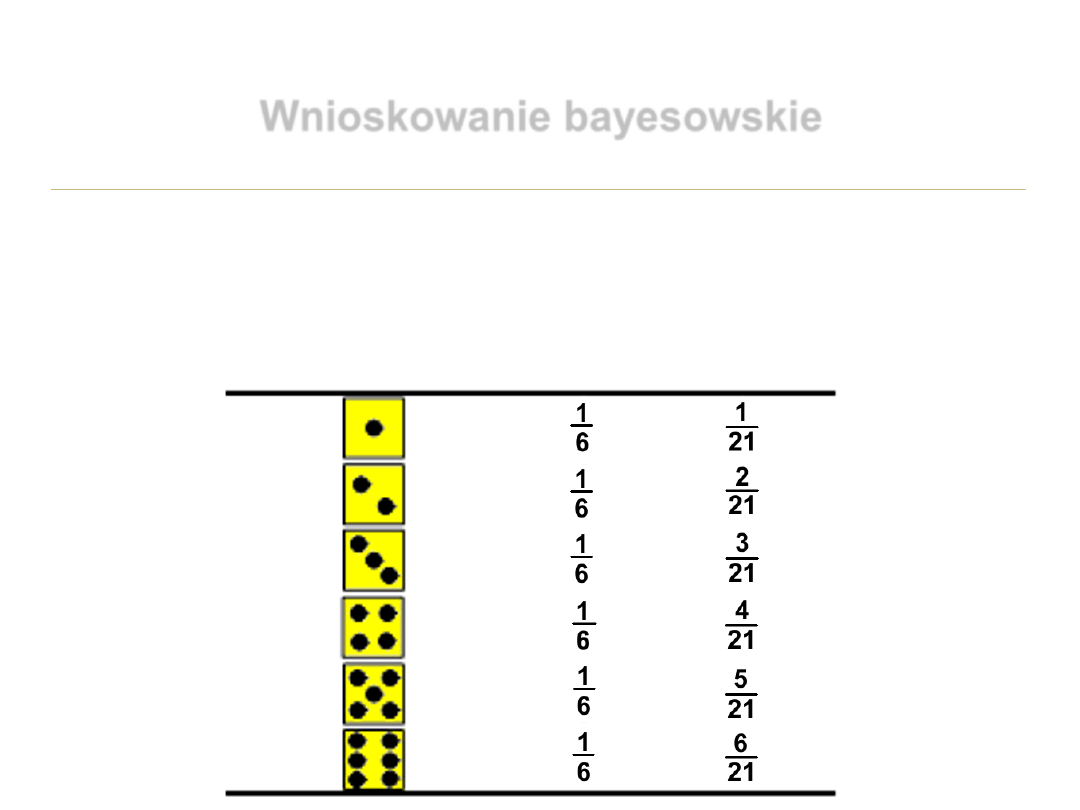
Wnioskowanie bayesowskie

100 kostek, 90 prawdziwych, 10 fałszywych
Prawdopodobieństwo P wyrzucenia oczek wynosi:

prawdziwa fałszywa

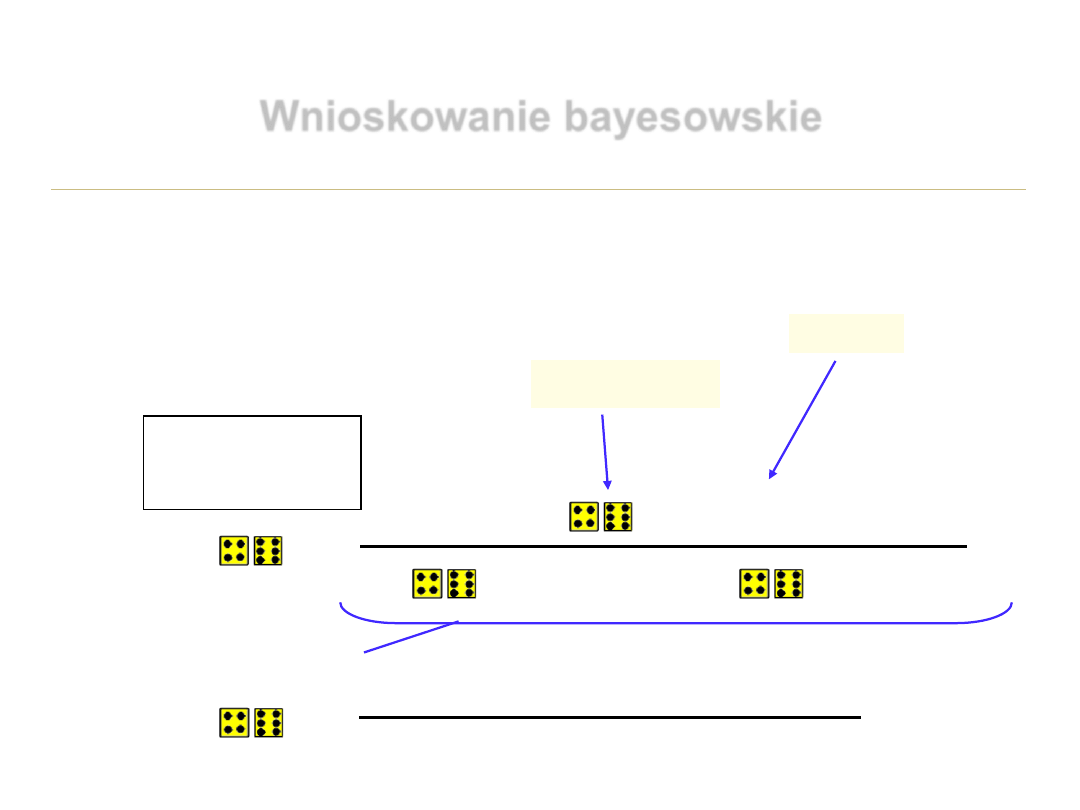
Wnioskowanie bayesowskie

Wyjęto jedną kostkę i dwa razy rzucono – za

pierwszym rzutem 4 oczka, za drugim 6.

Jakie jest prawdopodobieństwo, że kostka jest

fałszywa?

P [ | prawdziwa] = 1/6 x 1/6 = 1/36

P [ | fałszywa] = 4/21 x 6/21 = 24/441

P [fałszywa] / P [prawdziwa] = 1,93

Wnioskowanie bayesowskie

Wnioskowanie bayesowskie opiera się na prawdopodobień-

stwie a posteriori

(końcowym), które obrazuje jak zmieniła

się nasza opinia, czyli prawdopodobieństwo a priori
(początkowe) pod wpływem obserwacji.

prawdziwa +

fałszywa -

P [-| ] =

P [ |-] x P [-]

P [ |-] x P [-]x P [ |+ ] x P [+]

P [-| ] =

24/441 x 1/10
24/441 x 1/10 + 1/36 x 9/10

= 0,179

stała normalizująca

a priori

obserwacji

.

Zastosowanie formuły Bayesa

do rekonstrukcji filogenii

Bayesowskie oszacowanie filogenii opiera się na określeniu

wartości prawdopodobieństwa a posteriori drzewa.

s – liczba gatunków

B(s) –

liczba wszystkich możliwych drzew t

1

, t

2

, ... t

B(s)

dla s

gatunków

D – obserwowane dane tzn. alignment sekwencji lub macierz

morfologiczna

P (D|t

j

) x P (t

j

)

P (D|t

i

) x P (t

i

)

B(s)

j=1

∑

P (t

i

|D) =

Łańcuch Markowa Monte Carlo (MCMC)

Obliczenie prawdopodobieństwa a posteriori

obejmuje sumę wszystkich możliwych drzew i

wszystkich kombinacji długości gałęzi wraz z

modelem ewolucyjnym dla każdego z drzew, co
jest oprócz kilku bardzo prostych przypadków

niemożliwe do uzyskania drogą analityczną.

Zatem prawdopodobieństwo końcowe drzew z

konieczności musi być szacowane.

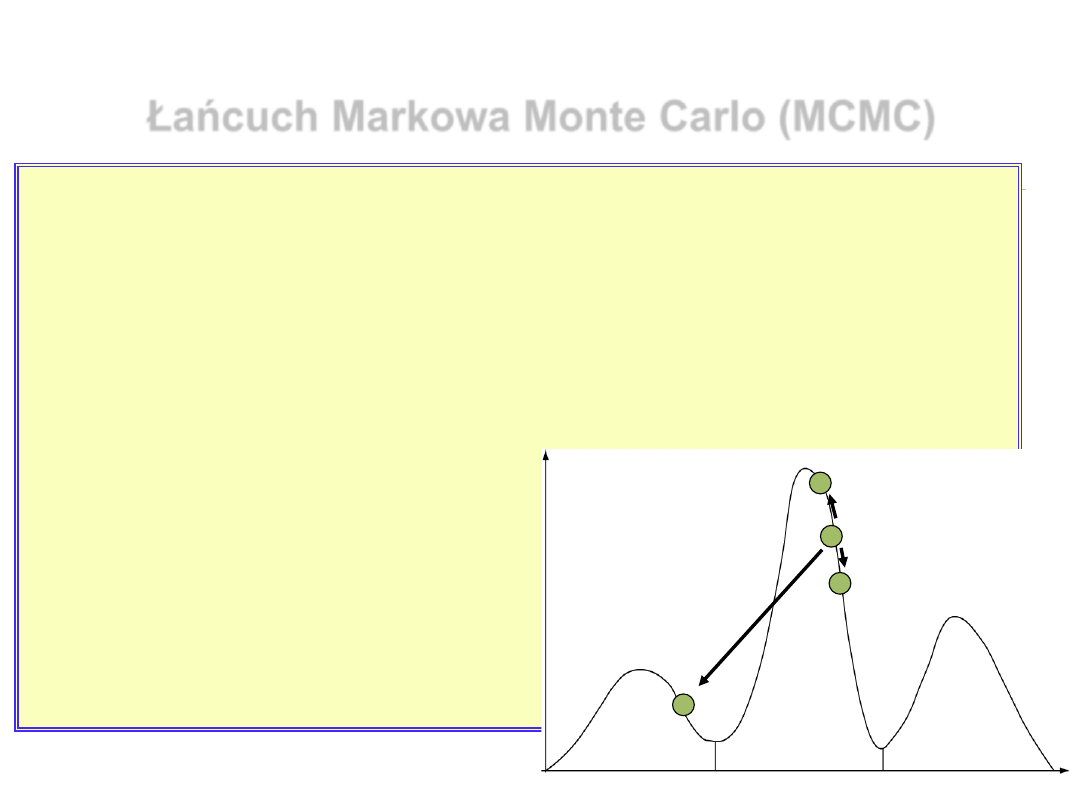
Konstrukcja MCMC

1. Zacznij w dowolnym miejscu przestrzeni parametrów = wybierz dowo lne

drzewo T ze zbi

oru wszystkich możliwych drzew dla danej liczby taksonów

2. Wybierz losowo drzewo T’

, które jest sąsiadem drzewa T z pkt . 1

3.

Przelicz stosunek prawdopodobieństw dla zaproponowanych drzew pr zy
danym modelu ewolucji cech R=P(T’)/P(T)

4.

Jeżeli R>=1 zaakceptuj nowe
drzewo ( T=T’

) i przejdź do pkt . 2

5.

Jeżeli R<1 wybierz losowo liczbę

z przedziału (0,1)
•

jeśli liczba ta jest mniejsza
od R to zaakceptuj nowe drzewo

•

jeśli nie, to obecne drzewo

pozostaw jako T

6.

Wróć do pkt . 2

Łańcuch Markowa Monte Carlo (MCMC)

zbiór wszystkich topologii

zawsze akceptuj

R>1

niekiedy akceptuj

R~1

pr

aw

dopodob

ieńs

tw

o

a

pos

ter

ior

i

nigdy nie
akceptuj

R<<1

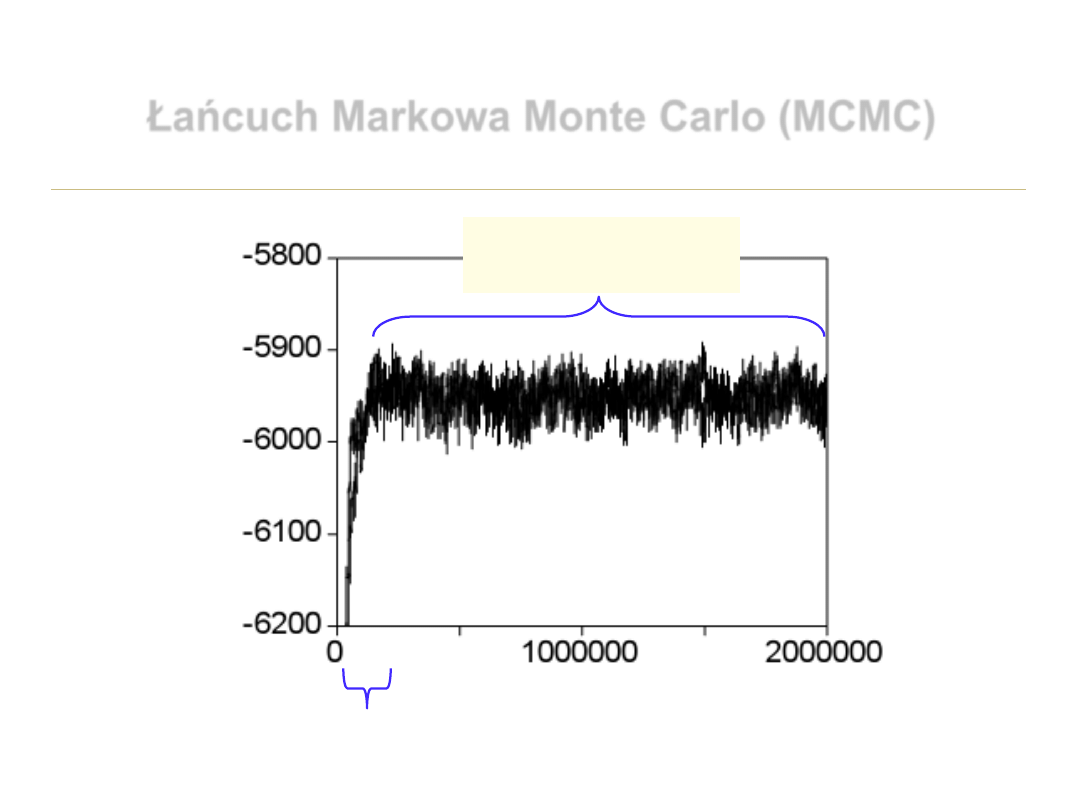
Łańcuch Markowa Monte Carlo (MCMC)

okres początkowy
(burn-in period)

okres zbieżności
(convergence period)

generacje

LnP

a

pos

ter

ior

i

Powiązany MCMC Metropolisa (Metropolis

Coupled MCMC, MCMCMC, (MC)

3

Idea algorytmu polega równoległym uruchomieniu n

łańcuchów Markowa, z czego jeden łańcuch operuje na

badanym rozkładzie prawdopodobieństwa P(t

i

|DX) jako

dystrybucji referencyjnej (tzw. zimna dystrybucja,

cold

distribution

), zaś pozostałe łańcuchy operują na

zmienionej dystrybucji, „podgrzanej” (

heated distribution

)

otrzymanej poprzez podniesienie rozkładu referencyjnego

do potęgi

β

i

, której wartość zawiera się w przedziale od 0

do 1.


T – czynnik „temperatury”

β

i

= 1/1+(i-1)T

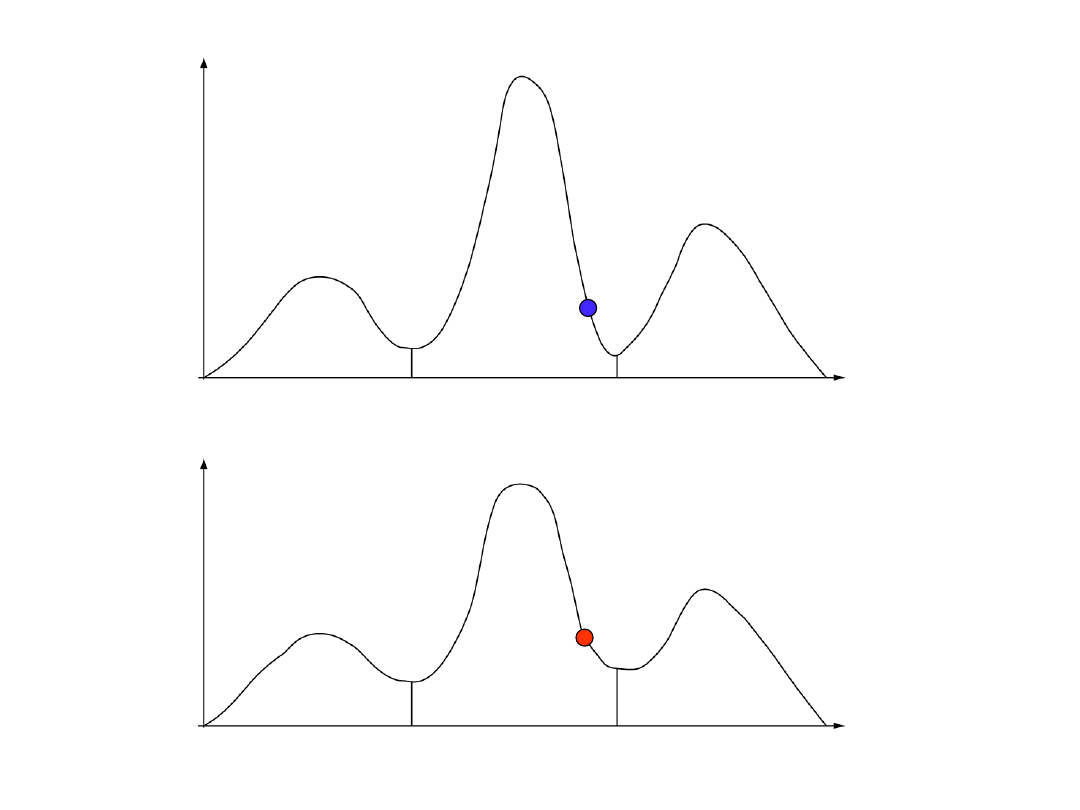
łańcuch zimny

łańcuch gorący

wg. prezentacji Freda Ronquista

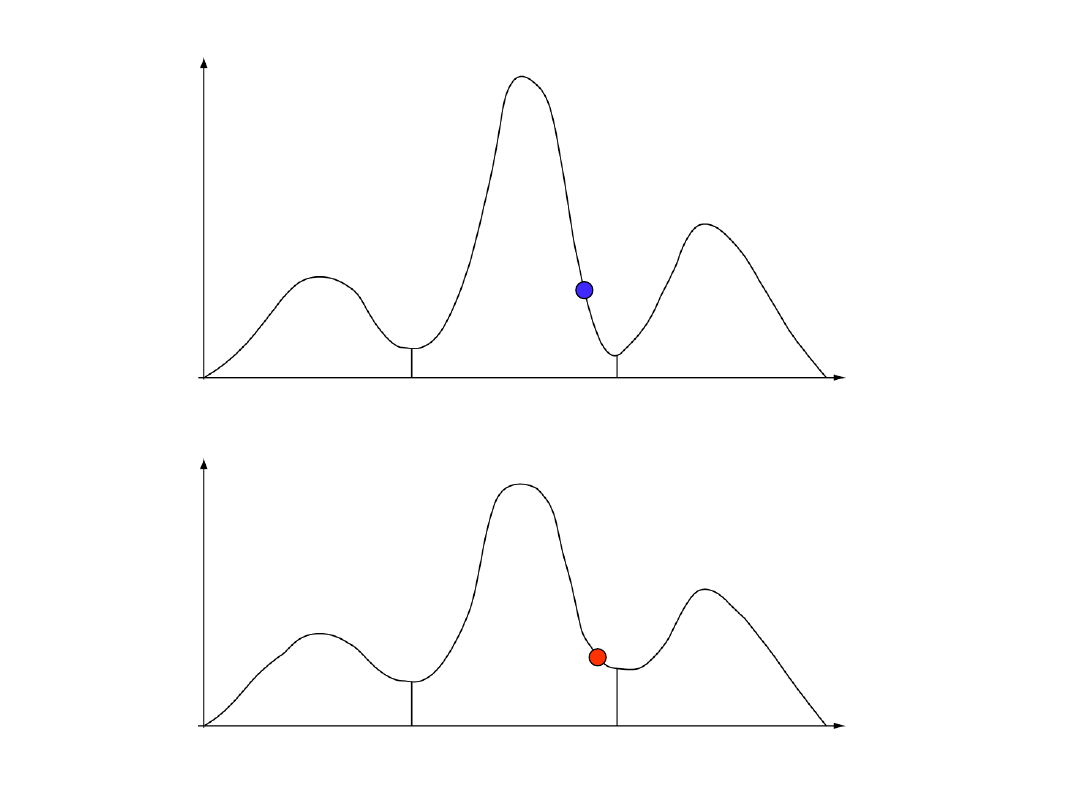
łańcuch zimny

łańcuch gorący

wg. prezentacji Freda Ronquista

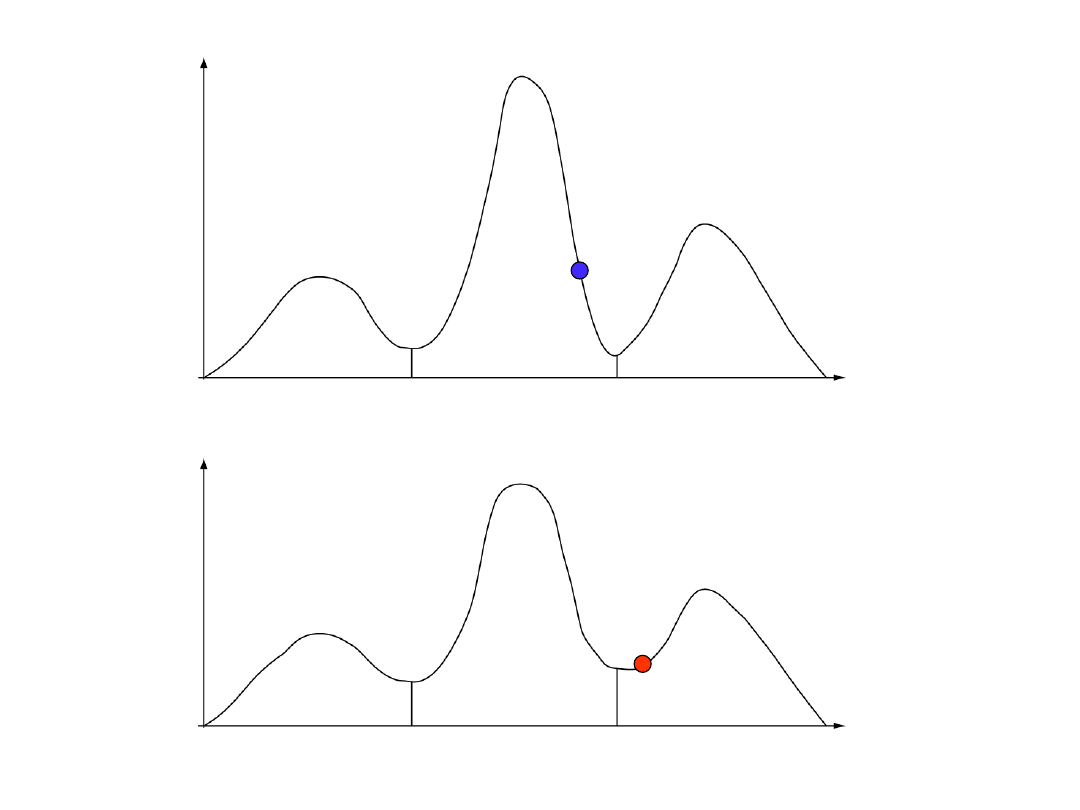
łańcuch zimny

łańcuch gorący

wg. prezentacji Freda Ronquista

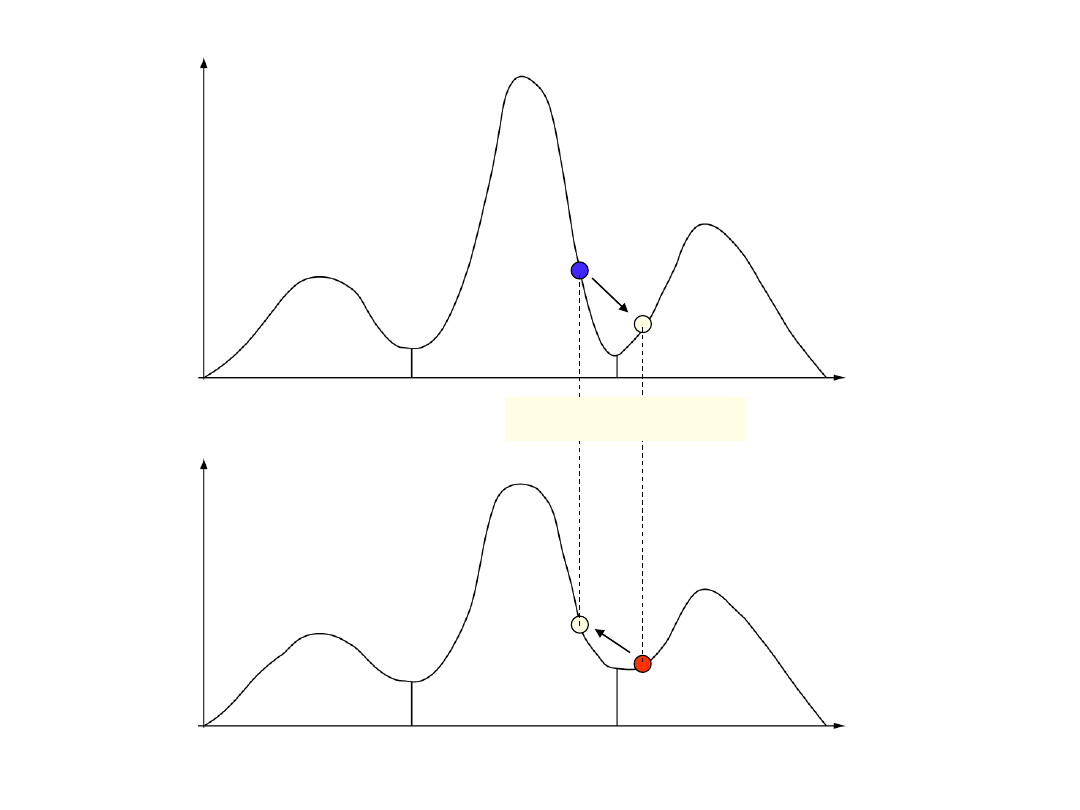
nieudana wymiana

łańcuch zimny

łańcuch gorący

wg. prezentacji Freda Ronquista

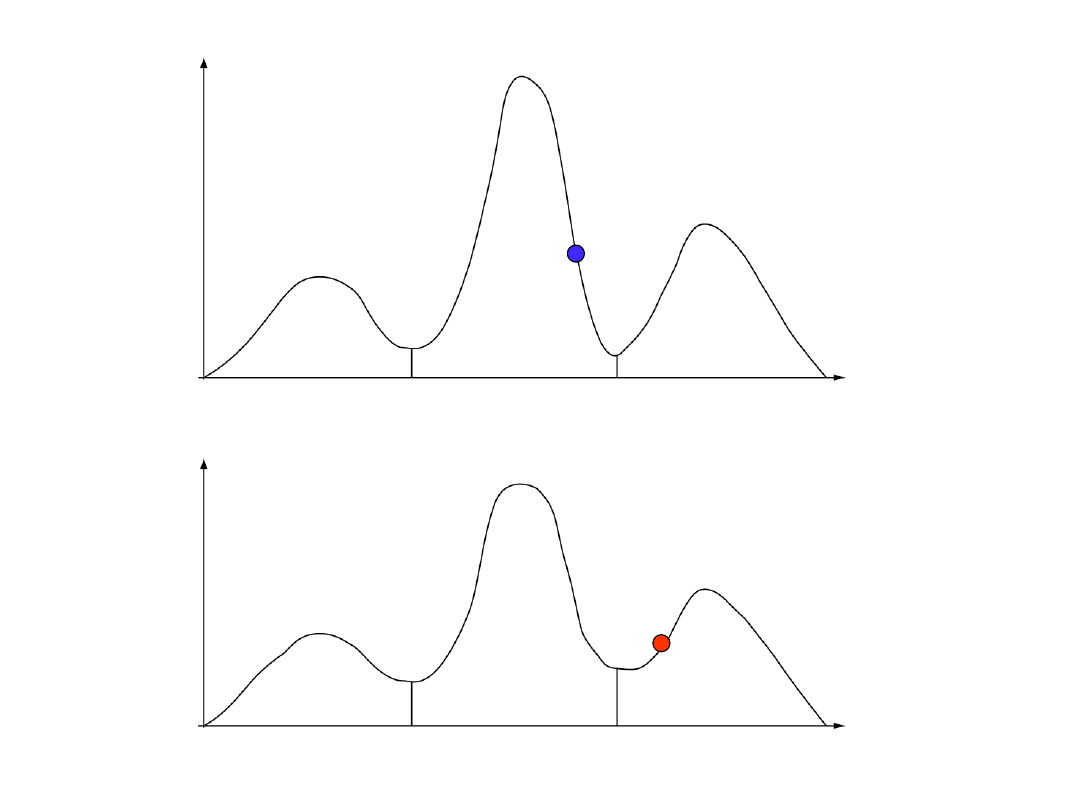
łańcuch zimny

łańcuch gorący

wg. prezentacji Freda Ronquista

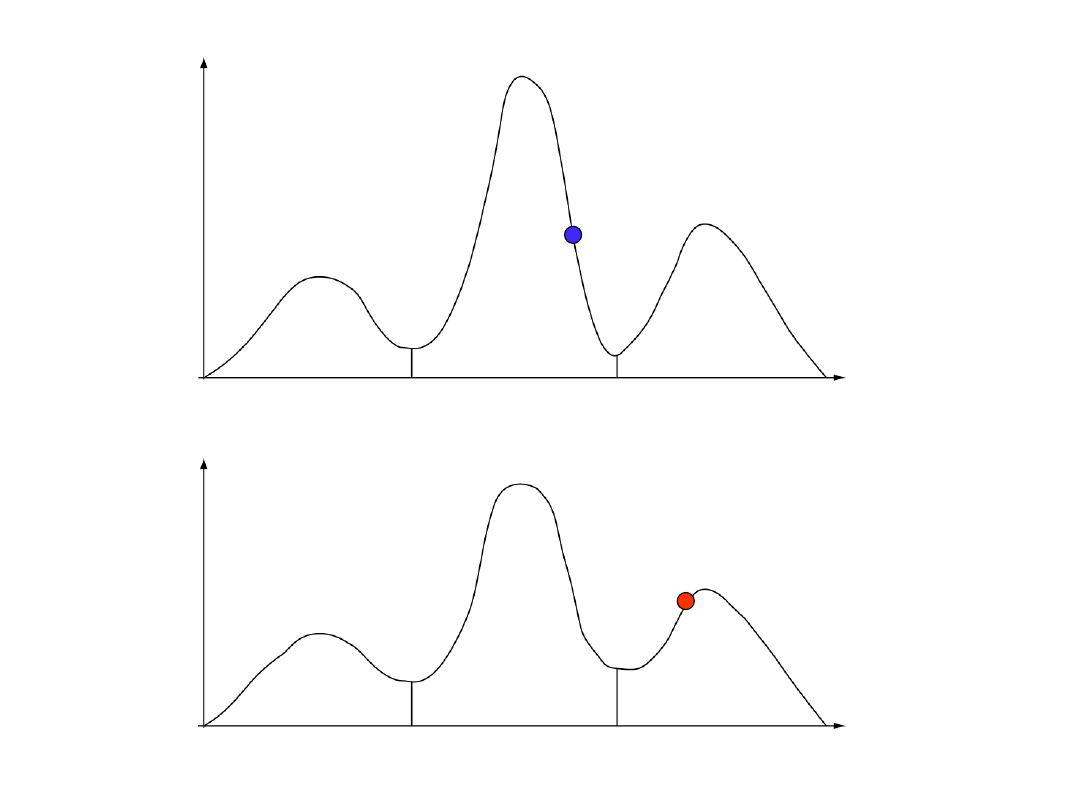
łańcuch zimny

łańcuch gorący

wg. prezentacji Freda Ronquista

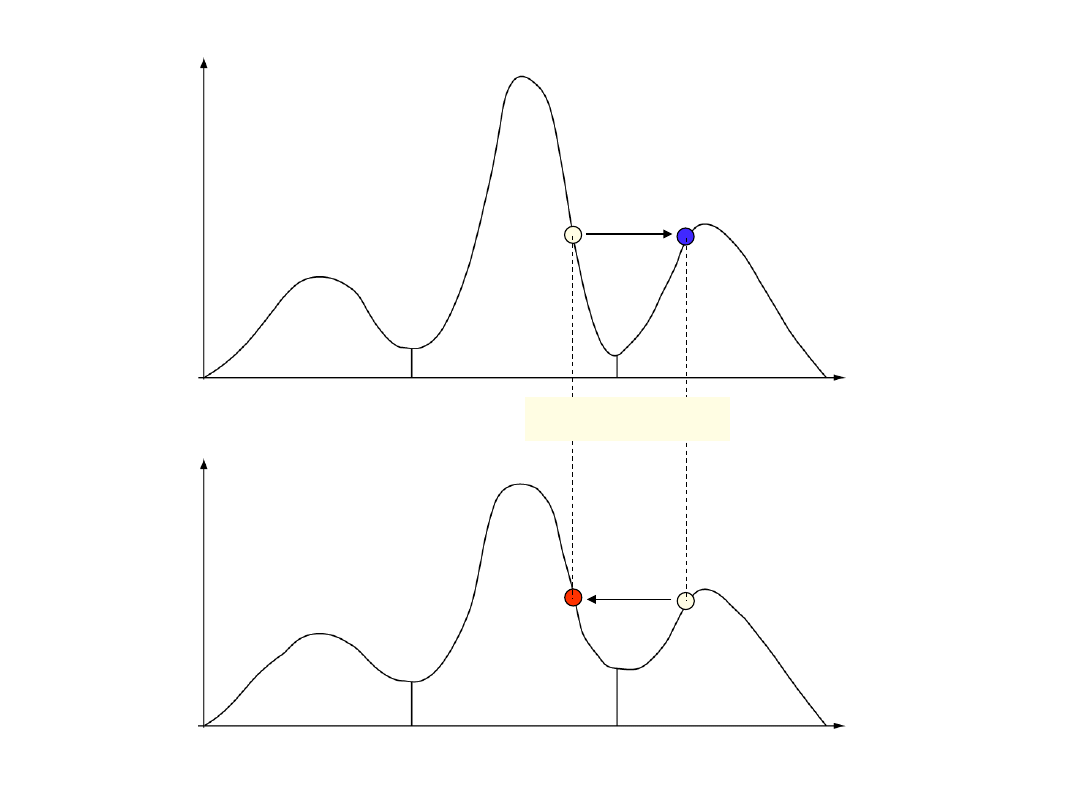
łańcuch zimny

łańcuch gorący

udana wymiana

wg. prezentacji Freda Ronquista

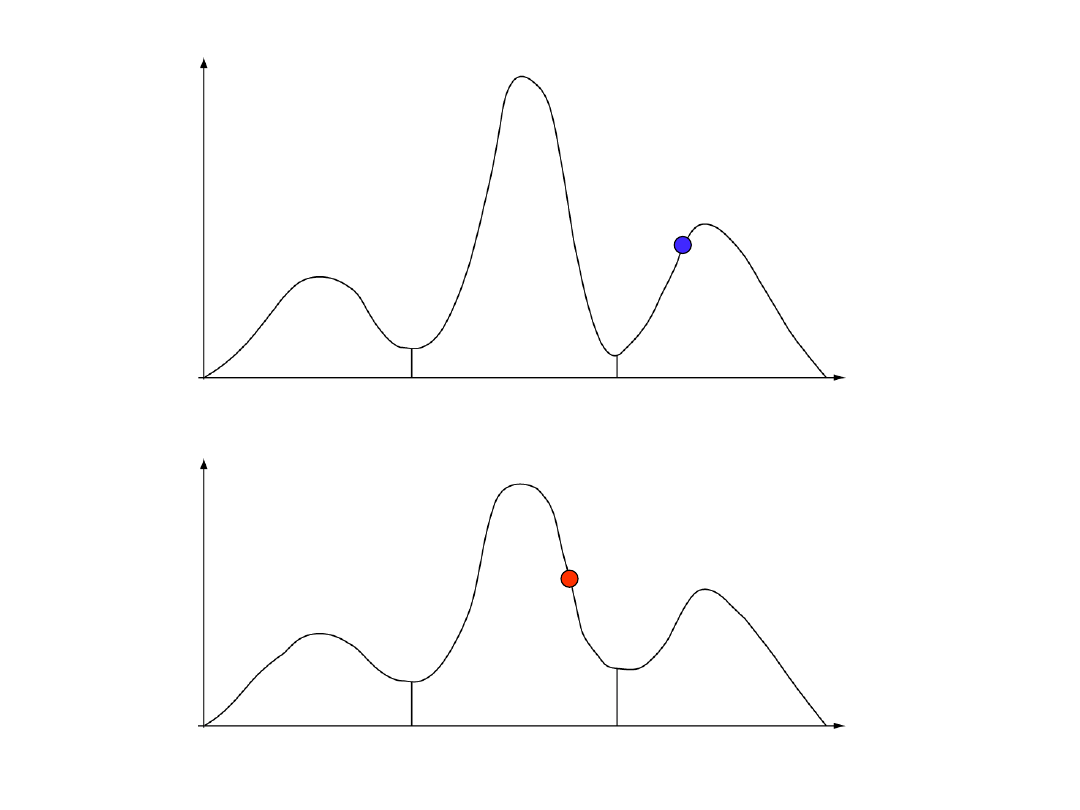
łańcuch zimny

łańcuch gorący

wg. prezentacji Freda Ronquista

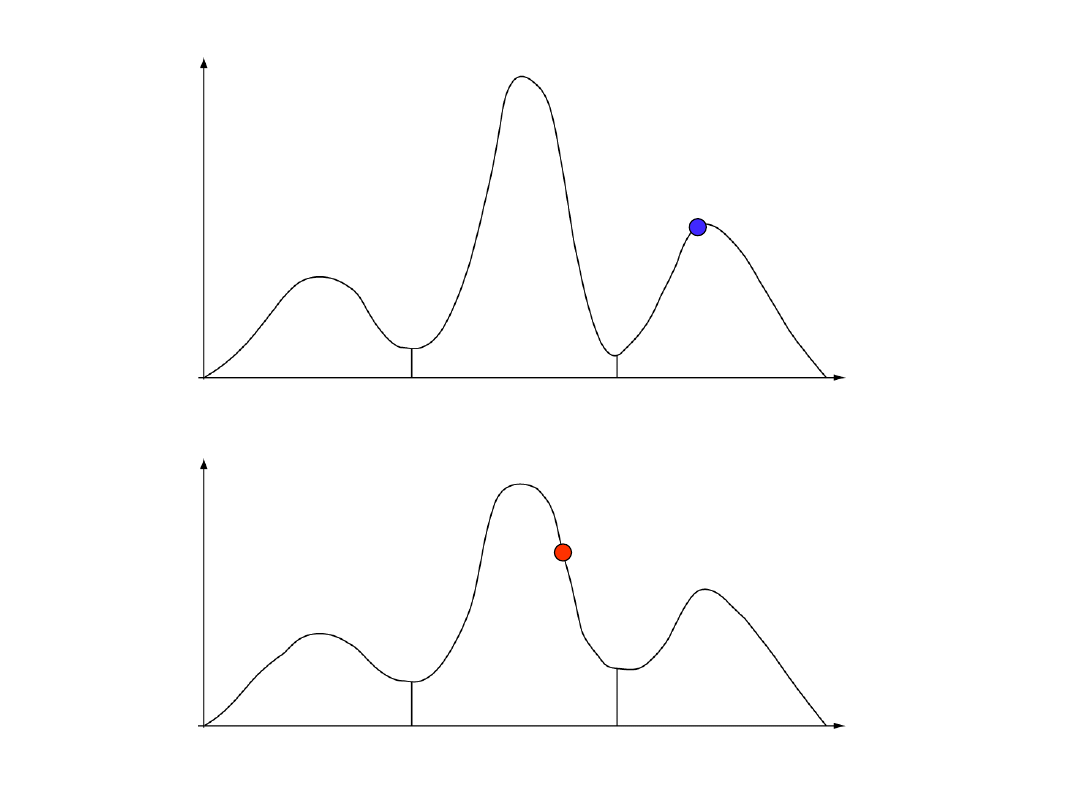
łańcuch zimny

łańcuch gorący

wg. prezentacji Freda Ronquista

łańcuch zimny

łańcuch gorący

udana wymiana

wg. prezentacji Freda Ronquista

łańcuch zimny

łańcuch gorący

wg. prezentacji Freda Ronquista

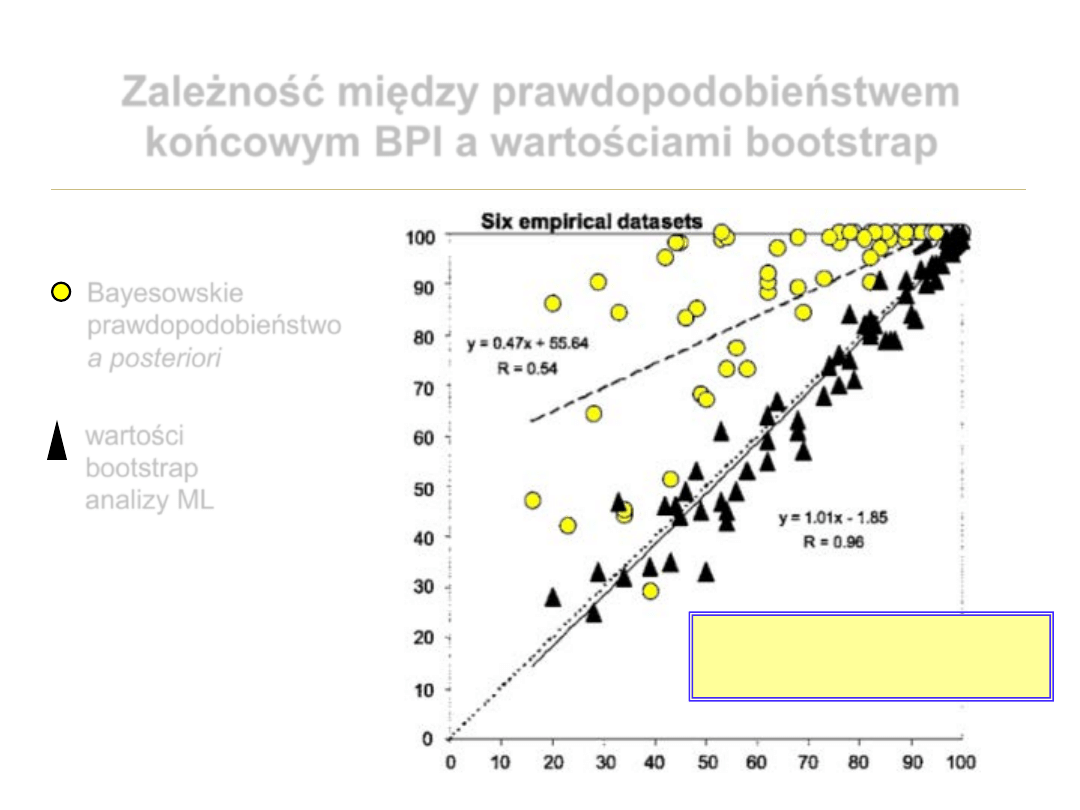
Zależność między prawdopodobieństwem

końcowym BPI a wartościami bootstrap

Bayesowskie

prawdopodobieństwo
a posteriori

wartości
bootstrap
analizy ML

wg. Douady et al. (2003)

95% BPI

≈ 70% boot.

• Maximum Likelihood

PHYML

Garli

MrBayes

• Wnioskowanie

Bayesowskie

MrBayes

Kalkulacja modeli substytucji

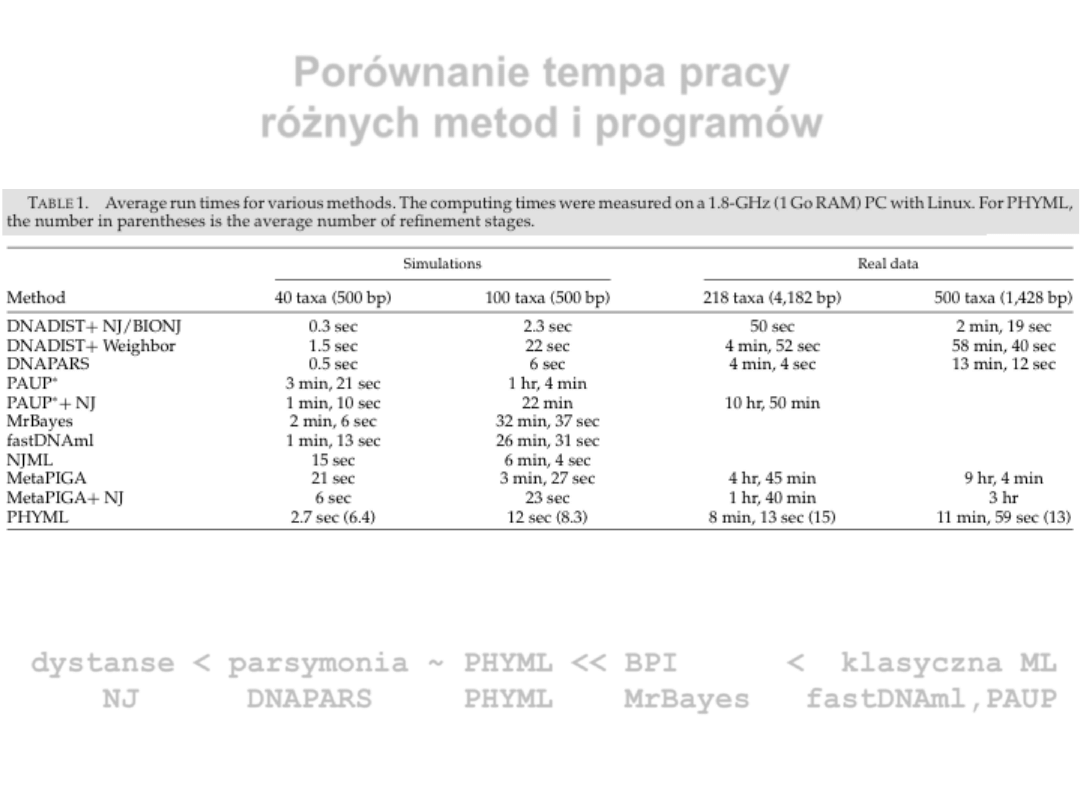
Porównanie tempa pracy

różnych metod i programów

dystanse < parsymonia ~ PHYML << BPI < klasyczna ML

NJ DNAPARS PHYML MrBayes fastDNAml,PAUP