
Podstawy
automatyki i
teorii maszyn
Wykład (2010/2011)
M. Zmysłowski na podstawie
wykładów dr hab. A. Kosiora (p. 2.8A)

Ro
zd
ział:
Wy
kł
ad
1
. –
Wpr
o
wadz
eni
e
d
o
t
eo
rii
m
asz
yn
2
Spis treści
Analiza mechanizmów krzywkowych metodą zastępowania par klasy 4 parami klasy 5 ................. 27
Metody analityczne wyznaczania prędkości i przyspieszeo mechanizmów krzywkowych ............... 28

Ro
zd
ział:
Wy
kł
ad
1
. –
Wpr
o
wadz
eni
e
d
o
t
eo
rii
m
asz
yn
3

Ro
zd
ział:
Wy
kł
ad
1
. –
Wpr
o
wadz
eni
e
d
o
t
eo
rii
m
asz
yn
4

Ro
zd
ział:
Wy
kł
ad
1
. –
Wpr
o
wadz
eni
e
d
o
t
eo
rii
m
asz
yn
5
Teoria maszyn

Ro
zd
ział:
Wy
kł
ad
1
. –
Wpr
o
wadz
eni
e
d
o
t
eo
rii
m
asz
yn
6
Wykład 1. – Wprowadzenie do teorii
maszyn
Literatura (również dla automatyki)
Podręczniki
„Podstawy teorii maszyn i automatyki” – T. Kołacin
„Podstawy teorii maszyn i mechanizmów” – A. Olędzki
„Teoria maszyn i mechanizmów” – Z. Parszewski
„Podstawy automatyki” – Z. Żelazny
Zbiory zadao
„Zbiór zadao do dwiczeo z PAiTM” – T. Kołacin, A. Kosior
„Zbiór zadao z podstaw automatyki” – D. Holejko, W. Kościelny, W. Niewczas
Wprowadzenie do teorii mechanizmów i maszyn
Maszyny i urządzenia mechaniczne to układy mas połączonych ze sobą ruchowo i
oddziałujących wzajemnie na siebie. Poszczególne masy będziemy nazywad ogniwami, bądź
członami.
Członem związany z układem odniesienia (nieruchomy) nazywamy podstawą. Dzielimy je na
sztywne i odkształcalne. Człony sztywne mają te same cechy, co bryły sztywne. Do członów
odkształcalnych zaliczamy liny, sprężyny, powietrze itp.
Dwa człony połączone ze sobą ruchowo (mające jeden punkt wspólny) i mogące wykonywad
ruch względny, nazywamy parą kinematyczną. Para może byd pojedyncza (2 człony), bądź
wielokrotna (gdy połączonych jest więcej członów w węźle). Zespół członów połączonych w pary
kinematyczne, to łaocuch kinematyczny.
Mechanizmem nazywamy łaocuch kinematyczny wykonujący określony ruch.
Maszyna to zespół mechanizmów wykonujący żądaną pracę, związaną z procesem
technologicznym, bądź przemianą energii.
W teorii mechanizmów pary kinematyczne dzielimy na klasy, a klasy na postaci. Podstawą
podziału na klasy jest ilośd stopni swobody, które odjęto każdemu członowi pary (np. para klasy I –
jeśli każdemu członowi w parze odjęto 1 stopieo swobody – zostało 5 stopni swobody). Pary dzielimy
na postaci według ilości odjętych przesunięd. 1. postad ma odjętą największą możliwą ilośd możliwych
przesunięd.
Połączenie członów w pary kinematyczne może byd siłowe, bądź kinematyczne. Połączenie
siłowe oznacza, że do realizacji połączenia członów koniecznie jest dociskanie siłą członów do siebie
(oddziaływanie siłowe).
Ro
zd
ział:
Wy
kł
ad
1
. –
Wpr
o
wadz
eni
e
d
o
t
eo
rii
m
asz
yn
7
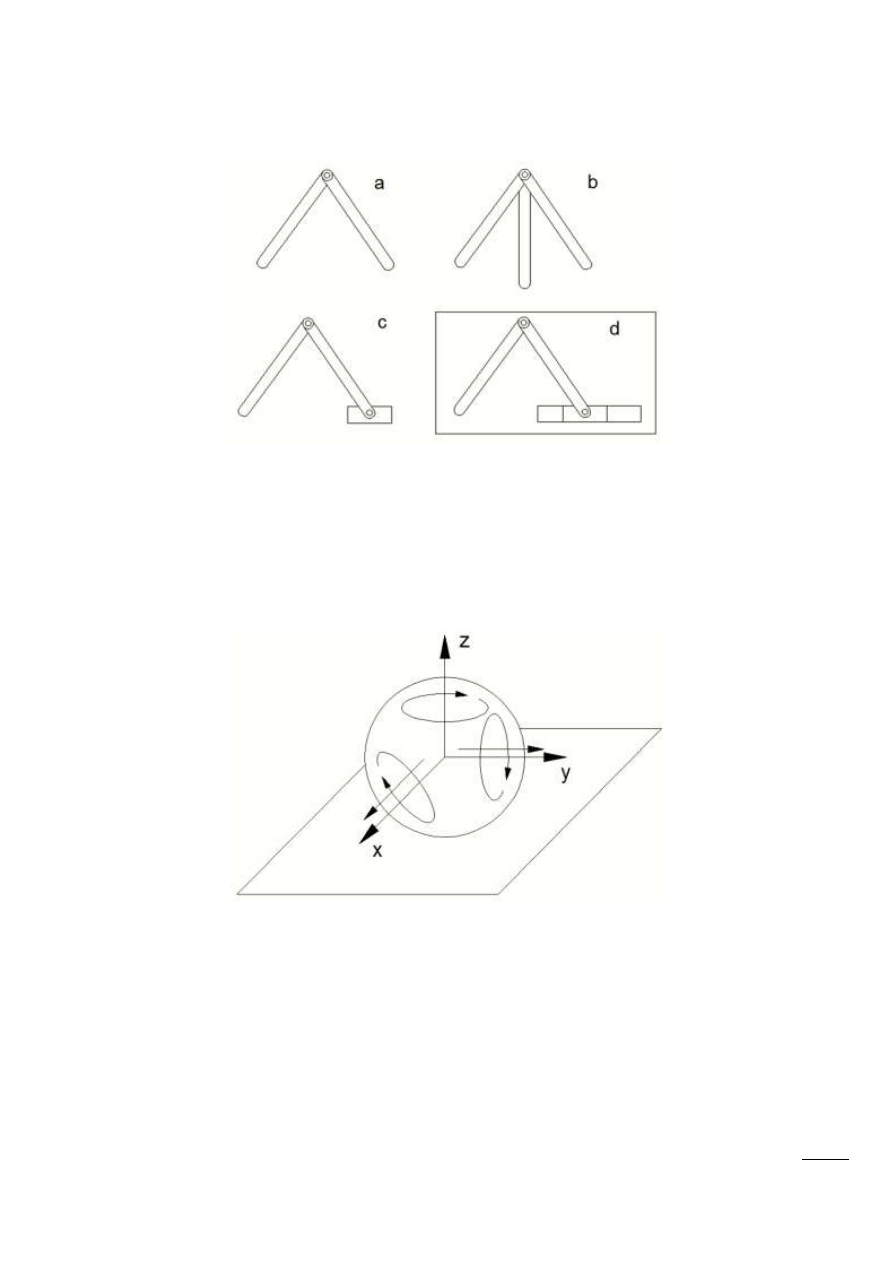
Pary kinematyczne mogą byd wyższe, lub niższe. Pary niższe – gdy występuje styk
powierzchniowy. W przypadku par wyższych występuje styk liniowy lub punktowy.
Rys. 1.1 – a – para kinematyczna, b – para wielokrotna, c – łaocuch kinematyczny otwarty, d –
łaocuch kinematyczny zamknięty
Klasyfikacja par kinematycznych
Para I klasy – para należy do I klasy jeśli każdy człon w parze posiada 5 stopni swobody
(odjęto po 1 stopniu). Utworzenie pary I klasy jest możliwe jedynie przez uniemożliwienie jednego
przesunięcia członu.
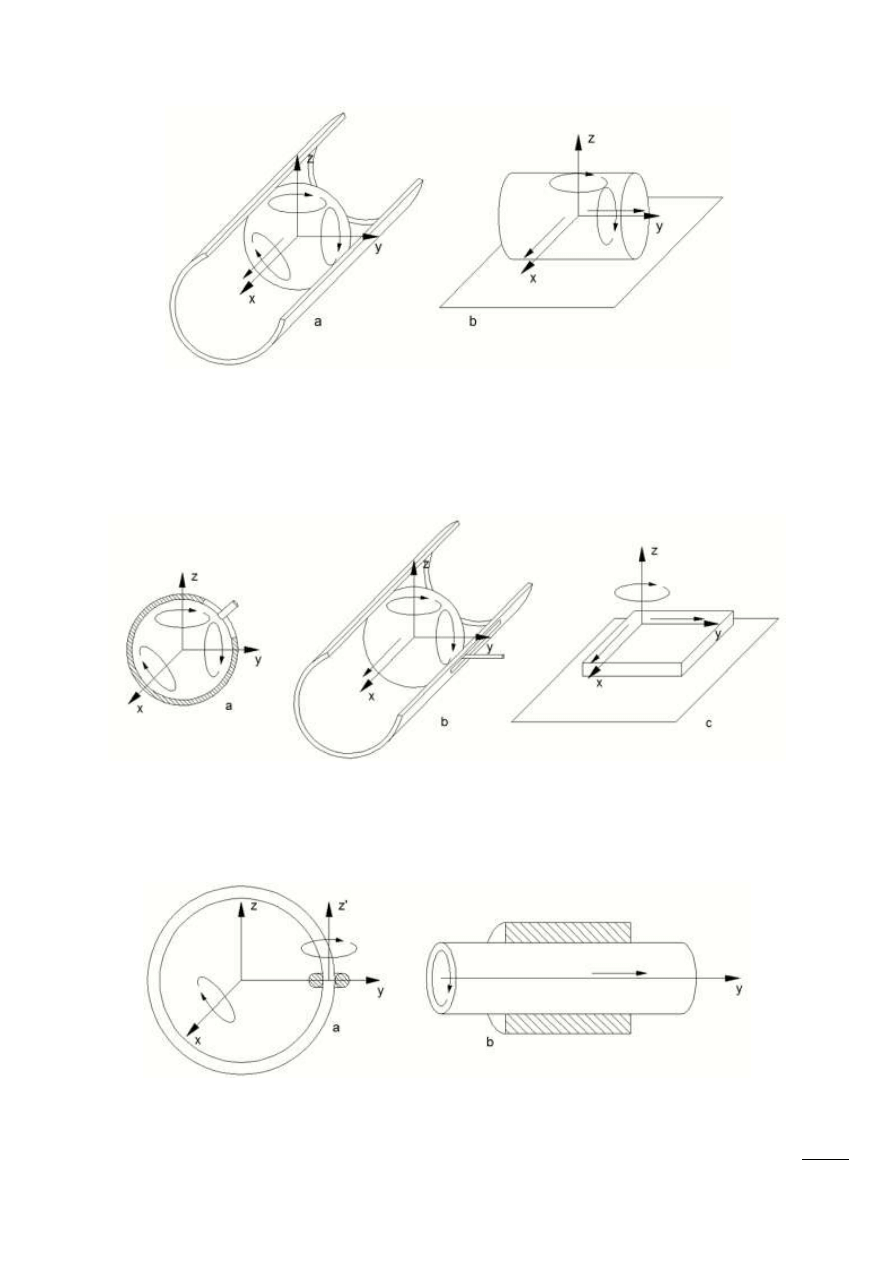
Rys. 1.2 – Przykład pary I klasy – przesunięcie w osi Z jest niemożliwe, ponieważ ruch w dół jest
blokowany przez płaszczyznę, natomiast po wykonaniu ruchu w górę, kula oderwałaby się od
powierzchni, przez co przestałyby one tworzyd parę kinematyczną.
Para II klasy – para należy do II klasy, jeśli człony tworzące parę mają 4 stopnie swobody.
Możliwe są dwie pary. Można zlikwidowad 2 przesunięcia lub odebrad 1 obrót i 1 przesunięcie.
Ro
zd
ział:
Wy
kł
ad
1
. –
Wpr
o
wadz
eni
e
d
o
t
eo
rii
m
asz
yn
8
Rys. 1.3 – a – para II klasy z odjętymi dwoma przesunięciami, b – para II klasy z odebranym jednym
obrotem i jednym przesunięciem.
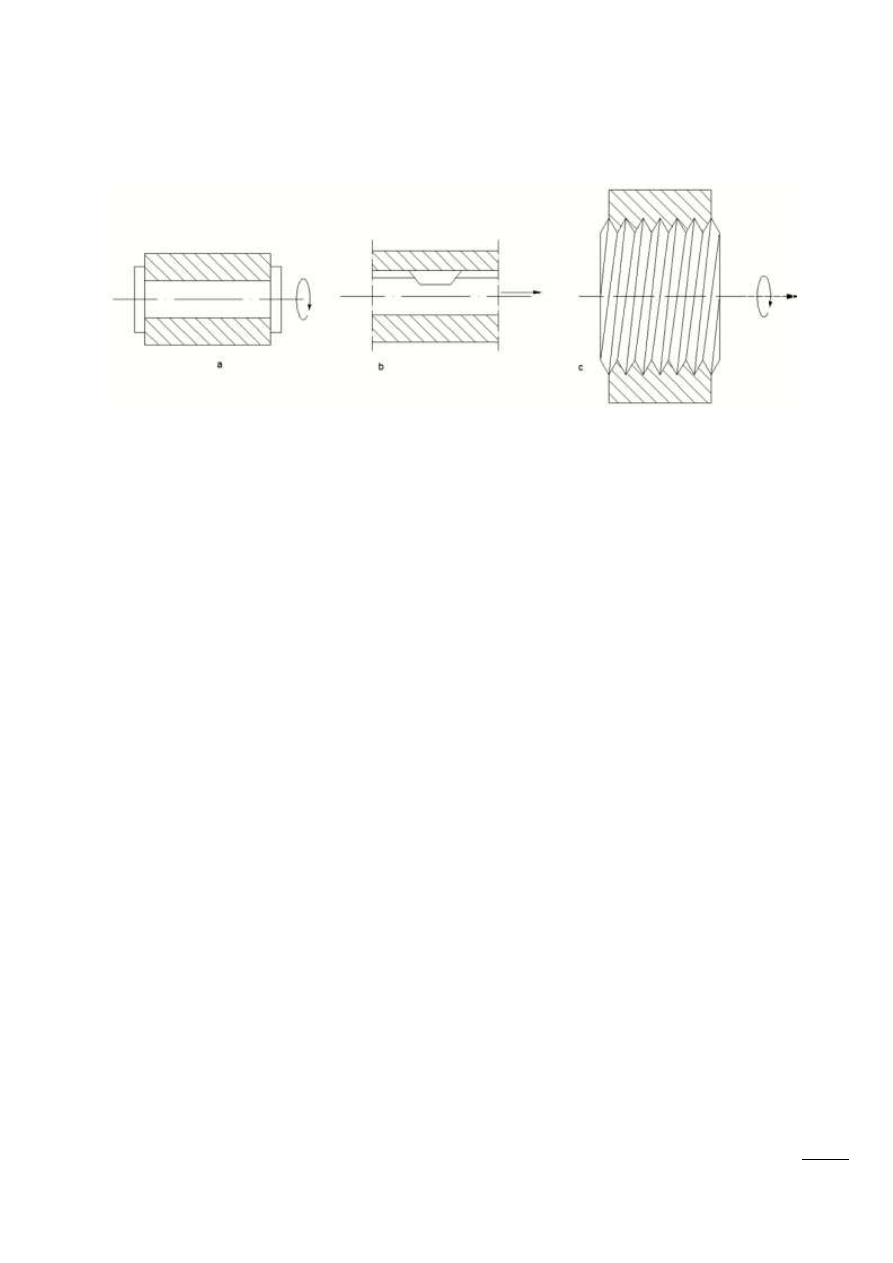
Para III klasy – para należy do III klasy, jeśli każdy człon posiada 3 stopnie swobody. Możliwe
są 3 pary, które uzyskuje się przez narzucenie więzów na 3 przesunięcia lub 2 przesunięcia i jeden
obrót, bądź na jedno przesunięcie i dwa obroty.
Rys. 1.4 – a – kulka w panewce ma odjęte 3 przesunięcia, b – kulka z bolcem w prowadzeniu ma
odjęte 2 przesunięcia i 1 obrót, c – płytka na powierzchni ma odjęte jedno przesunięcie i dwa obroty.
Para IV klasy – para należy do IV klasy, jeśli człony posiadają 2 stopnie swobody: 2 obroty,
bądź jeden obrót i 1 przesunięcie.
Rys. 1.5 – a – dwa pierścienie mające możliwośd się obracad i przesuwad, b – pręt w tulejce mający
możliwośd obrotu i przesunięcia.
Ro
zd
ział:
Wy
kł
ad
1
. –
Wpr
o
wadz
eni
e
d
o
t
eo
rii
m
asz
yn
9
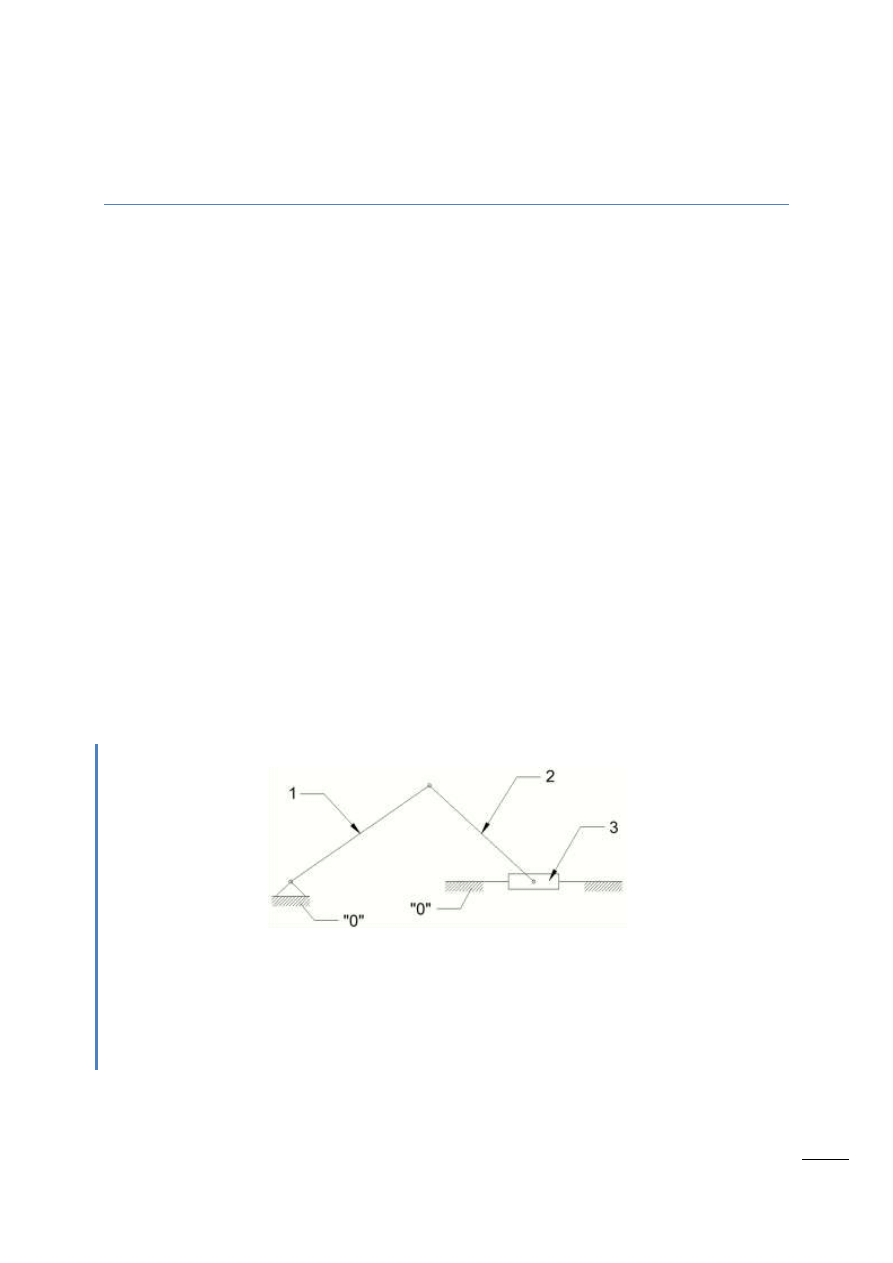
Para należy do V klasy, jeśli każdy z członów posiada 1 stopieo swobody. Możliwe są pary, w
których występuje możliwośd obrotu wokół jednej osi, przesunięcia wzdłuż jednej osi, bądź para
śrubowa.
Rys. 1.6 – a – element mający jedynie możliwośd obrotu w tulei, b – para postępowa, c – para
śrubowa (ruch wzdłużny jest związany z obrotowym, więc nie zalicza się jako dodatkowo odjęte
ograniczenie).
Pary w mechanizmach płaskich
Jeśli wszystkie punkty mechanizmu poruszają się w płaszczyznach równoległych do jednej
płaszczyzny, to mechanizm ten jest mechanizmem płaskim.
Pary w mechanizmach płaskich mogą byd jedynie IV lub V klasy. Para IV klasy ma tylko jedną
postad ruchu – obrót i przesunięcie (koło toczące się po szynie, ruch pary kół zębatych). Para V klasy
ma 2 postaci ruchu: obrót lub przesunięcie.
Ro
zd
ział:
Wy
kł
ad
2
. –
Wzo
ry
st
ru
ktura
ln
e,
kin
em
aty
ka
m
echan
iz
m
ó
w
i m
asz
yn
10
Wykład 2. – Wzory strukturalne,
kinematyka mechanizmów i maszyn
Wzory strukturalne
Ruchliwością mechanizmu nazywamy liczbę więzów, które należałoby nałożyd na człony
ruchome mechanizmu, aby je unieruchomid względem podstawy. Inaczej mówiąc jest to liczba stopni
swobody mechanizmu względem podstawy.
Gdzie:
s – liczba stopni swobody,
k – liczba członów,
p
1
… p
5
– liczba par od I do V klasy.
w – ruchliwośd mechanizmu
n – ilośd członów ruchomych (n = k – 1)
Dla mechanizmów płaskich:
Przykład
Rys. 2.1 – Mechanizm korbowo-wodzikowy
n = 5
p
4
= 0
p
5
: (0,1), (1,2), (2,3), (3,0)
p
5
= 4
w = 3 · 3 – 0 – 2 · 4 = 1
Ro
zd
ział:
Wy
kł
ad
2
. –
W
zo
ry
st
ru
ktura
ln
e,
kin
em
aty
ka
m
echan
iz
m
ó
w
i m
asz
yn
11
Więzy bierne
Więzy lub stopnie swobody nazywamy biernymi, jeśli usunięcie członów wprowadzających je
nie wpływa na ruch pozostałych członów.
Przykład
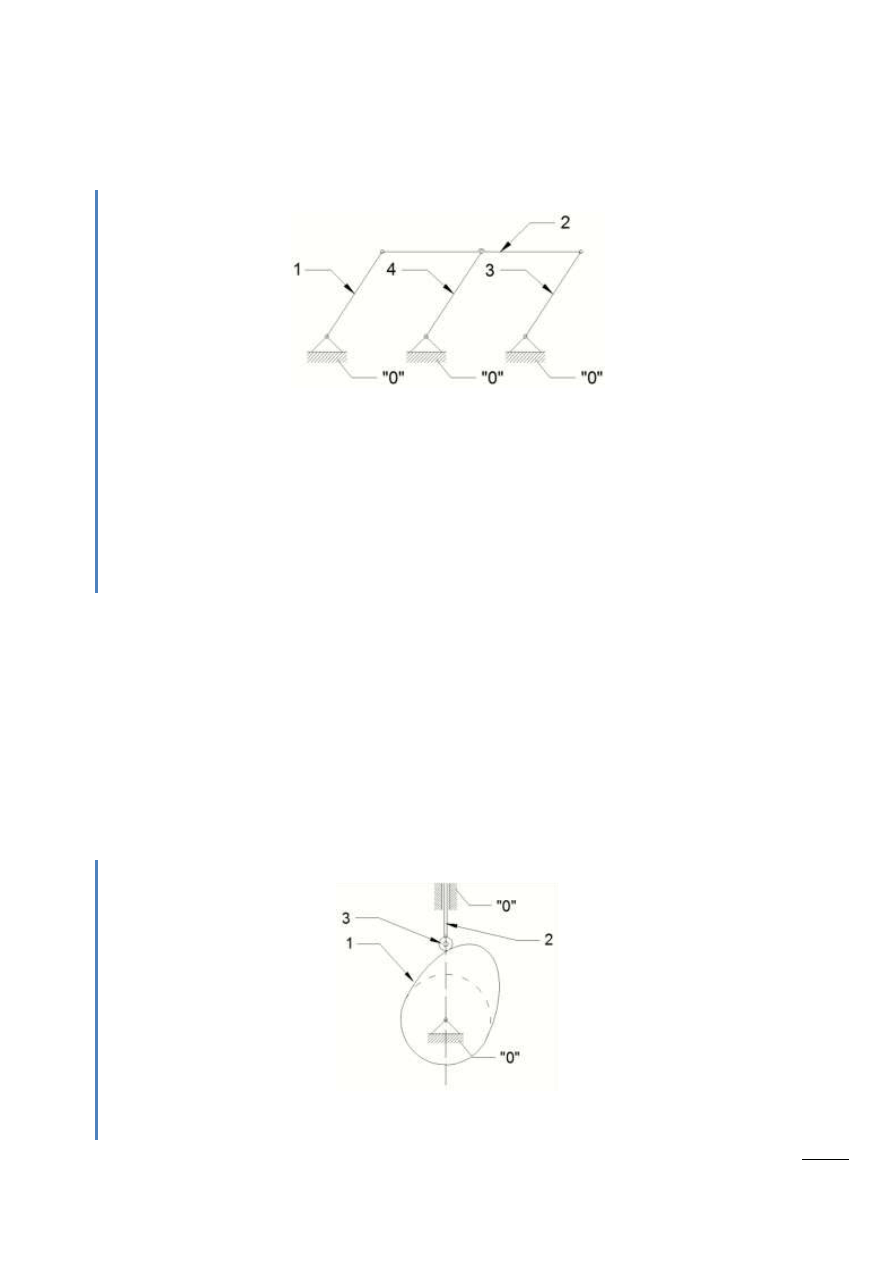
Rys. 2.2 – Mechanizm z więzami biernymi
n = 4
p
4
= 0
p
5
: (1,0), (1,2), (2,3), (3,0), (2,4), (4,0)
p
5
= 6
w = 3n – p
4
– 2p
5
= 3 · 4 – 0 – 2 · 6 = 0
Usunięcie członu nr 4 nie wpływa na ruch mechanizmu. Usuwając go uzyskujemy ruchliwośd
obliczeniową wynoszącą w = 1 (ruchliwośd praktyczna zarówno przed, jak i po usunięciu członu 4 cały
czas wynosi w = 1).
W praktyce konstrukcyjnej więzy bierne stosuje się ze względów wytrzymałościowych,
sztywności, korzystniejszego rozkładu sił itp. Więzy bierne zawsze komplikują układ, wprowadzając
statyczną niewyznaczalnośd i są niekorzystne ze względów wykonawczych. Dlatego zawsze gdy
możliwe jest równoważne rozwiązanie konstrukcyjne, bez więzów biernych należy bezwzględnie
unikad ich wprowadzania.
Zbędne stopnie swobody
Zbędne stopnie swobody nie mają wpływu na ruch mechanizmu jako całości. Dają one
pewne lokalne możliwości ruchu (np. jednego członu). Stosowanie zbędnych stopni swobody jest na
ogół pożądane, gdyż często służą zmniejszeniu oporów ruchu. Mimo to z rozważao kinematycznych
musza byd usunięte.
Przykład
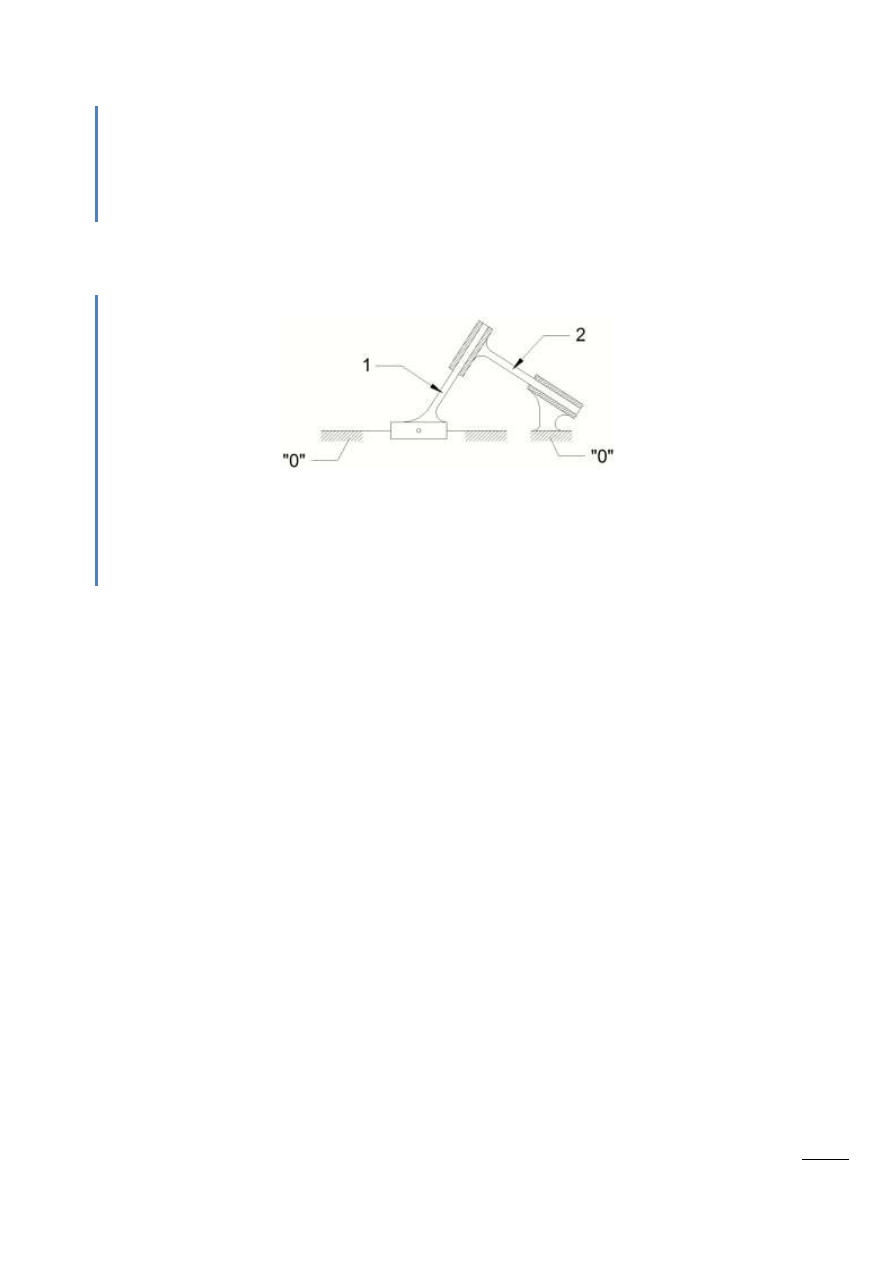
Rys. 2.3 – Mechanizm krzywkowy z rolką
p
4
: (1,3)
Ro
zd
ział:
Wy
kł
ad
2
. –
Wzo
ry
st
ru
ktura
ln
e,
kin
em
aty
ka
m
echan
iz
m
ó
w
i m
asz
yn
12
p
4
= 1
p
5
: (1,0), (2,0), (2,3)
p
5
= 3
w = 3n – p
4
– 2p
5
= 3 · 3 – 1 – 2 · 3 = 2
Usuwając rolkę (3) zmniejszymy ruchliwośd mechanizmu do wartości w = 1 i zwiększymy opory ruchu.
Mechanizmy postępowe
Mechanizmy postępowe składają się jedynie z par postępowych (nie występuje w nich obrót).
Przykład
Rys. 2.4 – Mechanizm postępowy
n = 2
p
5
: (1,0), (1,2), (2,0)
p
5
= 3
w = 2n – p
5
= 2 · 2 – 3 = 1
Klasyfikacja funkcjonalna mechanizmów
Klasyfikacja funkcjonalna mechanizmów dzieli je w zależności od wypełnianej funkcji. Uwzględnia
ona podstawowe cechy funkcjonalne i konstrukcyjne. Tak więc wyróżniamy następujące
mechanizmy:
cierne,
zębate,
pasowe/linowe/cięgnowe,
dźwigniowe,
krzywkowe,
przystankowe,
mechanizmy z elementami sprężystymi,
hydrauliczne/pneumatyczne
Kinematyka mechanizmów i maszyn
Cel i przegląd kinematyki
Kinematyka obejmuje zagadnienia związane z opisem ruchu bez uwzględnienia sił
działających (???). Badanie ruchu w tym przypadku polega na określeniu prędkości i przyspieszeo. Do
tego celu stosuje się metody analityczne, wykreślne, numeryczne lub kombinowane. Metody
wykreślne pozwalają szybko wyznaczyd położenie, prędkośd i przyspieszenie punktów mechanizmu.
Są jednak mniej dokładne niż pozostałe. W niektórych przypadkach celowe jest stosowanie metod
analitycznych, cyfrowych, bądź kombinowanych, zwłaszcza przy analizie mechanizmów, gdy zależy
nam na większej dokładności wyników.
Ro
zd
ział:
Wy
kł
ad
2
. –
Wzo
ry
st
ru
ktura
ln
e,
kin
em
aty
ka
m
echan
iz
m
ó
w
i m
asz
yn
13
Metody wykreślne kinematyki
Podstawowym zagadnieniem przy stosowaniu metod wykreślnych jest stosowanie
odpowiedniej podziałki. Podziałka to skalar określający stosunek wielkości rzeczywistej do
rysunkowej i posiadającej taki wymiar, aby na rysunku otrzymad wymiar w *cm+ bądź *mm+.
ϰ
l
– podziałka długości (bezwymiarowa)
ϰ
V
– podziałka prędkości
ϰ
p
– podziałka przyspieszeo
Wyznaczanie toru punktu
Tor punktu członu to miejsce geometryczne położeo, przez które przechodzi dany punkt w
czasie ruchu członów. Podczas wykreślania toru punktu mechanizmów zwykle oznaczamy na nich
odcinki odpowiadający określonym przedziałom czasu lub położeo pewnych członów mechanizmu
(na ogół członu napędzającego).
W teorii mechanizmów wyznaczamy tor punktu, który nazywamy torem ocechowanym.
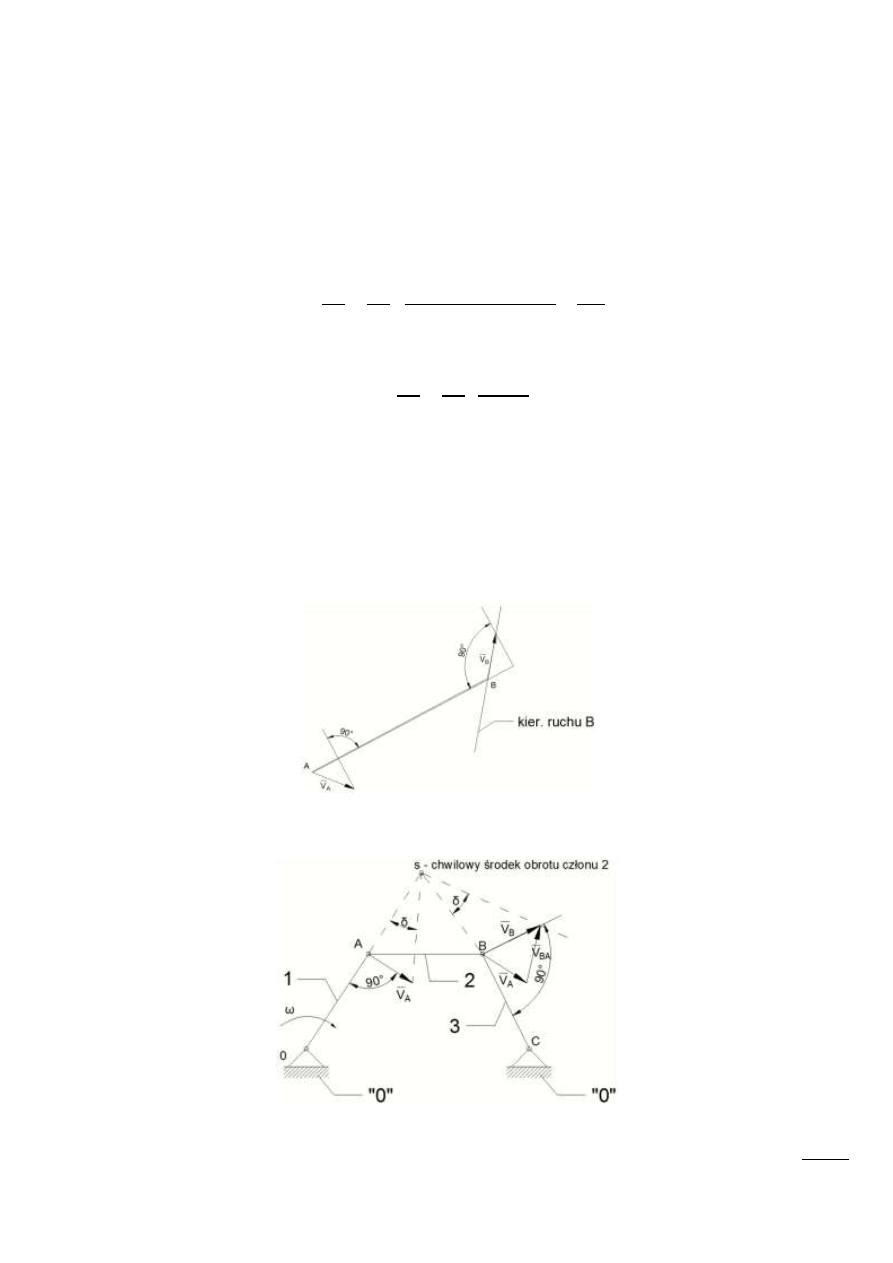
Rys. 2.5 – Wyznaczanie wektora prędkości punktu B na podstawie znajomości wektora prędkości
punktu A, oraz kierunku ruchu punktu B.
Rys. 2.6 – Wyznaczanie wektorów prędkości punktu B, oraz wektora prędkości punktu B względem A.
Ro
zd
ział:
Wy
kł
ad
3
. –
P
lan
y pręd
ko
ści i prz
yspi
eszeo
14
Wykład 3. – Plany prędkości i
przyspieszeń
Metoda planu wyznaczania prędkości punktu
Planem prędkości nazywamy figurę geometryczną będącą miejscem geometrycznym kooców
wektorów prędkości figury płaskiej, poruszającej się ruchem płaskim wykreślonym z jednego punktu.
Plan prędkości jest figurą podobną do badanej i obróconą w stosunku do niej o kąt prosty w
kierunku obrotu chwilowego. Zwykle punktem, z którego rysujemy równanie wektorowe nie jest
związany z figurą. Nazywamy go biegunem prędkości.
Przykład
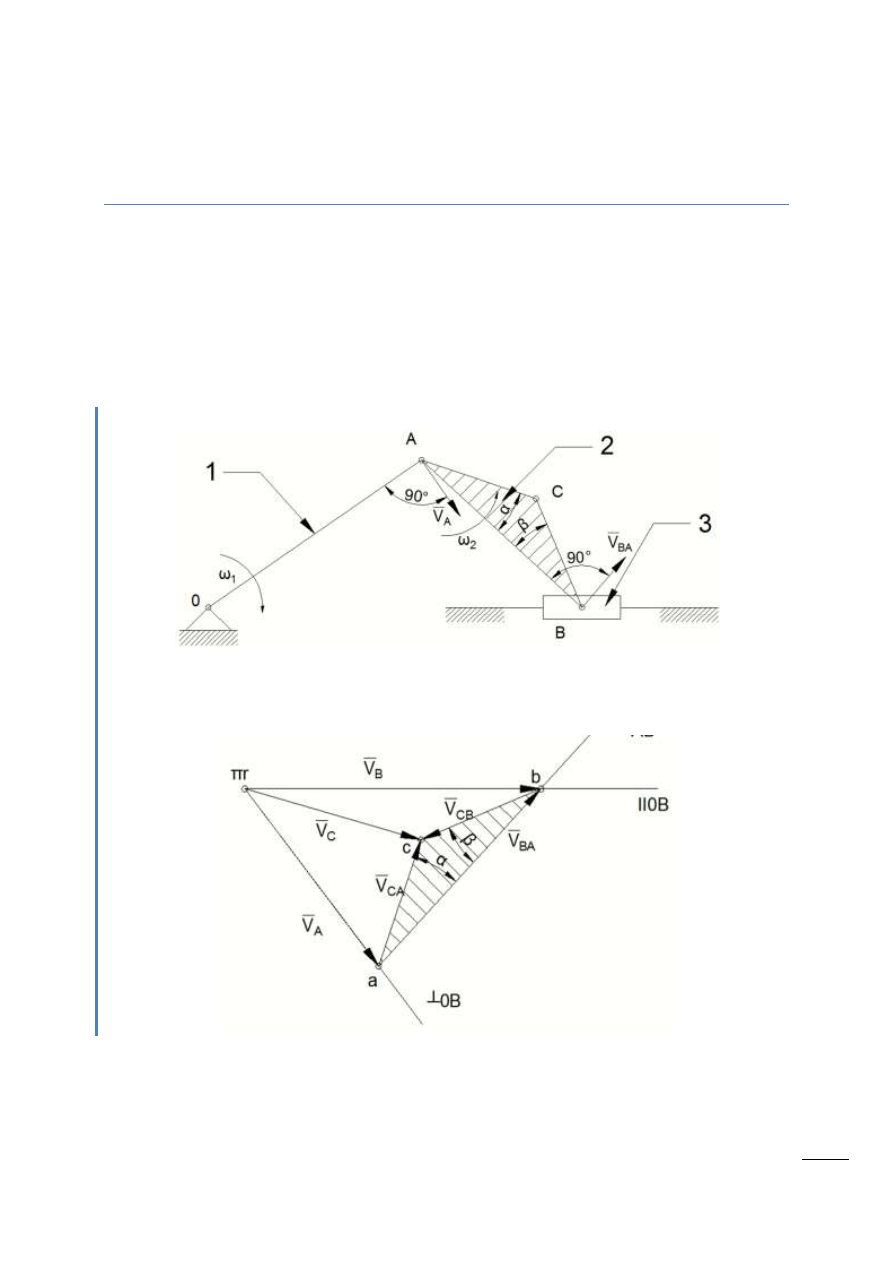
Rys. 3.1 – Mechanizm korbowo-wodzikowy z rozbudowanym członem 2.
Wyznaczanie przyspieszeń
(w ruchu złożonym)
(w ruchu płaskim)
Ro
zd
ział:
Wy
kł
ad
3
. –
P
lan
y pręd
ko
ści i prz
yspi
eszeo
15
Przykład
Rys. 3.3 – Wyznaczanie przyspieszeo w obracającym się pręcie
=
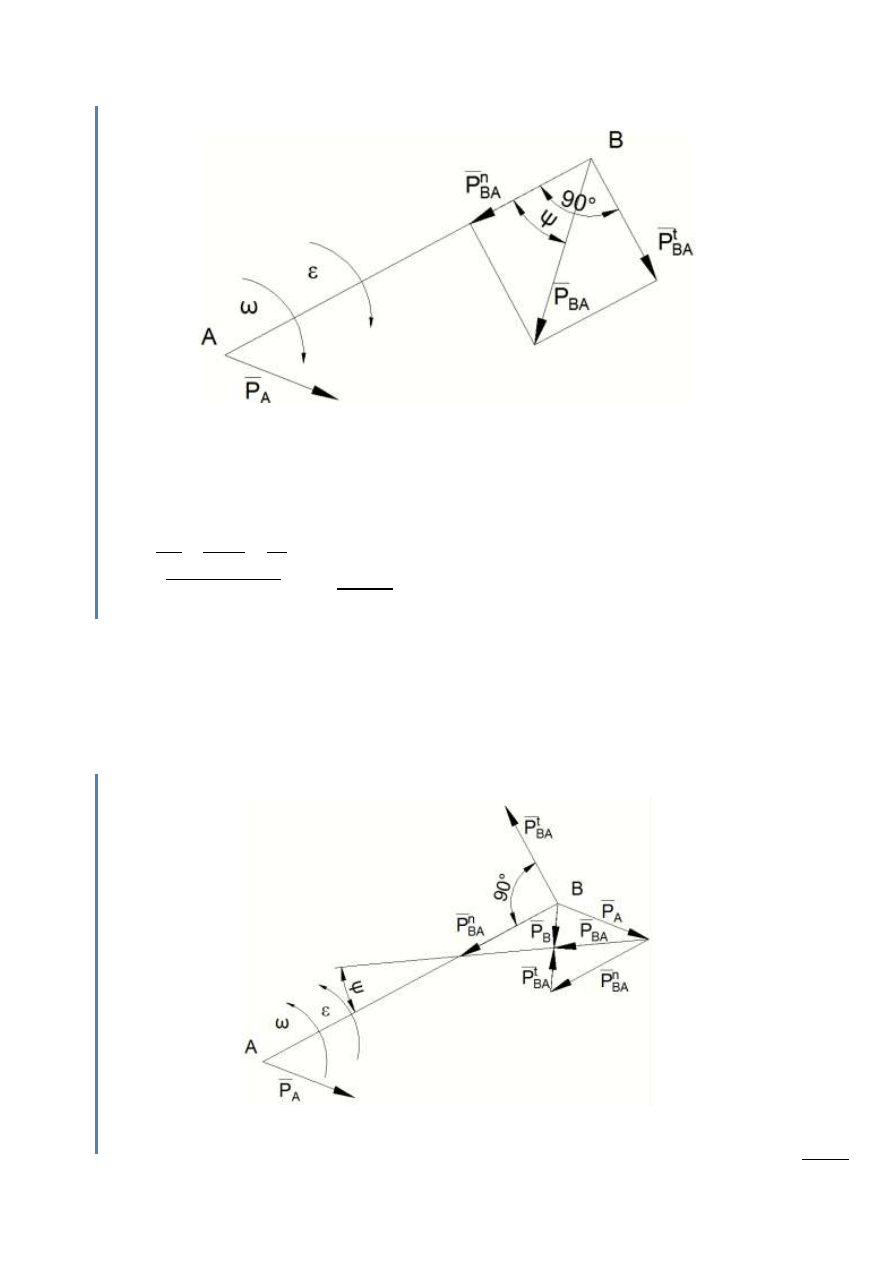
Metoda planu przyspieszeń
Planem przyspieszeo figury płaskiej poruszającej się ruchem płaskim nazywamy miejsce
geometryczne kooców wektorów przyspieszeo tej figury, wykreślonych z jednego punktu.
Plan przyspieszeo jest figurą podobną do figury badanej i obróconą o kąt θ = 180° - ψ w
stronę zgodną ze zwrotem przyspieszenia kątowego ε.
Przykład
Rys. 3.4 – Metoda planu przyspieszeo
Ro
zd
ział:
Wy
kł
ad
3
. –
P
lan
y pręd
ko
ści i prz
yspi
eszeo
16
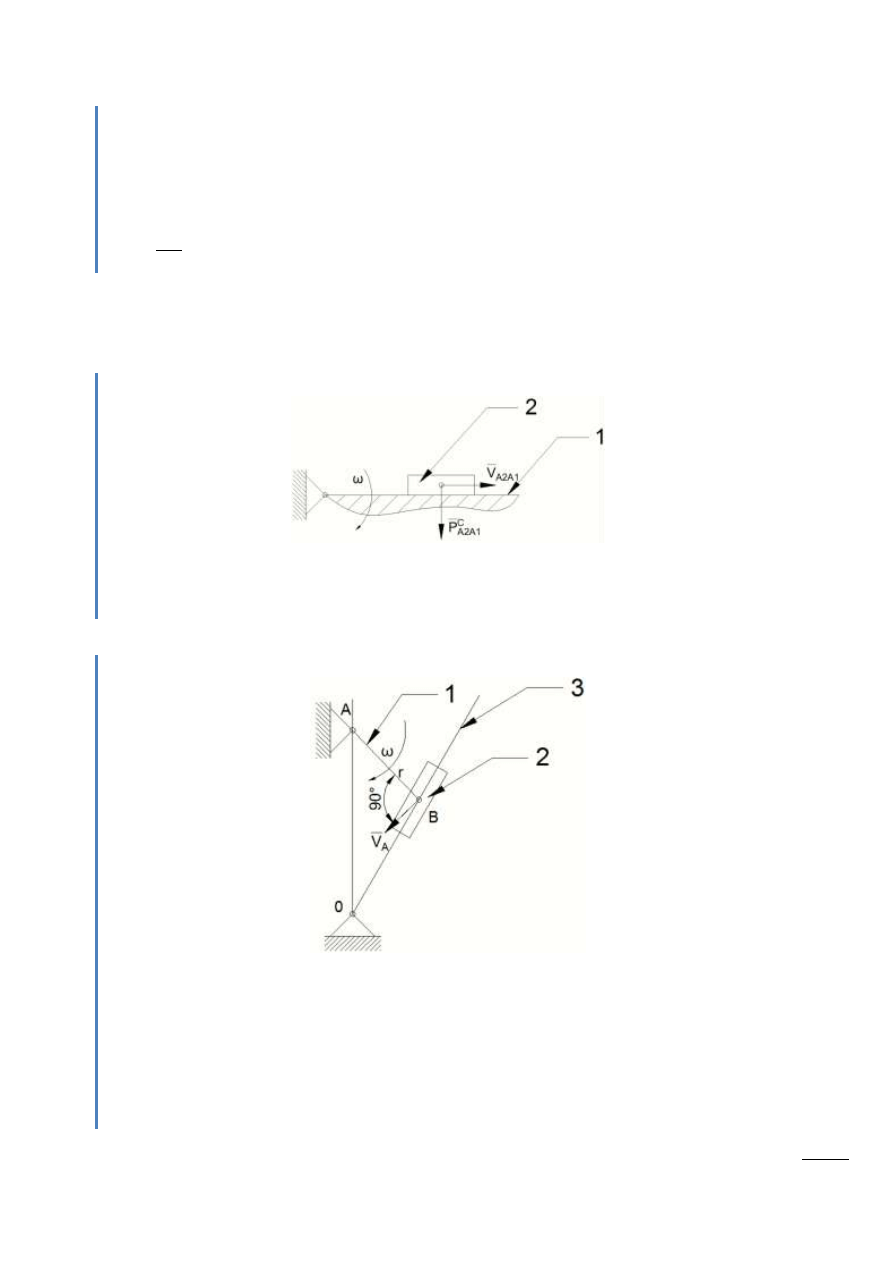
Plan przyspieszeń w przypadku występowania przyspieszenia Coriolisa
Gdy sąsiadujące człony wchodzą w skład pary postępowej, a ruch unoszenia jest obrotowy
występuje przyspieszenie Coriolisa.
Przykład
Rys. 3.5 – Układ z przyspieszeniem Coriolisa
Przykład
Rys. 3.6 – Mechanizm z przyspieszeniem Coriolisa
Ro
zd
ział:
Wy
kł
ad
3
. –
P
lan
y pręd
ko
ści i prz
yspi
eszeo
17
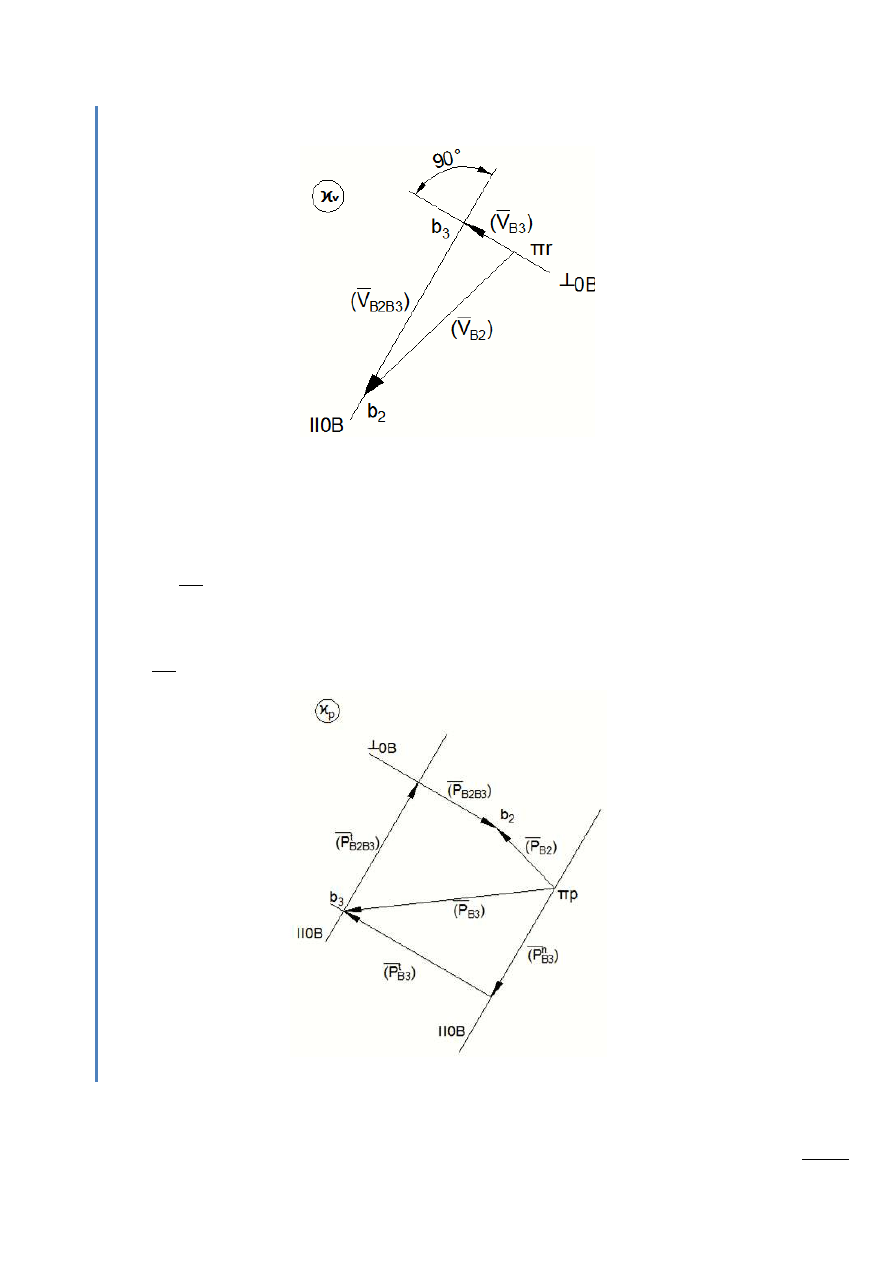
Rys. 3.7 – Plan prędkości
Rys. 3.8 – Plan przyspieszeo

Ro
zd
ział:
Wy
kł
ad
4
. –
M
eto
d
y anal
ity
czn
e
p
rędk
o
ści
i p
rz
yspi
eszeo
18
Wykład 4. – Metody analityczne
prędkości i przyspieszeń
Zasadnicza cechą metod analitycznych jest uzyskanie ogólnego wpływu parametrów (jak
wymiary członów, prędkośd, przyspieszenie członu napędowego itp.), bez potrzeby powtarzania
operacji. Czyni je to szczególnie przydatnymi w zagadnieniach syntezy mechanizmów mających
spełniad z góry określone warunki kinetyczne.
Dokładnośd metod wykreślnych jest ograniczone błędami rysunkowymi. Metody analityczne
pozwalają na uzyskanie dowolnie wysokiej dokładności.
Zasada metod analitycznych polega na uzyskaniu algebraicznych związków określających
położenie członów, tory punktów, ich prędkości i przyspieszenia w czasie ruchu mechanizmu.
Każdy mechanizm jako zamknięty łaocuch kinematyczny, może byd przedstawiony w postaci
zamkniętego wieloboku wektorów określających chwilowe położenie jego członów.
Położenie członów określamy za pomocą tak zwanych kątów skierowanych, określających
położenie wektorów względem przyjętego układu współrzędnych. W trakcie analizy nie wolno
zmieniad zwrotu kątów skierowanych. Kąty skierowany odmierzane są w jednym kierunku – obrotu
osi OX, do pokrycia się z kierunkiem i zwrotem danego wektora.
Równania toru:
Równania prędkości:
Równania przyspieszeo:
Ro
zd
ział:
Wy
kł
ad
4
. –
M
eto
d
y anal
ity
czn
e
p
rędk
o
ści
i p
rz
yspi
eszeo
19
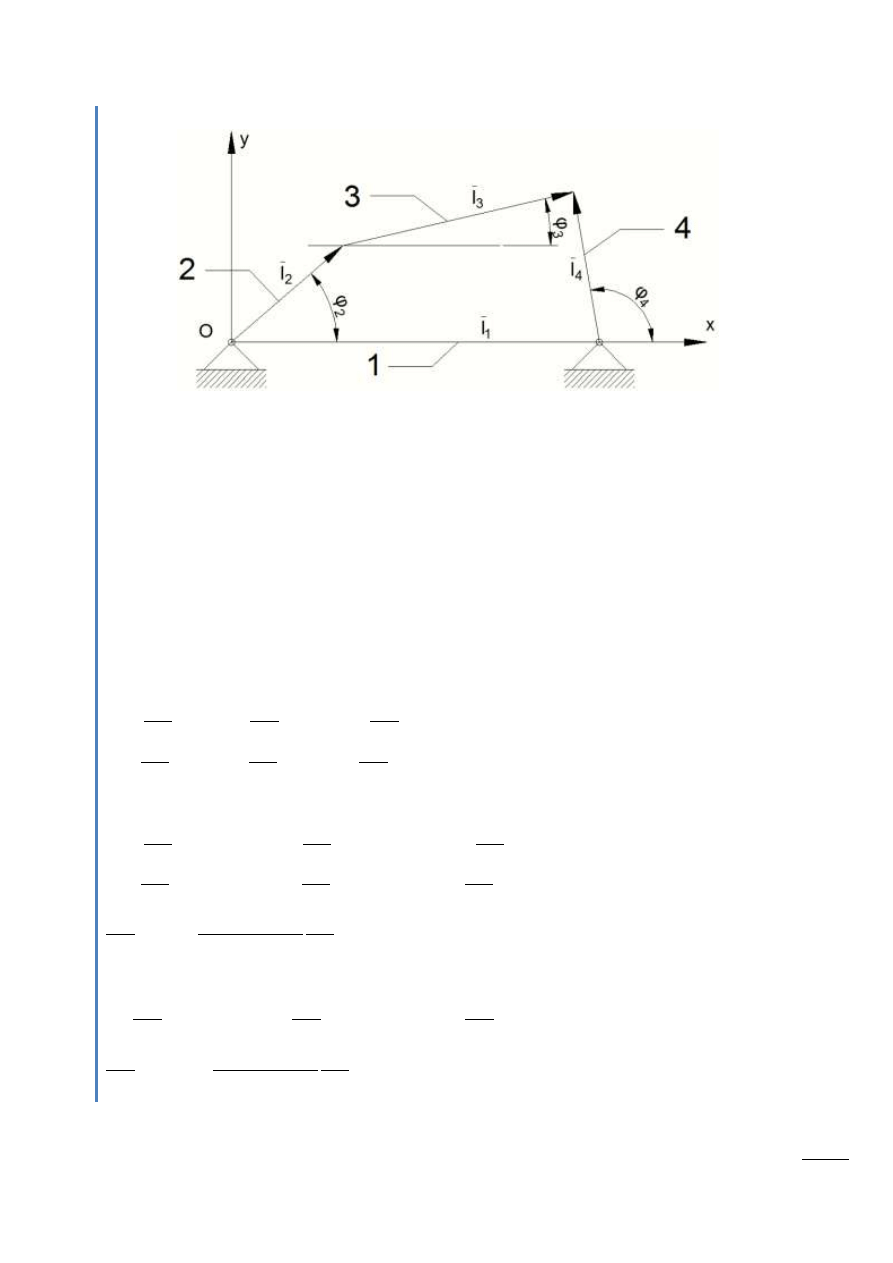
Przykład
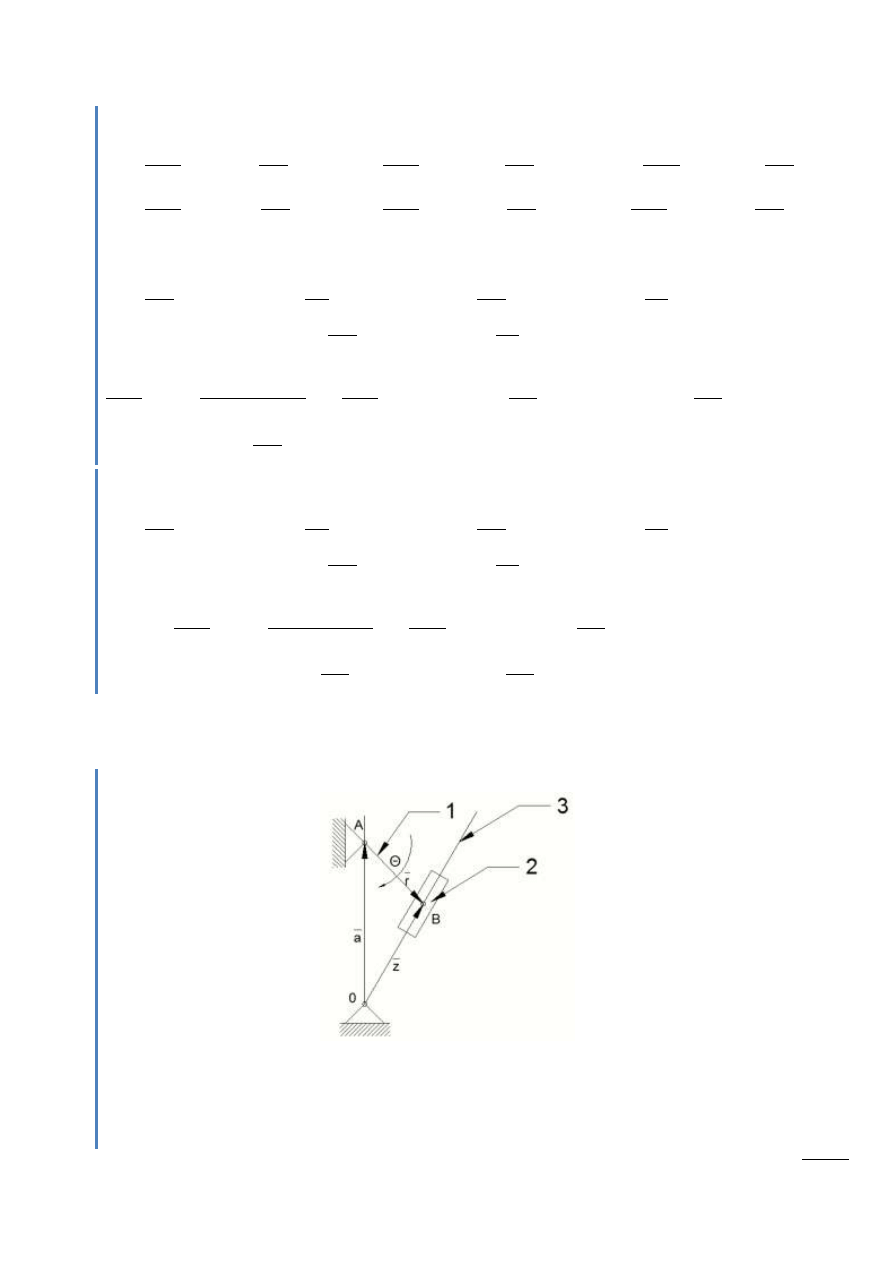
Rys. 4.1 – Oznaczenia kątów skierowanych w mechanizmie, dla którego wyznaczymy w dalszej części
metodą analityczną prędkości i przyspieszenia.
Obracamy układ współrzędnych o kąt +ϕ
3
i otrzymujemy:
Obracając układ współrzędnych o kąt +ϕ
4
otrzymujemy:
Ro
zd
ział:
Wy
kł
ad
4
. –
M
eto
d
y anal
ity
czn
e
p
rędk
o
ści
i p
rz
yspi
eszeo
20
Różniczkujemy jeszcze raz by uzyskad przyspieszenie:
Obracając układ współrzędnych o kąt +ϕ
3
otrzymamy:
Obracając układ o +ϕ
4
otrzymamy:
Wyznaczanie prędkości i przyspieszeń mechanizmu jarzmowego
Przykład
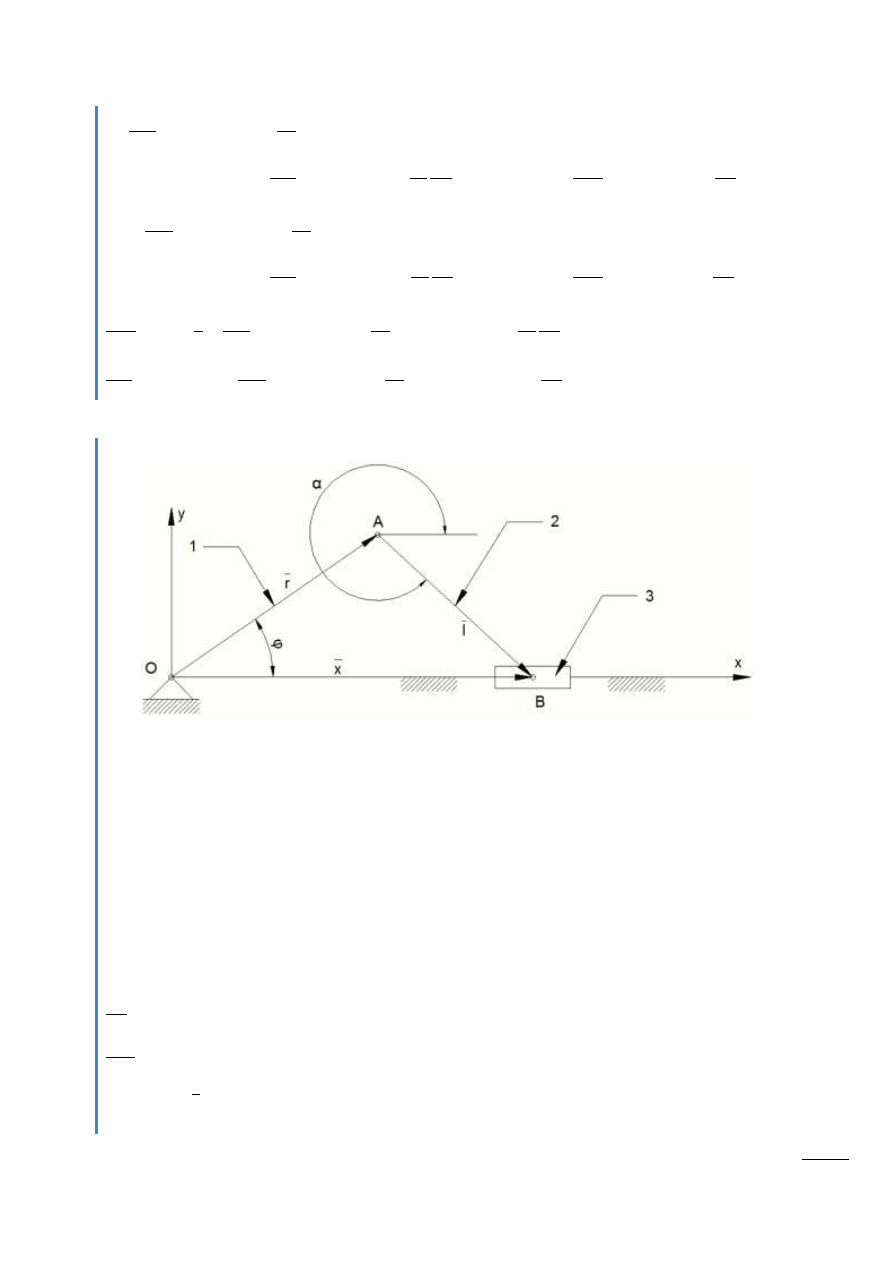
Rys. 4.2 – Mechanizm jarzmowy
B3

Ro
zd
ział:
Wy
kł
ad
4
. –
M
eto
d
y anal
ity
czn
e
p
rędk
o
ści
i p
rz
yspi
eszeo
21
Obracając układ współrzędnych o kąt +ψ otrzymamy:
Obracając układ współrzędnych o kąt +ψ otrzymamy:
Ro
zd
ział:
Wy
kł
ad
4
. –
M
eto
d
y anal
ity
czn
e
p
rędk
o
ści
i p
rz
yspi
eszeo
22
Wyznaczanie prędkości i przyspieszeń mechanizmu korbowo-wodzikowego
Przykład
Rys. 4.3 – Mechanizm korbowo-wodzikowy

Ro
zd
ział:
Wy
kł
ad
4
. –
M
eto
d
y anal
ity
czn
e
p
rędk
o
ści
i p
rz
yspi
eszeo
23
Ro
zd
ział:
Wy
kł
ad
5
. –
M
ech
an
iz
m
y
krz
yw
ko
we
24
Wykład 5. – Mechanizmy krzywkowe
Mechanizmem krzywkowym nazywamy mechanizm złożony z krzywki i popychacza. Zwykle
członem napędzającym jest krzywka. Popychacz może byd krążkiem lub ostrzem. Główną wadą
mechanizmów krzywkowych jest mała wytrzymałośd, szybkie zużywanie się, wrażliwośd na
uderzenia.
Analizę kinematyczną mechanizmów krzywkowych prowadzimy w celu wyznaczenia
przemieszczeo, prędkości i przyspieszeo popychacza w funkcji kąta obrotu krzywki. Analizę można
przeprowadzid metodą zastępowania pary IV klasy parą V klasy za pomocą planu prędkości i
przyspieszeo lub metodą analityczną. Można również przemieszczenia popychacza wyznaczyd
graficznie jako funkcję czasu lub kąta i przez różniczkowanie graficzne znaleźd prędkośd i
przyspieszenie.
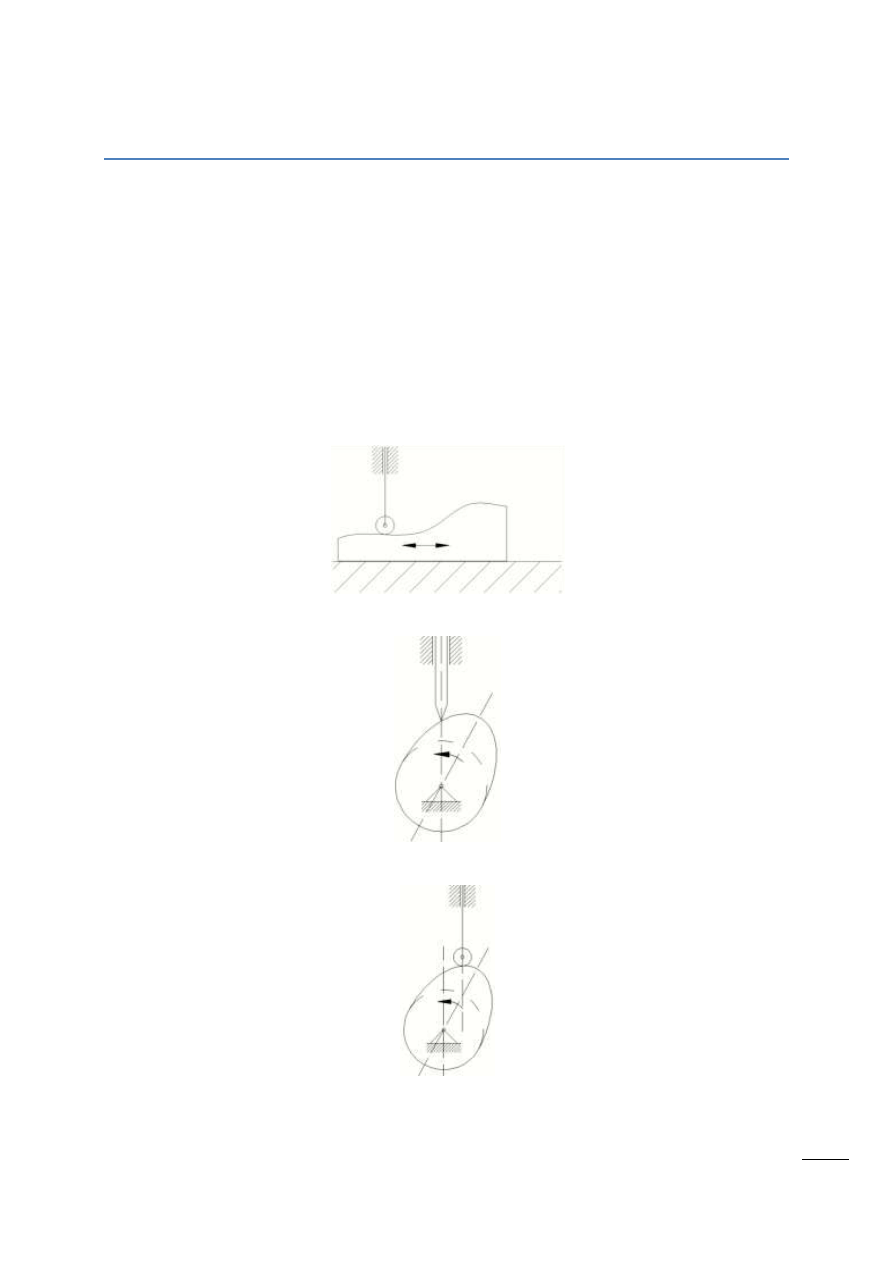
Rys. 5.1 – Krzywka o ruchu postępowym
Rys. 5.2 – Mechanizm z krzywką obrotową z popychaczem centralnym, ostrzowym
Rys. 5.3 – Mechanizm krzywkowy z popychaczem mimośrodowym krążkowym
Ro
zd
ział:
Wy
kł
ad
5
. –
M
ech
an
iz
m
y
krz
yw
ko
we
25
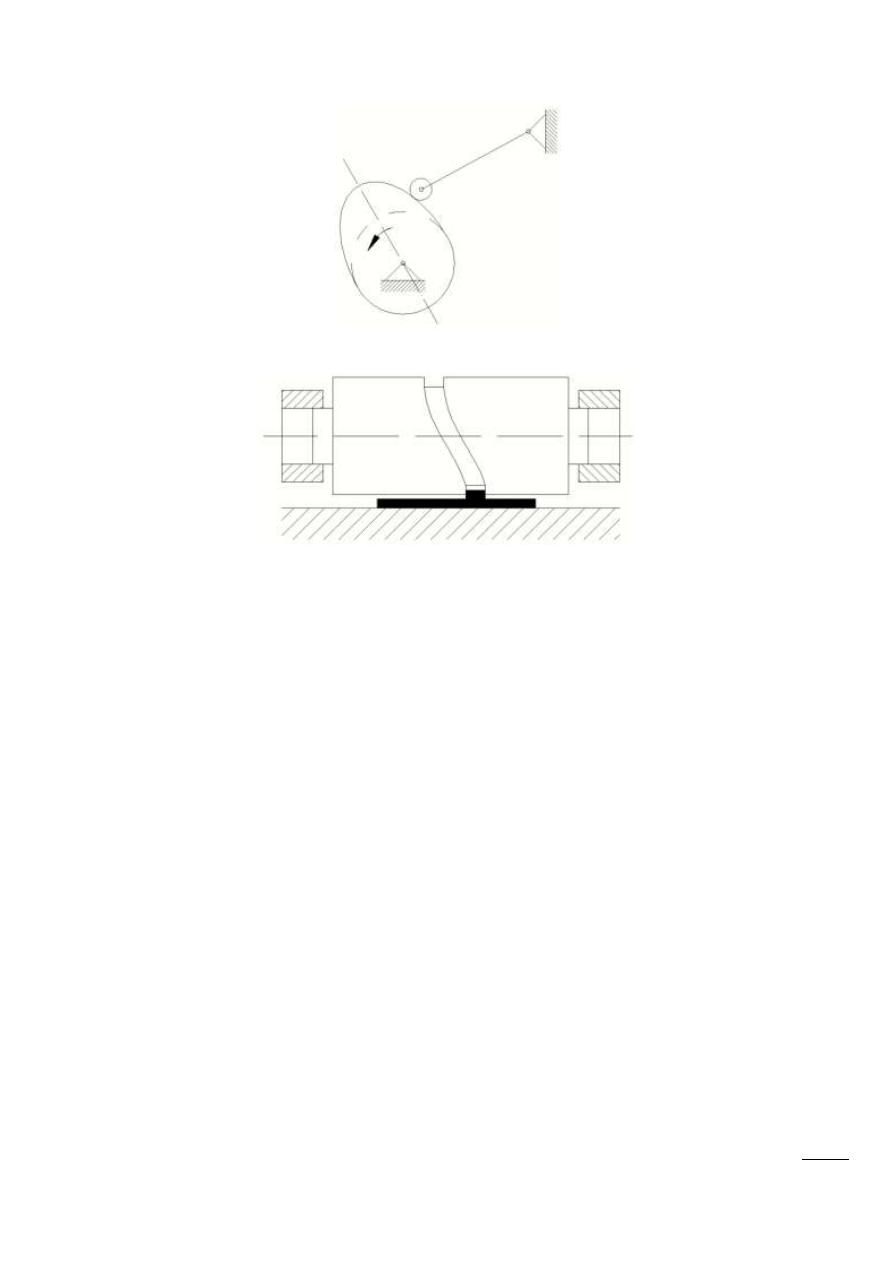
Rys. 5.4 – Mechanizm krzywkowy z popychaczem wahadłowym krążkowym
Rys. 5.5 – Mechanizm krzywkowy przestrzenny z krzywką walcową
Ro
zd
ział:
Wy
kł
ad
6
. –
An
ali
za i sy
n
teza m
echan
iz
m
ó
w
krz
ywk
o
wy
ch
26
Wykład 6. – Analiza i synteza
mechanizmów krzywkowych
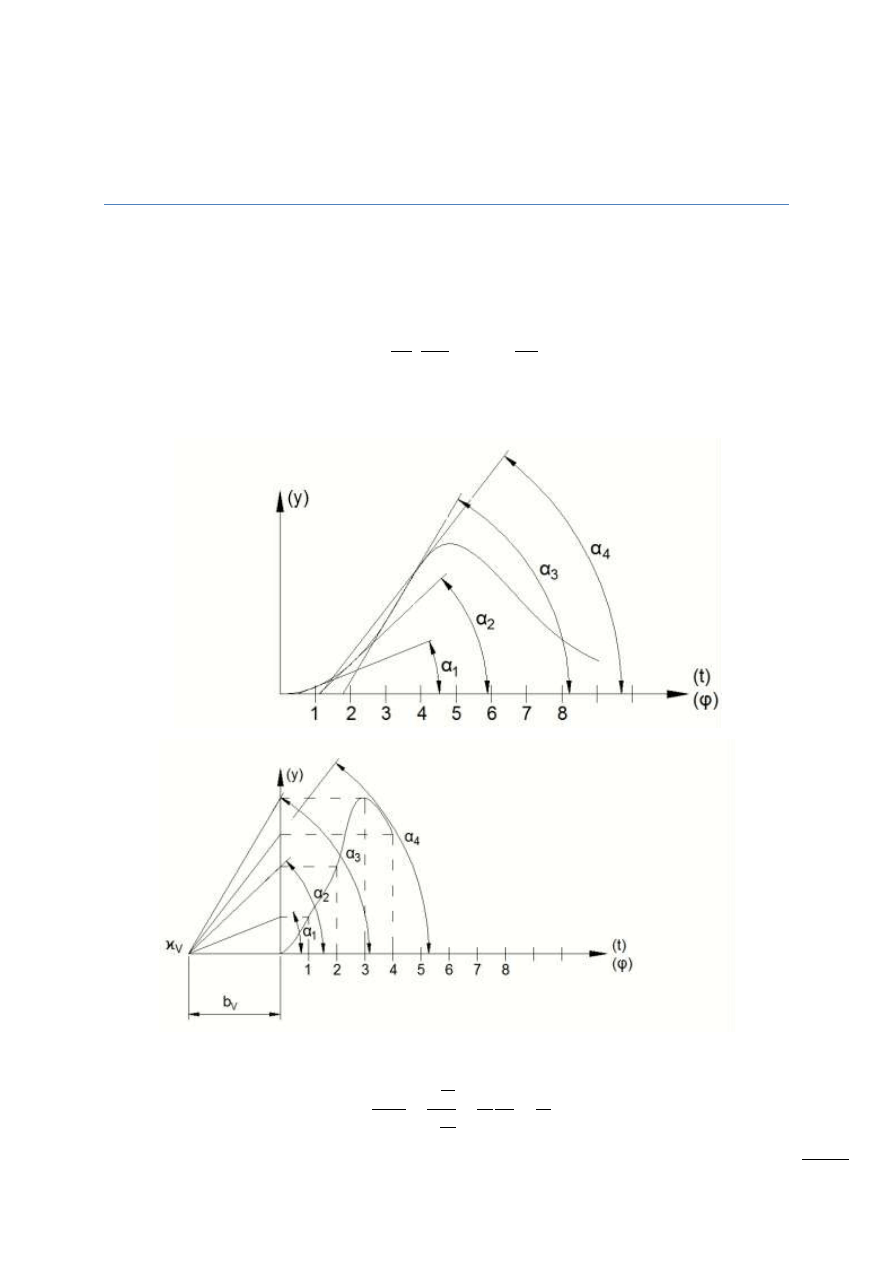
Metoda wykresów czasowych
Wykres przemieszczenia popychacza rysujemy przyjmując odpowiednią podziałkę czasu i
długości (k
t
, k
l
):
Przyjmując chwilę początkową t = 0 rozpatrywany punkt znajduje się w początku przyjętego
układu współrzędnych.
Rys. 6.1 – Różniczkowanie graficzne przemieszczenia popychacza
Ro
zd
ział:
Wy
kł
ad
6
. –
An
ali
za i sy
n
teza m
echan
iz
m
ó
w
krz
ywk
o
wy
ch
27
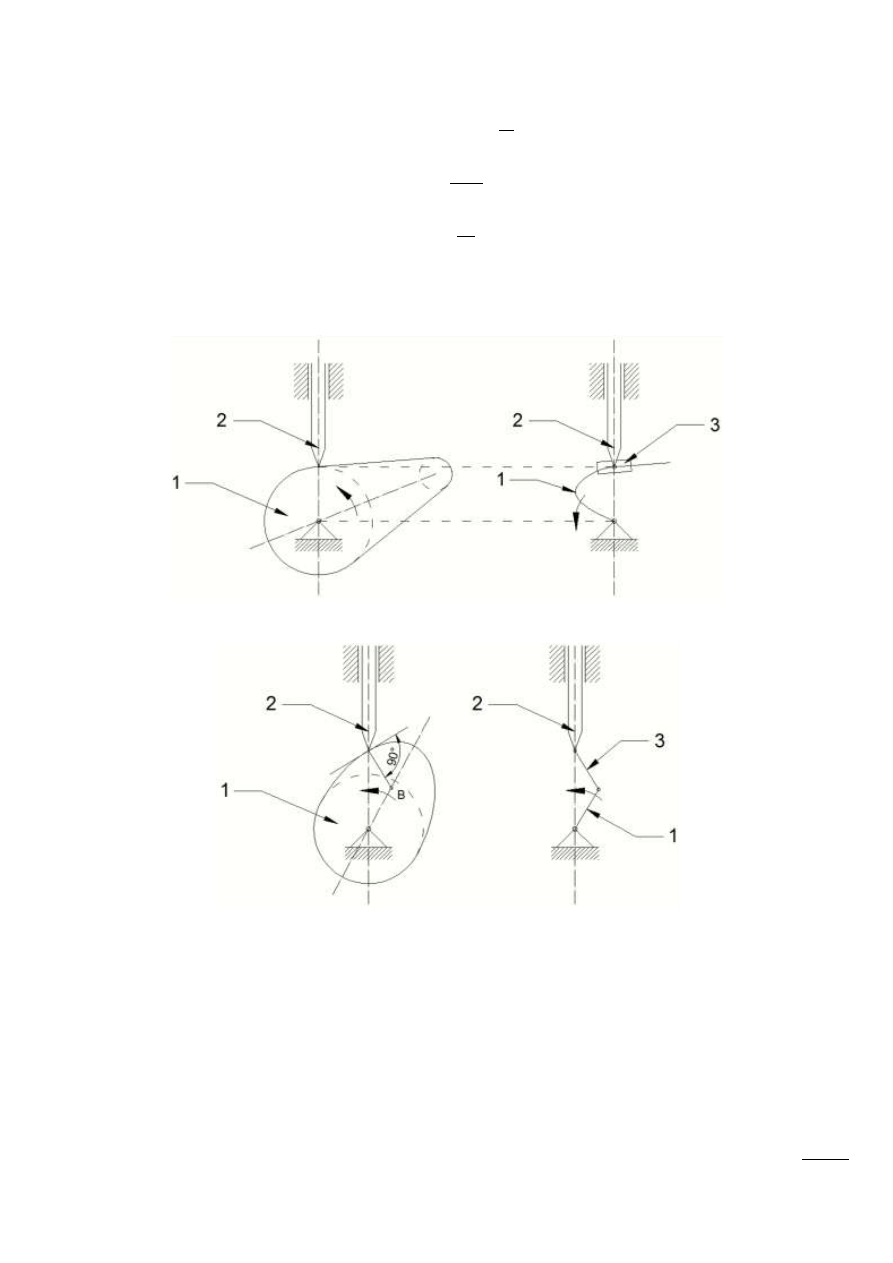
Analiza mechanizmów krzywkowych metodą zastępowania par klasy 4
parami klasy 5
Rys. 6.2 – Mechanizm krzywkowy i jego mechanizm równoważny
Rys. 6.3 – Mechanizm krzywkowy i jego mechanizm równoważny
Ro
zd
ział:
Wy
kł
ad
6
. –
An
ali
za i sy
n
teza m
ec
h
an
iz
m
ó
w
krz
ywk
o
wy
ch
28
Rys. 6.4 – Mechanizm krzywkowy i jego mechanizm równoważny
Metody analityczne wyznaczania prędkości i przyspieszeń mechanizmów
krzywkowych
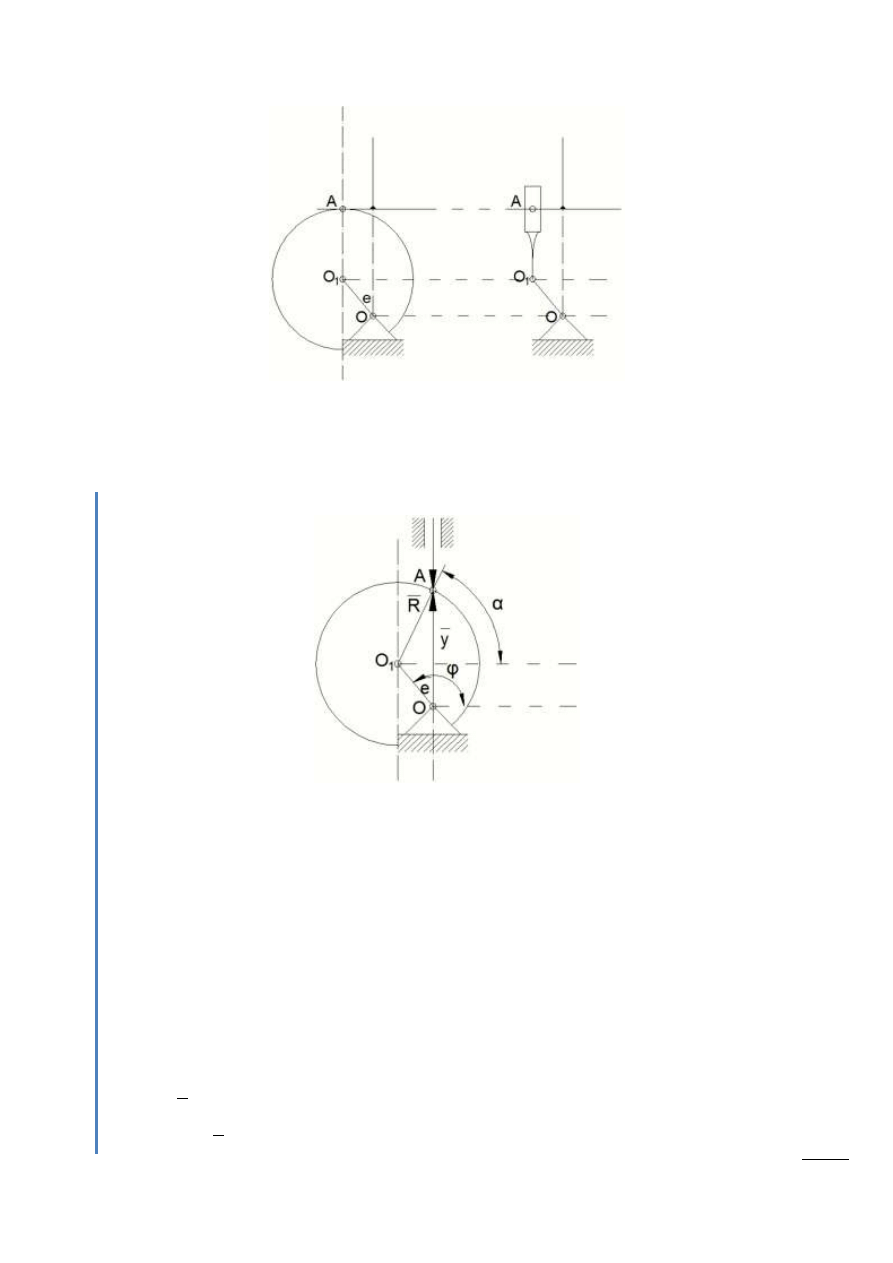
Przykład
Rys. 6.5 – Mechanizm krzywkowy
Z 1. równania:

Ro
zd
ział:
Wy
kł
ad
6
. –
An
ali
za i sy
n
teza m
echan
iz
m
ó
w
krz
ywk
o
wy
ch
29
Z 2. równania:
Razem uzyskujemy:
Synteza mechanizmów krzywkowych
W syntezie zajmiemy się projektowaniem mechanizmu krzywkowego, który spełnia z góry
zadane założenia (np. prędkości, przyspieszenia, położenia). Syntezę można przeprowadzid zarówno
na drodze analitycznej jak i wykreślnej.
Przykład
Zaprojektowad krzywkę harmoniczną, która będzie spełniania założony przebieg
przyspieszeo:
dla

Ro
zd
ział:
Wy
kł
ad
6
. –
An
ali
za i sy
n
teza m
echan
iz
m
ó
w
krz
ywk
o
wy
ch
30
dla
dla t = 0

Ro
zd
ział:
Wy
kł
ad
7
. –
D
yn
am
ika
m
echan
iz
m
ó
w
i m
asz
yn
31
Wykład 7. – Dynamika mechanizmów
i maszyn
W kinematyce mechanizmów analizuje się ich ruch (skutek) bez zajmowania się przyczyną,
która ten ruch powoduje. W tym celu zakłada się ruch członów napędzających i wyznacza ruch
członów napędzanych wynikający z ruchu członów napędzających. Nazywa się to analizą
kinematyczną mechanizmu lub maszyny.
Przyczyną powodującą ruch mechanizmu lub maszyny jest układ sił działających na
mechanizm lub maszynę. Dla realizacji założonego prawa ruchu mechanizmu lub maszyny niezbędne
jest przyłożenie odpowiedniego układu sił napędzających, równoważącego działania układu sił
obciążających mechanizm.
Siły napędzające (czynne) pochodzą od różnego rodzaju silników (ruch obrotowy) czy
siłowników (postępowy). Na obciążenie mechanizmu lub maszyny składają się siły oporu użytecznego
(siły bierne) np. siła skrawania w obrabiarce do metalu, siły oporu szkodliwego (siły tarcia w parach
kinematycznych, siły oporu aerodynamicznego) oraz siły ciężkości i bezwładności wynikające z ruchu
poszczególnych członów. Analiza przyczyn powodujących ruch mechanizmu lub maszyny nazywa się
analizą dynamiczną.
Wyznaczanie sił w mechanizmach z pominięciem sił bezwładności nosi nazwę analizy
statycznej. Jest ona szczególnym przypadkiem analizy dynamicznej. Zasada d’Alamberta
wprowadzająca siły bezwładności do podstawowych równao statyki pozwala rozwiązywad
zagadnienia dynamiki przy użyciu metod statyki. Analizę taką nazywa się kinetostatyczną.
Siły bezwładności
Układ sił bezwładności działających na dowolny człon sztywny można sprowadzid do siły
bezwładności:
oraz do momentu pary sił:
gdzie m – masa członu,
– przyspieszenie środka masy członu,
– moment bezwładności członu
względem osi prostopadłej do płaszczyzny ruchu i przechodzącej przez środek masy członu, –
przyspieszenie kątowe członu.

Ro
zd
ział:
Wy
kł
ad
7
. –
D
yn
am
ika
m
echan
iz
m
ó
w
i m
asz
yn
32
Rys. 7.1 Przyspieszenia i prędkości w pojedynczym członie
Metoda mas zastępczych (punktów zastępczych)
W wielu przypadkach gdy znamy przyspieszenia pewnych punktów członów, korzystniejszy
jest inny sposób sił bezwładności, polegający na zastąpieniu masy członu, kilkoma masami
skupionymi w punktach, których przyspieszenia znamy. Taką metodę nazywamy metodą skupionych
mas zastępczych. Warunki, które powinny spełniad skupione masy zastępcze, aby otrzymany dla nich
układ sił bezwładności był równoważny z rzeczywistym są następujące:
środek masy układu mas skupionych powinien pokrywad się ze środkiem masy członu
mechanizmu. Warunek ten dla układu płaskiego wyrażad się będzie wzorami:
gdzie
– współczynnik punktów, w których skupiono masy zastępcze.
Gdy początek układu współrzędnych pokrywa się ze środkiem masy członu, sumy wynoszą 0.
moment bezwładności układu mas zastępczych względem osi przechodzącej przez środek
mas, powinien byd równy momentowi bezwładności członu względem tej samej osi. W
przypadku układu płaskiego wyraża się to równaniem:
Pierwsze dwa warunki dają układ mas statycznie równoważny masie członów (bez
uwzględnienia bezwładności). Wraz z trzecim warunkiem dają układ mas dynamicznie równoważny.
Jeśli chcemy masę członu płaskiego zastąpid n masami skupionymi, musimy określid 3n parametrów
(każda masa określona jest 3 parametrami w postaci jej wielkości i 2 współrzędnych). Ilośd
parametrów, które możemy założyd dowolnie wyznaczamy z równania:
Ro
zd
ział:
Wy
kł
ad
7
. –
D
yn
am
ika
m
echan
iz
m
ó
w
i m
asz
yn
33
Najczęściej obieramy masy zastępcze w środkach przegubów i w środkach masy członów.
Masy zastępcze łatwo wyznacza się gdy są one rozmieszczone na jednej prostej, przechodzącej przez
środek masy członu.
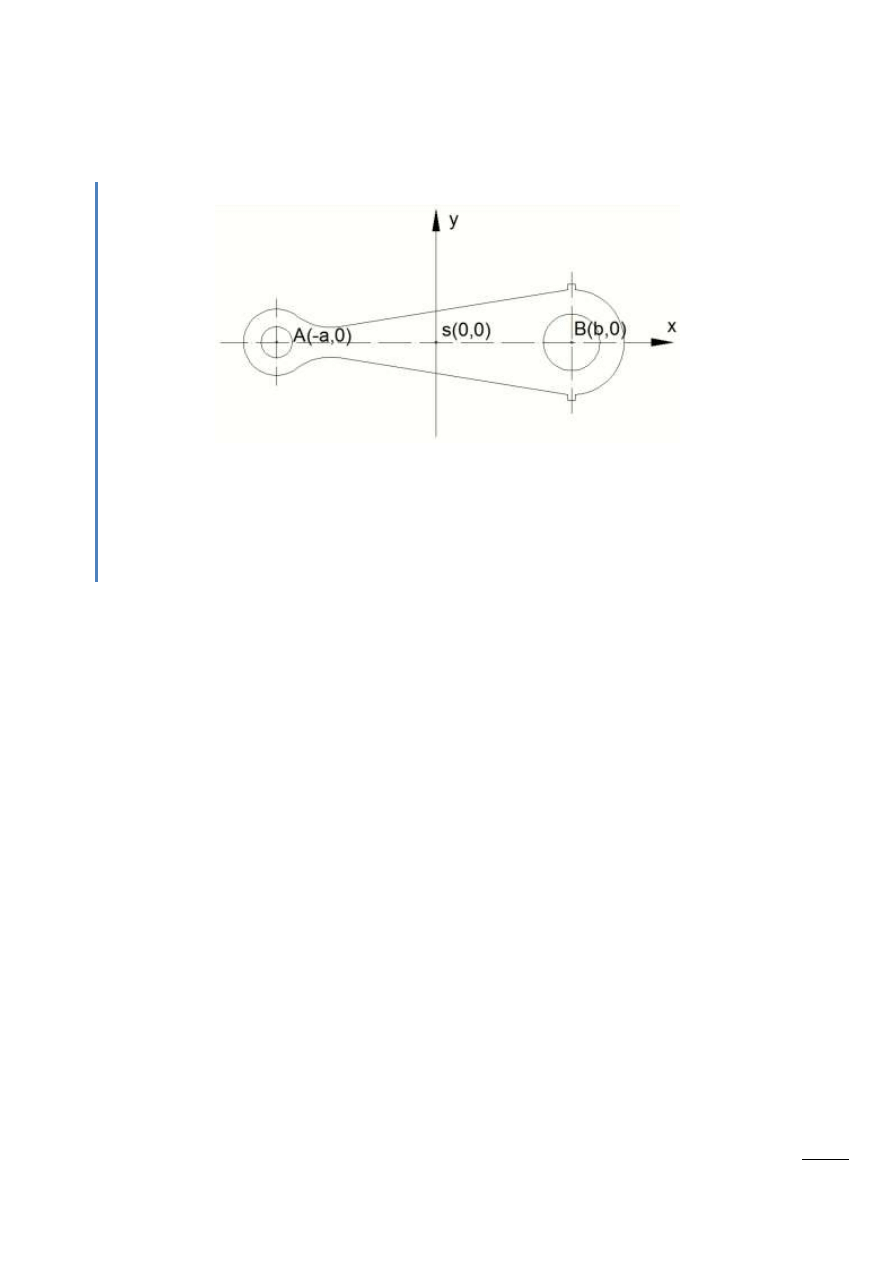
Przykład
Rys. 7.2 – punkty obrane na osi x (wzdłuż korby)
dla tego układu:
Ponieważ przyjęliśmy dowolne współrzędne musimy wyznaczyd masę punktu A, B oraz S.
Warunek wyznaczalności płaskiego łańcucha kinematycznego
Rozpatrzmy warunki jakie powinna spełnid liczba członów i liczba więzów kinematycznych
płaskiego łaocucha kinematycznego, by było możliwe wyznaczenie reakcji występujących w więzach
kinematycznych na podstawie statycznego warunku równowagi.
Reakcjami więzów w parach kinematycznych nazywamy siły oddziaływania jednego członu na
drugi. Warunkiem statycznej wyznaczalności mechanizmu płaskiego jest spełnienie równao
równowagi (rzutów sił i momentów sił) znanych z mechaniki:
Liczba równao które możemy ułożyd dla łaocucha kinematycznego mechanizmu o n członach
wynosi 3n. Tyle niewiadomych reakcji możemy wyznaczyd z równad mechaniki. Rozpatrzmy ile reakcji
występuje w łaocuchach kinematycznych mechanizmu płaskiego zawierającego pary kinematyczne V
i IV klasy.
Ro
zd
ział:
Wy
kł
ad
7
. –
D
yn
am
ika
m
echan
iz
m
ó
w
i m
asz
yn
34
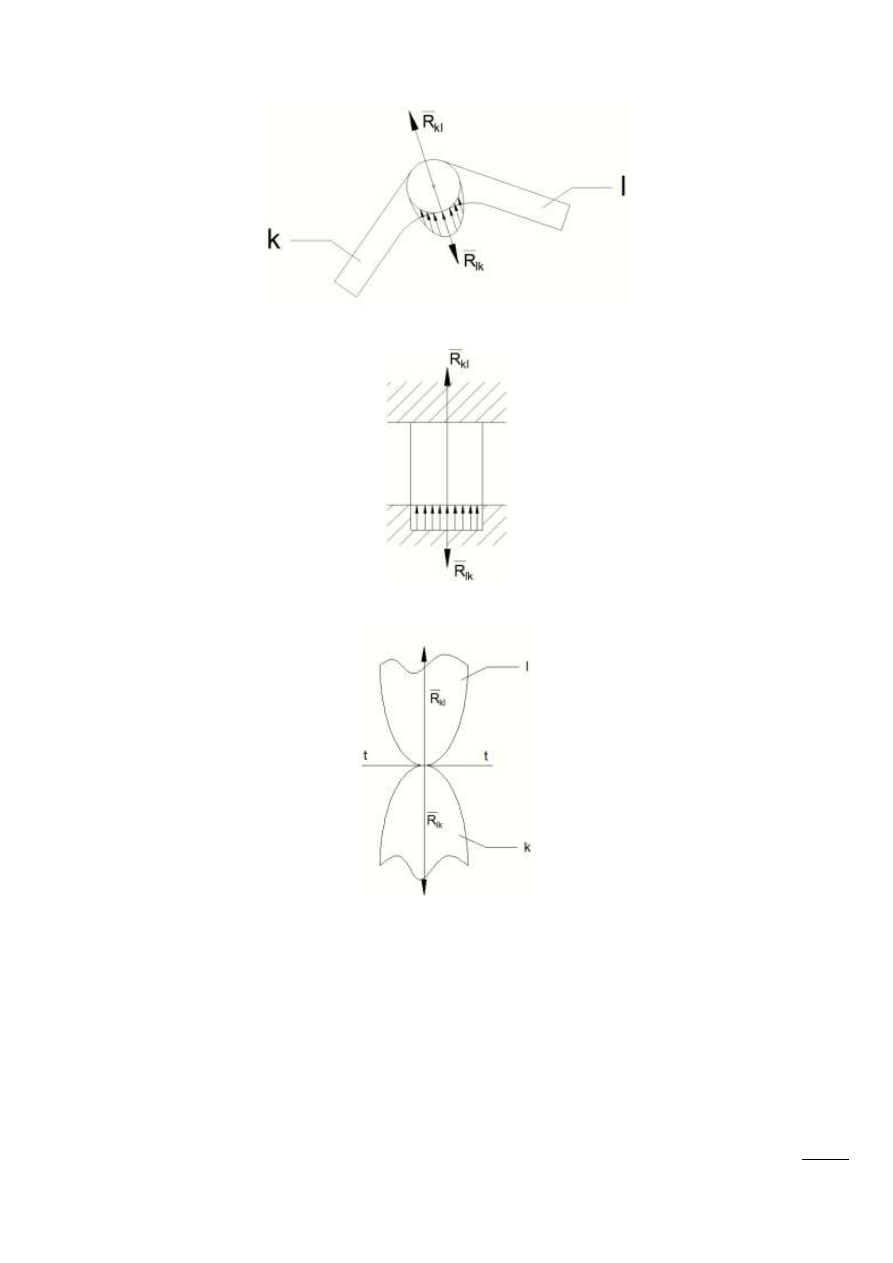
Rys. 7.3 – Para obrotowa (V klasa): wiadome: punkt przyłożenia; niewiadome: kierunek, wartośd.
Rys. 7.4 – Para postępowa (V klasa): wiadome: kierunek; niewiadome: punkt przyłożenia, wartośd.
Rys. 7.5 – Para V klasy – znane: punkt przyłożenia, kierunek; nieznane: wartośd.
W parze obrotowej V klasy mamy 1 niewiadomą (punk przyłożenia reakcji), bo musi
przechodzid przez oś przegubu. Wiadoma jest wartośd reakcji i jej kierunek. W parze postępowej V
klasy mamy także 1 wiadomą – kierunek reakcji, ponieważ musi on byd prostopadły do kierunku
ruchu. Nieznana jest wartośd i punkt przyłożenia reakcji. W parze IV klasy mamy 2 wiadome –
kierunek reakcji (prostopadły do krzywizn w punkcie styku) i punkt przyłożenia (punkt styku). Z
rozważao tych wynika, że w każdej parze V klasy mamy dwie niewiadome, a w parze IV klasy jedną.
Jeśli łaocuch kinematyczny składa się z par IV i V klasy, to ilośd niewiadomych wynosi 2p
5
+ p
4
. Aby
łaocuch kinematyczny płaski był statycznie wyznaczalny, to ilośd niewiadomych musi byd równa ilości
równao statyki. Otrzymamy więc warunek
. Warunek statycznej wyznaczalności

Ro
zd
ział:
Wy
kł
ad
7
. –
D
yn
am
ika
m
echan
iz
m
ó
w
i m
asz
yn
35
łaocucha kinematycznego mechanizmu jest identyczny z warunkiem istnienia grupy. Z równania tego
wynika, że grupa jest łaocuchem kinetostatycznie wyznaczalnym. Analiza kineto statyczna
mechanizmu sprowadza się do analizy grup strukturalnych na jakie może byd rozdzielony mechanizm.
Analiza musi byd rozpoczęta od grupy ostatniej w stosunku do członu napędowego.

Ro
zd
ział:
Wy
kł
ad
8
. –
Gru
p
y
36
Wykład 8. – Grupy
Każdy człon posiada trzy równania równowagi:
Klasyfikacja strukturalna mechanizmów płaskich
Klasę mechanizmu określa najwyższa klasa grupy wchodzącej w skład mechanizmu. Grupa
jest to łaocuch kinematyczny spełniający następujące warunki:
połączenie ruchome z podstawą wszystkich członów zewnętrznych łaocucha zamienia go w
układ sztywny, tzn. ruchliwośd jest równa 0, w = 0;
łaocucha spełniającego warunek pierwszy nie można podzielid przez rozłączenie członów na
łaocuchy spełniające ten warunek.
Człon napędowy nie należy do żadnej grupy i można go połączyd ruchowo z podstawą oraz z
grupą.
gdzie n to liczba członów w grupie, natomiast p
5
to liczba członów kinematycznych powstałych z
przyłączenia grupy do podstawy.
Pary IV klasy zamieniamy na pary V klasy.
Grupy dla n > 4 i p
5
> 6 występują bardzo rzadko.
Wyznaczanie reakcji w grupach klasy II
Dla grupy klasy II n = 2, p
5
= 3, zatem warunek grupy jest spełniony:
Ro
zd
ział:
Wy
kł
ad
8
. –
Gru
p
y
37
Wyznaczanie reakcji w mechanizmach można przeprowadzid metodą wykreślno-analityczną.
Metoda ta jest najprostsza i polega na wykreśleniu planu sił i analitycznym obliczeniu niezbędnych
wielkości. W obu przypadkach korzystamy z warunków równowagi sił i momentów. W metodzie
wykreślno-analitycznej posługujemy się wektorowymi równaniami sił oraz równaniami równowagi
momentów sił działających na człony grupy.
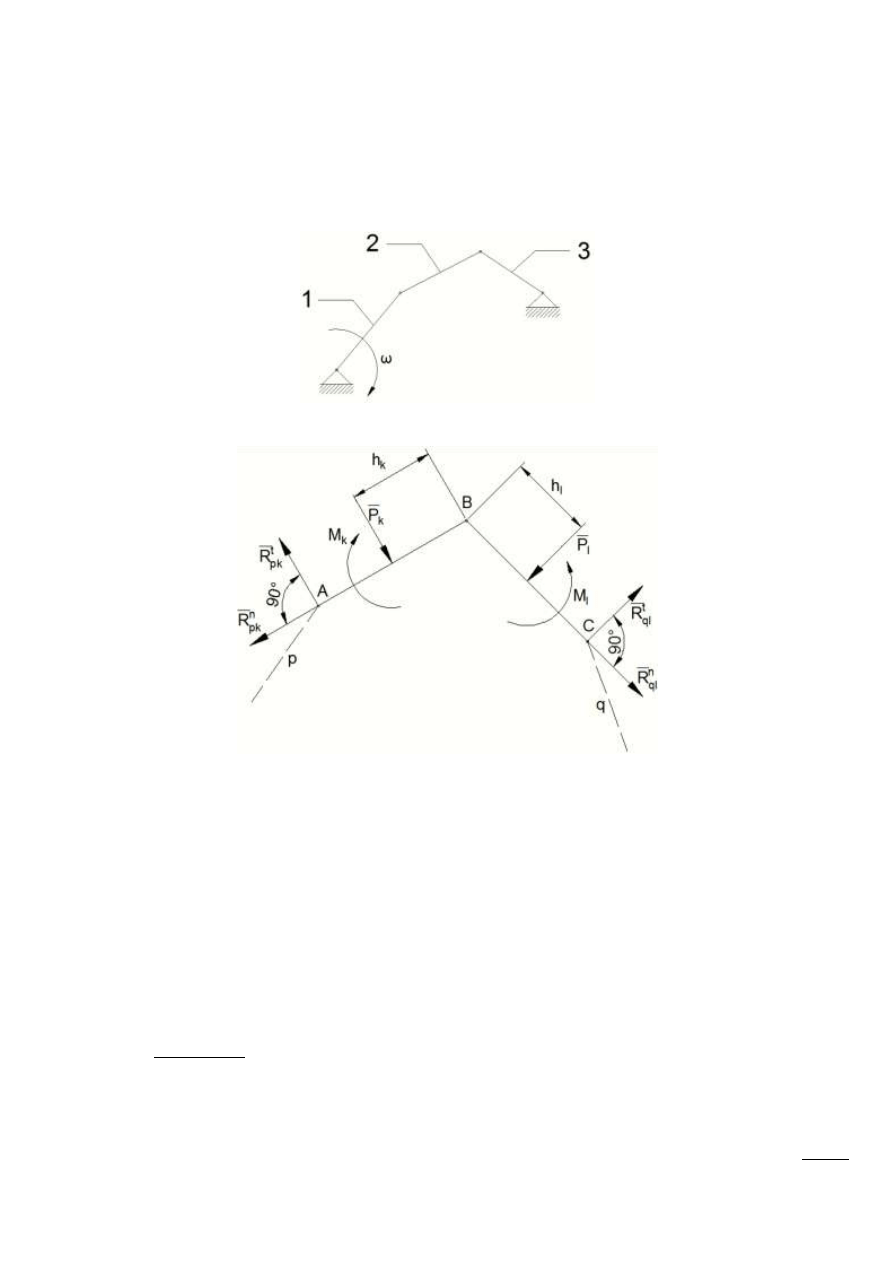
Rys. 8.1 – Przykładowa grupa
Rys. 8.2 – Reakcje wyznaczamy na kierunek równoległy i prostopadły do członu.
W punktach A i C zastępujemy więzy reakcjami R
pk
i R
ql
, które rozkładamy na kierynki
normalne (równoległe) oraz styczne (prostopadłe) do członów k i l. Układamy równania równowagi
momentów wszystkich sił względem punktu B. Ponieważ zwroty reakcji nie są nam znane, więc
przyjmujemy je dowolnie. Jeżeli po wyznaczeniu wartości reakcji z równania momentów, okaże się
ona ujemna, to jej zwrot należy przyjąd jako przeciwny.
Wyznaczanie momentów dla członu k:
Wyznaczanie momentów dla członu l:
Ro
zd
ział:
W
ykł
ad
8
. –
Gru
p
y
38
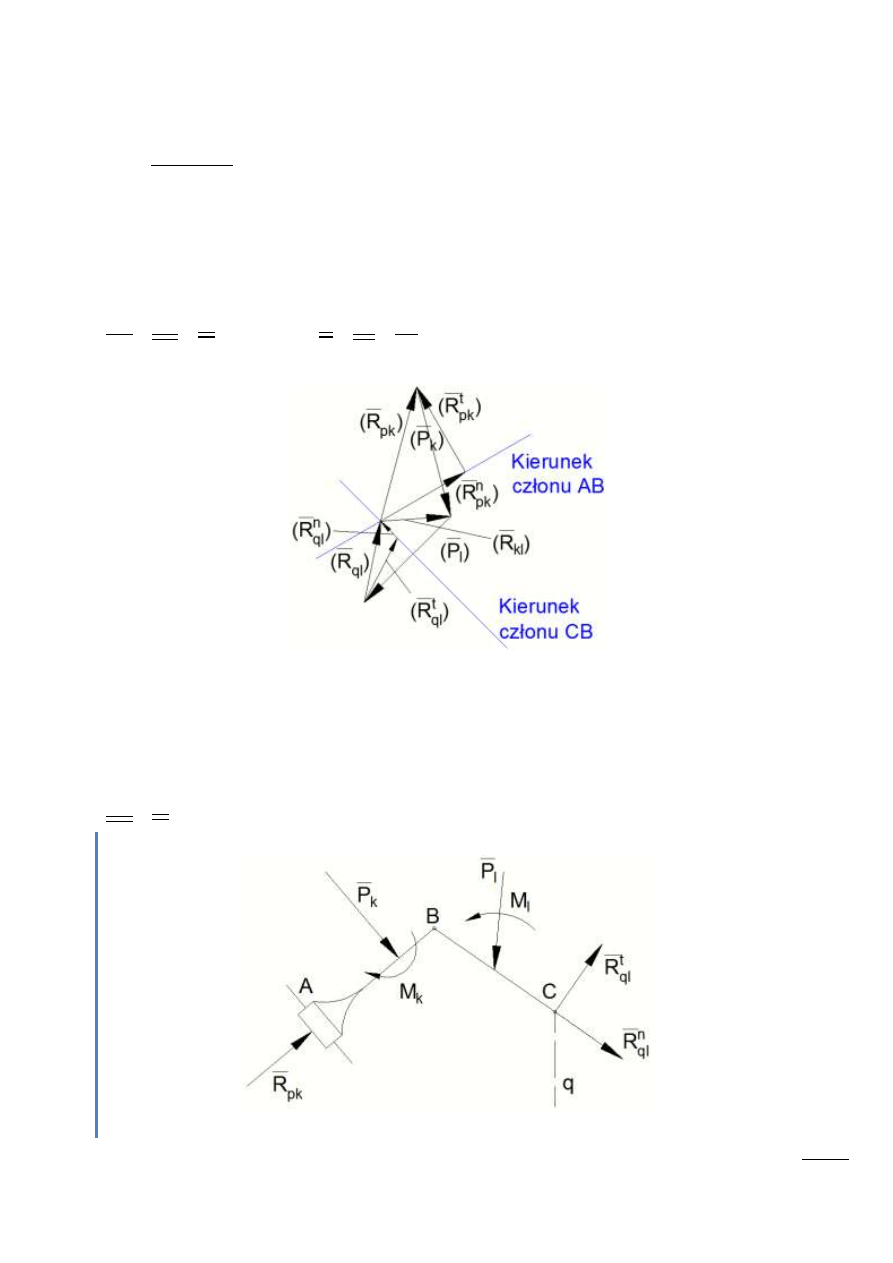
Piszemy równanie wektorowe dla całej grupy k-l:
Wykreślamy siły:
Rys. 8.3 – Rozrysowanie wektorów sił
Dla członu k:
Przykład
Rys. 8.4 – Grupa klasy II (postad 2)
Ro
zd
ział:
Wy
kł
ad
8
. –
Gru
p
y
39
Postępowanie:
1. punkt 2 z poprzedniego przykładu
2. punkt 3 z poprzedniego przykładu
3. punkt 1 z poprzedniego przykładu
Plan sił członu napędzającego
Człon napędzający tworzy z podstawą najczęściej parę obrotową lub postępową. Posiada on
jeden stopieo swobody względem podstawy. Rozpatrując człon napędzany łącznie z podstawą,
stwierdzamy, że warunek statycznej wyznaczalności nie jest spełniony. Liczba równao równowagi,
które możemy ułożyd dla członu napędzanego jest o 1 większa od liczby niewiadomych. Aby
zachodziła statyczna wyznaczalnośd, trzeba wprowadzid dodatkowe siły lub parę sił równoważącą
wszystkie siły przyłożone do członu napędzającego. Oznaczamy siłę równoważącą parę P
r
, a moment
równoważący M
r
.
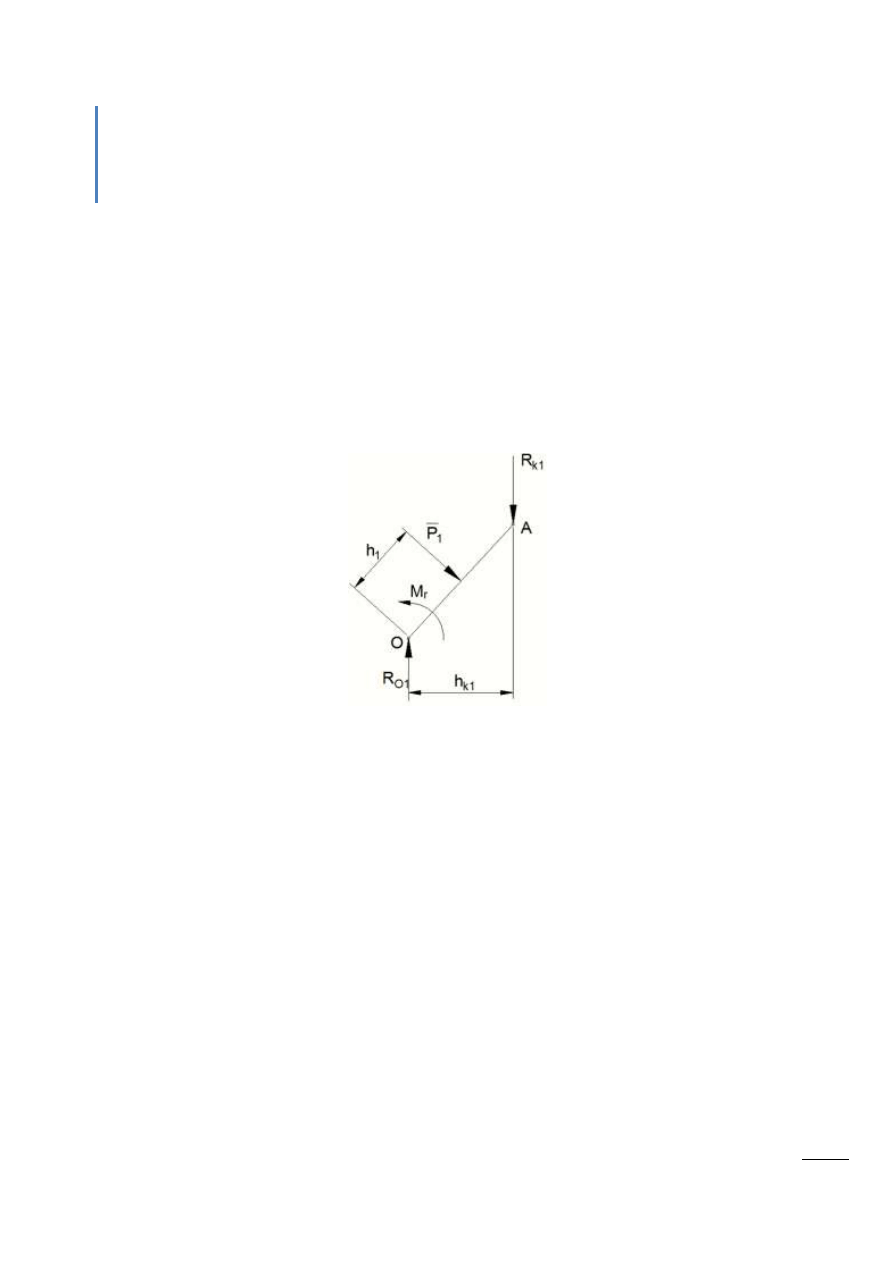
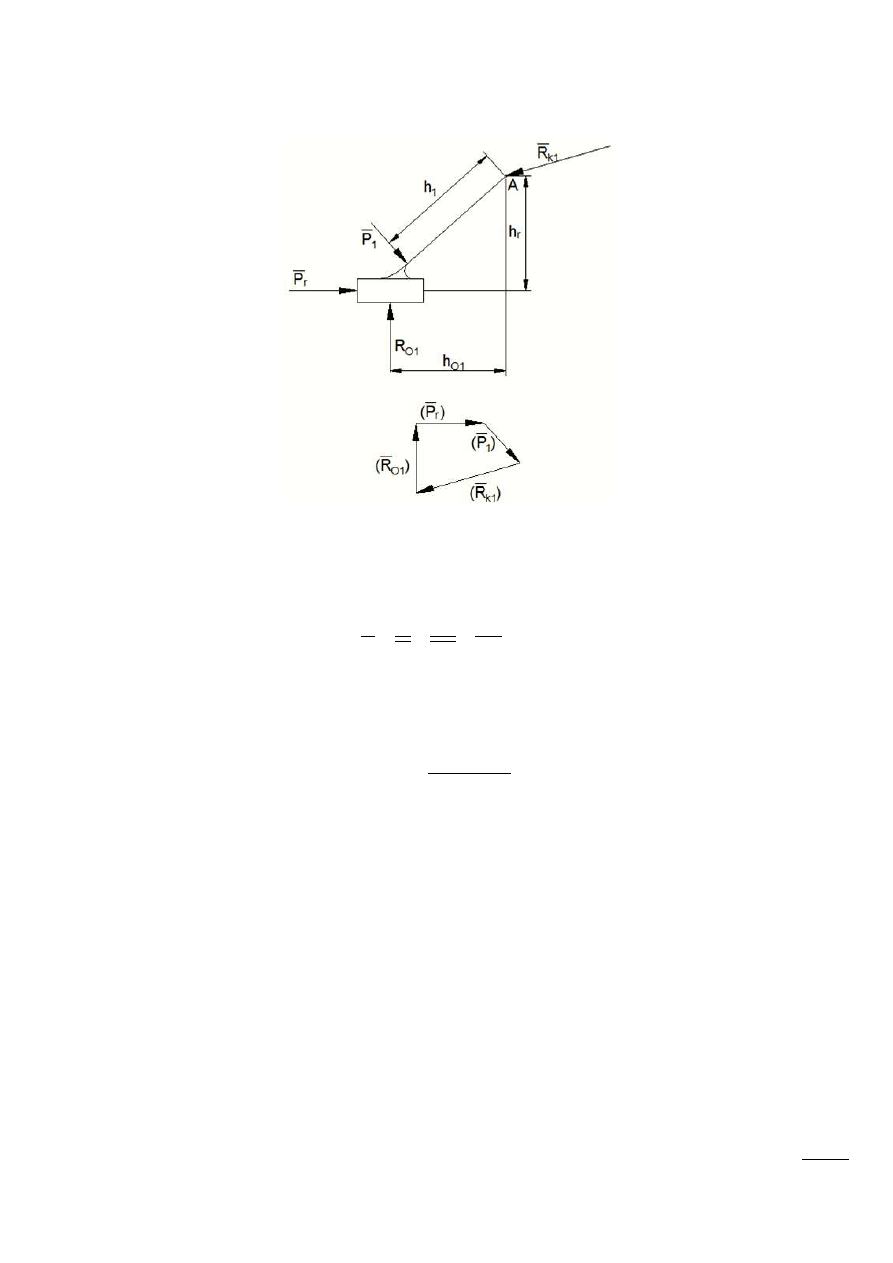
Dla członu napędzającego wykorzystującego ruch obrotowy:
Rys. 8.5 – Człon napędzany, wykonujący ruch obrotowy
Ro
zd
ział:
Wy
kł
ad
8
. –
Gru
p
y
40
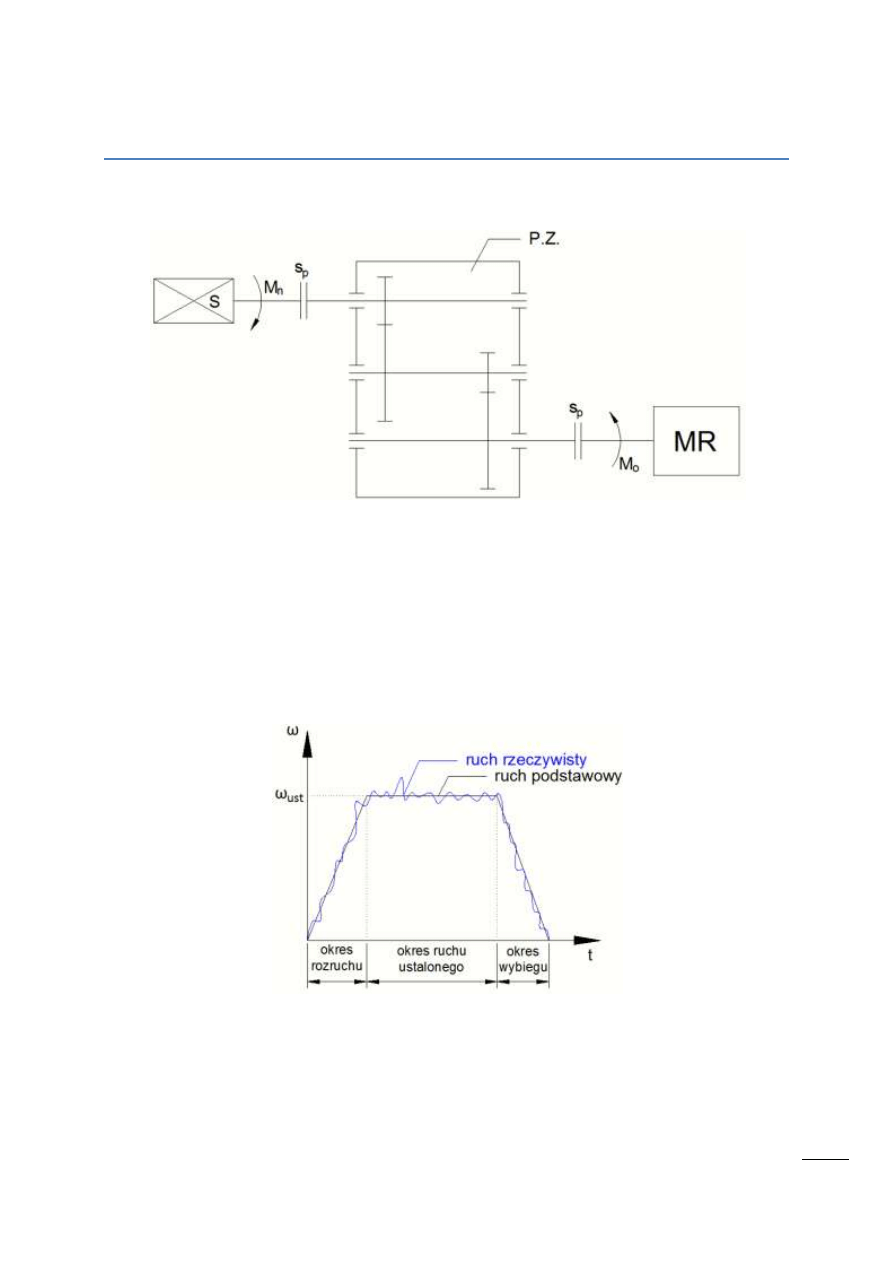
Dla członu napędzającego, wykonującego ruch postępowy:
Rys. 8.6 – Człon napędzający wykonujący ruch postępowy oraz suma wektorów sił w układzie.
Ro
zd
ział:
Wy
kł
ad
9
. –
D
yn
am
ika
m
asz
yn
41
Wykład 9. – Dynamika maszyn
Ruch maszyny pod działaniem sił
Rys. 9.1 – Maszyna robocza napędzana przez silnik. Przeniesienie napędu przez dwa sprzęgła oraz
przekładnie.
Dokładne określenie rzeczywistych przemieszczeo, prędkości, przyspieszeo i czasu ruchu
maszyny wymaga wyznaczenia przebiegu ruchu pod działaniem zadanych sił.
Wyznaczanie przebiegu ruchu maszyny można znacznie ułatwid jeśli masy wszystkich członów
ruchomych zastąpimy masą zredukowaną, umieszczoną na członie redukcji i zredukujemy do niego
wszystkie siły zewnętrzne działające na człony mechanizmu lub maszyny bez uwzględnienia sił
bezwładności.
Rys. 9.2 – Przebieg ruchu maszyny w czasie
W badaniach ruchu maszyny związanych w szczególności z projektowaniem maszyny,
rozdzielamy zagadnienie badania ruchu postępowania i ruchów dodatkowych – pasożytniczych.
Stosując znane z mechaniki metody można ułożyd równanie ruchu podstawowego maszyny.
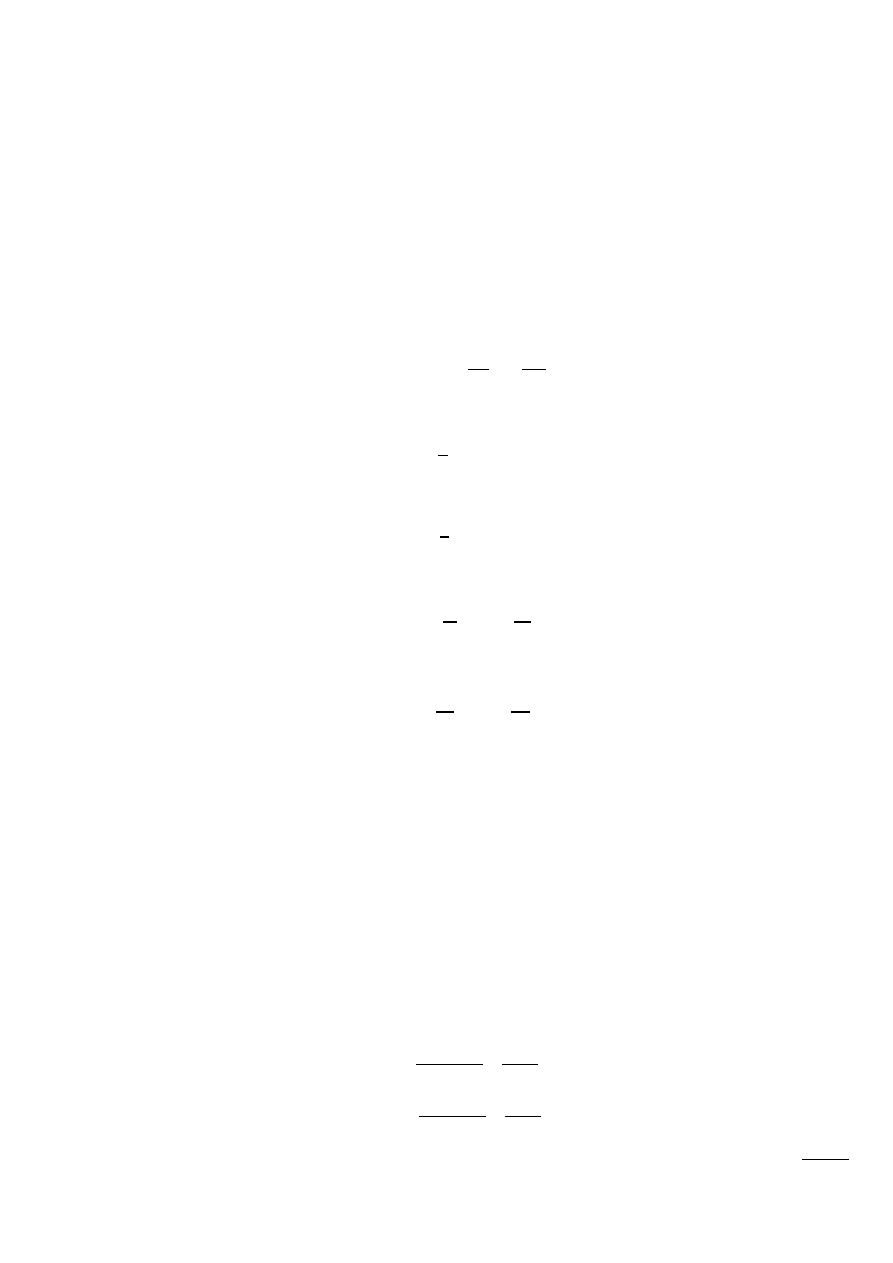
Ro
zd
ział:
Wy
kł
ad
9
. –
D
yn
am
ika
m
asz
yn
42
Redukcja mas
Zastępowanie układu mas członów ruchomych mechanizmu lub maszyny masą zredukowaną
skupioną w dowolnym punkcie lub zredukowanym momentem bezwładności członu redukcji
przeprowadza się korzystając z równości chwilowych wartości energii kinetycznych wszystkich
członów mechanizmów i członu redukcji:
Energia kinetyczna mechanizmu w dowolnej chwili równa jest sumie energii kinetycznych
poszczególnych jego członów. W przypadku ruchu płaskiego:
Energia kinetyczna członu redukcji wynosi w przypadku jego ruchu postępowego:
Energia kinetyczna członu redukcji w przypadku jego ruchu obrotowego:
Masa zredukowana:
Zredukowany moment bezwładności:
Redukcja sił
Zastępowanie układu sił zewnętrznych i momentów sił działających na ruchome człony
mechanizmu lub maszyny siłą zredukowaną, przyłożoną w dowolnie wybranym punkcie członu
redukcji lub momentem zredukowanym przyłożonym do członu redukcji, przeprowadza się
korzystając z równości chwilowych wartości mocy N
i
wszystkich członów mechanizmu i N
z
członów
redukcji. Zakładając kierunek siły zredukowanej zgodny z kierunkiem prędkości V
z
punktu redukcji,
moc członu wyniesie:
Moc chwilowa wszystkich członów mechanizmu lub maszyny wynosi:
Ro
zd
ział:
Wy
kł
ad
9
. –
D
yn
am
ika
m
asz
yn
43
Jako człon redukcji wybiera się najczęściej człon napędowy mechanizmu lub maszyny.
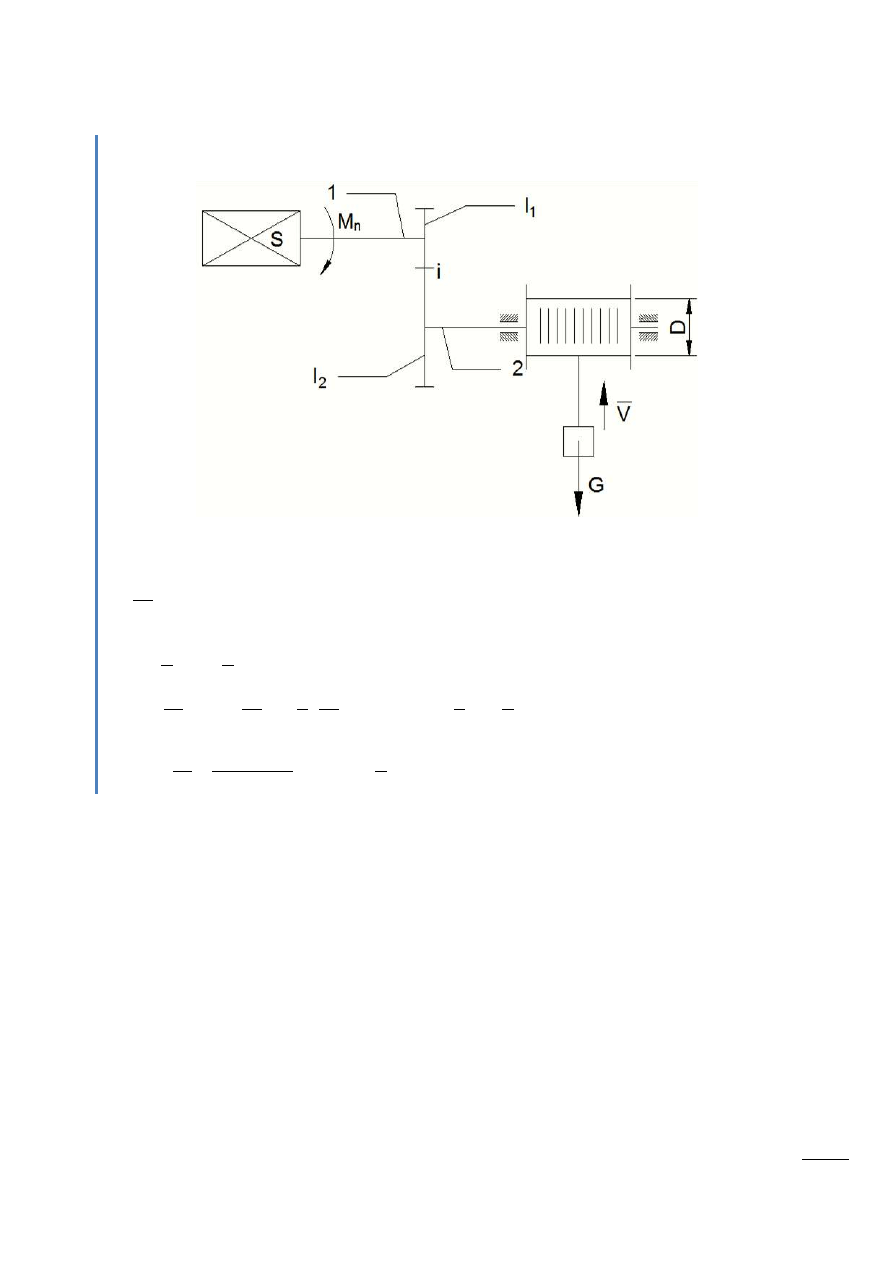
Przykład
Przeprowadzid redukcję układu pokazanego na rysunku na wał silnika.
Rys. 9.3 – Silnik działa momentem napędowym M
n
na wale 1. Poprzez przekładnię i bęben wciąga
przedmiot o ciężarze G. I
1
– moment bezwładności wału 1 łącznie z kołem zębatym i częściami
wirującymi silnika; I
2
– moment bezwładności wału 2 łącznie z kołem zębatym i bębnem.
Równanie ruchu maszyny
Ponieważ człon redukcji otrzymuje się w wyniku redukcji sił wyniku redukcji sił wychodząc z
warunków równości elementarnych praw, a redukcji mas wychodząc w warunku równowagi energii
kinetycznych, zatem przy badaniu ruchu członu redukcji, celowe jest wyjśd z zasady równowartości
energii kinetycznej i pracy:
Dla ruchu postępowego celowe jest wyrazid dE za pomocą masy zredukowanej m
z
. Różniczkę
pracy zaś za pomocą siły resztkowej P
z
, która stanowi różnicę siły czynnej P
c
i P
b
.
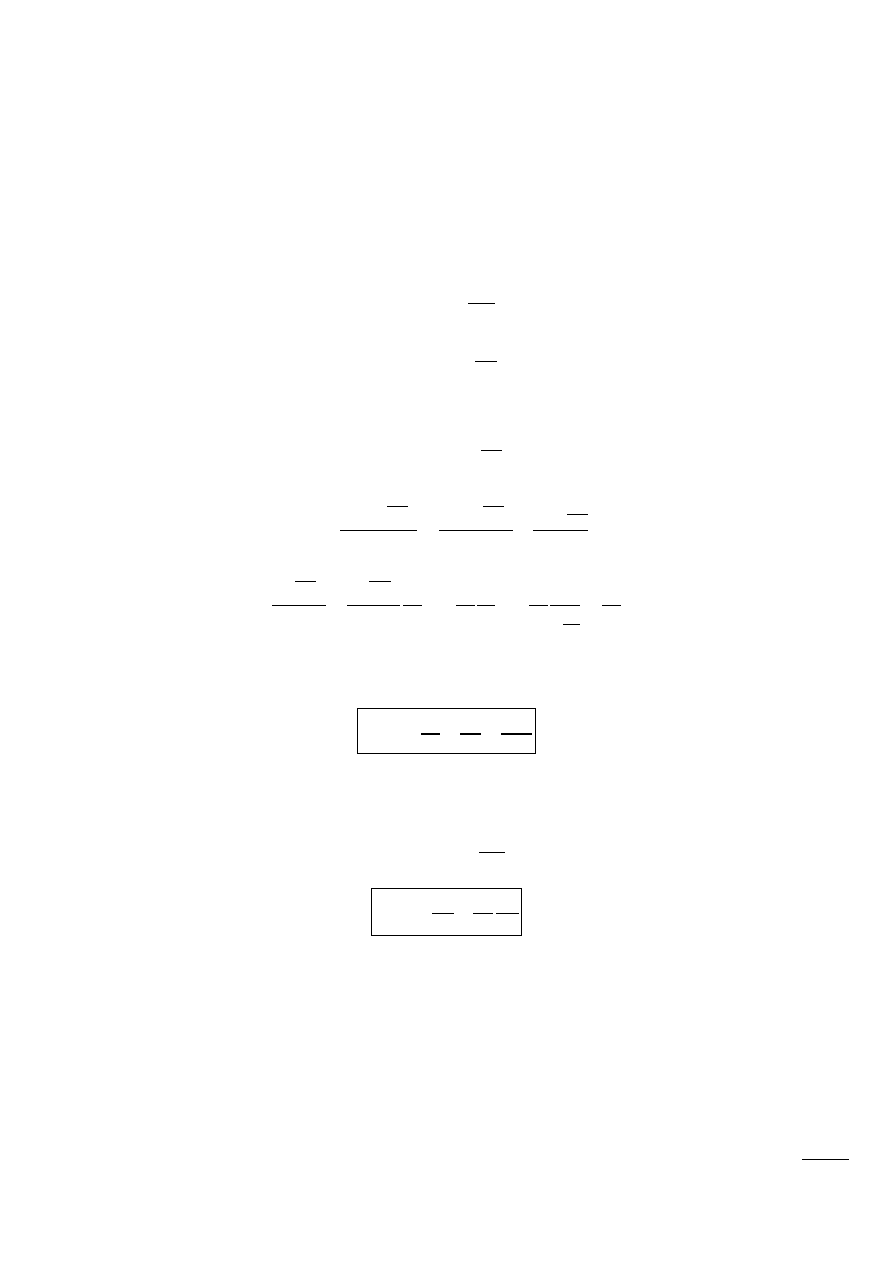
Ro
zd
ział:
Wy
kł
ad
9
. –
D
yn
am
ika
m
asz
yn
44
Dla ruchu obrotowego członu redukcji wygodnie jest wyrazid dE za pomocą zredukowanego
momentu bezwładności I
z
, a dl za pomocą zredukowanego momentu resztkowego M
z
, który stanowi
różnicę zredukowanego momentu czynnego i biernego.
Podstawiając do równania równości, otrzymamy:
Otrzymane równanie ruchu redukcji jest równaniem modelu dynamicznego mechanizmu lub
maszyny.
Dla ruchu postępowego członu redukcji:
Zaznaczone równania, to dynamiczne równania ruchu maszyny. Są to równania ogólne,
ważne zarówno dla maszyn, w których istnieje zmienne przełożenie, jak i dla maszyn o stałych
przełożeniach między członami.
Jeśli istnieje zmienne przełożenie w maszynie to zredukowany moment bezwładności jest
funkcją obrotu:

Ro
zd
ział:
Wy
kł
ad
9
. –
D
yn
am
ika
m
asz
yn
45
a moment zredukowany funkcją przemieszczenia:
Jeśli przełożenie nie zmienia się w trakcie ruchu, to:
i dynamiczne równania ruchu maszyny przyjmują wartośd:
Analizując ogólne równania różniczkowe maszyny, należy pamiętad, że:
Dynamiczne równania ruchu maszyny w postaci wygodnej w posługiwaniu się w przypadkach
gdy M
z
lub P
z
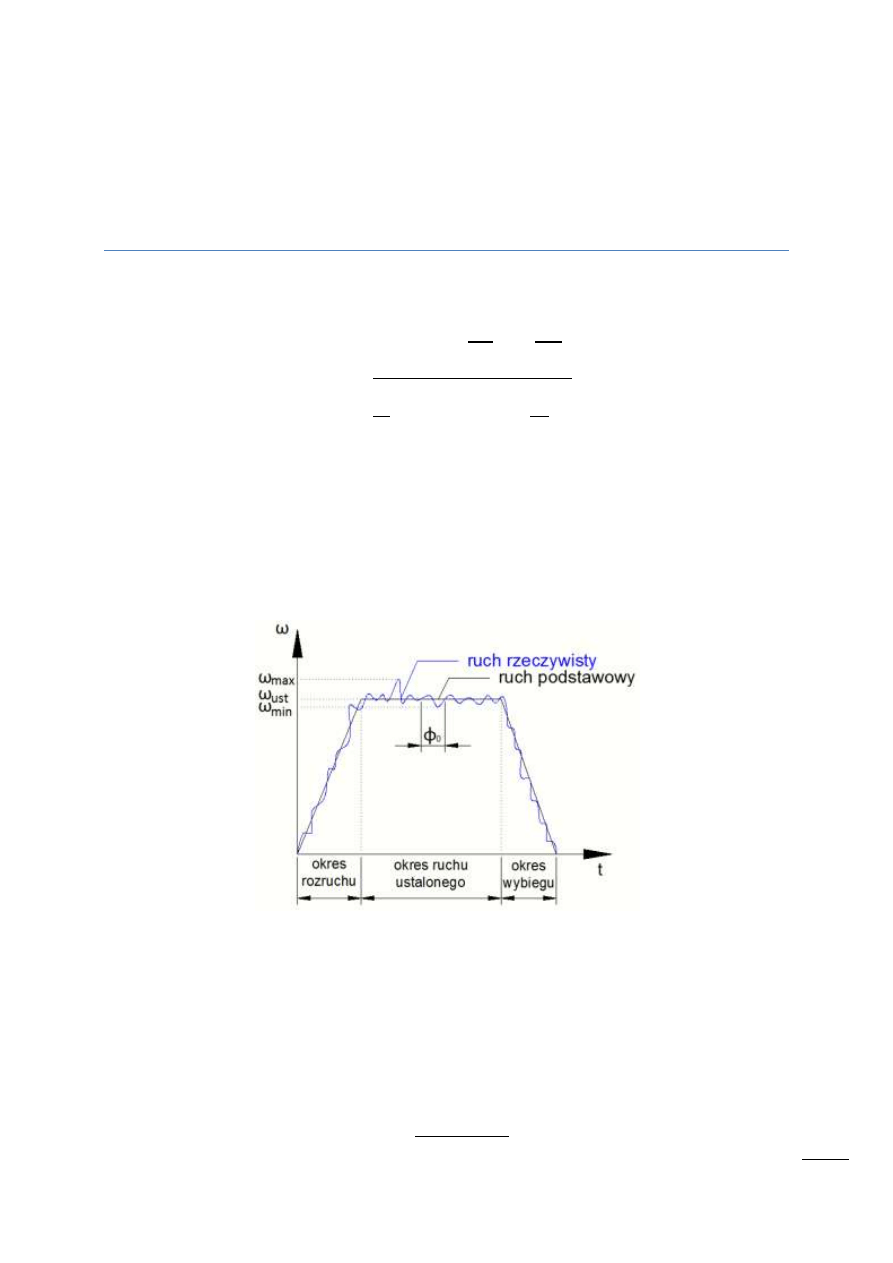
zależą od , a Iż czy M
z
zależą od lub s. W przypadkach gdy zredukowany
moment lub siła oraz moment bezwładności lub masa zredukowana są funkcjami położenia członu
maszyny, celowo jest ułożyd równanie ruchu maszyny w postaci energetycznej, korzystając w Prost z
równania równości energii kinetycznej i pracy.
Ro
zd
ział:
Wy
kł
ad
1
0
. –
N
ier
ó
wn
o
m
ierno
śd
b
ieg
u
m
asz
yn
y,
wpro
wadz
en
ie d
o
aut
o
m
aty
ki
46
Wykład 10. – Nierównomierność
biegu maszyny, wprowadzenie do
automatyki
gdzie:
I
zi
– moment bezwładności członu redukcji w dowolnym położeniu,
ω
i
– prędkość kątowa członu redukcji w dowolnym położeniu,
I
z0
– moment bezwładności członu redukcji w położeniu początkowym,
ω
0
– prędkość kątowa członu redukcji w dowolnym położeniu.
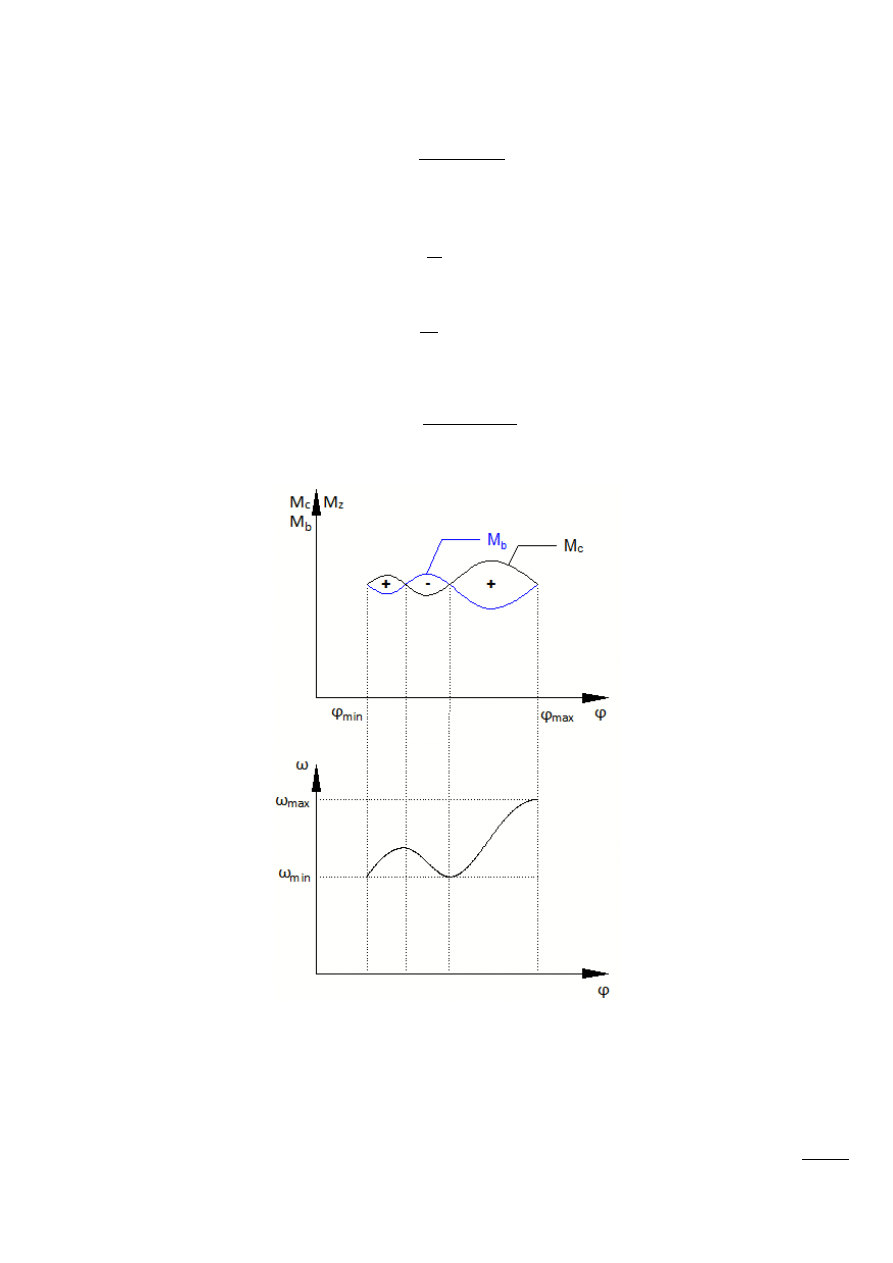
Rys. 10.1 – Minimalne i maksymalne wartości prędkości kątowej przy nierównomiernym biegu
maszyny w okresie ruchu ustalonego.
Nierównomierność biegu maszyny
Zmiana prędkości członu napędzającego maszyny w okresowym ruchu ustalonym nazywa się
okresową nierównomiernością biegu maszyny, w okresie jednego cyklu ruchu ustalonego lub
częściej stopniem nierównomierności biegu maszyny. Dla ruchu obrotowego nierównomiernośd
biegu maszyny wynosi:
Ro
zd
ział:
Wy
kł
ad
1
0
. –
N
ier
ó
wn
o
m
ierno
śd
b
ieg
u
m
asz
yn
y,
wpro
wadz
eni
e
d
o
aut
o
m
aty
ki
47
dla ruchu postępowego:
Prędkośd kątowa średnia:
gdzie T
c
to okres cyklu ruchu ustalonego.
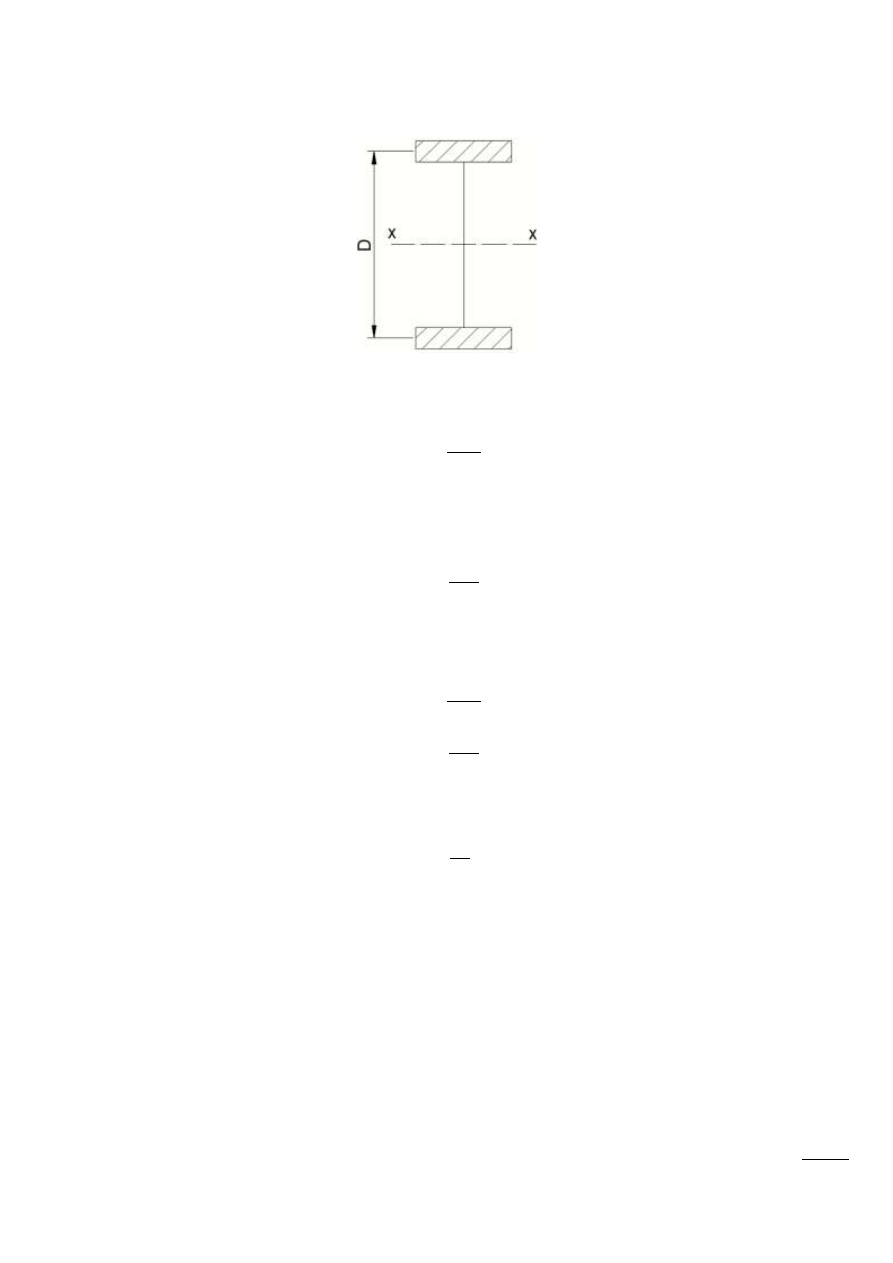
Rys. 10.2 – Przebiegi momentu czynnego i biernego.

Ro
zd
ział:
Wy
kł
ad
1
0
. –
N
ier
ó
w
n
o
m
ierno
śd
b
ieg
u
m
asz
yn
y,
wpro
wadz
eni
e
d
o
aut
o
m
aty
ki
48
Z równania tego wynika, że stopieo nierównomierności biegu maszyny jest tym większy im
większe jest nadwyżka pracy ΔL i tym mniejszy im większa jest prędkośd kątowa średnia i
zredukowany moment bezwładności. Najłatwiej jest zmniejszyd stopieo nierównomierności biegu
maszyny przez zwiększenie zredukowanego momentu bezwładności. Możemy to osiągnąd przez
odpowiedni dobór koła zamachowego.
gdzie:
I
zm
– zredukowany moment bezwładności maszyny,
I
k
– moment bezwładności koła.
Graniczne wartości stopnia nierównomierności biegu maszyny niektórych typów maszyn:
obrabiarki do metali – 1/5 do 1/50;
silniki spalinowe – 1/50 do 1/150;
generatory prądu zmiennego – 1/200 – 1/300.
Praktyczne zagadnienie regulacji okresowej nierównomierności biegu maszyny rozwiązuje się
za pomocą dodatkowej masy zamachowej, którą zawiera koło zamachowe. Zadaniem koła
zamachowego jest akumulowanie energii kinetycznej podczas przewagi sił napędzających nad
momentem sił oporu i oddawania tej energii maszynie podczas przewagi momentu biernego nad
czynnym.
Ro
zd
ział:
Wy
kł
ad
1
0
. –
N
ier
ó
wn
o
m
ierno
śd
b
ieg
u
m
asz
yn
y,
wpro
wadz
eni
e
d
o
aut
o
m
aty
ki
49
Wyznaczanie momentu bezwładności koła zamachowego
Rys. 10.3 – Koło zamachowe z masą rozłożoną na wieocu.
Dla koła zamachowego z rysunku 10.3 moment bezwładności wynosi:
Koło zamachowe konstruuje się skupiając jego masę głównie na wieocu o znanej średnicy D,
oznaczając średni promieo wieoca koła zamachowego przez r = D/2, a jego ciężar przez G. Zatem
moment bezwładności takiego koła będzie wynosił:
GD
2
– moment zamachowy
Moment bezwładności koła zamachowego wykonanego w formie tarczy o średnicy zewnętrznej D:
Koło zamachowe umieszcza się w różnych miejscach maszyny, na jednym z wałów
napędowych, na wale maszyny roboczej.

Ro
zd
ział:
Wy
kł
ad
1
0
. –
N
ier
ó
wn
o
m
ierno
śd
b
ieg
u
m
asz
yn
y,
wpro
wadz
eni
e
d
o
aut
o
m
aty
ki
50
Automatyka

Ro
zd
ział:
Wy
kł
ad
1
0
. –
N
ier
ó
wn
o
m
ierno
śd
b
ieg
u
m
asz
yn
y,
wpro
wadz
eni
e
d
o
aut
o
m
aty
ki
51
Wprowadzenie do automatyki
Automatyka jest dyscypliną naukową zajmującą się zagadnieniami automatycznego
sterowania procesu.
Sterowanie automatyczne polega na wywieraniu wpływu na przebieg procesu tak, by był on
zgodny z zamierzeniami. Istotą sterowania jest kontrola czynna polegająca na oddziaływaniu na
proces na podstawie pomiarów dokonywanych w czasie trwania procesu. Bardzo często spotykaną
formą sterowania automatycznego jest regulacja automatyczna polegająca na utrzymywaniu
wybranych wielkości procesu na żądanym poziomie lub zmienianiu ich na według określonego
programu.
Pojęcia podstawowe
Obiektem regulacji nazywamy układ fizyczny, w którym odbywa się aktualnie interesujący
nas proces sterowania. Obiekt regulacji jako układ fizyczny można opisad za pomocą jego
współrzędnych, to jest takich wielkości jak np. ciśnienie, temperatura, poziom cieczy, napięcie itp.
charakteryzujących zachowanie się układu oraz parametrów czyli np. mas układu, oporności,
przewodności cieplnych itp.
Sygnałem nazywamy dowolną wielkośd fizyczną występującą w procesie sterowania, będą cą
funkcją czasu wykorzystywaną do przekazywania informacji.
Informacją jest wartośd lub kształt przebiegu sygnału. Sygnałem może byd więc napięcie,
prąd lub częstotliwośd w układzie elektrycznym, ciśnienie w układzie pneumatycznym i
hydraulicznym, przesunięcie kątowe lub liniowe w układzie mechanicznym.
Wielkości fizyczne oddziałujące na obiekt z zewnątrz (przyczyna), nazywamy sygnałem
wejściowym. Ogólnie oznaczamy je symbolem x, a w przypadku gdy mamy do czynienia z tymi
samymi wielkościami fizycznymi nadajemy indeks „1” przy symbolu oznaczającym daną wielkośd
fizyczną. Wielkości wyjściowe z obiektu (skutki), nazywamy sygnałami wyjściowymi. Ogólnie
oznaczamy je symbolem y, bądź indeksem „2”, gdy sygnał wejścia i wyjścia przedstawiają te same
wielkości fizyczne. Jeżeli dwie wielkości fizyczne związane są ze sobą znaną zależnością
matematyczną, wówczas na podstawie przebiegu jednej z nich możemy określid zmiany drugiej, czyli
jeden z sygnałów zawiera informacje o drugim. Te zależności matematyczne zwykle daje się
przedstawid w postaci równania różniczkowego, a niekiedy równania algebraicznego. W przypadku,
gdy równanie algebraiczne jest liniowe, mamy do czynienia z zależnością proporcjonalną. Równanie
algebraiczne opisuje stan ustalony układu i nazywamy je równaniem statyki.
Charakterystyką statyczną układu nazywamy graficzne przedstawienie zależności wynikające
z równao statyki. W stanach nieustalonych, gdy sygnał wejściowy jest zależny od czasu, bądź też
układ po zmianie sygnału wejściowego nie osiągnął jeszcze nowego poziomu równowagi, związki
pomiędzy sygnałem wejściowym, a wyjściowym wyrażają się równaniami różniczkowymi. Równania
takie nazywamy równaniami dynamiki, gdyż opisują one właściwości dynamiczne układu.
Charakterystyką dynamiczną układu nazywamy graficzne przedstawienie rozwiązania
równania różniczkowego opisującego dany układ. Aby rozwiązad równanie różniczkowe, należy nie
tylko znad parametry układu, ale także wartości początkowe współrzędnych opisujących stan układu.
Ro
zd
ział:
Wy
kł
ad
1
0
. –
N
ier
ó
wn
o
m
ierno
śd
b
ieg
u
m
asz
yn
y,
wpro
wadz
eni
e
d
o
aut
o
m
aty
ki
52
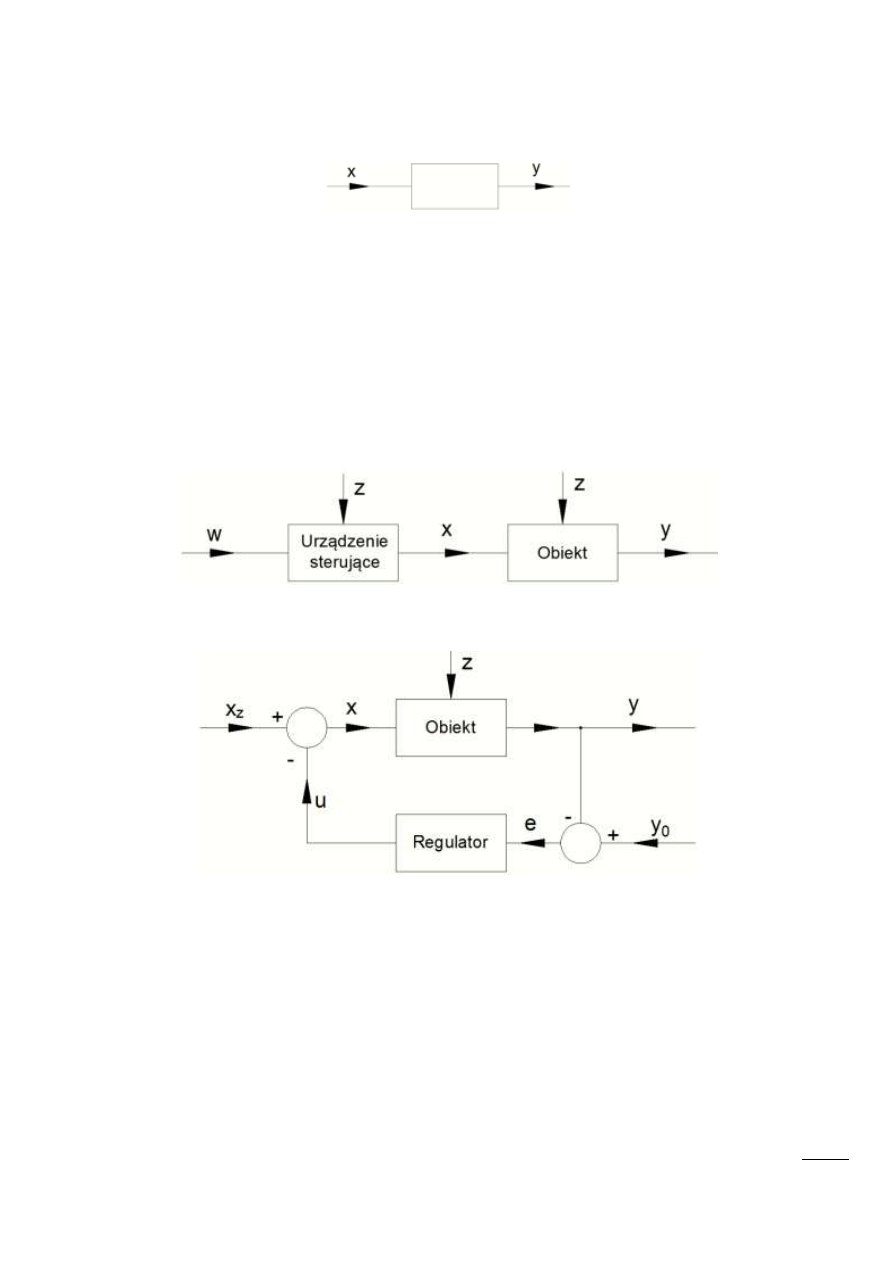
Elementem automatyki nazywamy układ fizyczny, w którym możemy wyróżnid sygnał
wejściowy i wyjściowy i oznaczamy go w sposób ukazany jak na rysunku:
Rys. 10.4 – Element automatyki
Strzałki na rysunku przedstawiają kierunki przechodzenia sygnału i oznaczają, iż nie
występuje oddziaływanie wsteczne. Oznacza to, że sygnał x nie jest zależny od y.
Układem automatyki nazywamy zespół elementów, biorących bezpośredni udział w
sterowaniu automatycznym danego procesu oraz elementów pomocniczych uporządkowany na
zasadzie ich wzajemnej współpracy, tzn. zgodnie z kierunkiem przekazywania sygnału. Możemy
wyróżnid dwa podstawowe rodzaje sterowania automatycznego:
sterowanie w układzie otwartym
sterowanie w układzie zamkniętym.
Rys. 10.5 – Otwarty układ sterowania; w – wymuszenie, y – wielkośd sterowana, z – sygnały
zakłócające, x – sygnał nastawiający.
Rys. 10.6 – Zamknięty układ sterowania; y – wielkośd regulowana, y
0
– wielkośd zadana, e – uchyb
regulacji (inaczej: ε – sygnał błędu),x
2
– sygnał zakłócający, u – sygnał nastawiający, x – wielkośd
wejściowa obiektu.
Ro
zd
ział:
Wy
kł
ad
1
1
. –
W
ła
ściwo
ści e
le
m
ent
ó
w
auto
m
aty
ki
53
Wykład 11. – Właściwości elementów
automatyki
W praktyce układy regulacji automatycznej zawierają większą liczbę elementów od
przedstawionych na rysunku z wykładu 10.
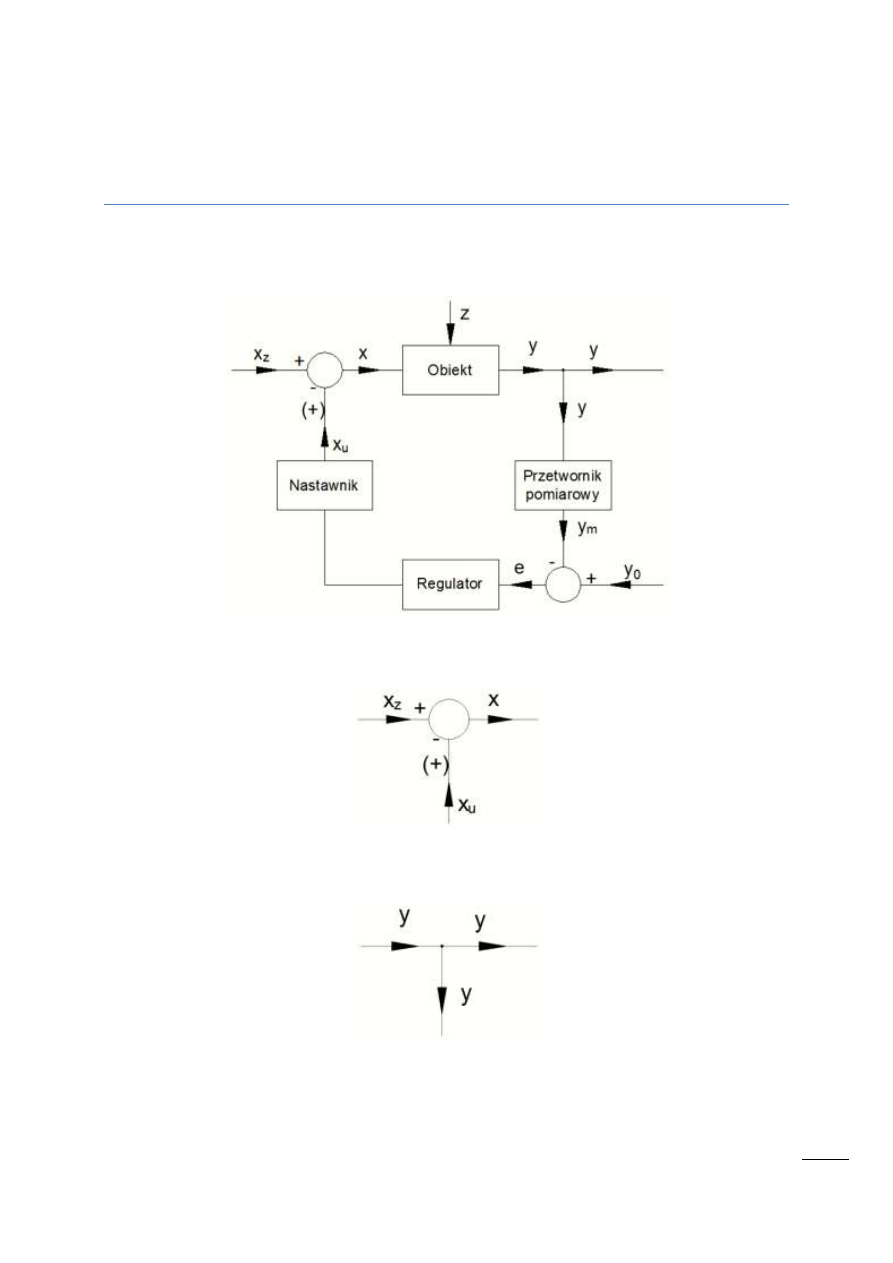
Rys. 11.1 – Układ automatyki z nastawnikiem i przetwornikiem pomiarowym
Rys. 11.2 – Węzeł sumacyjny
Rys. 11.3 – Węzeł informacyjny (zaczepowy)

Ro
zd
ział:
Wy
kł
ad
1
1
. –
W
ła
ściwo
ści e
le
m
ent
ó
w
auto
m
aty
ki
54
Układy regulacji automatycznej mogą służyd do regulacji napięcia generatorów, natężenia
przepływu substancji, ciśnienia gazu w zbiornikach, prędkości obrotowych, temperatury w piecach,
położenia narzędzia w obrabiarce kopiujące, stężenia substancji itp.
Aparatura regulacyjna (regulatory, przetworniki pomiarowe, nastawniki), może byd
mechaniczna, hydrauliczna, pneumatyczna, elektryczna lub mieszana, np. elektropneumatyczna.
Obiekt sterowania jest to proces technologiczny zachodzący w danym urządzeniu, przy czym
pożądany przebieg procesu wymaga odpowiedniego oddziaływania z zewnątrz.
Regulator to urządzenie, w którym określenie sygnału wykonawczego odbywa się przez
porównanie wartości sygnału zadającego i wartości sygnału pomiarowego odpowiadającego
wielkości regulowanej oraz przez dynamiczne uformowanie ich różnicy (wytworzenie sygnału
regulującego).
Uchyb regulacji (e), to różnica wielkości zadanej i regulowanej w układzie regulacji.
Przetwornik pomiarowy to element funkcjonalny, którego zadaniem jest zmiana postaci
wielkości regulowanej y lub zakresu wartości na wielkośd pomiarową y
m
o zakresie i postaci dogodnej
do porównania z wartością znaną y
0
.
Nastawnik jest elementem funkcjonalnym, którego zadaniem jest zmiana postaci lub zakresu
wielkości wyjściowej u z regulatora, na wielkośd o postaci i zakresie dogodnym do oddziaływania na
wejście obiektu.
Układ regulacji automatycznej, to układ zamknięty, w którym na urządzenie sterujące
oddziałuje wielkośd regulowana w obiekcie, a układ jest znamienny posiadaniem tzw. sprzężenia
zwrotnego.
Sprzężenie zwrotne to określony sposób oddziaływania wielkości wyjściowej (regulowanej)
układu na wielkości wyjściowe obiektu regulacji. Rozróżnia się sprzężenie zwrotne dodatnie i ujemne.
Zasady rachunku operatorowego
Zasady ogólne
Opis matematyczny danego elementu lub układu automatyki składa się w ogólnym
przypadku z dwóch części:
równania lub wykresu charakterystyki statycznej
równania różniczkowego lub operatorowego opisującego własności statyczne i dynamiczne w
otoczeniu wybranego na charakterystyce statycznej punktu pracy.
Jeżeli charakterystyka statyczna jest prostoliniowa, jako kompletny opis właściwości elementu lub
układu wystarczy podad równanie różniczkowe lub operatorowe, które opisuje wówczas własności
statyczne i dynamiczne w całym zakresie pracy, a nie tylko w otoczeniu wybranego punktu. Jeśli
charakterystyka statyczna jest krzywoliniowa, niezbędna jest znajomośd obu części opisu, gdyż
współczynniki równania różniczkowego są wówczas zmienne wzdłuż charakterystyki statycznej.
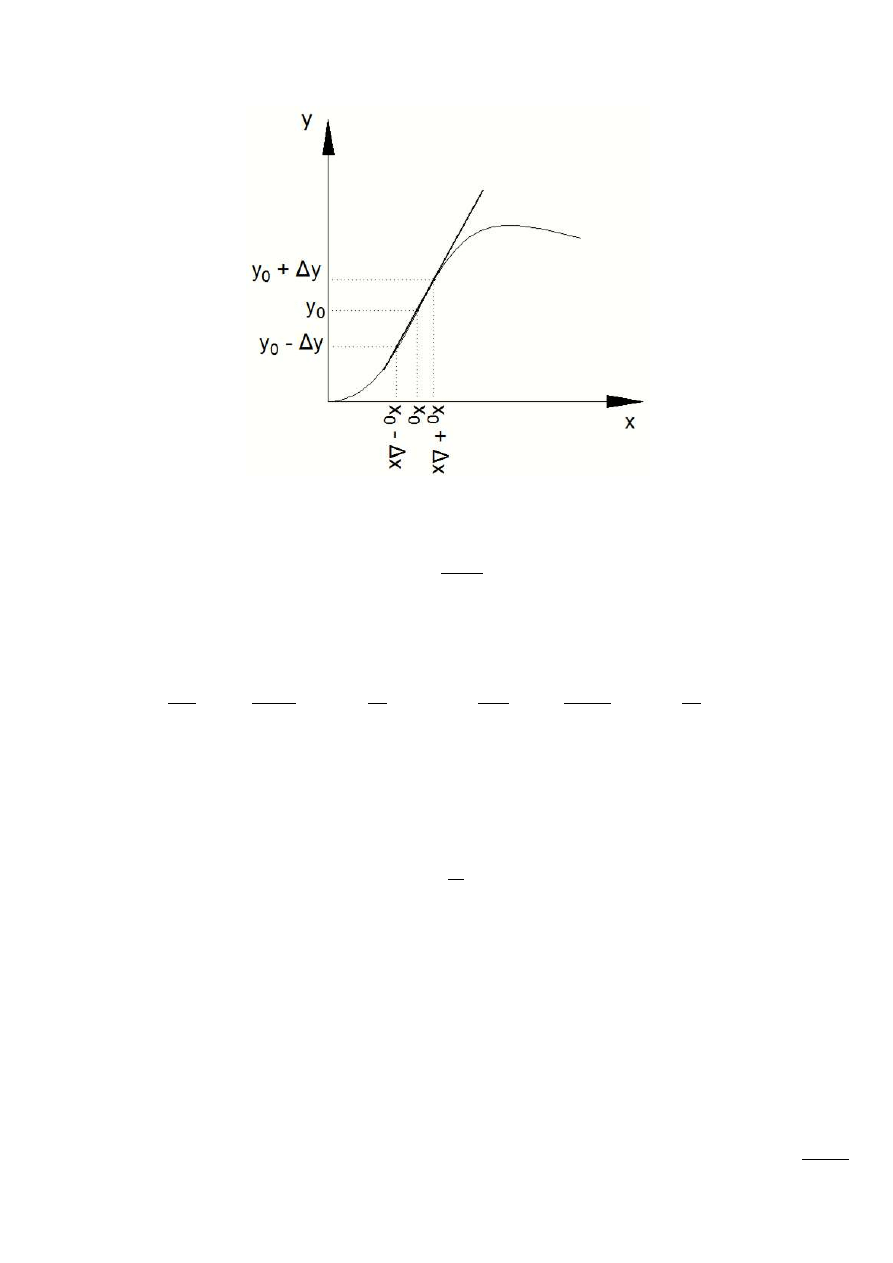
Linearyzacja polega na zastąpieniu krzywoliniowego odcinka charakterystyki statycznej w wybranym
punkcie. W przybliżeniu można wtedy traktowad charakterystykę statyczną jako prostoliniową, a
współczynniki równao różniczkowych jako stałe, ale tylko w otoczeniu danego punktu.
Ro
zd
ział:
Wy
kł
ad
1
1
. –
W
ła
ściwo
ści e
le
m
ent
ó
w
auto
m
aty
ki
55
Rys. 11.4 – Linearyzacja charakterystyki; (x
0
, y
0
) – punkt pracy.
Własności dowolnego elementu lub układu liniowego (zlinearyzowanego) można opisad za
pomocą równania różniczkowego posiadającego stałe współczynniki, którego postad ogólna jest
następująca:
y – wielkośd wyjściowa
x – wielkośd wejściowa
Własności dynamiczne ocenia się zwykle na podstawie przebiegów przejściowych
(nieustalonych) następujących po wprowadzeniu określonego sygnału wejściowego x(t).
Wyznaczanie tych przebiegów wymaga rozwiązania równania różniczkowego.
Przekształcenia Laplace’a
Przekształcenie Laplace’a umożliwia wprowadzenie równao różniczkowych do algebraicznych
i przez to znacznie ułatwia wykonanie potrzebnych działao algebraicznych. Przekształcenie Laplace’a
polega na tym, że daną funkcję czasu f(t) zwaną oryginałem, przekształcamy za pomocą ściśle
określonych działao matematycznych na inną funkcję F(s) zmiennej niezależnej s, zwanej
Ro
zd
ział:
Wy
kł
ad
1
1
. –
W
ła
ściwo
ści e
le
m
ent
ó
w
auto
m
aty
ki
56
transformatą. Przekształcenie funkcji f(t) na F(s) przeprowadza się w automatyce za pomocą
wyrażenia:
Stosując jednostronne przekształcenie Laplace’a używane w automatyce, zakłada się, że dla t < 0:
Nie wszystkie funkcje zmiennej rzeczywistej mają swoje transformaty. Aby można było
wyznaczyd transformaty funkcji f(t), muszą byd spełnione następujące warunki:
f(t) ma w każdym skooczonym przedziale wartośd skooczoną;
f(t) ma pochodną f’(t) w każdym przedziale skooczonym;
istnieje zbiór liczb rzeczywistych C, dla których
jest absolutnie zbierzna.
Właściwości i twierdzenia przekształcenia Laplace’a
Transformata iloczynu stałej przez funkcję:
Transformata sumy funkcji:
Transformata pochodnych funkcji:
gdzie
to wartośd początkowa funkcji f(t) (granica prawostronna).
Transformata 2 i n pochodnej:
Zajmowad się będziemy funkcjami f(t) dla których zwykle praktycznie stosowad będziemy
wzór w postaci uproszczonej.
Transformata całki funkcji:

Ro
zd
ział:
Wy
kł
ad
1
1
. –
W
ła
ściwo
ści e
le
m
ent
ó
w
auto
m
aty
ki
57
Twierdzenie o przemieszczeniu rzeczywistym:
Twierdzenie o przesunięciu zespolonym:
Twierdzenie o wartościach koocowych:
Twierdzenie o wartościach początkowych:
Najczęściej spotykana funkcja f(t) i odpowiadające im transformaty F(s) zostały zestawione w
tablicach. Jeśli mamy wyrażenie dane w postaci transformaty F(s), to możemy znaleźd odpowiadający
tej transformacie oryginał f(t) za pomocą przekształcenia odwrotnego zgodnie z podaną poniżej
zależnością:
gdzie ω to częstośd kołowa.
Transmitancja operatorowa (funkcja przejścia)
Transmitancją operatorową G(s) elementu lub układu nazywamy stosunek transformaty
wielkości wyjściowej y(s) do transformaty wielkości wyjściowej x(s) przy zerowych warunkach
początkowych.
Rodzaje wymuszeń
Przebiegiem przejściowym y(t) nazywamy przebieg w czasie wielkości wyjściowej y, po
wprowadzeniu sygnału wejściowego x(t) lub krócej: odpowiedź y(t) na wymuszenie x(t). Najczęściej
określa się odpowiedź y(t) na jedno z typowych wymuszeo.
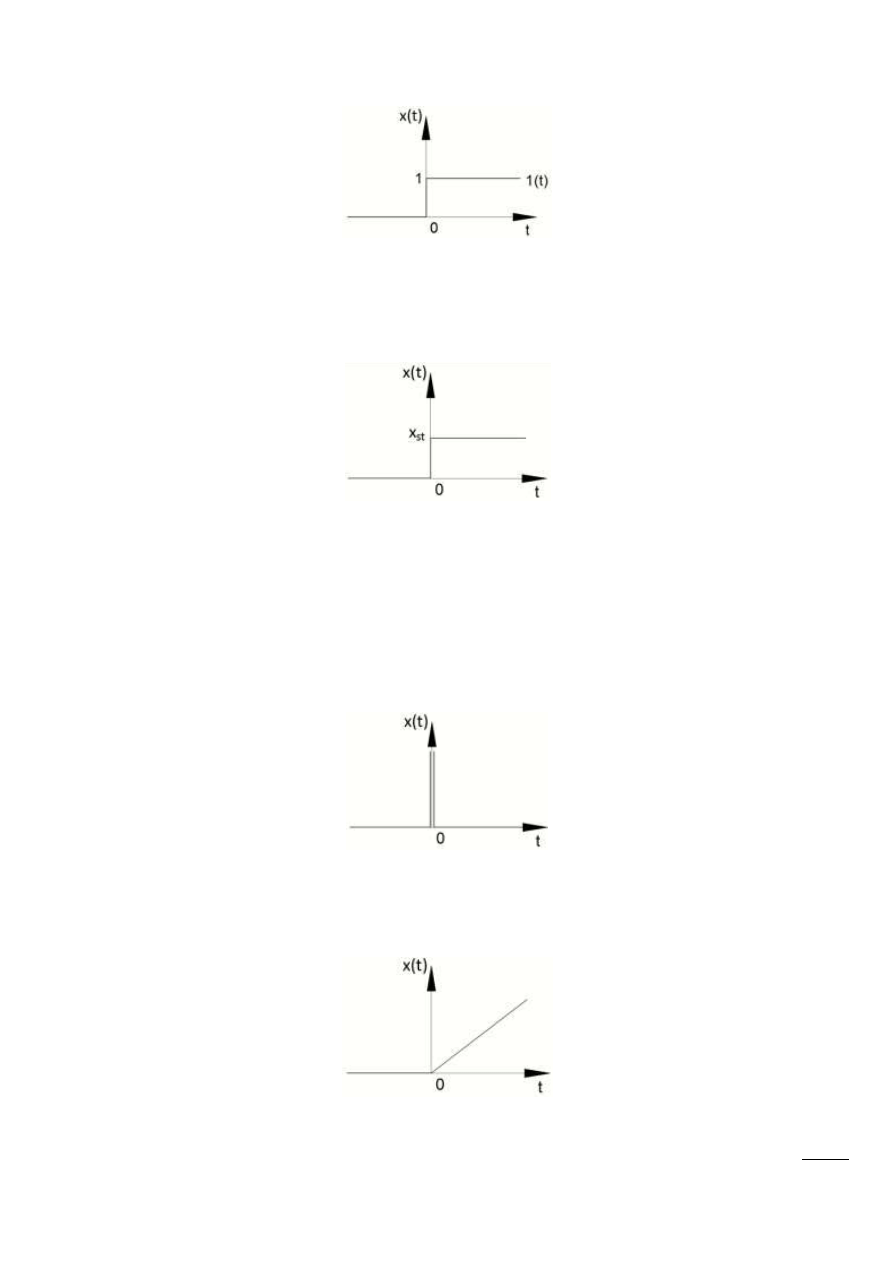
Wymuszenie jednostkowe – 1(t) (skok jednostkowy lub funkcja Heaviside’a):
Ro
zd
ział:
Wy
kł
ad
1
1
. –
W
ła
ściwo
ści e
le
m
ent
ó
w
auto
m
aty
ki
58
Rys. 11.5 – Wymuszenie jednostkowe
Wymuszenie skokowe:
Rys. 11.6 – Wymuszenie skokowe
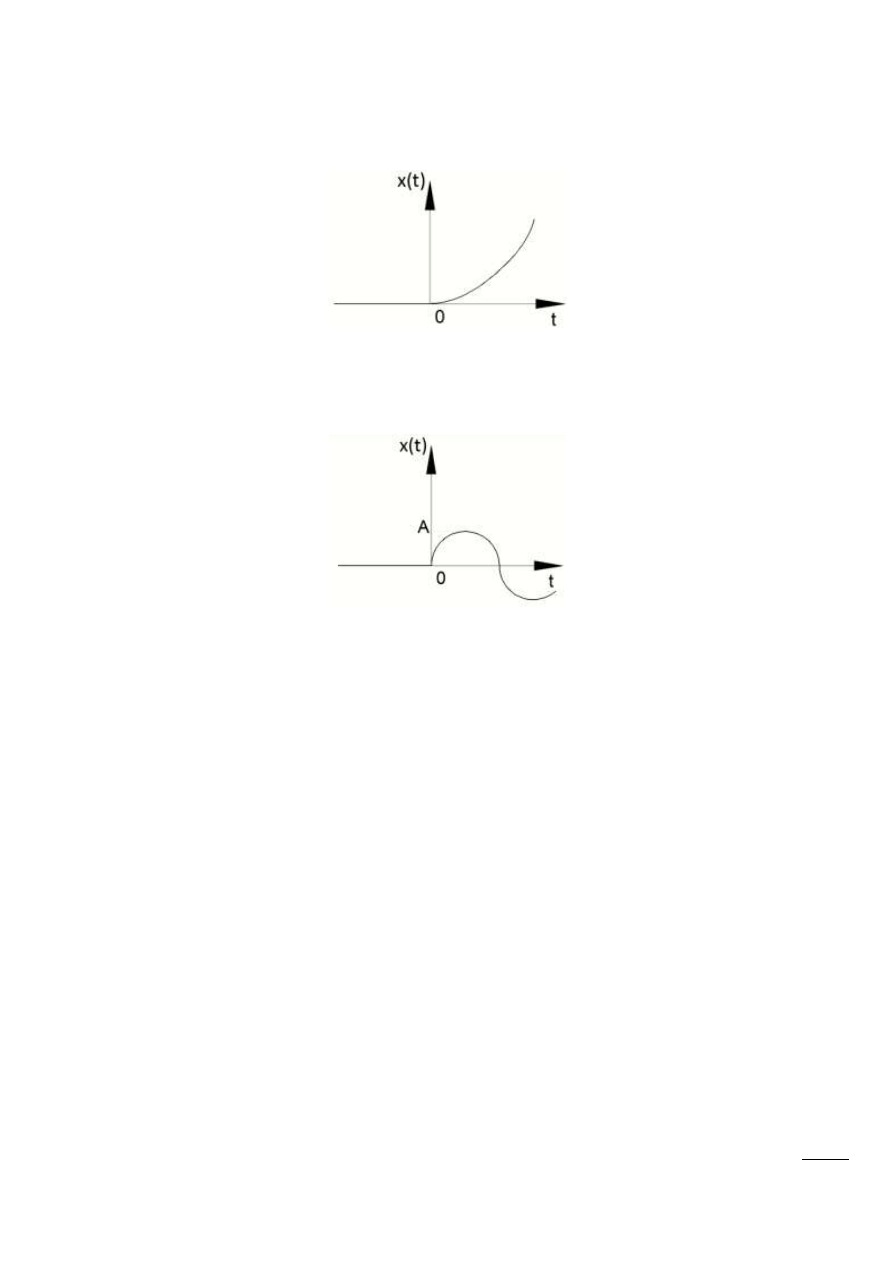
Wymuszenie impulsowe (funkcja Diraca):
Rys. 11.7 – Wymuszenie impulsowe
Wymuszenie liniowo narastające (skok prędkości):
Rys. 11.8 – Wymuszenie liniowo narastające
Ro
zd
ział:
Wy
kł
ad
1
1
. –
W
ła
ściwo
ści e
le
m
en
tó
w
auto
m
aty
ki
59
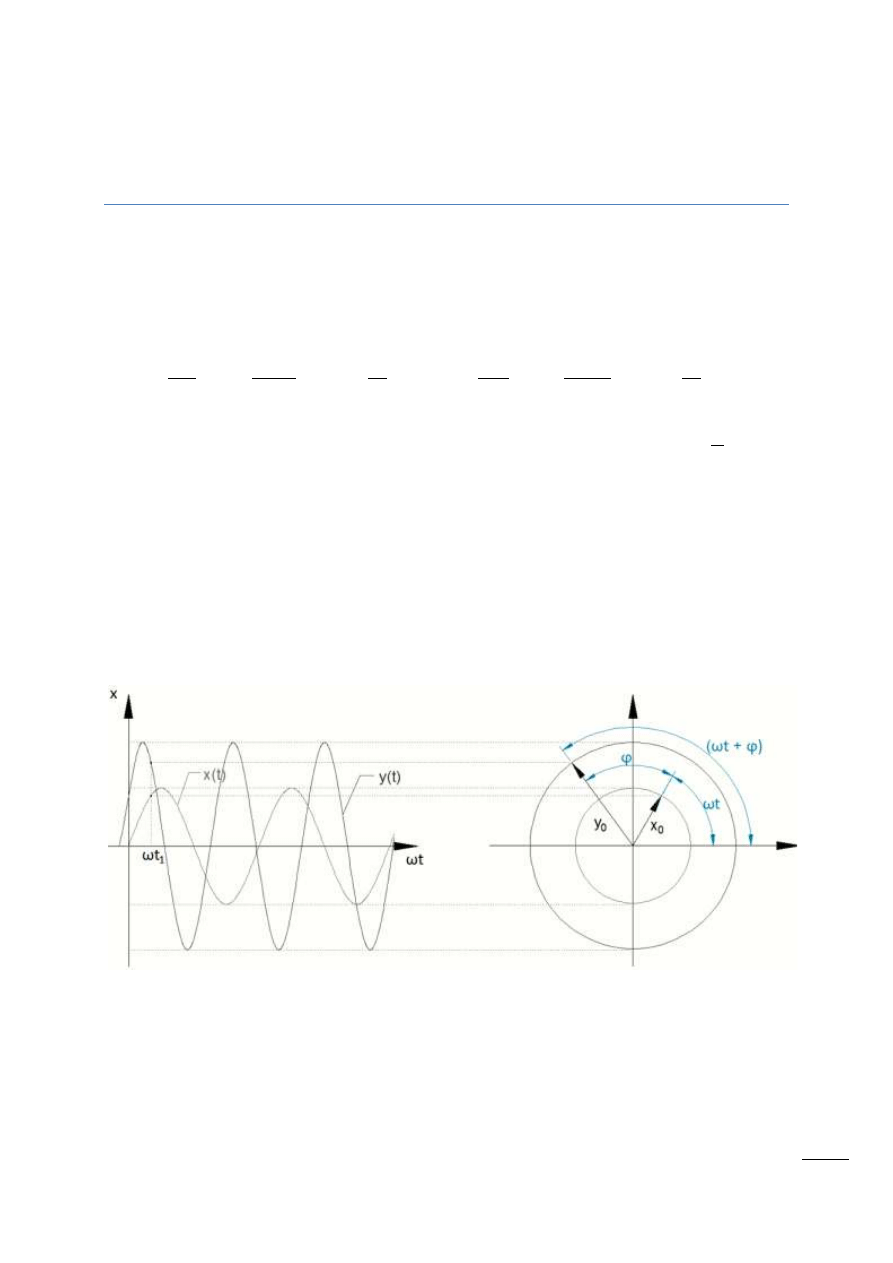
Wymuszenie paraboliczne (skok przyspieszenia):
Rys. 11.9 – Wymuszenie paraboliczne
Wymuszenie harmoniczne:
Rys. 11.10 – Wymuszenie harmoniczne
Ro
zd
ział:
Wy
kł
ad
1
2
. –
Bad
an
ie zach
o
wani
a układ
ó
w
a
u
to
m
aty
ki
60
Wykład 12. – Badanie zachowania
układów automatyki
Charakterystyki czasowe
Charakterystyką czasową nazywamy przebieg przejściowy y(t) przy ściśle określonym sygnale
wymuszającym x(t). Z omówionych rodzajów wymuszeo do wyznaczania charakterystyki czasowej
stosujemy zwykle wymuszenie jednostkowe przy zerowych warunkach początkowych.
Charakterystyka czasowa daje nam informację o tym, jak będzie zachowywał się układ
przechodząc z zerowego stanu ustalonego (y = 0) do nowego położenia równowagi
po
zadziałaniu na układ wymuszenia skokowego. Charakterystyka czasowa opisuje stan przejściowy
układu.
Charakterystyki częstotliwościowe
Oprócz stanów przejściowych ważne są także stany ustalone. Stan ustalony układu (tzw. stan
wymuszony) otrzymamy z rozwiązania szczególnego równania niejednorodnego (dla prawej strony
równej zero). Procesy ustalone badamy podając na wejście układy wymuszenie harmoniczne
. Na wyjściu otrzymujemy także funkcję sinusoidalną, ale o innej amplitudzie i
przesunięciu w fazie.
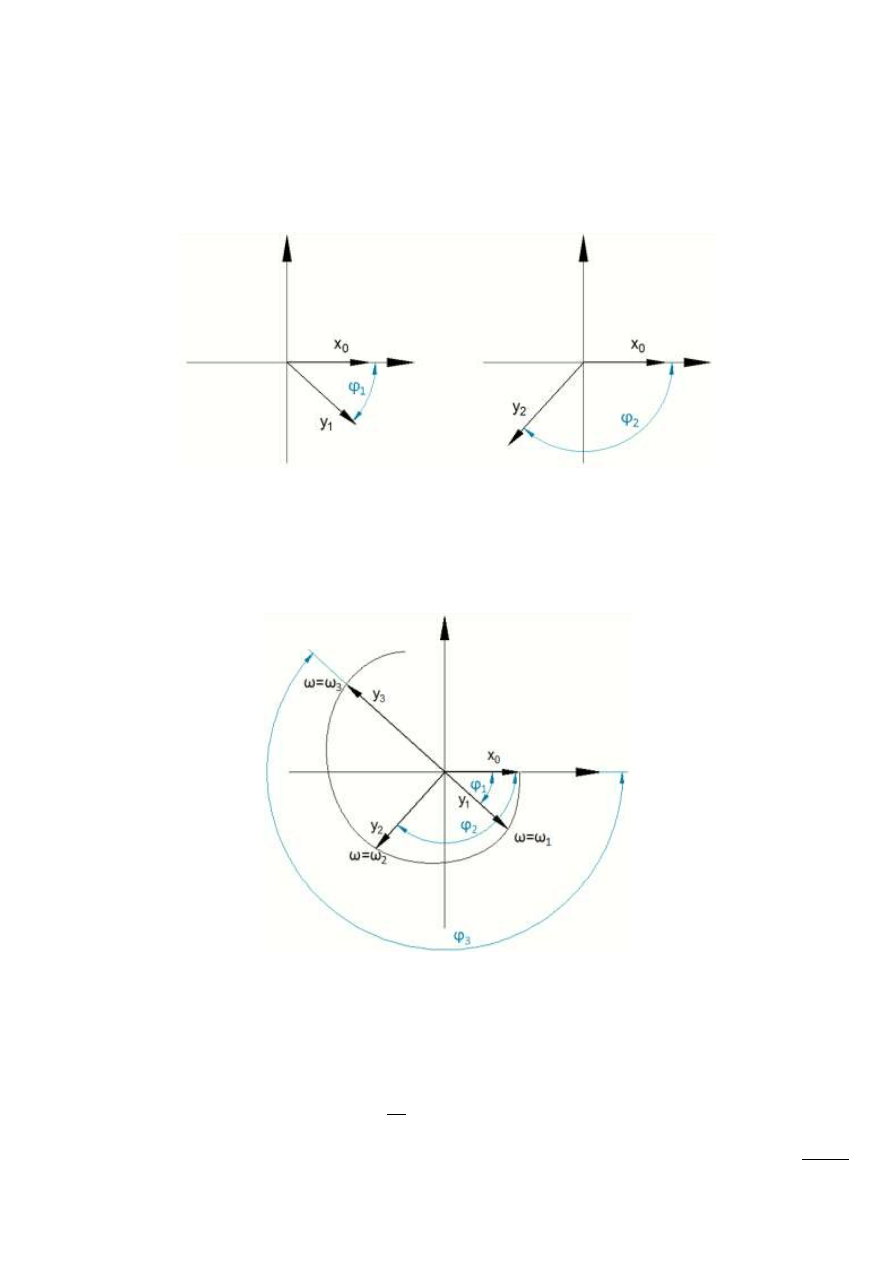
Rys. 12.1 – Przedstawienie wymuszenia i odpowiedzi w postaci wirujących wektorów
Jeżeli badamy układ przy częstotliwości wynoszącej ω
1
, to dla wymuszenia sinusoidalnego x(t)
otrzymamy następującą odpowiedź y(t) na wyjściu:
Ro
zd
ział:
Wy
kł
ad
1
2
. –
Bad
an
ie zach
o
wani
a układ
ó
w
a
u
to
m
aty
ki
61
Oraz dla innego ω = ω
2
:
Rys. 12.2 – Wymuszenia i odpowiedzi 1 i 2 w postaci wektorów wirujących
Wyznaczamy amplitudę i przesunięcie fazowe odpowiedzi od do . Jeśli drgania
y(t) porównujemy z x(t), możemy wektor x
0
umieścid na osi odciętych. Amplituda x
0
jest stała. Kąty
przesunięcia fazowego odmierzane są względem x
0
, a amplitudy odpowiedzi obrazują kooce
wektorów y.
Rys. 12.3 – Obraz wektorów odpowiedzi dla trzech różnych częstotliwości.
Harmoniczną funkcję możemy przedstawid w postaci liczb zespolonych:
Ro
zd
ział:
Wy
kł
ad
1
2
. –
Bad
an
ie zach
o
wani
a układ
ó
w
a
u
to
m
aty
ki
62
Podstawiając zależności na x(t) i y(t) w postaci zespolonej do równania opisującego
właściwości dowolnego układu liniowego otrzymamy taką zależnośd:
Z równania tego możemy obliczyd stosunek odpowiedzi układu do wymuszenia:
Wyrażenie nazywamy transmitancją częstotliwościową bądź widmową. Z otrzymanego
wzoru wynika, że jest funkcją zespoloną, zależną od ω. Moduł liczby zespolonej
przedstawia stosunek amplitudy odpowiedzi do wymuszenia, natomiast
przedstawia przesunięcie fazowe pomiędzy wymuszeniem, a odpowiedzią.
Porównujący wyrażenie na transmitancję operatorową z transmitancją widmową można zauważyd,
że transmitancję widmową możemy otrzymad z transmitancji operatorowej, podstawiając s = jω.
Ponieważ transmitancja widmowa jest funkcją zespoloną, można ją rozłożyd na częśd rzeczywistą i
urojoną:
Transmitancję widmową możemy przedstawid w prostokątnym układzie współrzędnych
zmieniając ω w zakresie od zera do nieskooczoności, w postaci wykresu:
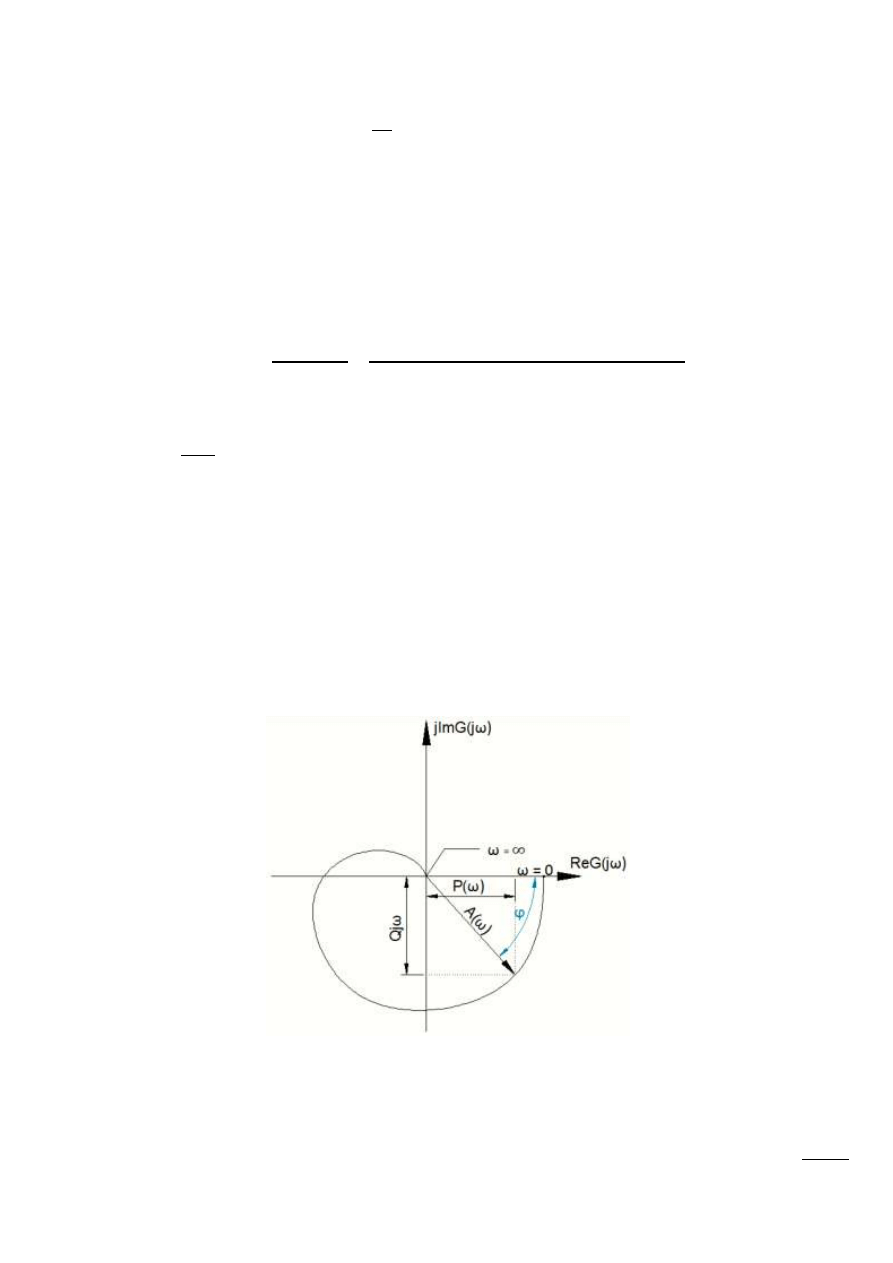
Rys. 12.4 – Transmitancja widmowa
Częstotliwościowa charakterystyka amplitudowo-fazowa jest to miejsce geometryczne
kooców wektorów, których długośd przedstawia stosunek sygnału wejściowego do amplitudy sygnału
Ro
zd
ział:
Wy
kł
ad
1
2
. –
Bad
an
ie zach
o
wani
a układ
ó
w
a
u
to
m
aty
ki
63
wyjściowego, a kąt mierzony od osi rzeczywistej przedstawia przesunięcie fazowe między
odpowiedzią, a wymuszeniem. Z przedstawionego rysunku wynikają związki:
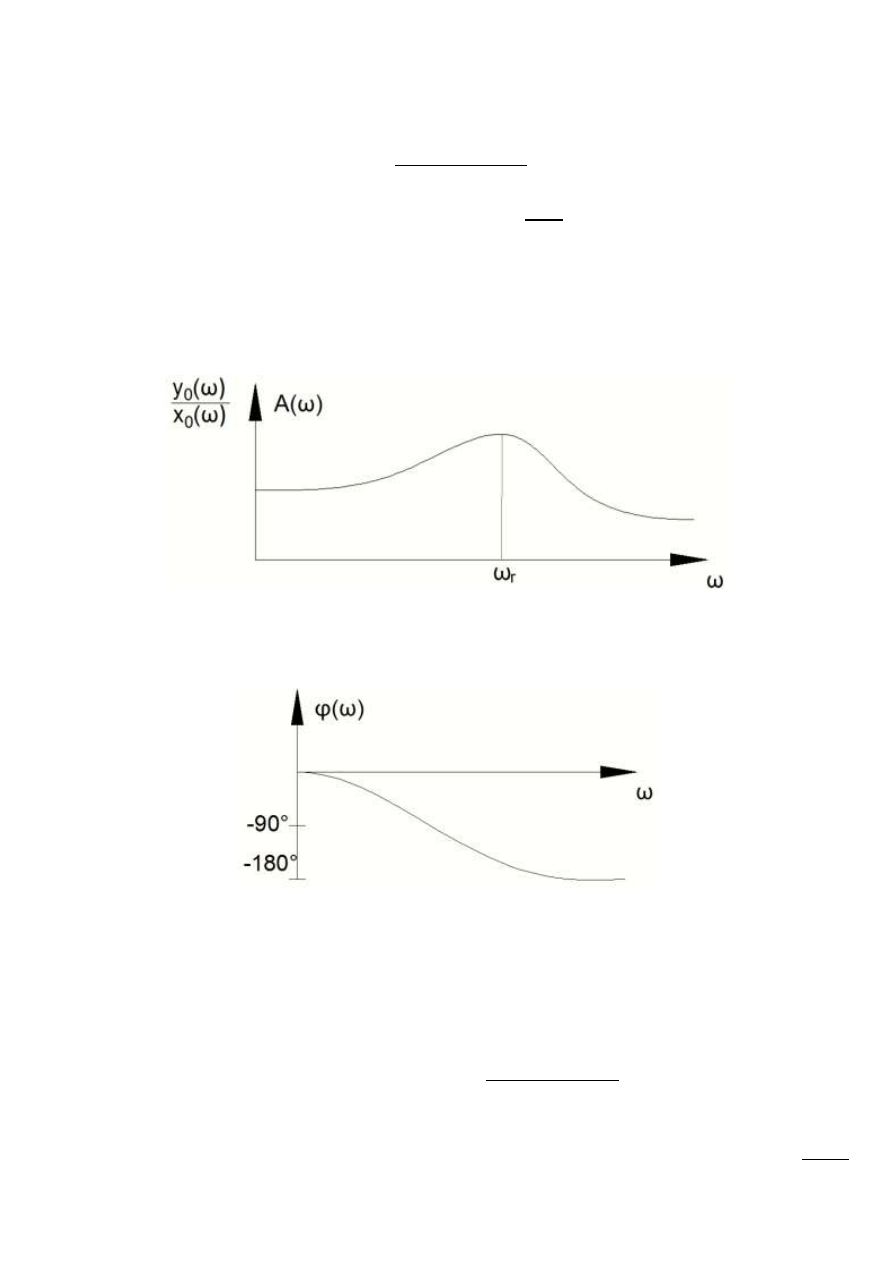
Rezonans będzie występował na charakterystyce w postaci punktu o maksymalnej odległości
od początku układu współrzędnych. Częstotliwością odpowiadającą temu punktowi jest częstotliwośd
rezonansowa ω
r
. Często ze względów praktycznych osobno badamy stosunki amplitud sygnałów oraz
ich wzajemne przesunięcie fazowe. Stosunek amplitud sygnałów nazywamy amplitudową
charakterystyką częstotliwościową.
Rys. 12.5 – Częstotliwośd rezonansowa na amplitudowej charakterystyce częstotliwościowej.
Wykres przesunięcia fazowego w funkcji częstotliwości nazywamy fazową charakterystyką
częstotliwościową.
Rys. 12.6 – Przykładowa fazowa charakterystyka częstotliwościowa
Charakterystyka logarytmiczna
Charakterystyka amplitudowa i fazowa są zazwyczaj przedstawione we współrzędnych
logarytmicznych. Logarytmiczną charakterystyką amplitudową nazywamy charakterystykę
amplitudową wykreśloną w skali logarytmicznej. Na osi odciętych odkładamy częstośd w skali
logarytmicznej, a na osi rzędnych amplitudę w skali logarytmicznej (często w dB).

Ro
zd
ział:
Wy
kł
ad
1
2
. –
Bad
an
ie zach
o
wa
n
ia u
kł
ad
ó
w
a
u
to
m
aty
ki
64
Rys. 12.7 – Przykładowy układ współrzędnych dla logarytmicznej charakterystyki amplitudowej
Logarytmiczną charakterystyka fazową nazywamy charakterystykę wykreśloną tak, że na osi
odciętych odkładamy częstotliwośd ω w skali logarytmicznej, a na osi rzędnych przesunięcie fazowe
ϕ(ω) w podziałce liniowej w stopniach lub radianach.
Rys. 12.8 – Przykład układu współrzędnych dla logarytmicznej charakterystyki fazowej
Właściwości statyczne i dynamiczne podstawowych elementów liniowych
Elementy liniowe klasyfikuje się najczęściej ze względu na ich właściwości dynamiczne.
Wyróżniamy 6 grup elementów podstawowych:
bezinercyjne (proporcjonalne)
inercyjne
całkujące
różniczkujące
oscylacyjne
opóźniające
Elementy bezinercyjne
Ogólna postad równania elementu bezinercyjnego jest następująca:
Ro
zd
ział:
Wy
kł
ad
1
2
. –
Bad
an
ie zach
o
wani
a układ
ó
w
a
u
to
m
aty
ki
65
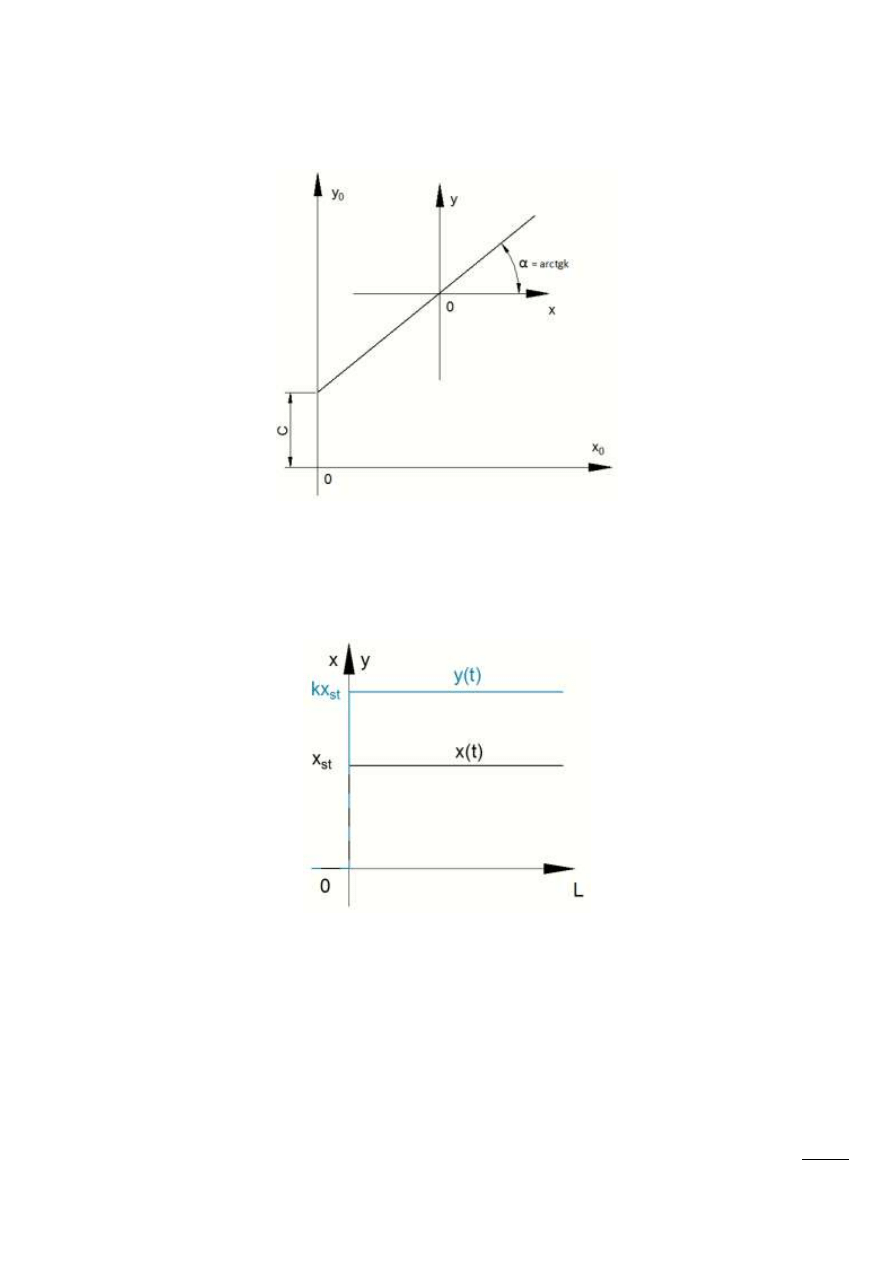
Równanie charakterystyki statycznej:
Rys. 12.9 – Charakterystyka statyczna elementu bezinercyjnego
Odpowiedź na wymuszenie skokowe elementu bezinercyjnego:
Rys. 12.10 – Wymuszenie skokowe i odpowiedź elementu bezinercyjnego
Charakterystyka częstotliwościowa, transmitancja widmowa:
Ro
zd
ział:
Wy
kł
ad
1
2
. –
Bad
an
ie zach
o
wani
a układ
ó
w
a
u
to
m
aty
ki
66
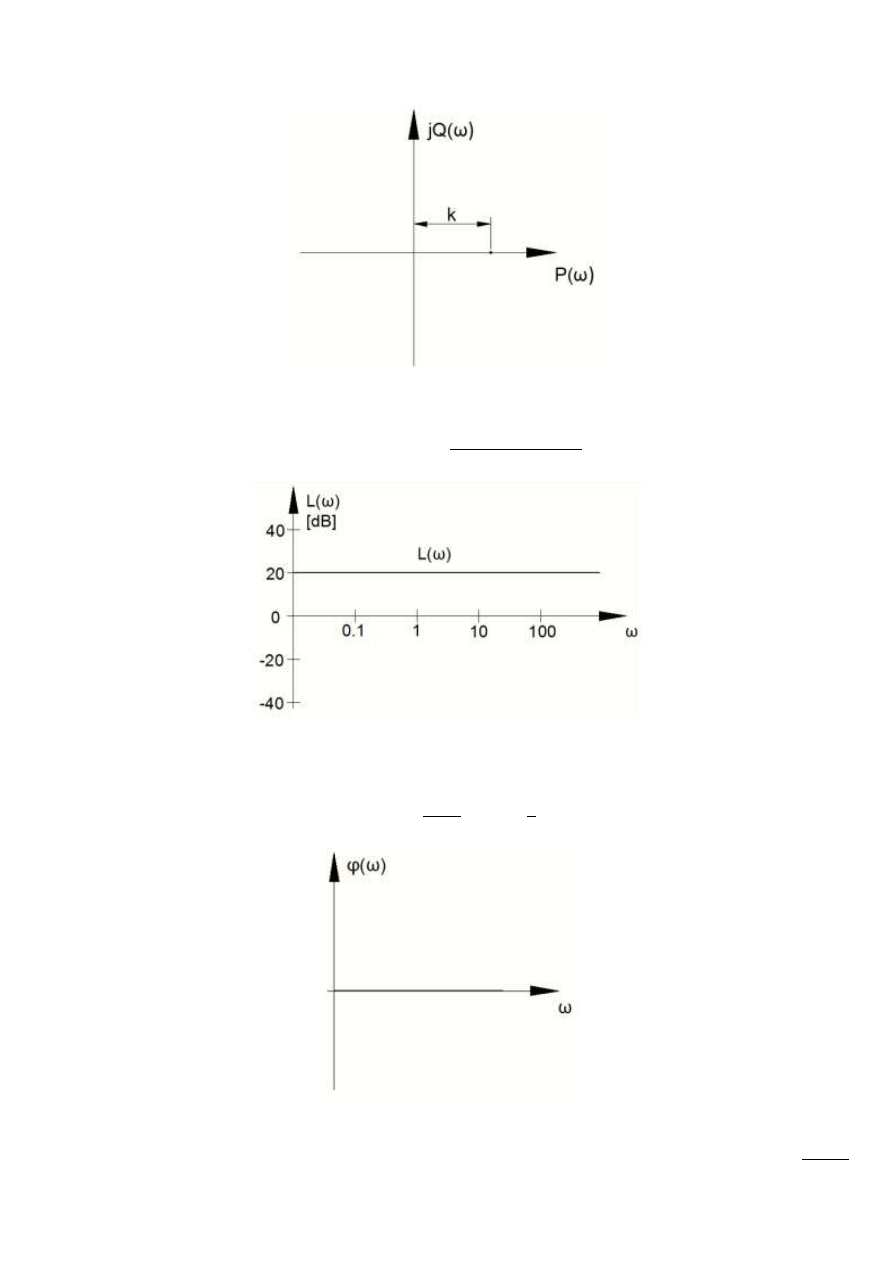
Rys. 12.11 – Transmitancja widmowa elementu bezinercyjnego
Logarytmiczna charakterystyka amplitudowa elementu bezinercyjnego:
Rys. 12.12 – Logarytmiczna charakterystyka amplitudowa elementu bezinercyjnego
Charakterystyka fazowa:
Rys. 12.13 – Charakterystyka fazowa elementu bezinercyjnego
Ro
zd
ział:
Wy
kł
ad
1
2
. –
Bad
an
ie zach
o
wani
a układ
ó
w
a
u
to
m
aty
ki
67
Przykład
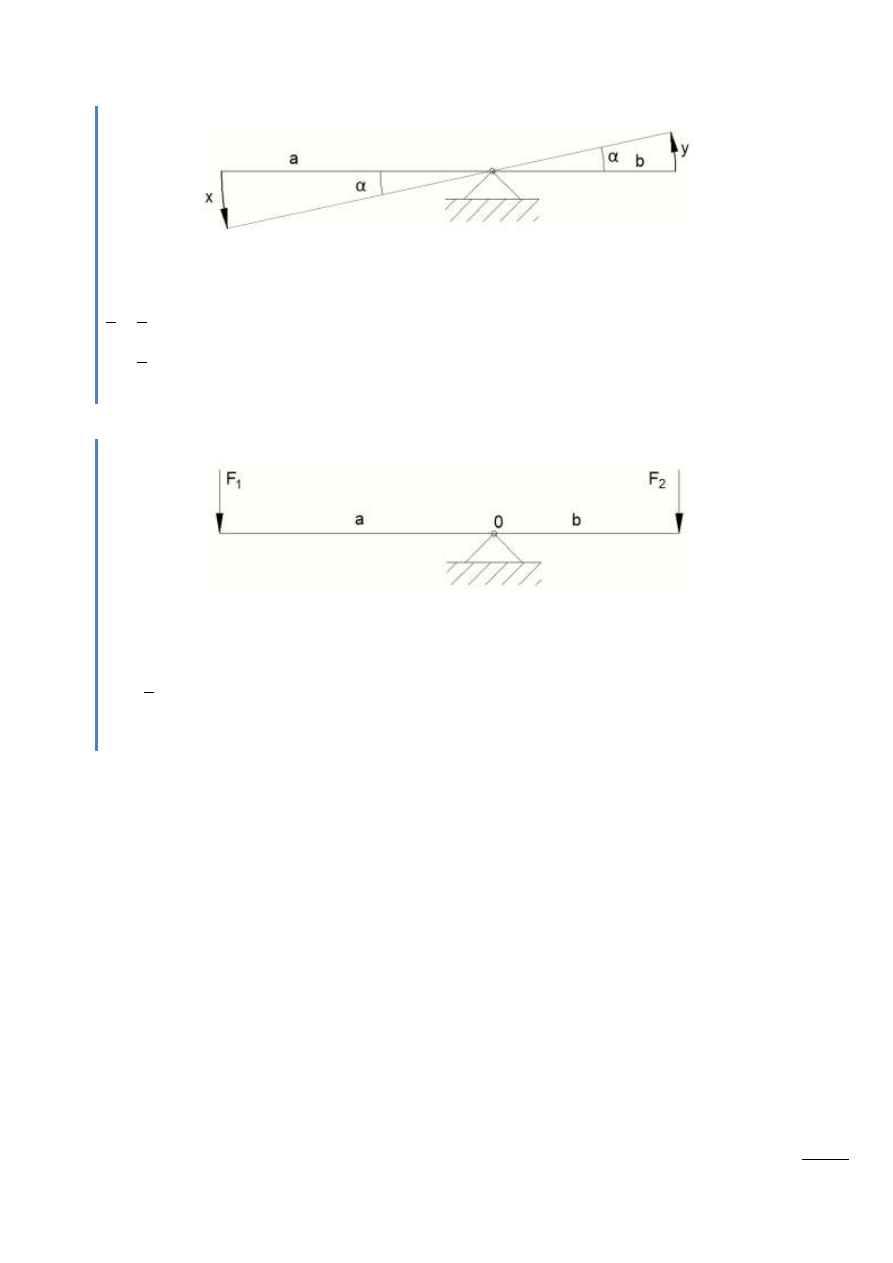
Rys. 12.14 – Przykład elementu bezinercyjnego
x – przesunięcie zadane na wejściu
y – przemieszczenie uzyskane na wyjściu
Przykład
Rys. 12.15 – Przykład elementu bezinercyjnego
Ro
zd
ział:
Wy
kł
ad
1
3
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki
68
Wykład 13. – Zachowanie elementów
automatyki
Elementy inercyjne I-rzędu
Równanie elementu
gdzie: T – stała czasowa
Transmitancja operatorowa
Charakterystyka statyczna
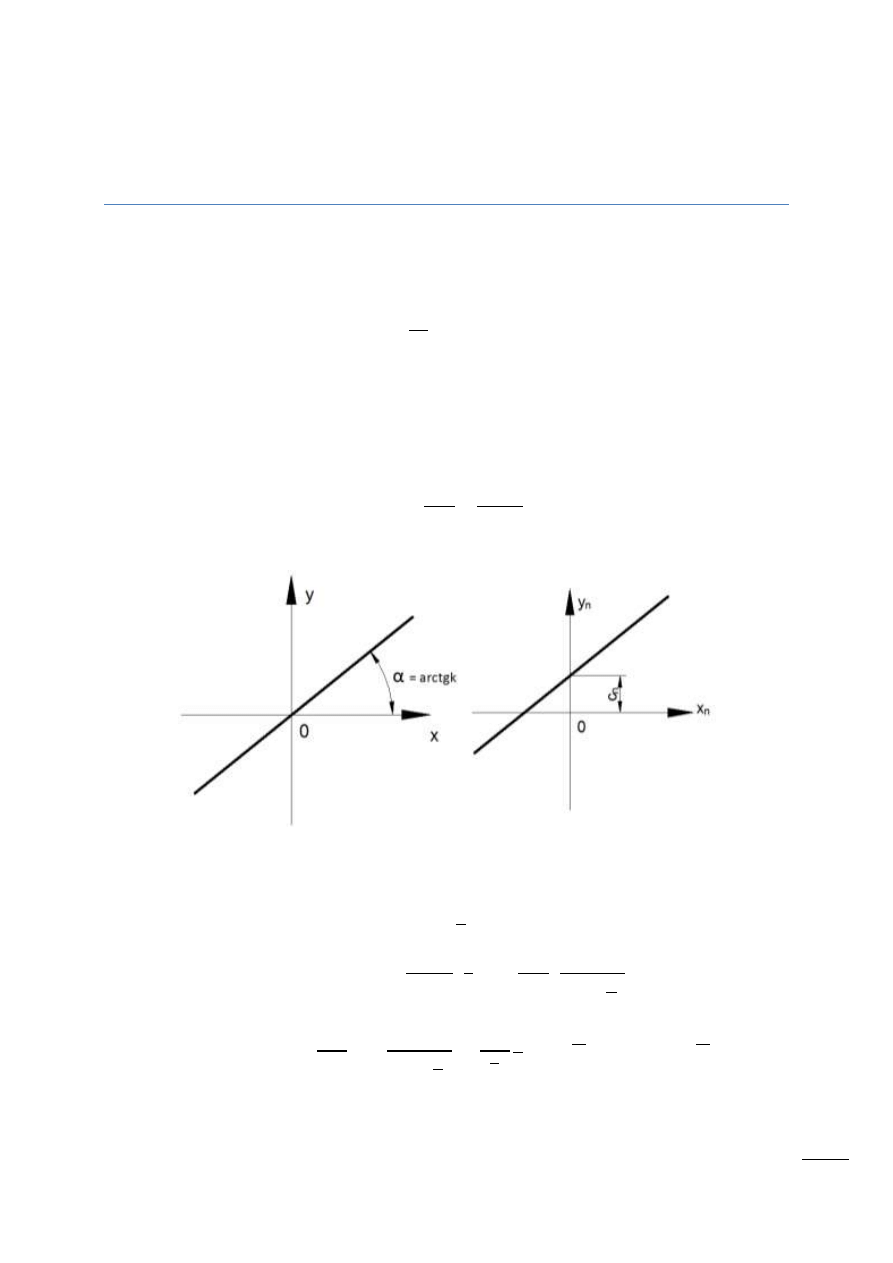
Rys. 13.1 - Charakterystyka statyczna y = kx
Odpowiedź na wymuszenie skokowe
Ro
zd
ział:
Wy
kł
ad
1
3
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki
69
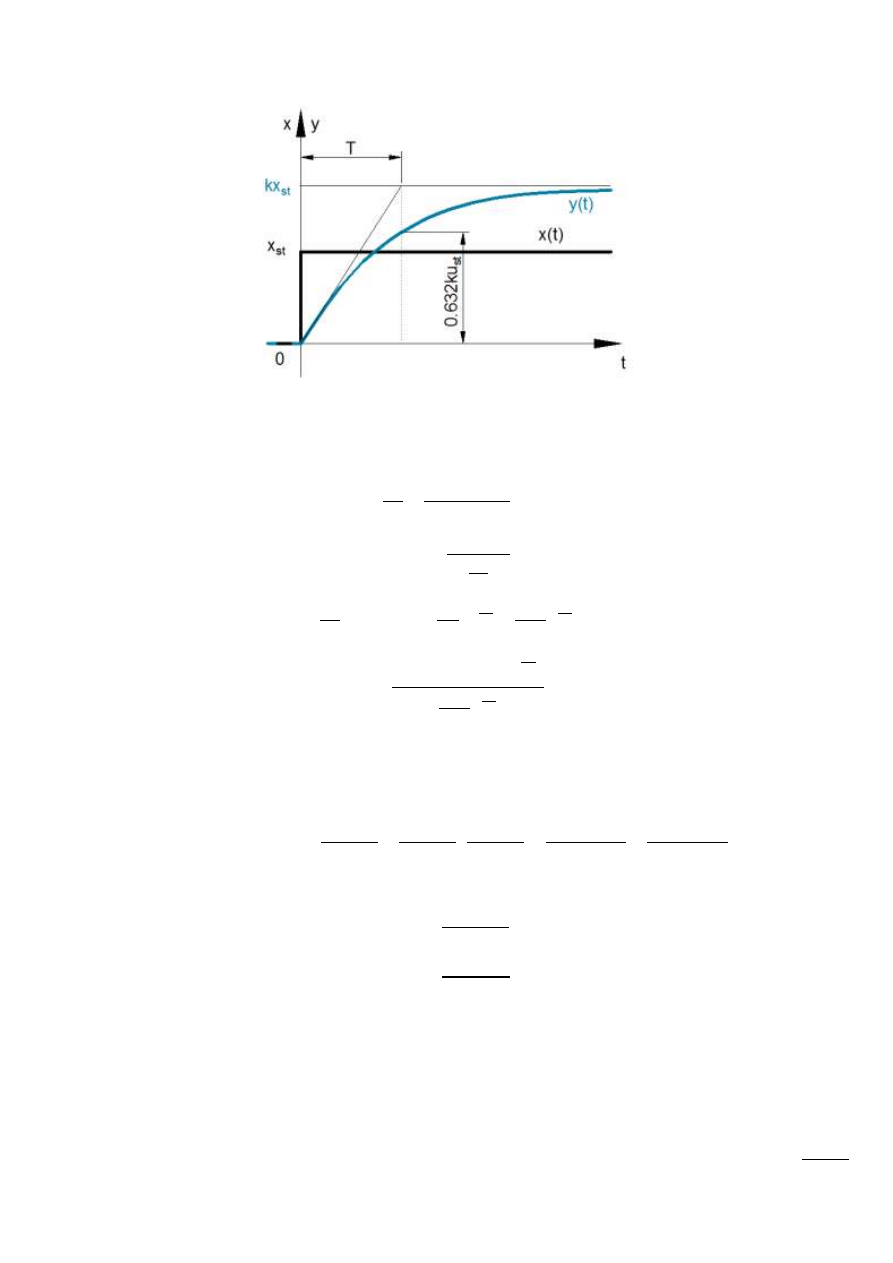
Rys. 13.2 – Odpowiedź na wymuszenie skokowe
Stałą czasową T można określid wystawiając styczną w dowolnym punkcie krzywej
wykładniczej y(t) i wyznaczając odcinek podstycznej na asymptocie.
Stałą czasową T można również określid jako czas od chwili T = 0 do chwili, kiedy y(T) osiągnie
wartośd 0.632 swojej wartości koocowej
Transmitancja widmowa
Ro
zd
ział:
Wy
kł
ad
1
3
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki
70
Rys. 13.3 – Transmitancja widmowa
Logarytmiczna charakterystyka amplitudowa
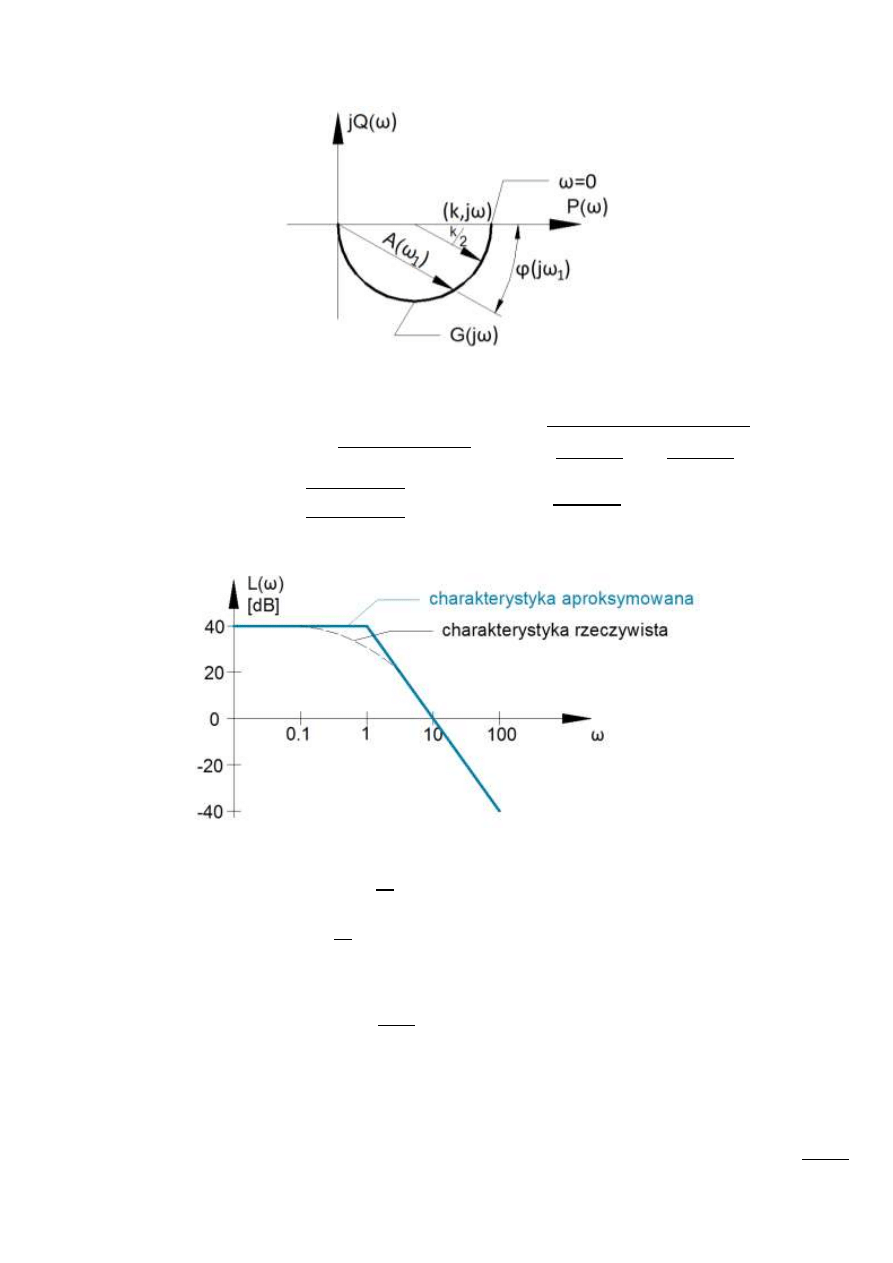
Rys. 13.4 – Charakterystyka amplitudowa dla k = 10
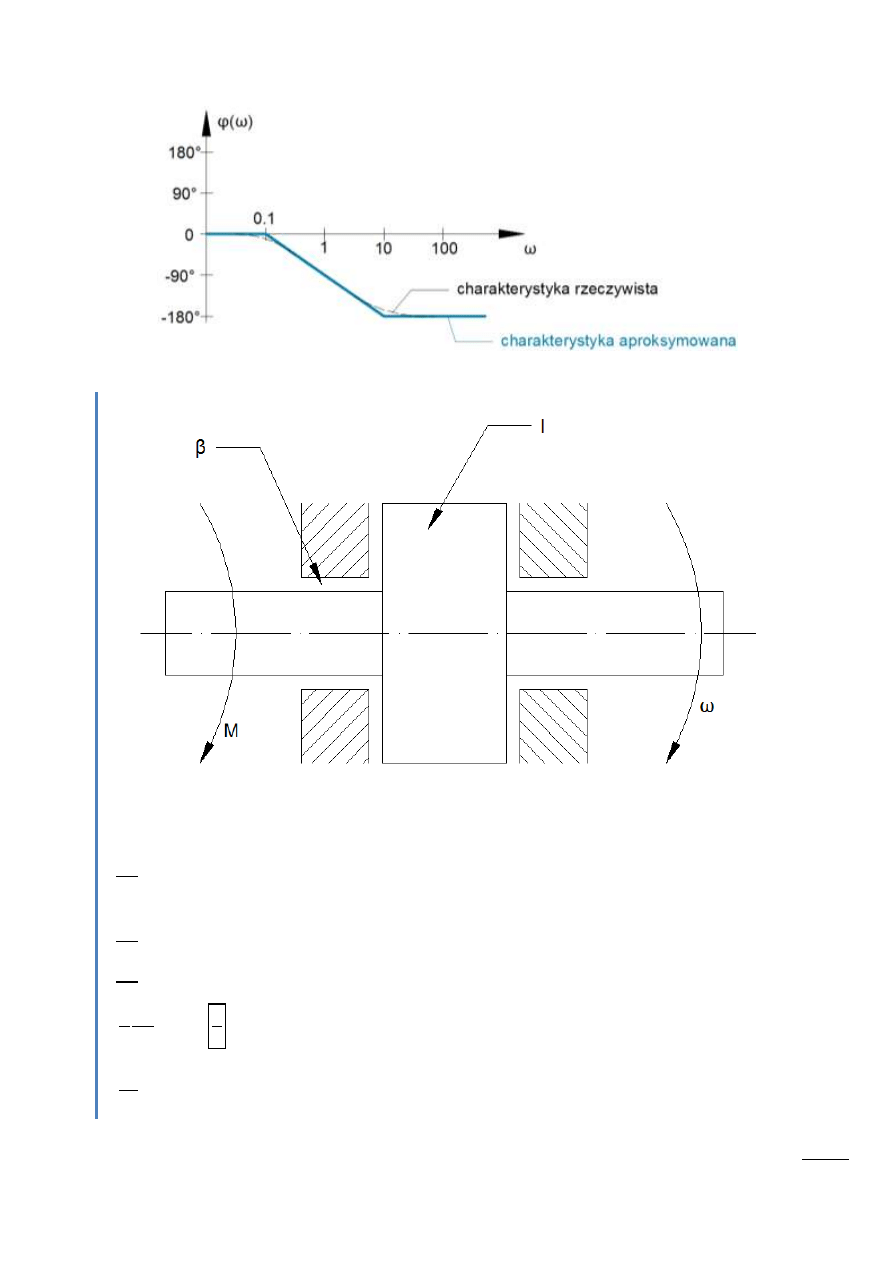
Logarytmiczna charakterystyka fazowa
Ro
zd
ział:
Wy
kł
ad
1
3
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki
71
Rys. 13.5 – Charakterystyka fazowa
Przykład
Rys. 13.6 – Masa o momencie bezwładności I, na obracającym się wale
wielkośd wej. – M – moment sił
wielkośd wy. – ω – prędkośd kątowa wału
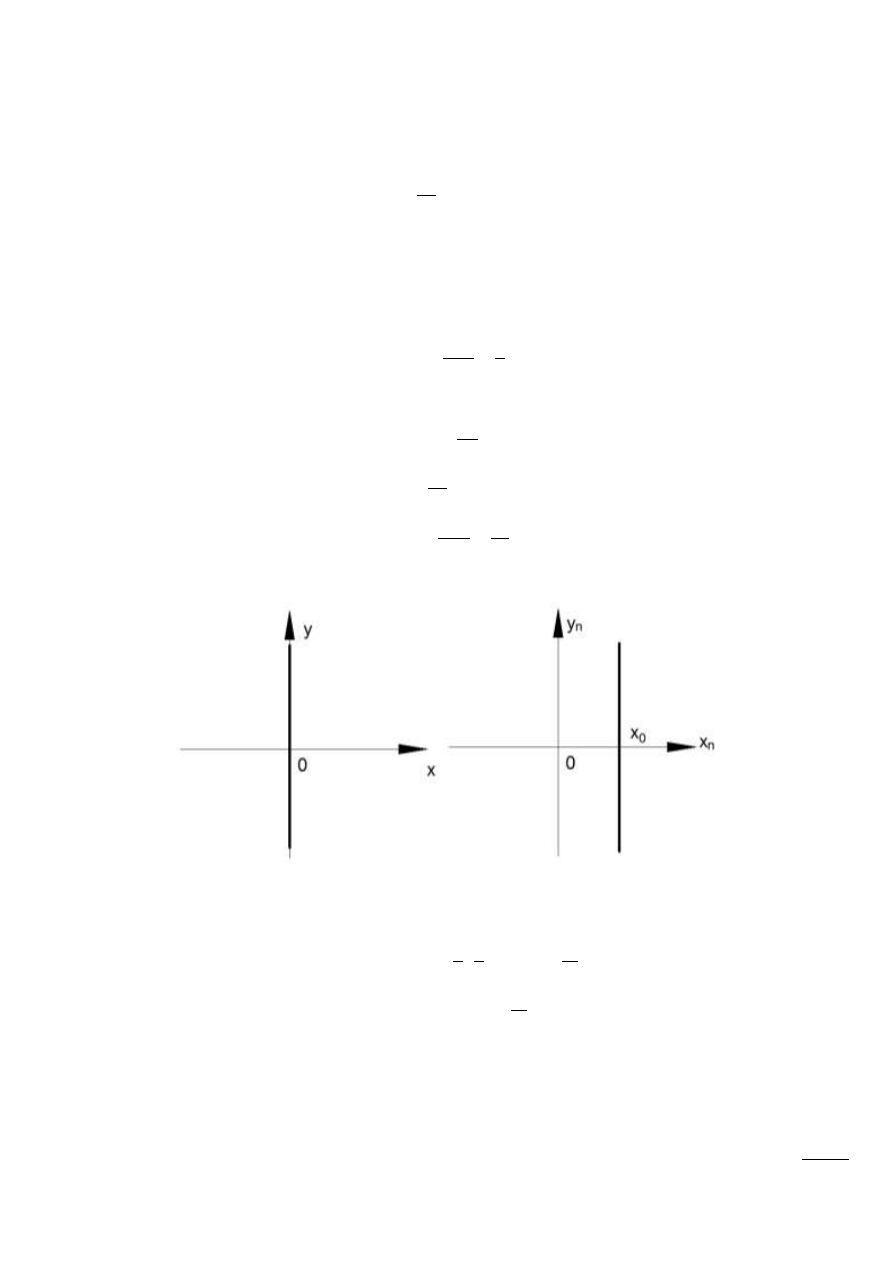
Ro
zd
ział:
Wy
kł
ad
1
3
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki
72
Elementy całkujące
Równanie elementu
Transmitancja operatorowa
dla k = 1/T:
Charakterystyka statyczna
Rys. 13.7 – Charakterystyka statyczna
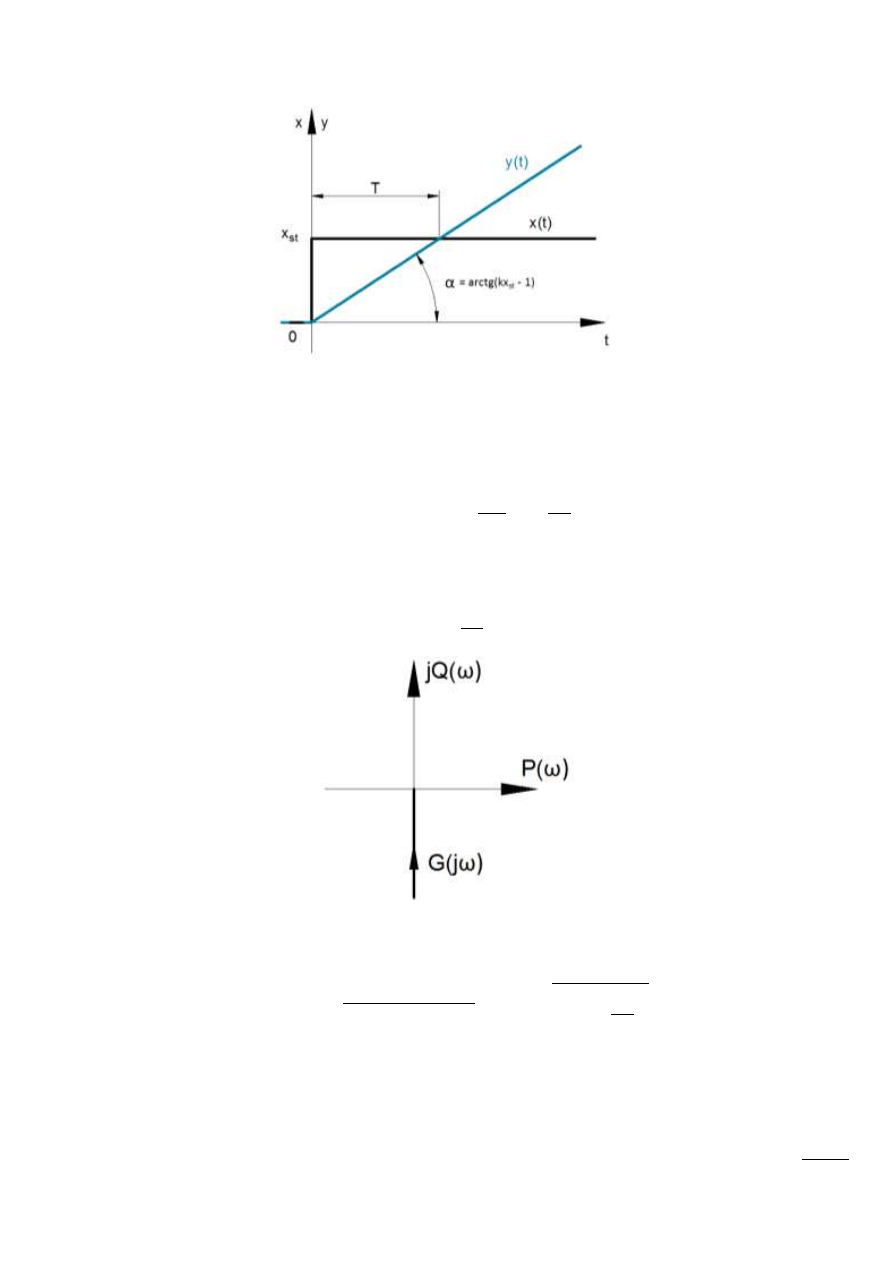
Odpowiedź na wymuszenie skokowe
Ro
zd
ział:
Wy
kł
ad
1
3
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki
73
Rys. 13.8 – Odpowiedź na wymuszenie skokowe
W przypadku szczególnym gdy wejście i wyjście są sygnałami jednoimiennymi współczynnik k
ma wymiar odwrotności czasu.
Transmitancja widmowa
Rys. 13.9 – Transmitancja widmowa
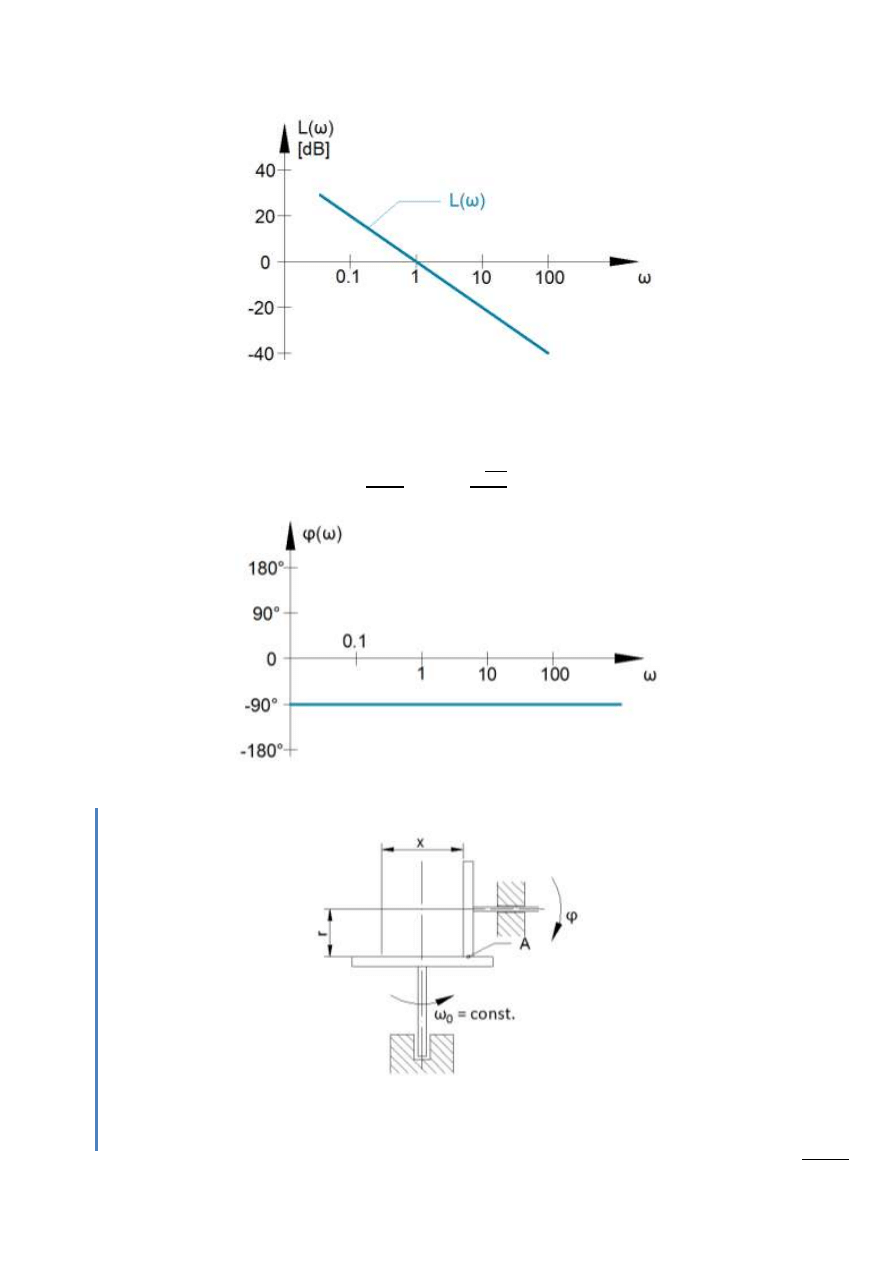
Logarytmiczna charakterystyka amplitudowa
Ro
zd
ział:
Wy
kł
ad
1
3
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki
74
Rys. 13.10 – Charakterystyka amplitudowa
Logarytmiczna charakterystyka fazowa
Rys. 13.11 – Charakterystyka fazowa
Przykład
Rys. 13.12 – Wirująca tarcza przesuwająca się po promieniu drugiej tarczy
x – w. wej. – przemieszczenie
ϕ – w. wyj. – kąt obrotu
Ro
zd
ział:
Wy
kł
ad
1
3
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki
75
Elementy różniczkujące
Równanie elementu
Transmitancja operatorowa
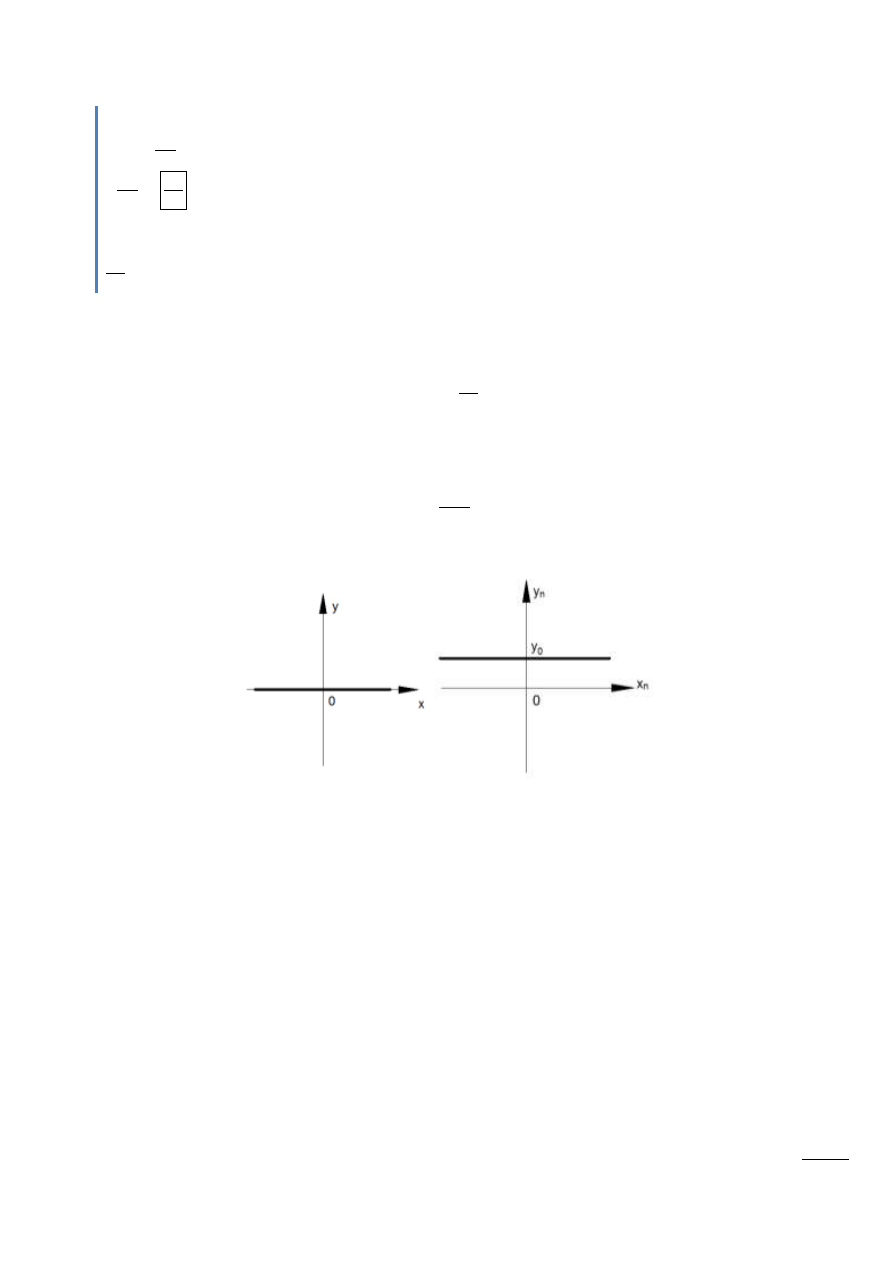
Charakterystyka statyczna
Rys.13.12 – Charakterystyki statyczne
Odpowiedź na wymuszenie skokowe
Ro
zd
ział:
Wy
kł
ad
1
3
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki
76
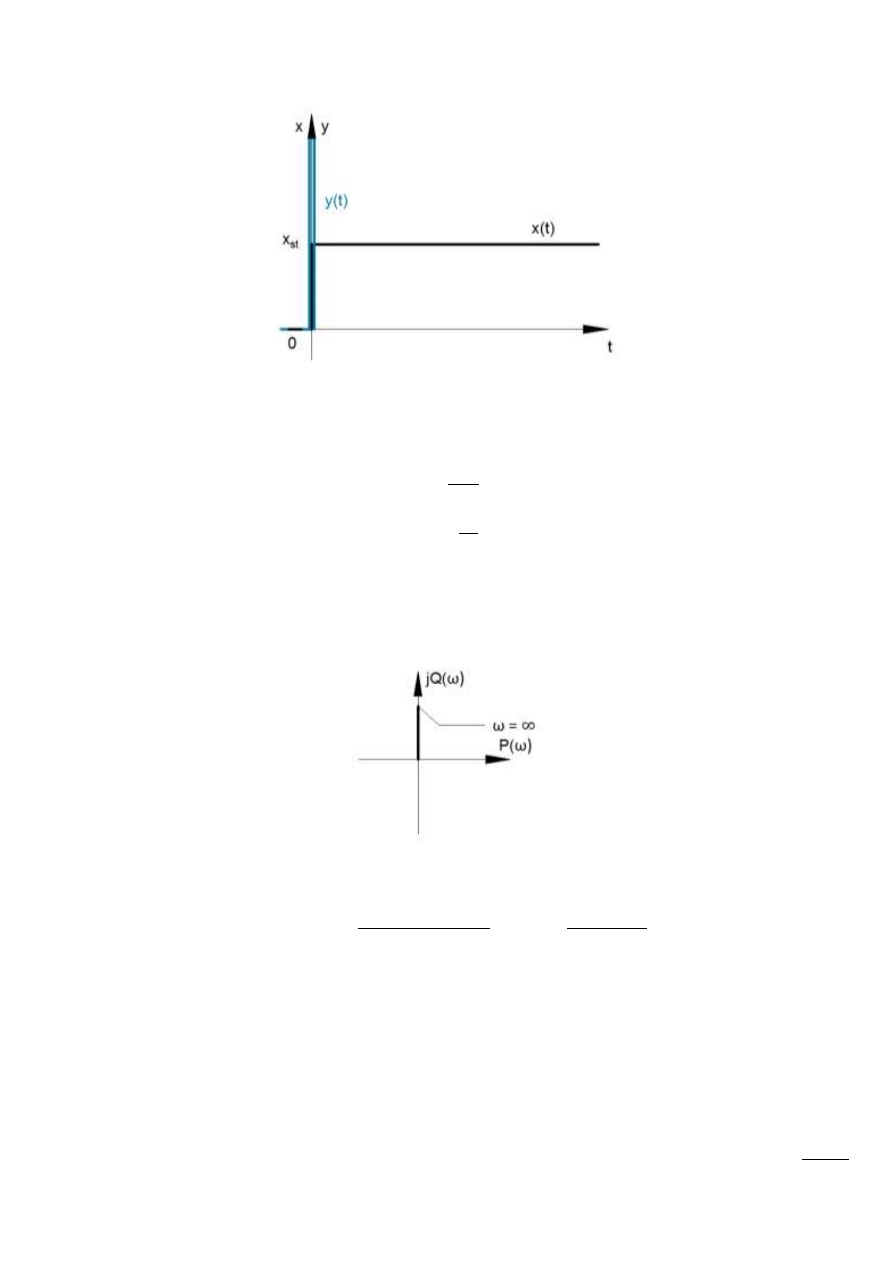
Rys. 13.13 – Odpowiedź na wymuszenie skokowe
Jeśli sygnały wejściowe i wyjściowe są sygnałami jednoimiennymi to równanie elementu ma
postad:
Transmitancja widmowa
Charakterystyka amplitudowo-fazowa
Rys. 13.14 – Charakterystyka amplitudowo-fazowa
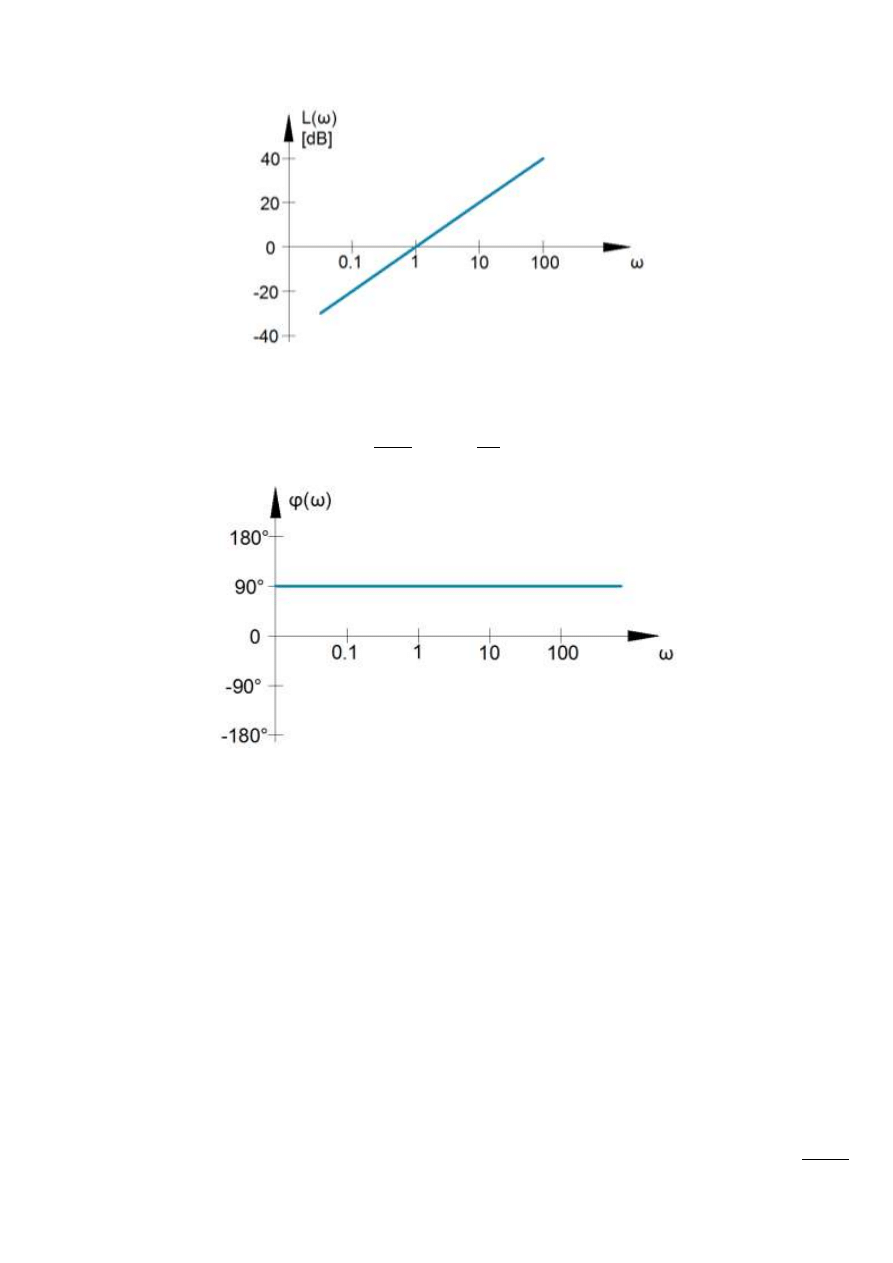
Logarytmiczna charakterystyka amplitudowa
Ro
zd
ział:
Wy
kł
ad
1
3
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki
77
Rys. 13.15 – Charakterystyka amplitudowa
Logarytmiczna charakterystyka fazowa
Rys. 13.16 – Charakterystyka fazowa
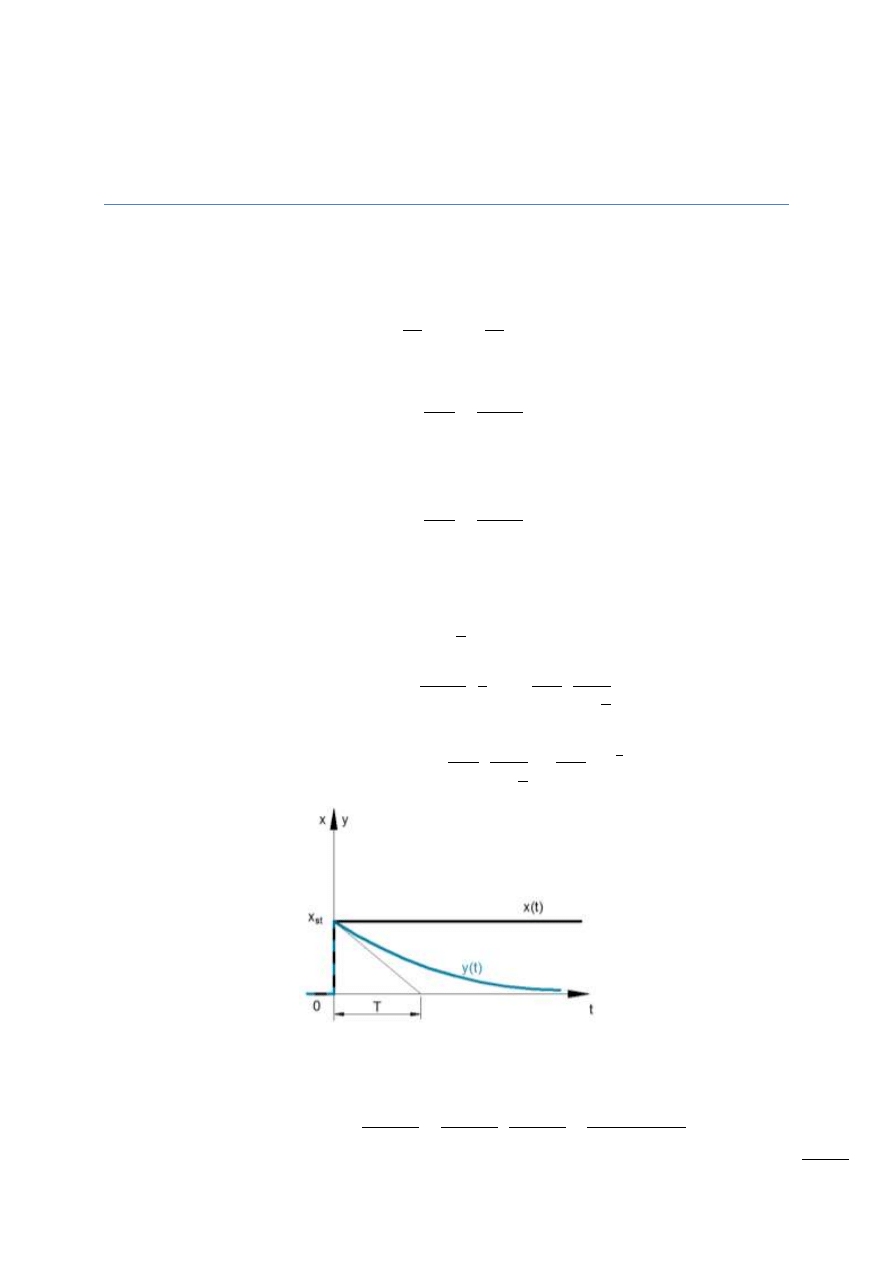
Ro
zd
ział:
Wy
kł
ad
1
4
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki c.d.
78
Wykład 14. – Zachowanie elementów
automatyki c.d.
Rzeczywiste elementy różniczkujące
Równanie elementu
Transmitancja operatorowa
Jeśli sygnały wejściowy i wyjściowy są sygnałami jednoimiennymi, to równanie elementu
zapisuje się w postaci (dla k = T):
Odpowiedź na wymuszenie skokowe
Rys. 14.1 – Odpowiedź na wymuszenie skokowe
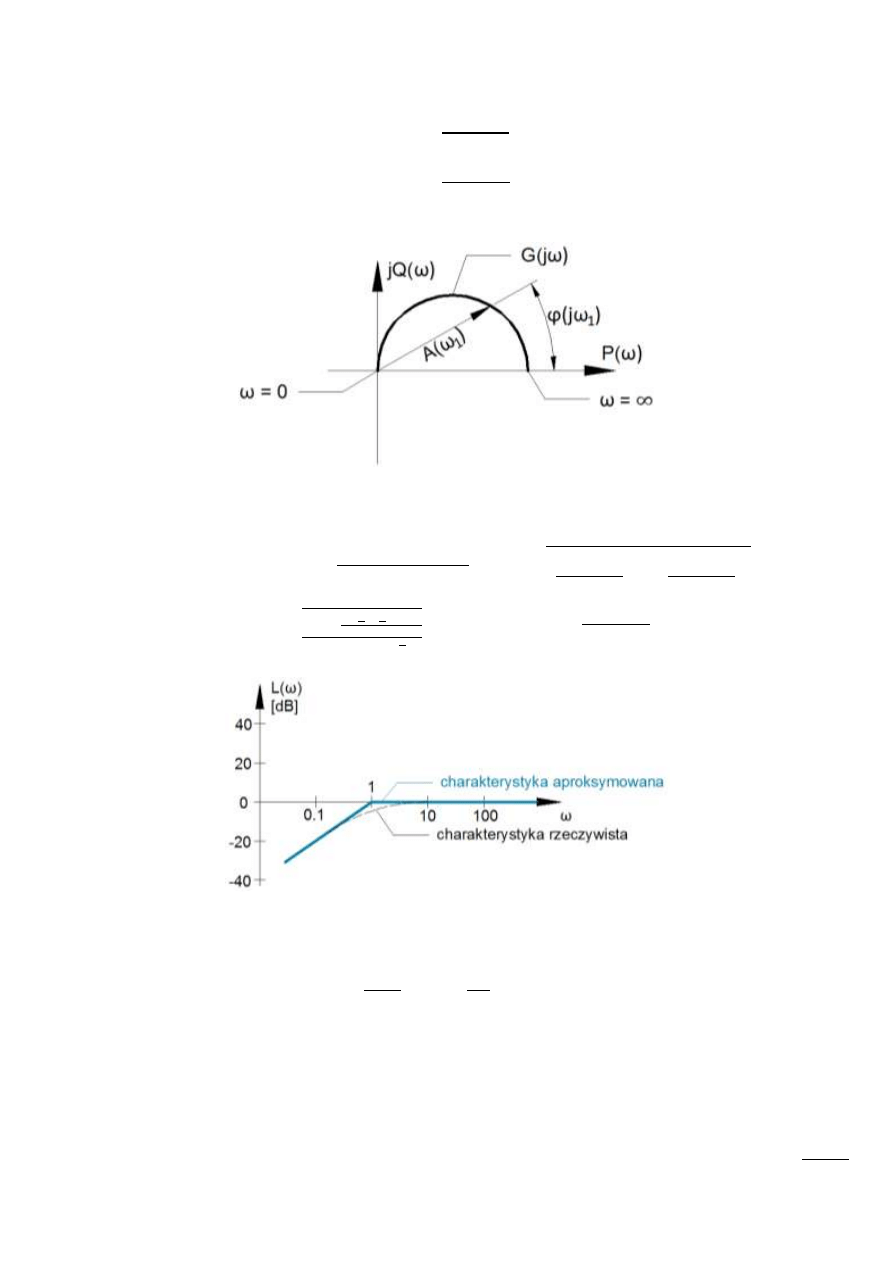
Transmitancja widmowa
Ro
zd
ział:
Wy
kł
ad
1
4
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki c.d.
79
Charakterystyka amplitudowo-fazowa
Rys. 14.2 – Charakterystyka amplitudowo-fazowa
Logarytmiczna charakterystyka amplitudowa
Rys. 14.3 – Charakterystyka amplitudowa
Logarytmiczna charakterystyka fazowa
Ro
zd
ział:
Wy
kł
ad
1
4
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki c.d.
80
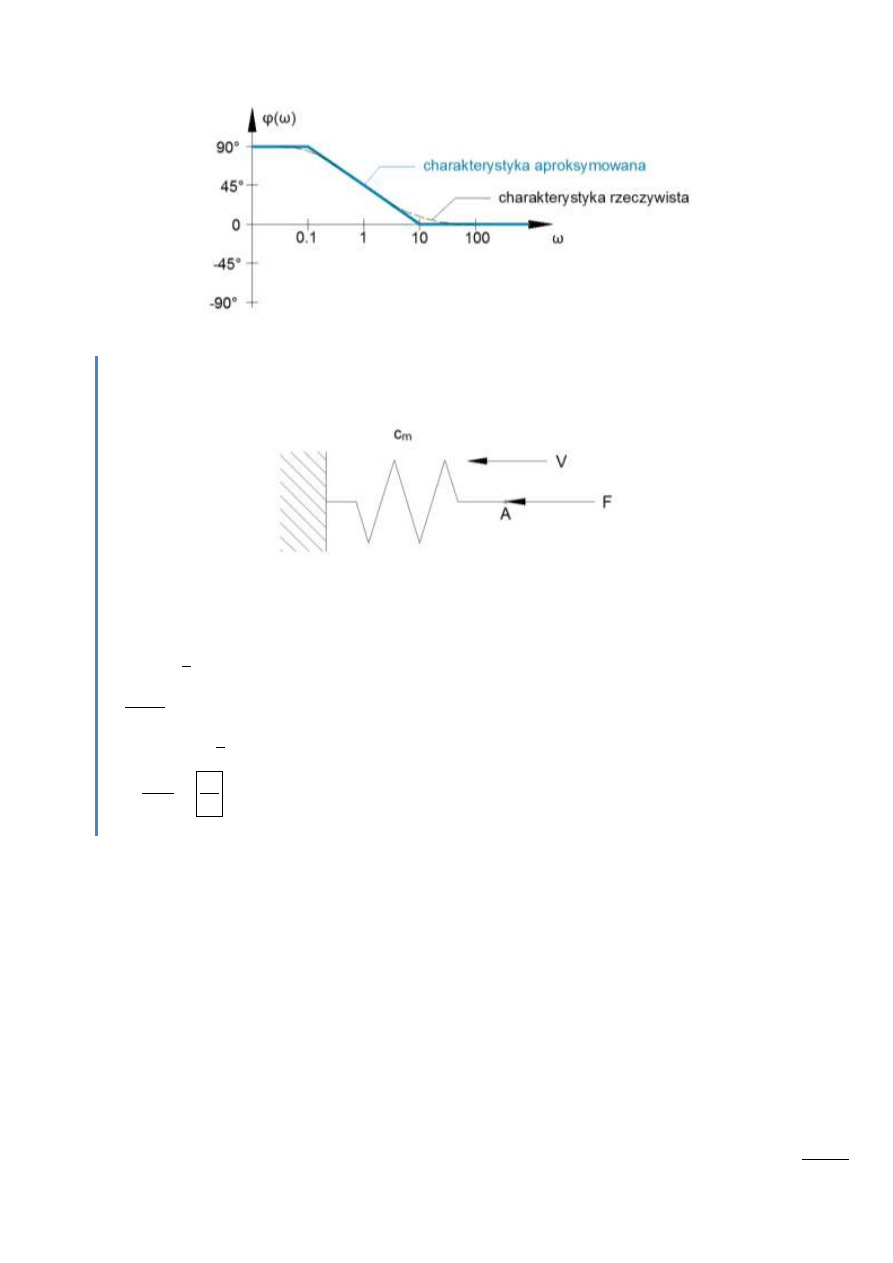
Rys. 14.4 – Charakterystyka fazowa
Przykład
Wyznaczyd transmitancję dla sprężyny o sztywności c
m
, przyjmując jako wielkośd wejściową
siłę F działającą na sprężynę, a jako wielkośd wyjściową prędkośd jej kooca.
Rys. 14.5 – Sprężyna poddana działaniu siły F

Ro
zd
ział:
Wy
kł
ad
1
4
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki c.d.
81
Przykład
Dla tłumika hydraulicznego pokazanego na rysunku wyznaczyd równanie różniczkowe i
transmitancję operatorową.
Rys. 14.6 – Model tłumika hydraulicznego
c
s
– sztywnośd sprężyny
h – współczynnik tłumienia
Elementy oscylacyjne
Równanie elementu
Transmitancja elementu

Ro
zd
ział:
Wy
kł
ad
1
4
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki c.d.
82
Charakterystyka statyczna
Rys. 14.7 – Charakterystyka statyczna
Transmitancja operatorowa
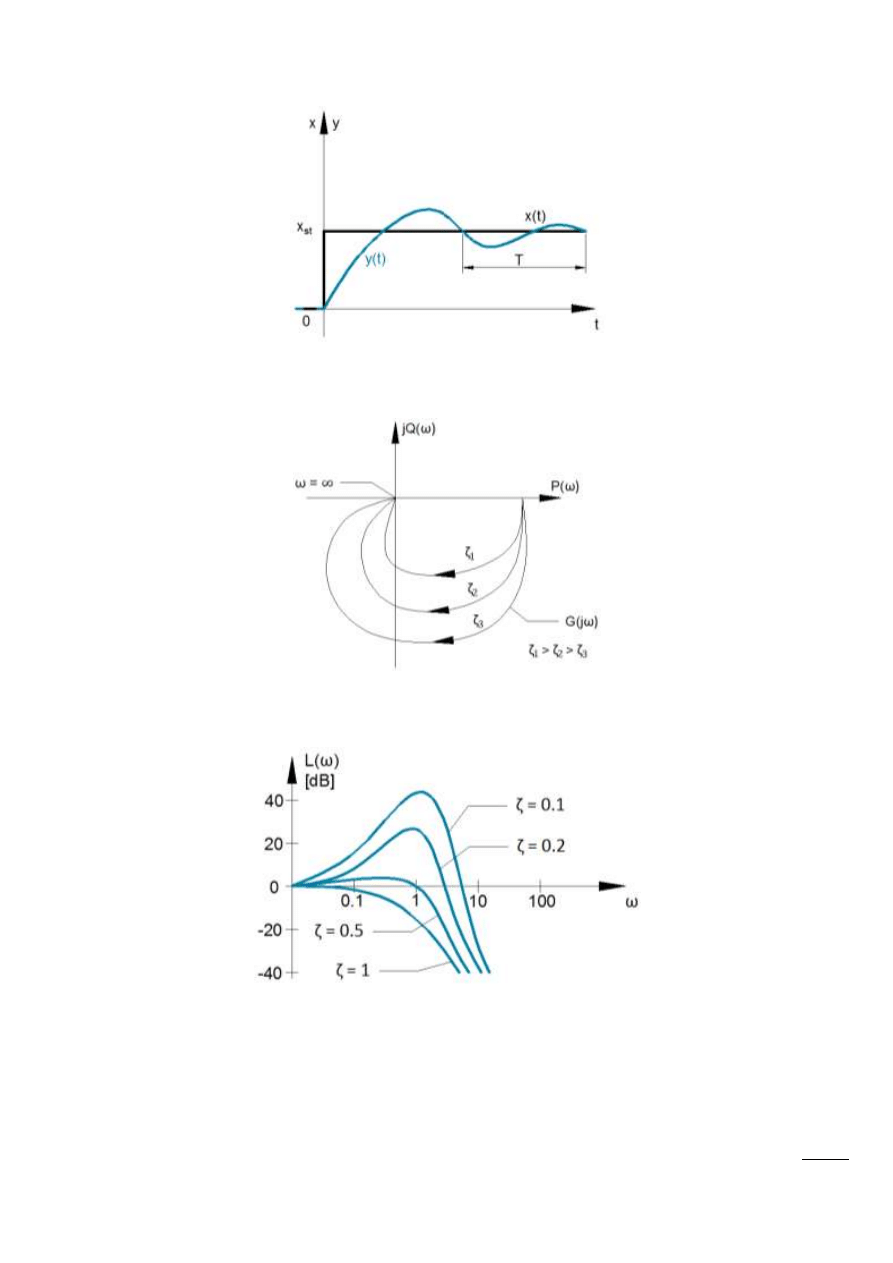
Odpowiedź na wymuszenie skokowe
Ro
zd
ział:
Wy
kł
ad
1
4
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki c.d.
83
Rys. 14.8 – Odpowiedź na wymuszenie skokowe
Transmitancja widmowa
Rys. 14.9 – Transmitancja widmowa
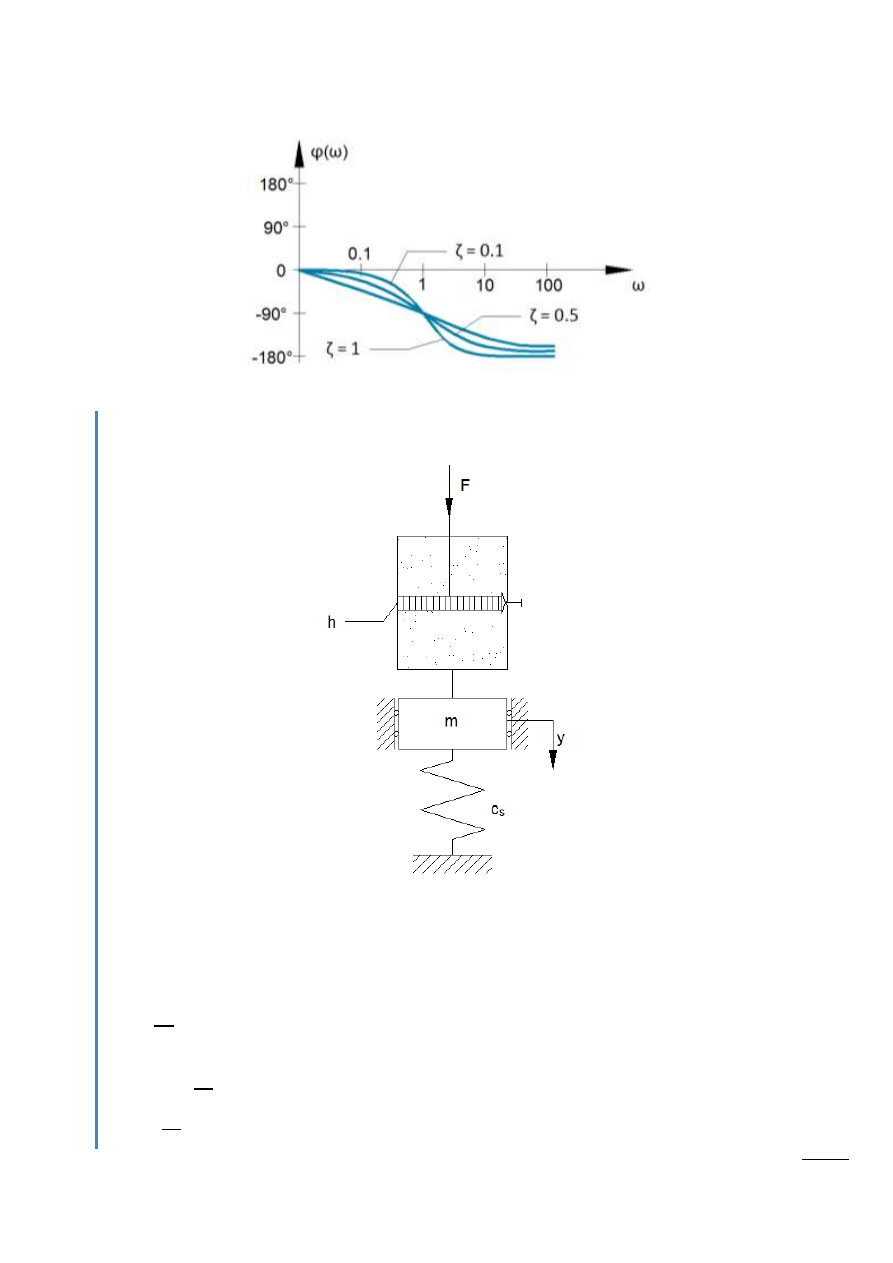
Logarytmiczna charakterystyka amplitudowa
Rys. 14.10 – Charakterystyka amplitudowa
Ro
zd
ział:
Wy
kł
ad
1
4
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki c.d.
84
Logarytmiczna charakterystyka fazowa
Rys. 14.11 – Charakterystyka fazowa
Przykład
Dla układu jak na rysunku wyznaczyd równanie i transmitancję operatorową
Rys. 14.12 – Układ tłumieniem
F – siła nacisku – wielkośd wejściowa
y – przemieszczenie – wielkośd wyjściowa
Ro
zd
ział:
Wy
kł
ad
1
4
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki c.d.
85
Elementy opóźniające
Równanie elementu
Transmitancja
Transmitancja operatorowa
Charakterystyka statyczna
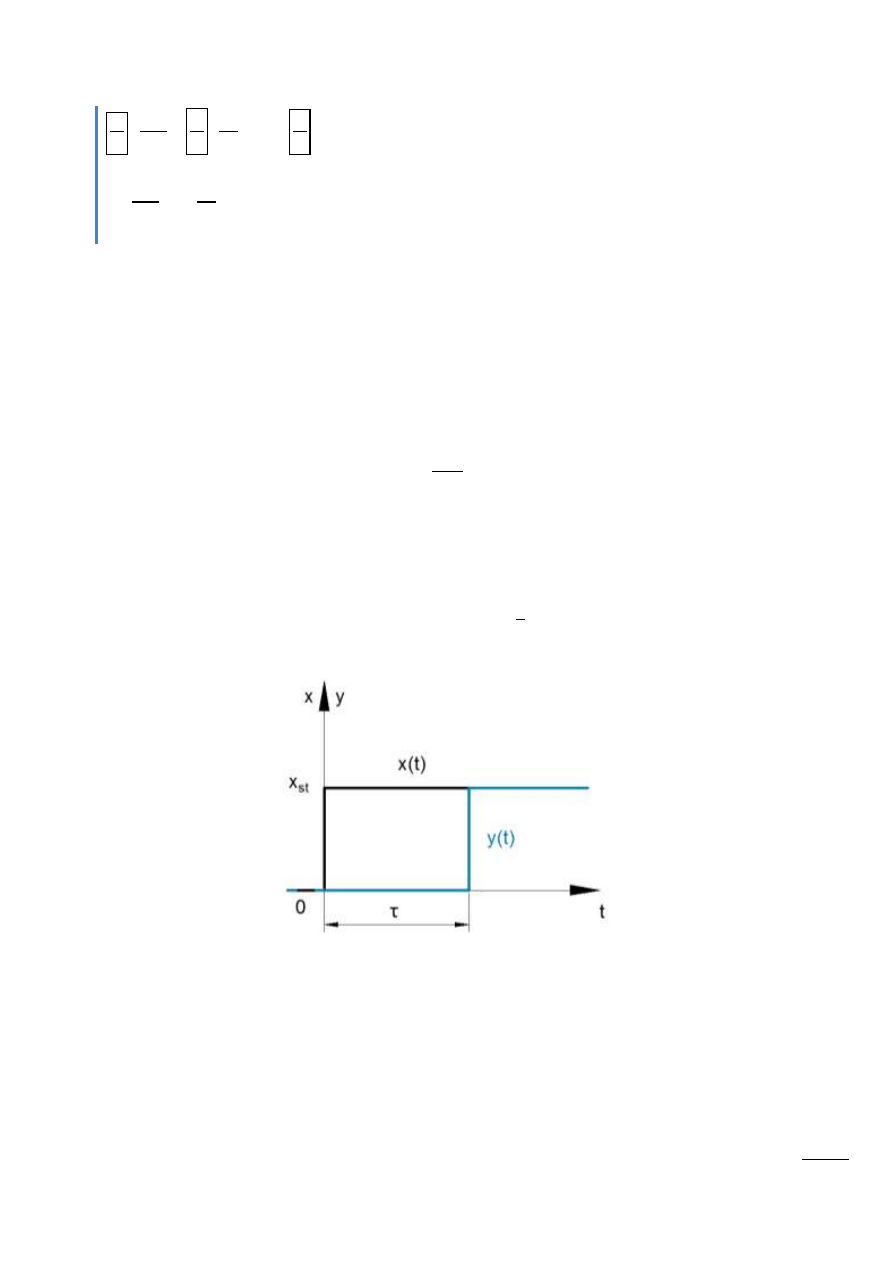
Odpowiedź na wymuszenie skokowe
Rys. 14.13 – Odpowiedź na wymuszenie skokowe
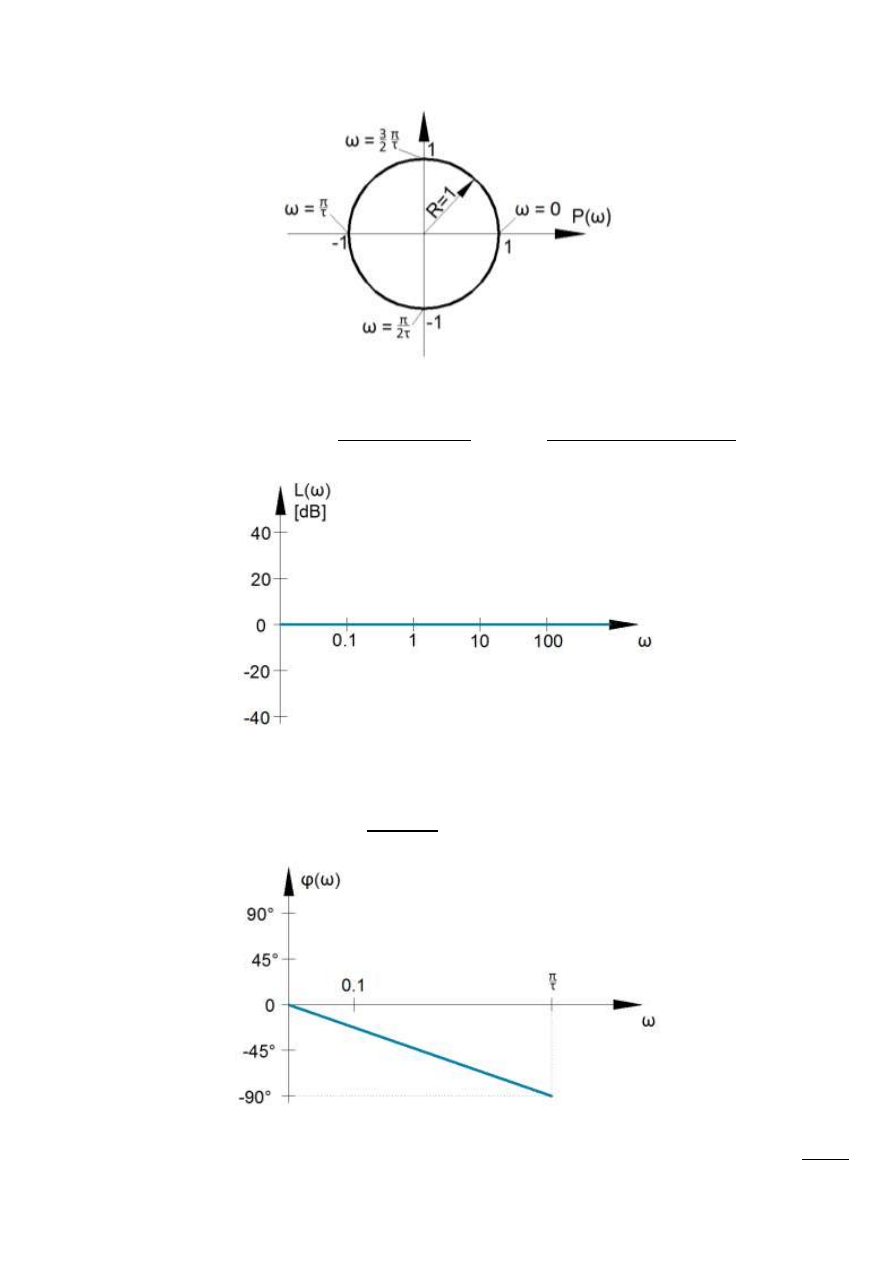
Transmitancja widmowa
Ro
zd
ział:
Wy
kł
ad
1
4
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki c.d.
86
Rys. 14.14 – Transmitancja widmowa
Logarytmiczna charakterystyka amplitudowa
Rys. 14.15 – Charakterystyka amplitudowa
Logarytmiczna charakterystyka fazowa
Rys. 14.16 – Charakterystyka fazowa

Ro
zd
ział:
Wy
kł
ad
1
4
. –
Zac
h
o
wani
e e
le
m
en
tó
w
au
to
m
at
yki c.d.
87
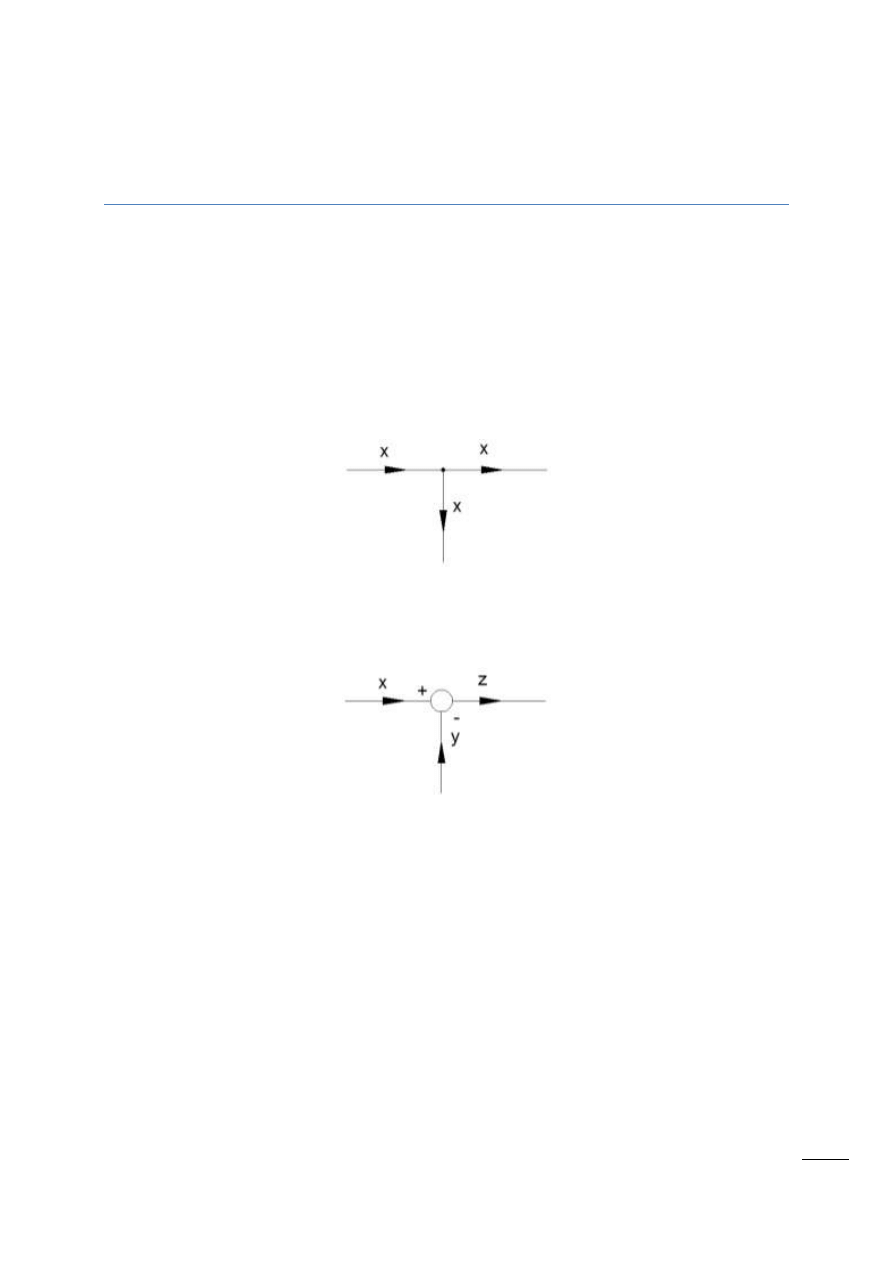
Ro
zd
ział:
Wy
kł
ad
1
5
. –
Sch
em
aty
bl
o
ko
w
e,
regu
lat
o
ry
, st
ab
iln
o
śd
88
Wykład 15. – Schematy blokowe,
regulatory, stabilność
Schematy blokowe zwane też strukturalnymi przedstawiają ogólną budowę (strukturę)
dowolnego elementu lub układu oraz podają kierunek przepływu sygnałów i związki (najczęściej
transmitancje) między sygnałami wejściowymi i wyjściowymi poszczególnych części tego elementu
lub układu.
Węzły informacyjne i sumacyjne
Węzły informacyjne (zaczepowe) – reprezentują na schematach blokowych urządzenia, które
pozwalają pobierad tę samą informację do kilku gałęzi układu.
Rys. 15.1 – Symbol graficzny węzła informacyjnego
Węzeł sumacyjny – reprezentuje na schematach blokowych urządzenia, w których zachodzi
algebraiczne (z uwzględnieniem znaków) sumowanie sygnałów.
Rys. 15.2 – Symbol graficzny węzła sumacyjnego.
z = x - y
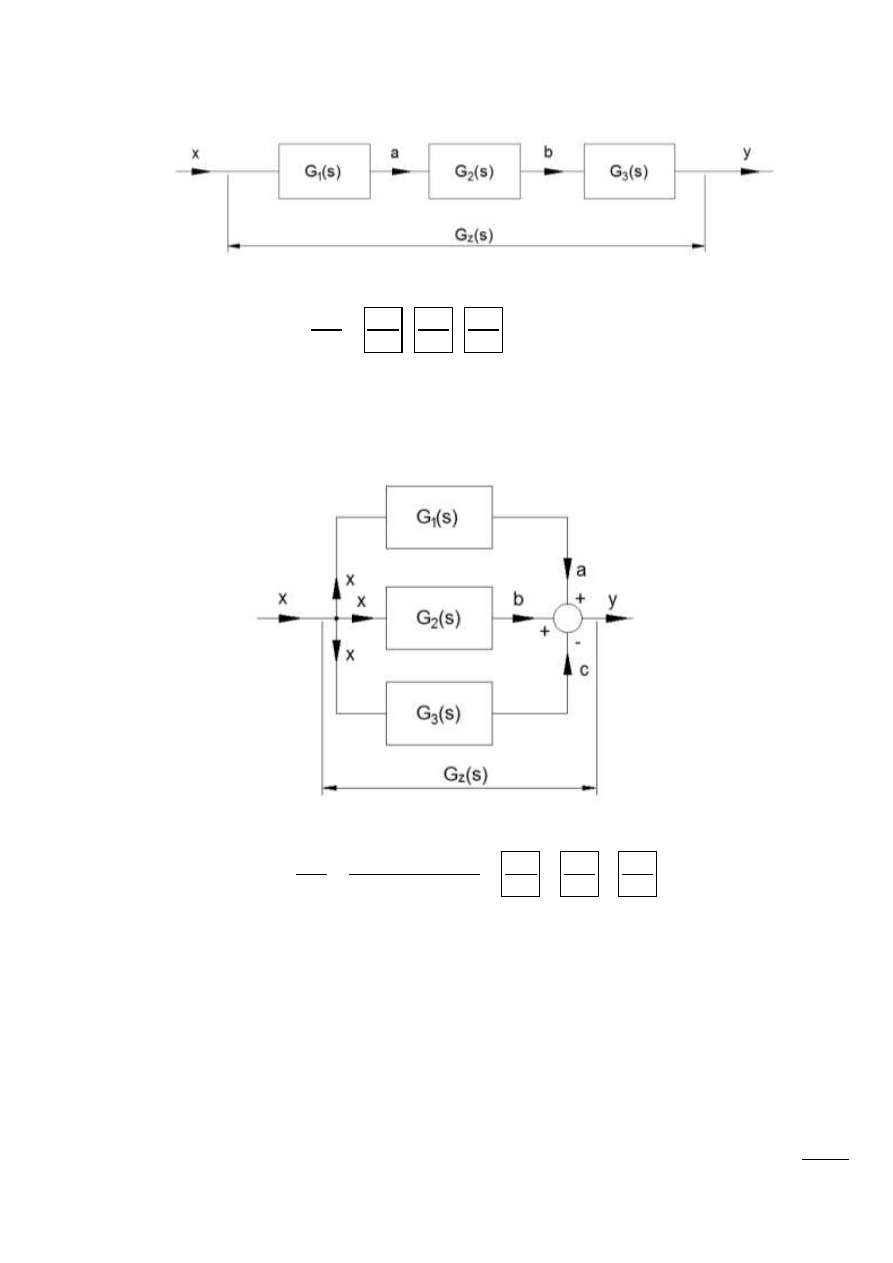
Przekształcenia schematów blokowych
Przekształcenia schematów blokowych pozwalają na wyznaczenie wypadkowej transmitancji
układu, którego struktura i transmitancje elementów składowych są znane.
Ro
zd
ział:
Wy
kł
ad
1
5
. –
Sch
em
aty
bl
o
ko
w
e,
regu
lat
o
ry
, st
ab
iln
o
śd
89
Połączenie szeregowe
Rys. 15.3 – Połączenie szeregowe
Ogólnie transmitancja szeregowego połączenia elementów jest równa iloczynowi
transmitancji tych elementów
Połączenie równoległe
Rys. 15.4 – Połączenie równoległe
Ogólnie transmitancja równoległego połączenia elementów jest równa algebraicznej sumie
(wraz z uwzględnieniem znaków) transmitancji tych elementów.
Jeżeli w dowolnej gałęzi schematu blokowego nie występuje żaden blok o określonej
transmitancji, to transmitancja takiej gałęzi jest równa jedności (wejście-są identyczne).
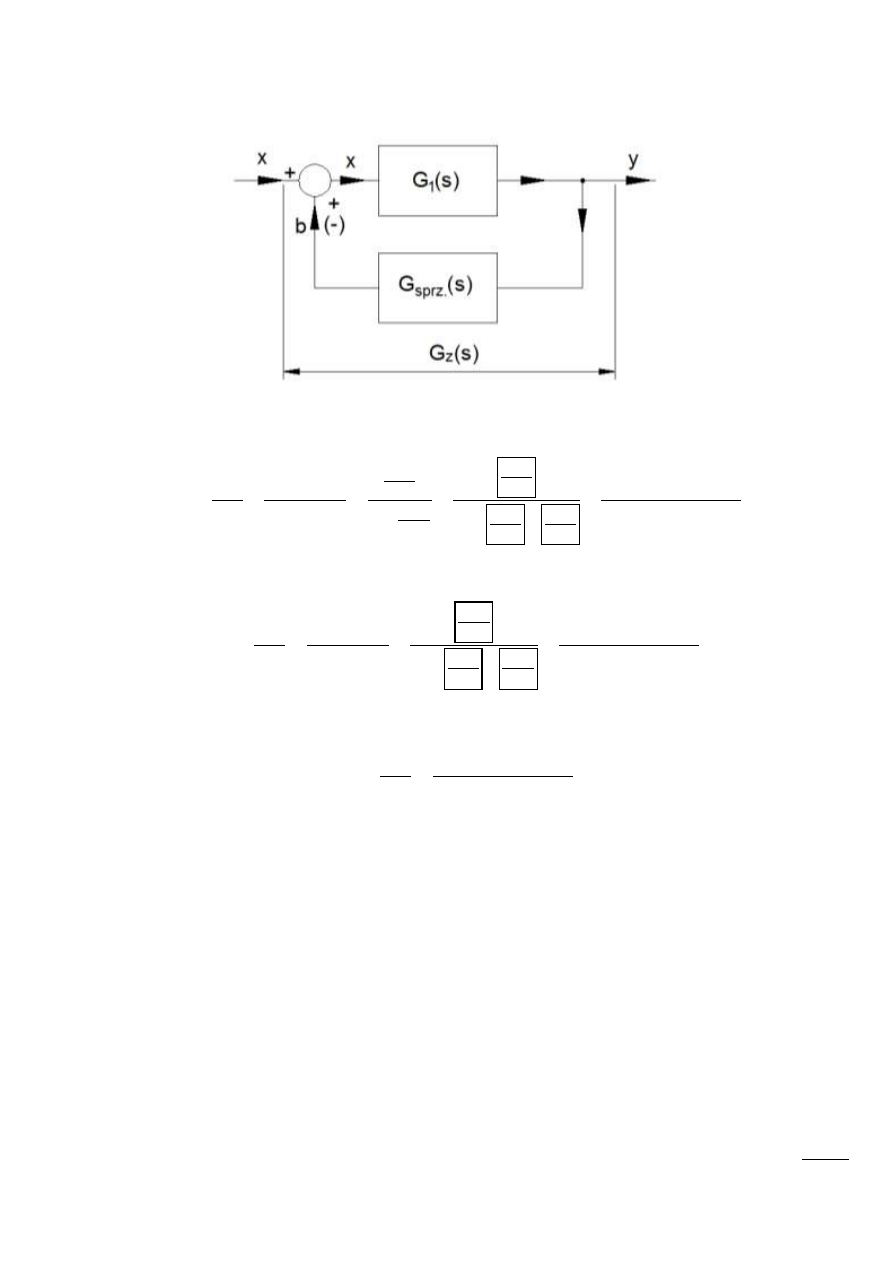
Ro
zd
ział:
Wy
kł
ad
1
5
. –
Sch
em
aty
bl
o
ko
w
e,
regu
lat
o
ry
, st
ab
iln
o
śd
90
Połączenie ze sprzężeniem zwrotnym
Rys. 15.5 – Układ ze sprzężeniem zwrotnym
Ogólnie:
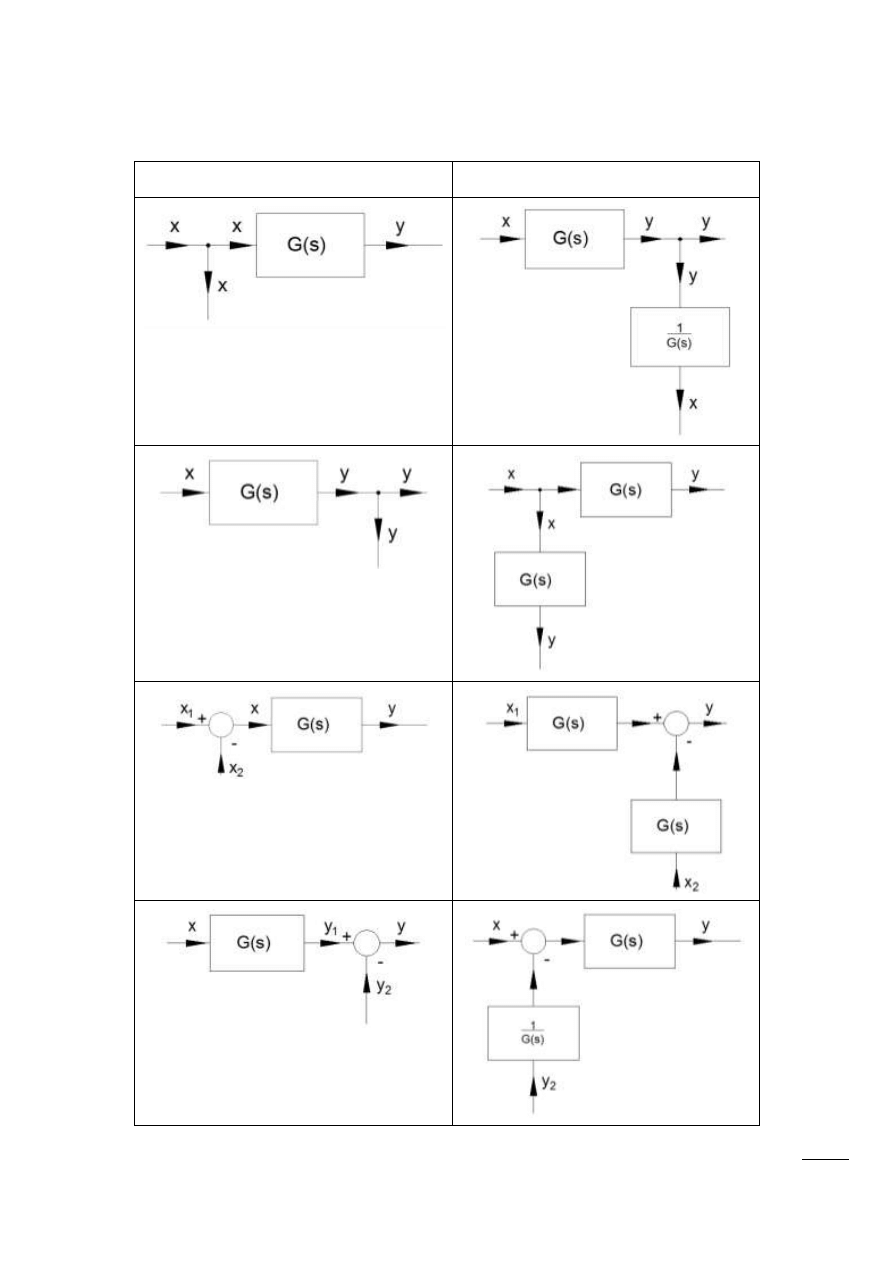
Ro
zd
ział:
Wy
kł
ad
1
5
. –
Sch
em
aty
bl
o
ko
w
e,
regu
lat
o
ry
, st
ab
iln
o
śd
91
Przesunięcia węzłów informacyjnych i węzłów informacyjnych
Schemat pierwotny
Schemat równoważny
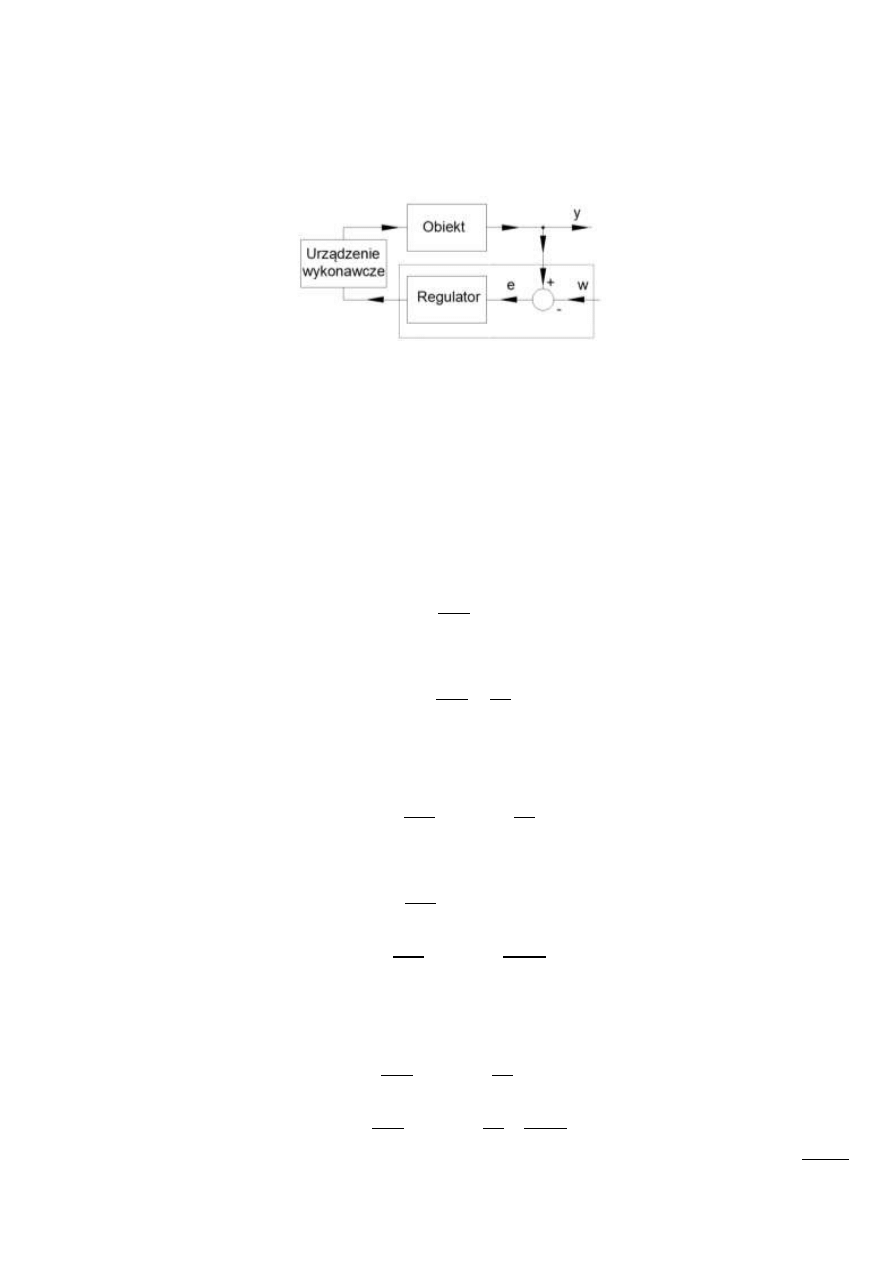
Ro
zd
ział:
Wy
kł
ad
1
5
. –
Sch
em
aty
bl
o
ko
w
e,
regu
lat
o
ry
, st
ab
iln
o
śd
92
Regulatory
Zadaniem regulatora jest wytworzenie sygnału sterującego obiektem regulacji w sposób
zapewniający jego pożądane zachowanie się.
Rys. 15.6 – Układ automatyki z regulatorem (w ramce)
Pracę regulatora charakteryzuje równanie różniczkowe według którego dla obiektu regulacji
zostaje wprowadzone działanie regulujące
Prawem regulacji nazywamy związek funkcjonalny jaki zachodzi między przyrostem sygnału
sterującego u, a przyrostem uchybu regulacji e.
Ze względu na własności dynamiczne, rozróżniamy następujące rodzaje regulatorów:
regulatory proporcjonalne (P)
regulatory całkujące (I)
gdzie T
i
– czas zdwojenia
regulatory proporcjonalno-całkujące (PI)
regulatory proporcjonalno-różniczkujące (PD)
gdzie T
d
– stała czasowa określająca działanie różniczkujące regulatora (czas wyprzedzenia)
regulatory proporcjonalno-całkująco-różniczkujące (PID)
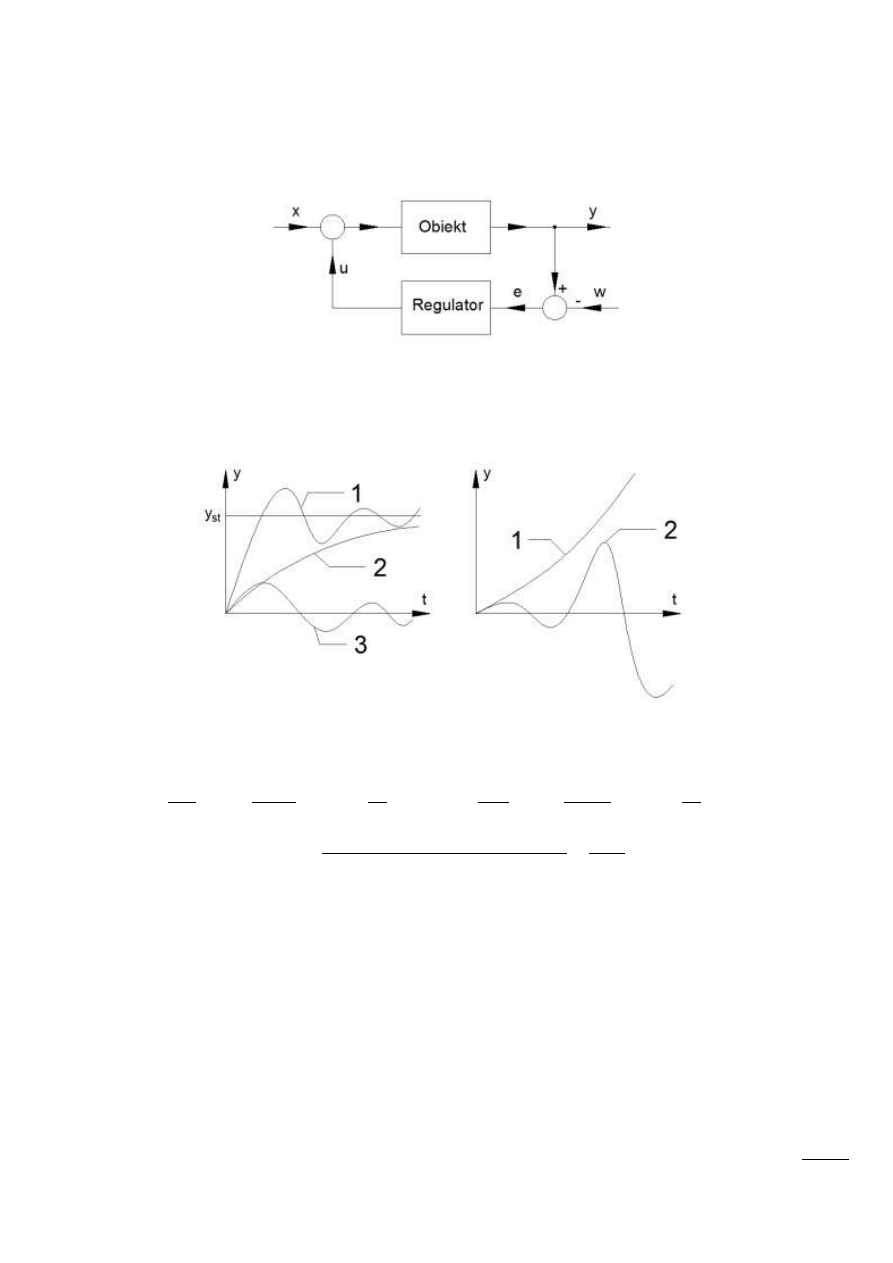
Ro
zd
ział:
Wy
kł
ad
1
5
. –
Sch
em
aty
bl
o
ko
w
e,
regu
lat
o
ry
, st
ab
iln
o
śd
93
Stabilność liniowych układów automatyki
Stabilnośd jest cechą układu polegającą na powracaniu do stanu równowagi stałej, po ustaniu
działania zakłócenia, które wytrąciło układ z tego stanu.
Rys. 15.7 – Zamknięty układ liniowy
Zamknięty układ liniowy będziemy uważad za stabilny jeśli przy każdej skooczonej wartości
x(t) i dla dowolnych warunków początkowych sygnał wejściowy y(t) będzie dążył do skooczonej
wartości ustalonej, do czasu t dążącego do nieskooczoności.
Rys. 15.8 – Układ stabilny (po lewej stronie); układ niestabilny (po prawej)
Ogólny warunek stabilności
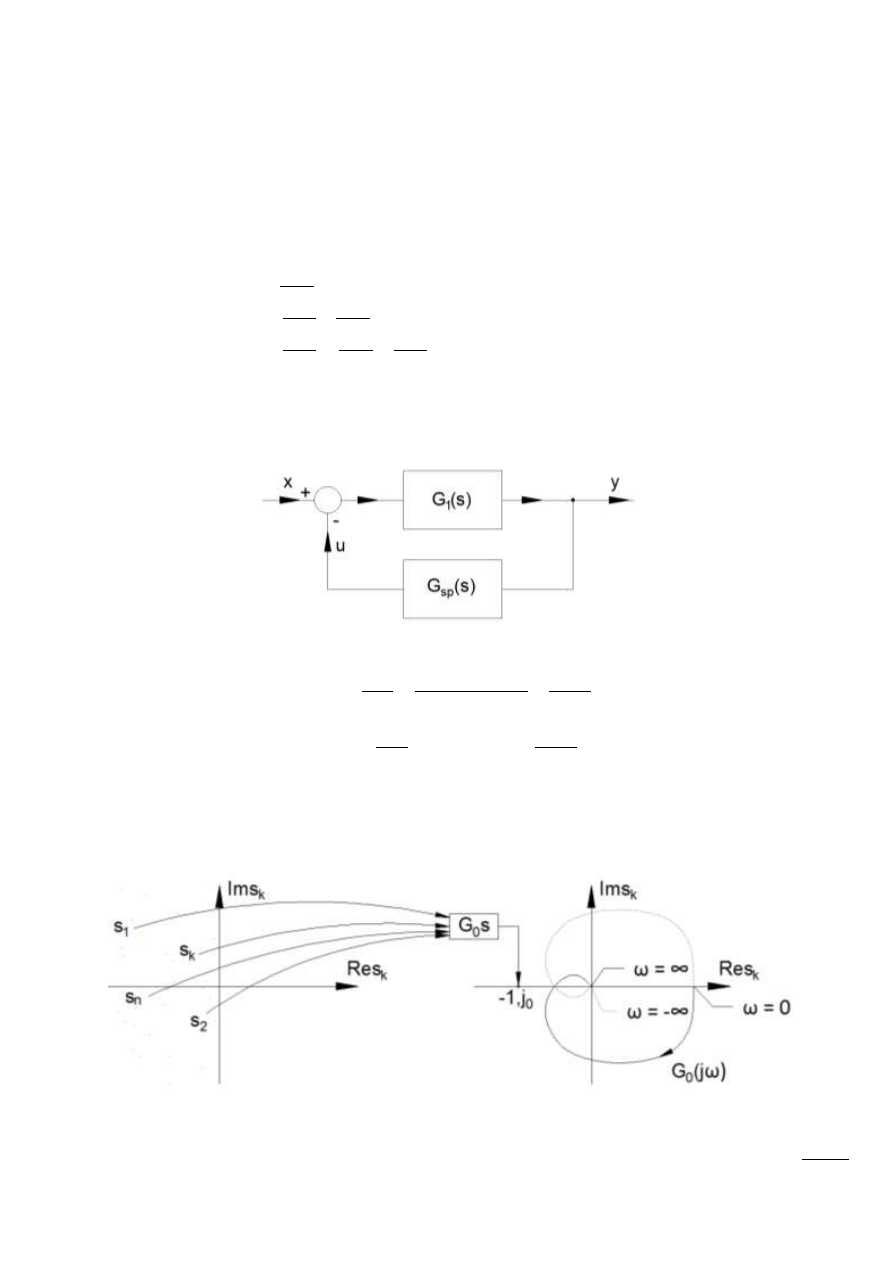
Ro
zd
ział:
Wy
kł
ad
1
5
. –
Sch
em
aty
bl
o
ko
w
e,
regu
lat
o
ry
, st
ab
iln
o
śd
94
Kryterium Hurwitza
Warunki:
1.
2.
Gdzie jest wyznacznikiem macierzy powstałej wg powyższego wzoru (i = n -2).
Kryterium Nyquista
Rys.15.9 – Układ ze sprzężeniem zwrotnym
Rys.15.10 – Odwzorowanie płaszczyzny Ims
k
(Res
k
)

Ro
zd
ział:
Wy
kł
ad
1
5
. –
Sch
em
aty
bl
o
ko
w
e,
regu
lat
o
ry
, st
ab
iln
o
śd
95
Jeżeli w obszarze ograniczonym krzywą
nie znajduje się punkt –j oznacza to, że
równanie nie ma pierwiastków o częściach rzeczywistych dodatnich. Jeśli układ otwarty jest stabilny i
punkt krytyczny (-1, j
0
) znajduje się na zewnątrz charakterystyki częstotliwościowej układu
otwartego, to układ ten będzie stabilny również po zamknięciu.
Document Outline
- Wykład 1. – Wprowadzenie do teorii maszyn
- Wykład 2. – Wzory strukturalne, kinematyka mechanizmów i maszyn
- Wykład 3. – Plany prędkości i przyspieszeń
- Wykład 4. – Metody analityczne prędkości i przyspieszeń
- Wykład 5. – Mechanizmy krzywkowe
- Wykład 6. – Analiza i synteza mechanizmów krzywkowych
- Wykład 7. – Dynamika mechanizmów i maszyn
- Wykład 8. – Grupy
- Wykład 9. – Dynamika maszyn
- Wykład 10. – Nierównomierność biegu maszyny, wprowadzenie do automatyki
- Wykład 11. – Właściwości elementów automatyki
- Wykład 12. – Badanie zachowania układów automatyki
- Wykład 13. – Zachowanie elementów automatyki
- Wykład 14. – Zachowanie elementów automatyki c.d.
- Wykład 15. – Schematy blokowe, regulatory, stabilność
Wyszukiwarka
Podobne podstrony:
Podstawowe zależności z teorii maszyn indukcyjnych
Maszyny wyk ad 4, Technologia żywności i żywienia człowieka, Maszynoznawstwo
Maszynoznastwo wyk ad 3, Technologia żywności i żywienia człowieka, Maszynoznawstwo
Podstawowe zależności z teorii maszyn indukcyjnych
WYK AD 13- 25-26-ZLN1-ZLN2 WSB w Gda sku-Podstawy zarz dzania-JB.x, PODSTAWY ZARZĄDZANIA
Wyk ad 8 sciaga, Studia - Automatyka, Przetwarzanie równoległe i rozproszone, egzamin, ściąga
Zagadnienia do wyk adu, PWr W9 Energetyka stopień inż, III Semestr, Podstawy automatyki
wyk ad VIII - tablica 1, Zarządzanie WSB Poznań (licencjat), II semestr, Podstawy finansów - dr Jani
Interpolacja, Automatyka i Robotyka, Semestr I, Podstawy Sterowania Robotów i Maszyn, Podstawy stero
robocik, Automatyka i Robotyka, Semestr I, Podstawy Sterowania Robotów i Maszyn, Projekt2
Podstawy Sterowania Robotów i Manipulatorów, Automatyka, Podstawy sterowania robotów i maszyn
PODSTAWY STEROWANIA ROBOTÓW I MASZYN, Automatyka, Podstawy sterowania robotów i maszyn, mój projekt
6 1 PodTel wyk ad Podstawy Mod Nieznany (2)
Wyk ad 1 sciaga, Studia - Automatyka, Przetwarzanie równoległe i rozproszone, egzamin, ściąga
Wyk ad 4 sciĄga, Studia - Automatyka, Przetwarzanie równoległe i rozproszone, egzamin, ściąga
Wyk ad 5 sciĄga, Studia - Automatyka, Przetwarzanie równoległe i rozproszone, egzamin, ściąga
wyk ad VIII - tablica 2, Podstawy finansów - dr Janina Kotlińska
więcej podobnych podstron