Podstawy sterowania robotów i maszyn

Temat : Zadanie odwrotne

Jakub Pędzik

Gr III

AiR III sem VI

Wstęp

Opierając się na zadaniu transformacji odwrotnej można stwierdzić, że jeżeli mamy macierz transformacji prostej manipulatora w postaci ogólnej określonej dla wszystkich n jego członów w postaci T_0i jak również mamy macierze transponowane wyznaczone dla poszczególnych ogniw manipulatora T ^-1_i , to idąc od kiści manipulatora - ogniwa n, mnożąc macierz To, kolejno przez macierz transponowaną ogniw n, n-1 n-2,... .,l uzyskamy model kinematyki odwrotnej danego manipulatora w postaci

co oznacza ,że dla wybranego i-tego ogniwa manipulatora mamy

Zadanie.

Wyznaczamy współrzędne konfiguracyjne;

Y₃

Y₂ L2

L3

X₂ X₃

P

L1

Z₁

Y₀

Z₀

X₀

X₁ Y₁

Rys.1. Schemat łańcucha kinematycznego manipulatora.

Dane:

L₁=0.9 [m]

L₂=0,6 [m]

L₃=0,3 [m]

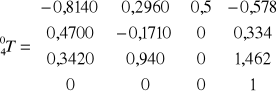
Macierze przekształceń:

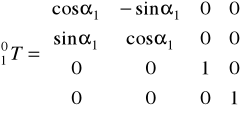
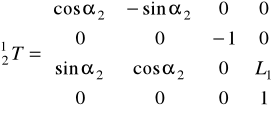
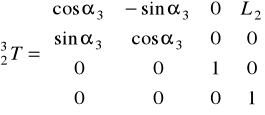
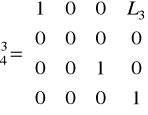
W celu wyznaczenia kątów
,
i
dokonujemy przekształcenia.

gdzie:

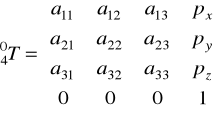
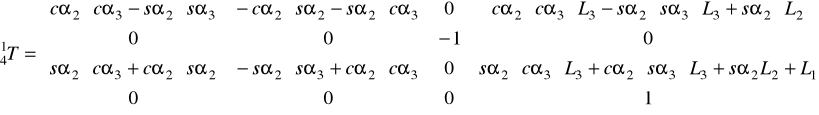
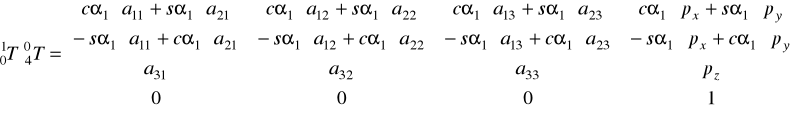
Porównując elementy z macierzy
i
obliczamy kąty
,
i
.

gdzie:

Po podstawieniu otrzymujemy:

Stosując wzór na różnicę kątów, otrzymujemy:

Ostatecznie rozwiązanie na
można być zapisane jako:

Uwzględniając położenie punktu P na podstawie danych wejściowych (-p_x,p_y) , kąt
jest równy:

Rozwiązując układ równań:

obliczamy kąt
:

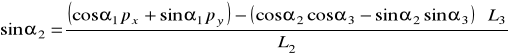
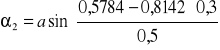
Kąt
obliczamy stosując wzór na sumę kątów:

Podstawiając do równania:

dane:

otrzymujemy:

Wyniki:

2

---