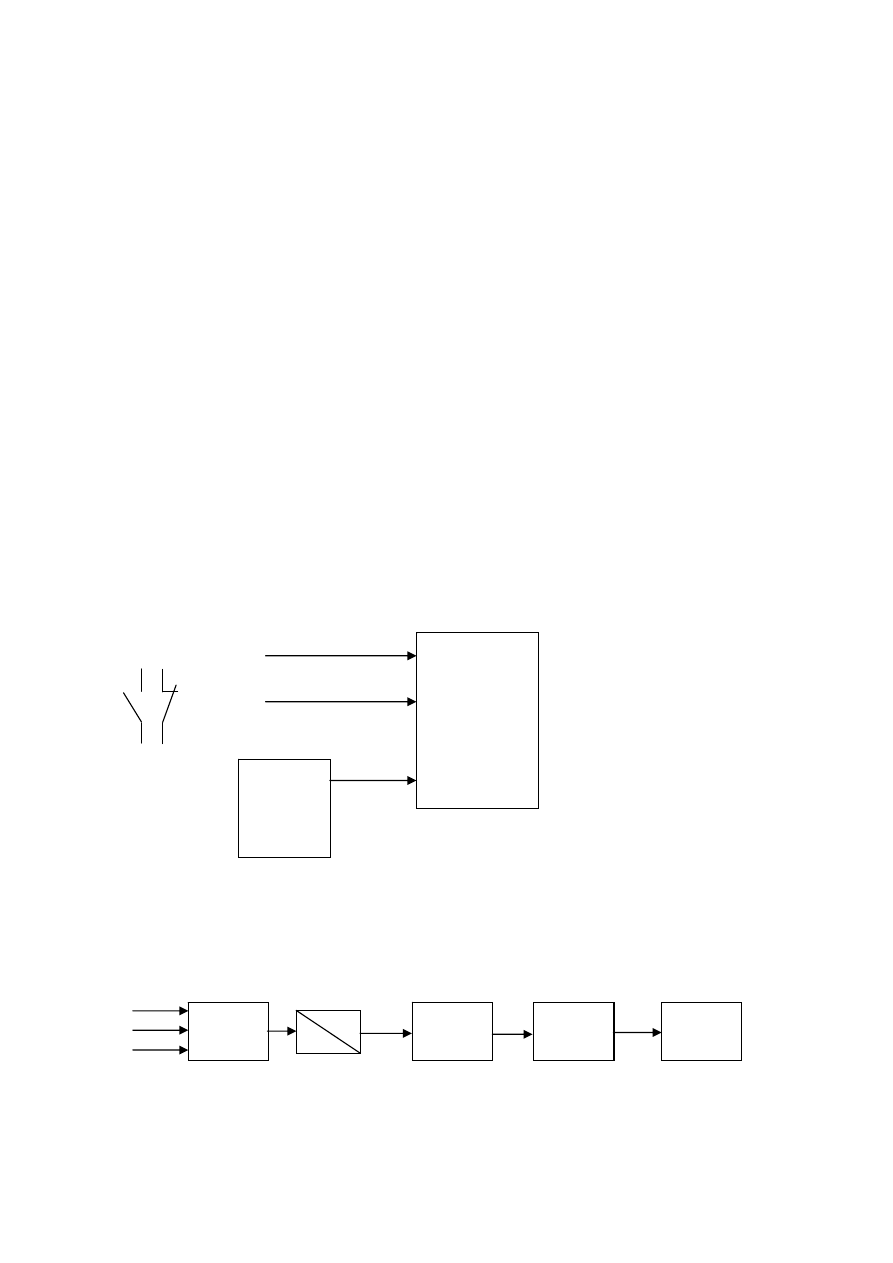
10. Zabezpieczenia cyfrowe

Początek: lata

70-te

Korzyści:

•

Możliwość łatwego komunikowania się między urządzeniami, zmniejszenie ilości

połączeń kablowych

•

Łatwość przechowywania dużych zasobów informacji

•

Możliwość realizacji złożonych algorytmów działania zabezpieczeń

•

Możliwość samotestowania urządzeń

•

Zredukowanie kosztu zabezpieczeń

Typy architektury zabezpieczeń cyfrowych:

•

Rozproszone urządzenia cyfrowe

•

Układy zintegrowane

Źródła informacji zabezpieczeń cyfrowych:

(I, U) sygnały analogowe

sygnały dwustanowe

z.c.

z.c.

Dyskretyzacja sygnałów analogowych

Sygnały

analogowe

Wstępne

Filtracja

Pomiary

Logika

A

C

Przetwarzanie

analogowa

cyfrowe

i decyzja

cyfrowe

1

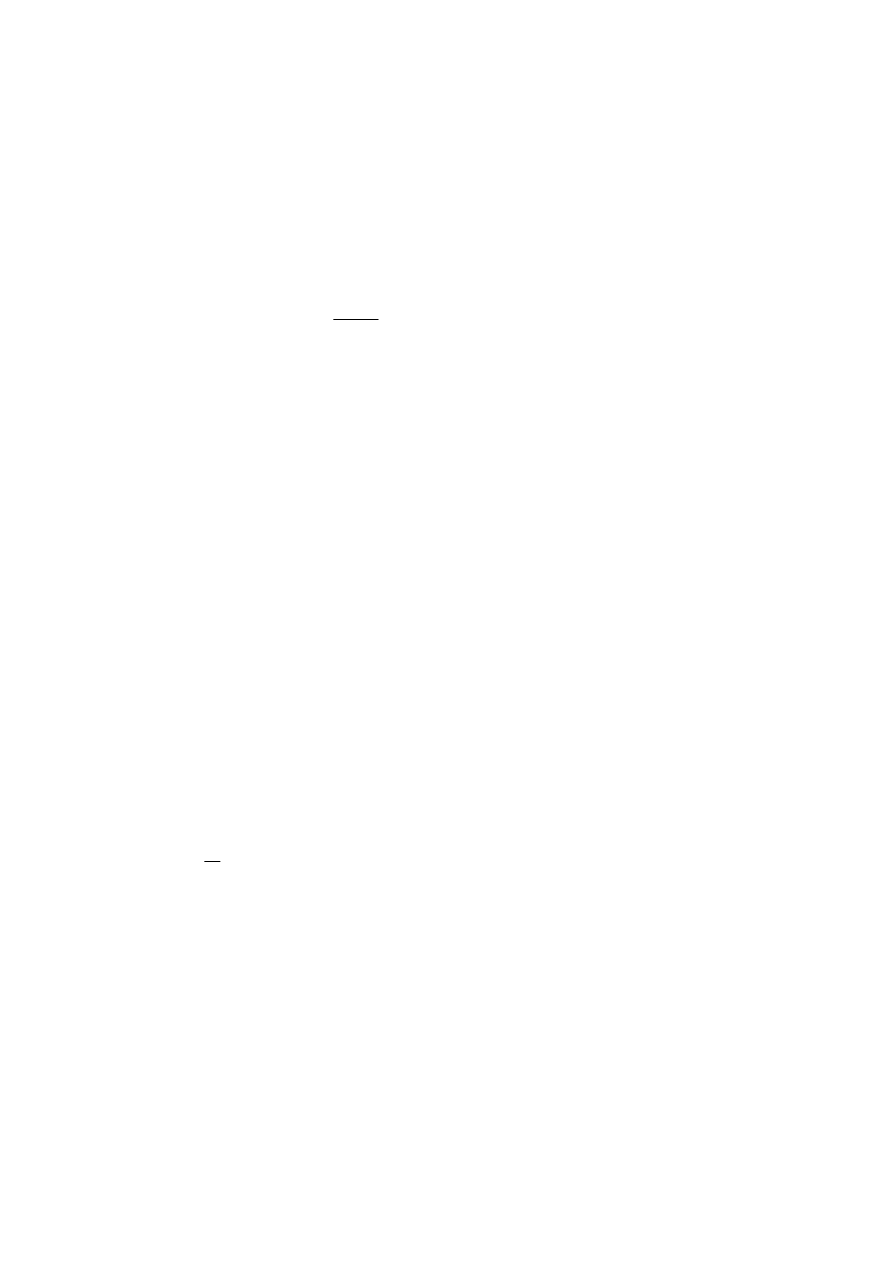
Filtracja analogowa - filtr analogowy dolnoprzepustowy, odfiltrowanie wyższych

częstotliwości zbędnych w dalszym procesie obróbki sygnału

Filtr A/C -

fi - częstotliwość próbkowania

fp

4

fi

⋅

≥

fp - częstotliwość sygnału przydatnego do dalszej obróbki

3

fp

fi

fc

fp

−

<

<

fc - częstotliwość odcięcia filtru

dolnoprzepustowego

Przetwornik próbkuje sygnał z częstotliwością fi zamieniając każdą z próbek na słowo

o długości m bitów (plus bit znaku).

Liczba dyskretnych stanów (przedziałów) odwzorowana słowem m-bitowym.

1

m

2

N

−

=

np. m=3 - długość słowa

7

1

3

2

N

=

−

=

0 0 0

0 0 1

0 1 0

0 1 1

1 0 0

1 0 1

1 1 0

1 1 1

N

Z

DZ

=

DZ - różnica wartości sygnału analogowego między dwoma sąsiednimi poziomami

cyfrowymi,

N - maksymalny zakres cyfrowy,

Z - maksymalny zakres analogowy

Pomiar: (Xmin, Xmax)

Xmin, Xmax - najmniejsza i największa spodziewana wartość sygnału analogowego

ε - wymagany względny poziom dokładności pomiaru sygnału analogowego

2

⎪

⎪

⎪

⎩

⎪⎪

⎪

⎨

⎧

⋅

ε

⋅

≥

⋅

≥

ε

≥

min

X

max

X

5

.

0

N

min

X

DZ

5

.

0

max

X

Z

Na podstawie obliczonego N oblicza się długość słowa przetwornika pomiarowego

Przykład:

Xmin = 1 V;

Xmax = 150 V,

ε = 0.01 (1%)

)

8192

13

2

(

;

13

m

;

7500

1

01

.

0

150

5

.

0

N

=

=

=

⋅

⋅

≥

Wstępne przetwarzanie cyfrowe

• Filtracja cyfrowa - wydobycie z sygnału mierzonego składowych o określonej

częstotliwości lub składowej symetrycznej

• Ortogonalizacja przebiegów sinusoidalnych - wyznaczenie składowych ortogonalnych -

amplitudy i fazy

Cyfrowa filtracja częstotliwościowa

• Filtry o nieskończonej odpowiedzi impulsowej (NOI), (IIR - infinite impulse response) -

filtry rekursywne

• Filtry o skończonej odpowiedzi impulsowej (SOI) - (FIR - finite impulse response) -

filtry nierekursywne

• Filtry Kalmana

3

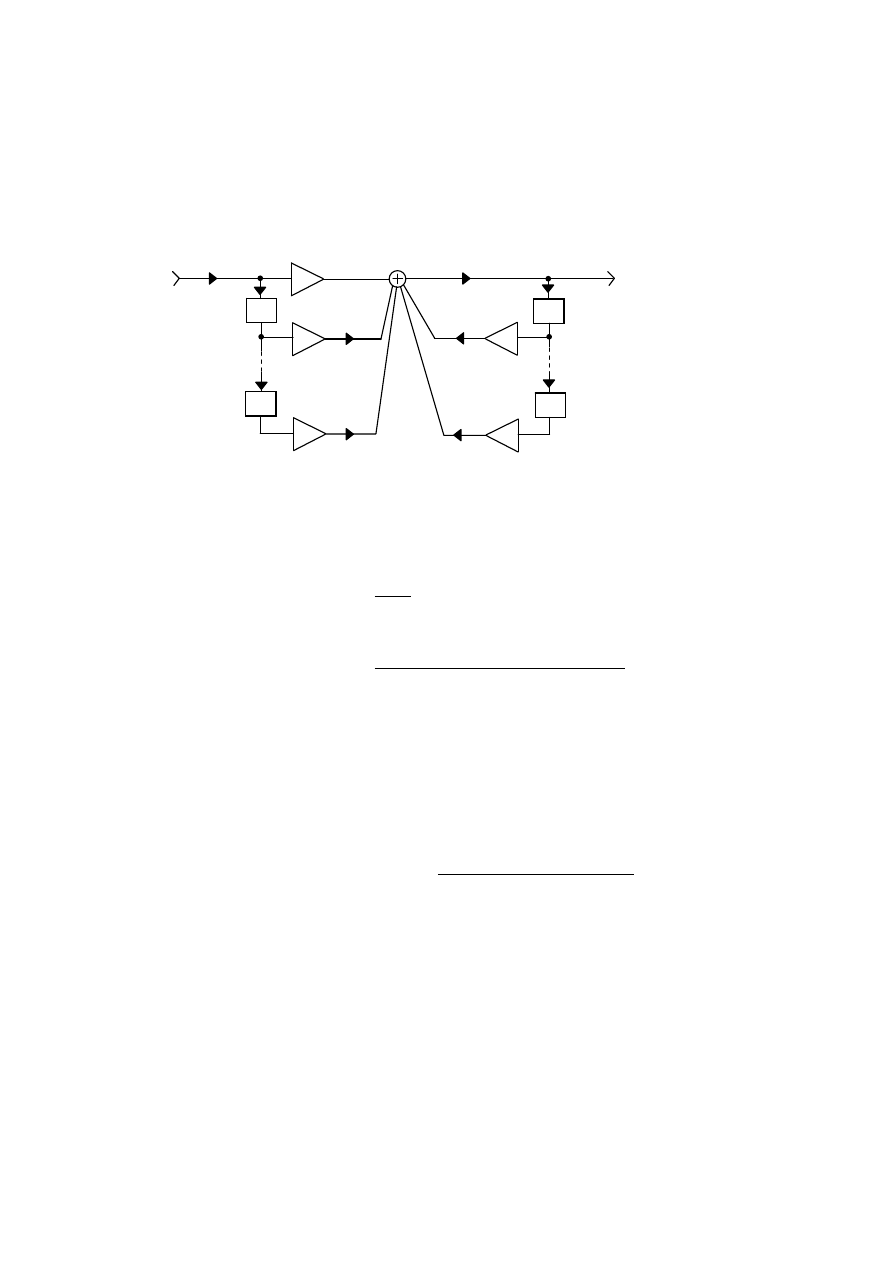
Filtr NOI

Reakcja na pobudzenie o skończonym czasie trwania jest (teoretycznie) nieskończenie długa

Z

-1

Z

-1

Z

-1

Z

-1

WEJ

WYJ

b

0

-a

q

-a

0

b

p

b

1

a

k

, b

k

> 0 - współczynniki wzmocnienia

Algorytm filtru NOI

Transmitancja filtru

)

z

(

X

)

z

(

Y

)

z

(

H

=

przy czym;

)

q

z

q

a

.........

1

z

1

a

0

a

(

1

p

z

p

b

.........

1

z

1

b

0

b

)

z

(

H

−

⋅

+

+

−

⋅

+

+

−

⋅

+

+

−

⋅

+

=

z -

wartość próbki

z

-k

-

opóźnienie próbki o k okresów próbkowania (czas: k

⋅Ti)

Przez dobór współczynników a

k

i b

k

można uzyskać filtr dolnoprzepustowy lub pasmowy.

Charakterystyka widmowa:

∑

∑

=

⋅

ω

⋅

⋅

−

⋅

+

=

⋅

ω

⋅

⋅

−

⋅

=

ω

q

0

k

)

i

T

k

j

exp(

k

a

1

p

0

k

)

i

T

k

j

exp(

k

b

)

j

(

H

T

i

- okres próbkowania

4

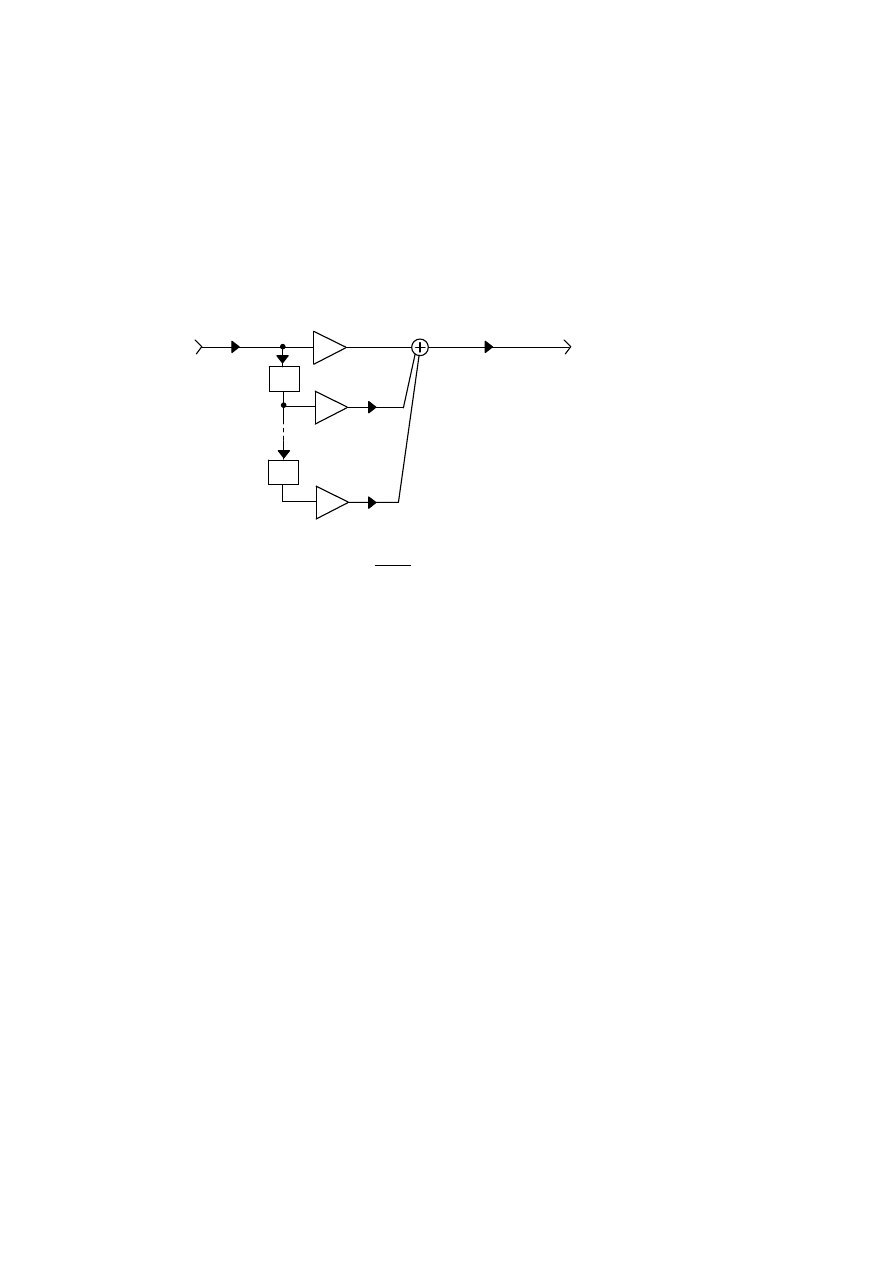
Filtr SOI

Reakcja na pobudzenie o skończonym czasie trwania jest skończona

Z

-1

Z

-1

WEJ

b

0

b

WYJ

p

b

1

Transmitancja filtru

)

z

(

X

)

z

(

Y

)

z

(

H

=

przy czym;

p

z

p

b

.........

1

z

1

b

0

b

)

z

(

H

−

⋅

+

+

−

⋅

+

=

z -

wartość próbki

z

-k

-

opóźnienie próbki o k okresów próbkowania (czas: k

⋅Ti)

Charakterystyka widmowa:

∑

=

⋅

ω

⋅

⋅

−

⋅

=

ω

p

0

k

)

i

T

k

j

exp(

k

b

)

j

(

H

T

i

- okres próbkowania

Dla filtrów SOI wprowadza się pojęcie okna filtru, którego długość odpowiada (n+1)

próbkom. Długość okna

i

T

)

1

n

(

w

T

⋅

+

=

. Kształt okna jest obwiednią

współczynników wagowych b

k

.

Przykłady okien i odpowiadających im widm:

5

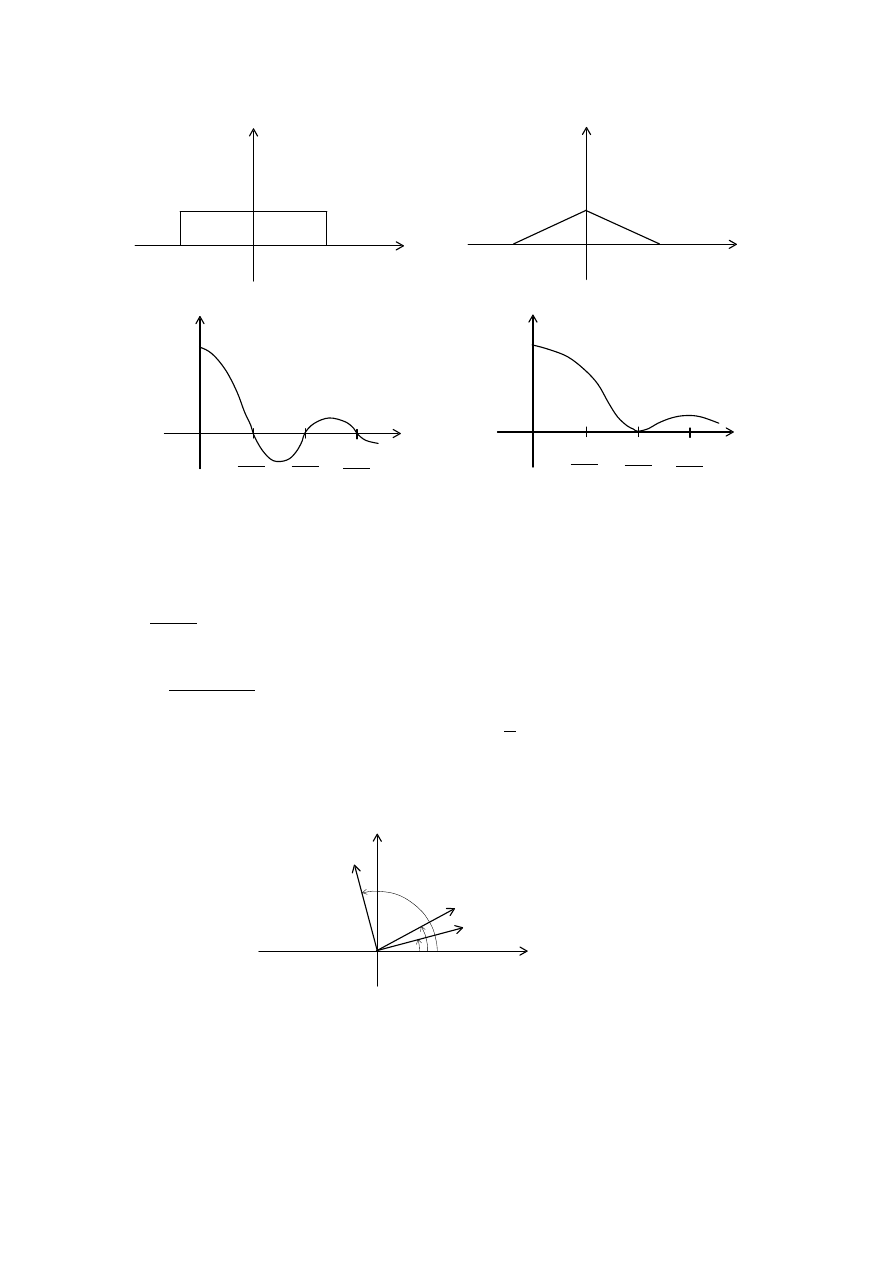
Ortogonalizacja sygnałów sinusoidalnych

Dany sygnał:

)

t

1

cos(

1

I

)

t

(

i

β

+

⋅

ω

⋅

=

Funkcje ortogonalne:

)

t

1

cos(

1

I

)

t

(

d

i

α

+

⋅

ω

⋅

=

)

t

1

sin(

1

I

)

2

t

1

cos(

1

I

)

t

(

q

i

α

+

⋅

ω

⋅

=

π

−

α

+

⋅

ω

⋅

=

α - dowolny kąt

h

t

0

-T

w

/2

T

w

/2

H

ω

w

T

2

π

w

T

4

π

w

T

6

π

h

t

0

-T

w

/2

T

w

/2

H

ω

w

T

2

π

w

T

4

π

w

T

6

π

i

d

β

i

α

i

q

α-π/2

6

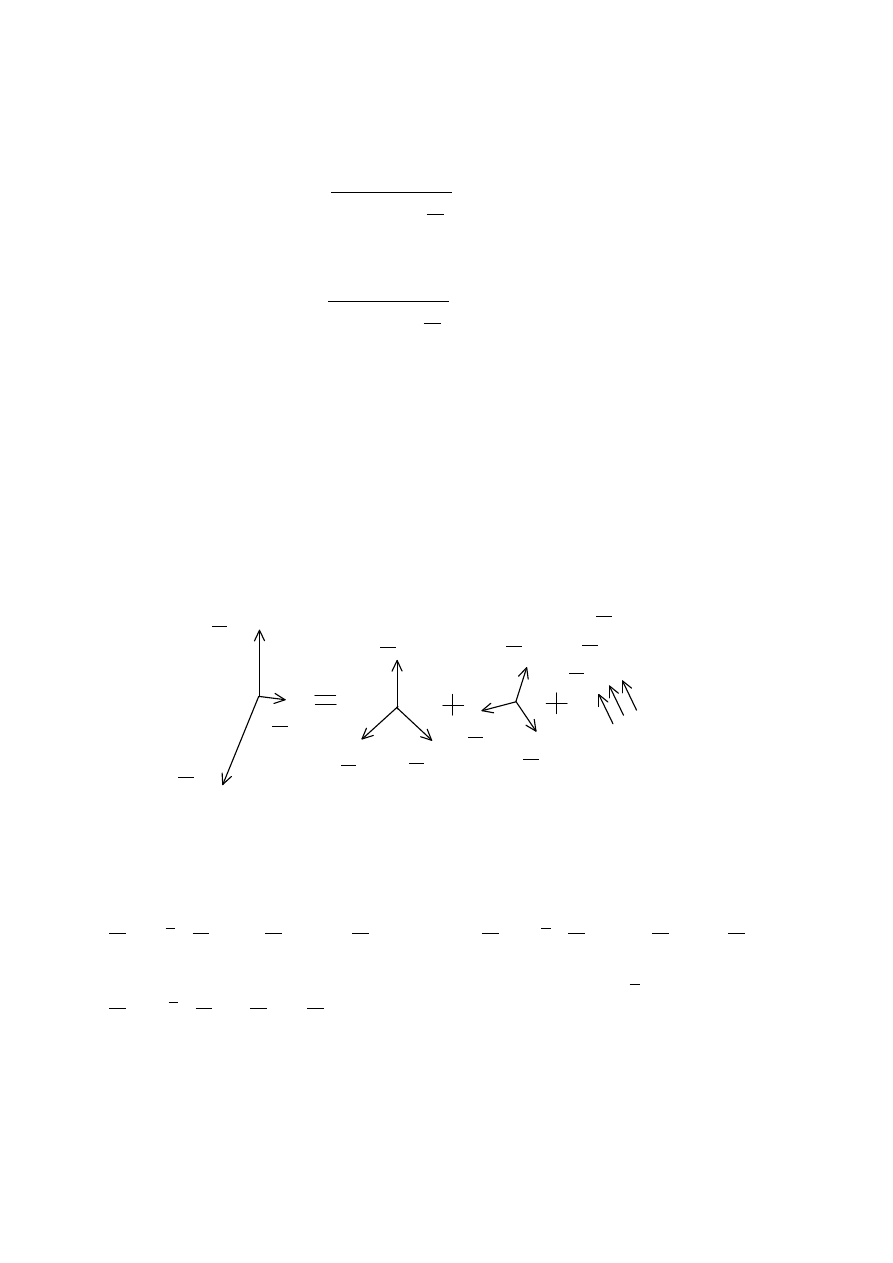
Dyskretne składowe ortogonalne

)

2

i

T

1

h

cos(

2

)

h

n

(

i

)

n

(

i

)

i

T

1

n

cos(

1

I

)

n

(

d

i

⋅

ω

⋅

⋅

−

+

=

α

+

⋅

ω

⋅

⋅

=

)

2

i

T

1

h

cos(

2

)

h

n

(

i

)

n

(

i

)

i

T

1

n

sin(

1

I

)

n

(

q

i

⋅

ω

⋅

⋅

−

−

=

α

+

⋅

ω

⋅

⋅

=

n - kolejna próbka sygnału

h - liczba próbek opóźnienia sygnału

T

i

- okres próbkowania

Filtracja składowych symetrycznych

Metoda składowych symetrycznych

Ilustracja

rozkładu niesymetrycznej gwiazdy wielkości fazowych na sumę trzech

układów symetrycznych: kolejności zgodnej, przeciwnej i zerowej

)

3

L

W

2

a

2

L

W

a

1

L

W

(

3

1

)

1

(

1

L

W

⋅

+

⋅

+

⋅

=

;

)

3

L

W

a

2

L

W

2

a

1

L

W

(

3

1

)

2

(

1

L

W

⋅

+

⋅

+

⋅

=

)

3

L

W

2

L

W

1

L

W

(

3

1

)

0

(

1

L

W

+

+

⋅

=

;

π

= 3

2

j

e

a

W

L1

W

L2

W

L3

W

L1

(1

)

W

L2

(1)

W

L3

(1

)

W

L1

(2)

W

L2

(2)

W

L3

(2

)

W

L1

(0)

W

L2

(0)

W

L3

(0)

7

Def.

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

⋅

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

⋅

=

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

3

L

I

2

L

I

1

L

I

a

2

a

1

2

a

a

1

1

1

1

3

1

)

2

(

I

)

1

(

I

)

0

(

I

;

)

3

2

j

exp(

a

π

⋅

=

Realizacja na próbkach (sposób naturalny):

)

n

(

3

L

i

)

n

(

2

L

i

)

n

(

1

L

i

)

n

(

)

0

(

i

3

+

+

=

⋅

)

3

m

n

(

3

L

i

)

3

m

2

n

(

2

L

i

)

n

(

1

L

i

)

n

(

)

1

(

i

3

−

+

⋅

−

+

=

⋅

)

3

m

2

n

(

3

L

i

)

3

m

n

(

2

L

i

)

n

(

1

L

i

)

n

(

)

2

(

i

3

⋅

−

+

−

+

=

⋅

m - liczba próbek w jednym oknie sinusoidy

Realizacja na próbkach (korzystanie z sygnałów zortogonalizowanych)

)

n

(

d

3

L

i

)

n

(

d

2

L

i

)

n

(

d

1

L

i

)

n

(

)

0

(

i

3

+

+

=

⋅

)

n

(

q

3

L

i

2

3

)

n

(

d

3

L

i

2

1

)

n

(

q

2

L

i

2

3

)

n

(

d

2

L

i

2

1

)

n

(

d

1

L

i

)

n

(

)

1

(

i

3

⋅

+

⋅

−

⋅

−

⋅

+

=

⋅

)

n

(

q

3

L

i

2

3

)

n

(

d

3

L

i

2

1

)

n

(

q

2

L

i

2

3

)

n

(

d

2

L

i

2

1

)

n

(

d

1

L

i

)

n

(

)

2

(

i

3

⋅

−

⋅

−

⋅

−

⋅

−

=

⋅

gdzie: i

L1d

, i

L2d

, i

L3d

, i

L1q

, i

L2q

, i

L3q

- składowe ortogonalne d i q prądów fazowych i

L1

, i

L2

, i

L3

.

Pomiar amplitudy

2

q

i

2

d

i

)

n

(

1

I

+

=

lub

)

h

i

T

1

sin(

)

h

n

(

q

i

)

n

(

d

i

)

n

(

q

i

)

h

n

(

d

i

)

n

(

1

I

⋅

⋅

ω

−

⋅

−

⋅

−

=

8

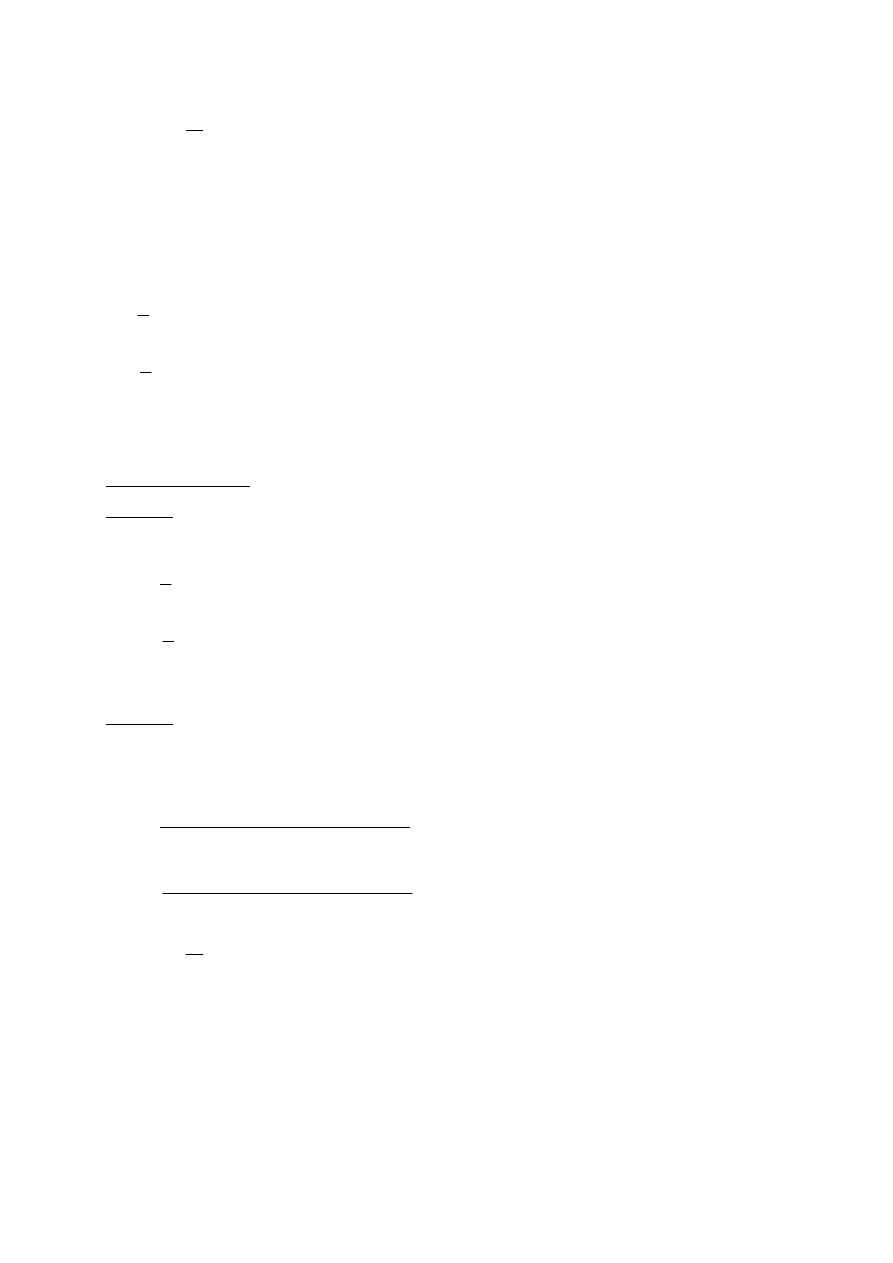
gdzie:

i

T

1

t

h

=

;

y

1

- dowolne opóźnienie sygnału ortogonalnego

Pomiar mocy czynnej i biernej

Def.:

ϕ

⋅

⋅

⋅

=

cos

1

I

1

U

2

1

P

moc

czynna

ϕ

⋅

⋅

⋅

=

sin

1

I

1

U

2

1

Q

moc

bierna

U

1

, I

1

- amplitudy podstawowych harmonicznych

Realizacja cyfrowa:

Sposób 1

Wykorzystanie składowych ortogonalnych podstawowej harmonicznej prądu i napięcia

)]

n

(

q

i

)

n

(

q

u

)

n

(

d

i

)

n

(

d

u

[

2

1

)

n

(

P

⋅

+

⋅

=

)]

n

(

q

i

)

n

(

d

u

)

n

(

d

i

)

n

(

q

u

[

2

1

)

n

(

Q

⋅

−

⋅

=

Sposób 2

Wykorzystanie składowych ortogonalnych bieżących i opóźnionych podstawowej

harmonicznej prądu i napięcia

)

h

i

T

1

sin(

2

)

h

n

(

q

i

)

n

(

d

u

)

n

(

q

i

)

h

n

(

d

u

)

n

(

P

⋅

⋅

ω

⋅

−

⋅

−

⋅

−

=

)

h

i

T

1

sin(

2

)

n

(

q

i

)

h

n

(

d

u

)

h

n

(

d

i

)

n

(

d

u

)

n

(

Q

⋅

⋅

ω

⋅

⋅

−

−

−

⋅

=

gdzie:

i

T

1

t

h

=

;

t

1

- dowolne opóźnienie

Istnieje wiele algorytmów obliczania mocy czynnej i biernej. Istotne są dwie ważne cechy:

- Odporność na zniekształcenie sygnałów (wyższe harmoniczne, odchylenie od częstotliwości

sieciowej),

9

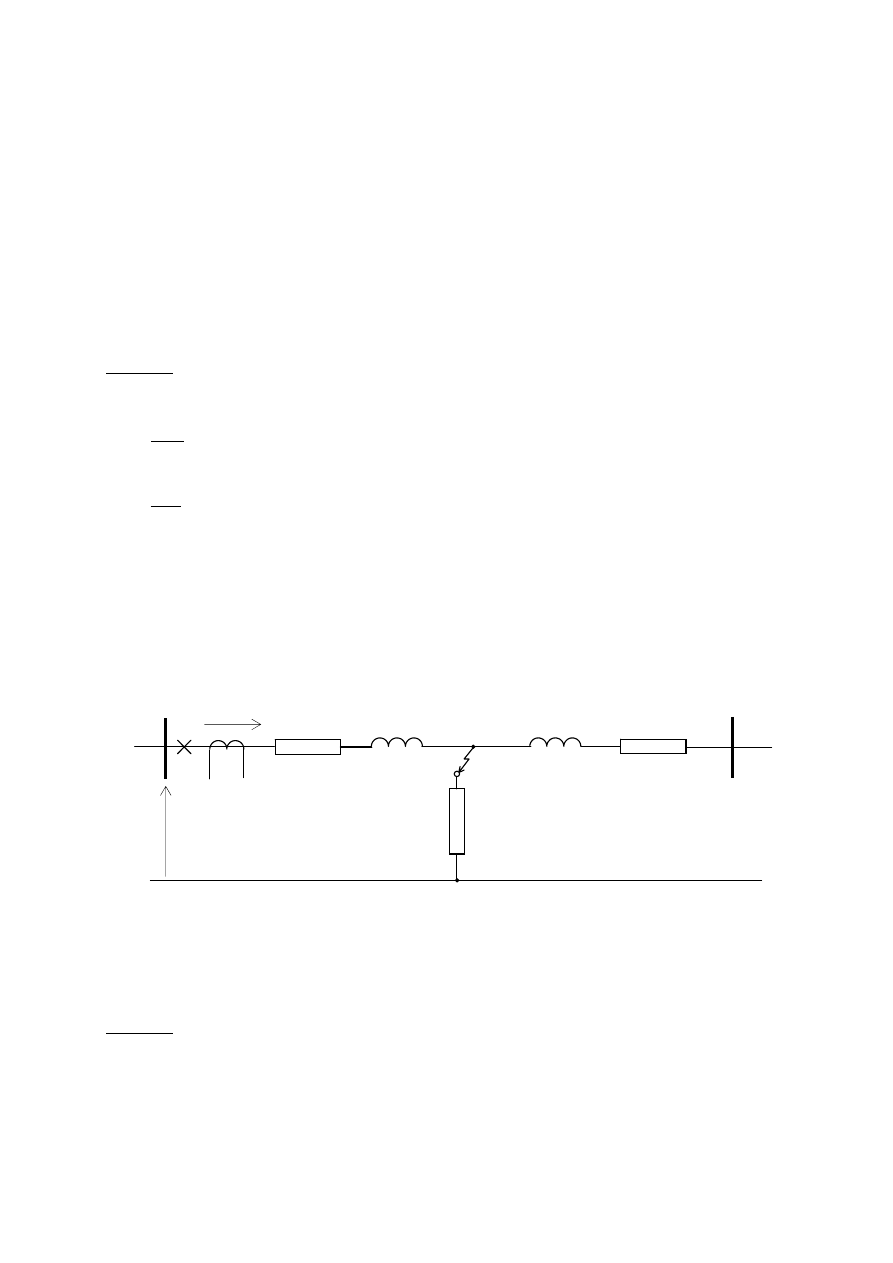
- Szybkość ustalania się wyniku pomiaru przy nagłej zmianie wartości sygnału (np. po

zwarciu).

Pomiar rezystancji i reaktancji do miejsca zwarcia

Pomiar rezystancji i reaktancji do miejsca zwarcia w układzie przedstawionym na

rysunku można zrealizować wg zależności:

Sposób 1

2

1

I

Q

2

z

X

⋅

=

2

1

I

P

2

z

R

⋅

=

gdzie: Q i P - fazowe moce czynne i bierne przesyłane od miejsca pomiaru w kierunku

uszkodzenia

I

1

- amplituda prądu płynącego przez uszkodzoną linię.

i

R

z

X

z

X

l

-X

z

R

l

-R

z

R

K

K

u

Rezystancja

przejścia R

K

wprowadza zafałszowanie pomiaru. Także zasilanie

dwustronne miejsca zwarcia wprowadza zafałszowanie.

Sposób 2

Układ jak na rysunku można opisać równaniem:

10

z

L

)

t

(

'i

z

R

)

t

(

i

)

t

(

u

⋅

+

⋅

=

gdzie:

- pierwsza pochodna prądu

)

t

(

'i

Zapisując to równanie dla dwóch chwil: t

1

i t

2

otrzymujemy:

z

L

)

1

t

(

'i

z

R

)

1

t

(

i

)

1

t

(

u

⋅

+

⋅

=

z

L

)

2

t

(

'i

z

R

)

2

t

(

i

)

2

t

(

u

⋅

+

⋅

=

i rozwiązując znajdujemy:

1

'i

2

i

2

'i

1

i

1

'i

2

u

2

'i

1

u

)

n

(

z

R

⋅

−

⋅

⋅

−

⋅

=

1

'i

2

i

2

'i

1

i

2

i

1

u

1

i

2

u

)

n

(

z

X

⋅

−

⋅

⋅

−

⋅

=

gdzie:

- wartości określone w chwili ,

1

'i

,

1

i

,

1

u

1

t

- wartości określone w chwili

.

2

'i

,

2

i

,

2

u

2

t

Wartości te określić można z zależności:

2

i

T

1

cos

2

)

1

n

(

u

)

n

(

u

2

u

⋅

ω

⋅

−

+

=

2

i

T

1

cos

2

)

1

n

(

i

)

n

(

i

2

i

⋅

ω

⋅

−

+

=

2

i

T

1

sin

2

)

1

n

(

i

)

n

(

i

2

'i

⋅

ω

⋅

−

−

=

Podobnie

można określić

z tym, że zamiast próbki (n) należy wstawić próbkę

(n-r), przy czym

.

1

'i

,

1

i

,

1

u

i

T

r

1

t

2

t

⋅

=

−

i

R

z

L

z

u

11

12

Opisany algorytm eliminuje wpływ składowej nieokresowej zawartej w sygnałach na

wynik pomiaru.

[1] Winkler W., Wiszniewski A.: Automatyka zabezpieczeniowa w systemach

elektroenergetycznych. WNT. Warszawa, 1999

[2] Wiszniewski A.: Algorytmy pomiarów cyfrowych w automatyce elektroenergetycznej.

WNT. Warszawa, 1990

[3] Szafran J., Wiszniewski A.: Algorytmy pomiarowe i decyzyjne cyfrowej automatyki

elektroenergetycznej. WNT. Warszawa, 2001

[4] Rosołowski E.: Cyfrowe przetwarzanie sygnałów w automatyce elektroenergetycznej.

Akademicka Oficyna Wydawnicza EXIT, Warszawa, 2002