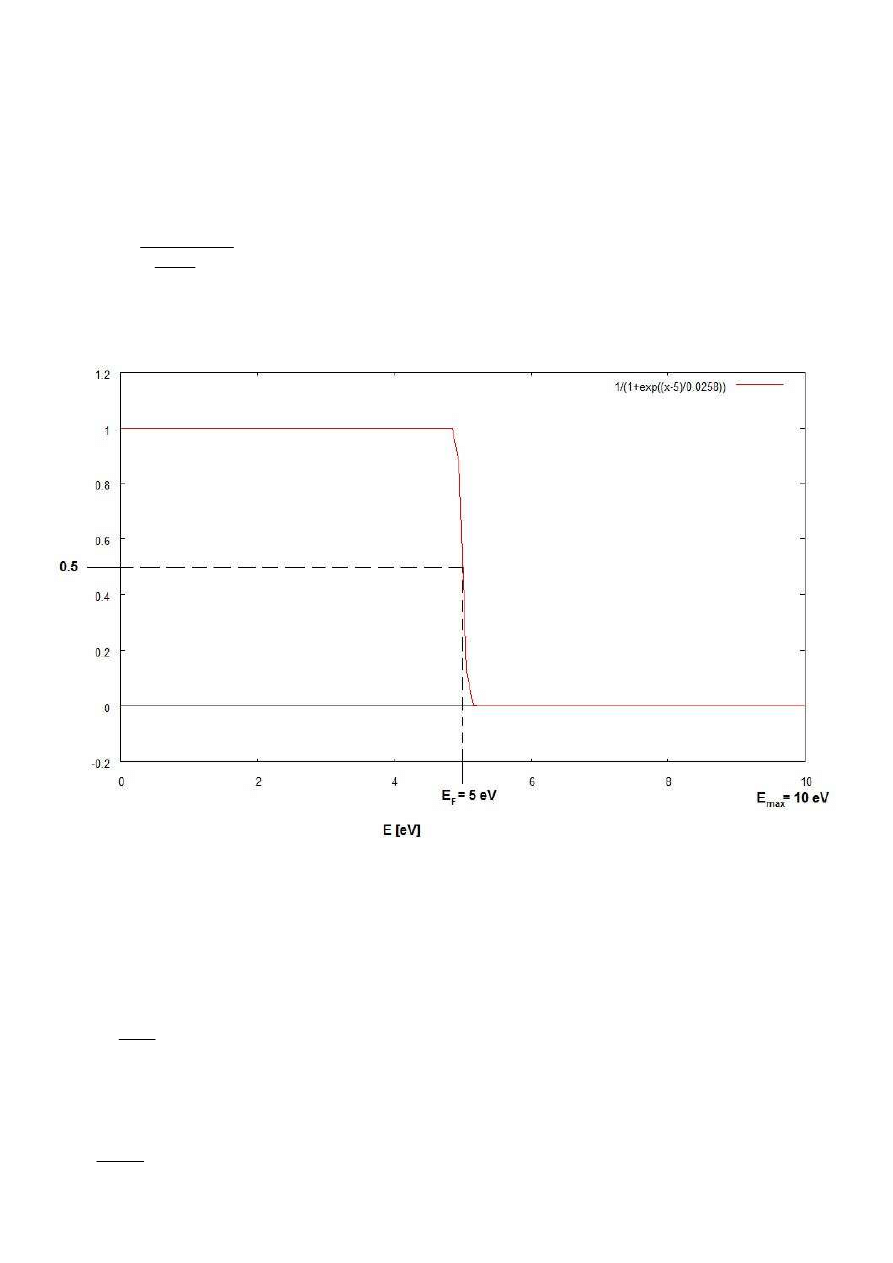
Koncentracja nośników w półprzewodnikach
Prawdopodobieństwem zajmowania danego stanu energetycznego przez fermiony rządzi
statystyka Fermiego-Diraca:
1
1
)
(
+
=
−
kT
E
E
F
e
E
f
, gdzie k jest stałą Boltzmanna, zaś
F
E
to energia Fermiego
Przykładowo, dla metali, w temperaturze ok. 300 K:
W przestrzeni odwrotnej poziom Fermiego tworzy kulę, znajdującą się w środku strefy Brillouina.
Stany poniżej poziomu Fermiego (wewnątrz kuli) są obsadzone, z kolei poza kulą – praktycznie puste. Prąd
jest przewodzony przez elektrony rozmyte na powierzchni kuli – jest ich o dwa rzędy wielkości mniej, niż
wewnątrz, ale i tak nie wszystkie biorą udział w przewodzeniu.
Na sferze o promieniu wyznaczanym przez wektor falowy k gęstość stanów jest jednorodna:
3
4
1
)
(
π
ρ
=
k
Gęstość zależy od energii, a ta jest proporcjonalna do kwadratu wektora falowego:
*
2
2
2
m
k
E
h
=
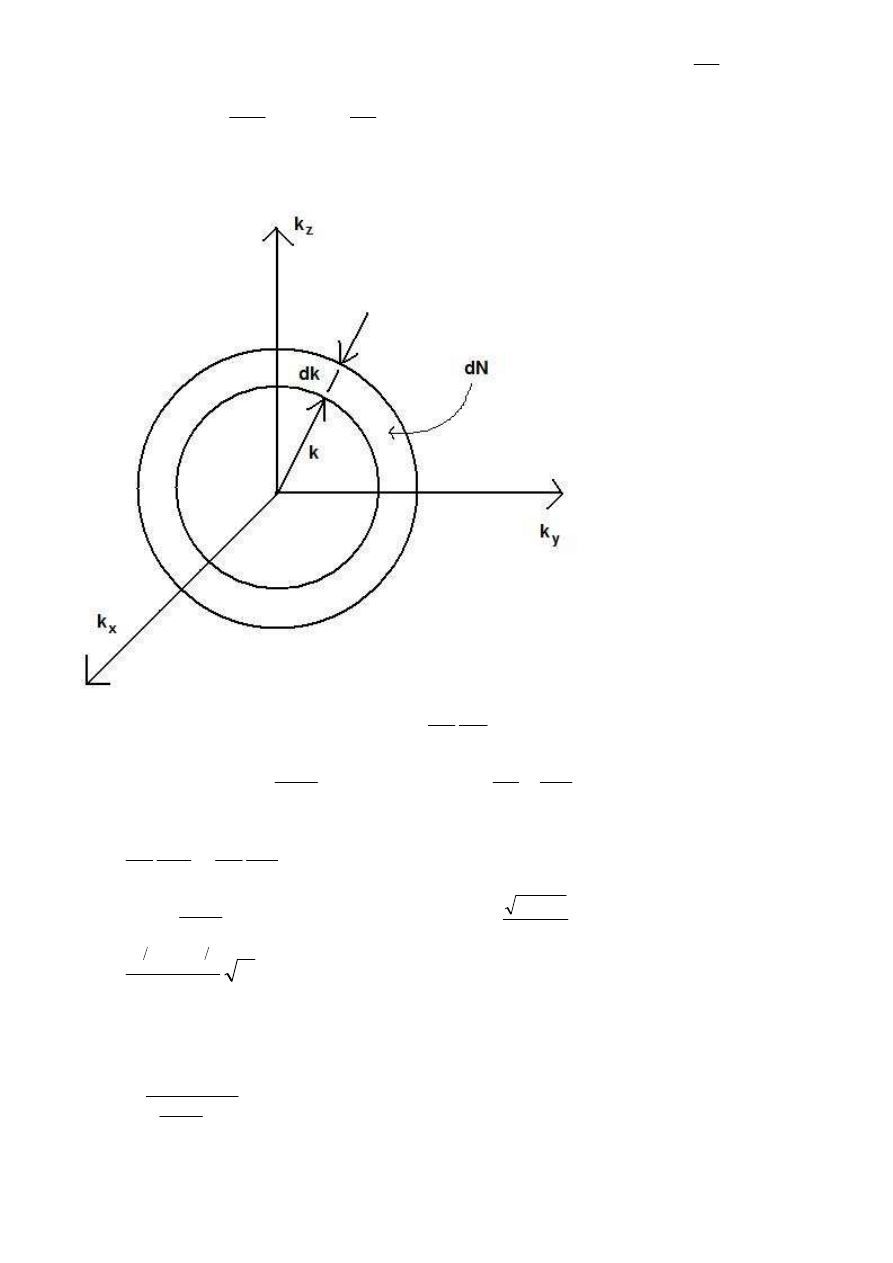
Gęstość nośników możemy wyrazić jako stosunek ich koncentracji do objętości:
dV
dN
k
=
)
(
ρ
stąd:
dk
k
dk
k
dV
k
dN
2
2
2
3
4
4
1
)
(
π
π
π
ρ
=
=
=
Jednocześnie możemy napisać:
dE
E
dN
)
(
ρ
=
Łącząc powyższe równości uzyskujemy:
dE
dk
k
E
2
2
)
(
π
ρ
=
Korzystając z zależności
*
2
2
2
m
k
E
h
=
obliczamy pochodną:
*
2
m
k
dk
dE
h
=
2
2
2
2
2
*
*
)
(
h
h
m
k
k
m
k
E
π
π
ρ
=
=
Z równania
*
2
2
2
m
k
E
h
=
mamy również wyrażenie na k :
h
E
m
k
*
2
=
, które wstawiamy tego powyżej:
E
m
E
3
2
2
3
2
1
*)
(
2
)
(
h
π
ρ
=
- jest to zależność prawdziwa na dnie pasma przewodnictwa, tam, gdzie nośniki przewodzą prąd
Nośnikami ładunku mogą być zrówno elektrony, o rozkładzie:
1
1
)
(
+
=
−
kT
E
E
e
F
e
e
E
f
,
jak i dziury, oznaczające brak elektronu:
e
d
e
d
E
E
E
f
E
f
−
=
→
−
=
)
(
1
)
(
, stąd:
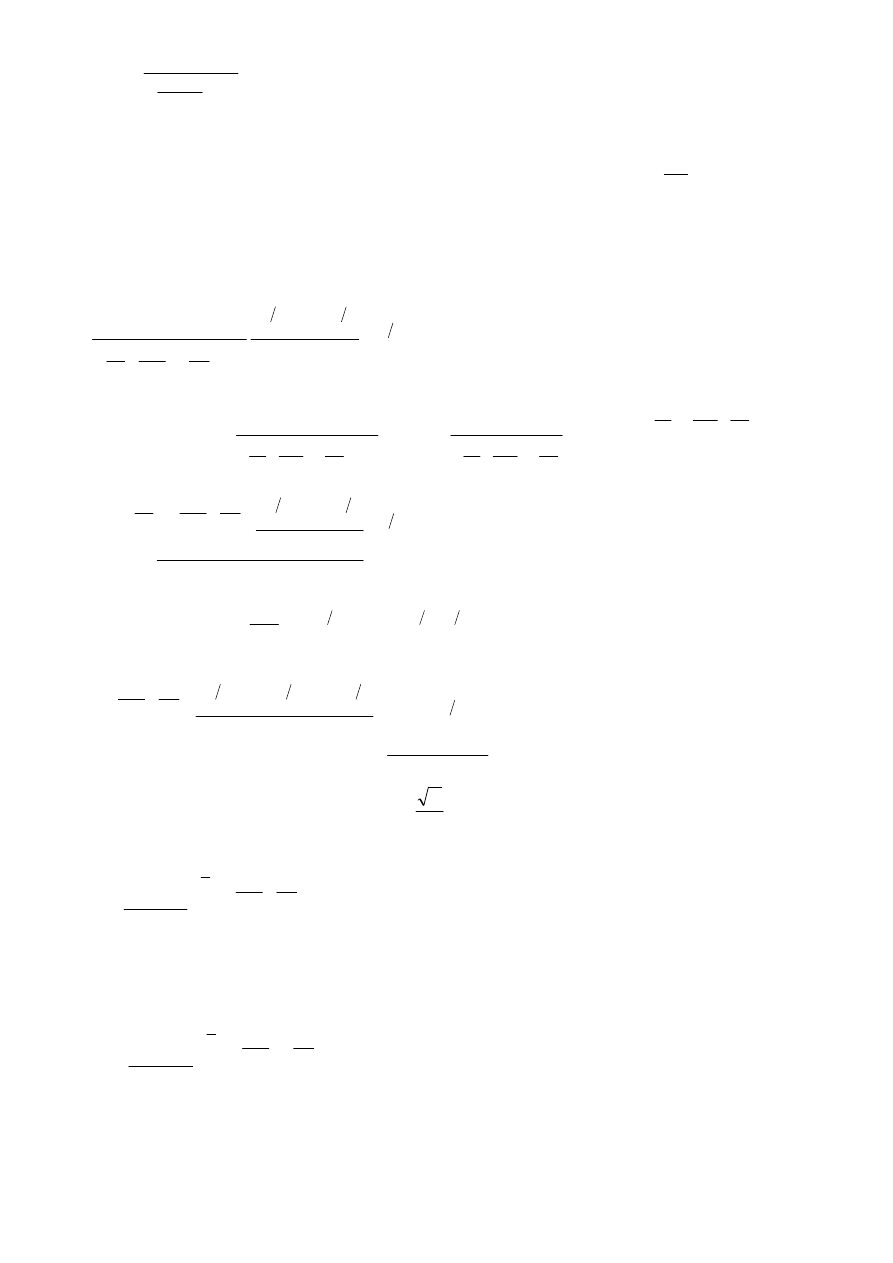
1
1
)
(
+
=
+
kT
E
E
d
F
d
e
E
f
- poziom Fermiego jest taki sam dla elektronów i dziur, znajduje się mniej więcej w połowie przerwy
energetycznej, tam też wybieramy poziom zerowy: przeskalowujemy energię
e
g
e
E
E
E
+
→
2
Koncentracja elektronów w paśmie przewodnictwa – całka po strefie Brillouina:
=
=
=
∫
∫
∞
0
)
(
)
(
)
(
)
(
e
e
e
SB
dE
E
E
f
dE
E
E
f
n
ρ
ρ
∫
∞
−
+
=
0
2
1
3
2
2
3
2
1
2
*)
(
2
1
1
e
e
kT
E
kT
E
kT
E
dE
E
m
e
e
e
F
g
e
h
π
Stosujemy przybliżenie:
kT
E
kT
E
kT
E
kT
E
kT
E
kT
E
kT
E
kT
E
kT
E
F
g
e
F
g
e
F
g
e
e
e
e
e
e
e
e
e
e
2
2
2
1
1
1
−
−
−
−
=
≈
+
∫
∞
−
−
⋅
=
0
2
1
3
2
2
3
2
1
2
*)
(
2
e
e
kT
E
kT
E
kT
E
dE
E
m
e
e
e
n
F
g
e
h
π
= const
Zamiana zmiennych:
kT
E
x
e
=
,
2
1
2
1
2
1
)
(
x
kT
E
e
=
,
dx
kT
dE
e
=
dx
x
e
kT
m
e
e
n
x
kT
E
kT
E
F
g
∫
∞
−
−
⋅
⋅
=
0
2
1
3
2
2
3
2
3
2
1
2
)
(
*)
(
2
h
π
||
2
π
Ostatecznie:
kT
E
kT
E
e
F
g
e
e
kT
m
n
2
2
3
2
*
2
2
−
=
h
π
- koncentracja elektronów w paśmie przewodnictwa
Wykonując analogiczne obliczenia w przypadku dziur otrzymalibyśmy:
kT
E
kT
E
d
F
g
e
e
kT
m
p
−
−
=
2
2
3
2
*
2
2
h
π
- koncentracja dziur w paśmie walencyjnym
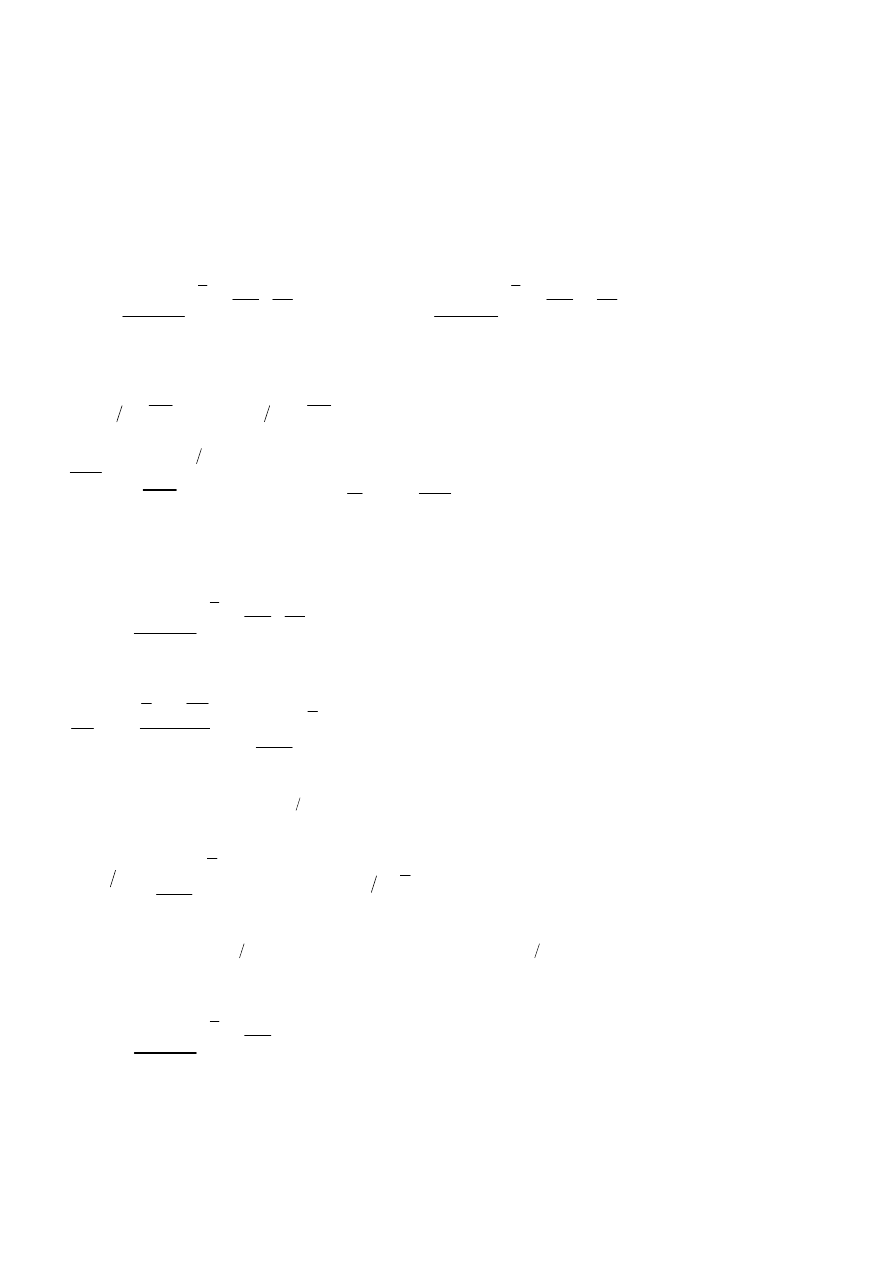
Półprzewodniki samoistne
Poziom Fermiego dla półprzewodnika niedomieszkowanego (samoistnego) oznaczamy symbolem
S
F
E
.
W półprzewodniku takim liczba elektronów jest równa liczbie dziur:
S
n
p
n
=
=
Korzystając ze wzorów:
kT
E
kT
E
e
F
g
e
e
kT
m
n
2
2
3
2
*
2
2
−
=
h
π
i
kT
E
kT
E
d
F
g
e
e
kT
m
p
−
−
=
2
2
3
2
*
2
2
h
π
Otrzymujemy zależność:
kT
E
d
kT
E
e
S
F
S
F
e
m
e
m
−
=
2
3
*
2
3
*
)
(
)
(
2
3
*
*
2
=
e
d
kT
E
m
m
e
S
F
*
*
ln
4
3
e
d
S
F
m
m
kT
E
=
→
Mając poziom Fermiego, możemy policzyć koncentrację nośników
S
n :
kT
E
kT
E
e
S
S
F
g
e
e
kT
m
n
2
2
3
2
*
2
2
−
=
h
π
4
3
*
*
ln
4
3
*
*
=
=
e
d
kT
m
m
kT
kT
E
m
m
e
e
e
d
S
F
Mnożymy ten wyraz przez
( )
2
3
*
e
m
:
( )
(
)
[
]
2
3
2
1
*
*
4
3
*
*
2
3
*
d
e
e
d
e
m
m
m
m
m
⋅
=
⋅
Wyrażenie
(
)
2
1
*
*
d
e
m
m
⋅
to masa zredukowana:
(
)
*
2
1
*
*
r
d
e
m
m
m
=
⋅
A więc:
kT
E
r
S
g
e
kT
m
n
2
2
3
2
*
2
2
−
=
h
π
- koncentracja samoistna zależy tylko od masy zredukowanej, przerwy energetycznej i temperatury