Fonony akustyczne
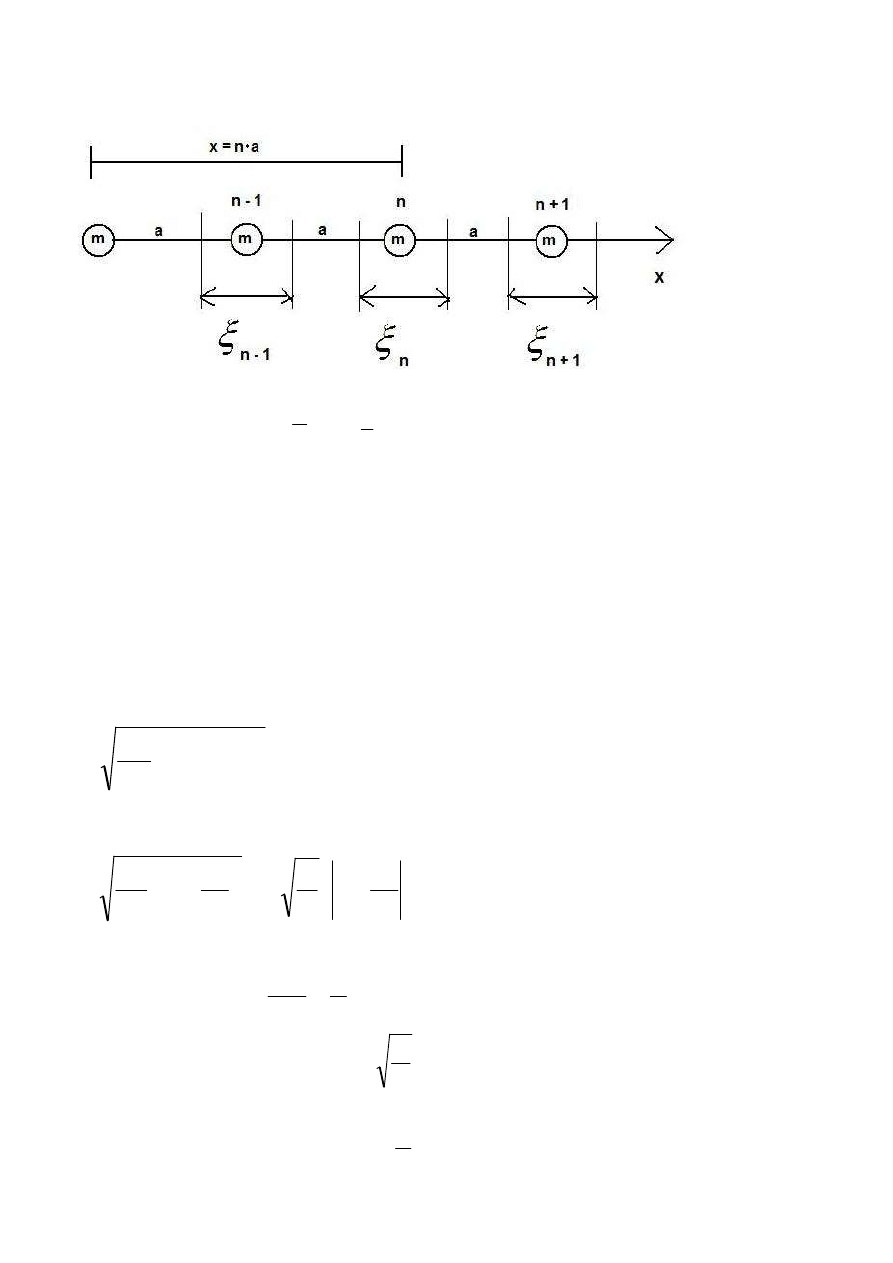
Fonony to drgania atomów w sieci kryształu. Najłatwiej jest je wyprowadzić z sieci liniowej:
Siła działająca na atom wychylony z położenia równowagi:
x
F
α
−
=
, gdzie
α
- stała siłowa
Z II prawa dynamiki Newtona:
a
m
F
w
=
← przyspieszenie = druga pochodna wychylenia po czasie:
n
n
n
n
n
m
ξ
α
ξ
α
ξ
α
ξ
α
ξ
−
+
−
=
+
−
1
1
&
&
(
)
1
1
2
+
−
+
−
=
n
n
n
n
m
ξ
α
ξ
α
ξ
α
ξ
&
&
-
n
- te równanie, dotyczące wychylenia
n
-tego atomu
Równanie to jest skojarzone z równaniem
1
−
n
i
1
+
n
.
Szukamy rozwiązania w postaci fali płaskiej:
(
)
qna
t
i
n
Ae
−
=
ω
ξ
, gdzie
x
na
=
to położenie atomu w sieci
(
)
2
2
−
+
=
−
−
iqa
iqa
e
e
m
α
ω
(
)
2
cos
2
2
−
=
−
qa
m
α
ω
(
)
qa
m
cos
1
2
−
=
α
ω
Korzystamy z własności funkcji trygonometrycznych:
x
x
x
x
x
x
2
cos
1
sin
2
sin
2
1
sin
cos
2
cos
2
2
2
2
−
=
→
−
=
−
=
2
sin
2
2
sin
4
2
qa
m
qa
m
⋅
=
=
α
α
ω
- jest to wyrażenie na dyspersję sieci
Najkrótsza możliwa fala akustyczna, jaka może się rozchodzić w ciele stałym:
a
2
min
=
λ
, stąd
a
q
π
λ
π
=
=
min
max
2
Dla małych
α
:
α
α
≈
sin
→
uq
qa
m
=
⋅
=
α
ω
, gdzie
u
- prędkość dźwięku w krysztale
Po skwantowaniu tego pola harmonicznego uzyskamy fonony – elementarne drgania atomów:
Energia całkowita drgań:
+
=
2
1
n
E
ω
h
- okazuje się, że dla
0
=
n
występują drgania zerowe (atomy w sieci nie mogą być nieruchome)
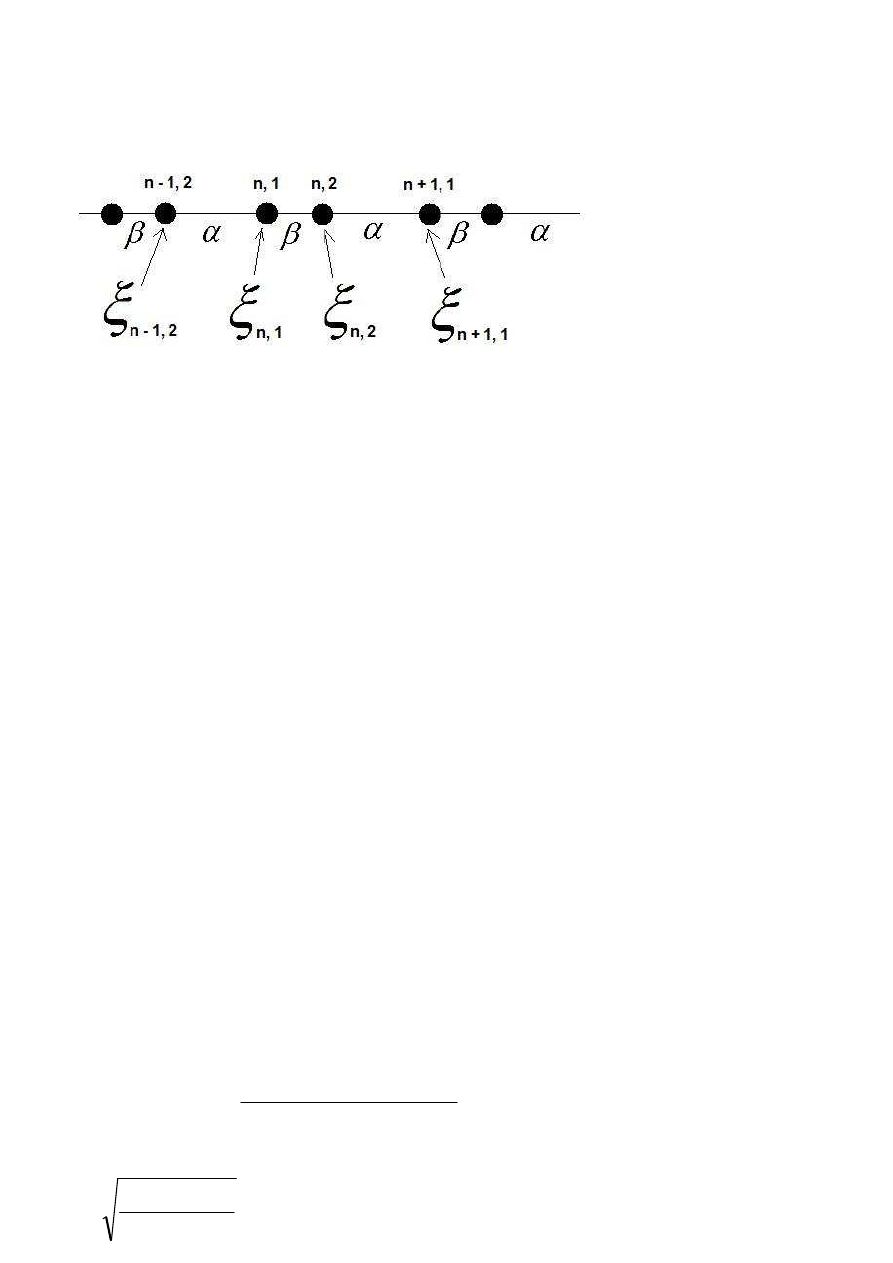
Fonony optyczne
Rozpatrujemy sieć, w której mamy po dwa atomy na węzeł:
1
,
2
,
1
,
2
,
1
1
,
1
n
n
n
n
n
m
ξ
β
ξ
β
ξ
α
ξ
α
ξ
−
+
−
=
−
&
&
2
,
1
,
1
2
,
1
,
1
,
2
n
n
n
n
n
m
ξ
α
ξ
α
ξ
β
ξ
β
ξ
−
+
−
=
+
&
&
(
)
qna
t
i
n
Ae
−
=
ω
ξ
1
,
(
)
qna
t
i
n
Ae
−
=
ω
ξ
2
,
Dla obu atomów częstość i wektor falowy są takie same, różne są natomiast amplituda i faza.
Otrzymujemy układ równań:
−
+
−
=
−
−
+
−
=
−
−
B
Ae
B
A
B
m
A
B
A
Be
A
m
iqa
iqa
α
α
β
β
ω
β
β
α
α
ω
2
2
2
1
=
−
+
+
−
−
=
+
−
−
+
−
0
]
)
[(
)
(
0
)
(
]
)
[(
2
2
2
1
ω
β
α
α
β
β
α
ω
β
α
m
B
e
A
e
B
m
A
iqa
iqa
W zapisie macierzowym:
=
−
+
+
−
+
−
−
+
−
0
0
)
(
)
(
)
(
)
(
2
2
2
1
B
A
m
e
e
m
iqa
iqa
ω
β
α
β
α
β
α
ω
β
α
Rozwiązanie nietrywialne istnieje wtedy, gdy wyznacznik macierzy
0
≠
.
0
)
)(
(
]
)
][(
)
[(
2
2
2
1
=
+
+
−
−
+
−
+
−
β
α
β
α
ω
β
α
ω
β
α
iqa
iqa
e
e
m
m
gdy przyjmiemy, że
m
m
m
=
=
2
1
, ilość rozwiązań się nie zmieni, a za to równanie się uprości:
0
)
cos
2
(
]
)
[(
2
2
2
2
=
+
+
−
−
+
qa
m
αβ
β
α
ω
β
α
2
δ
=
δ
ω
β
α
±
=
−
+
2
)
(
m
m
δ
β
α
ω
±
+
=
)
(
Gdy
0
=
q
,
2
2
2
2
)
(
2
β
α
αβ
β
α
δ
+
=
+
+
=
m
)
(
2
,
0
β
α
ω
ω
+
=
=
+
−
Gdy
a
q
π
=
,
2
2
2
2
)
(
2
β
α
αβ
β
α
δ
−
=
−
+
=
m
m
α
ω
β
ω
2
,
2
=
=
+
−
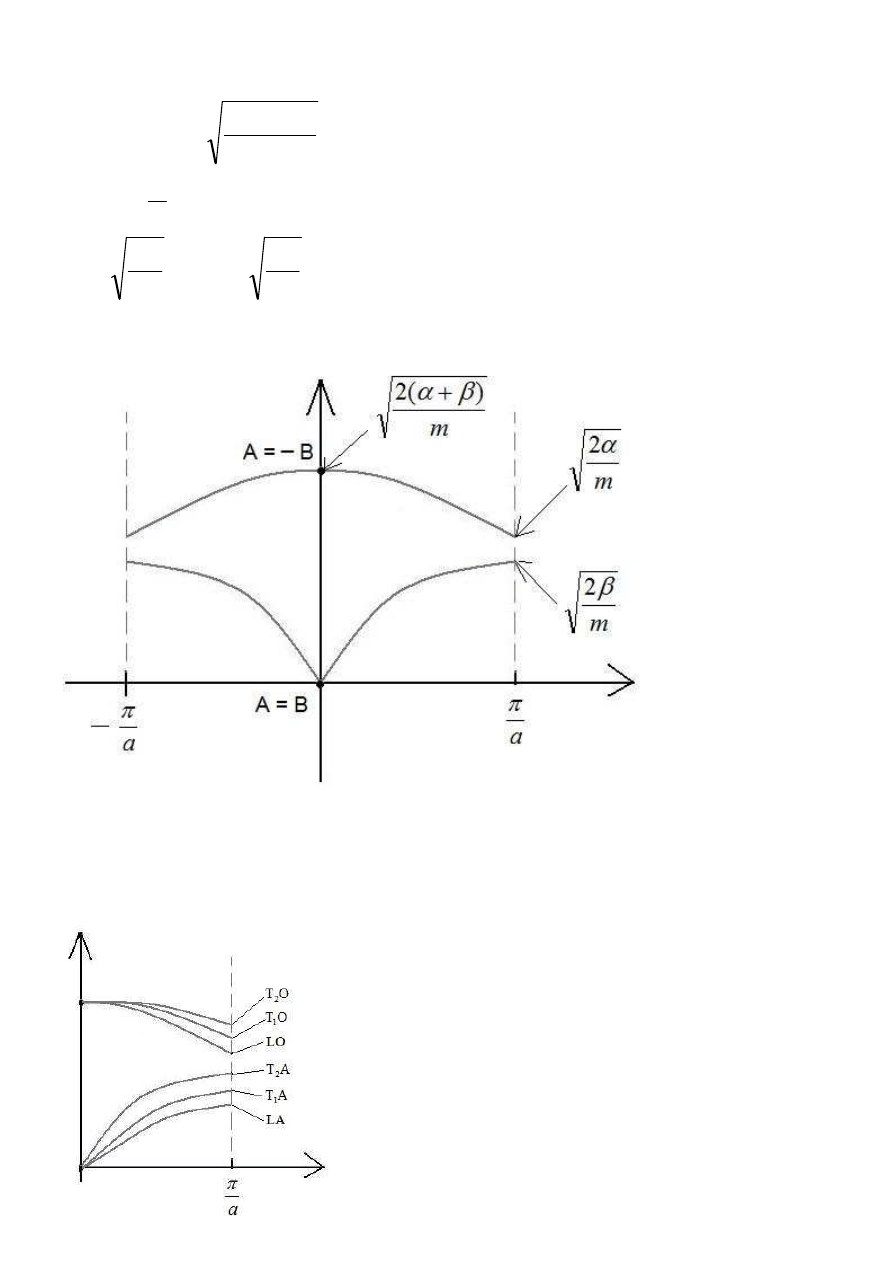
Jak zinterpretować to rozwiązanie?
Górna linia to drgania optyczne – atomy z jednego węzła wychylają się w przeciwne strony.
Dolna linia – drgania akustyczne, w których atomy z jednego węzła wychylają się w tę samą stronę.
Wśród tych drgań wyróżniamy jeszcze fale poprzeczne:
1
T
i
2
T
, oraz fale podłużne L.
Tworzą one tzw. gałęzie: 3 gałęzie akustyczne, oraz 3(n-1) gałęzi optycznych.