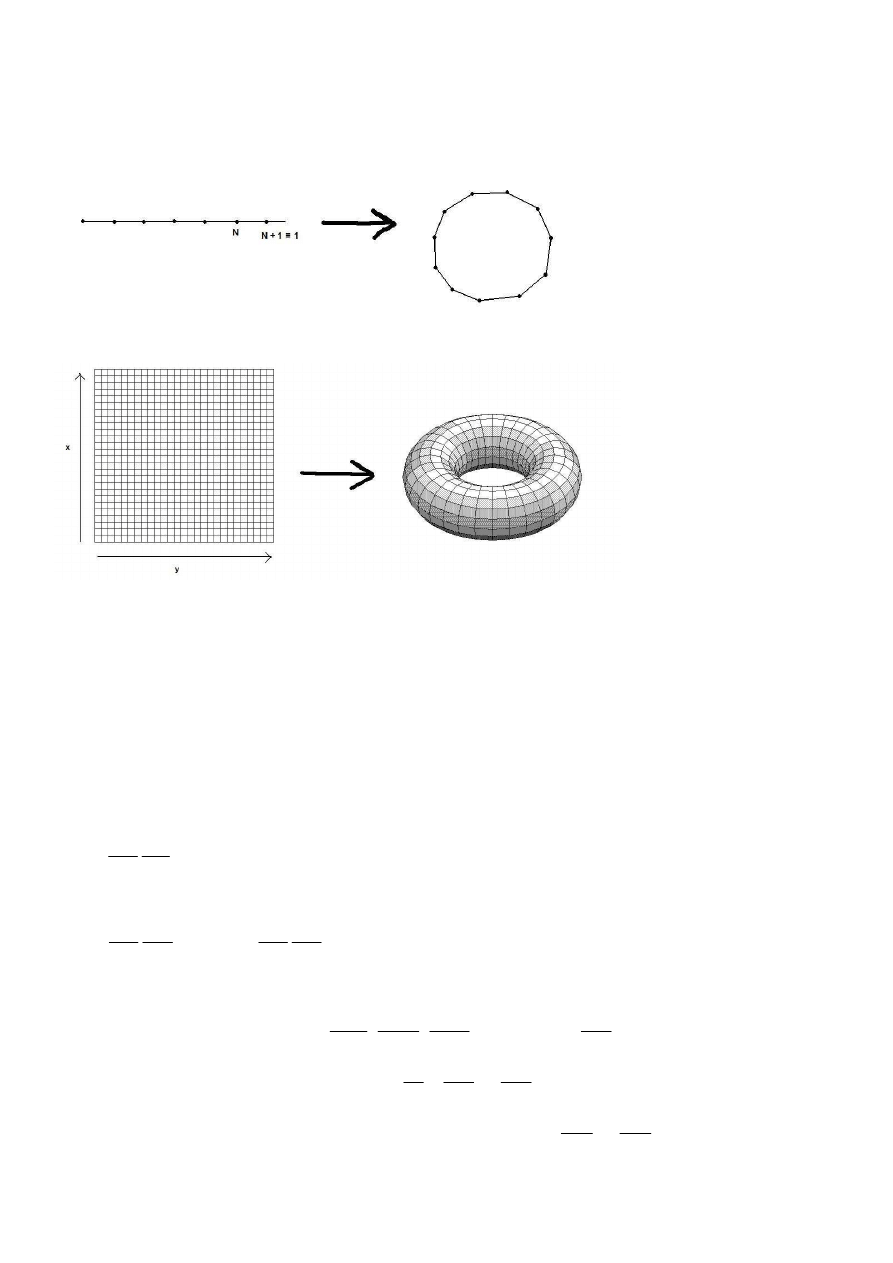
Warunki periodyczności Borna-Karmana:

Aby opisać kryształ o skończonej liczbie N atomów, musimy atomowi o indeksie

1

+

N

przypisać numer 1.

Można sobie wyobrazić, że gdy mamy jednowymiarowy kryształ, zamykamy go w „kryształ cykliczny”:

Z kolei kryształ 2-wymiarowy: w torus

(nie sposób sobie wyobrazić analogicznej operacji na krysztale 3-wymiarowym, ale dokonujemy tego w
rachunkach)

Funkcja Blocha musi zatem spełniać warunek:

)

(

)

(

1

1

)

(

1

1

x

u

e

a

N

x

u

e

k

x

k

i

k

a

N

x

k

i

x

x

=

+

+

, (gdy rozpatrujemy jeden kierunek, np.

x

)

1

1

1

=

a

N

k

i

x

e

, gdy

1

1

1

2 n

a

N

k

x

π

=

,

1

1

...,

,

3

,

2

,

1

N

n

=

Wynika stąd, że wektor falowy musi być równy:

1

1

1

2

N

n

a

k

x

n

π

=

Analogicznie dla pozostałych kierunków:

2

2

2

2

N

n

a

k

y

n

π

=

3

3

3

2

N

n

a

k

z

n

π

=

Wszystkich atomów mamy

3

2

1

N

N

N

N

⋅

⋅

=

Objętość komórki elementarnej:

V

L

L

L

N

a

N

a

N

a

V

k

3

3

2

1

3

3

2

2

1

1

8

2

2

2

π

π

π

π

=

⋅

⋅

=

⋅

⋅

=

, gdzie

V - objętość kryształu

Gęstość stanów w przestrzeni kryształu:

3

3

8

1

8

1

)

(

π

π

ρ

→

=

=

V

V

k

k

, jeśli przyjmiemy jednostkową objętość

Gdy uwzględnimy spin, gęstość stanów wzrośnie dwukrotnie:

3

3

4

1

4

)

(

π

π

ρ

→

=

V

k