Arkadiusz Ptak

Instytut Fizyki

Politechnika Poznańska

Podstawy nanotechnologii

Modelowanie i symulacje

molekularne

Modelowanie i symulacje molekularne

1.

Wprowadzenie

2.

Metody mechaniki molekularnej (klasycznej)

3.

Metody mechaniki kwantowej

•

metody ab-initio

•

metody półempiryczne

•

Metody DFT

PLAN

1. Wprowadzenie

a.

Czym s

ą

modelowanie molekularne i symulacje

b.

Zalety i ograniczenia

c.

Schemat metodologiczny

d.

Przybli

ż

enia, rodzaje oblicze

ń

e.

Obliczeniowe wyzwania

WPROWADZENIE

Modelowanie i symulacje molekularne

WPROWADZENIE

Modelowanie i symulacje molekularne

Modelowanie molekularne (MM)

- proces tworzenia modeli cz

ą

steczek, nanostruktur lub ich układów.

Modelowanie
- proces tworzenia modeli lub ich stosowanie.

Model
- system zało

ż

e

ń

, poj

ęć

i zale

ż

no

ś

ci mi

ę

dzy nimi pozwalaj

ą

cy opisa

ć

w

przybli

ż

ony sposób jaki

ś

aspekt rzeczywisto

ś

ci.

WPROWADZENIE

WPROWADZENIE

Czym jest modelowanie?

Symulacja
- przybli

ż

one odtwarzanie zjawiska lub zachowania danego obiektu za

pomoc

ą

jego modelu.

Symulacja molekularna jest rodzajem eksperymentu komputerowego,
którego przedmiotem s

ą

teoretyczne modele struktury i własno

ś

ci

cz

ą

steczek lub układów ponadcz

ą

steczkowych.

Symulacja jest implementacj

ą

modelu w czasie; pokazuje zachowanie

modelu.

WPROWADZENIE

WPROWADZENIE

Czym s

ą

symulacje molekularne?

Metody MiSM wykorzystuje si

ę

w:

- fizyce molekularnej (cz

ą

steczki)

- chemii obliczeniowej (cz

ą

steczki)

- biochemii i biologii obliczeniowej (biocz

ą

steczki)

- nanotechnologii (nanostruktury)

Czym s

ą

modelowanie i symulacje molekularne?

WPROWADZENIE

Czym s

ą

modelowanie i symulacje molekularne?

WPROWADZENIE

Ograniczenia:

• weryfikacja (przez falsyfikacj

ę

) – porównanie z danymi eksperymentalnymi;

je

ś

li brak, to sposoby po

ś

rednie:

- dane dla podobnych układów molekularnych (nanostruktur)
- stosowanie wielu metod MiSM
- poleganie na u

ż

yteczno

ś

ci wykorzystywanych w modelach teorii

(znajomo

ść

zało

ż

e

ń

i ogranicze

ń

)

• ograniczenia obliczeniowe, w tym sprz

ę

towe

Zalety i wykorzystanie:

• dodatek do istniej

ą

cych lub uzyskiwanych danych eksperymentalnych

• zdolno

ść

przewidywania wła

ś

ciwo

ś

ci nanoostruktur przed wykonaniem

eksperymentów (cz

ę

sto kosztownych)

• zdolno

ść

przewidywania wła

ś

ciwo

ś

ci nanoostruktur jeszcze nie wytworzonych

• główne

ź

ródło wiedzy w przypadku braku jakichkolwiek danych eksperymentalnych

(np. gdy konieczno

ść

wytworzenia ekstremalnych warunków eksperymentu: bardzo

wysoka lub niska temperatura, UHV, niewa

ż

ko

ść

itp..)

Zalety i ograniczenia

WPROWADZENIE

Zalety i ograniczenia MiSM

WPROWADZENIE

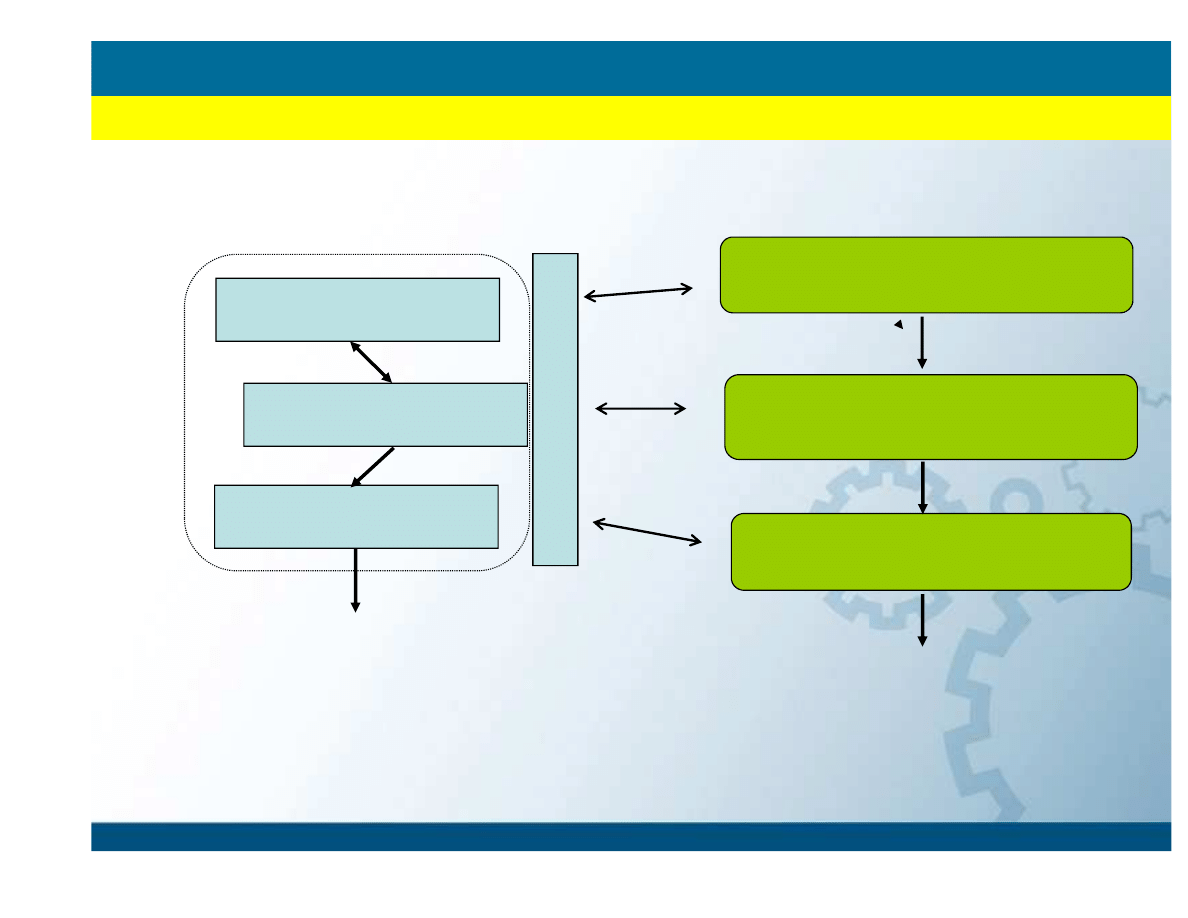
Schemat blokowy:

Visualization Tool

Compute Engine

Analysis Tool

U

se

r

in

te

rf

a

ce

Budowa wst

ę

pnego modelu

molekuły

Wybór silnika obliczeniowego

(rodzaju modelu teoretycznego)

Analiza obliczonych wła

ś

ciwo

ś

ci

Projekt MiSM

WPROWADZENIE

Dla wszystkich metod:

Przestrze

ń

homogeniczna (jednorodna) i izotropowa

Dla metod kwantowych:

Przybli

ż

enie Borna-Oppenheimera:

ruch j

ą

der atomowych znacznie wolniejszy ni

ż

elektronów

Szczegółowe zało

ż

enia dla konkretnych metod MiSM

(np. wprowadzenie dodatkowych pól fizycznych)

Zało

ż

enia ogólne

WPROWADZENIE

Zało

ż

enia ogólne

WPROWADZENIE

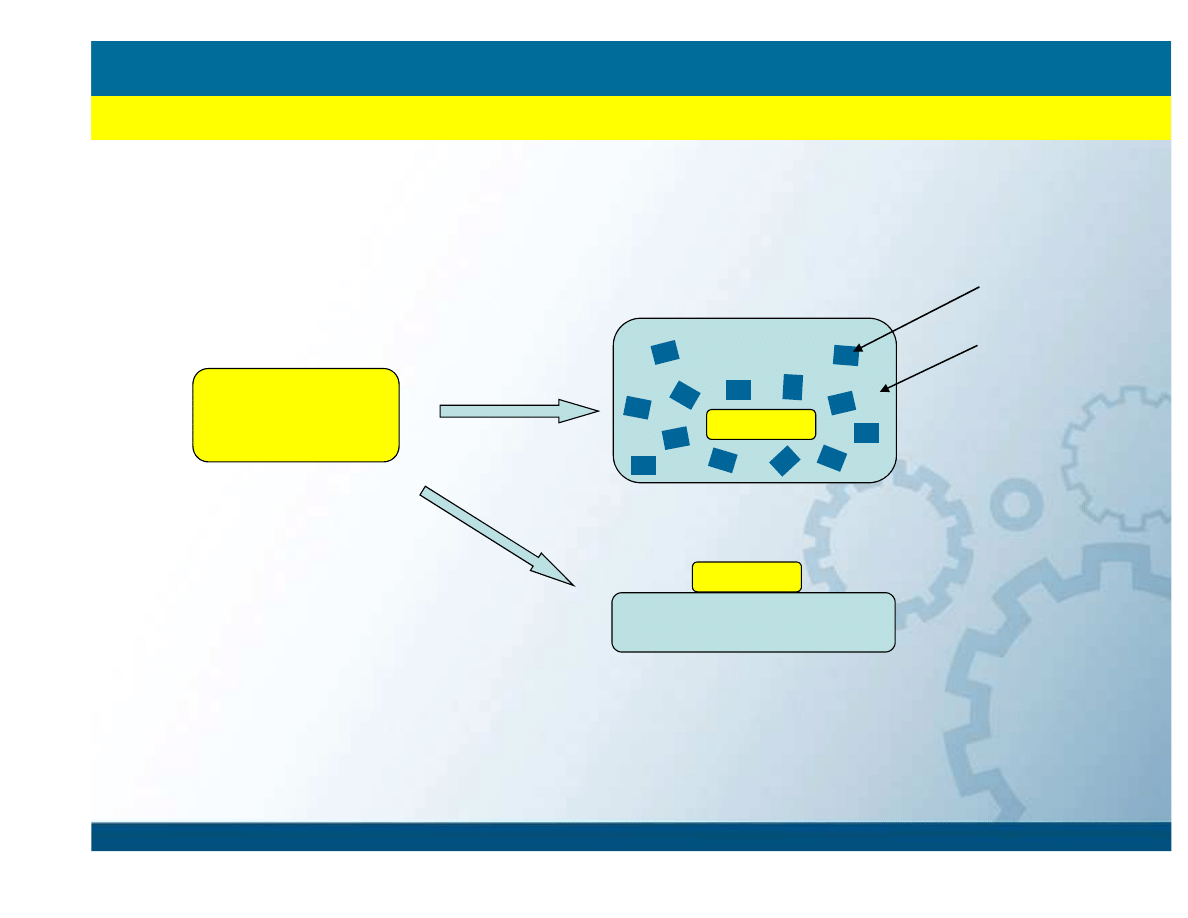
Molecule

in vacuo

Liquid

Metodologia

WPROWADZENIE

Solid

Metodologia

WPROWADZENIE

Otoczenie

explicite

continuous
phase

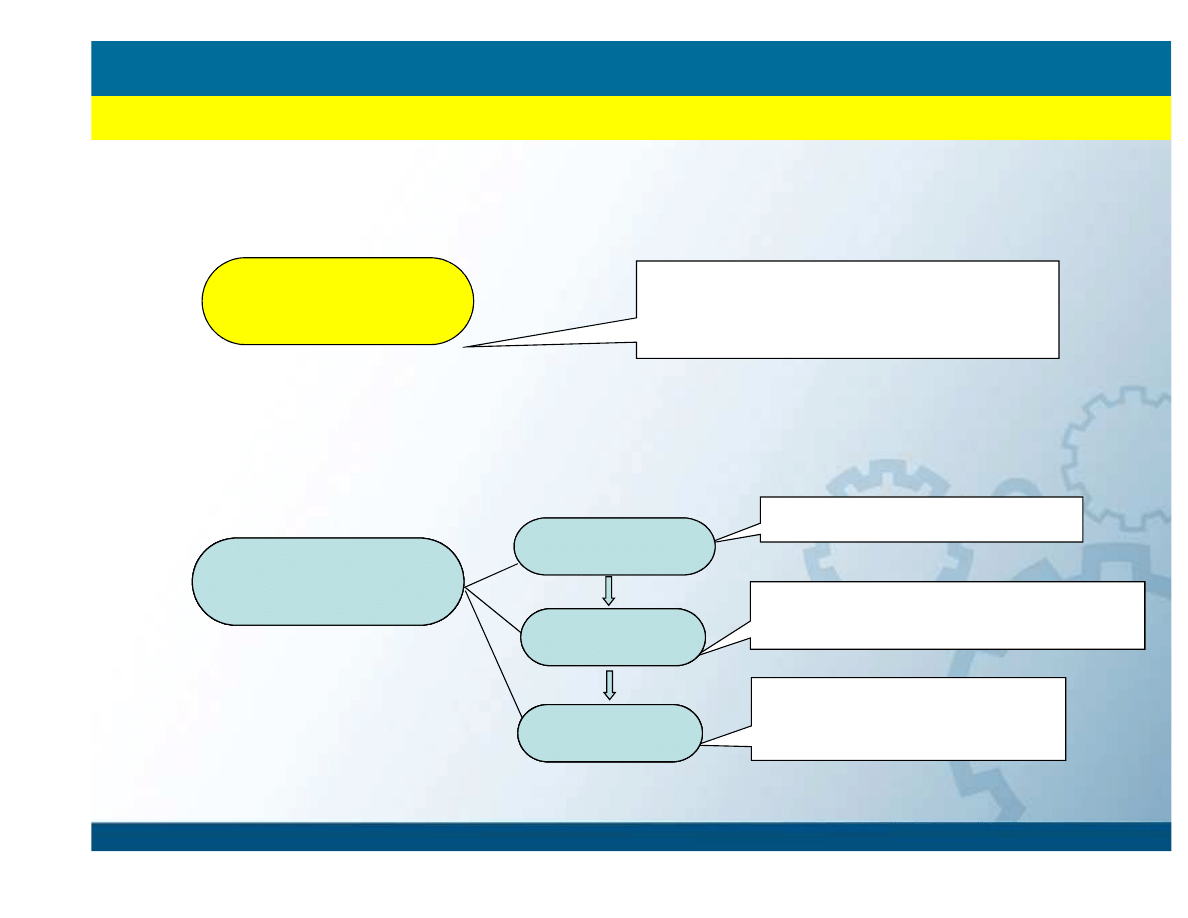
Classical physics

Quantum physics

Potential functions; Only effects related to
the arrangement of atomic nuclei;
not optical spectra for instance.

Ab initio

DFT

Semi-empirical

Self-consistent field (SCF)
or
Hartree-Fock calculations

Density Functional Theory
- based on some empirical knowledge

Based on empirical knowledge

Quantum physics

Ab initio

DFT

Quantum physics

Ab initio

Semi-empirical

DFT

Quantum physics

Ab initio

Metodologia

WPROWADZENIE

Teoria

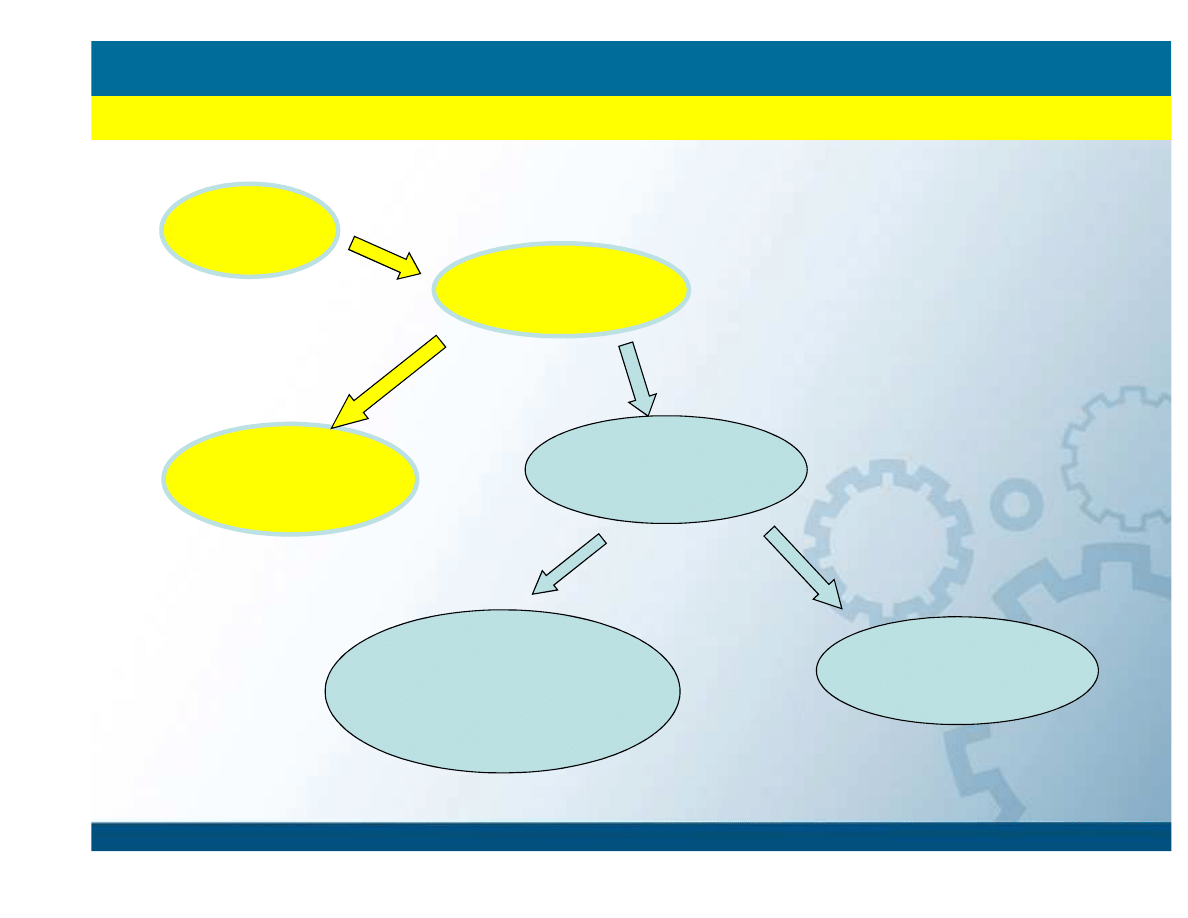
Geometry

optimization

Molecular

Dynamics

Calculation of orbitals

Simulation of spectra

Metodologia

WPROWADZENIE

Density of charge

Density of spin

Electrostatic potentials

Rodzaje oblicze

ń

Single Point

Metodologia

WPROWADZENIE

Energy landscape

x

y

E

Single Point

Geometry

optimization

Architektura komputerowa:

• wieloprocesorowe superkomputery (Cray, IBM)

• stacje robocze (Silicon Graphics, Sun, HP, IBM)

• klastery komputerowe (poł

ą

czone w sieci, grid)

• pojedyncze PC

Dwa aspekty:

• obliczenia

• wizualizacja

Hardware

WPROWADZENIE

Hardware

WPROWADZENIE

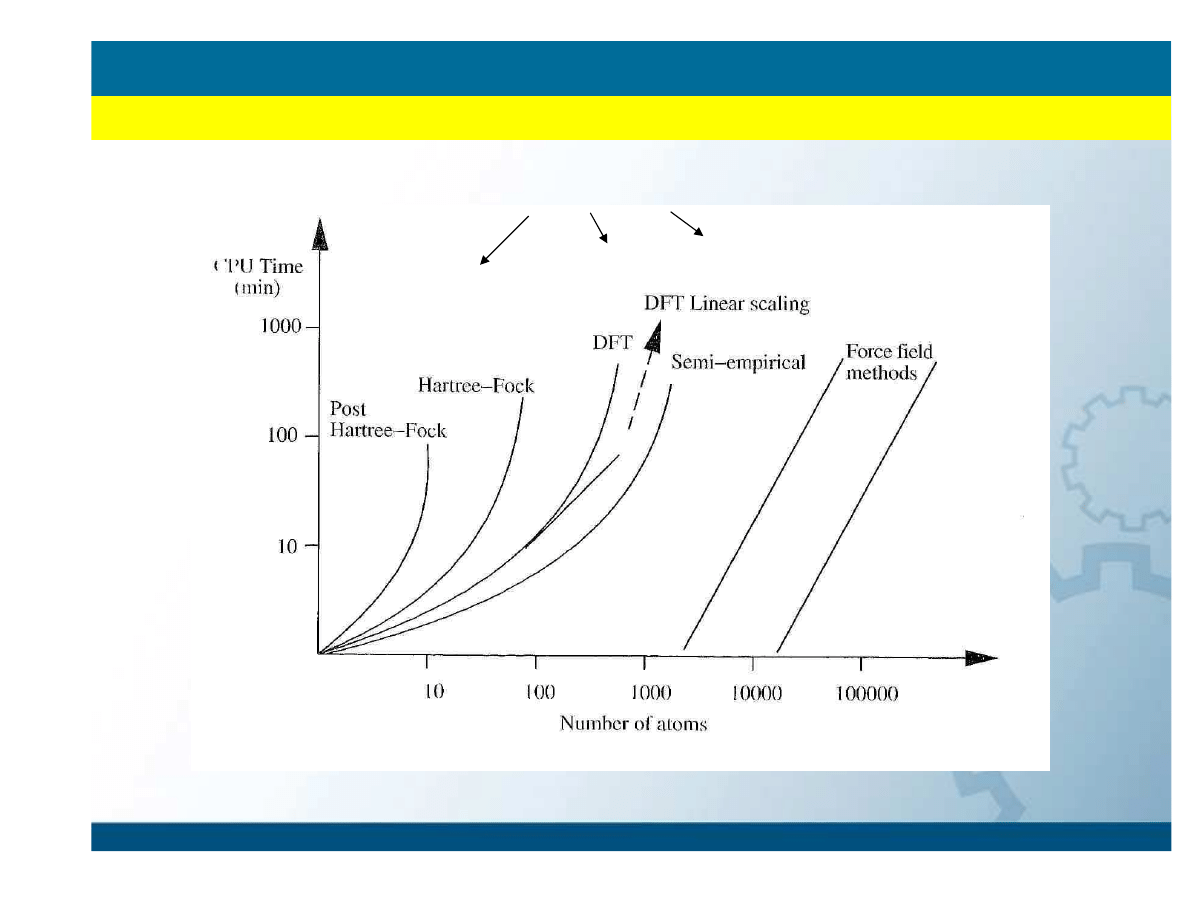
Metody klasyczne

Metody

półempiryczne

Ab initio

Ograniczenia sprz

ę

towe

WPROWADZENIE

DFT

Metody kwantowe

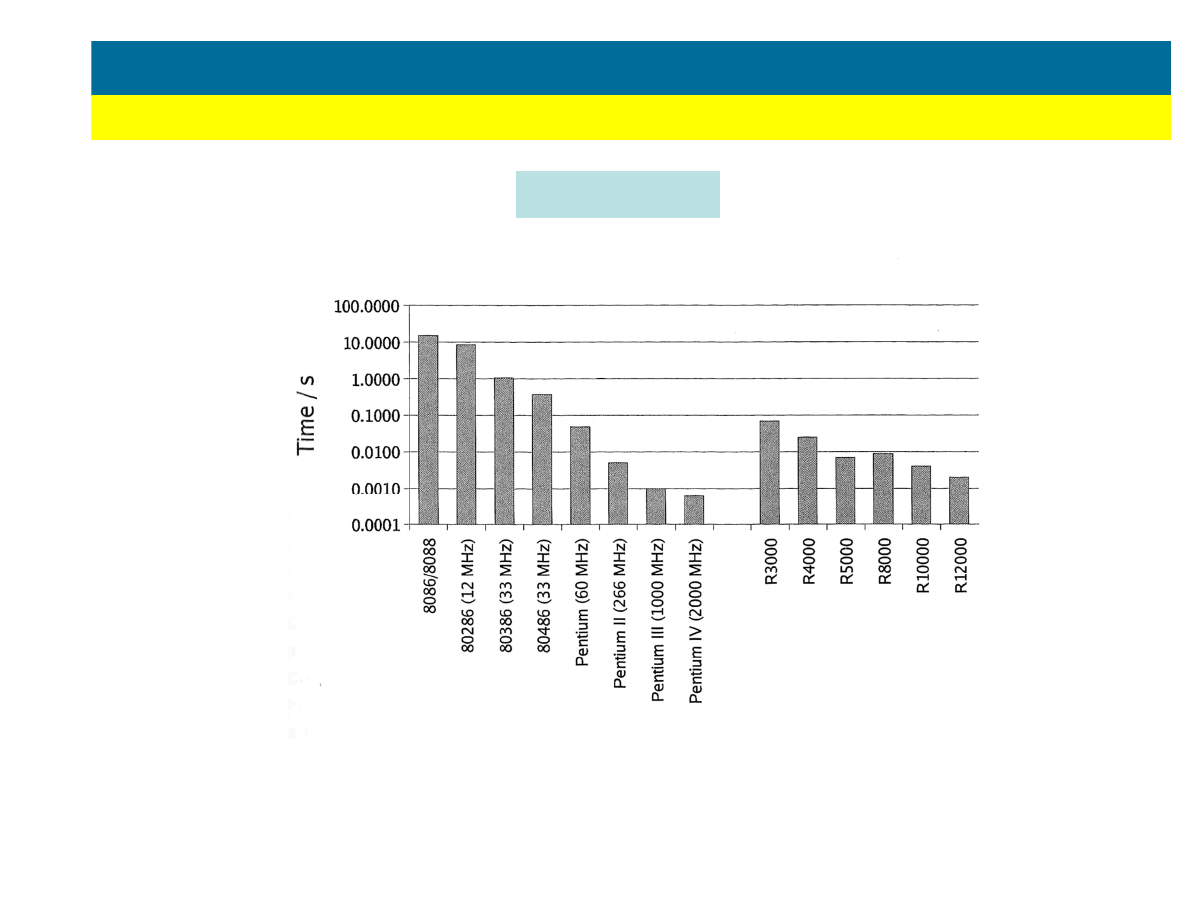
Post

ę

p

Intel

MIPS

WPROWADZENIE

Ograniczenia sprz

ę

towe

Przykłady:

• Insight II

• Gaussian

• NWChem

• SPARTAN

• HyperChem

• CACHe

• Materials Studio

• MAPS

• MaterialsExplorer

• NAMD

• Arguslab

Oprogramowanie

WPROWADZENIE

METODY

MECHANIKI KLASYCZNEJ

METODY MECHANIKI KLASYCZNEJ

1.

Mechanika molekularna

a.

Okre

ś

lenie modelu

b.

Potencjały oddziaływania

•

Potencjały wi

ą

za

ń

atomowych

•

Potencjały k

ą

tów wi

ą

za

ń

•

Potencjały torsyjne

•

Potencjały odziaływa

ń

van der Waalsa

•

Potencjał wi

ą

za

ń

wodorowych

•

Potencjał oddziaływa

ń

elektrostatycznych

c.

Optymalizacja geometrii (energii)

2.

Podstawy u

ż

ytkowania programów MM&S

a.

Budowanie cz

ą

steczek

b.

Optymalizacja struktury

Plan

METODY MECHANIKI KLASYCZNEJ

Plan

Model i Energia

• Cz

ą

steczka jest zespołem oddziałuj

ą

cych na siebie atomów

• Oddziaływania mo

ż

na opisa

ć

za pomoc

ą

prostych funkcji analitycznych

el

bonds

H

vdW

torsion

angle

stretch

tot

E

E

E

E

E

E

E

+

+

+

+

+

=

−

METODY MECHANIKI KLASYCZNEJ

Energia całkowita:

Model i Energia

METODY MECHANIKI KLASYCZNEJ

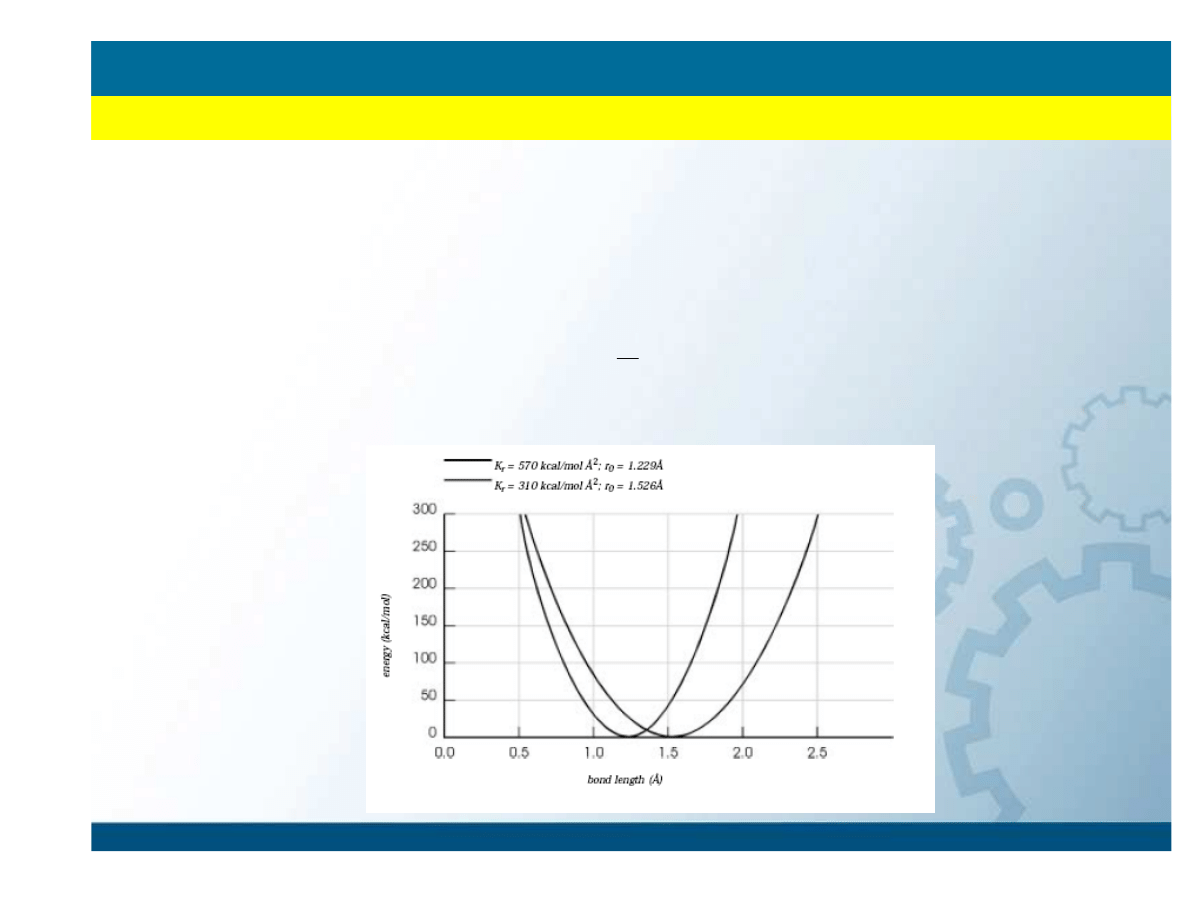
Bond stretching

(rozci

ą

ganie wi

ą

za

ń

)

∑

−

=

bonds

r

stretch

r

r

k

E

2

0

)

(

2

1

C-O

C-C

Pola siłowe

METODY MECHANIKI KLASYCZNEJ

Pola siłowe

METODY MECHANIKI KLASYCZNEJ

Bending

(zginanie)

∑

−

=

angles

bend

k

E

2

0

)

(

2

1

θ

θ

θ

Pola siłowe

METODY MECHANIKI KLASYCZNEJ

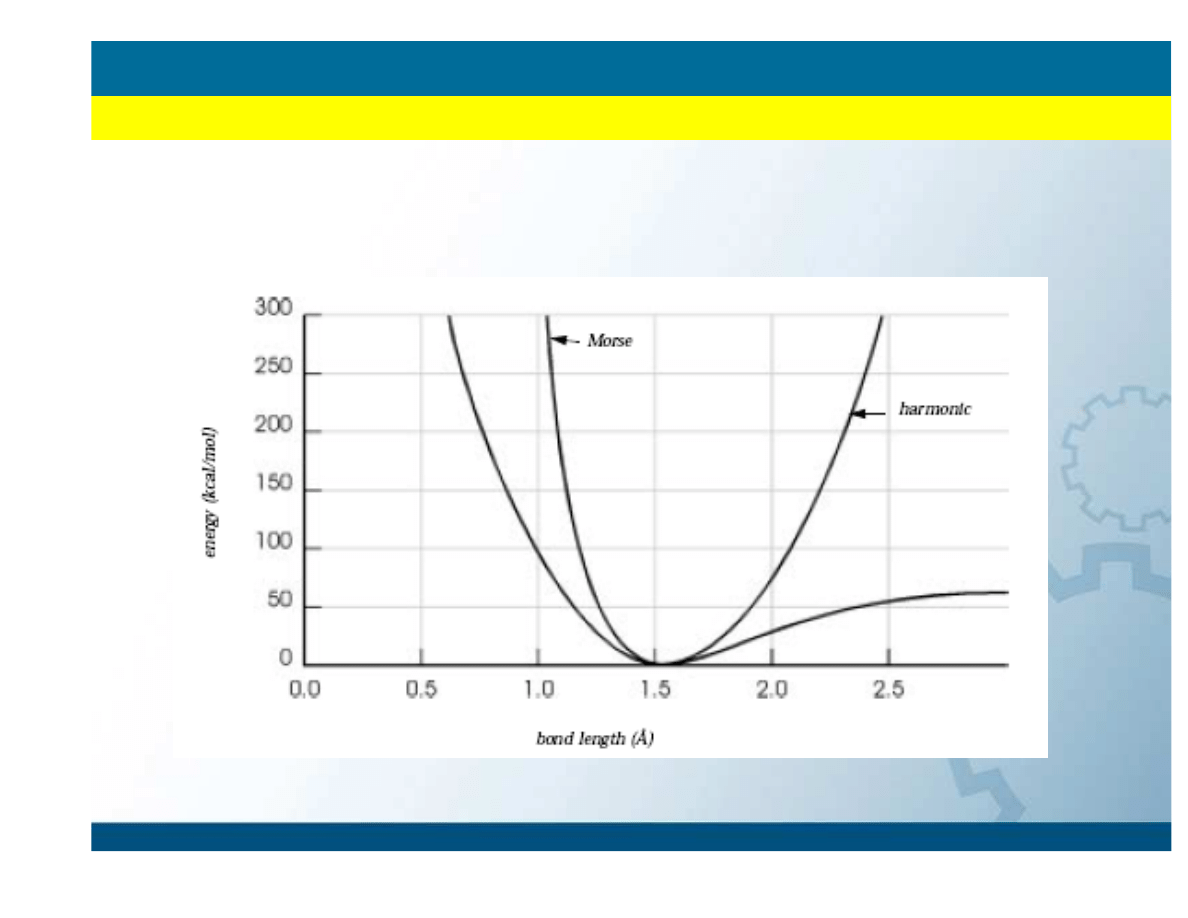
Dlaczego potencjał harmoniczny a nie Morse’a?

Pola siłowe

METODY MECHANIKI KLASYCZNEJ

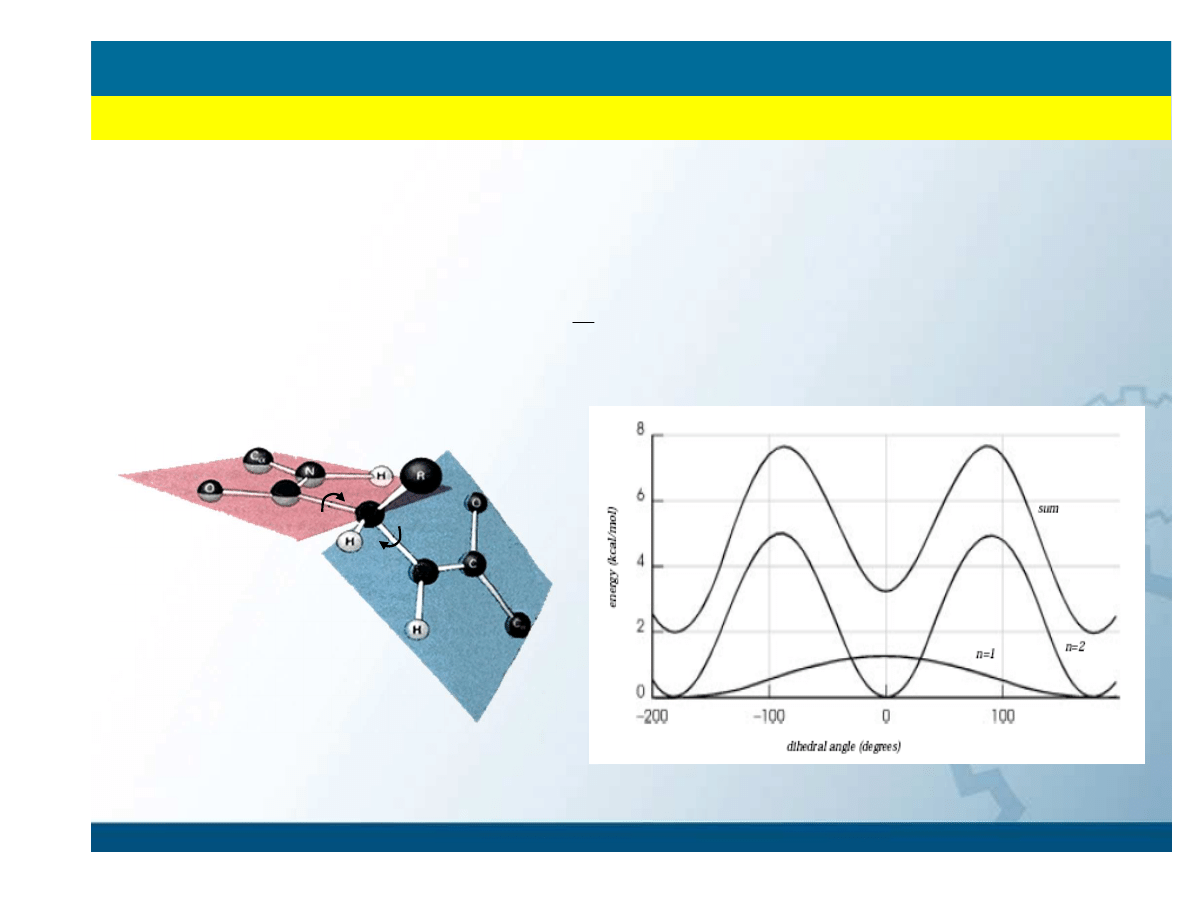
Torsions

(obroty torsyjne)

[

]

∑

Φ

−

Φ

+

=

dihedrals

n

dihedrals

n

V

E

2

0

)

cos(

1

2

1

HN-C=O

cis

trans

Pola siłowe

METODY MECHANIKI KLASYCZNEJ

C

α

αα

α

C

N

Φ

Φ

Φ

Φ

Ψ

Ψ

Ψ

Ψ

Pola siłowe

METODY MECHANIKI KLASYCZNEJ

Van der Waals interactions

(oddziaływania vdW)

∑

<

















−

=

j

i

ij

ij

ij

ij

vdW

R

B

R

A

E

6

12

Hydrogen bonding

(wi

ą

zania wodorowe)

∑

−

−

















−

=

bonds

H

ij

ij

ij

ij

bonds

H

R

D

R

C

E

10

12

Pola siłowe

METODY MECHANIKI KLASYCZNEJ

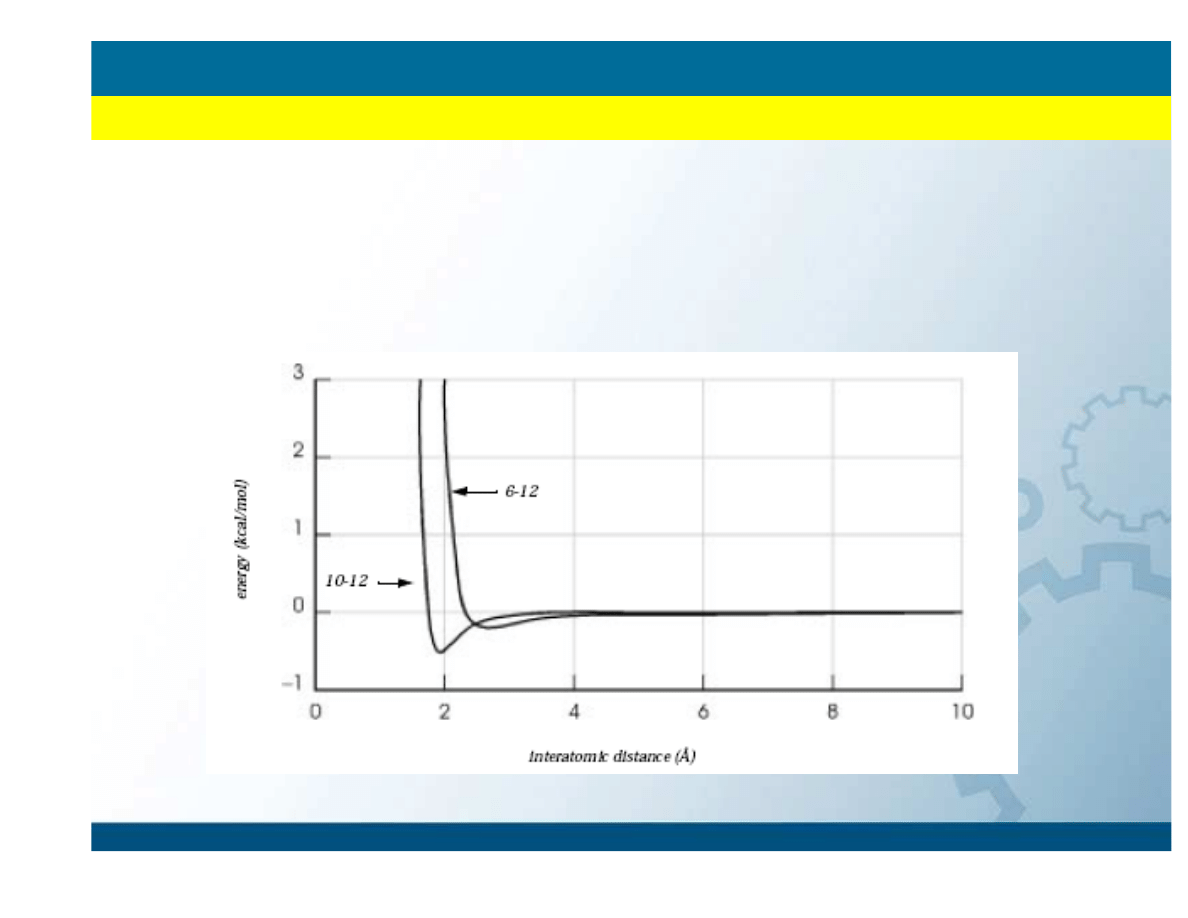
Porównanie potencjałów oddziaływa

ń

Van der Waalsa i

wi

ą

za

ń

wodorowych

Pola siłowe

METODY MECHANIKI KLASYCZNEJ

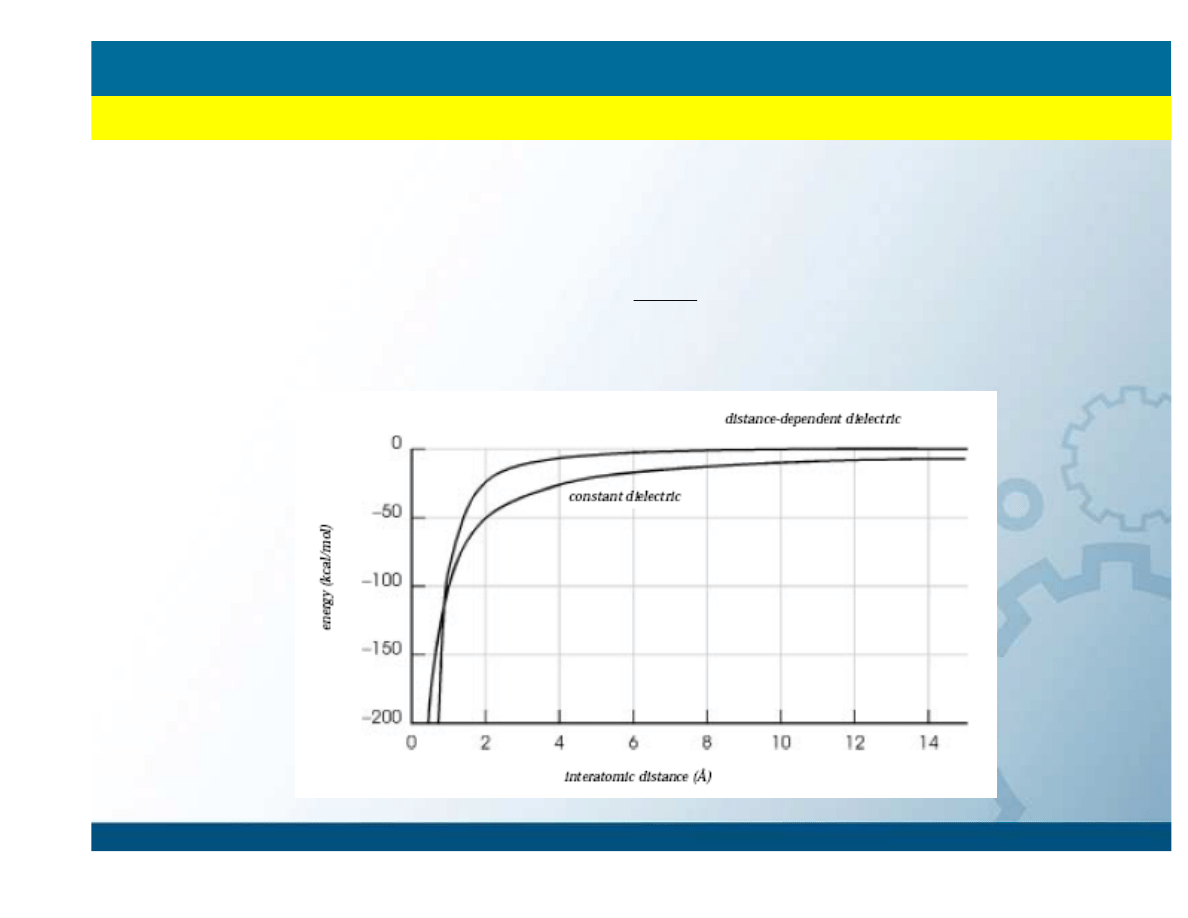
Electrostatic interactions

∑

<

















=

j

i

ij

j

i

el

R

q

q

E

ε

)

(

ij

R

ε

ε

=

Pola siłowe

METODY MECHANIKI KLASYCZNEJ

Systematyczne przesuwanie wszystkich atomów cz

ą

steczki

(nanostruktury) dopóki siła wypadkowa działaj

ą

ca na ka

ż

dy atom

nie wynosi zero.

Optymalizacja geometrii

METODY MECHANIKI KLASYCZNEJ