1. Programowanie strukturalne i obiektowe. 
2. Fala elektromagnetyczna: typy, paramet1. Programowanie struktry, właściwości. 
3. Tranzystory bipolarne i unipolarne: budowa, właściwości i zastosowania. 
4. Systemy ciągłe i dyskretne: klasyfikacja i opis. 
5. Zmienna losowa: właściwości i opis. 
6. Ciągła, dyskretna i szybka transformata Fouriera, widmo sygnału. 
7. Modulacje analogowe i cyfrowe. 
8. Wzmacniacze operacyjne: właściwości i we. 
13. Bazy danych i ich zastosowania. 
14. Przetwarzanie obrazów, metody ich zastosowania. 
15. Miary 

i oceny dokładności algorytmów przybliżonych. 

16. Systemy operacyjne komputerów. 
17. Zadania optymalizacji i techniki ich rozwiązywania. 
18. Systemy dynamiczne, opisy własności. 
19. Programowanie w systemie operacyjnym UNIX. 
20. Komputer, architektura i oprogramowanie. 
 
 
1. Programowanie strukturalne i obiektowe. 
Programowanie strukturalne 

– metodyka opracowywania, organizacji i pisania programów komputerowych, prowadząca do 

uzyskania programów o zwięzłych, przejrzystych i łatwych do analizy strukturach, wykorzystujących procedury (podprogramy) 
tworzone osobno dla realizacji określonych zadań i wywoływane w odpowiednich miejscach programu głównego. Opisywane są 
kolejno czynności, które muszą zostać wykonane, aby osiągnięty został cel zadania. Dane przekazywane poprzez wartości 
zwracane i argumenty funkcji. Zalecane jest unikanie zmiennych globalnych w związku z istnieniem niebezpieczeństwa zmiany 
wartości zmiennej przez dowolną funkcję. Obecnie prawie wszystkie popularne języki programowania spełniają wymogi 
programowania strukturalnego. Programowanie strukturalne cechuje się prostotą zapisu programu, dlatego jest bardzo 
przydatne zwłaszcza w początkowych fazach nauki programowania, chociaż ze względu na zużyty czas lub pamięć często nie 
jest optymalną metodą programowania. 
  
Programowanie obiektowe (ang. object-oriented programming) 

– metodyka tworzenia programów komputerowych, która  

definiuje programy za pomocą "obiektów" – elementów  łączących stan (czyli dane) i zachowanie (czyli procedury, tu: metody). 
Ob

iektowy program komputerowy wyrażony jest jako zbiór takich obiektów, komunikujących się pomiędzy sobą w celu 

wykonywania zadań. Podejście to rożni się od tradycyjnego programowania proceduralnego, gdzie dane i procedury nie są ze 
sobą bezpośrednio związane. Programowanie obiektowe ma ułatwić pisanie, konserwację i wielokrotne użycie programów lub 
ich fragmentów. Największym atutem programowania, projektowania oraz analizy obiektowej jest zgodność takiego podejścia z 
rzeczywistością– mozg ludzki jest w naturalny sposób najlepiej przystosowany do takiego podejścia przy przetwarzaniu 
informacji. Jest to najbardziej naturalny sposób rozumienia rzeczywistości;  podstawową cechą mózgu ludzkiego jest 
klasyfikacja 

–  łączenie występujących w rzeczywistości obiektów w grupy – klasy. Odbywa się to na podstawie wspólnych cech 

dla grup obiektów – w tym podobnych zachowań. 
  
Podstawowe cechy języków programowania, które czynią je obiektowymi, to: 

● 

abstrakcja 

– każdy obiekt w systemie jest abstrakcyjnym modelem, który może wykonywać zadania, opisywać i zmieniać 

swój stan oraz komunikować się z innymi obiektami bez ujawniania, w jaki sposób dane cechy zostały zaimplementowane 

● 

hermetyzacja - 

to sposób odizolowania  od otoczenia wybranych danych i funkcji (operujących na tych danych) 

zgromadzonych w jednej strukturze. Widoczne są tylko niezbędne fragmenty programu, natomiast zmienne i funkcje 
pomocnicze są ukryte i niedostępne z zewnątrz. Dzięki takiemu połączeniu programista uwalnia się od pamiętania o wszystkich 
szczegółach implementacyjnych, co zapewnia zmniejszenie liczby błędów oraz prostszą strukturę programu końcowego. Dla 

terminu hermetyzacja spotyka się również określenie enkapsulacja. Podobnie jak w innych językach programowania, 
hermetyzację można stosować bez klasycznych mechanizmów programowania obiektowego. 

● 

dziedziczenie - 

operacja, która powoduje przeniesienie danych i metod z klasy bazowej do potomnej. Mechanizm ten 

uwalnia programistę od ponownego tworzenia i implementowania struktur danych oraz funkcji działających na tych strukturach. 
Udostępnia on możliwość korzystania z własnej bądź cudzej pracy jedynie poprzez rozszerzanie już zaimplementowanych 
elementów. Nie ma więc konieczności ponownego definiowania tego, co raz już zostało zrobione. Warto pamiętać,  że 
d

ziedziczenie może dotyczyć rownież interfejsów, gdzie trzeba zachować większą ostrożność w stosowaniu tego mechanizmu.  

● 

polimorfizm - 

to najważniejsza cecha, która umożliwia dostosowanie działania obiektów do własnych oczekiwań poprzez  

łączenie funkcjonalności zarówno dziedziczonej, jak i  implementowanej samodzielnie. Idea polimorfizmu bazuje na tym, że 
użytkownik obiektu nie musi wiedzieć, czy konkretne zachowanie wykorzystywanego obiektu zostało zrealizowane 
bezpośrednio w tym obiekcie czy też w tym, po którym dziedziczy on swoje właściwości. Ponadto może się okazać,  że takie 
samo odwołanie do metody za każdym razem dotyczy innej akcji  (inaczej zdefiniowanej). Może się też okazać, że w zależności 
od poziomu dziedziczenia pozornie ta sama metoda (nazywa

jąca się tak samo) wykonuje inną akcję.  

  
Programowanie strukturalne zakłada tworzenie procedur i realizacje danego zagadnienie w oparciu o nie. Złożone dane 
przechowywane są w postaci struktur a sekwencja wywołań procedur (funkcji) realizuje proces danego zagadnienia. Język 
strukturalny nie posiada mechanizmów opisu  świata rzeczywistego, z tego powodu nie nadaje się do modelowania 
rzeczywistych procesów.  Ten sposób programowania nadaje się do tworzenia algorytmów, rzadziej jest wykorzystywany do 
modelow

ania zjawisk. Do tego typu zagadnień stosuje się podejście obiektowe. Dzięki mechanizmom polimorfizmu, 

dziedziczenia, hermetyzacji w  łatwy sposób można modelować zachowania obiektów istniejących w rzeczywistości, same zaś 
obiekty reprezentować przy pomocy klas definiujących obiekt, mający określone cechy (własności) czy też zachowania 
(metody).  
 
2.   

 

Fala elektromagnetyczna: typy, parametry, właściwości 

Promieniowanie elektromagnetyczne (fala elektromagnetyczna) 

– rozchodzące się w przestrzeni zaburzenie w postaci pola 

elektromagnetycznego. 
W  fali 

rozchodzącej się  w  próżni lub jednorodnym nieograniczonym ośrodku fala elektromagnetyczna jest  falą poprzeczną,  w 

której składowa elektryczna i magnetyczna są prostopadłe do siebie, a obie są prostopadłe do kierunku rozchodzenia się fali. 
Oba  pola  indukują  się  wzajemnie  –  zmieniające  się  pole  elektryczne  wytwarza  zmieniające  się  pole  magnetyczne,  a  z  kolei 
zmieniające się pole magnetyczne wytwarza zmienne pole elektryczne. 
 
Właściwości fal elektromagnetycznych mocno zależą od długości fali. Promieniowaniem elektromagnetycznym o różnej długości 
fali, są fale radiowe, mikrofale, podczerwień, światło, ultrafiolet, promieniowanie rentgenowskie i promieniowanie gamma. 
W  opisie  kwantowym 

promieniowanie  elektromagnetyczne  jest  traktowane  jako  strumień  nie  posiadających  masy  cząstek 

elementarnych zwanych fotonami

, których energia zależy od długości fali. 

Właściwości promieniowania elektromagnetycznego 
Widmo fal elektromagnetycznych 

 

Promieniowanie elektromagnetyczne demonstruje swe właściwości falowe zachowując się jak każda fala, ulegając interferencji, 
dyfrakcji

, spełnia prawo odbicia i załamania. W wyniku superpozycji fal elektromagnetycznych może powstać fala stojąca. 

Jednak  niektóre  właściwości  promieniowania  elektromagnetycznego  (szczególnie  jego  oddziaływanie  z  materią)  zależą  od 
długości fali (częstotliwości promieniowania) i dlatego dokonano podziału promieniowania elektromagnetycznego na zakresy ze 
względu  na  jego  częstotliwość.  Granice  poszczególnych  zakresów  są  umowne  i  nieostre.  Należy  je  traktować  szacunkowo, 
promieniowanie  o  tej  samej  długości  może  być  nazywane  falą  radiową  lub  mikrofalą  -  w  zależności  od  kontekstu.  Granice 
promieniowania  gamma  i  pro

mieniowania  rentgenowskiego  często  rozróżnia  się  z  kolei  ze  względu  na  źródło  tego 

promieniowania. Najdokładniej określone są granice dla światła widzialnego, gdyż są one zdeterminowane fizjologią ludzkiego 
oka. 

Fale radiowe  
Fale  radiowe  znajdują  bardzo  szerokie  zastosowanie  w  telekomunikacji,  radiofonii,  telewizji,  radioastronomii  i  wielu  innych 
dziedzinach  nauki  i  techniki.  W  technice  podstawowym  źródłem  fal  radiowych  są  anteny  zasilane  prądem  przemiennym 
odpowiedniej częstotliwości. Wiele urządzeń generuje też zakłócenia będące falami radiowymi, wymienić tu można na przykład: 
zasilacze  impulsowe,  falowniki  i  regulatory  tyrystorowe,  piece  indukcyjne

, spawarki, zapłon  iskrowy silników samochodowych, 

iskrzące  styki  urządzeń  elektrycznych.  Naturalne  źródła  fal  radiowych  to  między  innymi  wyładowania  atmosferyczne,  zorze 
polarne, radiogalaktyka. 

Mikrofale 
W  zależności  od  metody  wytwarzania  niekiedy  mikrofale  są  zaliczane  do  fal  radiowych,  albo  do  podczerwieni.Podstawowe 
zastosowania  mikrofal  to  łączność  (na  przykład  telefonia  komórkowa,  radiolinie,  bezprzewodowe  sieci  komputerowe)  oraz 
technika radarowa. Za

kres mikrofalowy jest również używany w radioastronomii, a odkrycie  mikrofalowego promieniowania tła 

miało  ważne  znaczenie  dla  rozwoju  i  weryfikacji  modeli  kosmologicznych.  Wiele  dielektryków  mocno  absorbuje  mikrofale,  co 
powoduje ich rozgrzewanie i jest wykorzystywane w kuchenkach mikrofalowych i w medycynie. 

Podczerwień  
Promieniowanie podczerwone jest nazywane również cieplnym, szczególnie w kontekście gdy jego źródłem są nagrzane ciała. 
Każde ciało o temperaturze większej od zera bezwzględnego emituje takie promieniowanie, a ciała o temperaturze pokojowej 
najwięcej  promieniowania  emitują  w  zakresie  długości  fali  rzędu  10  μm.  Przedmioty  o  wyższej  temperaturze  emitują 
promieniowanie  o  większym  natężenie  i  mniejszej  długości,  co  pozwala  na  pomiar  ich  temperatury  i  obserwację  za  pomocą 
urządzeń rejestrujących wysyłane promieniowanie. 
Technika rejestracji promieniowania podczerwonego emitowanego przez obiekty o temperaturach spotykanych w codziennych 
warunkach to Termowizja. 

Światło widzialne  

400-700 nm 

Ultrafiolet  

Promieniowanie  ultrafioletowe,  jest  zaliczane  do  promieniowania 

jonizującego,  czyli  ma  zdolność  odrywania  elektronów  od 

atomów i cząsteczek. W dużym stopniu określa to jego właściwości, szczególnie oddziaływanie z materią i na organizmy żywe. 
Słońce  emituje  ultrafiolet  w  szerokim  zakresie  spektralnym,  ale  górne  warstwy  atmosfery  ziemskiej  (warstwa  ozonowa) 
pochłaniają większość promieniowania z krótkofalowej części spektrum. Obserwacje astronomiczne w ultrafiolecie rozwinęły się 
dopiero  po  wyniesieniu  ponad  atmosferę  przyrządów  astronomicznych.  W  technice  ultrafiolet  stosowany  jest  powszechnie. 
Powoduje  świecenie  (fluorescencję)  wielu  substancji  chemicznych.  W  świetlówkach  ultrafiolet  wytworzony  na  skutek 
wyładowania  jarzeniowego  pobudza  luminofor  do  świecenia  w  zakresie  widzialnym.  Zjawisko  to  wykorzystuje  się  również  do 
zabezpieczania banknotów i w analizie chemicznej (Spektroskopia UV). Ultrafiolet o małej długości fali jest wykorzystywany do 
sterylizacji 

(wyjaławiania) pomieszczeń. 

Promieniowanie rentgenowskie  
Promieniowanie  rentgenowskie  jest  promieniowaniem  jonizującym.  Technicznie  promieniowanie  rentgenowskie  uzyskuje  się 
przeważnie poprzez wyhamowywanie rozpędzonych cząstek naładowanych. W  lampach rentgenowskich są to rozpędzone za 
pomocą  wysokiego  napięcia  elektrony  hamowane  na  metalowych  anodach.  Źródłem  wysokoenergetycznego  promieniowania 
rentgenowskiego  są  również  przyspieszane  w  akceleratorach  cząstki  naładowane.  Promieniowanie  rentgenowskie  jest 
wykorzystywane do wykonywania 

zdjęć rentgenowskich do celów defektoskopii i diagnostyki medycznej. 

Promieniowanie gamma 
Promieniowania gamma jest promieniowaniem jonizującym. Promieniowanie gamma towarzyszy  reakcjom jądrowym, powstaje 
w  wyniku  anihilacji 

–  zderzenie  cząstki  i  antycząstki,  oraz  rozpadów  cząstek  elementarnych.  Otrzymywane  w  cyklotronach 

promieniowanie hamowania i synchrotronowe również leży w zakresie długości fali promieniowania gamma, choć niekiedy bywa 
nazywane wysokoenergetycznym promieniowaniem rentgenowskim. Promienie gamma mogą służyć do sterylizacji żywności i 
sprzętu  medycznego.  W  medycynie  używa  się  ich  w  radioterapii  oraz  w  diagnostyce.  Zastosowanie  w  przemyśle  obejmują 
badania defektoskopowe.  
Mod fali elektromagnetycznej  
Mody  fali  elektromagnetycznej 

są  to  charakterystyczne  rozkłady  pola  elektromagnetycznego  w  propagującej  fali. 

Najprostszym  w  opisie  matematycznym  modem  fali  elektromagnetycznej  jest  poprzeczn

a  fala  płaska,  w  której  składowa 

elektryczna  i  magnetyczna  są  prostopadłe  do  siebie,  a  obie  są  prostopadłe  do  kierunku  rozchodzenia  się  fali.  Ze  źródła 
punktowego  rozchodzą  się  fale  kuliste.  Zależności  między  kierunkami  pola  elektrycznego,  magnetycznego  i  propagacji  oraz 
relacje fazowe w fali kulistej pozostają takie same, jak w fali płaskiej. Każdą falę rozchodzącą się w nieskończonym bezstratnym 
ośrodku  dielektrycznym,  niezbyt  blisko  źródła,  można  uważać  za  kulistą,  a  dostatecznie  mały  jej  wycinek  za  płaską. 
Promieniowanie  laserów  często  ma  gaussowski  profil  wiązki,  charakteryzujący  się  rozkładem  amplitudy  natężenia  pola 
elektrycznego w płaszczyźnie prostopadłej do osi wiązki opisanym funkcją Gaussa. 
Ogólnie wszystkie mody fali elektromagnetycznej można je podzielić na: 
§    falę  poprzeczną  (TEM  od  ang.  Transverse  ElectroMagnetic)  -  wektory  natężenia  pola  elektrycznego  i  indukcji  pola 
magnetycznego są prostopadłe do kierunku rozchodzenia się fali; 
§    TE  (ang.  Transverse  Electric)  -  mody,  dla  których  wektor  natężenia  pola  elektrycznego  jest  prostopadły  do  kierunku 
rozchodzenia się fali, a wektor indukcji pola magnetycznego nie; 
§    TM  (ang.  Transverse  Magnetic)  -  mody,  dla  których  wektor  indukcji  pola  magnetycznego  jest  prostopadły  do  kierunku 
rozchodzenia się fali, a wektor natężenia pola elektrycznego nie; 
§  mody hybrydowe - mody nie będące żadnym z powyższych - zarówno pole elektryczne, jak i magnetyczne mają niezerowe 
składowe w kierunku ruchu. 
Polaryzacja fali elektromagnetycznej 
Polaryzacja  fali  elektromagnetycznej  to  charakterystyczne  zachowanie  się  kierunków  wektorów  pola  elektrycznego  i 
magnet

ycznego.  Obecnie  zwyczajowo  przyjęto,  że  polaryzację  fali  elektromagnetycznej  określa  się  dla  jej  składowej 

elektrycznej (składowa magnetyczna jest do niej prostopadła). 

§  Polaryzacja jest liniowa, jeżeli kierunek wektora natężenia pola elektrycznego znajduje się cały czas w jednej płaszczyźnie, w 
kierunku prostopadłym do kierunku rozchodzenia się fali. 
§    Przy  polaryzacji  kołowej  pole  elektryczne  określane  wzdłuż  kierunku  ruchu  fali  ma  zawsze  taką  samą  wartość,  a  jego 
kierunek się zmienia w taki sposób, że koniec wektora opisującego zaburzenie zatacza okrąg w czasie jednego okresu fali. 
§  Przy polaryzacji eliptycznej natężenie pola elektrycznego określane wzdłuż kierunku ruchu fali ma zawsze wartość i kierunek 
taki, że koniec jego wektora zatacza elipsę. 
§  Istnieją bardziej złożone typy polaryzacji. 

Energia fali elektromagnetycznej 

W  fali  elektromagnetycznej  jej  pola  elektryczne  i  magnetyczne  niosą  ze  sobą  energię.  W  próżni  i  jednorodnym  idealnym 
dielektryku  składowe  elektryczne  i  magnetyczne  niesionej  energii  są  sobie  równe,  natomiast  w  ośrodku  o  niezerowym 
przewodnictwie elektrycznym są różne. 
Strumień  energii  przenoszonej  przez  falę  elektromagnetyczną  w  każdym  punkcie  przestrzeni  określa  wektor  Poyntinga 
zdefiniowany jako 

 

μ0 - przenikalność magnetyczna próżni 

 - 

natężenie pola elektrycznego 

 - indukcja pola magnetycznego. 

Prędkość fali elektromagnetycznej  
Prędkość rozchodzenia się fali elektromagnetycznej w próżni jest stała, nie zależy od jej częstości ani układu odniesienia. 

Nazywa się ją prędkością światła. Jest ważną stałą fizyczną, a jej wartość wynosi około 

. W ośrodkach 

materialnych prędkość fali elektromagnetycznej jest zawsze mniejsza niż w próżni. 
Oddziaływanie fali elektromagnetycznej z materią  
Rozchodzenie się fali w ośrodkach zależy od zarówno od właściwości tych ośrodków, jak i częstotliwości fali. 
§  Gdy długość fali duża w porównaniu z odległościami między cząsteczkami ośrodka może on być traktowany jako ciągły. Gdy 
jest dielektrykiem, fala się w nim rozchodzi, a zmienia się jej prędkość i długość. W ośrodkach przewodzących rozchodząca się 
fala  jest  tłumiona,  tym  bardziej,  im  większe  jest  ich  przewodnictwo.  Również  straty  dielektryczne  powodują  tłumienie  fali.  W 
dobre przewodniki (metale) fale o tej długości wnikają jedynie na niewielką głębokość, natomiast odbijają się. 
§    Gdy  długość  fali  staje  się  porównywalna  z  odległościami  międzyatomowymi  (rzędu  nm  -  promieniowanie  rentgenowskie) 
zaczynają przeważać efekty dyfrakcyjne. 
§  Gdy  długość fali jest się małe  w porównaniu  z odległościami międzyatomowymi promieniowanie  nazywa się przenikliwym, 
gdyż  ma  dużą  zdolność  penetracji  materii.  Kwanty  promieniowania  o  małej  długości  mają  jednak  tak  dużą  energię,  że  mogą 
jonizować atomy i rozbijać cząsteczki. 
§    W  dużym  stopniu  pochłaniane  są  również  kwanty  promieniowania  o  energii  odpowiadającej  różnicy  poziomów 
energetycznych 

elektronów i cząsteczek w materiale (pochłanianie rezonansowe). 

Opis teoretyczny  
Równania Maxwella w przestrzeni nie zawierającej ładunków (w próżni) można zapisać jako: 

 

 

gdzie 
H 

– wektor natężenia pola magnetycznego, 

E 

– wektor natężenia pola elektrycznego. 

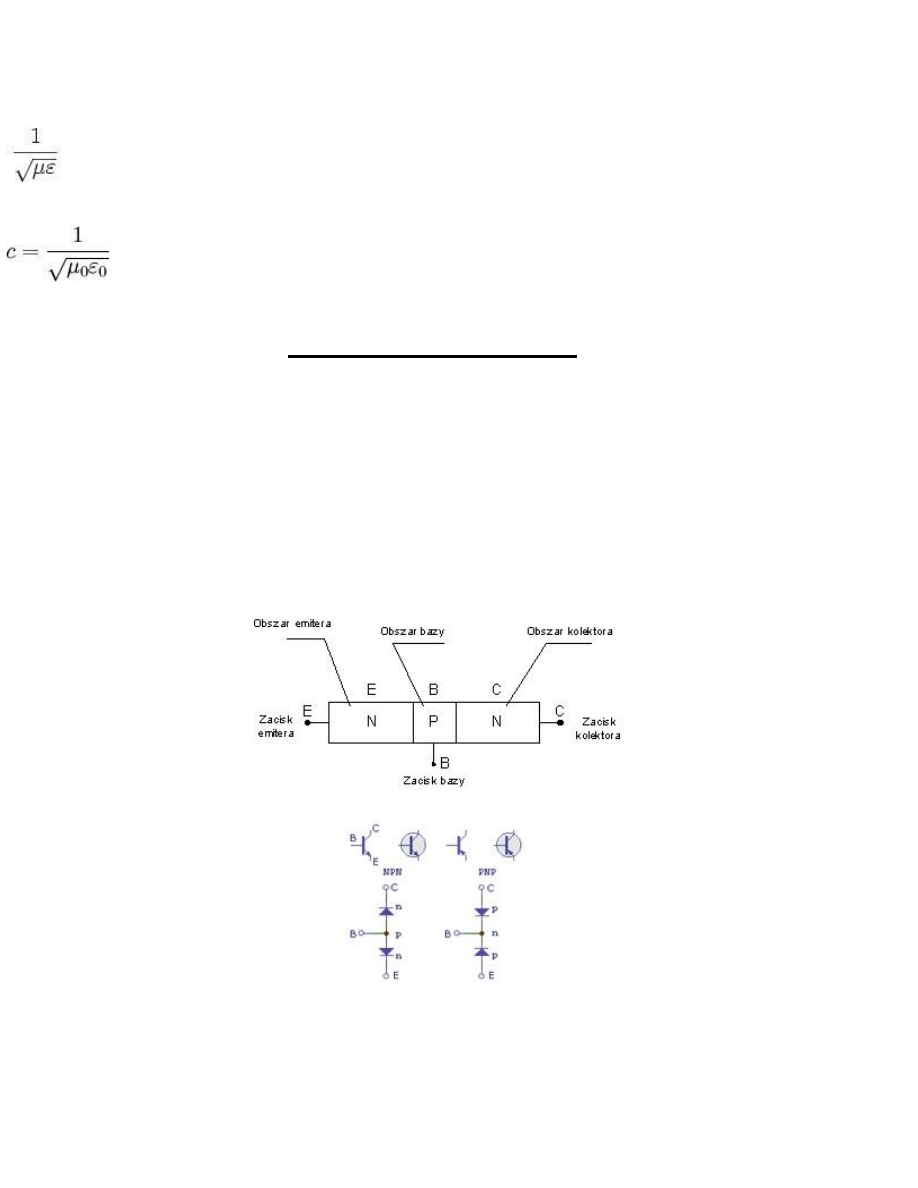
Równania te są liniowymi równaniami różniczkowymi fali rozchodzącej się z prędkością 

 

gdzie: 

ε  to  przenikalność  elektryczna,  a  μ  to  przenikalność  magnetyczna  ośrodka,  w  którym  rozchodzi  się  fala.  W  próżni 

prędkość ta jest prędkością światła w próżni i określa ją wzór: 

 

  
3. Tranzystory bipolarne i unipolarne: budowa, właściwości i zastosowania. 

Tranzystory bipolarne 

Wiadomości podstawowe 

Tranzystory  są  urządzeniami  półprzewodnikowymi  umożliwiającymi  sterowanie  przepływem  dużego  prądu,  za  pomocą  prądu 
znacznie mniejszego. Wykorzystuje się je do wzmacniania małych sygnałów oraz przetwarzania informacji w postaci cyfrowej. 
Nazwa "tranzystor" pochodzi z połączenia słów transfer i rezystor.  
    

Pierwszy tranzystor bipolarny zbudował rok później inny amerykański fizyk  - W.B. Shockley. Cała ta trójka za wynalezienie 

tranzystora otrzymała w 1956 roku Nagrodę Nobla.  
   

Nazwa bipolarne dotyczy tranzystorów, w których transport ładunków odbywa się za pośrednictwem obu rodzajów nośników 

jakie istnieją w półprzewodniku, tzn. elektronów i dziur. Półprzewodniki, w których na skutek nieregularności  sieci krystalicznej 
przeważają  nośniki  typu  dziurowego  nazywa  się  półprzewodnikami  typu  p  (niedomiarowymi),  gdy  przeważają  nośniki 
elektronowe nazywa się je półprzewodnikami typu n (nadmiarowymi).  
 

Tranzystor bipolarny składa się z trzech obszarów półprzewodnika o przeciwnym typie przewodnictwa, co powoduje powstanie 

dwóch złączy: p-n i n-p. 

 

Istnieją dwie możliwe konfiguracje złączy p-n i n-p prowadzące do powstania dwóch rodzajów tranzystorów bipolarnych. 

 

Zasada działania 

Zasada działania tranzystora bipolarnego omówiona zostanie na podstawie tranzystora NPN: 

 

  

    

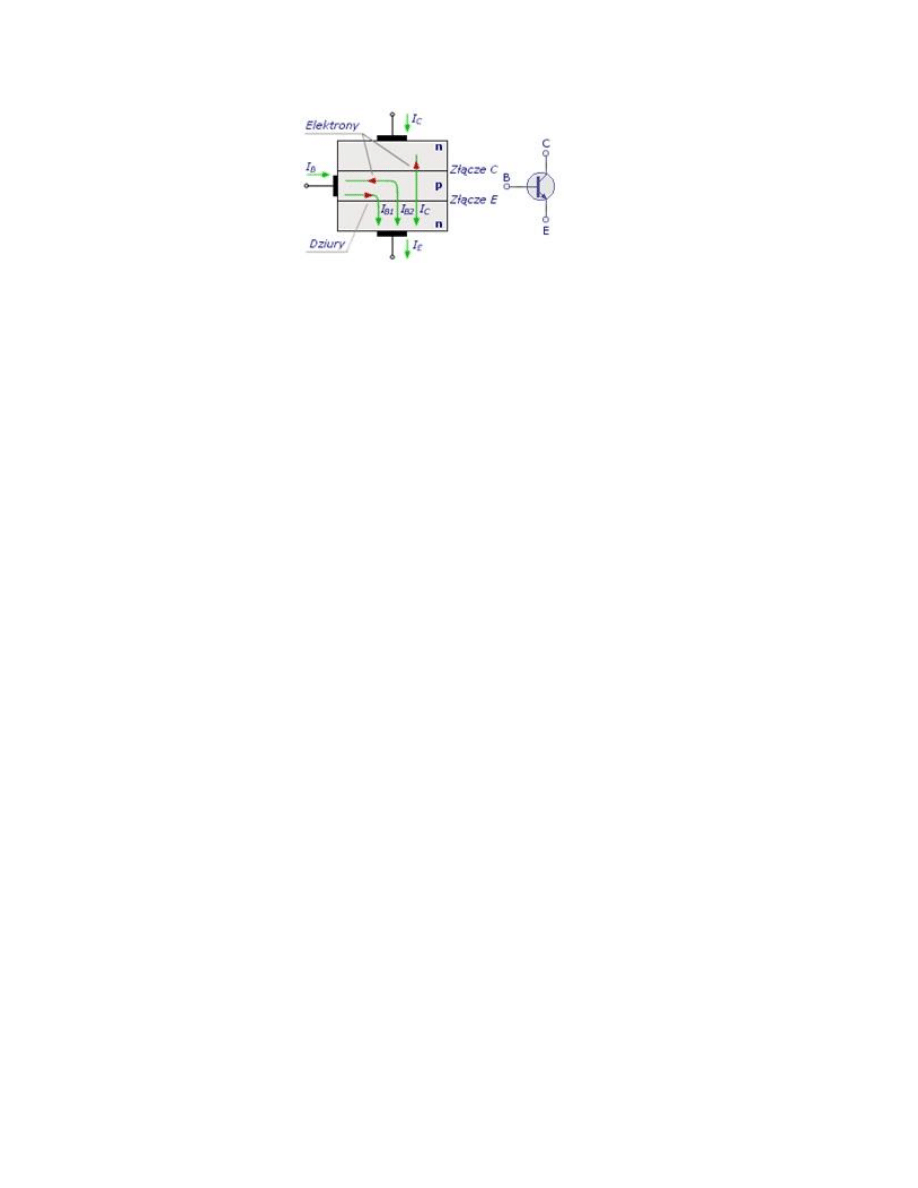
Przez złącze BE tranzystora npn przepływają nośniki większościowe ładunku, w tym przede wszystkim elektrony swobodne z 

emitera  (typ  n)  do  bazy.  Również  dziury  z  obszaru  bazy  (typ  p)  przepływają  przez  złącze  do  emitera.  Prąd  dziurowy  jest 
znacznie mniejszy ze względu na mniejszą liczbę dziur, wynikającą z mniejszej objętości emitera. Mniejsza część elektronów 
swobodnych  po  osiągnięciu  obszaru  bazy  wypełnia  istniejące  tam  dziury,  czyli  podlega  procesowi  rekombinacji.  Znacznie 
większa część elektronów swobodnych po znalezieniu się w obszarze bazy jest przyciągana przez kolektor i przepływa przez 
złącze BC spolaryzowane zaporowo, tak jak własne nośniki mniejszościowe bazy. Wypływające z emitera  elektrony swobodne 
tworzą prąd emitera IE, który rozdziela się w obszarze bazy na mały prąd bazy IB i duży prąd kolektora IC.

 

 

Podstawowe parametry tranzystora 

Bardzo ważnym jest aby strata elektronów w bazie była jak najmniejsza. Miarą tego na ile prąd kolektora odpowiada prądowi 
emitera  jest  współczynnik  a  nazywany  zwarciowym  współczynnikiem  wzmocnienia  prądowego  prądu  emitera  (współczynnik 
wzmocnienia prądowego tranzystora w układzie WB), definiowany jako: 
alfa = (I

C

-I

C0

)/I

E

 

    gdzie I

C0

 

jest prądem złącza kolektorowego spolaryzowanego zaporowo przy I

B

=0. 

    

Konstrukcja  tranzystora  bipolarnego,  a  głównie  małe  rozmiary  bazy  sprawiają,  że  stosunek  między  prądem  kolektora,  a 

prądem  bazy  jest  stały.  Stosunek  I

C

/  I

B

 

nazywa  się  współczynnikiem  wzmocnienia  prądowego  prądu  bazy  (współczynnik 

wzmocnienia prądowego tranzystora w układzie WE) i oznacza się symbolem beta. 
IE = IC + IB  
IC = beta * IB 
    

Zależność pomiędzy obydwoma współczynnikami opisuje równanie: 

beta = alfa / (1-alfa) 
    

Stały stosunek IC/ IB oznacza, ze pewnej wartości prądu bazy IB odpowiada określona wartość prądu kolektora IC. Można 

zatem  zmieniać  prąd  bazy  po  to  aby  uzyskiwać  b-krotnie  większe  zmiany  prądu  kolektora.  Uzyskuje  się  zatem  wzmocnienie 
przez tranzystor mocy sygnału sterującego. Większą moc sygnału w obwodzie kolektora otrzymuje się kosztem mocy czerpanej 
z zasilacza. 
    

Dla  sygnałów  zmiennoprądowych  o  małych  amplitudach  tranzystor  jest  czwórnikiem  liniowym.  Czwórnik  opisywany  jest  za 

pomocą  czterech  wielkości  wyrażających  napięcia  i  prądy  na  jego  wejściu  i  wyjściu.  Aby  móc  opisać  go  za  pomocą  układu 
równań dwóch zmiennych należy dwie z czterech wielkości czwórnika opisać za pomocą dwóch pozostałych. W zależności od 
tego,  które  ze  zmiennych  uznane  zostaną  za  zmienne  zależne,  a  które  za  zmienne  niezależne  otrzymać  można  6  różnych 
układów równań. Najczęściej wykorzystywane są jednak układy z parametrami: 
a) impedancyjnymi: 

U1 = z11I1 + z12I2  
U2 = z21I1 + z22I2 

 
b) admitancyjnymi: 

I1 = y11U1 + y12U2  
I2 = y21U1 + y22U2 

 
c) mieszanymi 

h (układ z parametrami hybrydowymi): 

U1 = h11I1 + h12U2  

I2 = h21I1 + h22U2 

  
    

Tranzystory, tak zresztą jak inne elementy elektroniczne, mają charakterystyczne dla siebie parametry graniczne, tzn. takie 

których przekroczenie grozi uszkodzeniem tranzystora. Są to: 
 
UEBOmax - 

dopuszczalne napięcie wsteczne baza-emiter  

UCBOmax - 

dopuszczalne napięcie wsteczne kolektor-baza  

UCEOmax - 

maksymalne dopuszczalne napięcie kolektor-emiter  

Icmax - 

maksymalny prąd kolektora  

IBmax - 

maksymalny prąd bazy  

Pstmax - maksymalna dopuszczalna moc strat 
  
    

Parametry  takie  jak  Icmax,  UCEOmax,  Pstrmax  wyznaczają  dopuszczalny  obszar  pracy,  który  nosi  również  nazwę 

"dozwolonego obszaru pracy aktywnej" w skrócie SOA (Safe Operating Area).  
    

Parametry  tranzystorów  bipolarnych  w  znacznym  stopniu  zależą  również  od  temperatury.  Prąd  zerowy  ICBO  jest  w 

przybliżeniu  wykładniczą  funkcji  temperatury  i  przy  jej  wzroście  o  10K  w  przybliżeniu  podwaja  swoją  wartość.  Tranzystory 
krzemowe  - 

ze  względu  na  małą  wartość  ICBO  -  mogą  być  stosowane  aż  do  temperatury  ok.  473  K  (200  C). Współczynnik 

wzmocnienia prądowego wzrasta na ogół ze wzrostem temperatury. Wzrost ten jest rzędu kilku procent na stopień kelwina. Przy 
stałej wartości prądu bazy, napięcie baza-emiter UBE za wzrostem temperatury maleje. 

 

Sposoby polaryzacji tranzystora 

Tranzystor składa się z dwóch złączy PN, które mogą być spolaryzowane w kierunku zaporowym lub przewodzenia. W związku 
z tym można wyróżnić cztery stany pracy tranzystora. 

  

Stan tranzystora

 

Kierunki polaryzacji złączy tranzystora

 

 

 

Złącze emiter-baza

 

Złącze kolektor-baza

 

Zatkanie

 

Zaporowy

 

Zaporowy

 

Przewodzenie aktywne

 

Przewodzenia

 

Zaporowy

 

Nasycenie

 

Przewodzenia

 

Przewodzenia

 

Przewodzenie inwersyjne

 

Zaporowy

 

Przewodzenia

 

 

 

   

 

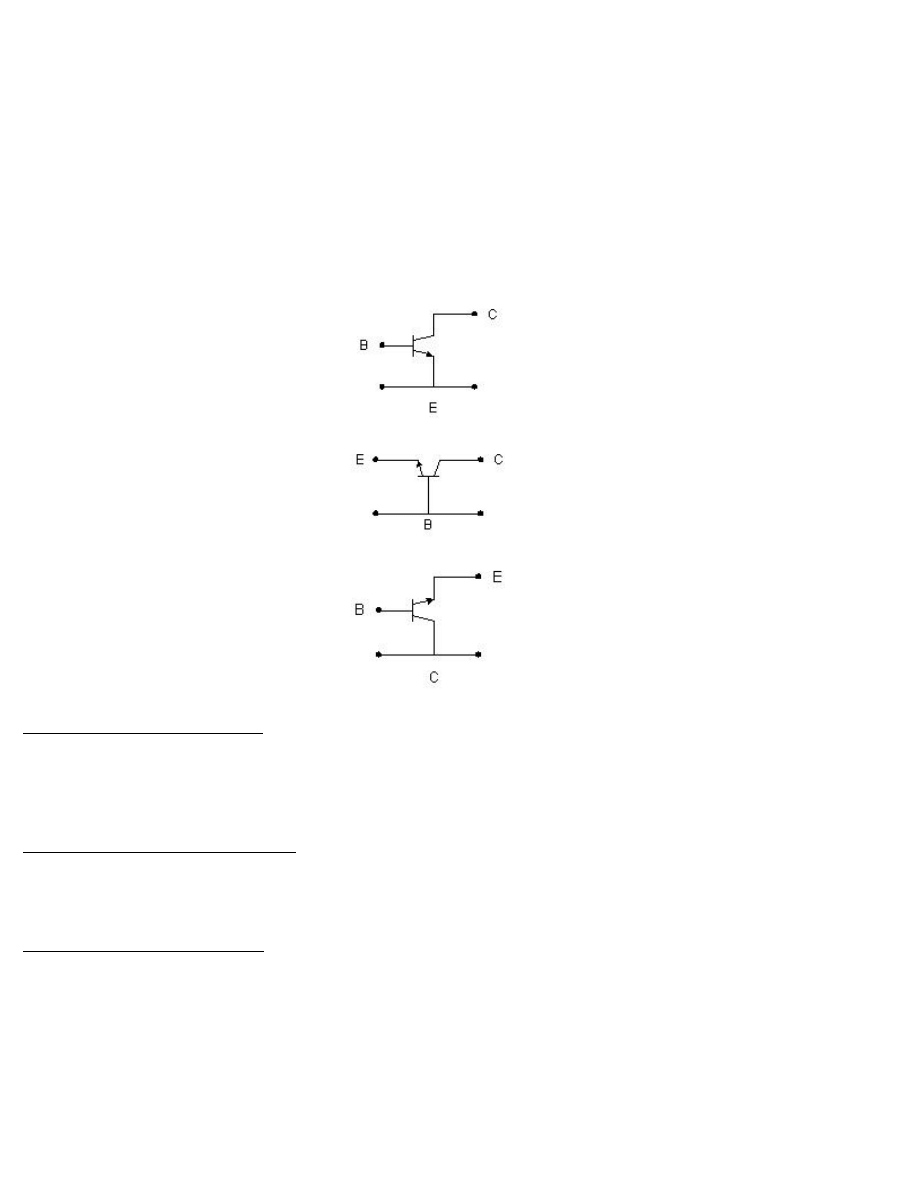
Najważniejszym  z  tych  nich  jest  obszar  pracy  aktywnej,  gdyż  to  właśnie  w  tym  obszarze  tranzystor  wykazuje  swoje 

właściwości wzmacniające, które są wykorzystywane praktycznie. 

 

 

Układy pracy tranzystora 

Tranzystor  jako  element  trójkońcówkowy,  czyli  trójnik  może  być  połączony  w  układzie  elektronicznym  w  rozmaity  sposób.  W 
matematycznym opisie tranzystora - 

trójnika - traktuje się go zwykle jako czwórnik, przyjmując jedną z końcówek jako wspólną 

dla wejścia i wyjścia. W zależności od tego, którą z końcówek wybieramy za wspólną, rozróżnia się konfiguracje: 
1. Układ ze wspólnym emiterem OE (WE) 

 

2. Układ ze wspólną bazą OB. (WB) 

 

3. Układ ze wspólnym kolektorem OC (WC) 

 

Wybór układu pracy jest zależny od przeznaczenia i rodzaju zastosowanego tranzystora. 
    

Tranzystor pracujący w układzie OE jest najczęściej używany w układach elektronicznych ponieważ charakteryzuje się: 

- 

dużym wzmocnieniem prądowym  

- 

dużym wzmocnieniem napięciowym  

- 

dużym wzmocnieniem mocy 

    

Napięcie wejściowe w OE jest odwrócone w fazie o 180 st. W stosunku do napięcia wejściowego. Rezystancja wejściowa jest 

rzędu kilkuset W, a wyjściowa wynosi kilkadziesiąt k W. 
    

Tranzystor pracujący w układzie OB. ma: 

- 

małą rezystancję wejściową  

- 

bardzo dużą rezystancje wyjściową  

- 

wzmocnienie prądowe bliskie jedności 

    Tra

nzystor w tym układzie pracuje przy bardzo dużych częstotliwościach granicznych, niekiedy nawet rzędu GHz. 

    

Tranzystor pracujący w układzie OC charakteryzuje się: 

- 

dużą rezystancją wejściową (co ma istotne znaczenie we wzmacniaczach małej częstotliwości)  

- 

wzmocnieniem napięciowym równym jedności (stąd jest nazywany również wtórnikiem emiterowym)  

- 

dużym wzmocnieniem prądowym 

Zastosowania 

Znaczenie tranzystorów dla obecnej techniki jest olbrzymie, o czym świadczy chociażby fakt, iż od ponad pół wieku  nikomu nie 
udało  się  zrealizować  innego  elementu  elektronicznego,  który  miałby  tak  szerokie  zastosowanie.  Tranzystory  są  używane 

wszędzie, od najprostszego wzmacniacza lub generatora do najbardziej skomplikowanego komputera. Procesory tych urządzeń 
zawiera

ją  w  sobie  miliony  tranzystorów.  Warto  też  podkreślić,  że  pierwszy  komputer,  może  bardziej  maszyna  licząca,  został 

zrealizowany na lampach elektronowych, które były pierwowzorami tranzystorów. Cechowały się podobnymi parametrami, ale 
były  bardziej  zawodne  niż  obecne  tranzystory,  choć  miały  lepsze  charakterystyki  przenoszenia.  Obecnie  producenci,  którzy 
zajmują się sprzętem audio ( przede wszystkim chodzi o wzmacniacze gitarowe) wracają do lamp i ponownie konstruują piece 
gitarowe na lampach elektronowych. 

 

Tranzystory polowe 

Wiadomości podstawowe 

 

Tranzystory  polowe  w  skrócie  FET  (Field  Effect  Transistor),  są  również  nazywane  unipolarnymi.  Działanie  tych  tranzystorów 

polega  na  sterowanym  transporcie  jednego  rodzaju  nośników,  czyli  albo  elektronów  albo  dziur.  Sterowanie  transportem  tych 
nośników,  odbywającym  się  w  części  tranzystora  zwanej  kanałem,  odbywa  się  za  pośrednictwem  zmian  pola  elektrycznego 
przyłożonego do elektrody zwanej bramką. 

 

    

Bramka jest odizolowana od kanału, a więc pomięidzy nią a pozostałymi elektrodami tranzystora polowego, znajdującymi się 

na obu końcach kanału (zwanych źródłem oraz drenem) występuje bardzo duża impedencją.  
    

Tranzystory polowe  zajęły obecnie miejsce tranzystorów bipolarnych,  zalicza się je do najczęściej stosowanych elementów 

dyskretnych. Rewelacyjne  efekty można  uzyskać, stosując tranzystory polowe  w połączeniu  z obwodami scalonymi,  zarówno 
dla niskich jak i wysokich częstotliwości 

 

Klasyfikacja tranzystorów polowych 

Istnieją dwie zasadnicze grupy tranzystorów polowych, różniących się sposobem odizolowania bramki od kanału. Pierwsza to 
tranzystory  polowe  złączowe  zwane  także  tranzystorami  JFET,  w  których  oddzielenie  bramki  od  kanału  jest  wykonane  za 
pośrednictwem  zaporowo  spolaryzowanego  złącza  p-n. W  drugiej  grupie  tranzystorów  polowych  bramka  jest  odizolowana  od 
kanału cienką warstwą izolatora, którym jest najczęściej dwutlenek krzemu. Tranzystory nazywane są tranzystorami z izolowaną 
bramką lub tranzystorami MOSFET.  
    

Tranzystory  MOSFET  można  podzielić  dalej  w  zależności  od  rodzaju  kanału  na  tranzystory  z  kanałem  wbudowanym  ( 

tranzystory  normalnie  załączone,  tranzystory  z  kanałem  zubożanym)  oraz  tranzystory  z  kanałem  indukowanym  (tranzystory 
normalnie wyłączone).  

 

Zasada działania tranzystora JFET 

Zasadę działania opisują poniższe rysunki: 

 

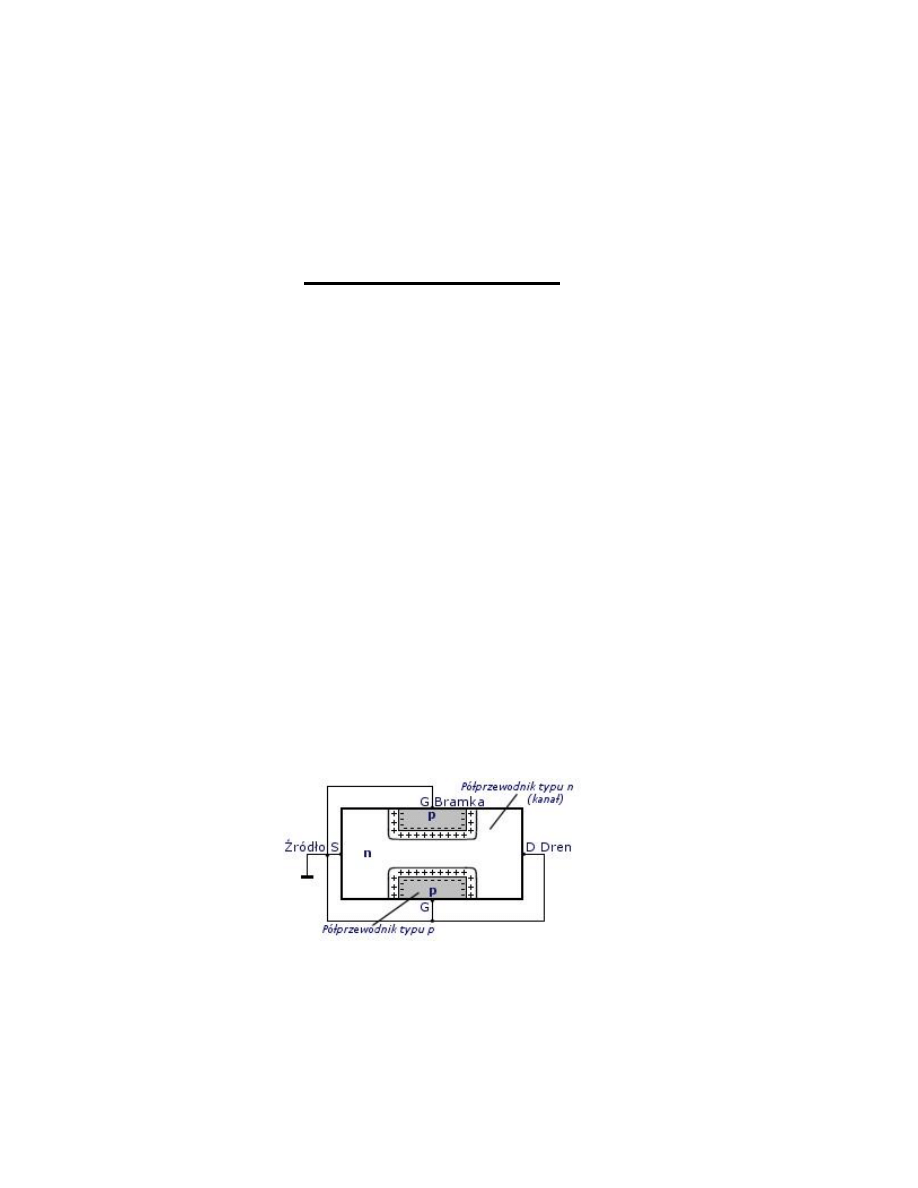
Jednorodny  obszar  półprzewodnika  występujący  między  drenem  i  źródłem  stanowi  kanał,  przez  który  płynie  prąd  i  którego 
rezystancję można  zmieniać przez  zmianę szerokości kanału. Zmianę szerokości kanału  uzyskuje się przez rozszerzenie  lub 
zwężenie warstwy zaporowej złącza p-n, a więc przez zmianę napięcia UGS polaryzującego to złącze w kierunku zaporowym. 

 

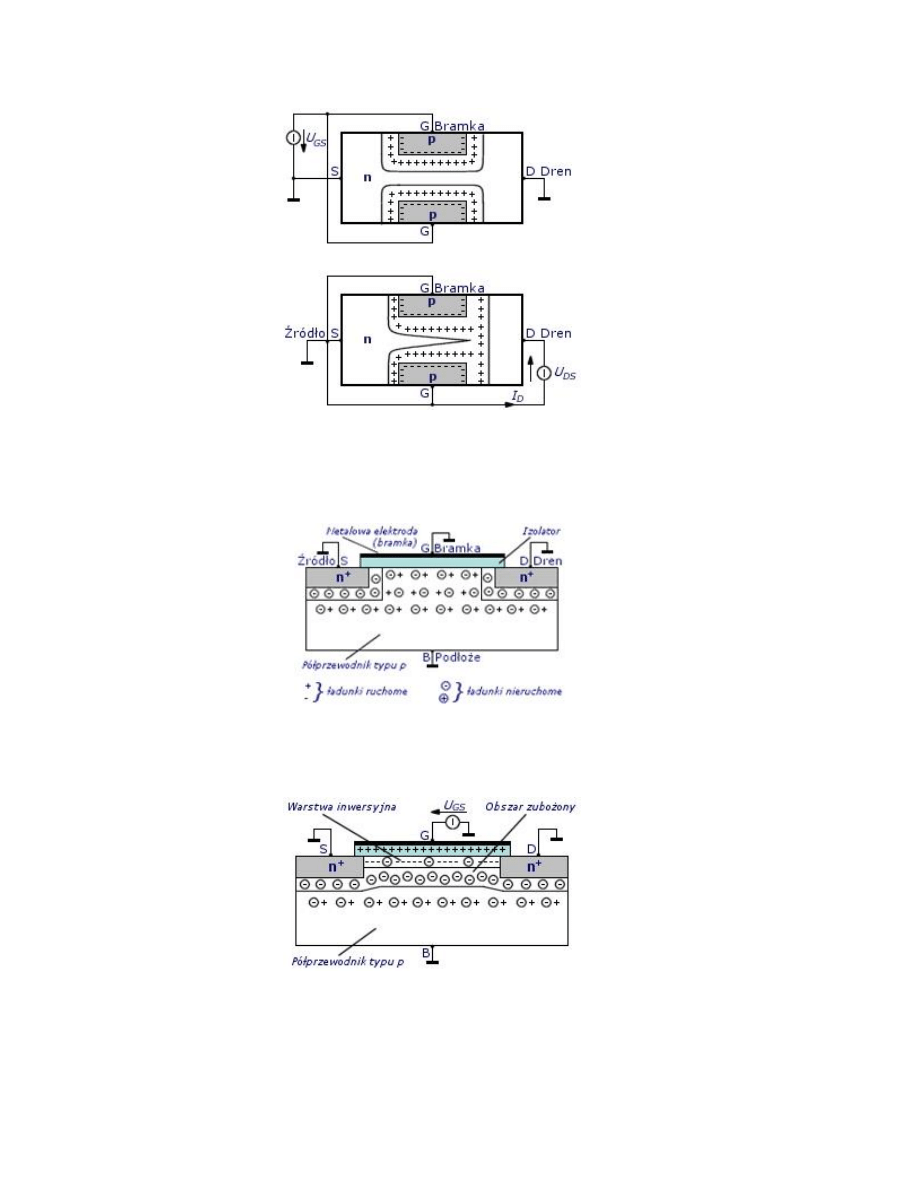
Dalsze zwiększanie napięcia UGS może spowodować połączenie się warstw zaporowych i zamknięcie kanału. 

 

Rezystancja będzie wówczas bardzo duża.  
Można powiedzieć, że tranzystor JFET jest swego rodzaju rezystorem sterowanym napięciow 

 

Zasada działania tranzystora MOSFET 

Poniżej przedstawiono zasadę działania tranzystora MOSFET z kanałem indukowanym typu n i podłożem typu p. 

 

 

   

Na powyższym rysunku przedstawiona jest sytuacja, w której polaryzacja drenu i bramki jest zerowa czyli UDS=0 i UGS=0. 

W  takiej  sytuacji  brak  jest  połączenia  elektrycznego  pomiędzy  drenem  i  źródłem  czyli  brak  jest  kanału.  Jeżeli  zaczniemy 
polaryzować bramkę coraz większym napięciem UGS>0 to po przekroczeniu pewnej wartości tego napięcia, zwanej napięciem 
progowym UT, zaistnieje sytuacja przedstawiona na poniższym rysunku.

 

 

   

 

Dodatni ładunek bramki spowodował powstanie pod jej powierzchnią warstwy inwersyjnej złożonej z elektronów swobodnych 

o dużej koncentracji oraz głębiej położonej warstwy ładunku przestrzennego jonów akceptorowych, z której wypchnięte zostały 
dziury. Powstaje w ten sposób w warstwie inwersyjnej połączenie elektryczne pomiędzy drenem a źródłem. Przewodność tego 
połączenia  zależy  od  koncentracji  elektronów  w  indukowanym  kanale,  czyli  od  napięcia  UGS.  Wielkość  prądu  płynącego 
powstałym kanałem zależy niemalże liniowo od napięcia UDS. Zależność ta nie jest jednak do końca liniowa, ponieważ prąd ten 

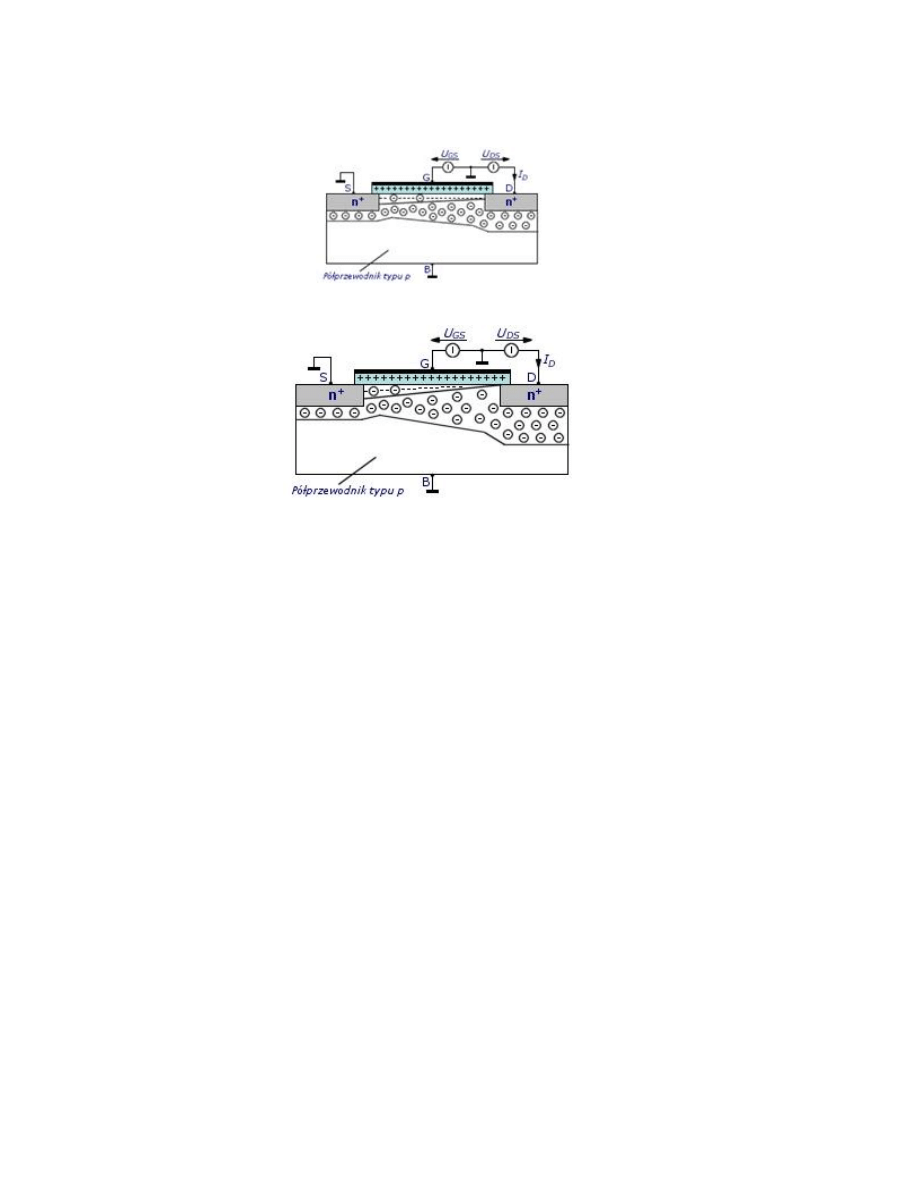
zmienia  stan  polaryzacji  bramki,  na  skutek  czego  im bliżej  drenu,  tym  różnica  potencjałów  pomiędzy  bramką  i  podłożem  jest 
mniejsza, a kanał płytszy.

 

 

Gdy  w  wyniku  dalszego  zwiększania  napięcia  UGS  przekroczona  zostanie  pewna  jego  wartość  zwana  napięciem  odcięcia 
UGSoff, lub wartość napięcia UDS zrówna się z poziomem napięcia UGS (UDS=UGS), powstały kanał całkowicie zniknie. 

 

    

Można  zatem  powiedzieć  iż  dla  małych  wartości  napięcia  dren-źródło  omawiany  tranzystor  typu  MOSFET  stanowi  liniowy 

rezystor, którego rezystancję można regulować za pomocą napięcia bramka-źródło.

 

 

Podstawowe parametry tranzystora oraz parametry różniczkowe gm i gds - ich sens fizyczny 

Tranzystory unipolarne opisuje się, między innymi za pomocą następujących parametrów: 

● 

Napięcie odcięcia bramka-źródło UGS(OFF) , czyli napięcie jakie należy doprowadzić do bramki, aby przy ustalonym 

napięciu UDS nie płynął prąd drenu. 

● 

Napiecie progowe UP - 

napięcie jakie należy doprowadzić, aby przez tranzystor popłynął prad 

● 

Prąd nasycenia IDSS prąd drenu płynący przy napięciu UGS=0 i określonym napięciu UDS. 

● 

Prąd wyłączenia ID(OFF) - prąd drenu płynący przy spolaryzowaniu bramki napięciem |UGS| > |UGS(OFF)| 

● 

Rezystancja statyczna włączenia RDS(ON) - rezystancja między drenem a źródłem tranzystora pracującego w zakresie 

liniowym charakterystyki ID = f(UDS) przy UGS=0; 

● 

Resystancja statyczna wyłączenia RDS(OFF) - rezystancja między drenem a źródłem tranzystora znajdującego się w 

stanie odcięcia 

● 

Dopuszczalny prąd drenu IDmax 

● 

Dopuszczalny prąd bramki IGmax 

● 

Dopuszczalne napięcie dren-źródło UDSmax 

● 

Dopuszczalne straty mocy Ptot max  

    

Właściwości  wzmacniające  tranzystora  określa  stosunek  zmiany  prądu  ID  do  zmiany  napięcia  sterującego  UGS  nazywany 

konduktancją wzajemną (transkonduktancją) gm: 

 

Drugi 

ważny parametr tranzystora gds zwany konduktancją drenu lub konduktancją wyjściową. 

 

Wykorzystując  wyprowadzone  powyżej  parametry  można  przedstawić  jeszcze  jeden  parametr  tranzystora  zwany 
współczynnikiem wzmocnienia napięciowego. 

 

ZASTOSOWANIE TRANZYSTORÓW UNIPOLARNYCH 

Tranzystory znajdują szerokie zastosowania w elektryce, elektronice, technice i podobnych dziedzinach. Ze względu na ilość 
tych zastosowań przedstawię tylko niektóre wybrane. Wzmacniacze. 
- 

Wzmacniacz o bezpośrednim sprzężeniu z tranzystorami MOS 

Wzmacniacz małej częstotliwości. 
Wzmacniacze różnicowe. 
Tranzystorowy wzmacniacz różnicowy posiada szereg istotnych zalet jako wzmacniacz małych sygnałów prądu stałego. Po 
pierwsze, ze względu na kompensowanie się temperaturowych zmian parametrów pary tranzystorów wpływ temperatury jest 
znacznie zmniejszony. Po drugie, sygnały sumacyjne mogą być właściwie wyeliminowane przy starannym zaprojektowaniu 
układu. 
Wyłączniki analogowe 
We współczesnych systemach telemetrii wielokrotnej szeroko stosuje się wyłączniki analogowe dla próbkowania odcinkami 
czasu sygnału wejściowego. Jest oczywiste, że takie wyłączniki powinny przenosić informację bez zniekształceń w stanie 
„włączony”,, mieć wystarczająco dużą rezystancję w stanie „wyłączony”, by przesłuch był znikomo mały mieć czas wyłączania 
rzędu części mikrosekundy. 
Zastosowania tranzystora polowego jako rezystora sterowanego napięciem 
Taki element jest przydatny do wielu zastosowań, wśród których przykładowo wymienimy następujące: 
- 

Tłumiki sterowane napięciowo. 

- 

Mostki z automatycznym równoważeniem. 

- 

Sterowaniem częstotliwością rezonansową oraz dobrocią filtrów aktywnych i pasywnych. 

- 

Mnożenie i dzielenie sygnałów analogowych. 

- 

Regulacja współczynnika sprzężenia zwrotnego we wzmacniaczu lub generatorze. 

- S

terownie napięciowe przesuwników fazowych. 

 

łą dziedzinę, to znaczy jest zdefiniowany dla każdej wartości argumentu (najczęściej czasu) w skończonym lub nieskończonym 
przedziale. 
Modelem deterministycznego sygnału ciągłego je 
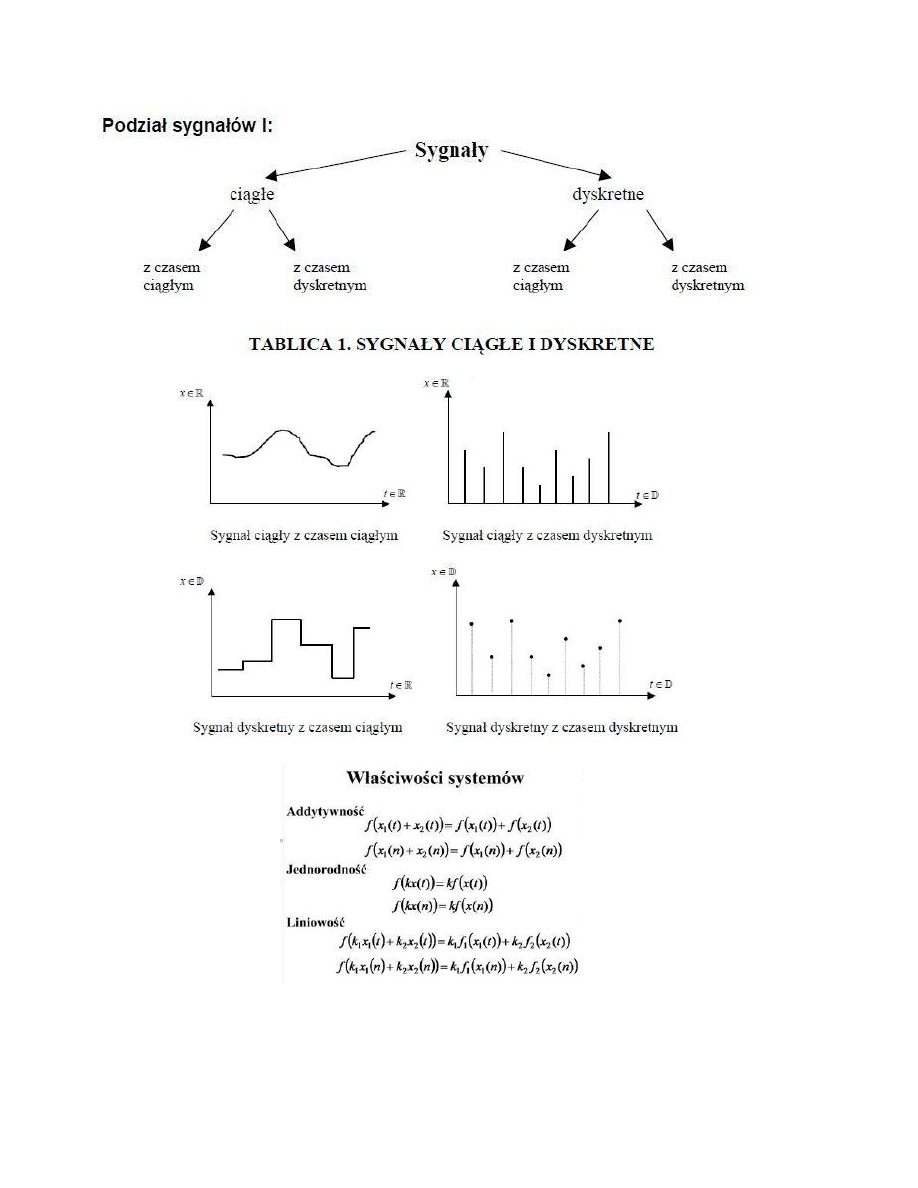
4. Systemy ciągłe i dyskretne: klasyfikacja i opis. 
Systemy ciągłe – wszystkie sygnały (wejściowe i wyjściowe) są funkcjami ciągłymi w czasie i mogą przybierać dowolną 
wartość z obszaru swojej zmienności. Układy te opisuje się zwykle równaniami różniczkowymi. 
Sygnał ciągły – sygnał, który ma ciągst funkcja określona w danym przedziale argumentu. Uwaga: funkcja ta nie musi być 
funkcją ciągłą, w szczególno 
ści może posiadać nieskończenie wiele punktów nieciągłości. 
Przeciwieństwem sygnału ciągłego jest sygnał dyskretny. 
 
Przykłady: 
Przykładem jednowymiarowego sygnału ciągłego jest przebieg zmian napięcia elektrycznego lub natężenia prądu powstały 
przez przetworzenie fali akustycznej na prąd. 
Przykładem dwuwymiarowego sygnału ciągłego jest obraz analogowy zarejestrowany na kliszy fotograficznej, gdzie odcienie 
szarości lub kolor zdefiniowane są dla każdego punktu na płaszczyźnie w granicach wynikających z rozmiaru kliszy. 
 
Sygnał analogowy – sygnał, który może przyjmować dowolną wartość z ciągłego przedziału (nieskończonego lub 
ograniczonego 

zakresem zmienności). Jego wartości mogą zostać określone w każdej chwili czasu, dzięki funkcji 

matematycznej opisującej dany sygnał. Przeciwieństwem sygnału analogowego jest sygnał skwantowany, nazywany również 
dyskretnym (w szczególności: cyfrowym). 
  
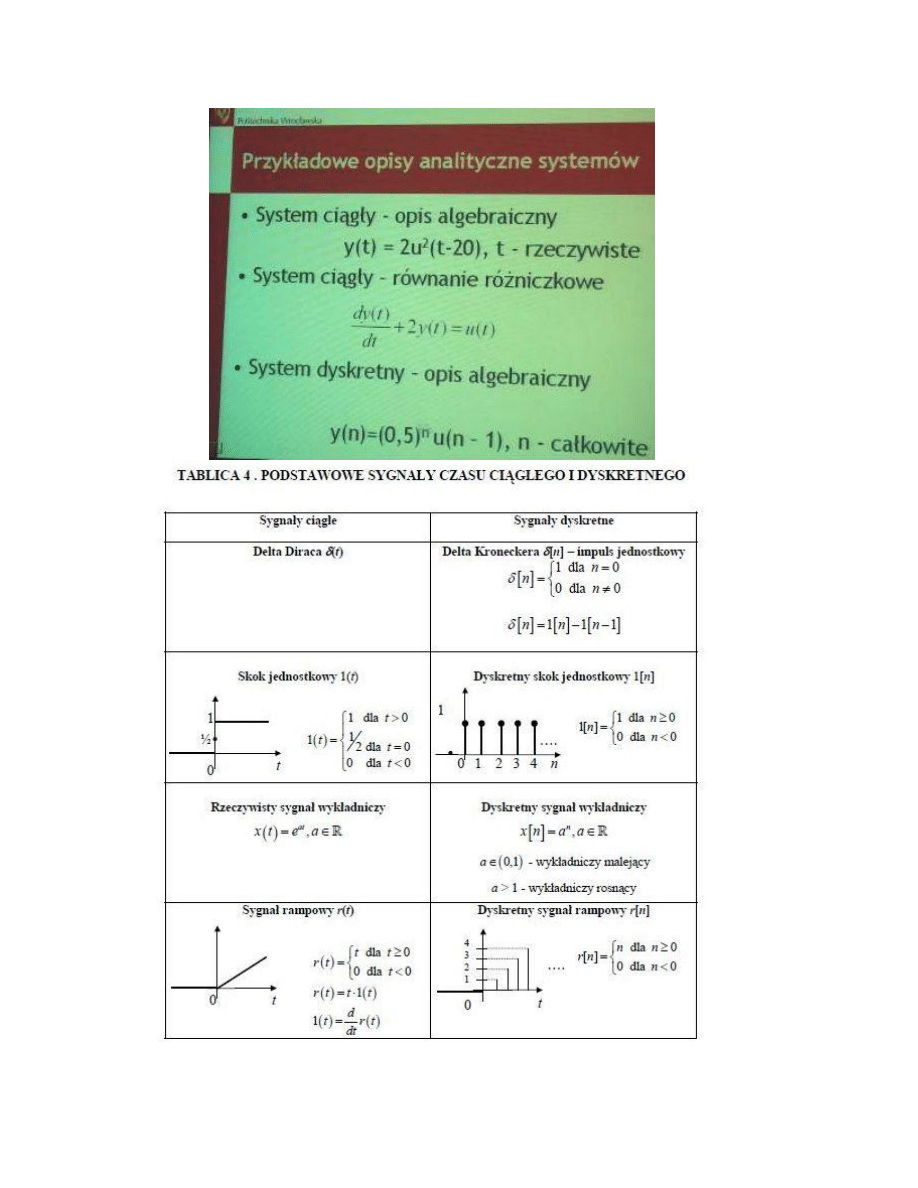
Systemy dyskretne 

– układ jest dyskretny, jeżeli przynajmniej jeden jego sygnał ma charakter dyskretny, tzn. przyjmuje tylko 

określone wartości dla określonych argumentów. Układy takie opisuje się zwykle równaniami różnicowymi. Przy przetwarzaniu 

sygnałów ciągłych (analogowych) na dyskretne (cyfrowe) mamy do czynienia z próbkowaniem i kwantyzacją. Przy 
przetwarzaniu sygnału dyskretnego na ciągły należy pamiętać o Twierdzeniu Kotielnikowa-Shannona i warunku Nyquista. 
 
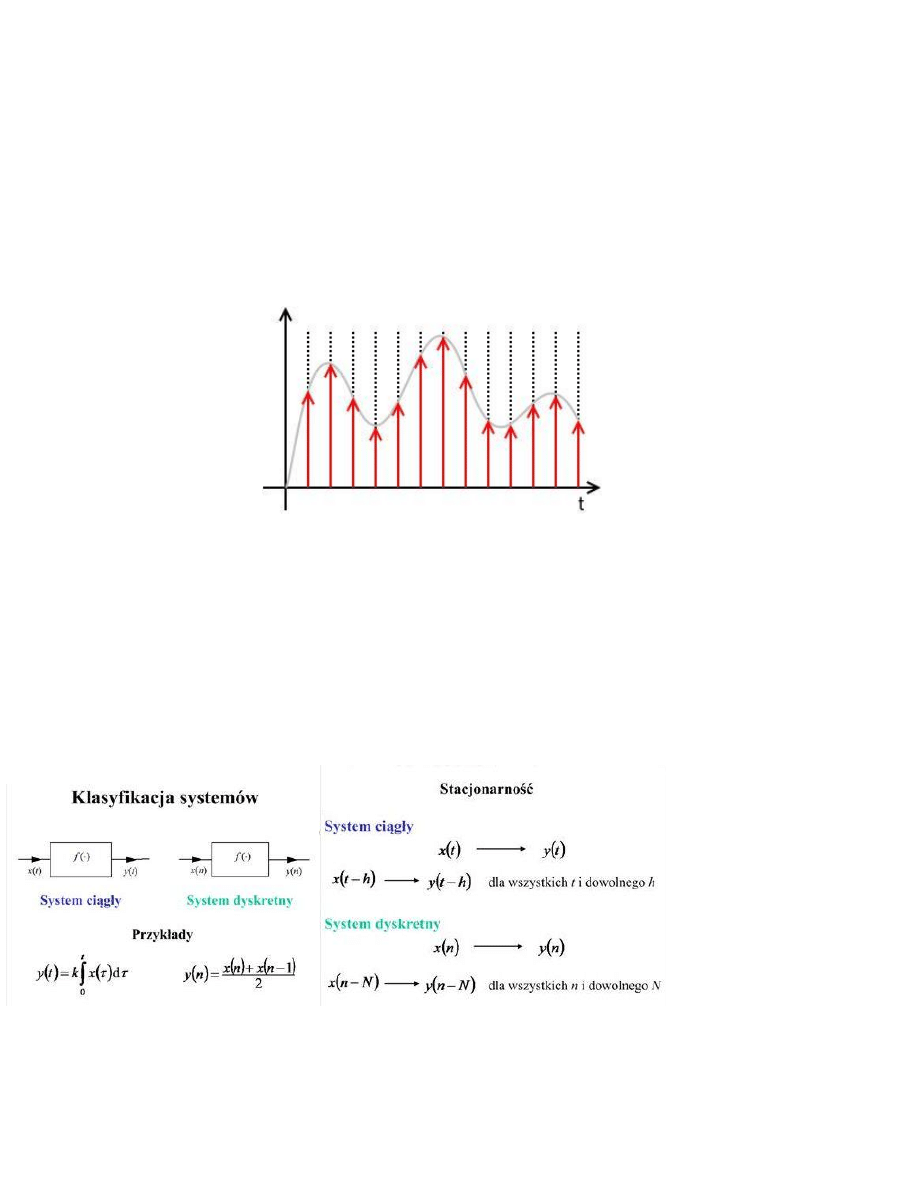
Sygnał dyskretny – model wielkości zmiennej, która jest określona tylko w dyskretnych chwilach czasu. Najczęściej jest to 
sygnał powstały poprzez próbkowanie sygnału ciągłego. 
W odróżnieniu od sygnału ciągłego, sygnał dyskretny nie jest funkcją zdefiniowaną dla ciągłego przedziału argumentów, lecz 
ciągiem liczbowym. Każda wartość ciągu nazywa się próbką (ang. sample). 
W odróżnieniu od sygnału cyfrowego, poszczególne próbki sygnału dyskretnego analogowego mogą przyjmować dowolne 
wartości z nieograniczonego lub ograniczonego zbioru. 
 

 

Rys1. sygnał dyskretny 

 

Sygnał cyfrowy – sygnał, którego dziedzina i zbiór wartości są dyskretne. Jego odpowiednikiem o ciągłej dziedzinie i ciągłym 
zbiorze wartości jest sygnał analogowy. Znaczenie tego terminu może odnosić się do: 
● 

wielkości fizycznej, która z natury jest dyskretna (np. liczba błysków lampy w ciągu godziny) 

● 

wielkości pierwotnie ciągłej i analogowej, która została spróbkowana i skwantowana (np. sygnał na wyjściu komparatora 

napięcia kontrolującego pewien proces w określonych chwilach) 
● 

każdej reprezentacji jednego z powyższych, w tym (najczęściej) w postaci ciągu liczb zapisanych w pamięci maszyny 

cyfrowej (np. plik komputerowy typu WAV). 
Współcześnie telekomunikacja i elektronika powszechnego użytku prawie całkowicie zostały zdominowane przez cyfrowe 
prz

etwarzanie sygnałów, które jest powtarzalne, bardziej niezawodne i tańsze od przetwarzania analogowego. 

  

 

 

 

  

 

 

 

 

 

 

 

  

 

 

 
 

  
5. Zmienna losowa: właściwości, opis. 
http://www.sendspace.com/file/oehewc 

(za dużo wzorów do kopiowania, sorry ;) - E) 

 
7. Modulacje analogowe i cyfrowe. 
Modulacje analogowe 

● 

Modulacje amplitudy 

– zmiana amplitudy 

- DSB-LC (inaczej AM) (ang. Double-Sideband Large Carrier)  
- DSB-SC (ang. Double-Sideband Suppressed Carrier)  
- SSB (ang. single-sideband modulation)  
- VSB (ang. vestigial-sideband modulation)  

● 

Modulacje kąta 

○ 

PM (ang. phase modulation) 

○ 

FM (ang. frequency modulation) 

 
1. Modulacje amplitudy 
 
1.1.  Modulacja AM 
Modulacja AM (ang. Amplitude Modulation

) zwana również A3 lub DSB-LC (ang. Double Sideband with Large Carrier) czyli 

dwuwstęgowa modulacja amplitudy z dużym poziomem fali nośnej. Modulacja AM była przez wiele lat powszechnie 
wykorzystywana w radiofonii w zakresie fal długich, średnich i krótkich. Obecnie nadal jest tam stosowana, chociaż ze względu 
na niską jakość odbioru (ograniczenie przenoszonego pasma i wrażliwość na zakłócenia) coraz mniej jest aktywnych 
nadajników tego typu. Modulację AM wykorzystuje się także w radiotelefonii CB (ang. Citizen’s Band) pracującej w paśmie 
obywatelskim 27MHz oraz w lotnictwie. W systemach z modulacją AM niewielkie różnice w częstotliwości nośnej w 
radiotelefonie pracującym jako nadajnik i w radiotelefonie pracującym jako odbiornik (nawet do ok. 1kHz) nie mają wpływu na 
jakość transmisji. Fakt ten ma duże znaczenie w przypadku urządzeń CB, które są sprzętem powszechnego użytku i powinny 
być tanie. Ponadto zaletą modulacji AM jest bardzo prosty układ demodulacji (tzw. detektor obwiedni, np. detektor szczytowy) 
pracujący bez konieczności odtwarzania przebiegu nośnej w odbiorniku co również ma wpływ na niską cenę odbiorników. 

 
1.1.1. Istota modulacji AM 
Modulacja fali nośnej polega na uzależnieniu amplitudy chwilowej sygnału zmodulowanego od wartości chwilowej sygnału 
modulującego . Funkcja modulująca jest liniową funkcją sygnału modulującego i reprezentuje amplitudę chwilową sygnału 
zmodulowanego . Współczynnik proporcjonalności zwany jest czułością modulatora, natomiast przy braku sygnału 
modulującego stanowi amplitudę sygnału zmodulowanego. 
 
1.2.  Modulacja DSB-SC 
Modulacja DSB-SC (ang. Double Sideband with Suppressed Carrier

) czyli dwuwstęgowa modulacja amplitudy ze stłumioną falą 

nośną. Sygnał DSB-SC zawiera tylko dolną i górną wstęgę boczną, a nie zawiera fali nośnej, co pozwala na poprawę 
efektywności wykorzystania mocy w systemie telekomunikacyjnym w porównaniu do systemu AM. Pasmo zajmowane przez 
sygnał DSB-SC jest jednak takie samo jak w przypadku modulacji AM. Ten rodzaj modulacji nie poprawia więc efektywności 
wykorzystania 

szerokości pasma. 

 
1.2.1. Istota modulacji AM 
W modulacji DSB-

SC harmoniczna fala nośna jest mnożona przez funkcję modulującą , stanowiącą tożsamościową funkcję 

sygnału informacyjnego. Zostaje zatem wytworzony sygnał zmodulowany , będący iloczynem sygnału modulującego i fali 
nośnej. 
 
1.3.  Modulacja SSB 
Modulacja  SSB  (ang.  Single  Sideband

)  zwana  również  J3  należy  do  grupy  sygnałów  jednowstęgowych  i  jest  najczęściej 

stosowana w praktyce. Sygnał SSB posiada widmo odpowiadające jednej wstędze bocznej (dolnej lub górnej) widma sygnału 
AM.  Nie  występuje  w  nim  prążek  fali  nośnej.  Stosowanie  tej  metody  modulacji  jest  o  wiele  efektywniejsze  w  porównaniu  do 
modulacji  DSB-

SC,  gdyż  lepiej jest wykorzystywana  przesyłana moc (dzięki eliminacji jednej  ze  wstęg  bocznych) jak również 

wykorzystanie dostępnej szerokości pasma kanału. Poprawa ta odbywa się bez utraty informacji, ponieważ pełna informacja o 
sygnale  modulującym  jest  przenoszona  w  jednej  wstędze  sygnału  zmodulowanego.  W  praktyce  SSB  jest  powszechnie 
stosowana  w  kr

ótkofalarstwie  i  w  radiotelefonii  CB.  Ze  względu  na  trudność  detekcji  sygnału  SSB,  w  praktyce  stosuje  się 

również  systemy  jednowstęgowe,  w  których  oprócz  wstęgi  bocznej  przesyła  się  również  falę  nośną  przytłumioną  20-70%  jej 
wartości nominalnej. Takie emisje oznacza się jako R3. Spotykane są również systemy, w których oprócz jednej wstęgi bocznej 
przesyłana jest pełna fala nośna. Takie emisje oznacza się H3. Systemy, w których stosowane są modulacje jednowstęgowe z 
pełną  lub  stłumioną  falą  nośną  charakteryzują  się  gorszym  wykorzystaniem  mocy  przesyłanej  niż  systemy  z  modulacją  J3. 
Pierwszy raz modulacja SSB została komercyjnie wykorzystana 7 stycznia 1927 r. w komunikacji radiowej między Londynem a 
Nowym  Jorkiem.  Modulacja  SSB  była  również  wykorzystywana  w  liniach  telefonicznych  jako  cześć  technologii  FDM 
(multipleksacja z podziałem częstotliwości). 
 
1.3.1. Istota modulacji SSB 
Zapis matematyczny sygnału z jednowstęgową modulacją amplitudy SSB powstaje w wyniku pomnożenia zespolonej 
harmonicznej fali nośnej przez zespoloną funkcję modulującą . Zespolona harmoniczna fala nośna jest sygnałem analitycznym 
odpowiadającym rzeczywistej harmonicznej fali nośnej. 
Postać zespolonej funkcji modulującej jest zależna od tego, czy wytwarzany sygnał SSB ma zawierać górną czy dolną wstęgę 
boczną. W przypadku wytwarzania sygnału SSB z górna wstęgą boczną (oznaczanego jako USB – Upper Sideband), 
zespolona funkcja modulująca stanowi sygnał analityczny, odpowiadający rzeczywistemu sygnałowi modulującemu.  
 
1.4.  Modulacja VSB 
Modulacja VSB (ang. Vestigial Sideband

) czyli modulacja z częściowo stłumioną wstęgą boczną. Stacje telewizyjne pracujące w 

systemie NTSC,PAL, SECAM czyli w analogowym formacie wykorzystują tę metodę jeśli video jest transmitowane w AM ze 
względu na dużą ilość danych. Może być również wykorzystywana w cyfrowej transmisji, takiej jak ATSC 8-VSB. Modem firmy 
Milgo 4400/48 (użyty w 1966r.) bazował na modulacji VSB i równomiernej zmiany odkodowywania aby zapewnić 4800 bitową 
transmisję w ponad 1600 Hz kanale. 

 
2. 

Modulacje kąta 

2.1. Modulacja FM 
Modulacja częstotliwości FM (ang. Frequency Modulation) zwana również F3 jest modulacją ciągłą harmonicznej fali nośnej, 
powszechnie stosowaną w radiofonii w zakresie fal ultrakrótkich, w transmisji sygnału w telewizji satelitarnej, sygnału fonii w 
systemach telewizji naziemnej, w krótkofalarstwie i w radiotelefonii CB. 
 
2.1.1. Istota modulacji FM 
W tym rodzaju modulacji, pulsacja chwilowa , a więc także częstotliwość chwilowa fali nośnej jest liniowo zależna od sygnału 
modu

lującego. Fazę chwilową sygnału zmodulowanego FM można wyznaczyć jako wynik całkowania pulsacji chwilowej po 

czasie t. W modulacji częstotliwości FM nie tylko pulsacja, ale także faza chwilowa zmienia się wraz ze zmianami sygnału 
modulującego. Faza chwilowa sygnału zmodulowanego FM składa się ze składnika liniowego narastającego z czasem oraz z 
chwilowej odchyłki fazy . Charakterystyczną cechą, odróżniającą ten rodzaj modulacji od modulacji fazy, jest fakt, że chwilowa 
odchyłka fazy w modulacji FM jest proporcjonalna do całki z sygnału modulującego ,a nie bezpośrednio do sygnału , jak ma to 
miejsce w modulacji fazy PM. W przeciwieństwie do modulacji analogowych, funkcja modulująca jest tutaj nieliniowa 
(eksponencjalna). Modulacja FM jest więc modulacją nieliniową. Rzeczywisty sygnał zmodulowany FM stanowi część 
rzeczywistą zespolonego sygnału analitycznego. 
 
2.2. Modulacja PM 
Modulacja PM (ang. Phase Modulation

) zwana również G3 jest modulacją ciągłą harmonicznej fali nośnej. Modulacja fazy jest 

rzadko  używana  w  systemach  analogowych,  gdyż  modulacja  częstotliwości  (FM)  pozwala  na  zastosowanie  prostszych 
modulatorów  i  demodulatorów  sygnału.  Sygnał  modulowany  fazowo  można  przekształcić  na  sygnał  modulowany 
częstotliwościowo i w ten sposób dokonuje się zazwyczaj demodulacji PM. Modulacja fazy jest natomiast szeroko stosowana w 
transmisji cyfrowej. 
 
2.2.1. Istota modulacji PM 
W tym rodzaju modulacji kąt fazowy fali nośnej jest liniowo zależny od sygnału modulującego. Pośrednio sygnał użyteczny 
wpływa także na pulsację (częstotliwość) chwilową sygnału zmodulowanego. W modulacji PM pulsacja chwilowa sygnału 
zmodulowanego jest liniowo zależna od pochodnej sygnału modulującego. Jest to istotna różnica w porównaniu z modulacją 
FM, w której pulsacja jest proporcjonalna bezpośrednio do sygnału . Rzeczywisty sygnał zmodulowany PM stanowi część 
rzeczywistą zespolonego sygnału analitycznego. 
 
Modulacje cyfrowe 

● 

PSK (phase-shift keying) 

● 

FSK (frequency-shift keying) 

● 

ASK (amplitude-shift keying) 

● 

QAM (quadrature amplitude modulation) 

 
1.1 PSK 
PSK (ang. Phase Shift Keying) kluczowanie fazy) 

– rodzaj modulacji cyfrowej, w której reprezentacja danych odbywa się 

poprzez dyskretne zmiany fazy fali nośnej. 
W przypadku PSK zmieniana jest faza sygnału. Istnieją dwie podstawowe metody wykorzystania fazy sygnału w ten sposób: 

● 

Poprzez kodowanie danych wprost za pomocą fazy, w tym przypadku demodulator musi mieć dostęp do sygnału 

odniesienia. 

● 

Popr

zez kodowanie danych za pomocą zmian fazy, czyli metodą różnicową, wtedy nie potrzebny jest sygnał odniesienia. 

Każdy rodzaj cyfrowej modulacji wykorzystuje skończoną liczbę sygnałów w celu reprezentacji danych. W przypadku PSK 
używana jest skończona liczba faz sygnału, każdej z nich przypisany jest unikalny układ bitów. Zazwyczaj każda faza dekoduje 

tę samą liczbę bitów. Każda sekwencja bitów tworzy symbol reprezentowany przez pojedynczą fazę.Demodulator, specjalnie 
dopasowany do sekwencji symboli, które tworzy modulator, określa fazę otrzymanego sygnału i na tej podstawie odtwarza 
oryginalne dane. Metoda ta wymaga specjalnego sygnału odniesienia, do którego odbiornik mógłby porównać sygnał otrzymany 
w celu określenia fazy. Takie systemy nazywane są systemami koherentnymi. 
 
1.2 FSK 
FSK (ang.) Frequency-Shift Keying 

– modulacja częstotliwości dla sygnałów cyfrowych, czyli kluczowanie z przesuwem 

częstotliwości. Przy stałej amplitudzie harmonicznego sygnału nośnego następuje zmiana częstotliwości: niższej dla symbolu 
"zera logicznego" i wyższej dla "jedynki logicznej" informacji binarnej, czasami przypisanie częstotliwości może być odwrotne. 
Sygnał zmodulowany może przechodzić z jednej częstotliwości w drugą z ciągłością jego fazy lub bez niej. Jest to równoważne 
sytuacji kiedy kluczowane są wyjścia dwóch niezależnych generatorów, albo parametry jednego generatora. 
 
1.3 ASK 
ASK (ang. Amplitude-Shift Keying) 

– kluczowanie amplitudy. Typ modulacji cyfrowej reprezentującej sygnał cyfrowy w postaci 

zmieniającej się amplitudy fali nośnej. Modulacja ASK jest odpowiednikiem analogowej modulacji AM (czyli DSB-LC). Fala 
nośna zwiększa lub zmniejsza swoją amplitudę w zależności od zmieniającego się ciągu bitów. W najprostszym przypadku 
logiczne 0 jest reprezentowane jako b

rak nośnej (amplituda równa 0) natomiast logiczne 1 jest sygnałem harmonicznym o 

określonej amplitudzie. W ASK faza oraz częstotliwość nośnej nie podlega żadnej zmianie. Taki sposób modulacji określa się 
często pojęciem OOK (on-off keying) i był wykorzystywany w przypadku komunikowania się za pomocą alfabetu Morse'a. 
Zaletami ASK są prostota działania oraz relatywnie małe koszty realizacji. Jednak modulacja ta jest silnie podatna na tłumienie 
oraz zakłócenia. Z tego powodu w praktyce wykorzystuje się ją niezwykle rzadko, głównie w transmisjach światłowodowych. 
 
1.4 QAM 
Modulacja QAM (ang. Quadrature Amplitude Modulation). Kwadraturowa modulacja amplitudowo-fazowa. Stosowana m.in. w 
transmisjach DVB-

C. Modulacja QAM jest kombinacją modulacji amplitudy i fazy. Dane formowane są w dwójki, trójki, czwórki 

itd., które odpowiadają zarówno amplitudzie jak i fazie. Tworzone są według diagramu konstelacji (ang.Constellation diagram). 
Nośna powstaje w wyniku sumowania dwóch przebiegów: kosinusoidalnego i sinusoidalnego (powstałego z przesunięcia 
cosinusoidy w fazie o π/2).Dane w postaci cyfrowej dzielone są na dwa strumienie. Następnie każdy strumień zamieniany jest 
na sygnał analogowy w przetworniku cyfrowo analogowym. Analogowy sygnał może przechodzić przez filtr dolnoprzepustowy 
(ang. Low Pass Filter

). W kolejnym etapie jeden sygnał mnożony jest przez nośną (ang. Carrier), a drugi przez nośną 

przesuniętą w fazie o π/2. Na koniec modulacji obydwa sygnały są sumowane i wysyłane jako sygnał QAM. 
 
8. Wzmacniacze operacyjn

e: właściwości i zastosowania. 

Właściwości i parametry. 
          Nazwa wzmacniacz operacyjny 

dotyczyła początkowo układów wzmacniających stosowanych w elektronicznych 

maszynach analogowych, wykonując operacje matematyczne typu: dodawanie, odejmowanie, całkowanie, różniczkowanie. 
Obecnie pojęcie to odnosi się do wzmacniaczy przeważnie o sprzężeniu bezpośrednim, dużym wzmocnieniu i z reguły 
przeznaczonych do pracy w zewnętrznym obwodem sprzężenia zwrotnego. Głównie zewnętrzny obwód sprzężenia zwrotnego, 
decyd

uje o właściwościach całego układu. Większość obecnie produkowanych wzmacniaczy operacyjnych ma wejście 

symetryczne (różnicowe) oraz niesymetryczne wyjście. 

         

 

         

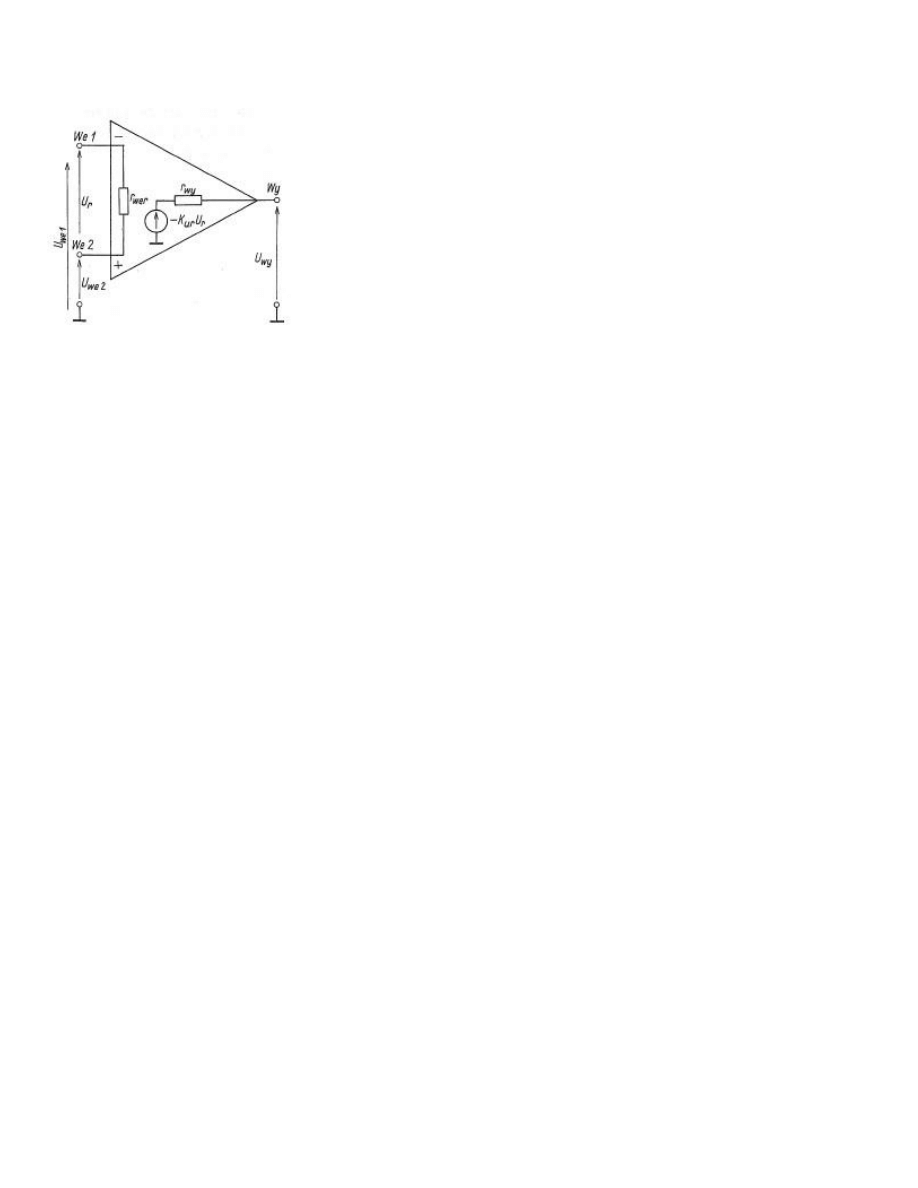
Rysunek jest dla tych, którzy nie pamiętają budowy. 

We1  oznaczone minusem , jest 

wejściem odwracającym (inwersyjnym), a wejście We2, oznaczone plusem – wejściem nie 

odwracającym (nieinwersyjnym).  
 
Jeżeli do wejścia odwracającego zostanie doprowadzone napięcie sinusoidalne, to przesunięcie fazowe między sygnałami 
wejściowym i wyjściowym będzie równe 180°. Przy doprowadzeniu tego samego napięcia do wejścia nieinwersyjnego 
przesunięcie wyniesie zero. Ważną właściwością wzmacniacza operacyjnego jest to, że gdy do obu wejść zostaną 
doprowadzone dwa identyczne sygnały, to sygnał na wyjściu powinien być równy zeru. 
Idealny wzmacniacz operacyjny powinien charakteryzować się: 
·         nieskończenie dużym wzmocnieniem napięciowym, 
·         nieskończenie dużą impedancją wejściową, 
·         zerową impedancją wyjściową, 
·         nieskończenie szerokim pasmem przenoszenia częstotliwości, 
·         nieskończenie dużym zakresem dynamicznym sygnału. 
  
Podstawowe parametry wzmacniacza rzeczywistego: 
1.     Wzmocnienie napięciowe różnicowe Kur. 
2.     Wzmocnienie napięciowe sumacyjne Kus. 
3.     Wsp

ółczynnik tłumienia sygnału sumacyjnego Hs. 

4.     Rezystancja (impedancja) wejściowa różnicowa rwe r (ẕwe r). 
5.     Rezystancja (impedancja) wejściowa sumacyjna rwe s (ẕwe s). 
6.     Rezystancja (impedancja) wyjściowa rwy (ẕwy). 
7.     Wejściowy prąd polaryzacyji Iwe. 
8.     Wejściowe napięcia niezrównoważenia Uwe n. 
9.     Wejściowy prąd niezrównoważenia Iwe n. 
10.  Dryfty: temperaturowy i czasowy wejściowego napięcia i prądu niezrównoważenia. 
11.  Parametry graniczne: maksymalne napięcie wejściowe Uwe max, maksymalne różnicowe napięcie wejściowe Uwe r max, 
maksymalne napięcie wyjściowe Uwy max, maksymalny prąd wyjściowy Iwy max. 
12.  Napięcie Uz i moc Pz zasilania. 
13.  Szerokość pasma częstotliwości: określona częstotliwością graniczną fg, marginesem wzmocnienia A i marginesem fazy α. 
14.  Parametry odpowiedzi na skok napięcia: czas narastania tn, szybkość narastania S, przeregulowanie (przerzut) δu. 
  
Zastosowanie wzmacniacza operacyjnego. 
1.     W układzie wzmacniacza odwracającego. 
2.     W układzie wzmacniacza nieodwracającego – sygnał wejściowy doprowadza się do wejścia nieodwracającego wzm. 
operacyjnego. 

3.     

Wtórnik napięciowy – przyjmując we wzm. nieodwracającym  nieskończoną wartość rezystancji wejściowej na wejściu 

odwracającym, uzyskuje się wtedy wzmocnienie napięciowe równe jedności. 
4.     Inwerter 

– kiedy napięcie wejściowe jest równe napięciu wyjściowemu ze zmienionym znakiem. 

5.     

Wzmacniacz różnicowy – powstaje w wyniku skojarzenia wzmacniacza odwracającego i nieodwracającego, w którym 

napięcie wyjściowe jest proporcjonalne do różnicy napięć wejściowych Uwe 2 i Uwe 1. 
6.     

Sumowanie napięć – kiedy założymy, że rezystancja wejściowa wzmacniacza jest równa nieskończoności, a rezystancje 

są równe otrzymujemy algebraiczne sumowanie napięć. 
7.     

Przetwornik prądu na napięcie – mała rezystancja wejściowa i wyjściowa, a jego napięcie wyjściowe jest proporcjonalne 

do prądu wejściowego  
 
8.     

Przetwornik napięcia na prąd – powoduje przepływ przez rezystancję obciążenia prądu proporcjonalnego do napięcia 

wejściowego. 
9.     W 

układzie różniczkującym  - kondensator C jest dołączony do wejścia odwracającego wzmacniacza operacyjnego, 

natomiast rezystor R 

między wejście a wyjście. 

10.  W 

układzie całkującym (integrator) – otrzymamy go włączając w obwód sprzężenia zwrotnego wzmacniacza, 

kondensator a na wejściu rezystor. 
11.  W diodowych generatorach funkcyjnych. 
12.  W 

układach logarytmujących. 

13.  W 

układach logarytmujących stosunek napięć – po połączeniu dwóch układów logarytmujących i wykorzystując 

wzmacniacz różnicowy. 
14.  Komparator 

– jeden z nielicznych układów w których brak jest sprzężenia zwrotnego. Służy do porównywania dwóch 

napięć lub do określenia zakresu, w których znajduje się napięcie porównywane. Na jedno z wejść wzmacniacza operacyjnego, 
np. na wejście odwracające, podaje się napięcie odniesienia Uod, a na drugie wejście napięcie porównywane Uwe. 
A także: 
1.     

Metody mnożenia bezpośredniego, w których wykorzystuje się zależność napięcia wyjściowego niektórych układów lub 

eleme

ntów od iloczynu wielkości wejściowych. 

2.     Metody modulacyjne

, w których sygnałami wejściowymi moduluje się niektóre parametry sygnałów zmiennych, a 

następnie na ich podstawie określa się iloczyn. 
 
 
 
9. Mikroprocesory: budowa, zastosowania.  
 
Mikroproc

esor jest to scalony układ elektroniczny sterowany rozkazami. Układ cyfrowy wykonany jako pojedynczy układ scalony 

o wielkim stopniu integracji zdolny do wykonywania operacji cyfrowych według dostarczonego ciągu instrukcji. Pełni on funkcje 
obliczeniowe (a

rytmetyczne), steruje przepływem danych  i współpracuje z urządzeniami zewnętrznymi, reaguj,,ąc na wysyłane 

przez nie sygnały. Wykonywane są w technologii LSI (mikroprocesory 8 – bitowe(, VLSI (mikroprocesory 16-bitowe i 32-bitowe) 
lub ULSI (mikroprocesory 64-

bitowe). Firmy wiodące prym w produkcji to: Intel, Motorola, MOS Technology oraz liczne zakłady 

dalekowschodnie. 
Komputer 
 
Mikroprocesor składa się z 3 zasadniczych bloków: 

● 

jednostki sterującej (CU, control unit) – jest to blok odpowiedzialny za pobieranie kodu z zewnętrznej pamięci programu, 

dekodowanie rozkazów, ustalanie adresów. W jego skład wchodzą między innymi rejestry rozkazów, licznik rozkazów, rejestr 
stanu. 

● 

jednostki wykonawczej (EU, execution unit) 

– jest to blok odpowiedzialny za wykonywanie zdekodowanego rozkazu przy 

pomocy jednostki arytmetyczno-logicznej (ALU 

– Arithmetic Logic Unit) oraz rejestrów (wewnętrznej pamięci mikroprocesora, 

zawierającej argumenty operacji oraz ich wyniki). W jego skład wchodzą między innymi rejestry danych i rejestry warunków. 

● 

jednostki adresowej (MU, memory unit) 

– blok odpowiedzialny za pobieranie dostarczanych poprzez magistralę danych z 

pamięci RAM. W jego skład wchodzą między innymi rejestry adresowe i wskaźnik stosu. 
 
 
Do komunikacji między tymi blokami i pamięcią służą magistrale:   

● 

magistrala danych - 

służy do przesyłania danych z/do pamięci i z/do urządzeń wejścia wyjścia, 

● 

magistrala adresowa - 

procesor umieszcza na tej magistrali, adres urządzenia lub pamięci, z ktorym aktualnie się 

komunikuje 

● 

magistral

a sterująca – jest zbiorem dodatkowych sygnałów sterujących Istotnym elementem rozróżniającym architekturę 

procesorów jest lista rozkazów. 
 
 
Wyróżniamy dwa główne typy: 

● 

CISC (Complex Instruction Set Komputer) 

– wykorzystywane rozkazy są różnej długości. Układ wykonujący instrukcje jest 

wspomagany pamięcią ROM, w której zapisane są ciągi operacji odpowiadające rozkazom – zmniejsza to obciążenie magistral. 

● 

RISC (Reduced Instruction  Set Komputer) 

– rozkazy mają przeważnie stałą długość i tworzą podstawowe operacje 

wykonywane przez procesor. Skutkuje to dużym obciążeniem magistrali ze względu na częste odwołania do pamięci. 

● 

VLIW (Very Long Instruction Word) 

– nazwa architektury mikroprocesorów z bardzo długim słowem instrukcji. Obecnie 

VLIW oparta jest o archit

ekturę RISC, najczęściej z czterema, maksymalnie ośmioma jednostkami obliczeniowymi. 

 
Zastosowanie: 
Mikroprocesor (w skrócie μP) łączy funkcje centralnej jednostki obliczeniowej (CPU) w pojedynczym półprzewodnikowym 
układzie scalonym. Pierwszy mikroprocesor działał w oparciu o słowa 4-bitowe, dzięki czemu tranzystory tworzące jego obwody 
logiczne mogły zmieścić się w jednym układzie. 
  
Mikroprocesor umożliwił rozwój mikrokomputerów w połowie lat 70. dwudziestego wieku. Przed tym okresem, elektroniczne 
CPU b

yły konstruowane z zajmujących wiele miejsca indywidualnych urządzeń przełączających, z których każde było 

odpowiednikiem zaledwie kilku tranzystorów. Poprzez zintegrowanie procesora w jeden lub kilka obwodów scalonych o coraz 
wyższej skali integracji (zawierających odpowiednik tysięcy lub milionów tranzystorów), stosunek możliwości do ceny procesora 
znacząco wzrósł. Od połowy lat siedemdziesiątych, dzięki intensywnemu rozwojowi układów scalonych, mikroprocesor stał się 
najbardziej rozpowszechnioną formą CPU, prawie całkowicie zastępując wszystkie inne. 
 
 
 
 
10. Sieci komputerowe: budowa, protokoły, zastosowanie. 
Mianem sieci komputerowej (Computer Network) określa się zespół komputerów i urządzeń końcowych, połączonych między 
sobą łączami komunikacyjnymi, umożliwiającymi przesyłanie danych. Dostęp komputera do sieci komputerowej odbywa się za 
pośrednictwem interfejsu sieciowego. W zależności od rozpiętości fizycznej sieci dzieli się na sieci lokalne (Local Area 
Network), sieci miejskie (Metropolitan Area Netw

ork) oraz sieci rozległe (Wide Area Network). Sieci LAN stosowane są często w 

biurach, fabrykach lub miasteczkach uniwersyteckich. Te pojedyncze sieci, często połączone są ze sobą w większe grupy, w 
ramach jednego miasta, tworzą sieć MAN. Wzajemne połączenie tych sieci pozwala podłączonym do nich komputerom na 
wymianę informacji. Idąc dalej, sieci miejskie ponłączono ze sobą w taki sposób, że rozciągają się na przestrzeni krajów oraz 
kontynentów, tworząc sieć WAN. Taką jedną, wielką światową 
siecią jest właśnie Internet. Takie zorganizowanie łączności pomiędzy komputerami o różnej architekturze oraz obsługiwanych 
przez różne systemy operacyjne, wymusiło ustalenie pewnych standardów komunikacji. Na zlecenie twórcy ARPAnetu, a dalej 
Internetu 

– agencji DARPA (Defense Advanced Research Project Agency) oraz zaangażowaniu MIT, stworzono protokoły 

TCP/IP. Technologia IP (Internet Protocol) odpowiedzialna jest za przekazywanie pakietów w sieci, natomiast TCP 
(Transmission Control Protocol) sprawdza, czy pakiety dota

rły nie zmienione i we właściwej kolejności. 

Sieci można podzielić za względu na rodzaj udostępnianych zasobów, np. P2P (łatwe w budowie, tanie, słaba ochrona danych, 
brak serwera głównego), klient–serwer (serwer gromadzi zasoby, nie ma użytkowników bezpośrednich, są wielodostępowi, 
posiadają pomocniczych klientów np. serwery plików, drukarek, aplikacji, pocztowe, bezpieczeństwa). 
 
Sieci można również podzielić ze względu na ich topologię: 
a) topologia gwiazdy - 

połączenia sieci LAN o topologii gwiazdy z przyłączonymi do niej urządzeniami rozchodzą się z jednego, 

wspólnego punktu, którym jest koncentrator (HUB), okablowanie całej sieci w tym przypadku opiera się na skrętce cztero 
parowej i kart sieciowych z wyjściem na UTP. Odległości pomiędzy komputerami a HUB’em nie powinny przekraczać odległości 
100 metrów. Odmiennie niż w topologii pierścienia, każde urządzenie przyłączone do sieci w topologii gwiazdy może uzyskiwać 
bezpośredni i niezależny od innych urządzeń dostępu do nośnika. W tym celu urządzenia te muszą współdzielić dostępne 
szerokości pasma koncentratora. Topologie gwiazdy stały się dominującym we współczesnych sieciach LAN rodzajem topologii. 
Są one elastyczne, skalowalne i stosunkowo tanie w porównaniu z bardziej skomplikowanymi sieciami LAN o ściśle 
regulowanych metodach dostępu. 
b) 

topologia pierścienia - każda przyłączona do sieci stacja robocza ma w ramach takiej topologii dwa połączenia, po jednym ze 

swoich najbliższych sąsiadów. Połączenie to opierało się na kablu koncentrycznym, przy wykorzystaniu kart sieciowych z 
wyjściem na BNC, oraz trójnika rozdzielającego sygnał. Połączenie takie musiało tworzyć fizyczną pętlę, czyli pierścień. Dane 
przesyłane były wokół pierścienia w jednym kierunku. Każda stacja robocza działa podobnie jak wzmacniak, pobierając i 
odpowiadając na pakiety do niej zaadresowane, a także przesyłając dalej pozostałe pakiety do następnej stacji roboczej 
wchodzącej w skład sieci. Pierwotna, pierścieniowa topologia sieci LAN umożliwiała tworzenie połączeń równorzędnych między 
s

tacjami roboczymi. Połączenia te musiały być zamknięte; czyli musiały tworzyć pierścień. Korzyść płynąca z takich sieci LAN 

polegała na tym, że czas odpowiedzi był możliwy do ustalenia. Im więcej urządzeń przyłączonych było do pierścienia, tym 
dłuższy był ów czas. Ujemna strona tego rozwiązania polegała na tym, że uszkodzenie jednej stacji roboczej najczęściej 
unieruchamiało całą sieć pierścieniową. 
c) topologia magistrali - 

wyróżnia ją to, że wszystkie węzły sieci połączone są ze sobą za pomocą pojedynczego, otwartego 

(czyli umożliwiającego przyłączanie kolejnych urządzeń) kabla. Kabel taki obsługuje tylko jeden kanał i nosi nazwę magistrali. 
Niektóre technologie oparte na magistrali korzystają z więcej niż jednego kabla, dzięki czemu obsługiwać mogą więcej niż jeden 
kanał, mimo że każdy z kabli obsługuje niezmiennie tylko jeden kanał transmisyjny. Oba końce magistrali muszą być 
zakończone opornikami ograniczającymi, zwanymi również często terminatorami. Oporniki te chronią przed odbiciami sygnału. 
Zawsze, g

dy komputer wysyła sygnał, rozchodzi się on w przewodzie automatycznie w obu kierunkach. Jeśli sygnał nie napotka 

na swojej drodze terminatora, to dochodzi do końca magistrali, gdzie zmienia kierunek biegu. W takiej sytuacji pojedyncza 
transmisja może całkowicie zapełnić wszystkie dostępne szerokości pasma i uniemożliwić wysyłanie sygnałów pozostałym 
komputerom przyłączonym do sieci. Typowa magistrala składa się z pojedynczego kabla łączącego wszystkie węzły w sposób 
charakterystyczny dla sieci równorzędnej, długość sieci w tej topologii nie powinna przekroczyć odległości 185 m (licząc od 
jednego terminatora do drugiego). Kabel ten nie jest obsługiwany przez żadne urządzenia zewnętrzne. Zatem wszystkie 
urządzenia przyłączone do sieci słuchają transmisji przesyłanych magistralą i odbierają pakiety do nich zaadresowane. Brak 
jakichkolwiek urządzeń zewnętrznych, w tym wzmacniaków, sprawia, że magistrale sieci lokalnych są proste i niedrogie. Jest to 
również przyczyną ograniczeń dotyczących odległości, funkcjonalności i skalowalności sieci. Topologia ta jest, więc stosowana 
praktyczna jedynie dla najmniejszych sieci LAN. Wobec tego obecnie dostępne sieci lokalne o topologii magistrali są tanimi 
sieciami równorzędnymi udostępniającymi podstawowe funkcje współdziałania sieciowego. Topologie te są przeznaczone 
przede wszystkim do użytku w domach i małych biurach. 
 
11. Sterowniki mikroprocesorowe i ich zastosowanie. 

Sterownik mikroprocesorowy to sterownik, którego architektura oparta jest na mikrokontrolerze pełniącym kluczową 
rolę w jego działaniu. Taki mikrokontroler np. MCS-51 jest odpowiedzialny za operacje numeryczne i logiczne 
związane ze sterowaniem. 
  

Przykładami sterowników mikroprocesorowych są np. Sterownik PLC, Regulator PID, Sterownik CNC, Sterownik 
PAC 
  
1. 

Sterownik PLC - 

uniwersalne urządzenie mikroprocesorowe przeznaczone do sterowania pracą maszyny lub 

urządzenia technologicznego. Sterownik PLC musi zostać dopasowany do określonego obiektu sterowania poprzez 
wprowadzenie do jego pamięci żądanego algorytmu działania obiektu. Cechą charakterystyczną sterowników PLC 
odróżniającą ten sterownik od innych sterowników komputerowych jest cykliczny obieg pamięci programu. Algorytm 
jest zapisywany w dedykowanym sterownikowi języku programowania. Istnieje możliwość zmiany algorytmu przez 
zmianę zawartości pamięci programu. Sterownik wyposaża się w odpowiednią liczbę układów wejściowych 
zbierających informacje o stanie obiektu i żądaniach obsługi oraz odpowiednią liczbę i rodzaj układów wyjściowych 
połączonych z elementami wykonawczymi, sygnalizacyjnymi lub transmisji danych. 
  
2. 

Regulator PID 

– (ang. proportional-integral-derivative controller – regulator proporcjonalno-całkująco-

różniczkujący) – w automatyce, regulator składający się z członu proporcjonalnego P o wzmocnieniu kp, 
całkującego I o czasie zdwojenia Ti oraz różniczkującego D o czasie wyprzedzenia Td. Jego celem jest utrzymanie 
wartości wyjściowej na określonym poziomie, zwanym wartością zadaną. 
Regulatora PID używa się np. do sterowania temperaturą procesu, w tym wypadku działa on jak bardzo dokładny 
termostat. Może również sterować ciśnieniem, natężeniem przepływu, składem chemicznym, siłą, prędkością i 
innymi sygnałami. Regulatory znajdują zastosowanie w przemyśle samochodowym, w tym przypadku ich zadaniem 
je

st utrzymywanie stałej prędkości samochodu bez względu na warunki jazdy (tzw. tempomat). 

  
Aby z regulatora PID zrobić regulator: 
● 

P (proporcjonalny), należy ustawić Ti=∞, Td=0 

● 

PD (proporcjonalno-

różniczkujący), należy ustawić Ti=∞ 

● 

PI (proporcjonalno-

całkujący), należy ustawić Td=0 

  
3. 

Sterownik CNC to typ sterownika mikroprocesorowego, który programuje się za pomocą tzw. G code'u. Nazwa 

sterownika pochodzi od typu sterowania CNC (Computer Numerical Control). Sterowniki te używane są m.in. do 
kontroli takich u

rządzeń jak: frezarki, tokarki a w szerszym zastosowaniu do sterowania robotami fabrycznymi, które 

pracują w tzw. trybie taśmy montażowej np. automaty składające podzespoły samochodowe. W nowoczesnych 
maszynach CNC stosuje się sterowniki pracujące na bazie komputera przemysłowego IPC w technologii "PC-based 
Automation". W tej technologii sterownik CNC działa programowo, a nie sprzętowo, tak jak to odbywało się w 
starego typu dedykowanych sterownikach. Działające w czasie rzeczywistym oprogramowanie TwinCAT zawiera 
jądro systemu CNC, PLC i steruje wszystkimi elementami nowoczesnej maszyny numerycznej. HMI czyli interfejs 
operatora współpracuje z systemem operacyjnym Windows XP który kontroluje wizualizację procesów i pozwala na 
profesjonalne sterowanie maszyn

ą. 

  
4. 

Sterowniki PAC zwane sterownikami automatyki są dużymi systemami sterownikowymi przeznaczonymi do 

obsługi złożonych procesów technologicznych. Wiele dotychczasowych sterowników PLC o największej wydajności 
zostało nazwanych przez producentów sterownikami PAC - przykładem jest tu firma Rockwell wraz ze swoją rodziną 
LOGIX (CompactLogix, ControlLogix). Granica pomiędzy dużymi i wydajnymi sterownikami PLC a sterownikami 
PAC jest obecnie słabo widoczna. 
Współczesne procesy sterowania wykorzystują ogromne ilości sygnałów i danych, począwszy od analogowych i 
cyfrowych urządzeń wejścia/wyjścia, poprzez szybkie kamery wysokiej rozdzielczości, a kończąc na wieloosiowych 

sterownikach ruchu. Takie zastosowania, jak: szybka produkcja, monitoring pracy maszyn w czasie rzeczywistym, 
sterowanie precyzyjne czy sterowanie złożonym procesem, wymagają deterministycznych systemów akwizycji, 
zaawansowanej analizy i algorytmów przetwarzania danych.Wyższej klasy sterowniki PLC w pewnym stopniu 
spełniają te wymagania. Jednakże do wydajnego przetwarzania tych danych trzeba zastosować odpowiednie środki 
informatyczne, m.in. procesory zmiennoprzecinkowe i duże zasoby pamięci. Sterowniki PAC integrują tego rodzaju 
gotowe składniki sprzętowe w ramach systemu czasu rzeczywistego, oferując w ten sposób wydajną platformę dla 
inżynierów automatyki 
 
 
 

 
 
13. Bazy danych i ich zastosowania. 
 
Bazy danych to strukturalne zbiory danych powiązane z systemem komputerowym umożliwiającym zarządzanie danymi, edycję, 
aktualizację, dodawanie, usuwanie, wyszukiwanie. Struktura zbiorów jest ściśle określona; zbiór posiada swoją strukturę, w 
związku z czym zawiera dane jednego konkretnego typu. Baza danych organizuje dane w tabele – kolekcje, element kolekcji 
opisuje obiekt, zdarzenie, każdy rekord tabeli (krotka) składa się z atrybutów. 
  
Podstawowe pojęcia: 
a) tabela 

– jest wizualnym przedstawieniem relacji. W jej budowie można wyróżnić: - wiersze (odpowiedniki krotek) – 

przechowują treść tabeli, muszą się od siebie różnić przynajmniej jedną wartością. Kolejność wierszy jest dowolna. 
Reprezentacja krotki w  terminologii relacyjnej to rekord. 
- 

kolumny (odpowiedniki atrybutów) – zawierają wartości z określonej dziedziny. Kolumny w jednej tabeli mogą mieć taką samą 

dziedziną, ale muszą różnić się nazwami. Kolejność kolumn jest dowolna. Reprezentacja  w terminologii relacyjnej to pole 
(przecięcie wiersza i kolumny) – składowa krotki. 
b) klucz - 

zbiór atrybutów (jednego lub wielu), którego wartość jednoznacznie identyfikuje każdą krotkę (wiersz) w relacji (tabeli). 

Wyróżniamy dwa główne rodzaje kluczy:  klucz główny oraz klucz obcy (atrybut lub kilka atrybutów danej relacji, które 
sąkluczem głównym w innej relacji) 
c) encja 

– podstawowy element modelowania relacyjnego. Nazwa  encji jednoznacznie identyfikuje typ lub klasę rzeczy, które 

opisuje. Należy definiować w przemyślany sposób nowe encje, ponieważ wszystkie się wzajemnie wykluczają; z tego powodu 
każde wystąpienie encji musi być wyraźnie odróżnialne od reszty instancji. Encje posiadająatrybuty, czyli charakteryzujące je 
cechy, przyjmujące wartości z określonego zbioru (dziedziny).  
d) związek – jest to powiązanie zachodzące pomiędzy określonymi atrybutami krotek lub tej samej relacji. Inaczej mówiąc jest to 
logiczne powiązanie między encjami. 
e) relacje 

– po podzieleniu danych na tabele i zdefiniowaniu pól kluczy podstawowych trzeba wprowadzić do systemu bazy 

danych informacje na temat sposobu poprawnego łączenia powiązanych danych w logiczną całość. W tym celu definiuje się 
relacje między tabelami: 

● 

relacja jeden-do-jednego 

– w tego typu relacji każdy rekord w tabeli A może mieć tylko jeden dopasowany rekord z tabeli 

B, i tak samo każdy rekord w tabeli B może mieć tylko jeden dopasowany rekord w tabeli A. Ten typ relacji spotyka się rzadko, 
ponieważ większość informacji powiązanych w ten sposób byłoby zawartych w jednej tabeli. 

● 

relacja jeden-do-wielu 

– jest najbardziej powszechnym typem relacji. W relacji jeden do wielu rekord w tabeli A może mieć 

wiele dopasowanych do niego rekordów w tabeli B, ale rekord w tabeli B ma tylko jeden dopasowany rekord w tabeli A. 

● 

relacja wiele-do-wielu 

– rekord w tabeli A może mieć wiele dopasowanych do niego rekordów w tabeli B i tak samo rekord 

w tabeli B może mieć wiele dopasowanych do niego rekordów w tabeli A. Jest to możliwe tylko przez zdefiniowanie trzeciej 
tabeli, której klucz podstawowy składa się z dwóch pól kluczy obcych z tabel A i B. Relacja wiele-do-wielu jest w istocie dwiema 
relacjami jeden-do-

wielu z trzecią tabelą. 

f) transakcja 

– jest to pewien przemyślany ciąg operacji, które mogą zostać wykonane w całości lub wcale 

g) perspektywa 

– nazywana również widokiem, jest tymczasową strukturą, którądefiniuje się na podstawie innej tabeli lub tabel. 

Może być używana prawie tak samo jak tabela. Nazwy kolumn w perspektywie nie muszą odpowiadać nazwom kolumn w 
źródłowych tabelach. 
  
Zbiór celów stawianych relacyjnym bazom danych: 

● 

wysoki poziom niezależności danych 

● 

przejrzysty wgląd w dane 

● 

uproszczenie operacji wykonywanych przez administratora na bazie danych 

● 

wprowadzenie p

rzystępnych reguł i wskazówek odnośnie zarządzania bazami 

● 

ujednolicenie sposobu zarządzania plikami 

  
Własności relacyjnej bazy danych:  

● 

widziana przez użytkownika jako zbiór relacji,  

● 

dostępny zbiór operatorów umożliwiający wydzielenie lub łączenie części relacji,  

● 

nie istnieją jawne powiązania między relacjami – realizowane są za pomocą danych,  

● 

język zapytań jest deklaratywny,  

● 

użytkownik nie musi znać fizycznej reprezentacji danych,  

● 

pełna niezależność danych.  

 
 
14. Przetwarzanie obrazów, metody ich zastosowania. 
Rozpoznawanie 
ad.23. Zadania i metody rozpoznawania obrazów 
Obraz jest to ilościowy opis obiektu, zdarzenia lub zjawiska. Ogólnie ujmując zadanie rozpoznawania obrazów polega na 
określaniu przynależności obrazów do pewnych klas w sytuacji braku apriorycznej informacji co do reguł przynależności, a 
jedyną dostępną informację stanowi zwykle tzw. ciąg uczący złożony z obiektów, których prawidłową klasyfikację znamy (tzw. 
rozpoznawanie z nauczycielem). 
Rozpoznawanie obrazów można zdefiniować dokładniej jako wieloetapowy proces przetwarzania informacji, podczas którego 
relatywnie duża ilość danych wejściowych zostaje przetworzona na mniejszą ilość danych użytecznych. Proces ten jest 
zakończony klasyfikacją, czyli przypisaniem obiektowi numeru klasy. 
o

biekt wejściowy ?

 

ekstrakcja parametrów ?

 wektor cech ?

 klasyfikacja ?

 klasa 

Schemat klasyfikacji bez nauczyciela: 
wektor cech (dane testowe) 

 klasyfikator 

wynik klasyfikacji 

Schemat klasyfikacji z nauczycielem: 
wektor cech (dane uczące) 

 klasyfikator 

 wynik klasyfikacji 

nauczyciel 

 

Wśród metod rozpoznawania obrazów wyróżnić można: 
a) metody fizjologiczne (biocybernetyczne), w których dąży się do naśladowania procesów umysłowych przez tworzenie modeli 
systemu nerwowego 
b) metody programowe (algoryt

miczne), w których głównym celem jest tworzenie formalnych metod opisu zadania 

rozpoznawania i związanych z nimi algorytmów możliwych do komputerowej realizacji 
 
Metody algorytmiczne: 
● 

algorytmy minimalnoodległościowe: stosuje się pewną przestrzeń metryczną, która definiuje odległość pomiędzy dwoma 

każdymi elementami tej przestrzeni (czyli mówi się o metryce – na przykład Euklidesa, Hamminga). Przykładami takich 
algorytmów są: 

- NM (Nearest Mean - 

najbliższej średniej) – zaliczany do metod wzroców, w których określenie przynależności nieznanego 

obiektu zależy od jego położenia w obszarze wzorca i-tej klasy (sami wyznaczamy wzorzec). Dla każdej klasy liczy się obraz 
przeciętny i uśrednia go po liczbie obrazów. Po wyznaczeniu wzorca liczy się odległość. 
- 

α-NN (Nearest Neighbour - najbliższego sąsiada) – podstawowy algorytm NN ma wadę związaną z jego wrażliwością na błędy 

ciągu uczącego S, ponieważ w przypadku, gdy choć jeden element ciągu uczącego zostanie niepoprawnie sklasyfikowany, to 
podobnie stanie się z całym jego otoczeniem. Dlatego też wprowadzone algorytm α-NN, który zawiera parametr α 
determinujący metodykę rozpoznawania. Parametr α jest małą liczbą całkowitą wybieraną arbitralnie. Zasadę działania tego 
algorytmu można przedstawić następująco: gdy zostaje zadana wartość α i mamy obiekt podlegający rozpoznawaniu, to 
wyznaczamy odległości tego obiektu od wszystkich obiektów ciągu uczącego S, następnie sortujemy elementy ciągu uczącego 
wg rosnących odległości, aby wyselekcjonować α początkowych elementów, potem zaś tworzymy podzbiory dla konkretnych 
klas, aby ostatecznie wyznaczyć funkcję przynależności. 
Algorytmy minimalnoodległościowe są w praktyce chętnie stosowane ze względu na prostotę i intuicyjność, a także dlatego, że 
dają stosunkowo dobre wyniki. Są one jednak kosztowne w realizacji, gdyż wymagają archiwizowania całego ciągu uczącego U 
w pamięci systemu rozpoznającego oraz czasochłonnego obliczenia odległości rozpoznawanego obiektu x od wszystkich 
elementów ciągu uczącego 

, co w ogólnym przypadku zmusza do stosowania dużych mocy obliczeniowych lub godzenia się 

z długim czasem obliczeń. 
● 

algorytm Bayes’a – jeżeli dysponujemy pełną informacją statystyczną, czyli posiadamy dla wszystkich klas wartości 

prawdopodobieństwa i rozkłady obrazów w klasie, to możemy wyprowadzić algorytm optymalny. Minimalizuje on średnie ryzyko. 
Wyznaczenie bayesowskiej reguły decyzyjnej sprowadza się do wyznaczenia dla każdej ustalonej obserwacji cech optymalnej 
decyzji. Algorytm Bayesa jest optymalny pod kątem średniego ryzyka, które definiuje przeciętne prawdopodobieństwo 
popełnienia błędu dla 0-1 funkcji strat. Wykorzystuje informacje probabilistyczną - gęstość obrazów w klasach. W praktyce 
realizowany przy pomocy estymatorów gęstości na podstawie ciągów uczących. Empirycznym odpowiednikiem alg. Bayesa jest 
alg. typu plug-

in (gdzie średnie ryzyko dąży do ryzyka Bayesa). Przy spełnieniu odpowiednich warunków pozwala on osiągnąć 

bardzo dobre wyniki rozpoznawania (właśnie jak typ plug-in). Dla 0-1 funkcji strat algorytm α-NN jest bliski algorytmowi Bayesa. 
 
Przekształcenia obrazu 
1. Przekształcenia kontekstowe obrazu 
  
1.1 Przekształcenia morfologiczne obrazu 
  
Przekształcenia  morfologiczne  są  jednymi  z  najważniejszych  operacji  w  komputerowej  analizie  obrazu,  gdyż  pozwalają  na 
bar

dzo  złożone  operacje,  związane  z  analizą  kształtu  cząstek,  ich  wzajemnego  rozmieszczenia  czy  też  na  złożone  procesy 

symulacji. Przekształcenia morfologiczne są jednym z najważniejszych operacji w komputerowej analizie obrazu, pozwalają na 
najbardziej złożone operacje związane z analizą kształtu elementów obrazu. Obecnie morfologia jest szeroko stosowana jako 
jeden z najbardziej użytecznych zestawów narzędzi przetwarzania i analizy obrazów. Morfologiczne podejście do przetwarzania 
obrazów jest bardzo naturalne. Obraz binarny rozważany jest jako zbiór, z kolei obraz o wielu poziomach szarości jako funkcja. 
Pojęcie filtru morfologicznego jest ściśle związane z pojęciem τ-odwzorowania, czyli operacji niezmiennej względem translacji. 
Filtr  morfologiczny  określany  jest  jako  dowolne  odwzorowanie  monotoniczne  i  niezmienne  względem  translacji,  lub  inaczej 
mówiąc,  dowolne  monotoniczne  τ-odwzorowanie.  Dzięki  temu  wynik  filtracji  jest  taki  sam  niezależnie  od  położenia  zbioru 
reprezentującego  obraz.  Przykładami  prostych  odwzorowań  są  dylacja,  erozja,  otwarcie  i  zamknięcie.  Można  jednak  podać 
wiele innych przykładów. Należy w tym miejscu zwrócić uwagę jeszcze na jeden fakt, iż wszystkie filtry morfologiczne można 
przedstawić  za  pomocą  erozji  i/lub  dylacji.  W  morfologii  sposób,  w  jaki  rozważane  są  obrazy,  sprawia  że  wiele  problemów 
związanych  z  klasycznym  przetwarzaniem,  może  być  rozwiązane  poprzez  mniej  lub  bardziej  skomplikowane  operacje 
morfologiczne. Wadą przekształceń morfologicznych jest duża złożoność obliczeniowa. 
 
Pr

zykładowe zastosowania: 

-Erozja 
-Dylatacja 

-otwarcie obiektu 
-

zamknięcie obiektu 

-

pogrubianie obiektów 

-

ściemnianie obiektów 

-szkieletyzacja 
-gradient morfologiczny 
 
Erozja 

jest  jednym  z  podstawowych  przekształceń  morfologicznych.  Jej  działanie  polega  na  obcinaniu  brzegów  obiektu  na 

obrazie. Dylatacja 

służy do zamykania małych otworów oraz zatok we wnętrzu figury. Obiekty zwiększają swoją objętość i jeśli 

dwa lub więcej obiektów położonych jest blisko siebie, zrastają się w większe obiekty. Dylatacja jest operacją odwrotną erozji. 
Erozje można dokonywać z podstawowymi parametrami oraz za pomocą obiektów strukturalnych zarówno obrazów binarnych 
jak i kolorowych. 
Kolejnymi funkcjami są operacje otwarcia i zamknięcia obiektu. Dwa opisane powyżej podstawowe przekształcenia 
morfologiczne posiadają wspólną wadę. Mianowicie w wyniku ich działania powierzchnia obiektów na obrazie ulega znacznej 
zmianie. Erozja przyczynia się do zmniejszania obiektów, a dylatacja do ich zwiększania. Sposobem na pozbycie się tej 
niedog

odności jest stosowanie tych dwóch przekształceń w parze. Istnieją dwie możliwości zestawienia ich razem, dające różne 

rezultaty. Są to operacje otwarcia i zamknięcia, które można zdefiniować jako:  
 
otwarcie = erozja + dylatacja, 
zamknięcie = dylatacja + erozja. 
Parametr n 

w obu funkcjach określa wielkość elementu strukturalnego użytego do wykonania operacji erozji i dylatacji. 

  
Następnymi operacjami są pogrubianie i ściemnienie obiektów. Polegają one na nałożeniu lub odcięciu wierzchniej warstwy 
obiektu 

znajdującego się na obrazie na przyłożeniu szablonu strukturalnego SE do każdego punktu obiektu w ten sposób, żeby 

punkt centralny pokrywał się z analizowanym punktem. W procesie ściemniania wartość punktu nie zmienia się, gdy SE 
pokrywa się z jego sąsiedztwem lub zmienia się wartość 0, gdy szablon SE pasuje do sąsiedztwa rozpatrywanego punktu. W 
procesie pogrubiania relacje są odwrotne. 
  
Szkieletyzacja 

to zbiór wszystkich punktów, które są w równych odległościach od co najmniej dwóch punktów należących do 

brzegu rozpatrywanego obiektu. Proces ten jest wykorzystywany do wyznaczania szkieletów (osiowych punktów) 
analizowanych figur. 
  
Gradient morfologiczny 

dla funkcji ciągłej L dwóch zmiennych x1 i x2 o ciągłych pochodnych jest zdefiniowany jako 

dwustronny wektor [dL/dx1,dL/dx2].  
 
1.2 Filtracja obrazu 
  
Filtracja to usuwanie szumu z obrazu. Intuicyjnie szum jest stochastycznym odchyleniem sygnału od jego wartości rzeczywistej. 
Zadaniem filtracji jest eliminacja tego szumu głównie za pomocą metod przetwarzania obrazu. W procesie przetwarzania 
obrazów filtry wykorzystywane są do szeregu operacji poprawy jakości i parametrów obrazów. 
  
Zastosowania to min. filtr Sobela, filtr wykrywający narożniki, filtr medianowy i uśredniający, filtry ekstremalne, filtr adaptacyjny 
oraz filtry uśredniające jak również filtracja wybranego fragmentu obrazu. 
  
2. Przekształcenia bezkontekstowe obrazu 
Przekształcenia  bezkontekstowe,  zwane  inaczej  przekształceniami  punktowymi,  są  to  przekształcenia  dotyczące  stopnia 
szarości  lub  nasycenia  barwy  każdego  punktu  obrazu  oddzielnie. W  przekształceniach  punktowych  wartości  stopnia  szarości 
lub nasycenia barwy poszczególnych punktów obrazu są wynikiem operacji algebraicznych prowadzonych tylko na tym punkcie 
- 

nie są brane pod uwagę punkty z jego otoczenia. 

Operacje nieliniowe są to przekształcenia, w których stopień szarości obrazu wynikowego jest zadaną funkcją nieliniową stopnia 
szarości obrazu źródłowego. Klasycznymi funkcjami tego typu są omówione w dalszej części funkcje: 
-   pierwiastkowania obrazu. 
-   logarytmowania obrazu. 
Operację pierwiastkowania stopni szarości lub nasycenia barwy danego punktu obrazu można zapisać w postaci: 
L2(m,n)=sqrt(L1(m,n)) 
Zastosowanie funkcji pierwiastkowej powoduje podwyższenie kontrastu w obszarze małych wartości L1(m,n). Otrzymany obraz 
wynikowy musi być odpowiednio znormalizowany omawianymi wcześniej metodami. 
Operację logarytmowania stopnia szarości lub nasycenia barwy danego punktu obrazu można zapisać w postaci: 
L2(m,n)=log(L1(m,n)+1) 
Zastosowanie 

funkcji kwadratowej powoduje podwyższenia kontrastu w obszarze dużych wartości L(m.n) (oznacza to generalne 

rozjaśnienie  obrazu  z  bardzo  silnym  różnicowaniem  najjaśniejszych  partii.  Otrzymany  obraz  wynikowy  również  musi  być 
odpowiednio znormalizowany. 
Prz

ekształceniom  arytmetycznym  poddawany  jest  stopień  szarości  lub  nasycenia  barwy  danego  punktu  obrazu.  Stopień 

szarości  lub  nasycenia  barwy  w  danym  punkcie  obrazu  wynikowego  jest  wynikiem  wykonanej  operacji  arytmetycznej  nad 
stopniem szarości lub nasycenia barwy w odpowiadającym mu punkcie obrazu źródłowego. 
Operacje  liniowe  są  to  przekształcenia,  w  których  stopień  szarości  obrazu  wynikowego  jest  liniową  funkcją  stopnia  szarości 
obrazu źródłowego. Do operacji liniowych można między innymi zaliczyć: 
-   dodawanie lub odejmowanie liczby k do obrazu. 
-   

mnożenie lub dzielenie obrazu przez liczbę k. 

Należy zwrócić uwagę, że operacje arytmetyczne prowadzone na obrazach mogą dawać zaskakujące rezultaty. Często w ich 
wyniku otrzymuje się jedynie jednolity biały lub czarny obszar, albo inne dziwne efekty. Związane jest to z faktem, że w obrazie 
wynikowym reprezentowanych jest jedynie 256 stopni szarości (od czerni, której odpowiada 0. do bieli, której odpowiada 255), 
lub 256 nasycenia barwy dla każdego koloru. Wynik operacji arytmetycznych czę-sto przekracza wartość 255 lub jest ujemny. 
Możliwe są tutaj trzy podejścia do otrzymanego wyniku: 
-   

wszystkie punkty o wartości równych lub wyższych od 255 są wyświetlane jako biel, natomiast wszystkie punkty o mniejszych 

lub 

równych zero jako czerń, "ten sposób prezentacji wyników operacji arytmetycznych to metoda nasycenia, 

-     

wszystkie  punkty  o  wartości  powyżej  255  są  traktowane  jako  wynik modulo  p  (p  =  256).  Ten  sposób  prezentacji  wyników 

operacji arytmetycznych to metoda modulo. 
-     

po  każdej  operacji  arytmetycznej  jest  wykonywana  normalizacja  obrazu.  Ten  sposób  prezentacji  wyników  operacji 

arytmetycznych to metoda z normalizacją albo metoda klasyczna. 
Normalizację  można  zdefiniować  jako  operację  punktową  polegającą  na  zmianie  wartości  stopni  szarości  poszczególnych 
punktów  obrazu  źródłowego  L1(m,n)  do  ustalonego  zakresu  tych  wartości  na  obrazie  wynikowym  L2(m,n),  według  zadanej 
funkcji  (najczęściej  liniowej).  Częstym  przypadkiem  występującym  w  praktyce  są  obrazy,  w  których  z  powodu  nadmiernego 
kontrastu  trudno  rozróżnić  w  pewnych  obszarach  szczegóły.  Na  przykład  fotografując  bramę  wjazdową  do  domu  o  fasadzie 
oświetlonej słońcem stajemy przed wyborem: 
-     

albo  prawidłowo  naświetlimy  tak  zwane  tło,  a  wtedy  wnętrze  bramy  po-zostanie  niemal  czarne  (czyli  nie  potrafimy  tam 

rozróżnić szczegółów), 
-   

albo też warunki ekspozycji dopasujemy do wnętrza bramy, co spowo-duje. że fasada budynku wyjdzie na zdjęciu jako jasna 

plama (oczywiście też bez szczegółów). 
 
 
15. Miary i oceny dok

ładności algorytmów przybliżonych. 

Algorytmy  przybliżone  (aproksymacyjne)  generują  przybliżone  rozwiązanie  zadania,  które  najczęściej  nie  jest  optymalne,  ale 
różni  się  od  niego  niewiele  w  sensie  przyjętej  miary  dokładności.  Algorytmy  przybliżone  stosowane  są  do  rozwiązywania 
problemów, dla których znalezienie rozwiązania dokładnego w rozsądnym czasie nie jest możliwe. W szczególności do tej grupy 
problemów należą problemy NP-trudne, których rozwiązania nie da się uzyskać w czasie wielomianowym. 
  

Korzystając  z  algorytmów  przybliżonych  istotna  jest  ocena  ich  dokładności,  czyli  oddalenie  skonstruowanego  rozwiązania  w 
sensie  wartości  funkcji  od  optimum.  Istnieją  różne  metody  oceny  dokładności  algorytmów  aproksymacyjnych.  Trzy 
najważniejsze to: oszacowanie najgorszego przypadku, ocena probabilistyczna i ocena eksperymentalna. 
  
Analiza najgorszego przypadku - 

jest to oszacowanie, które pokazuje, jaki jest maksymalny błąd rozwiązania wygenerowanego 

przez  algorytm  aproksymacyjny  w  stosunku  do  rozwiązania  optymalnego,  przy  czym  jest  to  niezależne  od  rozwiązywanej 
instancji danego problemu. Oszacowanie polega na znalezieniu takiej instancji rozwiązywanego problemu, dla której algorytm 
popełni  największy  błąd.  Błąd  ten  definiuje  się  jako  iloraz  wartości  funkcji  celu  rozwiązania  otrzymanego  algorytmem 
przybliżonym  przez  wartość  funkcji  celu  rozwiązania  optymalnego,  dla  problemu  minimalizacyjnego,  oraz  odwrotność  tego 
ilorazu, dla problemu maksymalizacyjnego. 
Zdefiniowano dwie wartości oszacowania najgorszego przypadku:  
– bezwzględne: 

, 

 - 

zbiór wszystkich instancji problemu  . 

- asymptotyczne: 

 

 
Ocena  probabilistyczna  - 

najgorszy  przypadek  nie  zawsze  jest  interesujący,  bo  jest  to  najczęściej  sztucznie  skonstruowany 

problem daleki od instancji problemów występujących w rzeczywistości. Pożądania wydaje się ocena średniego zachowania się 
algorytmu aproksymacyjnego. W analizie probabilistycznej przyjmuje się, że wartości parametrów są realizacjami niezależnych 
zmiennych losowych o takich samych rozkładach (i.i.d.). Dla tak określonego problemu 

,  gdzie  n 

jest liczbą generowanych 

wartości  parametrów,  zazwyczaj  najpierw  wykonuje  się  probabilistyczną  analizę  wartości,  która  pozwala  wyrazić  w  prosty 
sposób  asymptotyczną  wartość  optimum  funkcji  celu  OPT(

)  za  pomocą  parametrów  problemu.  Następnie  dokonuje  się 

probabilistycznej  ocena  badanego  algorytmu  aproksymacyjnego  A

,  traktując  wartość  rozwiązania  konstruowanego  przez  ten 

algorytm jako zmienną losową A(

). Wyróżnia się tutaj dwie miary oceny: 

 
– błąd względny, definiowany jako procentowe odchylenie od optimum: 

, 

 
-  

błąd bezwzględny - silniejsza miara zdefiniowana następująco: 

. 

 
W przypadku obu miar oceny bada się zbiegać do 0.  
Wyróżnia się trzy rodzaje zbieżności: 
 
– zbieżność z prawdopodobieństwem 1: 

 

 
- 

zbieżność według prawdopodobieństwa: 

, 

 
- 

zbieżność według średniej: 

 

 
Ocena eksperymentalna - 

służy do badania zachowania średniego (przeciętnego) rozwiązań konstruowanych przez algorytmy 

aproksymacyjne. Polega ona na porównaniu, w sensie wartości funkcji celu, rozwiązań skonstruowanych przez dany algorytm z 
rozwiązaniami optymalnymi dla dużej (reprezentatywnej) liczby konkretych przypadków rozważanego problemu. Ponieważ 
znalezienie optimum jest często bardzo trudne lub wręcz niemożliwe korzysta się z innych możliwości: 
● 

znalezienie wartości tzw. dolnego ograniczenia wyznaczanego przez osłabienie założeń w problemie wyjściowym, 

● 

porównanie wartości suboptymalnych rozwiązań z wartościami rozwiązań konstruowanych przez algorytmy wykładnicze, 

których obliczenia przerwano z powodu przekroczenia terminu wykonywania obliczeń, 
● 

porównanie z rozwiązaniami uzyskanymi przypadkowo. 

 
 
16. Systemy operacyjne komputerów. 
Zadaniem systemu operacyjnego jest przekształcenie surowego sprzętu w maszynę łatwą w użyciu. Wraz ze sprzętem tworzy 
o

n  maszynę wirtualną, która zapewnia: 

1) obsługę we/wy: uwalnia użytkownika od konieczności rozumienia złożoności sprzętu we/wy 
2) obsługę pamięci operacyjnej: O.S. powinien zapewnić podział pamięci pomiędzy procesy, użytkowników oraz obsługę 
pamięci wirtualnej. 
3) system plików: zazwyczaj działa w pamięci dyskowej. Umożliwia użytkownikowi pobieranie informacji za pośrednictwem 
nazw symbolicznych oraz pozwala nadać strukturę gromadzonym informacjom. 
4) ochronę zasobów i obsługę  błędów: w wielu współczesnych systemach z zasobów korzysta wielu użytkowników lub 
procesów  w jednym czasie. Zasoby użytkowników muszą być chronione przed skutkami działania innych procesów (oraz 
błędami samych użytkowników) 
5) współdziałanie programów: Maszyna wirtualna umożliwia współdziałanie programów tak, aby np. wyniki jednego mogły 
służyć jako dane wejściowe innych. 
6) sterowanie programami: Maszyna wirtualna zapewnia interfejs, za pośrednictwem którego użytkownik porozumiewa się z nią 
w języku wyższego poziomu niż maszynowy. 
  
Większość systemów operacyjnych stosowanych w mikrokomputerach stanowią:  
1) systemy dla indywidualnego użytkownika (MS-DOS, MS-Windows, MacOS, BeOS, ...). 
2) systemy sterowania procesami (przemysłowymi, kontrola środowiska, monitorowanie stanu pacjentów, ...).  
3) Systemy przepytywania plików (bazy danych).  4) Systemy przetwarzania transakcji (rezerwowanie miejsc w samolotach, 
operacje bankowe,...)  
5) Systemy wielodostępne (wielu użytkowników wykonujących różne zadania). 
  
Porównanie popularnych systemów operacyjnych komputerów osobistych (MS-DOS, rodzina MS-Windows, Unix/Linux): 
MS-

DOS należy do systemów, które pozwalają na wykonywanie tylko jednego programu (procesu). Systemy MS-Windows 9x, 

NT oraz 2000 Pro pozwalają na wykonywanie współbieżne kilku procesów. System MS-Windows 2000 Server oraz systemy 
UNIXopodobne pozwalają na wykonywanie wielu współbieżnych procesów oraz stworzenie wielu maszyn wirtualnych dla 
użytkowników. Systemy MS-DOS, MS-Windows 9x obsługują tylko maszyny jednoprocesorowe. Na maszynach z kilkoma 
procesorami można uruchamiać systemy firmy Microsoft oparte na technologii NT, a więc MS-Windows NT, 2000 oraz 
oczywiście UNIX/Linux.  
  
Aktualnie ważnym kierunkiem rozwoju systemów operacyjnych są systemy sieciowe. Porównajmy je pod względem 
oferowanych usług:  
1) serwery wydruku: wszystkie  systemy rodziny Windows potrafią udostępniać w sieci drukarki podłączone do dowolnego 
komputera. W  systemie Linux do drukowania uruchamia się specjalny proces. Można także skorzystać z pisania do pliku 
reprezentującego drukarkę (każde urządzenie we/wy w systemach Uniksowych jest reprezentowane przez plik). Jeżeli chcemy 

udostępnić drukarkę podłączoną do komputera z Linuksem w otoczeniu sieciowym systemów MS-W. można wykorzystać pakiet 
SMB (samba). 
2) Se

rwery aplikacji: Idea zdalnego uruchamiania aplikacji pojawiła się dla komputerów mainframe (dużych i drogich), aby 

efektywnie wykorzystać ich zasoby.  Łączenie się z systemem za pomocą terminala (zarówno w trybie tekstowym, jak i w  
środowisku graficznym X-Windows) i uruchamianie  aplikacji jest standardem w systemach Uniksowych. Z pozostałych rolę 
serwera aplikacji może spełniać jedynie MS-W. 2000 server. 
3) Serwery plikowe: swoje dyski w sieci mogą udostępniać wszystkie systemy oprócz MS-DOS (oczywiście jeśli nie zainstaluje 
się np. Novela). Systemy Windows serii 9x nie pozwalają jednak na swobodną kontrolę praw dostępu do plików. Kontrolę na 
poziomie zasobów zapewniają systemy MS-W. NT, 2000 oraz Linux z pakietem Samba. 
 
 
17. Zadania optymalizacji i tech

niki ich rozwiązywania. 

Celem optymalizacji dla danego problemu jest wyznaczenie rozwiązania, które jest najlepsze według przyjętego kryterium 
jakości (planowanej drogi, poniesionego kosztu itp.) spośród wszystkich rozwiązań dopuszczalnych. O  optimum w punkcje x 
(optymalnych wartościach decyzyjnych) można mówić, gdy wartość funkcji celu w tym punkcje jest najlepsza (najmniejsza lub 
największa) z możliwych do osiągnięcia. Funkcja minimalizowana/maksymalizowana nazywana jest funkcją celu, a limity 
zużycia zasobów ograniczeniami. 
  
Zadania optymalizacji: 
a) liniowe 
Są to zadania, w których optymalizuje się funkcję linową postaci: 

 

 

 

gdzie macierz A ma rozmiar m x n

. Współczynniki w wektorze c często zwane są cenami (albo kosztami). Najczęściej do 

rozwiązania stosuje się algorytm simplex. 
b) nieliniowe 
Są to zadania, w których optymalizuje się funkcje nieliniowe, zazwyczaj w postaci wypukłej. Można wyróżnić zadania z 
ograniczeniami i bez ograniczeń. W pierwszego rodzaju zadań są zdefiniowane funkcje ograniczające wartości poszczególnych 
zmiennych decyzyjnych, co powoduje,  że nie każde rozwiązanie jest dopuszczalne. W drugiego rodzaju zadań wszystkie 
rozwiązania są dopuszczalne. W zadaniach z ograniczeniami stosuje się tzw. funkcje kary za przekroczenie ograniczeń, często 
jednak także kary za zbliżenie do ograniczeń. 
  
Metody: 
zadania optymalizacji liniowe 

– Simpleks 

zadania optymalizacji nieliniowe 

– metody gradientowe i bezgradientowe: 

- 

gradientowe: największego spadku, zmodyfikowana metoda Newtona 

- bezgradientowe: Gaussa

–Seidla, Powella, metoda poszukiwań prostych 

  
Zadania optymalizacji nieliniowej w praktyce najczęściej występują z ograniczeniami. Wśród metod optymalizacji z 
ograniczeniami można wyróżnić cztery następujące podejścia: 
1. sprowadzanie probl

emu do postaci bez ograniczeń poprzez zastosowanie transformacji zmiennych niezależnych w taki 

sposób,  że funkcja celu pozostaje niezmieniona; 
2. modyfikacja funkcji celu przez wprowadzenie do niej wyrażenia reprezentującego karę za naruszenie ograniczeń; 
3.  modyfikacja kierunku poszukiwań w otoczeniu ograniczeń przez: 
- generowanie kierunku dopuszczalnego (np. metoda Zoutendijka), 
- rzutowanie kierunku gradientu (np. metoda Rosena); 
4.  tworzenie tzw. „ograniczonego sympleksu” (metoda complex) 

 
W typowym 

algorytmie poszukiwania minimum bez ograniczeń zaczynamy od jakiegoś punktu początkowego i generujemy 

kolejne punkty, które powinny przybliżać się do rozwiązania optymalnego. Typowe metody, w których wykorzystuje się 
pochodnąminimalizowanej funkcji (metody gradnientowe) charakteryzują się tym,  że iteracje zbiegają stopniowo do otoczenia 

punktu optymalnego  

, a następnie szybko do samego   . W wielu algorytmach optymalizacji bez ograniczeń, szczególnie w 

algorytmach gradientowych, wykorzystuje się ideę poszukiwania wzdłuż kierunku. Punktem wyjścia jest określenie punktu 
początkowego poszukiwań. Następnie w każdej iteracji wyznacza się koleiny kierunek poszukiwań (w różny sposób dla różnych 
metod) i przeszukuje kierunek w celu znalezienia punktu minimum (ma

ksuimum) wzdłuż kierunku, tzn. punktu o możliwie 

najlepszej wartości funkcji celu, położonego na prostej wyznaczonej przez aktualne przybliżenie rozwiązania optymalnego i 
kierunek poszukiwań. Tym co różni poszczególne metody jest sposób poszukiwań i zastosowana metoda minimalizacji 
kierunkowej. 
  
Metoda najszybszego spadku j

est najprostszą z metod kierunków poprawy. Oparta jest na modelu liniowym minimalizowanej 

funkcji. Jako kierunek poszukiwań przyjmuje się kierunek minus gradientu (

). Metoda najszybszego spadku jest 

jednak wolna i zawodna. 
  
Metodę Newtona w wersji podstawowej wprowadza się przy wykorzystaniu modelu kwadratowego minimalizowanej funkcji. 
Model kwadratowy otrzymujemy z obciętego rozwinięcia w szereg Taylora drugiego rzędu w punkcje aktualnego przybliżenia 
rozwiązania. W tej wersji nie przewiduje się minimalizacji w kierunku i w rezultacie metoda ta jest zbieżna tylko lokalnie (tzn. 
wtedy, gdy punkt początkowy jest dostatecznie blisko optymalnego). Aby zwiększyć obszar zbieżności stosuje się 
zmodyfikowaną wersję metody Newtona (poprawka Newtona jest stosowana do generacji kierunku poszukiwań). 
  
Metoda gradientów sprzężonych jest następną metoda opierająca się na modelu kwadratowym funkcji celu. W metodzie tej jako 
pierwszy kierunek przyjmuje

my kierunek minus gradientu (jak w metodzie najszybszego spadku), a w następnych iteracjach 

generujemy kierunki sprzężone na podstawie informacji o nowej pochodnej i poprzednim kierunku. 
  
Bezgradientowe metody 

minimalizacji w kierunku generalnie opierają się na założeniu o unimodalności funkcji celu. Funkcja jest 

unimodalna w przypadku, gdy ma tylko jeden punkt stacjonarny (tzn. taki, w którym zeruje się pierwsza pochodna funkcji). Do 
typowych metod bezgradientowej minimalizacji w kierunku należą: metoda złotego podziału oraz bezgradientowa metoda 
aproksymacji kwadratowej.  
 
 
18. Systemy dynamiczne, opisy własności. 
System dynamiczny przekształca sygnał wejściowy u(t) w sygnał wyjściowy y(t), czyli przekształca jedną funkcję czasu w inną. 
Na wartości wielkości wejściowych takiego systemu w chwili t mają wpływ nie tylko wartości wejściowe w tej właśnie chwili, ale 
również ich wartości w chwilach wcześniejszych od t. Reakcja układu dynamicznego zależy od warunków początkowych, 
pobudzenia i własności samego systemu. 
  
Możemy dokonać klasyfikacji systemów między innymi ze względu na następujące kryteria: 
a) ze względu na liniowość układu: 

● 

systemy liniowe 

– można je opisać za pomocą równań liniowych algebraicznych, różniczkowych, różnicowych lub 

całkowych 

● 

systemy nieliniowe 

– zawierają przynajmniej jeden element nieliniowy; w praktyce każdy układ jest nieliniowy, lecz zwykle 

w przybliżeniu zakłada się jego liniowość lub linearyzuje się jego nieliniową charakterystykę 
b) ze względu na charakter sygnałów: 

● 

systemy ciągłe – wszystkie sygnały wejściowe i wyjściowe są funkcjami ciągłymi w czasie i mogą przyjmować dowolną 

wartość z obszaru swojej zmienności. Zwykle opisuje się je przy pomocy równań różniczkowych 

● 

systemy dyskretne 

– przynajmniej jeden sygnał ma charakter dyskretny, czyli przyjmuje tylko określone wartości dla 

określonych argumentów. Zwykle opisuje się je równaniami różnicowymi. 
c) ze względu na liczbę wejść i wyjść: 

● 

systemy jednowymiarowe 

– jedno wejście i wyjście 

● 

systemy wielowymiarowe 

– wiele wejść i wyjśćd) ze względu na charakter zmienności wymuszeń i parametrów: 

● 

systemy deterministyczne 

– ich działanie można przedstawić za pomocą pewnej funkcji czasu 

● 

systemy stochastyczne 

– działanie systemu można przedstawić przy pomocy mechanizmów probabilistycznych 

(s

ygnałów losowych, rozkładów prawdopodobieństwa) 

e) ze względu na wpływ czasu na parametry: 

● 

systemy stacjonarne 

– o parametrach niezależnych od czasu 

● 

systemy niestacjonarne 

– o parametrach zależnych od czasu 

  
Do opisu systemów dynamicznych wykorzystuje się: 
 
a) Równanie różniczkowe/różnicowe 
Jest to podstawowy opis systemu dynamicznego, który jednoznacznie określa transmitancję. Rozwiązanie tego równania 
informuje w sposób jednoznaczny o tym, jaka przy danym warunku początkowym jest reakcja systemu na pobudzenie. 
Równanie to oblicza się zazwyczaj dwiema metodami: 

● 

metoda klasyczna 

– polega na wyprowadzeniu równania charakterystycznego, obliczeniu pierwiastków tego równania i 

wyznaczeniu stałych na podstawie warunków początkowych. Metoda ta jest ciężka do stosowania w przypadku równań 
wyższego rzędu. 

● 

metoda operatorowa 

– pozwala znacznie uprościć tok obliczeń. Polega ona na znalezieniu przekształcenia 

pozwalającego zastąpić równania różniczkowo-całkowe zwykłymi równaniami algebraicznymi. Stosuje się w tym celu 
transformatę Laplace’a. Systemy istniejące w rzeczywistości są z reguły nieliniowe, stąd opis liniowym równaniem 
różniczkowym jest jedynie przybliżeniem zachowań danego systemu. 
 
b) Transmitancję (funkcję przejścia) 
 
c) Współrzędne stanu 
W przypadku układów liniowych i nieliniowych coraz częściej stosuje się opis własności układu z użyciem współrzędnych stanu. 
Ten sposób opisu ma pewną przewagę nad opisem przy pomocy równania różniczkowego lub transmitancji, gdyż w ich 
przypadku trzeba przyjąć warunki początkowe równe zeru. 
  
Charakterystyką czasową układu nazywa się przebieg w czasie odpowiedzi układu na określony standardowy sygnał wejściowy, 
podany na wejście układu będącego w stanie równowagi. Stosowanie tych samych sygnałów wejściowych do badania różnych 
układów pozwala na porównanie właściwości dynamicznych tych układów i ich klasyfikację. Sygnały wejściowe do określania 
charakterystyk czasowych muszą mieć postaćumożliwiającą pełną identyfikację dynamiki układu.  
  
Do opisywania i porównywania własności dynamicznych układów oprócz charakterystyk w dziedzinie czasu stosuje się także 
charakterystyki w dziedzinie częstotliwości. Charakterystyka częstotliwościowa opisuje odpowiedź układu na wymuszenie 
harmoniczne (sinusoidalne) o częstotliwości zmieniającej się w określonym zakresie.