1
Obliczanie wsp
Obliczanie wsp
ó
ó
ł
ł
rz
rz
ę
ę
dnych na powierzchni
dnych na powierzchni
elipsoidy obrotowej
elipsoidy obrotowej
Problem obliczania współrzędnych geodezyjnych na powierzchni elipsoidy
obrotowej oraz azymutów i długości linii geodezyjnych nosi nazwę
przenoszenia wspó
ł
rz
ę
dnych.
Wyróżnia się dwa rodzaje problemu: tzw.
zadanie wprost
i
zadanie odwrotne
. Dotyczą one:
1.
zadanie wprost
: obliczenia współrzędnych geodezyjnych
B
2
,
L
2
punktu
P
2
i azymutu (odwrotnego)
A
21
linii geodezyjnej, gdy znane
są współrzędne geodezyjne
B
1
,
L
1
punktu
P
1
, długość linii
geodezyjnej
s
12
oraz azymut (wprost)
A
12
pod jakim linia geodezyjna
wychodzi z punktu
P
1
2.
zadanie odwrotne
: obliczenia długości linii geodezyjnej
s
12
łączącej
na powierzchni elipsoidy dwa punkty o znanych współrzędnych
P
1
(
B
1
,
L
1
) i
P
2
(
B
2
,
L
2
) oraz obliczenie azymutów linii geodezyjnej
(wprost i odwrotnego)
A
12
i
A
21
Podzia
Podzia
ł
ł
metody przeniesienia
metody przeniesienia
wsp
wsp
ó
ó
ł
ł
rz
rz
ę
ę
dnych
dnych
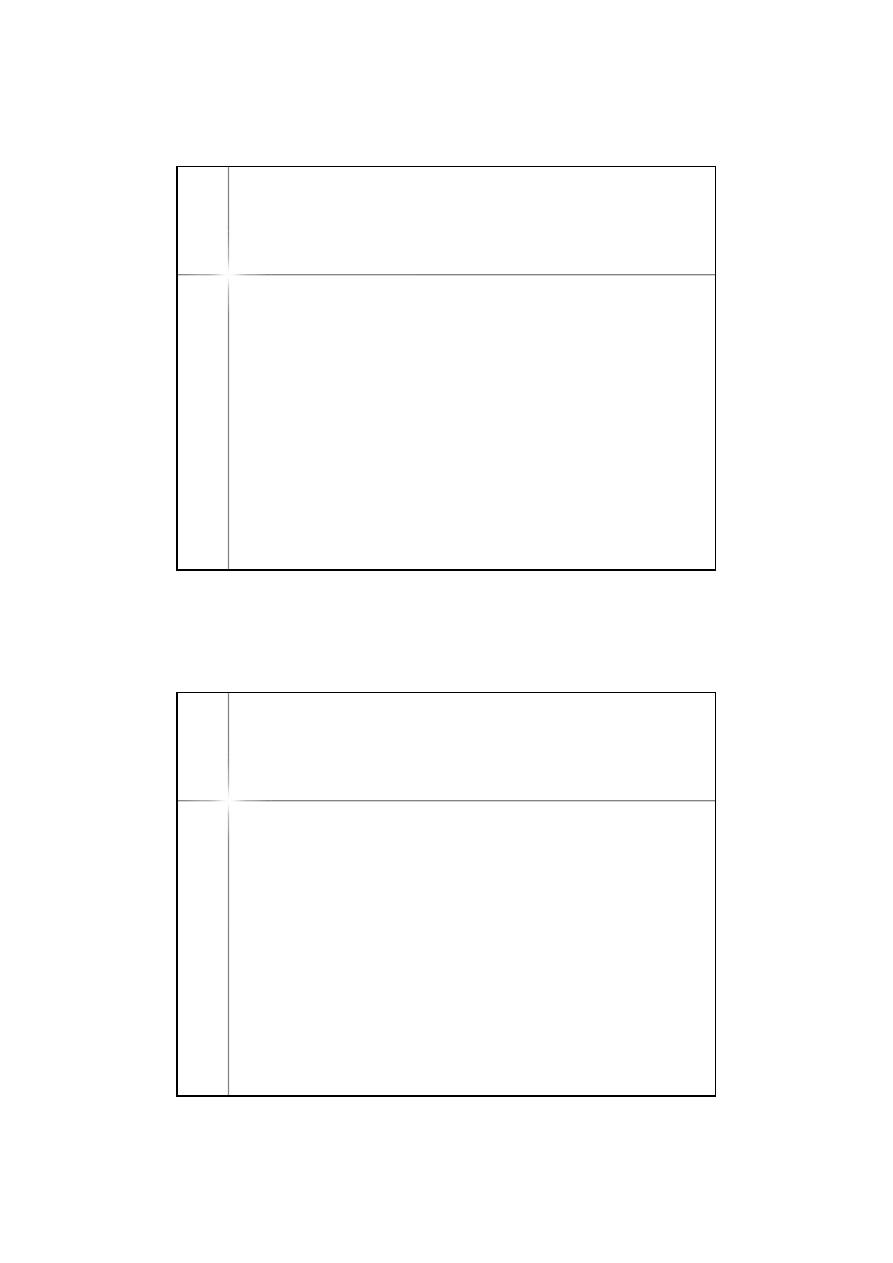
1. Metody bezpośrednie
– polegające na rozwiązaniu trójkąta
elipsoidalnego, którego dwa wierzchołki to początek i koniec linii geodezyjnej a
trzeci to biegun
2. Metody wykorzystujące szeregi potęgowe Legendre’a
–
polegają na rozwinięciu w szereg różnic
∆
B,
∆
L,
∆
A
względem parametru
naturalnego
s
3. Metody wykorzystujące punkt pomocniczy
– dla niewielkich
odległości („smukłych” trójkątów)
4. Za pomocą cięciw elipsoidy
– niekonwencjonalne, trójwymiarowe
podejście do problemu zaproponowane przez Mołodeńskiego
5. Całkowania numerycznego -
pewna odmiana metody 2,
z ograniczeniem się zazwyczaj do pierwszego wyrazu rozwinięcia
2
Metody bezpo
Metody bezpo
ś
ś
rednie
rednie
W metodach bezpośrednich budowano zazwyczaj pomocniczą kulę o
promieniu N
1
lub a. Do metod bezpośrednich należą metody Bessela,
Helmerta, Clarke-Robinsa, Levallois-Dupuy....
Metody wykorzystuj
Metody wykorzystuj
ą
ą
ce szeregi
ce szeregi
pot
pot
ę
ę
gowe
gowe
Legendre
Legendre
’
’
a
a
.
.
.
2
1
2
1
2
2
1
1
2
+
+
=
−
s
ds
B
d
s
ds
dB
B
B
..
.
2
1
2
1
2
2
1
1
2
+
+
=
−
s
ds
L
d
s
ds
dL
L
L
..
.
2
1
2
1
2
2
1
1
2
+
+
=
−
s
ds
A
d
s
ds
dA
A
A
Polegają na rozwinięciu w szereg Maclaurina różnic
∆B, ∆L i ∆A
względem parametru naturalnego, czyli długości linii geodezyjnej s.
Powolna zbieżność szeregów limituje ich wykorzystanie do odległości
rzędu 150-200 km. Do podstawowych metod tego typu należ metoda
średniej szerokości Gaussa.
3
Metody wykorzystuj
Metody wykorzystuj
ą
ą
ce punkt
ce punkt
pomocniczy
pomocniczy
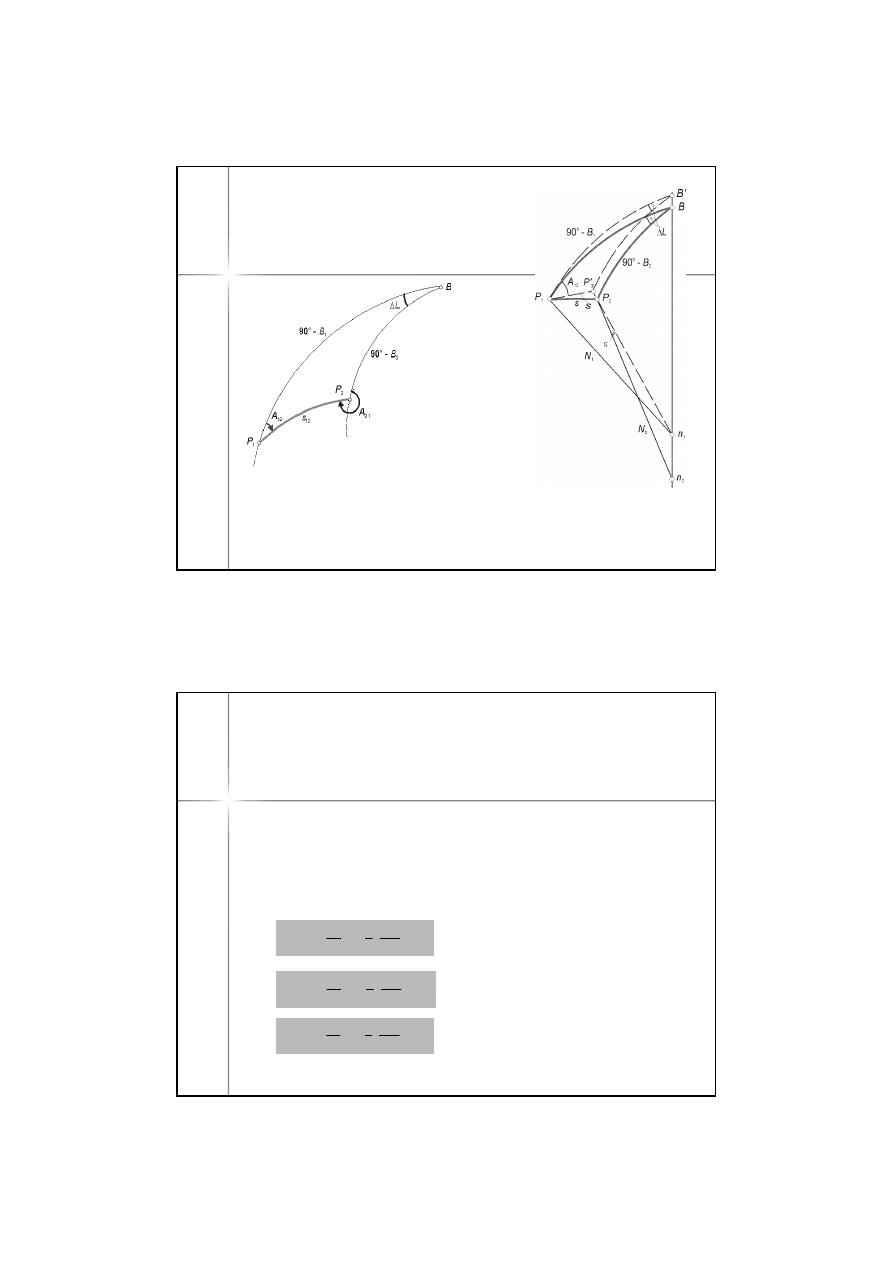
Punkt P
2
rzutuje się na południk punktu P
1
prowadząc przez punkt P
2
przekrój
normalny prostopadły do południka punktu P
1.
Metody stosowane dla małych
odległości (30-60 km; np.. Metoda Clarke’a)
Metody za pomoc
Metody za pomoc
ą
ą
ci
ci
ę
ę
ciw elipsoidy
ciw elipsoidy
4
Metoda
Metoda
Clarke
Clarke
’
’
a
a
(1)
(1)
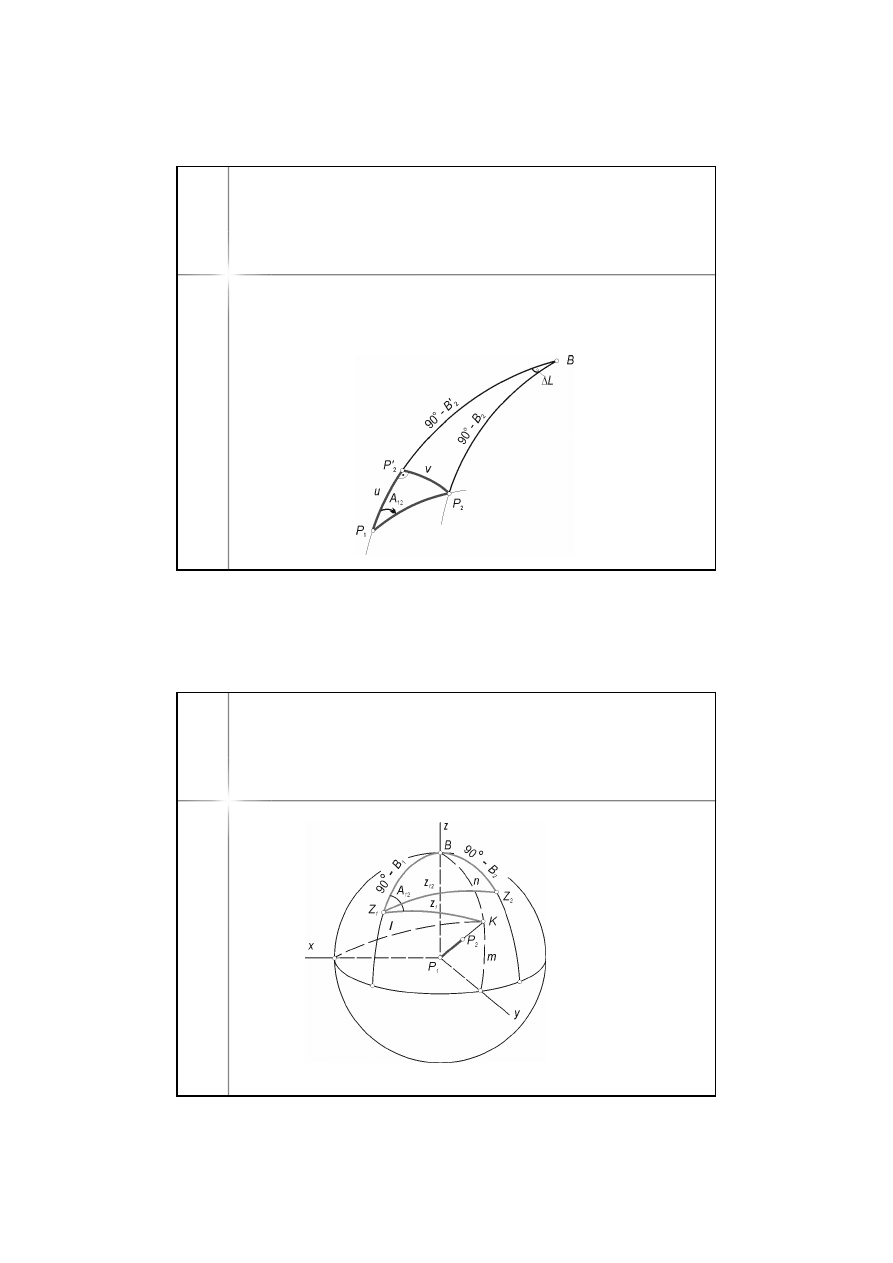
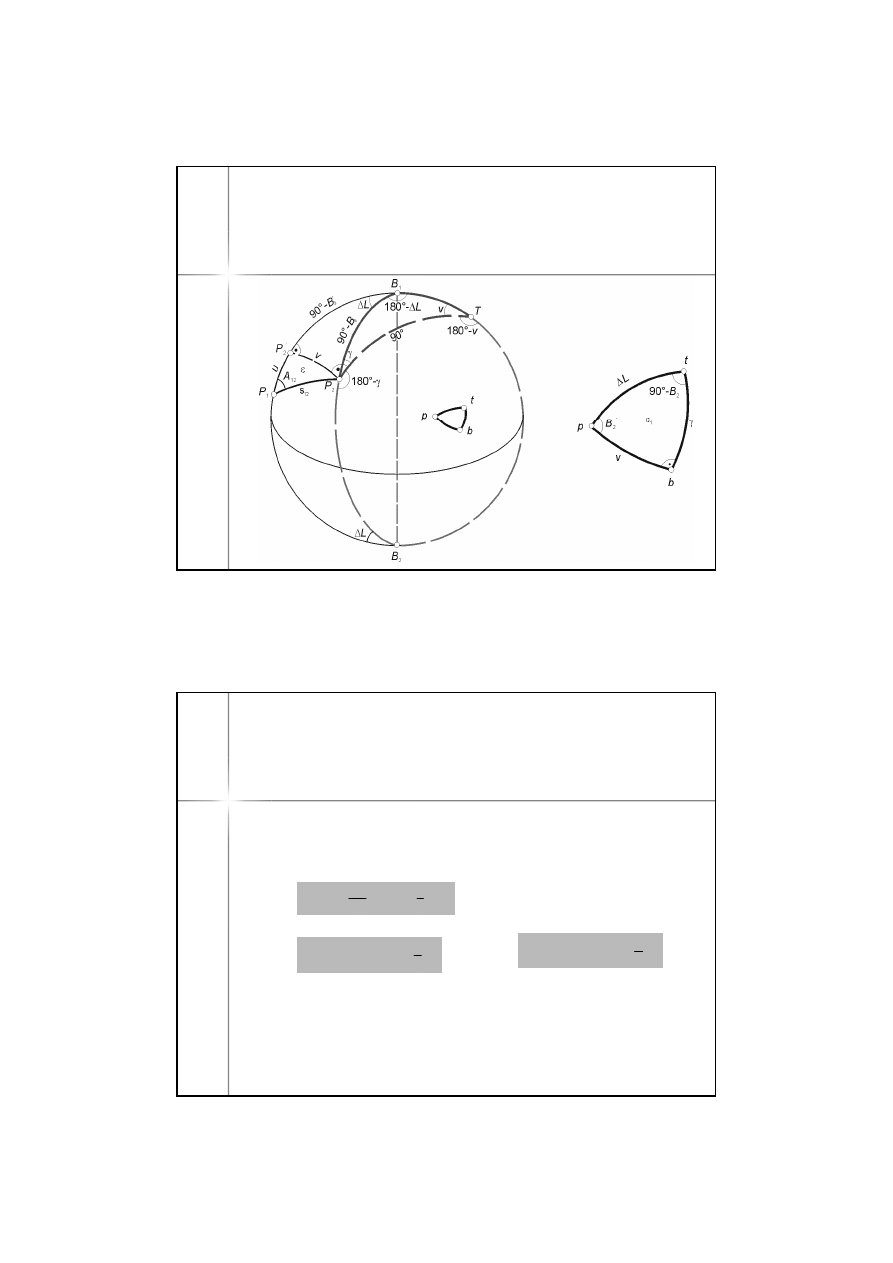
1.
Obliczamy średni promień
krzywizny w punkcie P
1
2.
Na sferze o promieniu R
1
rozwiązujemy mały trójką
sferyczny P
1
P
2
P
2
’ dowolną
metodą – otrzymujemy
długości u i v
)
3
1
sin(
)
3
2
cos(
12
12
12
12
ε
ε
−
=
−
=
A
s
v
A
s
u
Metoda
Metoda
Clarke
Clarke
’
’
a
a
(2)
(2)
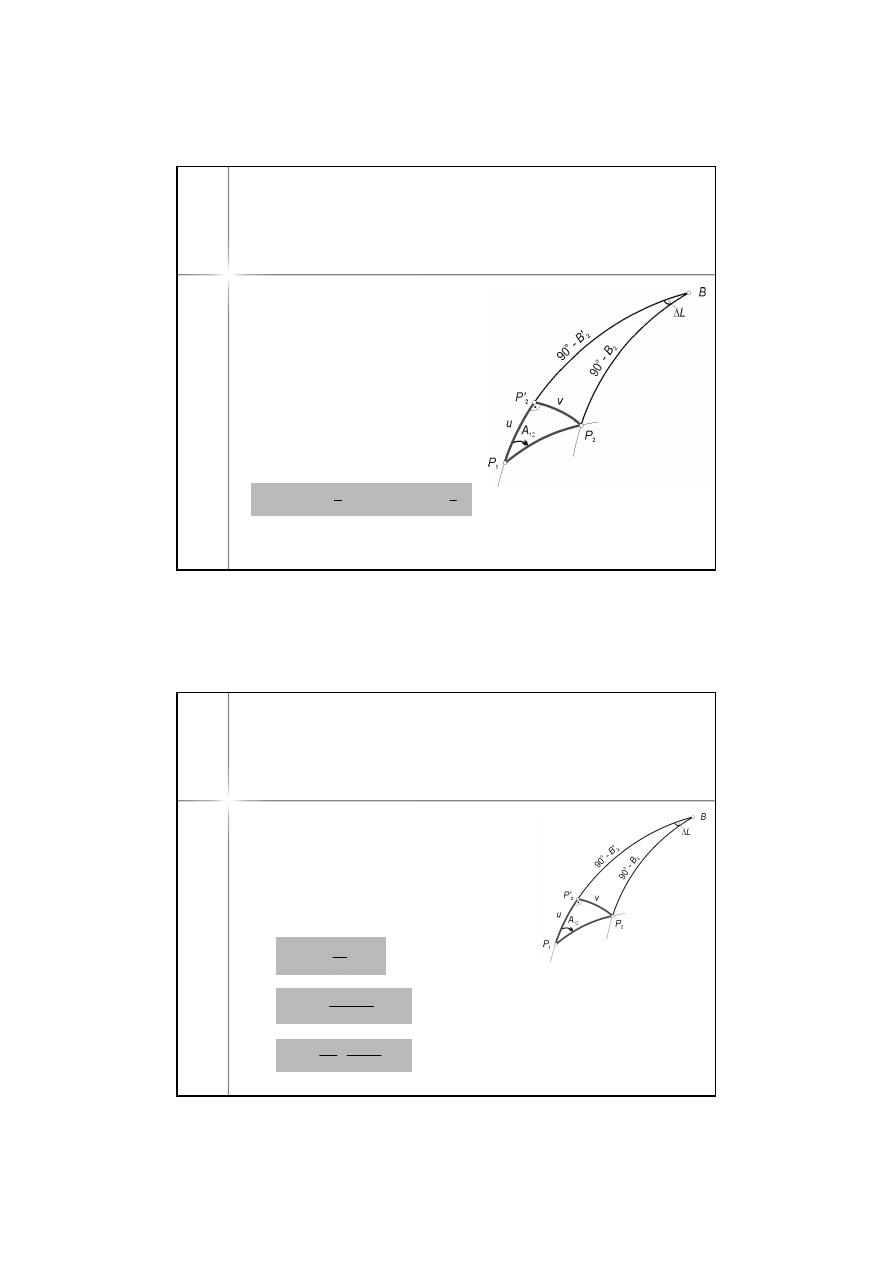
3.
Szerokość B
2
’ wyznaczamy na
podstawie znanej już długości u, licząc
wcześniej średni promień krzywizny
południka dla połowy długości u
4.
Szerokość B
2
wyznaczamy z trójkąta
P
2
’BP
2
z wzoru cosinusowego
2
2
2
2
tan
2
B
v
B
B
′
=
−
′
′ −
=
′ ′
′
B
B
v
M
N
B
2
2
2
2
2
2
2
tan
.
2
2
2
2
1
2
tan
2
B
N
M
v
M
u
B
B
m
′
′
′
−
+
=
po wstawieniu średniego promienia krzywizny w punkcie P
2
’
5
Metoda
Metoda
Clarke
Clarke
’
’
a
a
(3)
(3)
Metoda
Metoda
Clarke
Clarke
’
’
a
a
(4)
(4)
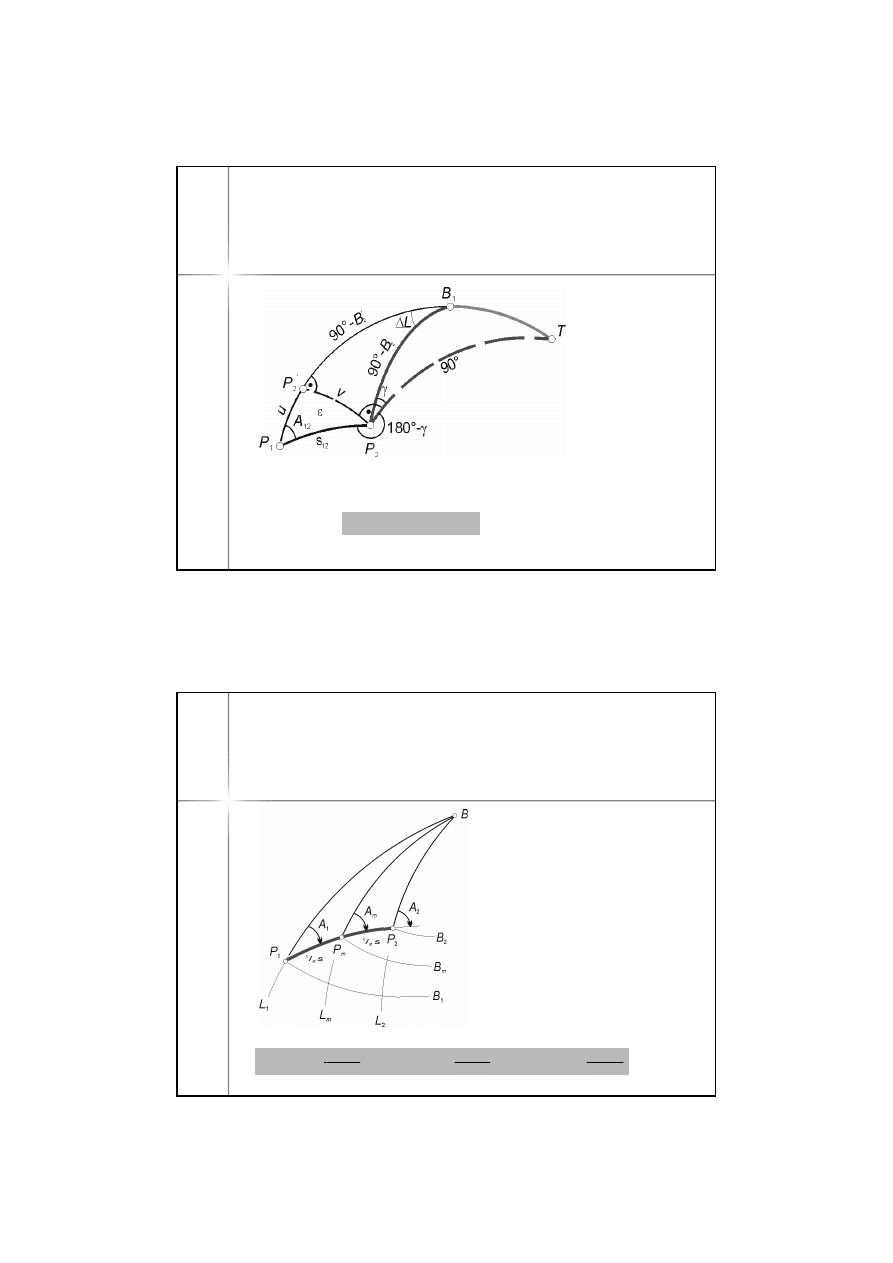
5.
W oparciu o trójkąt biegunowy
ptb
dostajemy wzory na długość
geodezyjną i zbieżność południków w punkcie p
2
L
L
v
N
B
2
1
2
2
1
1
3
=
+
′
+
sec (
)
.
ε
)
3
1
(
sin
)
(
1
2
1
2
ε
γ
−
′
−
=
B
L
L
)
3
2
(
sin
)
(
1
2
1
2
ε
γ
+
−
=
B
L
L
lub
6
Metoda
Metoda
Clarke
Clarke
’
’
a
a
(5)
(5)
Azymut odwrotny w punkcie P
2
wyniesie:
ε
γ −
+
±
=
o
180
12
21
A
A
Metoda
Metoda
ś
ś
redniej szeroko
redniej szeroko
ś
ś
ci Gaussa
ci Gaussa
(1)
(1)
B
B
B
B
B
L
L
L
L
L
A
A
A
A
A
m
m
m
≠
=
+
≠
=
+
≠
=
+
,
,
,
,
,
.
1
2
1
2
1
2
2
2
2
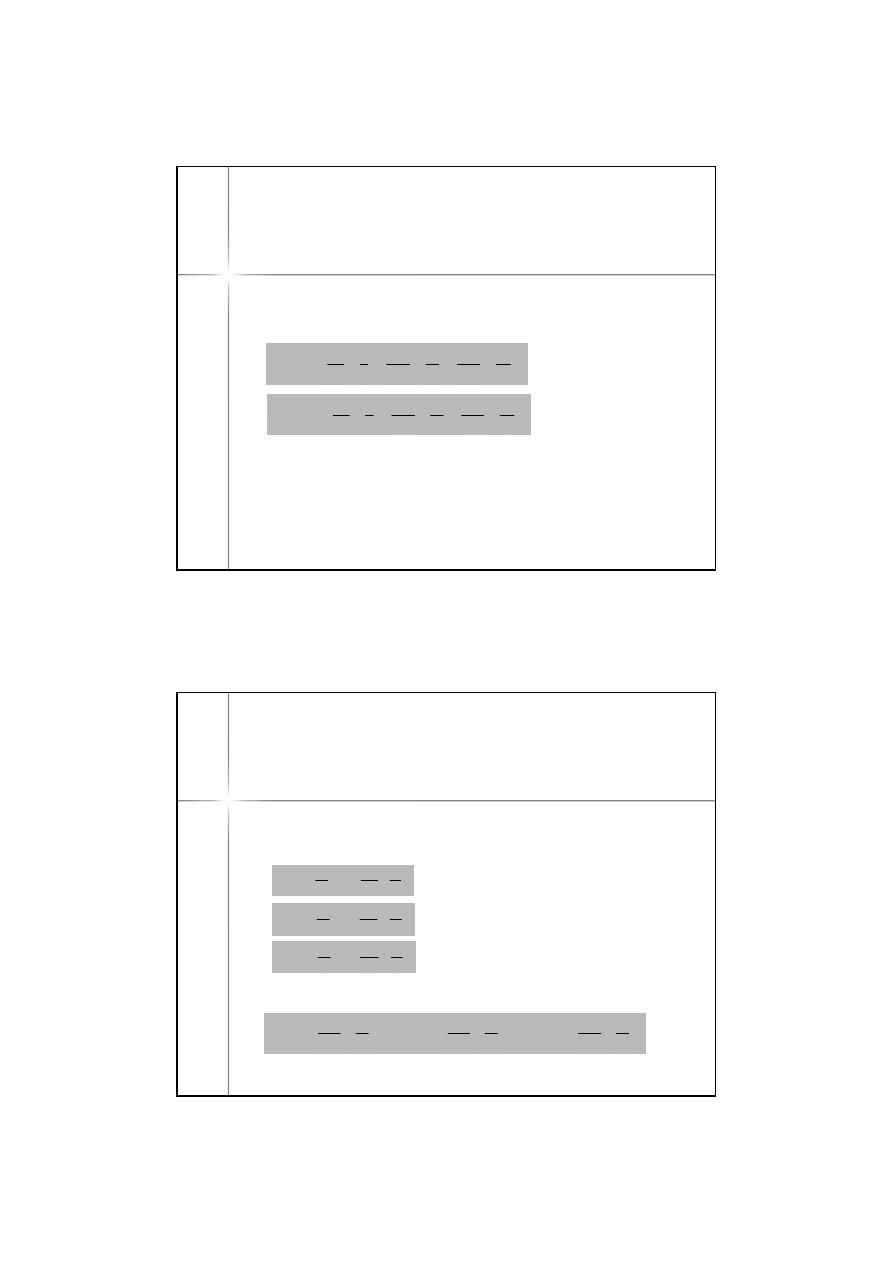
Gauss zaproponował metodę
wykorzystującą szeregi potęgowe
Legendre’a przyjmując za punkt
wyjściowy punkt w połowie
długości linii geodezyjnej
7
Metoda
Metoda
ś
ś
redniej szeroko
redniej szeroko
ś
ś
ci Gaussa
ci Gaussa
(2)
(2)
..
.
48
8
2
3
3
3
2
2
2
2
+
+
+
=
−
s
ds
B
d
s
ds
B
d
s
ds
dB
B
B
m
m
m
m
..
.
48
8
2
3
3
3
2
2
2
1
+
−
+
−
=
−
s
ds
B
d
s
ds
B
d
s
ds
dB
B
B
m
m
m
m
Rozwinięcie różnic
B
2
-B
m
i
B
1
-B
m
w szereg potęgowy wg koncepcji Gaussa
Przy założeniu, że parametr
s
rośnie od punktu
P
1
do
P
2
co drugi wyraz w
drugim wzorze jest ujemny. Analogiczne wzory można zapisać dla różnicy
długości geodezyjnych i azymutów.
(1a)
(1b)
Metoda
Metoda
ś
ś
redniej szeroko
redniej szeroko
ś
ś
ci Gaussa
ci Gaussa
(3)
(3)
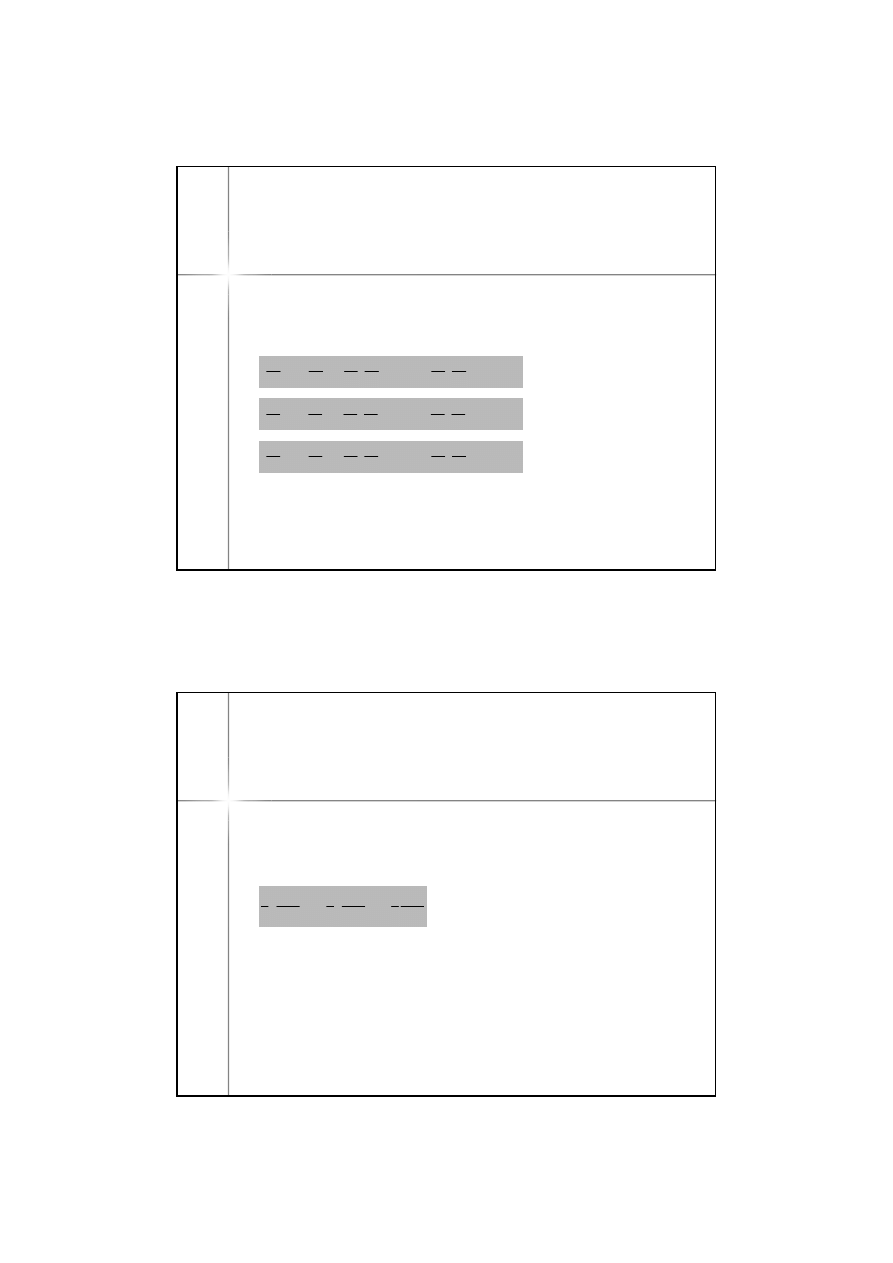
Odejmując stronami równania (1a) i (1b) dostaniemy:
..
.
24
3
3
3
1
2
+
+
⋅
=
−
s
ds
B
d
s
ds
dB
B
B
m
m
a dodając i dzieląc przez 2 otrzymamy:
..
..
8
,.
..
8
,.
..
8
2
2
2
2
2
2
2
2
2
+
=
−
+
=
−
+
=
−
s
ds
A
d
A
A
s
ds
L
d
L
L
s
ds
B
d
B
B
m
m
m
m
m
m
..
.
24
3
3
3
1
2
+
+
=
−
s
ds
L
d
s
ds
dL
L
L
m
m
..
..
24
3
3
3
1
2
+
+
=
−
s
ds
A
d
s
ds
dA
A
A
m
m
(2)
(3)
8
Metoda
Metoda
ś
ś
redniej szeroko
redniej szeroko
ś
ś
ci Gaussa
ci Gaussa
(4)
(4)
..
.
)
(
)
(
+
−
+
−
+
=
A
A
ds
dB
dA
B
B
ds
dB
B
ds
dB
ds
dB
m
m
P
m
∂
∂
∂
..
.
)
(
)
(
+
−
+
−
+
=
A
A
ds
dL
dA
B
B
ds
dL
B
ds
dL
ds
dL
m
m
P
m
∂
∂
∂
..
.
)
(
)
(
+
−
+
−
+
=
A
A
ds
dA
dA
B
B
ds
dA
B
ds
dA
ds
dA
m
m
P
m
∂
∂
∂
(4)
W celu znalezienia wartości pochodnych w punkcie
P
m
we wzorach
(2) i (3) Gauss zaproponował zastąpienie ich rozwinięciem w szereg
Taylora w otoczeniu punktu
P
zachowując tylko wyrazy I-go rzędu
Różniczki I-rzędu
dB
,
dL
i
ds
po parametrze naturalnym
s
wyprowadza
się wykorzystując zależności geometryczne dla podstawowego trójkąta
geodezyjnego i różniczkując równanie Clairauta
Metoda
Metoda
ś
ś
redniej szeroko
redniej szeroko
ś
ś
ci Gaussa
ci Gaussa
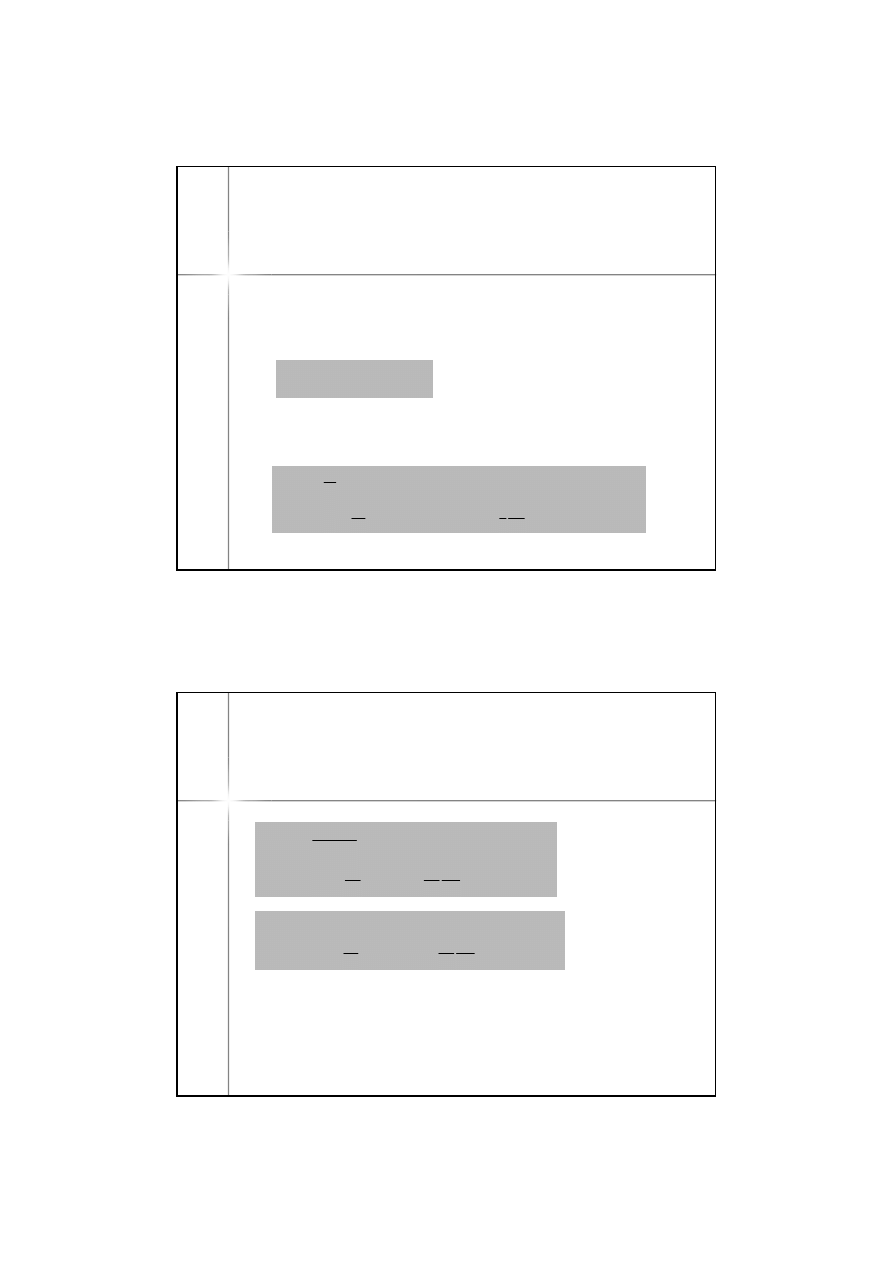
(5)
(5)
2
2
2
2
2
2
8
1
8
1
8
1
ds
B
d
ds
B
d
ds
B
d
P
m
≡
≈
Różnice
B
m
-B
i
A
m
-A
we wzorach (4) wyznaczyć można na podstawie
zależności (3), bowiem są to wielkości małe II-rzędu i zamiast
pochodnych w punkcie
P
m
wyznaczamy pochodne w punkcie
P
tzn.
i analogicznie dla
L
i
A
Podobnie można podejść do pochodnych wyższych rzędów w punkcie
P
m
w wyrażeniach (2) zastępując je pochodnymi w punkcie
P
, którego
współrzędne są średnią arytmetyczną współrzędnych końców linii
geodezyjnej!!!
9
Metoda
Metoda
ś
ś
redniej szeroko
redniej szeroko
ś
ś
ci Gaussa
ci Gaussa
(6)
(6)
Zachowując we wzorach (2) wyrazy do IV-rzędu włącznie (odrzucając
wyrazy, w których występuje 5-ta potęga
s
) oraz wprowadzając
oznaczenia:
b
B
B
l
L
L
e
B
t
B
=
−
=
−
= ′
=
2
1
2
1
2
2
2
,
,
cos
,
tan
,
η
dostaniemy dla odległości do 200km z dokładnością 0,0001” wzory (2)
w postaci:
B
B
s
N
V
A
l
B
t
b
V
t
t
2
1
2
2
2
2
2
2
2
2
2
2
2 2
1
1
24
2
3
2
1
8
1
4
−
=
+
=
+
+
−
− + +
cos
(
) ,
cos
(
)
(
) ,
∆Φ
∆Φ
η
η
η
η
(5a)
Metoda
Metoda
ś
ś
redniej szeroko
redniej szeroko
ś
ś
ci Gaussa
ci Gaussa
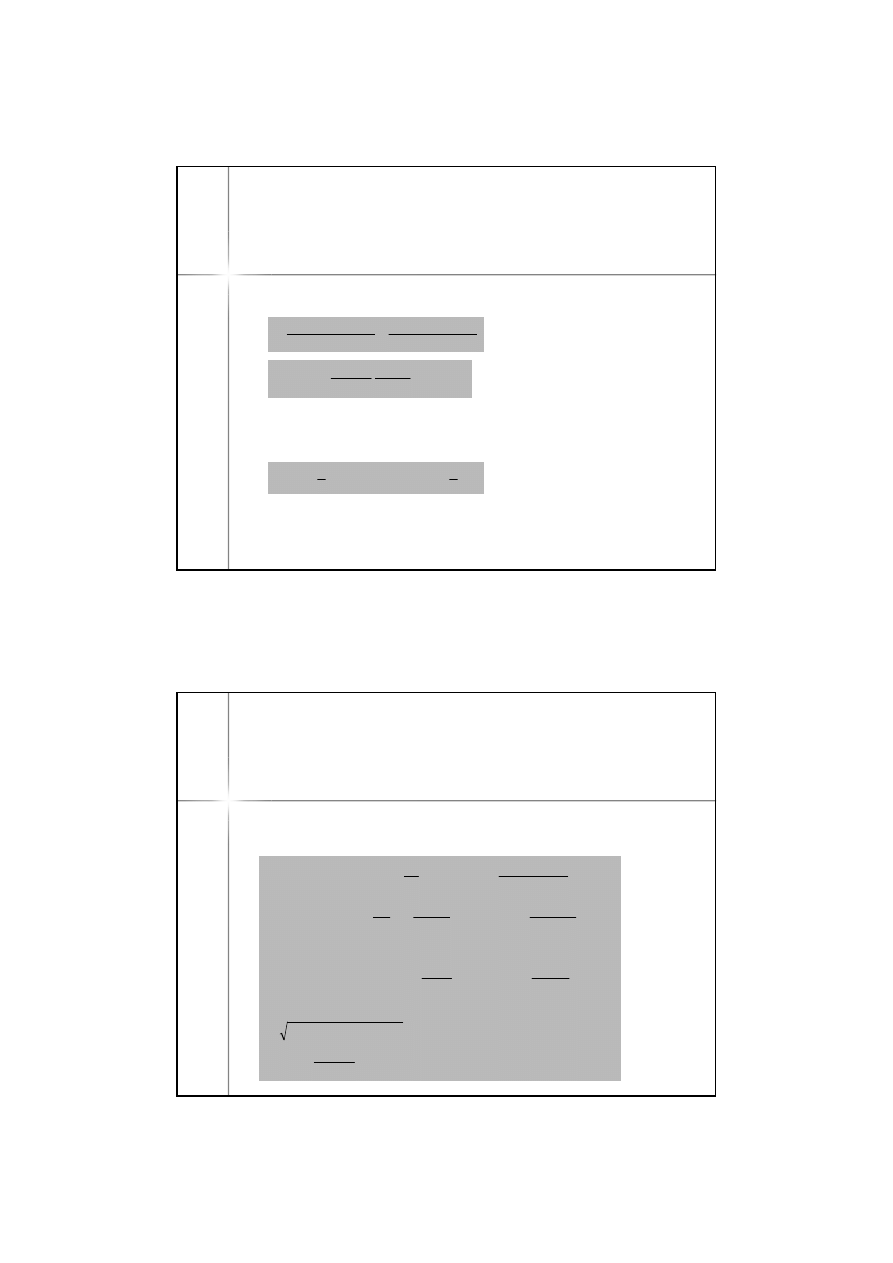
(7)
(7)
L
L
s
N
B
A
l
B
b
V
t
2
1
2
2
2
4
2
2 2
1
1
24
1
24
1
9
− =
+
=
−
+ −
cos
sin
(
) ,
sin
(
) ,
∆Λ
∆Λ
η
η
A
A
L
L
B
V l
B
b
V
2
1
2
1
2 2
2
2
4
2
4
1
1
12
1
24
3 8
5
−
=
−
+
=
+
+
+
(
) sin
(
) ,
cos
(
) .
∆α
∆α
η
η
Dla zadania
wprost
trzeba stosować postępowanie iteracyjne (co
najwyżej 2 kroki iteracyjne), rozpoczynając od współrzędnych
przybliżonych o dokładności co najmniej 5”
(5b)
(5c)
10
Metoda
Metoda
ś
ś
redniej szeroko
redniej szeroko
ś
ś
ci Gaussa
ci Gaussa
(8)
(8)
Zadanie odwrotne można rozwiązać odwracając zależności (5a,b,c)
s
B
B
N
V
A
L
L
N
B
A
=
−
+
=
−
+
(
)
(
) cos
(
)
cos
(
) sin
,
2
1
2
2
1
1
1
∆Φ
∆Λ
A
L
L
B
B
V
B
=
−
−
+
+
arctan
cos
.
2
1
2
1
2
1
1
∆Φ
∆Λ
(6a)
(6b)
Ze wzoru (6b) otrzymujemy azymut w punkcie P a ze wzoru (5c)
wartość różnicy
∆
A = A
2
-
A
1
i ostatecznie:
A
A
A
A
A
A
1
2
1
2
1
2
= −
= +
∆
∆
,
.
Metoda Gaussa była i jest najczęściej stosowana do rozwiązania
zadania odwrotnego
!
Metoda
Metoda
ś
ś
redniej szeroko
redniej szeroko
ś
ś
ci Gaussa
ci Gaussa
(9)
(9)
Po dalszych uproszczeniach dla odległości do 30 km wzory robocze dla
zadania odwrotnego mają postać :
(
)
( )
(
)
( )
( )
(
)
( )
(
) (
)
⋅
⋅
=
⋅
+
⋅
=
∆
⋅
+
+
⋅
∆
⋅
+
+
⋅
⋅
∆
=
∆
=
−
∆
⋅
−
+
⋅
∆
⋅
−
−
∆
⋅
∆
⋅
=
⋅
∆
⋅
−
+
+
⋅
∆
⋅
−
⋅
⋅
∆
⋅
=
⋅
−
A
s
A
s
A
A
s
A
s
s
B
V
B
L
B
L
A
A
A
B
V
t
B
L
L
B
M
A
s
B
V
t
B
L
B
L
N
A
s
cos
sin
tan
cos
sin
24
8
3
cos
12
1
1
sin
)
(
8
1
cos
24
2
1
1
2
cos
cos
24
9
1
cos
24
1
1
cos
sin
1
2
2
2
4
2
2
2
1
2
2
4
2
2
2
2
2
4
2
2
2
2
η
η
η
η
η
η

11
Metoda ca
Metoda ca
ł
ł
kowania numerycznego
kowania numerycznego
(algorytm
(algorytm
Kivioja
Kivioja
)
)
(1)
(1)
Jest to najprostsza metoda i na wskroś współczesna.
Polega na wykorzystaniu równań różniczkowych I-rzędu dla linii
geodezyjnej, a więc założeniu, że dzielimy ortodromę pomiędzy punktami
końcowymi
P
1
i
P
2
na n-części
ds
na tyle małych, aby przyjąć, że z
dokładnością numeryczną trójkąt rozpięty na
ds
możemy rozwiązać jako
trójkąt płaski.
Metoda ca
Metoda ca
ł
ł
kowania numerycznego
kowania numerycznego
(2)
(2)
B
N
A
ds
dL
cos
sin
=
const
c
A
B
N
=
=
⋅
⋅
sin
cos
M
A
ds
dB
cos
=
N
B
A
ds
dA
tan
sin
⋅
=
Podstawowe zależności wykorzystywane w metodzie całkowania
numerycznego to:
W przypadku azymutu A=90° lub 180° metoda w klasycznym ujęciu daje
błędny wynik!!! Wprowadzenie wzoru na różniczkę rozwiązuje ten
problem i sprawia, że metoda nie ma ‘numerycznie miejsc osobliwych’.

12
Metoda ca
Metoda ca
ł
ł
kowania numerycznego
kowania numerycznego
(3)
(3)
(algorytm post
(algorytm post
ę
ę
powania
powania
–
–
kolejne kroki oblicze
kolejne kroki oblicze
ń
ń
)
)
1.
Ustalamy długość
ds=s/n
, przy czym
ds
jeśli chcemy uzyskać
dokładność milimetrową współrzędnych element
ds<100-200m
(dla
uzyskania centymetrowej dokładność
ds<1-2km
)
2.
Wyznaczamy promienie krzywizny głównych przekrojów normalnych
N
i
M
w punkcie wyjściowym
P
1
M
a
e
e
B
N
a
e
B
i
i
i
i
=
−
−
=
−
(
)
(
sin
)
,
sin
1
1
1
2
2
2
3
2
2
3.
Obliczamy szerokość w połowie przyrostu
ds
z zależności:
B
B
B
i
m
i
i
=
+ 1
2
1
δ
( )
,
i
i
i
i
M
A
ds
B
cos
)
1
(
=
δ
gdzie
Metoda ca
Metoda ca
ł
ł
kowania numerycznego
kowania numerycznego
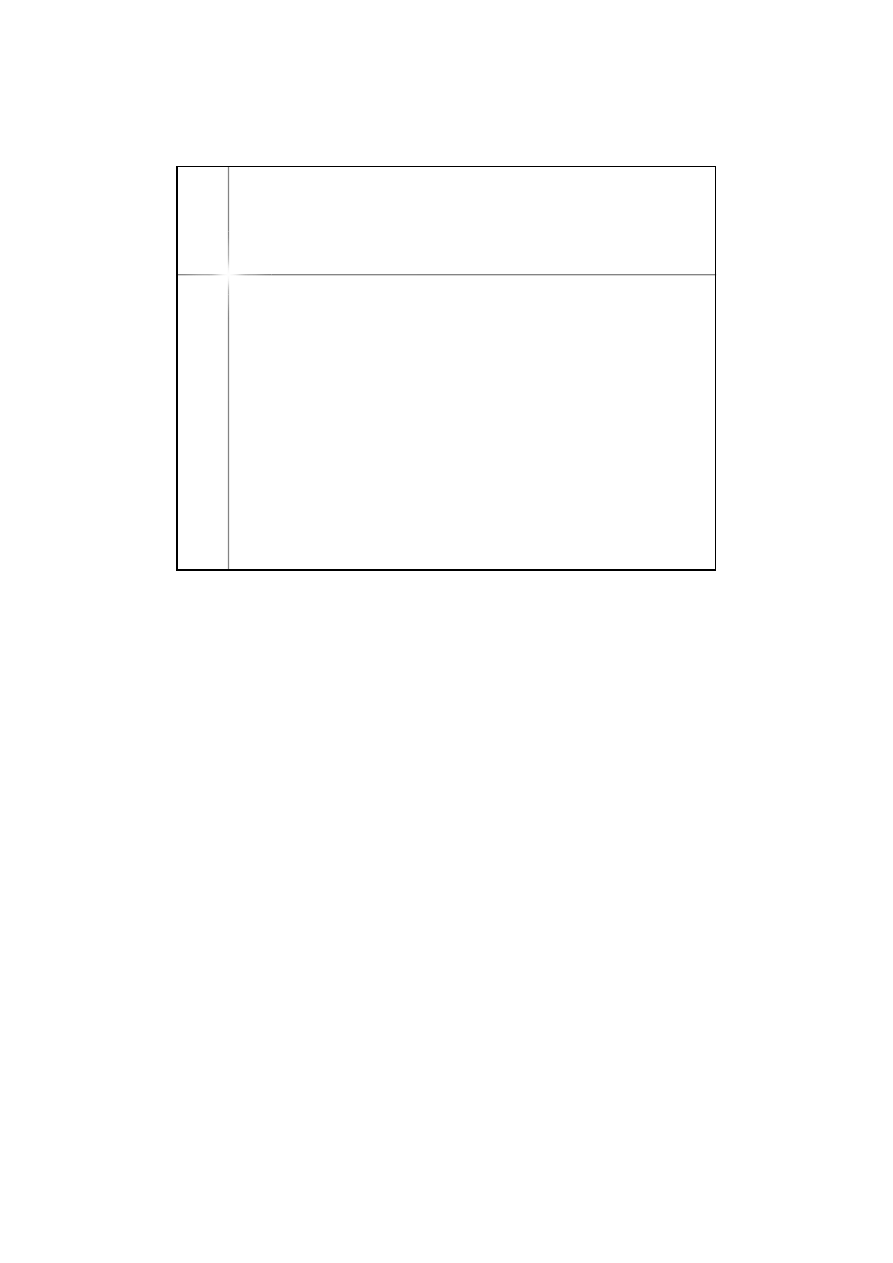
(4)
(4)
(algorytm post
(algorytm post
ę
ę
powania
powania
–
–
kolejne kroki oblicze
kolejne kroki oblicze
ń
ń
)
)
4.
Obliczamy promienie N i M dla punktu w połowie
ds
, a następnie
szerokość punktu
i+1
z zależności:
5.
Powtarzamy kroki 1-4 aż do osiągnięci punktu końcowego
m
i
i
m
m
i
m
i
m
m
i
i
m
m
m
i
m
m
i
i
m
m
i
m
i
i
i
i
i
i
i
i
i
i
i
i
i
A
A
A
N
B
A
ds
A
L
L
L
B
N
A
ds
L
B
B
B
M
A
ds
B
δ
δ
δ
δ
δ
δ
+
=
=
+
=
=
+
=
=
+
+
+
1
1
1
,
tan
sin
,
cos
sin
,
cos
∑
∑
∑
=
=
=
+
=
+
=
+
=
n
i
m
n
i
m
n
i
m
i
i
i
A
A
A
L
L
L
B
B
B
1
1
2
1
1
2
1
1
2
,
δ
δ
δ
13
Metoda ca
Metoda ca
ł
ł
kowania numerycznego
kowania numerycznego
(5)
(5)
1.
Przyjmuje się na wstępie przybliżoną długość linii geodezyjnej i
przybliżoną wartość azymutu
2.
Wykorzystując algorytm zadania wprost obliczamy współrzędne
punktu końcowego dla przyjętych wartości przybliżonych
3.
Obliczamy różnicę pomiędzy współrzędnymi uzyskanymi a
współrzędnymi punktu końcowego
4.
Na podstawie różnicy liczymy poprawki do azymutu i długości linii
geodezyjnej i powtarzamy kroki 2 i 3
5.
Obliczenia prowadzimy aż do uzyskania zgodności współrzędnych z
żądaną dokładnością
(np. 0.00001”)
Zadanie odwrotne rozwiązuje się wykorzystując algorytm z zadania
wprost w kolejnych 5 krokach:
Wyszukiwarka
Podobne podstrony:
3 GW Przeniesienie wsp (sem II Nieznany (2)
konspekty geodezja iiB przenies wsp ok
sciaga W5 W6 W7 W8 W9, Naika, stomatologia, Normy okluzji
si zalewska pri w5 w6
w4,w5,w6
Różne materiały i wsp. przenikania ciepła
Współczynnik przenikania c iepła podłogi wynosi 0
kalkulator wsp przenikania ciepła i oporu
~$ałowicz W5 (14 XI) W6 (21 XI 07) W7 (28 XI 07)
Ciałowicz W5 (14 XI) W6 (21 XI 07) W7 (28 XI 07)
OBLICZANIE WSPĂ“ĹCZYNNIKA PRZENIKANIA CIEPĹA U PRZEGRĂ“D GRANICZNYCH BILANSOWANA
kalkulatorU 02 07 Obl wsp przenikania ciepła Uk
kalkulatorU 02 07 Obliczanie wsp przenikania ciepła Uk wg PN EN ISO 6946 z 2004 oraz literatury fach
W6 Technika harmonogramów i CPM
w6 Czołowe przekładanie walcowe o zebach srubowych
W5 Zawiesia
W5 sII PCR i sekwencjonowanie cz 2
więcej podobnych podstron